Drgania harmoniczne

Ruchem drgającym nazywamy rych ciala zachodzący wokół stałego położenia równowagi Szczególnym rodzajem drgań są drgania harmoniczne, tj. okresowe, o stałej amplitudzie, opisane sinusoidą. Ze względu na prostotę opisu drgania harmoniczne są wykorzystywane do opisu wielu drgań rzeczywistych jako ich przybliżenie (lub poprzez rozkład na nie).

Najprostsze równanie opisujące drgania harmoniczne (dla ciężarka zawieszonego na sprężynie) ma postać:

mx'' (t) + kx(t) = 0.

Rozwiązaniem jest funkcja

x(t)=Asin(ωt+ϕ₀),

gdzie A - amplituda drgań, ω = 2πν = (k/m)^0.5, ω - częstość kołowa (ν - częstość drgań), k - współczynnik sprężystości, m - masa ciała, ϕ₀ - faza początkowa.

   Drgania tłumione.

Wszystkie ruchy doznają oporu, w grę wchodzi siła tarcia, gdy mamy do czynienia z ruchem po podłożu lub opór lepkości, gdy ruch odbywa się w powietrzu czy cieczy. Pokonanie sił tarcia czy lepkości wymaga zużycia energii. W przypadku ciał drgających strata energii powoduje tłumienie drgań. Przeanalizowaliśmy ruch oscylatora tłumionego, jeżeli wartość siły oporu jest proporcjonalna do wartości prędkości.
Siłę oporu można zapisać w postaci
znak "-" oznacza, że siła oporu ma przeciwny zwrot do prędkości ciała. Współczynnik γ zależy od warunków, w których ruch się odbywa, a także od rozmiarów i kształtu ciała (np. mniejszy od kształtów opływowych)

Równanie opisujące drgania tłumione przyjmuje postać:

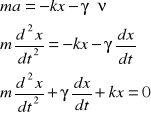
Korzystając z rachunku całkowego można udowodnić, że rozwiązaniem tego równania jest:

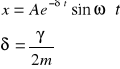
Amplituda drgań tłumionych wyraża się wzorem:

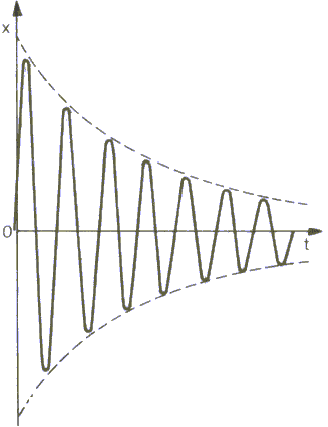
Ze wzoru wynika, że wartość amplitudy maleje wykładniczo w czasie.

Wspomniana strata energii powoduje wygasanie drgań. Częstość drgań tłumionych można przedstawić:

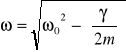
gdzie ω-częstotliwość drgań własnych

Wynika ω<ω₀ a zatem T>T₀

Okres drgań tłumionych jest dłuższy od okresu drgań swobodnych (nietłumionych) zachodzących pod działaniem takiej samej siły sprężystości.
W ciągu jednego okresu amplituda drgań ulega zmniejszeniu.

po zlogarytmowaniu otrzymamy

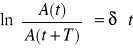
Wartość tę nazywamy dekrementem logarytmicznym amplitudy.

Ruch harmoniczny tłumiony z siłą wymuszającą

Jeżeli chcemy aby opory środka nie tłumiły drgań to na drgający punkt materialny musimy działać odpowiednio zmienno siłą;

Opis siły wymuszającej

F_w=F₀cosΩt [faza siły]

F=F_s+F_t+F_w=ma

Równanie różniczkowe drgań wymuszonych:

rozwiązanie:

x=Acos(ωt+Φ) [faza wychylenia] gdzie:

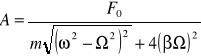
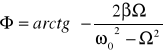
Widzimy więc ze w wyniku działania siły wymuszającej punkt materialny wykonuje drgania harmoniczne z pulsacją Ω tzn. z taką pulsacją z jaką zmienia się siła wymuszająca. Amplituda drgań wymuszonych jest ściśle określona i zależy od amplitudy siły wymuszającejF₀. oraz od jej pulsacji Ω. Również początkowa faza drgań Φ zależ od pulsacji Ω. Faza Φ jest różnicą fazy wychylenia i fazy siły.

Absorpcja mocy przez oscylator harmoniczny

Oscylator harmoniczny, wyidealizowany układ fizyczny - punkt materialny o masie m, na który działa siła proporcjonalna do chwilowego wychylenia x od pewnego położenia równowagi. Klasyczne równanie ruchu oscylatora harmonicznego ma postać:

punkt materialny wykonuje drgania harmoniczne o częstości kołowej

(A jest ich amplitudą, ϕ - stałą fazą).

???????????????????????????????????????????????????????????????????????????????????????

Składanie drgań współbieżnych

---