Zjawisko Halla. Wyznaczanie statycznych charaterystyk hallotronu i stałej Halla.

1). Cel ćwiczenia:

Celem ćwiczenia jest poznanie zjawiska Halla występującego w półprzewodnikach, wyznaczenie statystycznych charakterystyk hallotronu oraz wyznaczenie stałej Halla dla badanego półprzewodnika.

2). Zjawisko Halla i hallotrony.

W elementach galwanomagnetycznych wykorzystuje się zjawiska galwanoferrodynamiczne zachodzące w półprzewodnikach pod wpływem zewnętrznego pola magnetycznego. Do tego typu zjawisk należy efekt Halla.

Rys.1. Zasada działania hallotronu.

Efekt Halla polega na tym, że w materiale przewodzącym prąd elektronowy, dziurowy bądź jeden i drugi, poprzez działanie na ten materiał zewnętrznego pola magnetycznego o kierunku poprzecznym do kierunku przewodzenia prądu; uzyskuje się w nim pole elektryczne, a zatem i różnicę potencjałów wzdłuż prądu przewodzenia. Zjawisko to zachodzi zarówno w metalach jak i w półprzewodnikach. Rozważmy płaską prostopadłościenną płytkę półprzewodnika. Dla uproszczenia rozważań przyjmiemy że przewodzenie prądu w płytce odbywa się w oparciu o nośniki typu n (elektrony), oraz że ruchliwość nośników jest jednakowa. Wprowadźmy układ współrzędnych normalnych XYZ zorientowany jak na rysunku 1. Do płytki wzdłuż krawędzi I przeciwnie do zwrotu osi X jest przyłożone zewnętrzne pole elektryczne E. Pod wpływem tego pola nośniki uzyskują prędkość V_E o zwrocie zaznaczonym na rysunku, określona zależnością:

[m/s] (1)

Znak minus świadczy o przeciwnym zwrocie prędkości elektronów w stosunku do przyłożonego pola elektrycznego. Po umieszczeniu próbki w polu magnetycznym o indukcji B mającej zgodny ze zwrotem osi Z, na poruszające się z prędkością V_E elektrony działa siła Lenza o kierunku i zwrocie zgodnym z regułą prawej dłoni opisana:

F=-e * V_E * B *sin [N] (2)

e- ładunek elektronu,

 - kąt między wektorami V_E i B.

W dalszych rozważaniach przyjmiemy kąt   więc sin  Siła Lenza działa w płaszczyźnie prostopadłej do płaszczyzny utworzonej przez wektory V_E i B, przy czym dla nośników typu n jej zwrot jest zgodny z przyjętym na rys.1 zwrotem dodatnim osi Y. W wyniku działania tej siły pojawia się składowa V_F prędkości nośników o zwrocie zgodnym z siłą Lenza i określona zależnością:

V_F = -u_e * E_F [m/s] (3)

gdzie natężenie pola elektrycznego w kierunku siły F.

Wyrażając F przez (2) mamy:

V_F = -u_e * V_E * B [m/s] (4)

Wypadkowa prędkość ruchu nośników:

V = -(V_E+V_F) = -u_e*(E+V_E*B) [m/s] (5)

Prędkość ta określa gęstość prądu w płytce w kierunku V poprzez zależność:

J = -e*n*V [C * m/s] (6)

n- koncentracja nośników w obszarze płytki.

Podstawiając do (6) i (5) mamy:

J = u_e*e*n*(E+V_E*B) (7)

Określając gęstość J_E prądu w kierunku V_F dostajemy:

J_E = -e * n * V_E (8)

Podstawiając (8) do (7) mamy:

J = u_e*n*e*E - u_e*(J_E)_x*B (9)

Otrzymany wektor gęstości prądu w płytce można rozłożyć na składową podłużną gęstości (wzdłuż osi X) i składową poprzeczną gęstości (wzdłuż osi Y), przy czym składowa poprzeczna jest odpowiedzialna za występowanie efektu Halla możemy ją opisać:

J_y = - u_e*e*n*E_H (10)

gdzie natężenie pola elektrycznego Halla ([V/m]),

U_H - napięcie Halla,

a - szerokość płytki.

Otrzymujemy więc równość:

(11)

Wyrażając (J_E)_x w zależności od prądu sterującego według wzoru:

(12)

(13)

Więc zależność określająca napięcie Halla przyjmie postać:

(14)

gdzie:

(15)

Współczynnik R_H (stała Halla) jest parametrem charakteryzującym rodzaj przewodnika i ma różną wartość dla różnych materiałów. W szczególności dla półprzewodników typu n op7isany jest zależnością:

(16)

dla półprzewodników typu p:

(17)

Przy czym n i p oznaczają koncentrację odpowiednio elektronów i dziur, q - ładunek elektronu..

Z powyższych wzorów wynika, że polaryzacja napięcia Halla dla półprzewodników typu n lub p jest różna, badając znak napięcia Halla dla dowolnego rodzaju półprzewodnika przy znanym kierunku przepływu prądu i znanym kierunku wektora indukcji w płytce możemy określić dominujący rodzaj nośników w tym materiale.

3). Schemat układu pomiarowego:

Spis przyrządów:

• Magneśnica Ekl - 1

• Miniwoltomierz cyfrowy

• Miliamperomierz kl. 0.5 zakr. pom. 7 mA

• Amperomierz kl. 0.5 zakr. pom. 1.5 A

4). Wyniki:

5). Oszacowanie błędów pomiarów:

• błąd bezwzględny pomiaru I_X:

• błąd względny wybranego pomiaru I_X:

• błąd bezwzględny pomiaru I_m:

• błąd względny wybranego pomiaru I_m:

6). Wyznaczanie stałej Halla:

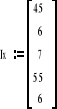
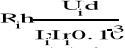
7). Oszacowanie błędu metodą różniczki zupełnej:

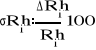
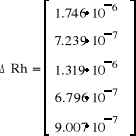
Wnioski i uwagi:

1. Badany hallotron jest elementem wrażliwym na zmiany położenia względem kierunku i zwrotu wektora indukcji magnetycznej. Ponieważ siła Lenza, mająca decydujące znaczenie w występowaniu zjawiska Halla zależy od sin kąta zawartego między kierunkami wektora prądu i wektora indukcji magnetycznej, więc zmiany tego kąta powodują zmiany napięcia Halla na wyjściu elementu.

2. Znaczna wartość napięcia asymetrii badanego hallotronu może być wynikiem występowania niewielkiego pola magnetycznego między biegunami magneśnicy nawet po wyłączeniu prądu magnesującego.

3. Charakterystyki statyczne obwodu wyjściowego hallotronu w funkcji wielkości wyjściowych mają przebieg zgodny z przewidywaniami teoretycznymi.

4. Uzyskana wartość stałej Halla odpowiada szacunkowo odpowiedniej wielkości dla tellurka rtęci.

5. Oszacowanie błędów pomiarów zostało wykonane w oparciu o znane błędy mierników .

Nie uwzględniono błędów wynikających z niedokładnego wyznaczenia wartości indukcji magnetycznej pola w szczelinie magneśnicy. Bez dokładnego pomiaru wartości tego parametru nie jest możliwe oszacowanie błędu tej wartości. Dlatego wyznaczona wartość stałej Halla może być znana tylko z dokładnością do jednego rzędu.

7

---