Badania operacyjne
Sformułowanie problemu
1. Wstęp
1.1. Wyodrębniły się:
modelowanie ekonometryczne (ekonometria w węższym sensie) - np. ustalanie związków przyczynowo-skutkowych ilościowych (przekrojowych i w czasie);
Buduje się modele postaci ![]()
w celu
weryfikacji teorii ekonomicznych,
prognozowania, przewidywania przyszłości,
symulacji.
badania operacyjne - metody optymalizacyjne, w których opis rzeczywistości jest połączony z wyborem najlepszej decyzji;
Przykłady:
ustalanie kolejności wykonywania zadań,
problem komiwojażera,
harmonogram zajęć,
dobór pracowników do zajęć, problem rozmieszczenia,
problem optymalnego wyboru.
wielowymiarowa analiza statystyczna - badanie związków i współzależności między dużą liczbą czynników (zmiennych).
Jak wydobyć informację o współzależności i związkach w dużych zbiorach danych (sieci neuronowe, algorytmy genetyczne, analiza skupień, analiza czynnikowa, analiza dyskryminacji, data mining)
Do rozwiązywania problemów stosujemy metody:
matematyczne;
statystyczne (algorytmy rozwiązywania zadań, dane);
informatyczne (przetwarzanie danych, algorytmy).
1.2. Podstawowym pojęciem stosowanym jest model. Model (matematyczny) jest to opis rzeczywistości (np. gospodarczej) za pomocą funkcji matematycznych, równań i nierówności (lub układów równań i nierówności). Model jest zawsze pewnym uproszczeniem rzeczywistości, powinien jednak uwzględniać cechy obiektów najbardziej istotne dla rozwiązywanego problemu.
Przykłady:
modelem kuli ziemskiej jest globus, modelem wycinka kuli ziemskiej jest mapa,
wzory (strukturalne) w chemii są modelami struktury powiązań między atomami w cząsteczce,
za pomocą grafów można modelować powiązania między ludźmi, sieć komunikacji miejskiej, przepływ dokumentów lub transakcji finansowych.
Zajmujemy się modelowaniem procesów podejmowania decyzji.
2. Metoda rozwiązania zadania
Musimy:
opracować model matematyczny problemu;
rozwiązać problem (jako zadanie matematyczne) metodami matematycznymi;
zinterpretować rozwiązanie w terminach problemu początkowego (np. ekonomicznego).
Ważna jest ponadto weryfikacja rozwiązania, ponieważ model może być niewłaściwie skonstruowany dla danego problemu.
Znalezieniem metody rozwiązania (algorytmu) zajmują się matematycy (na gruncie teoretycznym, aplikacyjnym - np. czy istnieje rozwiązanie, jak do niego dojść).
Algorytmy realizują programy komputerowe.
Zadaniem ekonomisty (socjologa, fizyka, geografa, psychologa) jest umiejętność wykonania przejścia (1) i (2)
3. Badania operacyjne
3.1. Badania operacyjne są ukierunkowane na podejmowanie decyzji. Zajmiemy się rozwiązywaniem problemów decyzyjnych, dotyczących optymalizacji w warunkach ograniczeń. Chodzi o to, żeby decyzje były jak najlepsze - zatem mamy cel działalności, który optymalizujemy.
3.2. W problemach ekonomicznych (również technicznych, fizycznych, innych) mamy często do czynienia z wyznaczaniem maksimum (lub minimum) funkcji rzeczywistej f w pewnym zbiorze argumentów. Ekonomiści (i nie tylko oni) mają duże „zachcianki” i ograniczone możliwości - czyli duże potrzeby i ograniczone zasoby.
Przykłady:
chcemy maksymalizować - sprzedaż, wielkość produkcji, zysk;
chcemy minimalizować - koszt przedsięwzięcia, czas wykonania zadania, straty;
Mamy ograniczone zasoby: kapitał, ludzie, materiały, czas.
Możemy wybierać sposób postępowania (sposób realizacji celu), ponieważ mamy wolną wolę, ale musimy uwzględnić ograniczoność zasobów. Jednak nawet przy spełnieniu tego warunku możemy podejmować różne decyzje.
3.3. Przykład
Piekarnia produkuje różne rodzaje pieczywa - chleb, bułki, bułeczki. Chce maksymalizować zysk ze sprzedaży, ale ma ograniczone: zasoby surowca, ludzi, możliwości produkcyjne. Może wybrać strukturę produkcji (ile chleba, ile bułek), ale ma ograniczenia (więcej chleba, to mniej bułek). Jest to problem decyzyjny. Decyzja jest to wybór jednego z możliwych wariantów postępowania (alternatyw). Decyzje możemy jakoś oceniać (np. jaki daje zysk).Są różne sposoby oceniania decyzji np. za pomocą liczb lub tylko porównując dwie decyzje i określając preferencje.
Należy wybrać najlepszy wariant z możliwych. Decydent (tj. podmiot podejmujący decyzję) ma więc pewne parametry (zmienne), którymi może sterować (lub przynajmniej je uwzględniać), ma cel działania (optymalizować ocenę decyzji), ma ograniczenia. Matematyk by powiedział: chcemy maksymalizować funkcję f(x) przy ograniczeniach ![]()
.
3.4. Przykład (dosyć prosty).
Należy na wybranym terytorium zlokalizować elektrownię. Jest 9 miejscowości, ale jest możliwych tylko 6 miejsc lokalizacji. Wybór miejsca powinien gwarantować ponoszenie najmniejszych kosztów eksploatacji (np. transport surowca, dowóz pracowników).
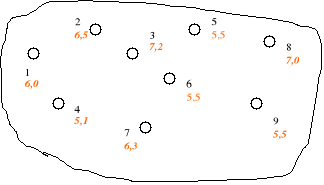
Niech ![]()
(i=1,...,9) - decyzje, ![]()
- zbiór decyzji,
![]()
- koszt decyzji ![]()
(w ustalonej jednostce)
![]()
- decyzje dopuszczalne, ![]()
![]()
- funkcja celu (funkcja kryterium), tutaj jest minimalizowana czyli ![]()
dla ![]()
Rozwiązanie: ![]()
oraz ![]()
(są to dwa rozwiązania alternatywne). Decyzja ![]()
daje minimum bezwarunkowe, ale jest to decyzja niedopuszczalna.
4. Rodzaje decyzji
Problemy decyzyjne dzieli się na 4 podstawowe klasy. Podział jest związany z ilością i jakością informacji, jaką dysponuje decydent.
Podejmowanie decyzji w warunkach:
pewności - proces jest zdeterminowany, ale zbiór decyzji dopuszczalnych jest liczny;
niepewności - proces jest stochastyczny (nie znamy prawdopodobieństwa wyniku),
ryzyka - proces jest stochastyczny, ale znamy prawdopodobieństwo wyniku,
częściowej informacji - proces jest stochastyczny, nie znamy prawdopodobieństwa wyniku, ale możemy je oszacować dzięki znajomości niektórych charakterystyk nieznanego rozkładu prawdopodobieństwa (np. wartość oczekiwana, wariancja).
Przykład
Jak najszybciej przejechać z punktu A do punktu B miasta.
są 3 drogi, mogą być „korki”,
znamy tyko parametry stochastyczne
czasu przejazdu
a)
b) znamy czasy przejazdu na odcinkach,
ale jest dużo możliwych tras, jest to
zadanie kombinatoryczne
5. Zagadnienie optymalnego wyboru (OW)
Zagadnienie optymalnego wyboru spełnia warunki:
Jest zdefiniowane pojęcie decyzji. Zbiór X wszystkich decyzji nazywamy przestrzenią decyzyjną.
Wyróżnia się podzbiór

decyzji dopuszczalnych.Decyzja ma służyć realizacji określonego celu. Umiemy oceniać stopień realizacji celu przez każdą decyzję (dopuszczalną).
Umiemy porównywać decyzje pod względem stopnia realizacji celu tzn. decyzja
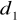
lepiej realizuje cel niż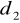
(lub tak samo lub nie gorzej). Rozumiemy, co to znaczy decyzja optymalna. Postępowanie prowadzące do jej wyznaczenia nazywamy procedurą optymalnego wyboru.
Związek modelu z rzeczywistością
Rzeczywistość |
Model |
Zbiór możliwych decyzji |
Przestrzeń decyzyjna X |
Decyzja |
element |
Ograniczenie |
zbiór |
Decyzja dopuszczalna |
|
Ocena decyzji |
f(x) - funkcja celu |
Porównywanie decyzji |
f(x) > f(y) |
Cel |
|
Decyzja optymalna |
|
Rozwiązanie dokładne, przybliżone |
|
Metody rozwiązywania zadania |
np. ciąg |
Metody rozwiązywania zadań:
dokładne - należy rozwiązać układ równań lub nierówności
iteracyjne - na ogół rozwiązanie jest wtedy przybliżone
W większości problemów metody rozwiązania dokładnego nie są znane. Stosuje się wtedy metody przybliżone (iteracyjne lub symulacje).
6. Zadanie programowania matematycznego
Rozważamy zagadnienia optymalnego wyboru pewnego typu. Można utworzyć dla tego typu odpowiedni model matematyczny. Zagadnienie to nazywamy zadaniem PM.
Każdą decyzję można przedstawić jako wektor w przestrzeni
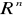
;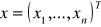
. Wówczas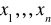
nazywamy zmiennymi decyzyjnymi. Są to parametry, które możemy wybierać.Decyzje dopuszczalne tworzą podzbiór
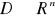
. Zbiór dopuszczalny D jest określony przez skończony układ równości i nierówności (nieostrych).Stopień realizacji celu można opisać przez funkcję rzeczywistą
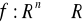
. Funkcję f nazywamy funkcją celu (lub funkcją kryterium). Wartość f(x) jest stopniem realizacji decyzji opisanej przez wektor x. Zbiór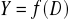
jest wtedy zbiorem dopuszczalnych ocen (stopnia realizacji celu).Decyzja x jest:
lepsza niż z wtedy i tylko wtedy, gdy f(x)>f(z),
tak samo dobra wtedy i tylko wtedy, gdy f(x)=f(z).
Decyzja

jest optymalna, gdy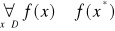
.
Poszukujemy decyzji optymalnych, co oznaczamy ![]()
Używa się notacji 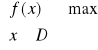
Rozważa się problem minimalizacji: ![]()
. Sprowadza się to do maksymalizacji funkcji -f(x).
Rozważa się też optymalizację jednocześnie wielu celów ![]()
, na ogół sprzecznych ze sobą (programowanie wielokryterialne).
Rysunek przedstawia jednowymiarowe zadanie: 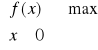
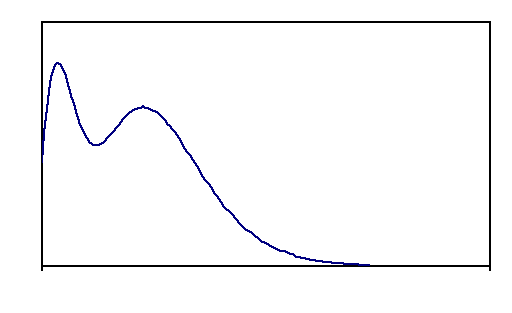
Ta funkcja ![]()
(dla![]()
) ma maksimum absolutne i maksimum lokalne. Ma minimum lokalne, ale nie ma minimum absolutnego. Ponadto inf f = 0. W celu rozwiązania zadania szukania ekstremów trzeba sprawdzić wartości funkcji na brzegu zbioru D, czyli f(0).
7. Szczególne problemy PM
W rozważaniach analizy matematycznej funkcja f może być skomplikowana (mieć wiele punktów nieciągłości, nieróżniczkowalna). W praktycznych zastosowaniach funkcja f nie jest na ogół zbyt skomplikowana. Rozważa się funkcje: wypukłe, liniowe, kwadratowe, ilorazowe (iloraz funkcji liniowych).
Zbiór dopuszczalny D może być ograniczony lub nie (w szczególności może okazać się zbiorem pustym). Na ogół nie jest zbyt skomplikowany np. na płaszczyźnie może to być prostokąt, trójkąt, wielokąt, koło, półprosta. Można go opisać za pomocą warunków równości i nierówności postaci:
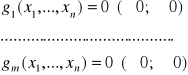
Czasami zapisujemy warunek w postaci: ![]()
. Równości i nierówności ![]()
można sprowadzić do postaci nierówności ![]()
.
Funkcje ![]()
(i=1,...,m) mogą być w szczególności: liniowe, kwadratowe, wypukłe itp. Zauważmy, że ograniczenia są nieostre. Dzięki temu zbiór D na ogół jest zbiorem domkniętym.
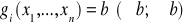
są to warunki ograniczające (ograniczenia).
Wyróżniamy wśród nich tzw. warunki brzegowe, postaci ![]()
. Oznacza to, że zmienne decyzyjne nie mogą być ujemne. Często wynika to z interpretacji ekonomicznej tych zmiennych.
Rozważamy zadania programowania: liniowego, kwadratowego, wypukłego, ilorazowego.
Niekiedy zmienne decyzyjne
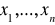
mogą przyjmować tylko wartości całkowite (wynika to z interpretacji tych zmiennych). Mamy do czynienia wtedy z programowaniem całkowitoliczbowym (ogólniej: programowaniem dyskretnym). Wyróżniamy też problemy, gdy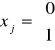
(programowanie binarne). Niekiedy występują zadania mieszane: część zmiennych jest dyskretnych, część - binarnych, część - ciągłych.
Przykład 1
Zakład wytwarza dwa produkty A i B. Ich ceny zbytu wynoszą odpowiednio 3Є i 4Є. Należy opracować dzienny plan produkcji zakładu tak, aby wartość produkcji zakładu liczona w cenach zbytu była jak największa.
Produkcja jest limitowana przez dostępny czas pracy maszyn i surowiec podstawowy. Dzienny limit czasu pracy maszyn wynosi 500 minut. Zakład może każdego dnia dysponować 350kg tego surowca.
Sztuka wyrobu A wymaga 1 minuty czasu pracy maszyn, natomiast sztuka wyrobu B - 2 minuty.
Na wyprodukowanie sztuki wyrobu A zużywa się 1kg surowca, na wyprodukowanie sztuki wyrobu B - również 1kg surowca.
Jednostkowy zysk ze sztuki A wynosi 2Є, a ze sztuki B - 1Є. Zakład jest zainteresowany tylko takim programem dziennej produkcji, przy którym będzie osiągał zysk co najmniej 600Є.
Budowa modelu
Co jest celem działania? - produkcja wyrobów A i B
O czym chcemy decydować? - o rozmiarach dziennej produkcji A i B
Jakie są warunki działania i środki? - praca maszyna
surowiec podstawowy
(założenia podane w opisie)
Jakie jest kryterium oceny decyzji? - maksymalna wartość produkcji w cenach zbytu
Zmienne decyzyjne:
![]()
- dzienna produkcja A (w sztukach)
![]()
- dzienna produkcja B (w sztukach)
Funkcja celu (wartość produkcji w cenach zbytu):
![]()
Ograniczenia:
maszyny ![]()
(na sztukę 1 i 2 min, łącznie ![]()
500 minut)
surowiec ![]()
(na sztukę 1 i 1 kg, łącznie ![]()
350 kg)
minimalny zysk ![]()
(na sztukę 2 i 1 Є, łącznie ![]()
600 Є)
Warunki brzegowe:
![]()
,![]()
Rozwiązanie
podać przykłady decyzji dopuszczalnych:
(300,0) f=900
(350,0) f=1050
(300,50) f=1100
(250,100) f=1150
okazuje się, że (250,100) jest decyzją optymalną
rozwiązania dopuszczalne znajdują się w trójkącie o współrzędnych (300,0), (350,0), (250,100) [por. interpretacja geometryczna].
Przykład 2
Firma produkuje dwa produkty X1 i X2. Do wyprodukowania każdego z tych produktów potrzebne są 3 maszyny: A, B i C.
Aby wyprodukować 1 egzemplarz produktu X1 maszyna A musi pracować 3h, B - 1h, C - 1h. Dla produktu X2 odpowiednie czasy pracy maszyn wynoszą: A - 2h, B - 2h, C -1h.
Wyprodukowanie jednego produktu X przynosi zysk 500zł, jednego produktu Y - 350zł.
Istnieją ograniczenia dotyczące czasu pracy maszyn. Maszyna A może pracować 24h na dobę, B - 16h, C - tylko 9h. Zakładając, że wszystkie maszyny są zawsze dostępne ustalić liczbę produkowanych egzemplarzy X1 i X2, które dają dziennie największy zysk.
Funkcja celu
![]()
Ograniczenia czasu pracy:
dla maszyny A:![]()
dla maszyny B:![]()
dla maszyny A:![]()
Warunki brzegowe:
![]()
,![]()
Rozwiązanie
(6,2), f=4050
BAD_OPER01
1
B
A
2
1
A
Zastosowanie rozwiązania (np. podjęcie decyzji)
Interpretacja ekonomiczna
(i weryfikacja)
Rozwiązanie zadania matematycznego
Model matematyczny
Problem ekonomiczny (decyzyjny)
B
punkt przegięcia
max loc
min loc
max abs
brzeg
inf
f(x)=W4(x)e-x
![]()
Wyszukiwarka