Wykład 1 21.02.01
Mechanika płynów zajmuje się :
równowagą płynów,
ruchem płynów,
mechanicznymi oddziaływaniami płynów na ciała w nich zanurzone i ściany ograniczające jego objętość.
Działy mechaniki :
hydrostatyka,
hydrokinematka,
hydrodynamika.
Płyny ulegają odkształceniom postaciowym, gazy ulegają odkształceniom objętościowym, ciecze nie ulegają odkształceniom objętościowym.
Ciała stałe, ciecze, gazy wykazują budowę molekularną.
Płyn jako ośrodek ciągły :
płyn rzeczywisty zastępuję model teoretyczny,
w modelu teoretycznym zakłada się że płyn jest ośrodkiem ciągłym, pomija się budowę molekularną i chaotyczne ruchy cząsteczek,
podstawową objętość płynu stanowi elementarna objętość płynu dV=dxdydz.
Siły działające w płynie :
Siły
wewnętrzne zewnętrzne
powierzchniowe masowe
siły masowe czynne siły bezwładności (d'Alemberta)
siły wewnętrzne - wywołane wzajemnym oddziaływaniem bezpośrednio sąsiadujących elementów mas leżących wewnątrz obszaru,
siły zewnętrzne - wynik działania mas nie należących do wydzielonego obszaru na poszczególne masy tego obszaru.
Pole sił powierzchniowych :
siły powierzchniowe zewnętrzne :
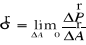
przyłożone na powierzchni płynnejjednostkowa siła powierzchniowa (naprężenie) :
P - wektor główny sił działających na element o powierzchni A
![]()
Pole sił masowych :
![]()
- siła masowa działająca na element płynu o masie m w objętości V,
![]()
- wektor jednostkowy siły masowej,
X,Y,Z - współrzędne siły jednostkowej,
![]()
Wymiar jednostkowej siły masowej :
Podstawowe własności płynów :
![]()
1. Gęstość :
![]()
- wg definicji makroskopowej dla cieczy niejednorodnych :
![]()
- interpretacja na poziomie mikroskopowym :
m - masa molekuły [kg], n - liczba molekuł [1/m3].
![]()
2. Gęstość właściwa : [m3/kg]
3. Ciężar właściwy : γ [N/m3]
![]()
- dla płynów niejednorodnych : G - ciężar płynu [N], V obj. [m3]
Dla gazów doskonałych
4. Ściśliwość płynów :
zdolność
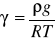
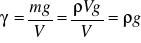
do zmniejszenia objętości pod wpływem sił zewnętrznych
wielkość charakterystyczna - współczynnik ściśliwości : p [m2/N],
odwrotność współczynnika ściśliwości - moduł sprężystości k=1/p,
![]()
![]()
jeżeli :
![]()
to :
więc :
![]()
ciecze rzeczywiste są nieściśliwe
5. Rozszerzalność cieplna :
- zdolność do zwiększania objętości pod wpływem temperatury,
- wielkość charakteryzująca współczynnik rozszerzalności cieplnej T [1/K],
![]()
6. Napięcie powierzchniowe : σ [N/m]
σ=P/l P - siła na granicy faz, l - długość przekroju na który działa siła P
7. Lepkość :
- własność płynu dzięki której pojawiają się siły ścinające - uwidacznia się w ruchu płynu,
- miara : dynamiczny współczynnik lepkości : = m2/s
kinematyczny współczynnik lepkości : =ρ [Ns/m2],
- prawa Newtona dla ruchu uwarstwionego :
- naprężenie styczne; dv/dn - gradient prędkości
W zależności od kształtowania się naprężeń stycznych w płynie w przepływie warstwowym płyny dzielimy na :
newtonowskie,
nienewtonowskie.
Przepływ warstwowy to taki gdzie elementy płynu nie przemieszczają się prostopadle do głównego wektora prędkości.
Wykład 2 28.02.01
Podstawowe prawo równowagi płynu :
Siły masowe :
X,Y,Z - składowe jednostkowej siły masowej,
Siły powierzchniowe działające od ciśnienia są skierowane od płynu do powierzchni.
Siły na ścianę o powierzchni dydz :
Suma sił w kierunku osi X :
Analogicznie dla pozostałych kierunków.
Warunek równowagi płynu d'Alemberta :
Suma sił działających w kierunku każdej osi kartezjańskiego układu współrzędnych jest równa 0.
Dla osi X :
Analogicznie dla pozostałych osi.
Sumujemy :
elementarna zmiana ciśnienia w płynie jest równa elementarnej zmianie sił masowych.
Równowagą cieczy w jednorodnym polu grawitacyjnym :
Szukamy C : dla warunków brzegowych na powierzchni cieczy :
Stąd ciśnienie w dowolnym punkcie :
γh - ciśnienie hydrostatyczne
gdzie :
h = z - z0
h - zagłębienie punktu M pod zwierciadłem
Jeżeli p0=pa (ciśnienie atmosferyczne) p=pa+γh
to ciśnienie p nazywamy ciśnieniem bezwzględnym,
różnicę p-pa nazywamy ciśnieniem względnym.
Klasyfikacja ciśnień :
p - ciśnienie bezwzględne,
pa - ciśnienie atmosferyczne = 1013 hPa,
pn - nad ciśnienie,
pp - pod ciśnienie.
Jeżeli p > pa to p - pa = pn > 0
Jeżeli p < pa to p - pa = pp < 0
metra słupa wody
1 bar = 105 Pa
Ciśnienie jest skalarne tzn. we wszystkich kierunkach działa z tą samą wartością.
Własności ciśnienia :
stałe we wszystkich kierunkach,
prawo Pascala : w zamkniętym naczyniu zmiana ciśnienia w dowolnym jego punkcie powoduje zmianę ciśnienia w całej cieczy o tę samą wartość.
P2=P1F2/F1
Przykład : Dane :
P,D,d,m,H, γ
Px = ?
Nie dzielimy przez 2, bo ciśnienie w każdym kierunku jest stałe.
Urządzenia do pomiaru ciśnienia :
piezometr : cienka rurka połączona z obszarem badanym.
zbiornik ciecz impulsowa w rurce
nadciśnienie panujące w zbiorniku
Wykład 3 07.03.01
manometr jednoramienny :
mierzy nadciśnienie,
podłączony do obszaru wypełnionego gazem (nie cieczą),
warunek równowagi względem poziomu zwieciadła cieczy manometrycznej w zbiorniku :
a/A - przełożenie manometru
manometr Recknagla :
manometr różnicowy z rurką pochyłą,
do pomiaru małych ciśnień,
warunek równowagi względem poziomu zwierciadła cieczy manometrycznej w zbiorniku :
manometr cieczowy typu MUR :
ρi - ciecz impulsowa,
ρm - ciecz manometryczna,
1 - zawory odcinające,
2 - zawory odpowietrzające,
3 - zawór wyrównawczy,
4 - zawór spustowy.
Równowaga względna w naczyniu wirującym dookoła osi pionowej :
równowaga względna - stan w którym płyn pozostaje w spoczynku względem naczynia, a naczynie znajduje się w ruchu obrotowymciecz w ruchu obrotowym podlega siłom :
grawitacji : m*g,
odśrodkowej : mω2r.
Wykład 4 14.03.01.
g - przyspieszenie ziemskie - jednostkowa siła masowa,
przyspieszenie kątowe można rozłożyć :
Równanie powierzchni swobodnej :
całkując :
dla warunków brzegowych :
Powierzchnia swobodna - (powierzchnia o p=const - powierzchnia ekwipotencjalna) - jest to powierzchnia zwierciadła. Kształt można wyznaczyć z równania :
Równanie paraboloidy obrotowej :
Dla dowolnego punktu :
całkując :
dla warunków brzegowych :
Punkt A(0,0,0) :
Punkt B(R,0) :
Punkt C(R,H) :
Punkt D :
Parcie hydrostatyczne - jest to siła powierzchniowa wywierana przez ciecz na pozostające z nią w kontakcie ciała :
Ciśnienie bezwzględne w dowolnym punkcie cieczy w polu grawitacyjnym :
parcie elementarne :
parcie całkowite :
moment statyczny pola F :
jeżeli ciśnienie na zewnątrz ściany = p0 :
parcie hydrostatyczne :
Przykład : wyznaczyć parcie hydrostatyczne na dno i ściany naczynia :
Wyznaczanie siły parcia na ściany metodą graficzną w oparciu o rozkład ciśnienia hydrostatycznego :
P=V - objętość bryły parcia której podstawą jest rozkład hydrostatyczny
Parcie hydrostatyczne płaskie poziome nie zależy od objętości cieczy zawartej w zbiorniku a jedynie od pola przekroju tej powierzchni i wysokości słupa cieczy w zbiorniku.
Wykład 5 21.03.01.
Wyznaczanie punkty przyłożenia parcia hydrostatycznego :
Moment wypadkowego parcia jest równy sumie momentów elementarnych.
yN - odległość środka parcia od osi X,
IX - moment bezwładności pola F względem osi X
Wg Steinera : IX=IS+ys2F,
zN - zagłębienie środka parcia :
xN - odległość środka parcia od osi Y :
IXY - moment odśrodkowy figury
Parcie na powierzchnie zakrzywione :
dFZ - rzut elementarnej powierzchni na płaszczyznę YZ,
dFX - rzut elementarnej powierzchni na płaszczyznę XY,
Parcie :
zS - zagłębienie środka rzutu figury na płaszczyznę pionową od zwierciadła wody.
z*dFX=dV, V - objętość bryły zawartej pomiędzy powierzchnią zakrzywioną a płaszczyzną zwierciadła wody.
Kierunek działania wyznaczamy z równania :
Przykład :
Wyznaczyć parcie na ściany i dno zbiornika walcowego o promieniu R zakończonego półkulą.
Parcie hydrostatyczne :
Uwzględniając nadciśnienie po :
Wykład 6 28.03.01.
Równowaga ciał pływających :
Równowagę oceniamy oddzielnie w przypadku ciał pływających przy całkowitym zanurzeniu i ciał pływających przy zanurzeniu całkowitym.
Równowaga ciał całkowicie zanurzonych :
Ciało pozostaje w spoczynku poziomym bo wypadkowa sił wzdłuż osi x jest równa zero.
Składowa pionowa :
Siła wyporu przyłożona w środku geometrycznym ciała zanurzonego :
Warunek równowagi (spoczynku) :
W-G=0 => W=G
Momenty sił MG i MW będą powodowały powrót ciała do
pozycji wyjściowej - równowaga trwała.
Moment sił wywracający - utrata równowagi
- równowaga nietrwała
Równowaga obojętna
Oceny ciała pływającego w całkowitym zanurzeniu po jego wychyleniu od pionu dokonujemy na podstawie położenia środka ciężkości i środka geometrycznego.
Ciała częściowo zanurzone :
Prawo Archimedesa :
Siła wyporu jest co do wartości równa
ciężarowi wypartej przez to ciało cieczy.
Sw' - rzeczywisty środek wyporu,
SW - to byłby środek wyporu
gdyby nie nastąpiła zmiana
kształtu obszaru zanurzonego
SC - nie ulega przesunięciu.
W' i G dają moment prostujący
Po wychyleniu z położenia równowagi ciało znajduje się pod wpływem pary sił G i W' oraz momentu obrotowego M0
M0' - moment siły W' względem osi X równy sumie momentów M0 i MK (pochodzi od siły wyporu klinów WK względem osi X).
Jeżeli :
To :
Ponieważ :
m - wysokość metacentryczna
m<0 a>IX/V - równowaga chwiejna
m=0 a= IX/V - równowaga obojętna
m>0 a< IX/V - równowaga trwała
V - objętość zanurzona,
a - odległość środka ciężkości ciała i środka geometrycznego części zanurzonej,
IX - moment bezwładności,
Za IX podstawiamy IMIN -jest to moment bezwładności tej osi której moment jest najmniejszy,
Wykład 7 4.04.01.
Kinematyka płynów
Kinematyka płynów :
geometryczny opisem ruchu płynów, bez wnikania w pole sił powodujących przepływ,
wykorzystanie zasady analizy matematycznej, co wymaga przyjęcia założenia że płyn jest ośrodkiem ciągłym pod względem masy i odkształceń postaciowych jak i objętościowych,
masa i odkształcenia traktowane są jako ciągłe funkcje czasu,
założenie ciągłości masy ruchy wszystkich elementów płynu są od siebie zależne,
założenie ciągłości odkształceń elementów płynu powstanie obok pola prędkości ruchu postępowego, pola prędkości obrotowych i pola prędkości odkształceń.
Zadania kinematyki :
określenie pola prędkości v,
określenie pola przyspieszeń a,
dla dowolnego elementu w dowolnym czasie.
Znajomość pola prędkości i przyspieszeń => wyznaczenie pola ciśnień p i gęstości.
Parametry ruchu płynów :
prędkość,
przyspieszenie,
ciśnienie.
Klasyfikacja przepływów :
Przepływ :
nieustalony (niestacjonarny) - parametry przepływu zależą od czasu i współrzędnych położenia,
ustalony (stacjonarny) - parametry przepływu nie zależą od czasu lecz jedynie od położenia,
Przepływ trójwymiarowy :
nieustalony,
ustalony,
Przepływ dwuwymiarowy :
płaski - między dwiema równoległymi płaszczyznami, do których wektory prędkości są równoległe,
osiowosymetryczny - /v= v(r,z,t)/ wszystkie elementy płynu leżące na tym samym okręgu poruszają się z taką samą prędkością (np. przepływy w rurociągu, dyfuzory, dysze o przekroju kołowym, osiowy przekrój brył obrotowych).
Przepływ jednowymiarowy : parametry ruchu zależą od jednej współrzędnej /położenia/ - stosowany w obliczeniach hydraulicznych.
Analityczny opis przepływów :
metoda Lagrange'a - analiza wędrowna,
metoda Eulera - analiza lokalna.
Metoda Lagrange'a :
rozpatrujemy ruch elementów płynu wzdłuż ich toru,
elementy płynu charakteryzuje się za pomocą współrzędnych jakie posiadł w chwili t=t0.
Jest to metoda teoretyczna, gdyż ciężko jest śledzić konkretny element płynu.
Opisanie za pomocą równoważnego układu równań analitycznych :
Jeżeli t jest zmienną, to równania te stanowią równanie toru elementu płynu, który w chwili t=t0 przechodził przez punkt P0(a,b,c).
Jeżeli t jest stałą a współrzędne są zmiennymi to równania opisują przestrzenny rozkład elementów płynu w danej chwili t.
Wyróżniony element płynu
przebędzie drogę :
z prędkością :
wektorowe pole prędkości :
wektorowe pole przyspieszeń :
gdzie :
Metoda Eulera :
polega na badaniu zmian, jakim w czasie przepływu podlega prędkość elementu płynu, przepływający przez wybrany w obszarze poruszającego się płynu punkt,
opis parametrów zgodny ze sposobem prowadzenia bezpośrednich pomiarów,
pole prędkości :
czyli :
współrzędne Eulera :
wektor przyspieszeń pochodna zupełna wektora prędkości pochodna substancjalna :
- zmiana wektora prędkości wiąże się ze zmianą położenia dx, a zmiana położenia następuje podczas zmiany czasu dt.
pochodna pochodna
lokalna unoszenia
Pochodną substancjalną wyznacza się analogicznie dla pozostałych parametrów przepływu, zarówno dla wielkości wektorowych jak i skalarnych.
Tor i linia prądu :
Tor - droga jaką zakreśla element płynu w ruchu.
W metodzie Lagrange'a tor opisują równania 1-3 po wyeliminowaniu czasu.
W metodzie Eulera tor opisują równania różniczkowe trajektorii :
Linia prądu - jest to linia do której w danej chwili w każdym jej punkcie wektory prędkości elementu płynu, leżących na tej linii są styczne.
linie prądu nie mogą się krzyżować,
wyrażone dla dwóch różnych chwil na ogół się nie pokrywają.
Różniczkowe równania linii prądu.
Warunek styczności :
K - kontur - powierzchnia zawarta w obszarze linii prądu ale nie będąca linią prądu, to zbiór linii prądu tworzących powierzchnię, a poprowadzone przez każdy punkt konturu nazywamy rurką prądu, płyn wewnątrz to struga. Jeżeli ogranicza dowolną skończoną powierzchnię to rurkę prądu uogólniamy do powierzchni prądu. Strumień - płyn zawarty wewnątrz powierzchni prądu.
Przykład :
Dla przepływu płaskiego nieustalonego opisanego funkcjami vx=x+t, vy=y+t, określić :
linię prądu przechodzącą w t=0 przez punkt A(1,1),
tor tego elementu płynu, który w chwili t=0 znajdował się w punkcie A
Równanie linii prądu :
całkując :
dla :
zatem równanie linii prądu przechodzącego w chwili t=0 przez punkt A to :
x = y
Wykład 9 18.04.01.
Struktura pola prędkości płynu
Elementarny ruch dowolnego elementu płynu złożony jest z :
prostego przesunięcia (postępowego),
obrotu elementu,
odkształcenia objętościowego (zmiana długości boków i objętości elementu),
odkształcenia postaciowego elementu (zmiana kątów kształtu elementu).
Odpowiednio odróżnia się :
prędkość ruchu postępowego,
prędkość wirowania,
prędkość odkształcania.
Prędkość odkształceń kątów elementu płynu :
Zmiana kształtu wynika ze zmiany prędkości w kierunku osi x.
Średni kąt obrotu (względem osi z) :
Prędkość kątowa odkształcenia postaciowego elementu to średni kąt obrotu krawędzi odniesiony do jednostki czasu :
W płaszczyźnie Oxy :
W płaszczyźnie Oyz :
W płaszczyźnie Oxz :
Prędkości kątowe odkształcenia objętościowego :
Prędkości kątowe obrotu i odkształcenia po pomnożeniu przez odpowiedni wymiar liniowy elementu wyrażają odpowiednio prędkość wirowania lub prędkość odkształcenia.
Równanie linii wirowej (linii prądu) :
Rotacja wektora prędkości :
Rotacją wektora prędkości v nazywa się następującą zależność :
Zależność pomiędzy składowymi rotacji a składowymi prędkości kątowej chwilowego obrotu xyz jest następująca :
Równanie ciągłości płynu :
Przepływ trójwymiarowy nieustalony płynu nieściśliwego : v=f(x,y,z,t); p=f(x,y,z,t).
Strumień masy - masa przepływająca w jednostce czasu przez daną powierzchnię.
Jednostkowa zmiana strumienia
Jeżeli zapiszemy to jako równanie analityczne : strumień * pole powierzchni * czas = masa
Suma przyrostów masy w objętości elementu w czasie dt :
Przyrost masy wynika ze zmiany gęstości po czasie dt.
Zmiana masy w elemencie płynu wskutek zmiany gęstości :
Pochodne cząstkowe strumieni :
Równanie ciągłości przepływu nieustalonego płynu ściśliwego :
Zmiany gęstości w zależności od położenia
I równanie w czasie
div - dywergencja prędkości = zmiana wektora prędkości (pochodna substancjalna).
Dla ruchu ustalonego płynu ściśliwego ρ 0
Dla ruchu ustalonego płynu nieściśliwego ρ = const.
Sens fizyczny dywergencji wektora prędkości :
Podstawowe równanie opisujące ciągłość przepływu ruchu nieustalonego :
Dywergencja wektora prędkości określa względną zmianę szybkości zmiany objętości płynu :
Dla przepływu ustalonego płynu nieściśliwego dV/dt=0 to divv=0
Natężenie przepływu :
Objętość płynu przepływająca w jednostce czasu lub masa przepływająca w jednostce czasu.
Objętościowe natężenie przepływu :
Jeżeli ρ=ρ(x,y,z,t) to posługujemy się masowym natężeniem przepływu :
Dla płynu nieściśliwego :
Dynamika :
Różniczkowe równanie ruchu Eulera płynu doskonałego :
Płyn doskonały - pozbawiony lepkości.
Siły masowe czynne :
Siły masowe bezwładności :
Zasada d'Alemberta :
Suma rzutów sił na dany kierunek równa jest zero
Analogicznie dla osi y i z
Ogólne równanie ruchu Eulera :
Ruch ustalony pf(t)
Potencjał :
W polu grawitacyjnym :
Całkując :
Równanie Bernouliego :
Równanie Bernouliego obowiązuje tylko dla przepływu ustalonego dla cieczy nieściśliwej /założenie że ρ=const/. Przedstawia ono sumę energii potencjalnej i kinetycznej jednostki ciężaru przepływającej cieczy :
Energia na jednostkę ciężaru :
Wysokość Ek jednostki ciężaru
przepływającej cieczy :
Wysokość ciśnienia zwiększająca
wartość EP przepływającej cieczy :
Wartość energii całkowitej w każdym przekroju jest stała.
Równanie ciągłości strumienia :
Równanie ciągłości strumienia :
Fv=const F1v1=F2v2
Q=Fv
Wysokość p0 to wysokość ciśnienia statycznego.
Wysokość prędkości to wysokość ciśnienia dynamicznego.
Suma ciśnień statycznych i dynamicznych to ciśnienie całkowite w strumieniu.
Rurka Pitota :
Rurka Prandtla :
k - współczynnik poprawkowy uwzględniający dokładność wykonania rurki na zaburzenia przepływu.
Zwężka Venturiego :
Dwa pierścienie z otworami na zbierają ciśnienie z całego obwodu przekroju.
Wykład 13 16.05.01.
Równanie Bernouliego jako całka różniczkowego równania ruchu Eulera.
Przemiana adiabatyczna :
Jeżeli :
Stąd :
Różniczkując :
Podstawiając :
Równanie Bernouliego opisujące przepływ gazu podlegającego przemianie adiabatycznej przyjmuje postać :
Przepływ w przewodach zamkniętych.
przepływ ustalony,
przepływ cieczy lepkiej nieściśliwej,
obowiązuje półempiryczna forma równania Bernouliego.
Półempiryczna forma równania B. umożliwia zbilansowanie energii w dwóch rozpatrywanych przekrojach 1 i 2.
Warunek przepływu ustalonego.
Ruch ten nazywamy uwarstwionym (laminarnym). Płyn porusza się ze stałą prędkością w poszczególnych warstwach.
Kryterium przepływu laminarnego stanowi liczba Reynoldsa :
Przepływ laminarny - brak wektora turbulencji
Przepływ turbulentny.
Przepływ turbulentny dzielimy na 3 strefy przepływu :
I - strefa rur hydraulicznie gładkich, - = f(Re)
II - strefa przejściowa ruchu burzliwego, - = f(Re,)
III - strefa kwadratowej zależności strat hydraulicznych od prędkości przepływu. - = f()
Ustalany na podstawie chropowatości bezwzględnej ścian przewodu oraz grubości warstwy podlaminarnej.
Chropowatość bezwzględna - średnia wysokość występków nad powierzchnię przewodu.
Dzieląc ją przez średnicę, obliczamy chropowatość względną.
W zależności od rodzaju przepływu zmienia się wielkość strat hydraulicznych.
Przeszkody :
dyfuzor konfuzor
Laminarny :
Burzliwy (równanie Collebrooke'a - White'a) :
Strefa II :
Strefa I :
Blassius :
Prandtl - Karman :
Przewody krótkie - w nich straty miejscowe są nieporównywalnie małe w stosunku do strat na długości.
W przypadku gdy straty te nie stanowią więcej niż 10-15 % strat na długości w obliczeniach pomijamy wyznaczanie strat liniowych a uwzględniamy je w głównym bilansie energii, powiększając lub wprowadzając pojęcie długości zastępczej przewodu o jaką należałoby ją powiększyć ażeby wyznaczone na jej podstawie straty na długości równoważyły straty w przewodach.
Charakterystyka hydr. przewodu :
Interpretacja graficzna równania Bernouliego.
Powinna obejmować podanie poziomu odniesienia i podanie wartości ciśnień piezometrycznych, energi rzeczywistej i energii dyspozycyjnej
Wykres Ancony piszemy tylko dla przewodu, a nie w zbiorniku.
Spadek hydrauliczny :
Mechanika Płynów - Wykład 1
- 6 -
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
n
v+dv
dn v
n
dv/dn
![]()
![]()
dx
![]()
z ![]()
y x
dz
dy
![]()
![]()
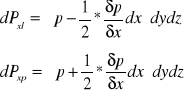
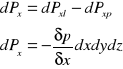
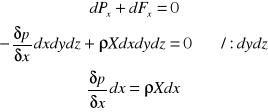
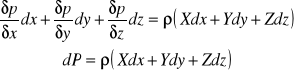
0 x
z0 z
p0 - ciśnienie zewnętrzne
h M(x,y,z) H
z
g p0 Hγ
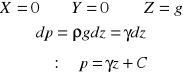
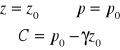
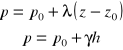
pn pp
p pa
p pa
![]()
p0
γ1
γ2
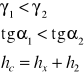
P1 P2
D
C
T1
T2
F1
F2
P P
P
m
D
d
H
Px P
![]()
Pa
P0
H γ Δh
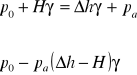
p1
p2
0 0 h1 H
h2
a
γm=ρmg
A
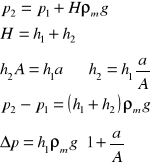
p1
p2 l
h2 h1 H
α
A
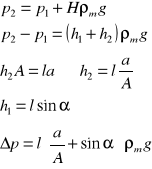
pa pb
2
1
1 H
ρi
h
H2
H1
ρm
4
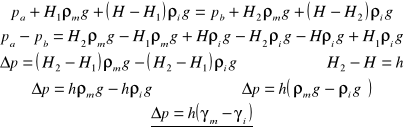
z
ω
r
M ω2x
z0
ω2y x
g
y
z
ω
r
M ω2x
z0
ω2y x
g
y
r 2x
M
2x 2r
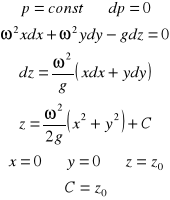
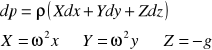
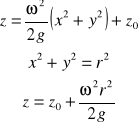
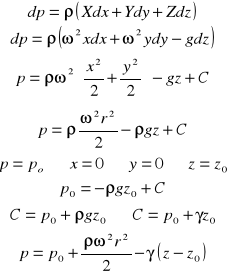
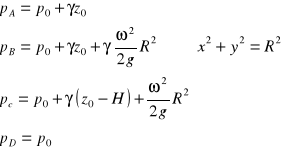
z
C
D
z0 A B
x
y
p0
zS zN z dP z
P
x
y
dF
F
y x
xN yN
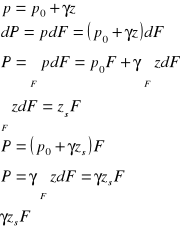
pa
c h
h/2
b
a
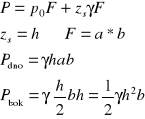
![]()
p0
zS zN z dP z
P
x
y
dF
F
y x
xN yN
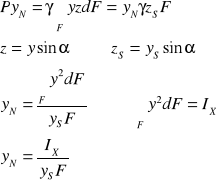
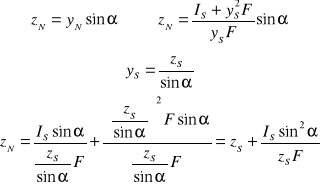
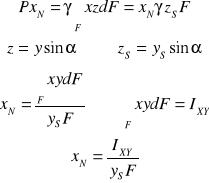
dFX
0 D C x
zS z
A dPZ dP
FZ dFZ dPX
B
dF
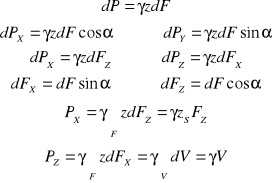
![]()
![]()
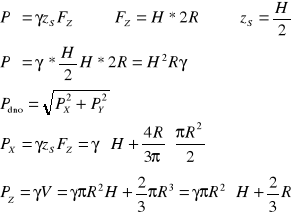
h
po
H
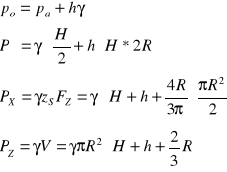
γ
γs S
Px Px
G
FR
PZ
![]()
![]()
W W'
SG SG'
SC SC'
G G'
W W'
SC SC'
SG SG'
G G'
W W'
SC SC'
SG SG'
G G'
Oś pływania
W
SG
SW
G
m M dWK
ysin
y y
dF a W W'
Sc
SW G SW'
e1 e2
![]()
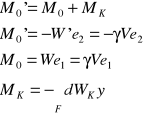
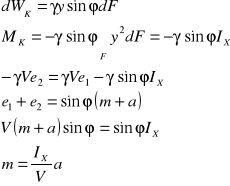
![]()
![]()
![]()
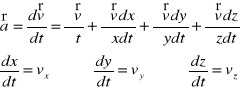
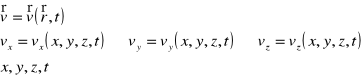
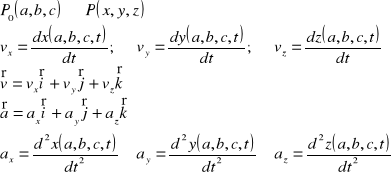
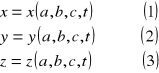
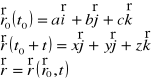
z
P0(t0)
r0
r P(t0+t)
k c z
i j a x y
b
x y
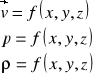
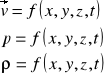
z
v
ds
K
k
i j y
x
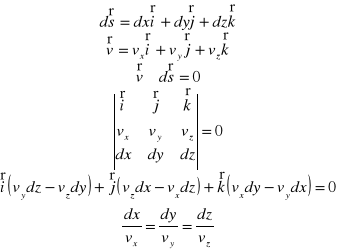
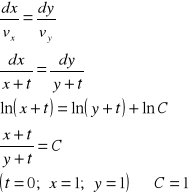
y
d
y
d
vy
vx x
x
![]()
![]()
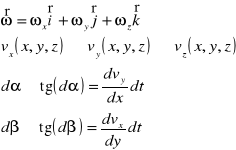
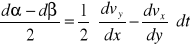
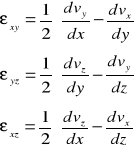
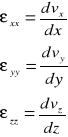
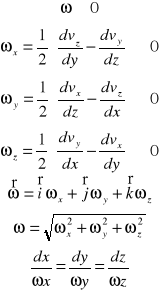
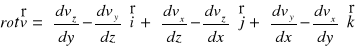
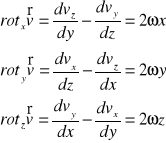
z
vyρ
dy
vxρ
dz
dx
vzρ
x
y
![]()
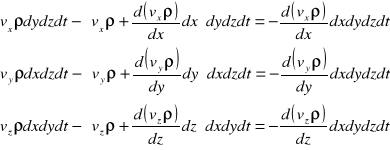
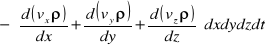
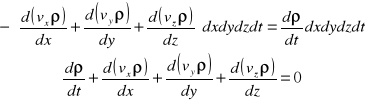
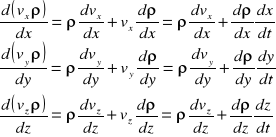
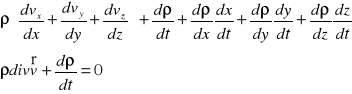
![]()
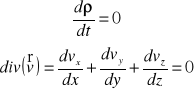
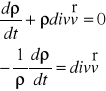
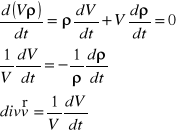
dF
v
F
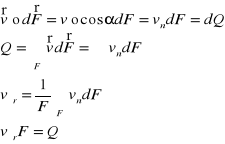
![]()
![]()
(p+dp/dz*dz)dxdy
z
pdxdz
pdydz z (p+dp/dx*dx)dydz
x
z
(p+dp/dy*dy)dxdz pdxdy
x
y
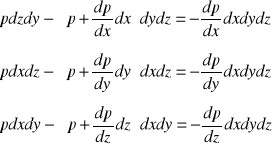
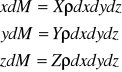
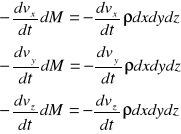
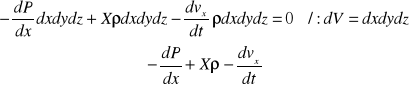
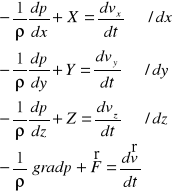
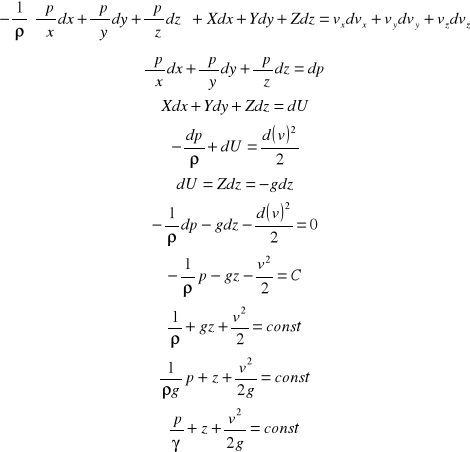
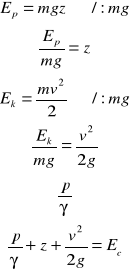
Linia energii dyspozycyjnej
Linia ciśnień piezometrycznych
p1
z1 linia położenia p2
z2=0
powierzchnia porównawcza
![]()
![]()
![]()
v0 v10
p0 p1max
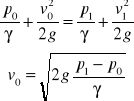
p0 p1
v0 γ v1
γm H
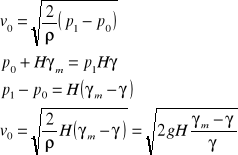
p0
v0
1
2
p0 p1
H
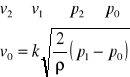
0 1
p0 p1 d
D
v0 v1
30
h1 h2
H

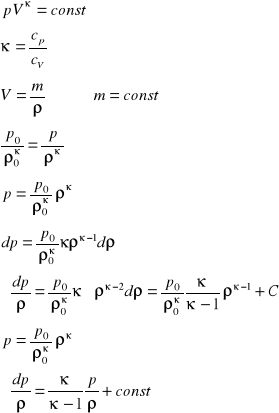
![]()
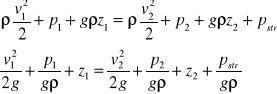
![]()
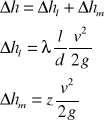
Rdzeń przepływu (jądro)
Warstwa podlaminarna
![]()
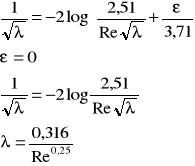
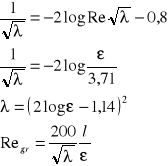
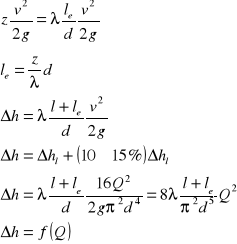
Linia energii dyspozycyjnej
Linia ciśnień piezometrycznych
![]()
![]()
![]()
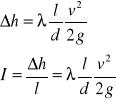
Wyszukiwarka