1. Kinematyka

(pogrubione - zadania rozwiązane w skrypcie)

1.1. Samochód pokonał trasę z miejscowości A do miejscowości B w ciągu 1 godziny i 20 minut. Jaka była średnia prędkość samochodu na tej trasie, jeśli wiadomo, że długość drogi między miejscowościami A i B wynosi 96 km?

1.2. Pierwszą połowę drogi pojazd przebył z prędkością v₁ a drugą z prędkością v₂. Obliczyć średnią prędkość pojazdu na trasie. Obliczenia numeryczne wykonać dla,
,
. Na wykresie prędkości przedstawić geometrycznie drogę przebytą przez pojazd.

1.3. Biegacz przebiegł połowę trasy z prędkością
, a drugą połowę z inną prędkością v₂. Gdyby biegł cały czas ze stałą prędkością
to czas potrzebny na przebycie całej trasy nie zmieniłby się. Oblicz wartość prędkości v₂.

1.4. Pociągi A i B jadą po sąsiednich torach z prędkościami odpowiednio v_A i v_B. Oblicz prędkość względną pociągu B względem A, gdy pociągi poruszają się a) w przeciwne strony, b) w tę samą stronę. Obliczenia numeryczne wykonać dla
,
.

1.5. Łódź płynie z prądem rzeki z przystani A do B w czasie
, a z B do A w czasie
. Ile czasu trzeba, aby łódź spłynęła z przystani A do B z wyłączonym silnikiem?

1.6. Prędkość łodzi względem wody w spoczynku wynosi v₁. Woda płynie w rzece z prędkością v₂. Jak należy skierować łódź, aby przepłynąć rzekę w kierunku prostopadłym do brzegów? W jakim czasie łódź przepłynie rzekę o szerokości L? Przedstaw graficznie układ prędkości. Obliczenia numeryczne wykonaj dla
,
,
.

1.7. Z jaką największą prędkością może iść podczas deszczu człowiek, tak aby deszcz nie padał mu na nogi, jeżeli człowiek ten trzyma parasol, którego brzeg znajduje się na wysokości
i w odległości
przed człowiekiem? Krople deszczu spadają pionowo z prędkością
.

1.8. Motocyklista przejechał
drogi z prędkością
i pozostałe
drogi z prędkością
. Znaleźć średnią prędkość motocyklisty na całym odcinku drogi.

1.9. Biegacz przebiegł dwie trzecie trasy z prędkością
, a pozostałą część z inną prędkością v₂. Gdyby biegł cały czas ze stałą prędkością
to czas potrzebny na przebycie całej trasy nie zmieniłby się. Oblicz wartość prędkości v₂.

1.10. Pasażer pociągu elektrycznego, poruszającego się z szybkością
, zauważył, że drugi pociąg o długości
(jadący w przeciwnym kierunku) minął go w czasie
. Znaleźć prędkość v₂ drugiego pociągu.

1.11. Znaleźć prędkość motorówki na stojącej wodzie, jeżeli podczas ruchu z prądem rzeki szybkość tej motorówki względem brzegu wynosi
a podczas ruchu pod prąd
. Jaka jest prędkość v_p prądu wody w rzece?

1.12. Samochody A i B jadą, w kierunkach wzajemnie prostopadłych, w stronę tego samego skrzyżowania z prędkościami odpowiednio:
i
. Oblicz prędkość względną samochodu B względem A. Wykonaj rysunek zaznaczając odpowiednie wektory prędkości.

1.13. Samolot leci z miasta A do miasta B, położonego względem A o
na wschód. Prędkość samolotu względem powietrza wynosi
. Obliczyć czasy przelotu: t_a - przy bezwietrznej pogodzie oraz t_b - gdy na całej trasie wieje wiatr z południa na północ z prędkością
. Wykonać rysunki.

1.14. Motocyklista rusza ze stałym przyspieszeniem
. Po 0,6 min od chwili rozpoczęcia ruchu zatrzymuje go policjant. Czy motocyklista będzie musiał zapłacić mandat z powodu przekroczenia dozwolonej prędkości 60 km/h?

1.15. Aby móc oderwać się od ziemi samolot musi osiągnąć prędkość
. Znaleźć czas rozbiegu i przyspieszenie samolotu, jeżeli długość rozbiegu wynosi
. Założyć, że ruch samolotu jest jednostajnie zmienny.

1.16. Samochód porusza się z prędkością
. Na drodze
jest hamowany i zmniejsza swą prędkość do
. Zakładając, że ruch samochodu jest jednostajnie zmienny, znaleźć przyspieszenie i czas hamowania.

1.17. W czasie t prędkość v₀ poruszającego się ciała wzrosła n razy. Oblicz stałe przyspieszenie ciała, prędkość średnią oraz drogę przebytą przez ciało w czasie t. Obliczenia numeryczne wykonaj dla
,
,
. Na wykresie prędkości przedstaw graficznie drogę przebytą przez ciało w czasie t.

1.18. W ruchu prostoliniowym prędkość ciała jest następującą funkcją czasu:
. a) Określ ruch ciała. b) Oblicz drogę przebytą przez ciało w czasie
.

1.19. Dwa samochody jechały jednakowo długo. Pierwszy z nich połowę czasu jechał z przyspieszeniem a a drugą połowę czasu z przyspieszeniem 2a. Drugi z kolei pierwszą połowę czasu jechał z przyspieszeniem 2a a drugą z przyspieszeniem a. Który z nich przebył dłuższą drogę? Przedstaw tę drogę na wykresie prędkości w funkcji czasu.

1.20. Zależność drogi s przebytej przez ciało od czasu t w ruchu prostoliniowym podaje równanie
, gdzie
,
,
. Znaleźć: a) zależność prędkości v i przyspieszenia a od czasu t; b) drogę przebytą przez ciało oraz prędkość i przyspieszenie ciała po upływie 2s od rozpoczęcia ruchu.

1.21. Dwa ciała poruszają się ruchem jednostajnie przyspieszonym. Stosunek ich przyspieszeń wynosi 2:3, stosunek czasów trwania ich ruchu jest 3:4. W jakim stosunku pozostają drogi przebyte przez te ciała?

1.22. Samochód jadący z prędkością
w pewnej chwili zaczął hamować tak, że zatrzymał się po upływie
. Zakładając, że ruch samochodu był jednostajnie zmienny, wyznacz przyspieszenie a samochodu oraz drogę s, jaką przebył on od chwili rozpoczęcia hamowania.

1.23. Znaleźć czas wznoszenia się windy, zakładając, że jej ruch podczas ruszania i hamowania jest jednostajnie zmienny o przyspieszeniu równym, co do wartości bezwzględnej
, a na środkowym odcinku drogi jej ruch jest jednostajny z prędkością
. Wysokość, na jaką wznosi się winda
. Sporządzić wykres prędkości windy od czasu trwania jej ruchu.

1.24. W ruchu prostoliniowym zależność drogi przebytej przez ciało od czasu jest:
. a) Określ ruch ciała. b) Oblicz prędkość ciała po przebyciu drogi
.

1.25. Dwa samochody jechały jednakowo długo. Pierwszy z nich połowę czasu jechał z przyspieszeniem a a drugą 3a. Drugi z kolei pierwszą połowę czasu jechał z przyspieszeniem 2a a drugą z przyspieszeniem a. Który z nich przebył dłuższą drogę? Który z nich osiągnął większą prędkość końcową?

1.26. Ciało spada z wieży. W chwili t₀, gdy przebyło ono drogę równą d, z punktu położonego o h niżej od wierzchołka wieży zaczęło spadać drugie ciało. Oba ciała spadają na ziemię w tej samej chwili. Wykazać, że wysokość wieży jest równa
.

1.27. Spadające swobodnie ciało pokonało w czasie pierwszych dwóch sekund 1/2 całej drogi. Znajdź wysokość z jakiej spadło to ciało. Przyjmij przyspieszenie ziemskie
.

1.28. Ciało spada swobodnie z wysokości
. Z jaką prędkością v ciało uderzy o ziemię? Na jakiej wysokości h₁ prędkość ciała będzie równa połowie prędkości końcowej? Przyjmij wartość przyspieszenia ziemskiego
.

1.29. Ciało spadające swobodnie ma w punkcie A prędkość
, a w punkcie B prędkość
. Obliczyć odległość między punktami A i B. Przyjmij
.

1.30. Spadający swobodnie kamień ma w punkcie A prędkość
. Jaką prędkość będzie on miał w punkcie B położonym o
poniżej punktu A (przyspieszenie ziemskie
)?

1.31. Ciało spada swobodnie na ziemię z wysokości H. Na jakiej wysokości prędkość tego ciała będzie n razy mniejsza od jego prędkości końcowej? Obliczenia numeryczne wykonaj dla
,
.

1.32. W urządzeniu kafarowym służącym do wbijania pali ruchomy ciężar podnoszony jest ruchem jednostajnym na wysokość 4,9 m z prędkością 0,98 m/s, a następnie spada swobodnie na pal. Znaleźć liczbę uderzeń ciężaru na minutę. Przyjmij
.

1.33. W jakim czasie swobodnie spadające ciało przebędzie n-ty metr swojej drogi?

Wskazówka: Przedstaw drogę przebytą przez ciało w postaci następującego iloczynu:
, gdzie
.

1.34. Znaleźć prędkość początkową, z jaką wyrzucono ciało pionowo do góry, jeżeli na wysokości
(licząc od punktu wyrzucenia ciała) znajdowało się ono dwukrotnie w odstępie czasu
. Nie uwzględniać oporu powietrza. Przyjąć przyspieszenie ziemskie równe
.

1.35. W rzucie poziomym prędkość końcowa ciała jest n = 3 razy większa od prędkości początkowej. Prędkość początkowa ciała wynosi
. Obliczyć wysokość początkową rzutu. Przyspieszenie ziemskie
.

1.36. Kula pistoletowa wystrzelona poziomo przebiła dwie pionowo ustawione kartki papieru, umieszczone w odległościach
i
od pistoletu. Różnica wysokości na jakich znajdują się otwory w kartkach wynosi h = 5 cm. Oblicz prędkość początkową kuli. Przyspieszenie ziemskie
.

1.37. Z wierzchołka góry wyrzucono ciało w kierunku poziomym z prędkością
. Znaleźć składowe wektora przyspieszenia, styczną i normalną do toru, po czasie
od chwili wyrzucenia. Przyjmij
.

1.38. Jaki powinien być czas opóźnienia zapłonu granatu wyrzuconego z prędkością v₀ pod kątem  do poziomu, aby wybuch nastąpił w najwyższym punkcie toru? Przyspieszenie ziemskie g jest dane.

1.39. Kamień rzucono pod kątem  do poziomu nadając mu prędkość początkową
.

a) Narysuj tor kamienia. Na rysunku zaznacz wektory prędkości w chwili początkowej i w najwyższym punkcie toru, wektor przyspieszenia oraz zasięg rzutu.

b) Oblicz czas trwania ruchu i zasięg rzutu.

Przyjmij wartość przyspieszenia ziemskiego
.

1.40. Od rakiety, wznoszącej się pionowo do góry, w momencie, gdy ma ona prędkość v₁ odczepia się na wysokości h niepotrzebny już zbiornik paliwa. Obliczyć czas spadania t oraz prędkość v₂, z jaką zbiornik opada na ziemię. Przyspieszenie ziemskie g - dane. Opór powietrza pominąć.

1.41. Ciało rzucono pionowo do góry z prędkością początkową
. Znaleźć odstęp czasu między chwilami, kiedy ciało znajdowało się na połowie maksymalnej wysokości. Zaniedbać opór powietrza. Przyjąć przyspieszenie ziemskie
.

1.42. W rzucie poziomym zasięg równy jest wysokości początkowej. Prędkość początkowa ciała wynosi v₀. Obliczyć czas trwania rzutu oraz prędkość końcową ciała. Obliczenia numeryczne wykonać dla
,
.

1.43. Z dachu domu rzucono poziomo kamień z prędkością v₀. Oblicz składową przyspieszenia kamienia prostopadłą do toru po czasie t. Obliczenia numeryczne wykonaj dla
,
.

1.44 Z armaty wystrzelono pocisk pod kątem
do poziomu z prędkością początkową
. W układzie współrzędnych XOY znajdź współrzędne położenia ciała (tj. współrzędne x, y) oraz współrzędne prędkości (tj. współrzędne v_x, v_y) po czasie
, gdzie t_c - czas trwania rzutu. Przyjąć przyspieszenie ziemskie
.

1.45. Pod jakim kątem do poziomu wyrzucono ciało, jeżeli wiadomo, że maksymalna wysokość, na jaką wzniosło się ciało, jest cztery razy mniejsza od zasięgu rzutu? Nie uwzględniać oporu powietrza.

1.46. Pod jakim kątem do poziomu należy skierować strumień wody, aby jego maksymalne wzniesienie było równe zasięgowi w kierunku poziomym?

47. Minutowa wskazówka zegara jest
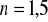
    raza dłuższa od wskazówki godzinowej.

a) Ile razy większa jest prędkość liniowa końca wskazówki minutowej od prędkości liniowej końca wskazówki godzinowej? b) Oblicz stosunek przyspieszeń dośrodkowych końców obu wskazówek.

1.48. Punkt materialny porusza się po okręgu o promieniu
ze stałym co do wartości przyspieszeniem stycznym
. Po jakim czasie t₁ od chwili rozpoczęcia ruchu przyspieszenie dośrodkowe a_d będzie co do wartości dwa razy większe od przyspieszenia stycznego?

1.49. Kolarz rozpoczynając jazdę pierwsze
jedzie ruchem jednostajnie przyspieszonym. Jaką prędkość osiąga po tym czasie, jeżeli promień kół rowerowych
, a przyspieszenie kątowe tych kół
?

1.50. Karuzela wykonuje w ciągu minuty
obrotów. Oblicz, jaką prędkość kątową, liniową i przyspieszenie dośrodkowe ma człowiek, który siedzi na karuzeli. Promień toru, po którym porusza się człowiek, wynosi
.

1.51. Oblicz przyspieszenie dośrodkowe ciała znajdującego się na równiku Ziemi. Porównaj je z przyspieszeniem spadku swobodnego
. Przyjmij, że promień równikowy Ziemi wynosi 6380 km, a okres jej obrotu 24 h.

1.52. Motocyklista startuje do wyścigu rozgrywanego na torze kołowym o promieniu
. W ciągu czasu
wartość jego prędkości wzrasta jednostajnie od 0 do
. Jaka była wartość przyspieszenia stycznego (liniowego) i kątowego motocyklisty? Oblicz przyspieszenie dośrodkowe motocykla w chwili
. Jaki kąt tworzył w tym momencie wektor przyspieszenia wypadkowego ze styczną do toru?

1.53. Samochód mając prędkość
zaczyna hamować bez poślizgu poruszając się przy tym ruchem jednostajnie opóźnionym. Do całkowitego zatrzymania się przebył on drogę
. Wiedząc, że promień kół samochodu wynosi
znajdź opóźnienie kątowe kół podczas hamowania.

5

---