MN jako nauka: badaniesposobów rozwiązania zadania matematycznego za pomocą działań arytmetycznych.
MN jako sztuka: wybór procedury rozwiązania która jest “najlepiej” dostosowana do danego zadania.
ŹRÓDŁA BŁĘDÓW PRZY ROZWIĄZYWANIU PROBLEMU:
Powstają w dwóch obszarach:
Przy matematycznym formułowaniu zadania.
Podczas wykonywania obliczeń:
Błędy grube ⇐ stosowanie komputerów w obliczeniach zmniejszyło prawdopodobieństwo ich występowania.
Błąd metody lub obcięcia ⇐ rozwiązywanie problemu w postaci przybliżonej, mogącej się różnić od postaci pierwotnej.
Błąd zaokrąglenia ⇐ nieskończone rozwinięcia dziesiętne (lub dwójkowe w komputerze) trzeba zaokrąglać.
DEFINICJE BŁĘDÓW:
wart. dokładna = wart. przybliżona + błąd bezwzględny WD = WP + BB
Błąd względny (BW): ![]()
RERGUŁA ZAOKRĄGLEŃ:
Liczba x jest poprawnie zaokrąglona na d-tej pozycji do liczby x(d) jeżeli błąd zaokrąglenia ε jest taki, że ![]()
Jeżeli ![]()
⇒ można wybrać zaokrąglenie “w dół” lub “w górę”.
CYFRY ZNACZĄCE:
wartość dokładna: x
wartość przybliżona: y
k-ta cyfra dziesiętna liczby y jest znacząca wtedy gdy:
![]()
BŁĄD WARTOŚCI FUNKCJI:
BB funkcji: ![]()
TEORIA STATYSTYCZNA BŁĘDU ZAOKRĄGLENIA:
Rozkład sumy n wzajemnie niezależnych błędów, przy n→∞, dąży do rozkładu normalnego.Przy obliczeniach, w których występuje n działań: max. błąd bezwzględny (BB)max jest proporcjonalny do n; błąd prawdopodobny BP jest proporcjonalny do ![]()
.
ALBEBRA MACIERZY
Macierz: Uporządkowany zbiór m x n liczb rozmieszczonych w postaci prostokątnej tabeli o m wierszach i n kolumnach nazywamy macierzą.
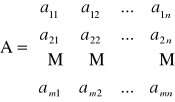
aij (i=1,2,...,m ; j=1,2,....,n) - elementy macierzy
A = [ aij] - Jest to macierz typu m x n inaczej dim A = mxn
m = n → macierz kwadratowa
m ≠ n → macierz prostokątna
m = 1, n >1→ macierz (lub wektor) wierszowy
m > 1, n = 1→ macierz (lub wektor) kolumnowy
m = 1, n >1 → macierz (lub wektor) wierszowy
m > 1, n = 1→ macierz (lub wektor) kolumnowy
Ważne macierze:
macierz przekątniowa (lub diagonalna) - macierz kwadratowa m x n o własności: aii ≠ 0, aij = 0 dla i≠j
(wszędzie zera poza główną przekątną)
macierz jednostkowa I - jeżeli na głównej przekątnej są
jedynki a wszędzie indziej zera.
symbol Kroneckera 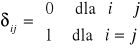
⇒ I = [δij]
macierz zerowa 0 - jeżeli wszystkie elementy macierzy aij = 0
macierz symetryczna - macierz kwadratowa o własności: aij = aji
macierz asymetryczna - macierz kwadratowa o własności: aij = -aji
Podstawowe działania na macierzach:
Równość macierzy: dim A = dim B A = B → aij = bij
Dodawanie dwóch macierzy: dim A = dim B = dim C
C = A + B → cij = aij + bij
Własności:
A + B = B + A
A + 0 = A
A + ( B + C ) = ( A + B ) + C
Odejmowanie dwóch macierzy: dim A = dim B = dim C
C = A - B → cij = aij - bij A - B = A + (-B)
Mnożenie macierzy przez liczbę: dim B = dim A
B = αA = Aα → bij =α aij
Własności:
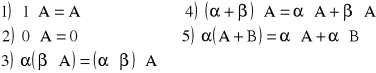
Mnożenie macierzy przez macierz:
Dane: dim A = m x n dim B = n x q
tzn. liczba kolumn A = liczbie wierszy B
Określamy macierz C, taką, że dim C = m x q, której współczynniki określone są wzorem:![]()
wtedy: ![]()
← macierz C jest iloczynem macierzy A i B.
![]()
Własności: (A, B, C - macierze; α - skalar (liczba)
Transpozycja macierzy: A → AT
Macierz transponowana powstaje z macierzy wyjściowej przez zamianę wierszy z kolumnami. B = AT → bij = aji
dim A = m x n → dim B = dim AT= n x m.
Własności:
(AT)T = A
(A + B)T = AT + BT
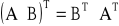
Wniosek: Macierz identyczna ze swoją macierzą transponowaną jest macierzą symetryczną. AT = A aij = aji czyli: macierz symetryczna jest macierzą kwadratową, której elementy są symetryczne względem przekątnej głównej.
Twierdzenie: Iloczyn macierzy i jej macierzy transponowanej jest macierzą symetryczną, ![]()
![]()
Wyznacznik macierzy kwadratowej
An x n = [ aij] uporządkowana tablica liczb. Tej tablicy przypisujemy pewną liczbę W obliczana wg ściśle określonych reguł i zwaną wyznacznikiem:
W = det A = 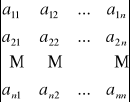
= ![]()
SPOSÓB OBLICZANIA WYZNACZNIKA:
Krok 1: Z kolejnych wierszy macierzy wybieramy po jednym elemencie, każdy leżący w innej kolumnie.
Wybieramy wszystkie możliwe kombinacje.
Krok 2: Dla każdej możliwości określa się najmniejszą liczbę przestawień t odpowiedniej permutacji, przywracającą naturalny porządek 1,2, 3, . . . , n.
Reguła obliczania liczby przestawień:
Idąc w danej permutacji od lewej doprawej strony sumuje się ilość cyfr po prawej stronie kolejnej cyfry, które są od niej mniejsze.
Krok 3: Tworzy się sumę iloczynów elementów wybranych w kroku 1 opatrzonych znakiem “+” gdy ilość przestawień stowarzyszonej permu-tacji wyznaczona w kroku 2 jest parzysta lub znakiem “-“ jeżeli jest nie-parzysta.
Ogólnie: dla macierzy An x n
![]()
gdzie sumowanie jest rozciągnięte na wszystkie możliwe permutacje j1, j2, j3, . . ., jn ciągu liczb 1, 2, 3, ..., n zaś t jest liczbą przestawień.
Wyznacznik macierzy diagonalnej: iloczyn wyrazów głównej przekątnej.
Własności wyznacznika:
Zamiana dwóch wierszy macierzy zmienia znak wyznacznika.
Pomnożenie wiersza przez liczbę powoduje pomnożenie wyznacznika przez tą samą liczbę.
Jeżeli dwa wiersze w macierzy są identyczne to wyznacznik jest równy zero.
Dodanie do jednego wiersza innego wiersza pomnożonego przez dowolną liczbę nie zmienia wartości wyznacznika.
Wyznacznik macierzy transponowanej jest taki sam jak macierzy oryginalnej.
Uwaga: Własności 1 ÷ 4 dotyczą również kolumn macierzy ← konsek-wencja własności 5 (det AT = det A ).
Definicja: Macierz, której wyznacznik jest równy zeru nazywamy macierzą osobliwą.
Numeryczne wyznaczanie wartości wyznacznika:
Korzystając z własności że mnożąc jeden wiersz przez liczbę i dodając go do drugiego wyznacznik się nie zmienia, wyznacznik macierzy oryginalnej przekształcamy do wyznacznika macierzy diagonalnej.
INNA METODA WYZNACZANIA WARTOŚCI WYZNACZNIKA MACIERZY
Dana jest macierz kwadratowa. Usuwamy z A i - ty wiersz i j - tą kolumnę → macierz Aij dim Aij =(n-1) ×(n-1)
Podwyznacznik macierzy A odpowiadający elementowi aij:
minor (aij) = (-1)i+j det Aij
Wtedy zachodzi:
![]()
ROZKŁAD MACIERZY NA SKŁADOWĄ SYMETRYCZNĄ I ASYMETRYCZNĄ
Dana jest A = [aij] Można napisać: 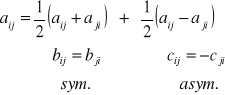
czyli A = B + C
gdzie:
![]()
![]()
MACIERZ TRÓJKĄTNA
Macierz kwadratowa, której elementy położone ponad (lub pod) główną przekątną są równe zeru.
Dolna macierz trójkątna:
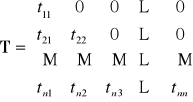
T = [tij] tij= 0 dla j>i
Górna macierz trójkątna:
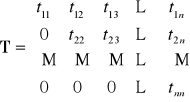
T = [tij] tij= 0 dla i>j
Wyznacznik macierzy trójkątnej: ![]()
ROZKŁAD MACIERZY KWADRATOWEJ NA ILOCZYN DWÓCH MACIERZY TRÓJKĄTNYCH
Dana jest nieosobliwa macierz An x n (det A ≠0)
wtedy: ![]()
L = [lij] - dolna macierz trójkątna
U = [uij] - górna macierz trójkątna
taka, że uii = 1

Inny rozkład:
![]()
![]()
= [lij] - dolna macierz trójkątna taka, że lii = 1
![]()
= [uij] - górna macierz trójkątna

Ogólnie: ![]()
Jeżeli macierz A jest symetryczna, to zachodzi AT = A
Wtedy: ![]()
Ale równocześnie: ![]()
Zatem (z porównania):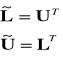
jeżeli A jest symetryczne.
NORMA MACIERZY KWADRATOWEJ
Norma - to miara “wielkości” macierzy. ![]()
Największa suma w bezwzględnych wartości elementów w kolumnie.
Norma Euklidesowa: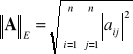
MACIERZ ODWROTNA DO DANEJ MACIERZY
Dana jest macierz kwadratowa An x n nieosobliwa. Macierzą odwrotną do macierzy A jest macierz B spełniająca
warunek: ![]()
tzn. 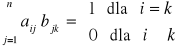
Macierz odwrotną B oznacza się najczęściej przez A-1.
Własności:
(AT)-1=(A-1)T
Jeżeli A jest symetryczna, to A-1 jest również symetryczna.
(A

B)-1 = B-1
A-1(A-1)-1 = A
METODY WYZNACZANIA MACIERZY ODWROTNEJ
Metoda 1: Wykorzystując definicję podwyznacznika (minora) macierzy A:
B = A-1 → ![]()
Metoda 2: Korzystając z rozkładu macierzy A na iloczyn macierzy trójkątnych.
Niech: ![]()
Wtedy: ![]()
WARTOŚCI WŁASNE MACIERZY KWADRATOWEJ
Wartościami własnymi kwadratowej macierzy A są liczby λi będące rozwiązaniami równania wyznacznikowego:
![]()
To równanie nazywamy równaniem charakterystycznym i ma ono postać:
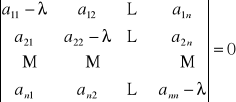
![]()
Wyznaczanie największej co do wartości bezwzględnej wartości własnej:
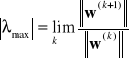
gdzie: ![]()
![]()
- dowolny niezerowy wektor początkowy
![]()
- norma wektora - wart. bezwzględna max. składowej.
UKŁADY LINIOWYCH RÓWNAŃ ALGEBRAICZNYCH
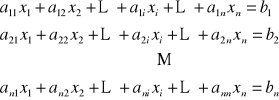
m - liczba równań
n - liczba niewiadomych
m > n - brak rozwiązań
m < n - nieskończenie wiele rozwiązań n-m zmiennych można przyjąć dowolnie
m = n - jedno rozwiązanie (jeżeli det A ≠0)
Typy zagadnień:
Macierze pełne ale nieduże (n<30) - metody dokładne eliminacji.
Macierze rzadkie ale być może duże (n>100) - metody iteracyjne.
Złe uwarunkowanie macierzy:
![]()
Niech: xd - rozwiązanie dokładne, x0 - rozwiązanie przybliżone. Zatem: b - Axd = 0 oraz b - Ax0 = r - wektor reszt r = A(xd - x0) i stąd xd - x0 = A-1rJeżeli niektóre elementy A-1 są bardzo duże, to x0 może znacznie się różnić od xd nawet gdy wektor reszt r jest mały.
To zachodzi gdy detA jest bliski zeru - macierz A jest źle uwarunkowana.
Źródła błędów:
Błędy współczynników A i b.
Błędy zaokrągleń w czasie obliczeń.
Błąd metody.
Metody rozwiązania:
dokładne:

metody iteracyjne:

METODA WYZNACZNIKÓW
A x = b → An x n= [aij] bn x 1= {bi} xn x 1= {xi}
Wyznacznik główny macierzy A: D = det A
Wyznacznik macierzy Aj powstałej z A przez zastąpienie
j -tej kolumny kolumną wyrazów wolnych b: Dj = det Aj
Wzory Cramera:
![]()
Analiza rozwiązań:
D ≠ 0 - układ oznaczony, jedno rozwiązanie.
D = 0 , Dj ≠ 0 - układ sprzeczny, brak rozwiązań.
D = 0 , Dj = 0 - układ jednorodny, wiele rozwiązań.
Wariant eliminacji Gaussa - redukcja Gaussa-Jordana
Kolumnę wyrazów wolnych traktujemy jako dodatkową kolumnę macierzy. Korzystając z tego, że możemy mnożyć wiersze przez liczbę i dodawać do ich wierszy doprowadzamy do tego żeby na głównej przekątnej były same niewiadome a pod nią i nad nią były same zera. Doprowadzi to do tego, że niewiadoma będzie się równała wyrazowi z kolumny wyrazów wolnych.
METODA ![]()
ROZWIĄZANIA UKŁADU RÓWNAŃ
A x = b det A ≠ 0
A = ![]()
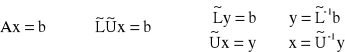
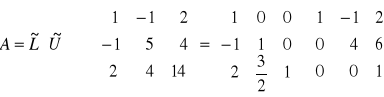
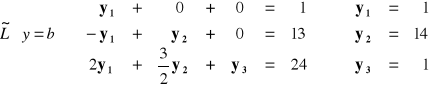
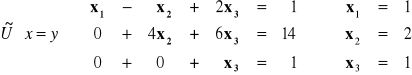
METODY ITERACYJNE
![]()
x(0) - przybliżenie początkowe
x(k+1) = Fk(x(k),x(k-1),. . . . . .,x(k-l))
Fk - funkcja iteracyjna
Zalety:
Mogą być lepsze od metod dokładnych pod względem czasu obliczeń;
Są bardziej ekonomiczne pod względem wykorzystania pamięci komputera;
Nie przekształca się oryginalnych równań - mniejsze błędy zaokrągleń.
Dany jest układ równań: ![]()
![]()
stąd:
![]()
![]()
To sugeruje wzór iteracyjny postaci:
![]()
![]()
Metoda iteracji prostej (Jacobiego):
gdzie C = I - A
tzn. 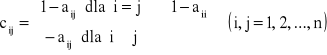
Warunki zbieżności procesu iteracyjnego:
![]()
lub ![]()
Warunek zakończenia procesu iteracyjnego: ![]()
![]()
- założona dokładność
Iteracja prosta Gaussa:
![]()
Z równania “i” wyznaczamy xi:
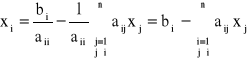
To sugeruje następujący wzór iteracyjny:
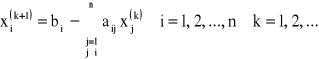
Iteracja prosta polega na tym że wyznaczamy niewiadome.
W zerowej iteracji pod niewiadome podstawimy 0 i obliczamy niewiadome następnej iteracji podstawimy je do równania i obliczamy znowu niewiadome następnej iteracji. Robimy to do momenty gdy różnica między niewiadomą następnej iteracji od poprzedniej będzie mieściła się w granicach błędu.
METODA ITERACJI SEIDLA:
![]()
Metoda Seidla jest podobna do metody prostej Gaussa z tym, że obliczając którąś niewiadomą w danej iteracji wykorzystujemy do liczenia następnej niewiadomej danej iteracji a nie czekamy na obliczenie wszystkich niewiadomych w danej iteracji i dopiero wtedy je wykorzystujemy co robimy w metodzie prostej Gaussa.
METODA NADRELAKSACJI: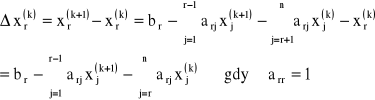
Stąd:
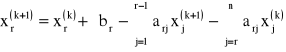
Wprowadzamy wzór zmodyfikowany:
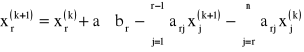
gdzie α - współczynnik nadrelaksacji z zakresu <1,2÷1,45>
WIELOMIANY
Wielomian potęgowy
![]()
Obliczanie wartości wielomianu dla zadanej wartości zmiennej x → schemat Hornera:
![]()
Obliczanie kolejnych pochodnych wielomianu:
![]()
![]()
![]()
![]()
Znajdowanie wielomianu (n-1) stopnia który w punktach ![]()
przyjmuje wartości ![]()
.
![]()
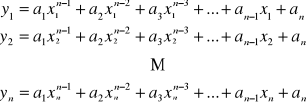
Jest to liniowy układ n równań z n niewiadomymi ![]()
.
![]()
gdzie
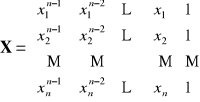
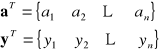
Zatem: ![]()
← współczynniki poszukiwanego wielomianu.
Wielomiany Lagrange'a
Dany jest ciąg wartości: x1 , x2 , x3 , . . . . . , xi , . . . . , xn.
Na tym ciągu tworzy się ciąg wielomianów Lagrange'a , tzn, wielomianów potęgowych stopnia
(n-1) L1(x) , L2(x), . . . , Ln(x) o własności:
![]()
Postać wielomianu Lagrange'a:
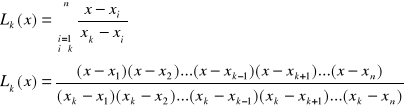
Inna postać wielomianu Lk(x) :
![]()
Współczynniki aki można obliczyć wykorzystując własność: ![]()
Wektor współczynników k-tego wielomianu:
![]()
Macierz współczynników:
![]()
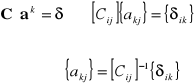
Zastosowanie wielomianów Lagrange'a:
Wielomian , który w zadanych punktach xk osiąga zadane wartości yk (k=1,2, . . . ,n).
![]()
Wielomiany Hermite'a:
Dany jest ciąg punktów: x1, x2, x3, . . . . . ., xn.
Wielomian Hermite'a - wielomian potęgowy stopnia (nm-1) spełniający warunki:
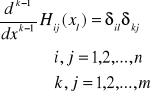
(k-1) pochodna wielomianu Hlk w punkcie x = xl przyjmuje wartość 1 , a w pozostałych punktach wartość 0.
Wszystkie pozostałe pochodne we wszystkich punktach przyjmują wartość 0.
UWAGA: pochodna rzędu zerowego = sama funkcja.
Jeżeli m = 1 tzn. najwyższa pochodna = pochodna zerowa, czyli sama funkcja, to wielomian Hermite'a = wielomian Lagrange'a.
![]()
Zwykle ograniczamy się do m = 2 ograniczamy się do wartości funkcji i jej pierwszej pochodnej.
m = 2
k = 1 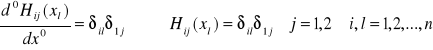
k = 2 ![]()
![]()
czyli
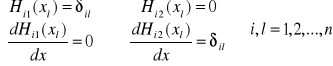
Wielomiany i szeregi Czebyszewa
![]()
Wielomian Czebyszewa k-tego stopnia:
![]()
Wzór rekurencyjny na tworzenie wielomianów:
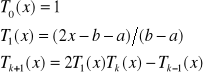
Szereg Czebyszewa: rozwinięcie funkcji w szereg względem wielomianów Czebyszewa :
![]()
Pierwsza pochodna rozwinięcia funkcji w szereg Czebyszewa:
![]()
Pochodne wielomianów Czebyszewa → różniczkowanie wzorów rekurencyjnych określających te wielomiany.
INTERPOLACJA FUNKCJI
Nie jest znana postać funkcji y=f(x) ale znamy jej wartości ![]()
w wybranych punktach xi i=1,2, . . .,n.
![]()
- interpolacja
![]()
- extrapolacja
Interpolacja liniowa
W przedziale ![]()
zawierającym x funkcję ![]()
aproksymujemy prostą ![]()
.
Interpolacja kwadratowa
W przedziale ![]()
zawierającym x funkcję ![]()
aproksymujemy wielomianem 2 stopnia (parabolą) ![]()
METODA KOLOKACJI
Dany jest ciąg punktów ![]()
Poszukiwaną funkcję ![]()
przybliżymy w postaci: ![]()
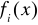
- znane, przyjęte przez nas dowolnie funkcje, które intuicyjnie najlepiej odwzorowują charakter poszukiwanej funkcji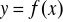
Na przykład, można przyjąć:
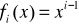
- wielomian potęgowy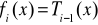
- szereg Czebyszewa
Współczynniki ai wyznaczymy żądając aby poszukiwana funkcja przeszła dokładnie przez wszystkie dane punkty, tzn. aby był spełniony warunek: ![]()
Zatem![]()
Oznaczając
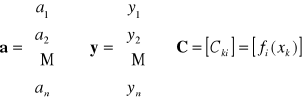
otrzymujemy układ równań liniowych względem a o postaci
![]()
i współczynniki ai wielomianu są określone.
Inny sposób postępowania:
Bezpośrednie wykorzystanie wielomianów Lagrange'a:
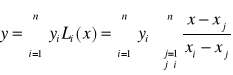
METODA NAJMNIEJSZYCH KWADRATÓW
Dany jest ciąg punktów ![]()
Poszukiwaną funkcję ![]()
przybliżymy w postaci:
![]()
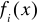
- znane, przyjęte przez nas dowolnie funkcje, które intuicyjnie najlepiej odwzorowują charakter poszukiwanej funkcji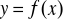
Nie można zastosować metody kolokacji do wyznaczenia ai , gdyż liczba związków typu ![]()
jest większa od liczby niewiadomych.
Przy założonych ai błąd spełnienia k-tego warunku:
![]()
czyli
![]()
Współczynniki ai trzeba dobrać tak, aby sumaryczna miara błędu była najmniejsza.
Błąd sumaryczny (wariancja):
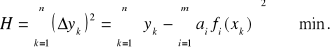
Warunek konieczny minimum: ![]()
Wszystkie pochodne cząstkowe ![]()
są równe zeru w punkcie minimalnym.
Czyli: 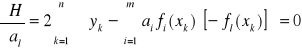
Oznaczmy: 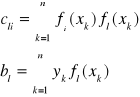
Wtedy: 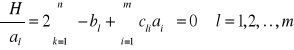
Co prowadzi do układu równań: ![]()
![]()
Miara błędu niezależna od liczby punktów:
Odchylenie standardowe ![]()
RÓŻNICZKOWANIE NUMERYCZNE
Powody:
Zbyt skomplikowana analityczna postać funkcji.
Wartość funkcji znana tylko w punktach.
Metoda I: Przybliżamy daną funkcję wielomianem interpolacyjnym, a następnie wielomian ten różniczkujemy.
Metoda II: Pochodną funkcji zastępujemy ilorazem różnicowym:
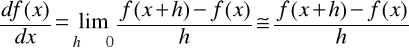
lub inaczej:
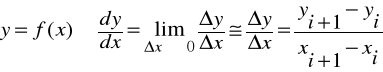
Rodzaje ilorazów różnicowych:
Iloraz zwykły:
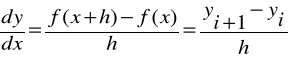
Iloraz wsteczny:
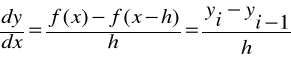
Iloraz centralny:
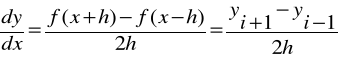
Inaczej:
Ad. 1 f(x) zastępujemy prostą y =a x + b poprowadzoną przez x i x + h. ![]()
Ad. 2 f(x) zastępujemy prostą y = a x + b poprowadzoną przez x-h i x.![]()
Ad. 3 f(x) zastępujemy parabolą y = a x2 + b x +c poprowadzoną przez x-h , x i x+h. ![]()
Pochodne wyższych rzędów:
Iloraz zwykły:
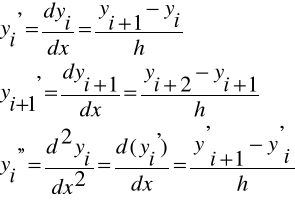
Zatem: 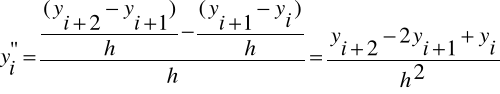
Podobnie: 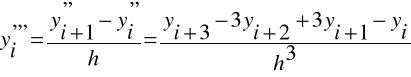
Identycznie obliczamy wyższe pochodne korzystając z ilorazów wstecznych i ilorazów centralnych.
CAŁKOWANIE NUMERYCZNE
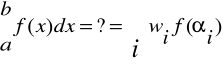
wi - wagi
![]()
- punkty z przedziału <a,b>
Funkcję f(x) aproksymujemy (przybliżamy) wielomianem P(x).
Można przybliżać jednym wielomianem w całym przedziale <a,b> - wzór kwadratur Gaussa.
Można przedział <a,b> podzielić na podprzedziały i w każdym podprzedziale przybliżać różnymi wielomianami tego samego (niskiego) stopnia - wzór trapezów, wzór Simpsona.
Wzór trapezów:
Przedział <a,b> dzielimy na n równych podprzedziałów o długości
h = (b - a)/n.
W każdym podprzedziale f(x) zastępujemy prostą a x + b.
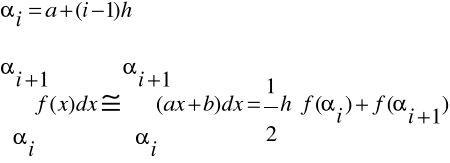
Zatem: 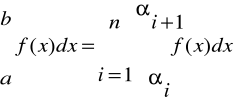
Stąd:
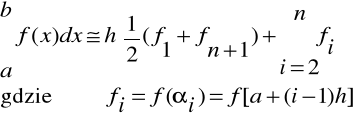
Wzór Simpsona:
Przedział <a,b> dzielimy na n równych podprzedziałów o długości
h = (b - a)/n.
W każdym podprzedziale f(x) zastępujemy parabolą a x2 + b x + c.
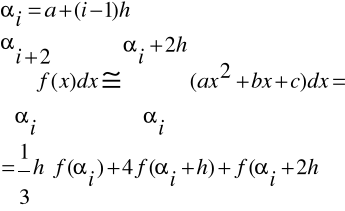
Niech ![]()
Zatem: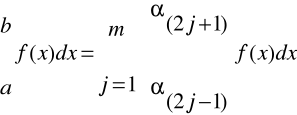
Stąd:
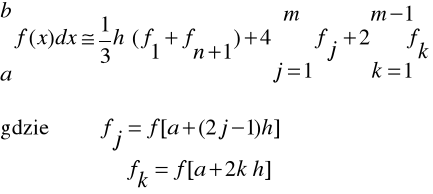
Wyszukiwarka