Metody oceny wartości projektów inwestycyjnych.

Wprowadzenie

Rozwój firmy i zdolność do konkurencyjności zależy od stałego dopływu idei dotyczących nowych technologii i metod obniżania kosztów produkcji. Implikuje to powstanie projektów inwestycyjnych, które oceniane są pod kątem ich efektywności. Istotna część każdego biznes planu to analiza finansowo ekonomiczna. W sposób syntetyczny pokazuje prawdopodobne dochody i wydatki oraz udziela odpowiedzi na pytanie: czy projekt jest opłacalny?. Matematyka finansowa stanowi istotne narzędzie rachunku gospodarczego, jest bowiem ściśle powiązana z rachunkiem wartości w aspekcie dynamicznym. Uwzględnienie dynamicznych własności wartości i kapitału stanowi ważny przejaw współczesnego myślenia ekonomicznego, a podstawową dziedziną zastosowań matematyki finansowej są obliczenia dotyczące stopy zwrotu kapitału zaangażowanego w przedsięwzięcia.

Decyzja o podjęciu inwestycji jest podejmowana w tedy gdy w pewnym sensie "suma" wartości dodatnich, korzyści wynikających z projektu, będzie większa niż, związanych z inwestycją wydatków. Stosowane są różne rodzaje wskaźników efektywności ekonomicznej.

Wszelkie wskaźniki efektywności ekonomicznej można podzielić na:

• statyczne, gdy przyjmuje się, że wartość pieniądza jest taka sama niezależnie od momentu pozyskania tej kwoty,

• dynamiczne, gdy podstawą do obliczeń są wartości dyskontowane.

Metody oceny wartości projektów inwestycyjnych zostały przedstawione na przykładzie fikcyjnych inwestycji. Przedstawione dane wyjściowe nie należy analizować pod względem kompletności, ponieważ mają jedynie na celu pokazanie technik tworzenia podstaw do podjęcia decyzji ekonomicznych.

Tradycyjny wskaźnik efektywności ekonomicznej

Najczęściej spotykanym statycznym kryterium oceny efektywności ekonomicznej jest prosty czas wzrostu nakładów SPBT. Jest on definiowany jako czas potrzebny do odzyskania nakładów inwestycyjnych poniesionych na realizację danego przedsięwzięcia. Jest liczony od momentu uruchomienia inwestycji do chwili, gdy suma korzyści brutto uzyskanych w wyniku realizacji inwestycji zrównoważy poniesione nakłady. W przypadku, gdy roczne korzyści brutto Zi są stałe wartość SPBT można obliczyć z wyrażenia

SPBT = - I/Zi

gdzie I oznacza wysokość poniesionych nakładów inwestycyjnych. Znak minus wynika z przyjętej konwencji gdzie wydatki określa się w postaci wartości ujemnych.

Wskaźnik ten cechuje duża poglądowość i prostota. Podstawową jego wadą jest to, że nie uwzględnia on całego okresu funkcjonowania przedsięwzięcia, lecz skupia uwagę inwestora na jego fazie początkowej. Służy zazwyczaj do wstępnej oceny efektywności przedsięwzięcia dając poglądową ocenę czasu zamrożenia aktywów finansowych z inwestycji.

Dynamiczne wskaźniki efektywności ekonomicznej.

Stosuje się cztery zasadnicze metody oceny wartości projektów inwestycyjnych na podstawie których podejmuje się decyzje o ich realizacji:

• okres spłaty,

• wartość zaktualizowana netto (NPV)

• wewnętrzna stopa zwrotu (IRR),

• zmodyfikowana wewnętrzna stopa zwrotu (MIRR)

Czynnik czasu

Strumienie środków finansowych inwestowanych (wypływających) i otrzymywanych dochodów (wpływających) przyjmują różne wartości w zależności od okresu ich powstania. Strumienie pieniężne w różnych okresach czasu (latach) są dyskontowane na moment rozpoczęcia realizacji projektu. Dyskontowanie polega na ustaleniu wartości obecnej przyszłych przepływów środków pieniężnych w okresie trwania inwestycji, jest to procedura prowadząca do porównywalności wartości pieniężnych pochodzących z różnych momentów czasu. Jeżeli koszt uzyskania kapitału jest określony, to wartość czynnika dyskontowego d_t oblicz się wg wzoru:

d_t =

dla t = 0,1,2,.....,n.

gdzie :

i - koszt kapitału projektu (stopa dyskontowa),

n - okres realizacji i eksploatacji inwestycji, lata.

Wartości zdyskontowane oblicza się na podstawie zależności:

CF _t · d_t =

dla t = 0,1,2,....,n.

gdzie :

CF_t - oczekiwany przepływ środków pieniężnych w okresie t,

pozostałe oznaczenia jak wyżej.

Przykład liczbowy 1.

Firma rozważa możliwość realizacji jednego z dwóch projektów inwestycyjnych X , Y. Nakłady inwestycyjne w obu przypadkach są jednakowe i wynoszą 150 tys. zł. Koszt kapitału w postaci przykładowo oferowanej przez bank stopy dyskontowej wynosi i = 20%. Okres eksploatacji oraz dochody w postaci strumieni środków pieniężnych przedstawia tabela 1.

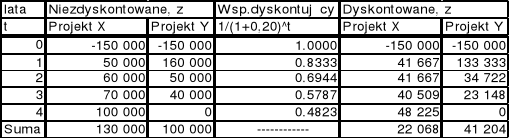
Tabela 1. Porównanie wartości niezdyskontowanych i dyskontowanych strumieni pieniężnych.

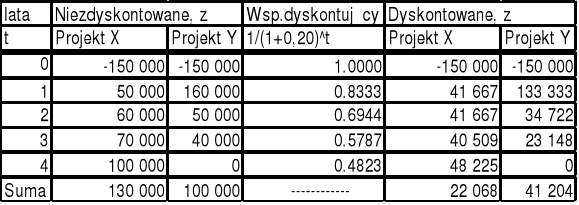
Porównując strumienie niezdyskontowane i dyskontowane otrzymuje się sprzeczne informacje dotyczące wartości projektów inwestycyjnych. W pierwszym przypadku bardziej opłacalna jest inwestycja dotycząca projektu X, w drugim zaś projektu Y.

Bezpośrednia suma strumieni pieniężnych nie uwzględnia zmiennej wartości pieniądza w czasie, którą reprezentuje koszt kapitału w wysokości i=20%. Każdy kapitał charakteryzuje się kosztem jego pozyskania lub też oczekiwanym dochodem w przypadku jego zainwestowania.

Okres spłaty

Okres spłaty określa się jako oczekiwana liczbę lat niezbędnych dla odzyskania zainwestowanych nakładów.

Obliczenia prowadzi się poprzez kumulowanie strumieni pieniężnych, dodając do ujemnej wartości "długu na nakłady inwestycyjne" wpływy w kolejnych latach, aż do momentu uzyskania wartości dodatniej. Następuje to w roku spłaty kredytu.

Aby ustalić dokładną wartość okresu spłaty dzieli się należności w ostatnim roku przez wpływ na koniec tego roku i dodając liczbę lat na rok przed zakończeniem spłaty.

s = s₁ +

gdzie:

s- okres spłaty w latach,

s₁ - liczba lat na rok przed zakończeniem spłaty,

s₂ - nie pokryty koszt inwestycji na początku roku ostatniej spłaty,

s₃ - wpływy środków pieniężnych w ciągu roku ostatniej spłaty.

Kryterium oceny jest okres spłaty, im krótszy tym lepszy. Przykład liczbowy przedstawiają rysunki 1 i 2 gdzie dane liczbowe zaczerpnięto z przykładu 1 (tab. 1.)

Jeżeli projekty wzajemnie się wykluczają, to wyżej ceniony jest projekt charakteryzujący się krótszym okresem spłaty (projekt Y). Pod pojęciem wzajemnie wykluczające rozumie się odrzucenie jednego projektu w przypadku przyjęcia drugiego. Na przykład, zainstalowanie taśmociągu wyklucza transport samochodami. Jeżeli nakłady inwestycyjne są realizowane jednorazowo w momencie t=0, to okres spłaty jest ustalony zgodnie z następującymi zależnościami:

Rok "k" w którym nastąpi sprawdzenie poniższej zależności, licząc od t=1, jest rokiem spłaty kredytu:

CF₀ +

gdzie:

CF₀ - nakład inwestycyjny na początku realizacji projektu

wartość ujemna t=0,

CF_t - dochód w kolejnym roku inwestowania t = 1,2,....,k ,

k - rok w którym suma przychodów przekroczy pierwszy raz wartość zainwestowanych nakładów,

Okres spłaty "s" ustala się zgodnie z poniższa zależnością:

s = (k - 1) +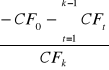

pozostałe oznaczenia jak wyżej.

Okres spłaty stosowany jest jako wskaźnik ryzykowności projektu.

Przykład liczbowy 2.

Projekt X: okres spłaty

Skumulowane

wartości :

s(x) = 2+ 40 / 70 = 2,57 lat

Projekt Y: okres spłaty

Skumulowane

wartości:

s (y) = = 150/160 = 0,94 lat

Rys. 1. Przepływ skumulowanych strumieni pieniężnych przy określeniu okresu spłaty.

Projekt X: okres zdyskontowanej spłaty

Skumulowana

wartość:

s_d(x) = 3 + (26,1/48,2) = 3,54 lat

Projekt Y: okres zdyskontowanej spłaty

s_d(y) = 1 + (16,7/34,7) = 1,48 lat

Rys.2. Przepływ zdyskontowanych, kumulowanych strumieni przy określeniu okresu spłaty.

Wartość zaktualizowana netto (NPV).

Wartość zaktualizowana netto jest metodą klasyfikującą projekty inwestycyjne na podstawie wartości bieżących przyszłych przepływów środków pieniężnych netto. NPV jest definiowane jako wartość uzyskana przez dyskontowanie, przy stałej stopie i oddzielenie dla każdego okresu, różnic między wpływami i wydatkami pieniężnymi, które powstają w okresie trwania projektu. Wartości zaktualizowane sald pieniężnych poszczególnych okresów są dodawane dla otrzymania NPV dla projektu. Stopa dyskonta, albo stopa graniczna powinna być równa stopie oprocentowania kredytów długookresowych albo stopie procentowej płaconej przez kredytobiorcę. Jeżeli obliczona wartość NPV jest dodatnia, efektywność inwestycji jest większa od stopy granicznej. Projekt z dodatnią NPV należy uznać za możliwy do przyjęcia, pod warunkiem dodania niezbędnego marginesu błędu dla uwzględnienia skutków niepewności i ryzyka. Jeżeli NPV jest ujemne projekt powinien być odrzucony. Jeżeli projekty są wzajemnie wykluczające, należy wybrać projekt z wyższym NPV.

Zastosowanie tej koncepcji polega na następującym postępowaniu:

NPV = CF₀ +
+
+ ...+
=

gdzie:

CF_t - oczekiwany przepływ środków pieniężnych w okresie t,

i - koszt kapitału projektu inwestycyjnego, stopa dyskonta.

Przykład liczbowy 3.

Firma budowlana biorąca udział w przetargu na roboty budowlane rozpatruje opłacalność przygotowanej oferty. Uwzględnia między innymi ceny rynkowe robót budowlanych, koszty zagospodarowania placu budowy, koszty ogólne budowy i zarządu oraz przewidywany strumień dochodów. Prognozowane przepływy pieniężne w tys. zł. zawierające oczekiwaną w tym okresie inflację przedstawia poniższy rysunek.

i = 15%

-400,0

-147,8

151,2

197,3

200,1

0,8 tys. zł.

Rys. 3. wartość zaktualizowana netto NPV)

Stopę procentową reprezentującą koszt zainwestowanego kapitału przyjęto w wysokości 15%. Podstawiając ww. dane do wzoru , otrzymuje się:

NPV = -400 -
+
+
+
= 0,8 tys. zł.

Jak wynika z przeprowadzonej analizy, wygranie przetargu przy założonym poziomie cen robót budowlanych prowadzi do dochodu netto, będącego na granicy opłacalności przedsięwzięcia. Przedstawione w przykładzie nr 1 porównanie wariantów inwestycyjnych poprzez zdyskontowanie strumieni pieniężnych sprowadza się właśnie do metody wartości zaktualizowanej netto (NPV)

Wewnętrzna stopa zwrotu (IRR)

Metoda oceny wartości inwestycji, polega na znalezieniu takiej stopy procentowej IRR, która zrównuje wartość zaktualizowaną przyszłych dochodów z kosztem inwestycji.

IRR to stopa dyskontowa, przy której wartość zaktualizowana wydatków pieniężnych równa się wartości zaktualizowanej wpływów pieniężnych. Inaczej, to stopa dyskontowa przy której zaktualizowana wartość efektów równa się wartości nakładów inwestycyjnych, a NPV=0. IRR może być interpretowana jako roczna pieniężna stopa zwrotu netto (czyli w znaczeniu finansowym dochód albo zysk) zainwestowanego kapitału albo też interpretowana jako najwyższa stopa oprocentowania kredytów w warunkach po opodatkowaniu, po której możliwe jest zgromadzenie środków dla projektu. Metoda IRR musi być stosowana ze szczególną ostrożnością w przypadkach, kiedy znaczne ujemne salda pieniężne powtarzają się w późniejszych okresach projektu.

Odpowiada na pytanie: przy jakiej stopie procentowej IRR nastąpi zrównanie przyszłych wpływów z kosztami projektowanej inwestycji ?

CF₀ +
+
+ ... +
= 0

= 0

Interpretację graficzną powyższej zależności przedstawia rys. 4.

i = ?%

0,00 tys. zł.

Rys.4. Interpretacja graficzna ocena wartości inwestycji metoda wewnętrznej stopy zwrotu.

-1000 +
+
+
+
= 0

Obliczenia odręcznie, bez kalkulatora finansowego lub komputera, przeprowadza się metoda prób i błędów, podstawiając próbne wartości IRR, aż do momentu kiedy obie strony równania będą równe zero. Przykładowa wartość IRR z zagadnienia przedstawionego na rys. 4 wynosi 14,5% i jest granicznym kosztem kapitału przy którym nie ponosi się strat. Wyższa stopa procentowa powoduje ujemne wartości ocenianego projektu inwestycyjnego.

Przykład liczbowy 4.

Dla danych z przykładu nr 1 obliczyć IRR, która doprowadzi do zrównania wydatków inwestycyjnych ze strumieniem dochodów pieniężnych. Dla projektu X wyliczony dochód z inwestycji przy i=20% wynosił 22,068 tys. zł. Szukając dochodu 0 przyjmując metodą prób i błędów stopy procentowe i=25% oraz i=30%. Obliczenia dla projektu X przedstawia tabela 2. Analogicznie można ustalić wartości wewnętrznej stopy zwrotu dla projektu Y z przykładu 1.

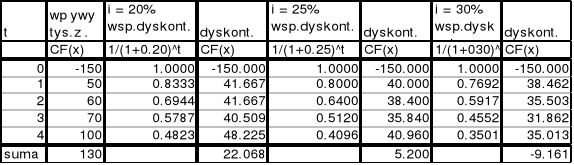
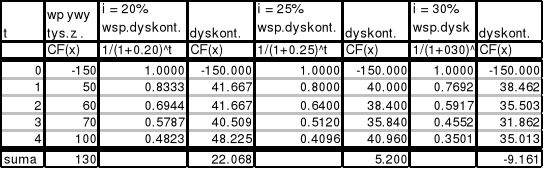
Tabela 2. Wewnętrzna stopa zwrotu projektu X.

Dla danych liczbowych projektu X w tys. zł warunek ma postać

150 =
+
+
+

Na podstawie powyższego równania można stwierdzić, że przy stopie dyskontowej równej 26,72% wydatki równe są korzyściom i przyjmując taki projekt do realizacji inwestor ani nie traci ani nie zarabia. Właśnie o tym informuje warunek NPV=0.

Jeśli porówna się wartości kosztu kapitału z wewnętrzną stopą zwrotu to otrzyma się informację o tym, czy projekt jest korzystny dla firmy, czy nie. W metodzie tej ocena wartości projektów inwestycyjnych sprowadza się do porównania wewnętrznej stopy zwrotu z ceną rynkową kapitału. Jeżeli zachodzi warunek:

IRR>CC, to ocena projektu jest pozytywna, CC - koszt kapitału,

Przyjęcie projektu przyczyni się do zwrotu poniesionych nakładów a także powstanie nadwyżka o której informuje różnica pomiędzy IRR a CC. Dla projektu X koszt kapitału wynosi 20%, podczas gdy wewnętrzna stopa zwrotu równa się 26,72%. Firma realizując ten projekt zwróci inwestorom całość poniesionych nakładów (100%), koszt kapitału (20%), a ponad to pozostanie 6,72% w postaci nadwyżki ponad poniesione obciążenia finansowe związane z uruchomieniem i eksploatacją projektu.

Zmodyfikowana wewnętrzna stopa zwrotu (MIRR).

W ocenie efektywności projektów inwestycyjnych istotne znaczenie ma problematyka uwzględniania przewidywanej stopy reinwestycji. Stopa reinwestycji - to stopa procentowa informująca o poziomie rentowności osiąganej z tytułu bieżącego inwestowania osiąganych przez firmę dodatnich przepływów pieniężnych (zysków). Stopa zwrotu uzyskiwana z tytułu reinwestycji jest zazwyczaj różna od wewnętrznej stopy zwrotu projektu. Stąd też nosi nazwę zmodyfikowanej wewnętrznej stopy zwrotu.

MIRR to taka wartość stopy dyskontowej, która zrównuje zaktualizowaną wartość końcową dodatnich przepływów pieniężnych z wartością bieżącą ujemnych przepływów pieniężnych, czyli:

=

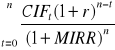
gdzie:

COF_t - ujemny przepływ pieniężny w roku t,

CIF_t - dodatnie przepływy pieniężne w roku t,

r - stopa dyskontowa stosowana przez inwestora (koszt kapitału),

n - okres obliczeniowy (w latach), będący sumą okresu budowy (ponoszenia) nakładów i okresu osiągania dodatnich przepływów pieniężnych

MIRR - wewnętrzna stopa zwrotu uwzględniająca przewidywaną stopę reinwestycji

Lewa strona równania określa bieżącą (zaktualizowaną) wartość ujemnych przepływów kapitałowych, obliczoną przy stopie dyskontowej równej kosztowi kapitału inwestora. Licznik prawej strony równości określa natomiast wartość przyszłą (na koniec ostatniego roku obliczeniowego) dodatnich przepływów pieniężnych otrzymaną przy założeniu, że będą one reinwestowane po koszcie kapitału.

Projekty inwestycyjny przyjmuje się do realizacji, gdy zmodyfikowana wewnętrzna stopa zwrotu przewyższa koszt kapitału, czyli MIRR > r. W przypadku stosowania zmodyfikowanej stopy zwrotu do wyboru jednego spośród kilku dostępnych projektów wybiera się ten, którego wartość MIRR jest największa. Oczywistym jest, że wyboru należy dokonywać ze zbioru tych projektów, których wartość MIRR jest większa od kosztu kapitału.

Wnioski końcowe.

Praktycznie zawsze projekty inwestycyjne związane są w większej lub w mniejszej mierze z ryzykiem i niepewnością, ponieważ odnoszą się zawsze do przyszłości. Ryzyko dotyczy sytuacji, w których prawdopodobieństwo zaistnienia zdarzeń w przyszłości jest określona na podstawie dostępnej wiedzy z przeszłości. Niepewność dotyczy sytuacji, w których prawdopodobieństwo zaistnienia zdarzeń w przyszłości jest określane na podstawie subiektywnych sytuacji. Należy przy tym zawsze pamiętać, że analiza nie daje pewności, że przedsięwzięcie zakończy się powodzeniem. Pozwala jednak zmniejszyć ryzyko niepowodzenia projektu, ale nie jest go w stanie wyeliminować. Mimo to nie znaleziono lepszego sposobu, który przed zainwestowaniem kapitału pozwalał by inwestorowi sprawdzić jakie wyniki (zysku lub straty) przyniesie dane przedsięwzięcie na rynku.

Bibliografia:

1. "Finanse i firma"

Edward W. Dawis, John Pointon

Warszawa 1997

2. "Matematyka i statystyka finansowa"

Praca zbiorowa pod redakcją Edwarda Nowaka

Warszawa 1994

3. "Zastosowanie matematyki finansowej"

M. Dobija, E. Smaga

Kraków 1993

t =4

t = 3

t = 2

t = 1

100

70,0

60,0

-150,0

50,0

t = 0

130,0

30,0

-40

-100,0

-150,0

t =4

t = 3

t = 2

t = 1

0

40

50,0

-150,0

160,0

t = 0

200,0

200,0

160

10,0

-150,0

t =4

t = 3

t = 2

t = 1

48,2

40,5

41,7

-150,0

41,7

t = 0

-26,1

22,1

-66,6

-108,30

-150,0

t =4

t = 3

t = 2

t = 1

0

23,1

34,7

-150,0

133,3

t = 0

41,2

41,2

18,1

-16,7

-150,0

lata

t = 4

t = 3

t = 1

t = 2

t = 0

200

tys. zł

350

300

-170

-400

t = 1

t = 2

t = 3

t =4

- 1000

500

100

300

100

t = 0

1000

---