Nr ćwiczenia: 102 |
Data:
21.03.2014 |
Imię i nazwisko: Garczyński Oskar Gajewski Kamil |
Wydział Fizyki Technicznej |
Semestr: |
Grupa: 2 |
|
Prowadzący: |
Przygotowanie:
|
Wykonanie:
|
Ocena: |
|||
Temat ćwiczenia: Wyznaczanie modułu sztywności metodą dynamiczną.
Podstawy teoretyczne
Wyznaczenie moduł sztywności można dokonać stosując metodę statyczną lub dynamiczną. Metoda statyczna przeznaczona jest dla cienkich prętów i drutów a dynamiczna dla znacznych przekrojów.
W ćwiczeniu wykorzystamy metodę dynamiczną gdyż badany drut ma niewielki przekrój. Jest on swym górnym końcem przymocowany do nieruchomego uchwytu, zaś na dolnym przymocowany jest wibrator. Wibrator składa się z dwóch skrzyżowanych płaskowników na których są przymocowane kołki umożliwiające nakładania obciążeń.
![]()
Skręcając wibrator o pewien kąt powodujemy wystąpienie w drucie momentu sił sprężystości. Działający moment stara się przywrócić stan równowagi. Zwolniony wibrator zacznie wykonywać ruch drgający czyli harmoniczny o okresie
gdzie: I- moment bezwładności, D - moment kierujący.
![]()
Moment kierujący wyznaczamy z zależności
![]()
Wyznaczenie momentu bezwładności nieobciążonego wibratora jest trudne, dlatego staramy się weliminować tę wielkość poprzez umieszczenie tzw. obciążenia wstępnego. Wówczas moment bezwładności zwiększy się o I1, a wzór przyjmie postać
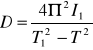
Przekształcając powyższe zależności można się pozbyć I a tym samym wyznaczyć moment kierujący który przedstawia poniższy wzór
![]()
Ostateczne równanie modułu skręcenia przyjmuje postać
gdzie: l - długość drutu, r - promień drutu, T - okres drgań wibratora nieobciążonego lub obciążonego wstępnie, T1 - okres drgań wibratora obciążonego znanymi masami.
Dodatkowy moment bezwładności można uzyskać poprzez nakładanie walców (obciążeń) o znanych masach na odpowiednie kołki. Znając odległości walców od osi wibratora d oraz ilość walców N, a także ich masę zgodnie z twierdzeniem o osiach równoległych Steinera można wyznaczyć moment bezwładności układu zgodnie z zależnością:
I1=NI0+Nmd2
gdzie: I0 - moment bezwładności pojedynczego walca względem jego osi symetrii.
Wyniki pomiarów
Długość drutu: 160 ± 0,1 [cm]
Średnica drutu (d): 0,99 ± 0,01 [mm]
Waga [g] +-1g |
Δm |
Średnica [mm] +-1mm |
Δd |
Średnia arytmetyczna średnicy |
Średnia arytmetyczna wagi |
Odchylenie standardowe Średniej arytm. |
94 |
0 |
31,8 |
0,025 |
31,775 mm |
0,094 kg |
Waga: 0,405144
Średnica: 0,0664295
|
91 |
3 |
31,2 |
0,575 |
|
|
|
95 |
1 |
32,0 |
0,225 |
|
|
|
93 |
1 |
32,0 |
0,225 |
|
|
|
95 |
1 |
31,7 |
0,075 |
|
|
|
93 |
1 |
31,8 |
0,025 |
|
|
|
96 |
2 |
31,9 |
0,125 |
|
|
|
94 |
0 |
32,0 |
0,225 |
|
|
|
92 |
2 |
31,6 |
0,175 |
|
|
|
94 |
0 |
31,8 |
0,025 |
|
|
|
94 |
0 |
31,6 |
0,175 |
|
|
|
95 |
1 |
31,9 |
0,125 |
|
|
|
Okres drgań T0 = 4,21s
Odległości kołków wibratora od jego środka:
d1= 43mm
d2= 92 mm
d3= 143 mm
Wyznaczanie okresu wahań obciążonego wibratora dla kilku rozkładów mas:
(10 okresów)
A) odważniki nr 1,2,3,4 - 1 minuta 30 sekund= 90s
B) odważniki nr 1,5,2,6,3,7,4,8 - 1 minuta 43 sekundy=103s
C) odważniki (wszystkie zawieszone) - 1 minuta 48 sekund=108s
Średni przybliżony czas 1 okresu obciążonego wibratora = 10s.
Obliczenia
Rozkład mas A
IA= (1/2* 0,094*(0,0159)^2) +(1/2* 0,091*(0,0156)^2)+ (1/2* 0,095*(0,016)^2)+ (1/2* 0,093*(0,016)^2)= 0,00004701895 [kg*m2]
I= 4*0,09325*(0,143)2= 0,007627477
I1=0,00004701895 + 0,007627477 = 0,00767449595 [kg*m2]
Rozkład mas B
IB=0,00004701895+ (1/2* 0,095*(0,01585)^2) +(1/2* 0,093*(0,0159)^2)+ (1/2* 0,096*(0,01595)^2)+ (1/2* 0,094*(0,016)^2)=0,00009495288375 [kg*m2]
I2=0,00009495288375+0,007627477+4*0,09450*(0,092)2= 0,01092182188375 [kg*m2]
Rozkład mas C
IC=0,00009495288375+ (1/2* 0,092*(0,0158)^2) +(1/2* 0,094*(0,0159)^2)+ (1/2* 0,094*(0,0158)^2)+ (1/2* 0,095*(0,01595)^2)= 0,0001421355925 [kg*m2]
I3= 0,0001421355925+0,007627477+0,003199392+4*0,09375*(0,043)2=0,0116623795925 [kg*m2]
Średni błąd ΔI
Δm=1g=0,001kg
Δd=0,1cm=0,001m
ΔR=0,1cm= 0,001m
gdzie R- promień walca
d- średnica walca
ΔI= Δm (R2/2 + d2) + m(R ΔR + 2d Δd)= 0,000 008602981953 [kg*m2]
Moduł sztywności
G1= 75564267815,38462 [N*m-2*rad-1]
G2= 83613307647,93905 [N*m-2*rad-1]
G3= 71426188279,12533 [N*m-2*rad-1]
Ostatecznie:
I= 0,001009 ±0,000009 kg*m2
Średnia arytmetyczna modułu sztywności
![]()
= 7,6867921247483*1010[N*m-2*rad-1]
![]()
≈7,69*1010[N*m-2*rad-1]
Średnia arytmetyczna masy walców
= 93.83333 [g]
Odchylenie standardowe średniej średnicy walców
= sqrt(1/(12-1)•((31.8-31.775)² +(31.2-31.775)² +(32-31.775)² +(32-31.775)² +(31.7-31.775)² +(31.8-31.775)² +(31.9-31.775)² +(32-31.775)²+(31.6-31.775)² +(31.8-31.775)² +(31.6-31.775)² +(31.9-31.775)²)) =
=sqrt(1/11•((0.00063)+(0.33062)+(0.05063)+(0.05063)+(0.00562)+(0.00063)+(0.01563)+(0.05063)+(0.03062)+(0.00063)+(0.03062)+(0.01563))=
= sqrt(0.05295) ≈ 0.23012
0.23012/3,46410=0,06643
Odchylenie standardowe masy walców
sqrt(1/(12-1)•((94-93.83333)²+(91-93.83333)²+(95-93.83333)²+(93-93.83333)²+(95- 93.83333)²+(93-93.83333)²+(96-93.83333)²+(94-93.83333)²+(92-93.83333)²+(94-93.83333)²+(94-93.83333)²+(95-93.83333)²)) =
=sqrt(1/11•((0.02778)+(8.02776)+(1.36112)+(0.69444)+(1.36112)+(0.69444)+(4.69446)+(0.02778)+(3.3611)+(0.02778)+(0.02778)+(1.36112))
= sqrt(1.9697) ≈ 1.40346
1.40346/3,46410=0,40514
Odchylenie standardowe modułu sztywności
sqrt(1/(3-1)•((75564267815.38461-76867921247.483)²+(83613307647.93906-76867921247.483)²+(71426188279.12534-76867921247.483)²))
= sqrt(1/2•((1699512271021908000)+(45500237691457490000)+(29612457698910736000))
= sqrt(38406103830695070000) ≈ 6197265835.08365
6197265835.08365/1,73205= 3577994766,36567 (≈3,6*109)
Dyskusja błędów
W trakcie wykonywania doświadczenia pojawiły się błędy przypadkowe, których nie dało się uniknąć. Konieczne było zastosowanie stopera a dokładność pomiaru przy jego użyciu i przy uwzględnieniu czynnika ludzkiego była dość niska w porównaniu np. do pomiaru przy użycia czujnika fotoelektrycznego. Duży wpływ miał również błąd pomiaru średnicy druta. Nie bez znaczenia były także różnice w wychylaniu wibratora co powodowało otrzymanie niedokładnych okresów drgań.
Wnioski
Otrzymana średnia wartość modułu skręcania (7.69*1010) dla stali jest nieznacznie inna niż podawana przez tablice fizyczne(G![]()
). Różnica ta spowodowana jest błędami pomiarowymi.
Moment bezwładności układu jest sumą poszczególnych momentów bezwładności walców w układzie.
Wzrasta on proporcjonalnie do sumy ich mas i w zależności od odległości od osi obrotu.
![]()
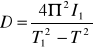
![]()
Wyszukiwarka