1.Skład paliw.
-substancje palne: węgiel , wodór, siarka,
-balast; popiół , woda (CaSO4,SiO2)
C+H+S+O+N+W+A=100%
2.Stany węgla.
a) roboczy
CR+HR+SR+OR+NR+WR+AR=100%
WR=Wn+WP
Wn- wilgotność higroskopijna
Wp- wilgotność przemijająca
b) analityczny
Ca+Ha+Sa+Oa+Na+Wa+Aa= 100%
Wa=Wn
c) suchy
Cs+Hs+Ss+Os+Ns+As= 100%
Siarka w węglu występuje w 3 postaciach (2 palne i 1 niepalna ). Siarka niepalna znajduje się w popiele.
Ss=S0+Spir
S0 - siarka organiczna,
Spir - siarka pirytowa
Sc=S0+Spir+SSO4
Sp= S0+Spir
Sp - siarka palna
- substancja palna
Cp+Hp+Sp+Op+Np= 100%
Sp=Sp0+Sppir
- substancja organiczna
Co+Ho+So+Oo+No= 100%
So=So
3.Skład popiołu.
- popiół wewnętrzny - pozostałości nieorganiczne z surowców z których powstał węgiel,
- popiół zewnętrzny - zanieczyszczenia z pokładu dostające się podczas tworzenia tego popiołu.
Skład chemiczny:
SiO2, Al2O3, CaO, MgO, TiO2, K2O, NO2, CaSO4, Fe2O3, od składu chemicznego zależy temp. Topnienia popiołu.
4.Zawartość części lotnych.
Jest podstawą klasyfikacji węgla. Węgle o wysokiej zawartości części lotnych to węgle energetyczne, węgle o małej zawartości to węgle koksownicze. Zawartość części lotnych bada się przez odgazowanie próbki.
Zawartość części lotnych w paliwach:
drewno-71%, torf-60-70%, węgiel brunatny-44-60%, węgiel kamienny-10-44%, antracyt-2-10%.
5.Skład paliw ciekłych.
|
C |
H |
S |
A |
benzyna |
85 |
15 |
0,015 |
0 |
nafta |
86 |
14 |
0,015 |
0,0005 |
Olej nap. |
87 |
13 |
0,1 |
0,002 |
mazut |
88 |
11 |
0,2-0,35 |
O,02 |
6.Paliwa gazowe.
- gaz ziemny wysoko metanowy ok. 94% zaw. metalu,
- gazy sztuczne powstające w procesie zagazowania.
W składzie będziemy uwzględniać max. Zawartości danego składnika.
- składniki palne CO+H2+CH4+C2H6+C3H8+C4H10+C5H12+C6H14+HsS
+C2H2+C2H4+C3H6+C4H8+C5H10
- składniki niepalne
CO2+SO2+O2+N2+He
W procesach spalania udział bierze też powietrze:
O2- 78,084%
N2- 20,946%
Ar - 0,97%
7.Obliczanie zapotrzebowania powietrza do spalania paliw stałych i ciekłych.
a) reakcje spalania węgla :
C + O2 CO2
1 kmol C + 1 kmol O2 1 kmol CO2
12,011 kg C + 32 kg O2 44,011 kg CO2
b) spalanie wodoru
H2 + ˝ O2 H2O
1 kmol H2 + ˝ kmol O2 1 kmol H2O
2 kg H2 + 16 kg O2 18 kg H2O
C+H+S+O+N+W+A = 100%
n'c = C/100*12,01 [kmol H/kg paliwa]
n'H2= H/100*2,016[kmol H/kg paliwa]
n'S2= S/100*32,064[kmol S/kg paliwa]
n'O2= O/100*32[kmol O/kg paliwa]
n'N2= N/100*28,014[kmol N/kg paliwa]
n'H2O= W/100*18,016[kmol H20/kg paliwa]
8.Kilomolowe zapotrzebowanie tlenu do spalania.
Potrzeba tyle tlenu aby spalić węgiel wodór i siarkę.
nO2t = nc +½n'H2 + n'S - n'O2 [kmol O2/kg paliwa]
t - teoretycznie
n'CO= CO/100*22,4136 [kmol CO/kg paliwa]
n'H2= H2/100*22,4136 [kmol H2/kg paliwa]
n'CH4= CH4/100*22,4136 [kmol CH4/kg paliwa]
nO2t= 1/100*22,4136[0,5(CO + H2) + ∑(1,5n + 0,5)CnH2n+2 +∑1,5n*CnH2n+ 1,5 H2S + 2,5C2H2 - O2] [kmol O2/Nm3g]
VO2t=0,01[0,5(CO+H2)+∑(1,5n+0,5)CnH2n+2+∑1,5n*CnH2n+1,5H2S + 2,5C2H2 - O2] [Nm3O2/Nm3g]
Vpow t=1/100*0,209436[0,5(CO + H2) + ∑(1,5n + 0,5)CnH2n+2 +∑1,5n*CnH2n+ 1,5 H2S + 2,5C2H2 - O2][kmol pow./Nm3g]
Vpow.= λ/100*0,209436[0,5(CO + H2) + ∑(1,5n + 0,5)CnH2n+2 +∑1,5n*CnH2n+ 1,5 H2S + 2,5C2H2] [Nm3pow./Nm3g]
9.Wydajność wentylatora powietrza przy kotle.
Vpow.= Q*λ/100*0,209436[0,5(CO + H2) + ∑(1,5n + 0,5)CnH2n+2 +∑1,5n*CnH2n+ 1,5 H2S + 2,5C2H2] [Nm3pow./s]
Przy ogrzanym powietrzu:
Vpow.= Q*λ/100*0,209436[0,5(CO + H2) + ∑(1,5n + 0,5)CnH2n+2 +∑1,5n*CnH2n+ 1,5 H2S + 2,5C2H2]*[(273,15+ tp)/273,15)][m3pow./s]
Q[Nm3g/s]
10.Obliczanie objętości i składu spalin przy spalniu zupełnym i całkowitym paliw ciekłych i stałych.
Spalanie jest zupełne jeżeli w składzie spalin nie ma produktów niezupełnego spalania (CO). Spalanie jest całkowite jeżeli w składzie popiołu nie ma produktów palnych.
Jeżeli spalanie jest zupełne i całkowite to:
n''CO2= n'c ('' odnosi się do produktów spalania
n''sw= n''CO2 +n''SO2+n''H2O+n''O2+n''N2 (spaliny wilgotne)
n''ss= n''CO2 +n''SO2+n''O2+n''N2 (spaliny suche).
n''sw= n''CO2 +n''SO2+n''H2O+n''O2+n''H2
n''CO2=n'c
n''SO2=n'S
n''H2O=n'N2+n'H2O+x*[(nO2t *λ)/0,20946)] (ze spalonego wodoru z wilgoci paliwa z wilgoci O2)
x=n''H2O/npow.
n''N2=n'N2+(0,79054/0,209446)nO2t
n''O2=(λ-1)nO2t
n''sw= n'C +n'S+n'H+n'N2+n'H2O+(1+x) [(nO2t *λ)/0,20946)][kmol spalin/kg paliwa]
nC2t=0,01[C/12 + H/4 + S/32 - O/32][kmol O2/kg paliwa]
VO2t=22,4136/100[C/12 + H/4 + S/32 - O/32][Nm3O2/kg paliwa]
Kmol gazu w temp. 0oC i ciśnieniu 1,01325 zajmuje 22,4136m3
Vpow.=22,41356/100*0,20946[C/12 + H/4 + S/32 - O/32][Nm3pow./kg pow.]
λ=Vpow./Vpow.t
λ zależy od kinstrukcji kotła i paliwa
CO NO
λSpt
Vpow.=B*Vpow. (jeżeli przy kotle jest wentylator powietrza)
B -zużycie węgla B[kg/s]
Vpow.=B*(22,41356/100*0,20946)[C/12 + H/4 + S/32 - O/32][Nm3pow./s]
Vpow.=B*(22,41356/100*0,20946)[C/12 + H/4 + S/32 - O/32]*[273,15+tpow/273,15][m3pow/s] (gdy powietrze doprowadzone do kotła jest grzane).
11.Zapotrzebowanie powietrza do spalania paliw gazowych.
a) CO + ½O2 CO2
1 kmol CO +½ kmol O2 1 kmol CO2
28 kg CO + 16 kg O2 44 kg CO2
b) CH4 + 2O2 CO2 + 2H2O
1 kmol CH4 +2 kmol O2 1 kmol CO2+ 2 kmol
H2O
16 kg CH4 + 64 kg O2 44 kg CO2 + 36 kg
H2O
c) CnH2n+2+(1,5n+0,5)O2 nCO2+(n+1)H2O
1 kmol CnH2n+2 +(1,5n+0,5) kmol O2 n kmol
CO2+(1,5n+0,5)kmol H2O
(14n +2)kg CnH2n+2 +32(1,5n+0,5) kg O2
44 kg CO2+18(n+1)kg H2O
d) C2H4+3O2 2CO2+2H2O
1 kmol C2H4+ 3kmol O2 2kmol CO2+2kmol
H2O
28kg C2H4+36kg O2 88kg CO2+ 36kg H2O
e) CnH2n+1,5nO2 nCO2+nH2O
1kmol CnH2n +1,5n kmol O2 n kmol CO2+
n kmol H2O
14n kg CnH2n+48n kg O2 44n kg CO2+18n kg
H2O
f) H2S+1,5O2 H2O+SO2
1 kmol H2S+1,5 kmol O2 1kmol H2O+1kmol
SO2
34kg H2S+ 48kg O2 18kg H2O+64kg SO2
g) C2H4+2,5O2 2CO2+H2O
1kmol C2H4+2,5kmol O2 2 kmol CO2+1kmol
H2O
26kg C2H4+80kg O2 88kg CO2+18kg H2O
nO2t=˝n'CO+˝n'H2+∑(1,5n+0,5)n'CnH2n+2+∑1,5
n' CnH2n+2+1,5n'H2S+2,5n'C2H2+n'O2[kmol/Nm3]
n''sw=0,01[C/12 + H/2 + S/32 + N/28 + W/18]
+(1+x) [(nO2t *λ)/0,20946)][kmol spalin/kg
paliwa]
Vsp=22,4136{ 0,01[C/12 + H/2 + S/32 + N/28+
W/18](1+x) [(nO2t /0,20946)-no2t]}[Nm3 sp/kg
pal.
Vsp=B*22,4136{ 0,01[C/12 + H/2 + S/32+
N/28+W/18](1+x) [(nO2t /0,20946)-no2t]}[Nm3
/s]
Vsp=B*22,4136{ 0,01[C/12 + H/2 + S/32+
N/28+W/18](1+x) [(nO2t /0,20946)-no2t]}*
[(273,15+tp)/273,15][1,01325/Psp][m3sp/s]
12.Obliczanie objętości i składu spalin przy zupełnym i całkowitym spalaniu.
zupełne - jeśli w składzie spalin w spalaniu nie ma produktów spalin niezupełnych
niezupełne - jeżeli w gazowych produktach spalania są takie składniki np. CO2
całkowite - jeżeli w stałych produktach spalania nie ma części palnych
niecałkowite - jeżeli w stałych produktach spalania w popiele i żużlu znajdują się części palne.
Wzory dla spalania zupełnego i całkowitego:
n''CO2=n'c
n''sw=n''CO2+n''SO2+n''H2O+n''O2+n''N2
n''sw-spaliny wilgotne zawierające parę
n''ss=n''sw-n''H2O
W kotłach o temp. > 100o spaliny wychodzące do komina są wilgotne (jedynie w niektórych kotłach do wyjścia komina kierowane są spaliny < 100o- spaliny suche.
n''sw=n''SO4+n''H2O+n''H2+n''O2
n''CO2=n'c
n''SO2=n'S
nH2O=nH2+nH2O+ x*[(nO2t *λ)/0,20946)]
x- kilomolowy wspólczynnik wijgotności
nH2O- zespolony wodór z wilgocią paliwa i powietrza
n''N2=n'N2+(0,79054/0,2946)*nO2t*λ
n''O2=(λ-1)nO2t
n''sw=n'c+ n's+ n'H2+ n'N2+ n'H2O+(1+x)* (nO2t *λ/0,20946)[kmol/kg paliwa]
n'sw=0,01*(C/12 + H/2 + S/32 + N/28 + W/18)+(1+x)( nO2t *λ/0,20946)[kmol/kg paliwa]
Vsp=22,4136[0,01(C/12 + H/2 + S/32 + N/28 + W/18)+(1+x)( nO2t /0,20946)- nO2t[kmol/kg paliwa]
Vsp= B*Vsp
Vsp= BVsp*[(273,15*tp)/273,15]*(1,01325/Psp)[m3sp/s]
13.Udziały procentowe w spalinach .
a)w spalinach suchych
[CO2]=(n''CO2/n''ss)*100
n''ss=n''sw-n''H2O
[SO2]=(n''SO2/n''ss)*100
[N2]=(n''N2/n''ss)*100
[O2]=(n''O2/n''ss)*100
b) w spalinach wilgotnych
[CO2]=(n''CO2/n''sw)*100
[SO2]=(n''SO2/n''sw)*100
[H2O]=(n''H2O/n''sw)*100
[N2]=(n''N2/n''sw)*100
[O2]=(n''O2/n''sw)*100
14.Objętość i skład spalin przy spalaniu paliw gazowych.
Skład paliw gazowych:
14 składników palnych i 5 niepalnych
CO+H2+CH4+C2H6+C3H8+C4H10+C5H12+C6H14+C2H4+C3H6+C4H8+C5H10+H2S+C2H2+CO2+SO2+N2+O2+H2=100%
Skład paliw wilgotnych
n''sw = CO2+SO2 +H2O+N2+O2+H2
n''CO2=n'CO+∑n*n'CnH2n+2+∑n*n'CnH2n+2+2n'C2N2+n'CO2
n''SO2=n'H2S+n'SO2
n'H2O=n'H2+∑(n+1)n'CnH2n+2+∑n*n'CnH2n+2+n'H2S+n'C2H2+x*( nO2t*λ /0,20946)
n''N2=n'H2
n''O2=(λ-1)nO2t
n''sw- suma tych składników
n''sw=n'H2O=n'CO+n'H2+∑(2n+1)n'CnH2n+2+∑2n*n'CnH2n+2+2n''H2S+3n'C2H2+n'SO2+n'N2+n'H2+(1+x)*( nO2t*λ /0,20946)-nO2[kmol sp./Nm3g]
n''sw=1/100*22,4136[CO+H2+∑(2n+1)CnH2n+2+∑2nCnH2n+2+2H2S+3C2H2+CO2+SO2+N2]+(1+x)*[(nO2t*λ)/o,20946]-nO2t[kmol sp/Nm3g]
Vsw=0,01[CO+H2+∑(2n+1)CnH2n+2+∑2nH2n+2+2H2S+3C2H2+CO2+SO2+N2+]+22,4136(1+x)*[(nO2t*λ)/o,20946]-nO2t [kmol sp/Nm3g]
Objętość w jednostce czasu
Vsp=Q{Vsw} [Nm3g/s]
Rzeczywista objętość spalin uwzględniając ciśnienie
Q{Vsp} [273,15+(tsp*1,01324)]/[273,15*Ps][m3sp/s]
15.Obliczanie składu spalin przy spalaniu niezupełnym i niecałkowitym paliw stałych.
n''CO2≠n'c
n'c=n''CO2+n''CO+n''c
n''sw=n''CO+n''CO2+n''SO2+n''H2O+n''N2+n''O2
n''CO- nie da się obliczyć można to określić tylko na podstawie pomiarów ss (w spalinach suchych mierzy analizator)
[CO]=(n''CO2/n''ss)*100
n''ss=n''sw-n''ss
n''CO=([CO]/100)*n''ss
n''CO2=n'c-n''CO-n''C=n'c-[([CO]/100)*n''ss]-[A2*C2/B*12]
[([CO]/100)*n''ss]-z analizy spalin
[A2*C2/B*12]- z analizy żużlu
n''SO2=n'S
n''H2O=n'N2+( 0,79054*nO2t /0,20946)+ λ
n''O2=(λ-1) +½ n'C n'CO+n''C
Analiza żużla
B[kg/s] zużycie węgla
A2[kg/s] ilośc popiołu w czasie
C2[kgC/kgŻ]
n''C=[A2*C2/B*12]
n''ss=1-½ [CO/100] [n'C+ n'S+ n'N2+(+[0,79054/0,02946]*λ-1)nO2+][kmolsp/kgp]
Vsp=22,4136[{1/(1-½([CO]/100)}[0,01(C/12+S/32+N/22)+( λ+(0,79054/0,20946) λ-1)nO2t]+0,01(H/2+W/18)+X*( nO2t+λ /0,20946)][Nm3/kg paliwa]
Vsp=BVsw[Nm3sp/s]
Vsp=BVsw[(273,15+tsp)/273,15]*(1,01325/Ps)[m3sp/s]
Ps - ciśnienie spalin
16.Pomiar kontrolowany spalania
-mierzymy miernikiem zawartość CO2
-mierzymy miernikiem zawartość O2
[CO2max]=n''CO2/[n'c+n's+n'N2[(0,79054/0,20946)*nO2t]+λ]
λ=1
n''CO=0
n''C=0
λ≈[[CO]/[CO2max]]
Co2max zależy od rodzaju paliwa
Paliwo |
CO2max[%] |
Koks Węg. Kamienny Węg. Brunatny Drewno Plej Gaz ziemny |
20,5-21 18,5-19,2 18,5-19,5 19,0 15,6 12-13 |
17.Obliczanie efektów energetycznych procesów spalania
Efekty energetyczne trzeba najperw jednoznacznie sprecyzować w warunki odniesienia.
Warunkami odniesienia są :
-węgiel C(S) -stan stały(grafit lub węgiel bezpostaciowy)
-siarka S(S)-stan stały
-wodór H2(g)-stan gazowy w molekułach 2-atomowych
-tlen O2(g) -stan gazowy w molekułach 2-atom.
-azot N2(g) - stan gazowy w molekułach 2-atom.
Produkty spalania:
-tlenek węgla CO(g)
-dwutlenek węgla CO2
-dwutlenek siarki SO2
1) C(S)+O2(g)→CO2(g)+ΔQ
Chemicy przypisują energię produktu spalania. Substraty w stanie pierwotnym mają en=0
ΔHc=0
ΔHO2=0
ΔHCO2=ΔQ
2) H2(g)+ ½C2(g)→H2Og+ΔQ1}inna energia dla wod
H2(g)+ ½O2(g)→H2Og+ΔQ2 }y w stanie ciek.i gaz.
ΔHH2 = 0
ΔHO2 = 0
ΔHH2Og =ΔQ1
ΔHH2Og = ΔQ2
ΔHc - entalpia chemiczna albo ciepło spalania
1) C(S)+O2(g)→CO2(g)+ΔQ
ΔHc=-ΔHCO2=ΔQ
ΔHC=-ΔHCO2=394086[kJ/kmol]-ene.1kmolagrafitu
ΔhC=[ΔHC/12,011]=32800[kJ/kgC]-energia 1 kg węgla czystego chemicznie(grafitu)-tyle trzeba energii by zniszczyć siatkę krystaliczną ΔhC=[ΔHC/12,011]=[407315/12,011]≈33900[kJ/kgc]-energia 1 kg węgla bezpostaciowego(tutaj nie musimy niszczyć siatki krystalicznej)
1) H2(g)+ ½O2(g)→H2O(g)+ΔQ1
ΔHH2=-ΔHH2Og=242174[kJ/kmol]-energia 1kmol wodoru nieskroplonego.
ΔhH2=[242174/2,016]=121000[kJ/kg]-wodór nieskroplony.
H2(g)+ ½O2(g)--> H2Oc+ΔQ2
ΔH 2H2=-ΔH2Oc=286248[kJ/kmol]-skroplony
Δh2H2=[286248/2,016]=143200[kJ/kgH2]-tutaj wodór skroplony(otrzymujemy jeszcze energię ze skroplenia)
2)S(S)+O2(g)SO2(g)+ΔQ
ΔHS=-ΔHSO2=334820[kJ/kmolS]
Δhs=(334820/32,066)=10400[kJ/kg]
Ciepłem spalania będziemy nazywać ilość ciepła powstającego w wyniku całkoitego i zupełnego spalania jednostkowej ilości paliwa (1 kg lub 1 Nm3) w suchym powietrzu po ochłodzeniu produktów spalania do temp. substratów (temp.odniesienia To=298,15 oK)jeżeli woda w produktacie spalania jest w stanie ciekłym .
Wartością opałową paliwa Qw będziemy nazywać ilośc ciepła powstałą w wyniku zupełnego i całkowitego spalania jednostkowej ilości paliwa w suchym powietrzu po ochłozeniu produktów spalania do temp. substratu (temp. odniesienia T0)jeżeli woda zawarta w produktach spalania jest w stanie gazowym
Qc=339*C+1432(H-O/8)+104S[kJ/kg paliwa]
Qw=339*C+1210(H-O/8)+104S-25W[kJ/kg paliwa]
QC=126,28*CO+127H2+398CH4+697C2H6+991C3H8+1285 C4H10+1579 C5H12+1873 C6H14+630 C2H4+912 C3H6+1214 C4H8+1507 C5H12+257H2S+580 C2H2[kJ/Nm3g]
Qw=126,28CO+107,87H2+358,32CH4+637,32 C2H6+912,11 C3H8+1185,7 C4H10+1459,8 C5H12+1736,36 C6H14+860 C3H6+590,29 C2H4+1135 C4H8+1404 C5H10+237H2S+560 C2H2[kJ/Nm3g]
18.Bilans energetyczny i sprawnościowy.
I0
D[kg/s]
B[kg/s] iwz
B*Qw=Q0+ΔQ
Straty ΔQ=BQw-Q0
Metoda bezpośrednia jest metodą doświadczalną.Metoda pośrednia jest metodą teoretyczną.
η={[D(i0-iwz)]/(B*Qw)}
D- natężenie przepływu wody lub pary w kotle.
Pomiaru dokonuje się przepływomierzem.
Zasada działania przepływomierza:
- w rurociągu płynie woda lub para,
spadek ciśnienia
D=kΔP
Iwz- entalpia wody we wlocie do kotła
Metodą pośrednią wyznaczamy sprawnośc kotła od 100% odejmujemy sumę strat w %
η=100% -∑Si * %
∑Si%=Sg%+Sn%+Sw%+Spr%+Sz%
niezupełna strata %
Sg%=Vss*[{([CO]/100)*12628}/Qw]*100
Sag%=Vss*{12628[CO]/Qw}
Sn%=[33900A2C2/B*Qw]*100
19.Straty wylotowe.
Sw%=[(Ispalin-Ipow.)/Qw]*100
S%= [(Ispalin-Ipow.)/Qw]*(100-Sn%)-jeżeli spalanie całkowite i zupełne
Isp=∑ViCpitsp
Isp=(n''CO*CpCO+n''CO2*CpCO2+n''SO2*CpSO2+n''H2O*CpH2O+n''N2*CpN2+n''O2*CpO2)*tsp[kj/kmol]
Isp=22,4136(n''CO*CpCO+n''CO2*CpCO2+n''SO2*CpSO2+n''H2O*CpH2O+n''N2*CpN2+n''O2*CpO2)*tsp[kj/kmol]
Ipow=Vpow*Cp pow*tpow
V[Nm3pow/kg pow]
Cp pow[kJ/Nm3pow}
Wzór uproszczony
Sw%=(tsp-tpow)/[CO2]
[CO2]- zawartość CO2 w ss
Q - współzależny od rodzaju wilgotności paliwa.
Np.
a=0,7 tsp=130o tp=30o
Strata promieniowania
Ao na podstawie wykresów
0,6
0,5
0,4
0,3
0,2
0,1
100 200 300
20.Temperatura w palenisku.
Bilans cieplny po stronie spalin tego kotła B*Qw*ηp+B*Vpow*Cp pow(tpow- t0)=B*Q*ηp*σ+B*Vsp*Cpsp(tsp-t0)
B*Qw*ηp-w komorze paleniskowej
B*Vpow*Cp pow(tpow- t0)-palensko z ogrzanym powietrzem
B*Q*ηp*σ- ciepło przekazane ekranem w komorze paleniskowej (rury w których odparowywuje się wodę)
B*Vsp*Cpsp(tsp-t0)-ciepło unoszone ze spalinami
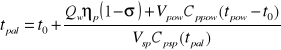
Cpsp=[n''COCpco+ n''CO2CpCO2+ n''SO2CpSO2+ n''H2OCpH2O+ n''N2CpN2+ n''O2CpO2]/[ n''CO+n''CO2+n''SO2+n''H2O+n''N2+n''O2]
Wyznaczenie temp. w palenisku:
1.Zakładamy pewną wartość temp. w palenisku.
2.Dla tej temp. określamy Cp poszczególnych składników
3.Wyznaczamy dla tej temp. średnią wartość ciepła właściwego spalin.
4.Wyznaczamy ciepło właściwe powietrza dla przyjętej temp. powietrza
5.Podstawiamy do wzoru założenia:
σ=0,4
Cp=0,98
oraz Cpsp i Cppow
i wyznaczamy temp. paleniska
6.Przyrównujemy założą temp. w palenisku i wykorzystujemy ją do obliczenia Cpsp z temp. w palenisku
TEORIA REAKTORÓW JĄDROWYCH
Historia energetyki jądrowej rozpoczyna się od teorii względności Alberta Einsteina (ΔE=Δmc2). Przewidział, że można uzyskać energię wyniku defektu masy. Masa się zmniejsza - wydziela się energia. Elementarne składniki materii (elektron proton, neutron). Energia jądrowa wyzwala się wtedy, gdy następują zmiany w jądrze atomowym. Paliwa rozszczepialne - z jednego dużego jądra atomowego powstaje jedno duże. Warunkiem rozszczepienia jest pochłonięcie neutronu. Paliwa syntezy - z dwóch małych jąder powstaje jedno. 1897 - odkrycie elektronu Thompson, 1932 - odkrycie neutronu - Chedwick, 1938 - Mahn, Strassmann - pierwsze pojedyncze rozszczepienie jądra atomowego (przypadkowo). 1940 - teoretyczne wyjaśnienie Bohra. 2.XII.1942 - USA - Termi uruchomił pierwszy reaktor jądrowy. 6 i 9.VIII.1945 Hiroshima i Nagasaki - zrzucenie bomby atomowej. 27.VI.1954 pierwsza elektrownia jądrowa (ZSRR). Jeżeli przyjąć, że okresem połowicznego rozkładu jest czas, po którym N=1/2 N0 to jest to czas połowicznego rozkładu.
![]()
Średni czas życia:
Def. 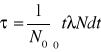
![]()
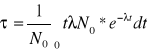
![]()
![]()
N0 - liczba wszystkich rozpadów
Średni czas życia dłuższy od półokresu rozpadu.
Liczbę rozpadów na jedną sekundę nazywamy aktywnością. Jednostka 1Ci = 3,7*1010 (rozp./sek.) 1Ci - Curie
1Bq (bekerel) = 1 rozp./sek.
1Ci - aktywność jednego grama rada.
Proces rozszczepienia jądra.
Jest to specjalny rodzaj reakcji - jądro rozpada się na dwie niekoniecznie równe części. Rozszczepienie następuje w reaktorze jądrowym. Cechą charakterystyczną rozszczepienia (oprócz podziału jądra na 2) jest wydzielanie ok. 2-3 neutronów i ok. 200 MeV energii.
Rdzeń składa się z na przemian z płyt urona i grafitu. Pręty silnie pochłaniające neutrony. Pręty do góry.
Pręty: 1 - regulacyjne - regulują moc reaktora, 2 - kompensacyjne, kompensują nadmiar paliwa 3 - awaryjne, służą do awaryjnego wyłączenia reaktora.
Energia otrzymana to:
- kinetyczna (wyrzucanie elementów procesów rozszczepiania)
- cieplna,
- promieniowania (α,β,γ)
Paliwa naturalne - uran (tylko) - zdolne do rozszczepiania i utworzenia układy krytycznego. Układ krytyczny - tam następuje reakcja łańcuchowa samowyzwalania)
Paliwem jądrowym ze skorupy ziemskiej jest izotop uranu 235
Skład wydobywanego uranu:
zawartość masy atomowe
92U234 - 0,006 % 234,11
92U238 - 99,282 % 238,12
92U235 - 0,712 % 235,127
92U235 - tylko ten uran nadaje się na paliwo, bo mała masa, a duża wydzielana energia.
Kiedy konstruowano pierwszą bombę atomową to uran zamieniono na gaz UF6 (sześciofluorek uranu) i w polu magnetycznym rozdzielono uran 92U235. Uran zależy od aktynowców: 89Ac , 90Tn, 91Pa, 92U, (33Np - ten występuje sporadycznie) Występują w ziemi.
94Pu, 95Au, 96Cn, 97Bk, 98Ct, 97Es, 100Fm, 101Mr, 102No - wytwarzane sztucznie.
103Lw, 104Kw - nie są aktynowcami.
Półokresy rozpadu.
T1/2 (U235) = 8,91 * 109 lat.
T1/2 (U238) = 4,98 * 109 lat.
W czasie reakcji jądrowych powstają:
ma nadmiar neutronów β- β-
U238 + n 92U239 ------93Np239 ----- 94Np239 - trwały
23,5 min 2,3 dnia
β- β-
90Th239 + n90Th233 -----91Pa233 ------ 92U233 - trwały
22 min 24,7 dnia
94U239; 92U233 - to 2 paliwa sztuczne
Właściwości Uranu:
U - metal srebrny - temperatura topnienia 1132 stopnie C
- temperatura wrzenia 3818 stopni
- temp. przejścia:
+ ortogonalna 668 stopni
+ tetrogonalna 668 - 774 stopni
+ regularna 774 - 1138 stopni
- gęstość 19,04 * 103 kg/m3
- wartość energetyczna 81,959040 MJ/kg U238
Wartość energetyczna U235 jest 3 miliony razy większa od paliw konwencjonalnych. Model kroplowy jądra - działają tam: - siły Culombowskie (przyciągania; elektrostatyczne), - siły drgające, - siły powierzchniowe (przeciwdziałające rozpadowi).
Jądro się rozpadnie jeśli siły drgające będą duże, a wzbudzi się jeśli przyjmie neutron: powstaje wtedy energia wzbudzenia powyżej której jądro ulega rozpadowi. Progowa wartość energii wzbudzenia, która może wywołać wzbudzenie nazywa się energią aktywacji. Jądro rozpada się, gdy: EWzb >Ea
EWzb - energia wzbudzenia wywołana neutronem
Ea - pewna energia właściwa dla danego jądra
Dla U233, U235, Pu239 - energia wzbudzenia wyzwalająca się w jądrze atomowym w wyniku pochłonięcia termicznego n (tzn. jego energia = 0) jest większa od energii aktywacji - dlatego jądra te mogą być rozszczepione n termicznie.
Dla U238 i Th232 energia w wyniku pochłonięcia n termicznego jest mniejsza od Ea, dlatego nie mogą być rozszczepione przez n termiczne. Dlatego n muszą posiadać dużą energię termiczną.
Energia wzbudzenia n termicznych i Ea dla niektórych ciężkich jąder.
Jądro tarcza |
Jądro wzbudzone |
Energia (MeV) wzbudzenia |
Energia (MeV) aktywacji |
Z2/A liczba / liczba masowa / atomowa |
U233 U235 U238 Th232 Pu239 |
U234 U236 U239 Th233 Pu240 |
6,6 6,4 4,9 5,1 6,4 |
4,6 5,3 5,5 6,5 4,0 |
36,4 36,0 35,5 34,4 34,5 |
Produkty rozszczepienia i energia rozszczepienia.
92U235 + 0n1 57La147 + 35Br87 + 2*0n1 - bardzo prawdopodobne rozszczepienie.
Badanie produktów rozszczepienia U235 wykazały, że istnieje więcej niż 60 różnych produktów rozszczepienia o masach atomowych 72-158. Oznacza to, że istnieje więcej niż 30 różnych produktów rozszczepienia. Ok. 97% przypadków rozszczepienia daje dwie grupy produktów: lekkich:85-104 masy atomowe, ciężkich: 130-149.
W najbardziej prawdopodobnych rozpadach 6% daje produkty o masach atomowych. Produkty rozszczepienia mają zbyt wiele n aby mogły być trwałe. Większość z nich jest w stanie wzbudzonym i każdy z produktów wzbudzenia zapoczątkowuje swój szereg rozszczepieniowy (tzw. łańcuch rozszczepień) Poszczególne człony łańcuchów rozpadają się najczęściej przez rozpad β-. Jednym z najdłuższych jest rozpad ksenonu.
β- β- β- β-
54X140 -- 55Cs140 -- 56Ba140 ---- 57La140 ---- 58Ce140 - trwałe
165 66,5 12,8 dni 40 godz.
Przykład krótkiego łańcucha „Neodym”
β- β-
60Nd147 --- 61Pm147 --- 62Sm147 (T1/2 = 1011 lat)
11 dni 4 lata
Energia rozszczepienia
Najbardziej znamienną cechą rozszczepienia jest energia. Wartość jej na jedno rozszczepienie wynosi: ok. 200 MeV. Wartość tej energii można obliczyć różnymi metodami:
a) w oparciu o bilans masy substratu i produktu.
Defekt masy, a nie materii (żadna cząstka nie ginie) są one inaczej poukładane.
ΔE=Δmc2
U235+ 0n1 Mo95 + La139 + 2* 0n1 + ΔE
Masa substratu:
U235 - 235,124 jma
n - 1,00897 jma
Ms = 236,133 jma
Masa produktów:
Mo95 - 94,946 jma
La139 - 138,955 jma
Mp = 235,919 jma
ΔM = Ms - Mp = 239,133 - 235,919 - 0,214 jma
M jma = 931,5 MeV
ΔE ≅ 199 MeV
jma - jednostki masy atomowej
b) w oparciu o bilans masy wiązania.
Bilans energii wiązania
Ew/A - energia wiązania przypadająca na 1 proton
1 - energia wiązania typu miedź, żelazo
Ciężkie się rozszczepiają, lekkie się łączą. Proces rozpadu i syntezy dążą do powstania pierwiastków o masie atomowej ok. 60 jma (Fe, Cu), których jest najwięcej w przyrodzie.
U235 + n Mo95 + La139 + 2n + ΔE
ΔE = Σ Ewp - Σ Ews
Σ Ewp - suma energii produktów wiązania
Σ Ewp = M(Mo) * Ew/A(Mo) + M(La) Ew/A(La)
Σ Ews = M(U236) Ew/A(U236)
Σ Ewp = 95 * 8,63 + 139 * 8,35 = 1980,5 MeV
Σ Ews = 236 * 7,5 = 1770 MeV
ΔE = 1980,5 - 1770 = 210,5 MeV
Rodzaj energii:
- energia wyzwolona natychmiastowo
- energia wyzwolona z opóźnieniem (promieniowanie)
Rodzaj energii |
U235 (MeV) |
Pu234 (MeV) |
U233 (MeV) |
U258 (MeV) |
Energia wyzwalana natychmiastowo: - energia kinetyczna fragmentów rozszczepienia - energia kinetyczna neutronów rozszczepionych - energia natychmiastowego promieniowania γ Energia wyzwalana z opóźnieniami: - energia promieniowania β- fragmentów rozszczepionych - energia promieniowania γ fragmentów rozszczepienia - energia unoszona przez neutrino |
167
5
8
9
7
11 |
172
6
7
9
7
11 |
163
5
7
9
7
11 |
163
5
7
9
7
11 |
Razem energia rozszczepienia |
207 |
212 |
202 |
202 |
Neutrony rozszczepione
Neutrony jako nienaładowane cząstki elementarne mają szereg własności. Liczne reakcje jądrowe wywołane przez neutrony mają szerokie zastosowanie. Najważniejszą rolę odgrywają neutrony w reakcjach rozszczepienia izotopów. Zastosowanie w medycynie. Ilość neutronów powstających z rozszczepienia jądra zależy od energii dostarczonego neutronu, rodzaju energii. U235 (ν=2,47) ; U233 (ν=2,5) ; Pa239 (ν=2,94).
Dla U235 0 MeV (ν=2,47); 0,5 MeV (ν=2,8); 1 MeV (ν=2,83)
Ilość neutronów powstających w procesie rozszczepienia ma charakter statystyczny.
Liczba neutronów powstających w jednym rozszczepieniu |
Liczba przypadków na 1000 rozszczepień |
||||||
0 1 2 3 4 5 |
27 138 339 352 13034W ok. 99% są to neutrony natychmiastowe wyzwolone w czasie 10-14 s. 1% emitowane jest ze znacznym opóźnieniem (od ułamka sekundy do kilkudziesięciu sekund) są to neutrony opóźnione - przydatne przy sterowaniu reaktora. Można je podzielić na 5 grup ze stałymi rozpadu.U235Pa239U233U238 |
Th232 |
|||||
Razem na jądro rozszczep. Razem na 1 neutr. rozszcz.
Razem |
0,0158 0,0064
0,64 |
0,0061 0,0021
0,21 |
0,0066 0,0026
0,26 |
0,0402 0,0157
1,57 |
0,0495 0,022
2,2 |
||
Be9 + He4 C12 + 0n1 + 5,76 MeV źródło (α,n)
Ra - Be wytwarza neutrony przez dłuższy czas.
Be(γ,n); H2(γ,n)H; źródło (γ,n). Posiadają one zawsze równą energię. Energia wiązania dla wodoru wynosi: 2,23 MeV, a dla Berytu 1,6 MeV i dlatego można te jądra rozszczepiać cząstką γ
Neutron w reaktorze może wywołać 4 rodzaje reakcji:
- zderzenie elastyczne (neutron i zderzający się obiekt - zachowana energia kinetyczna)
- zderzenie nieelastyczne (część energii kinetycznej zużywana jest na coś innego)
- pochłonięcie elektronu powodujące rozszczepienie
- pochłonięcie elektron nie powodujące rozszczepienia (wychwyt radiacyjny)
Całkowity przepływ czynny (prawdopodobieństwo wystąpienia reakcji
σt = σe + σin + σf + σr
Oddziaływane neutronów z ośrodkiem.
Do mierzenia tego oddziaływania służą przekroje czynne. Mikroskopowy przekrój czynny - prawdopodobieństwo zajścia reakcji jądrowej w odniesieniu do σ (cm2). Jednostką jest 1 Barn = cm2 * 10-24. Przekrój czynny - stosunek liczby reakcji zdarzeń danego typu w 1 cm3 ośrodka.
![]()
σ - mikroskopowy przekrój czynny na daną reakcję, c - liczba reakcji w 1 cm3 w czasie 1 sek. n - gęstość neutronów na 1 cm3 V - prędkość neutronów cm/s, N - liczba jąder na 1 cm3
Dla lepszego zilustrowania σ przyjmujemy takie rozumowanie:
Niech równoległa wiązka neutronów monoenergetycznych pada prostopadle na powierzchnię 1 cm2. Taka wiązka nazywa się prądem neutronów.
σ = c/(Na*I)
Na σ = C/I = 1
σ - mikroskopowy przekrój czynny (cm2 *10-24)
I - prąd neutronów [n/(cm2 * s)]
Jeżeli liczba C=I to Na σ = 1
Wartość przekroju czynnego dla różnych reakcji wyznacza się doświadczalnie:
N - liczba jąder w 1 cm płytki
N dx - liczba jąder w warstwie o grubości dx
Nσ dx - liczba reakcji danego typu w warstwie o grubości dx
-dI/I = Nσ dx
Ix=I0*e-Nσ dx
Stąd σ=1/N * x * ln(I0/Ix)
Miarą takiego przekroju jest stosunek wartości prądu neutronów przed i za obiektem. Wielkość Nσ nazywać będziemy mikroskopowym przekrojem czynnym i ma wymiar (cm-1) jest to suma przekrojów czynnych wszystkich neutronów w cm2.
Przekroje czynne poszczególnych składników możemy dodawać.
Σ = Σ1 + Σ2 + Σ3 + ....
Σ = σ1 * N1 + σ2 * N2 + σ3 * N3 + ....
Ix = I0 * e-Σx
Rodzaje przekrojów czynnych - istnieją 4 rodzaje reakcji neutronów z ośrodkiem. Neutron w ośrodku może zderzać się z jądrami albo być pochłonięty.
σt = σs + σa t - total, s - scattering, a - absorption
Zderzenia niesprężyste - gdy część Ek zostanie zamieniona np. na Ep na wzbudzenie
σs = σe + σi (e - elastic - sprężyste, i - inlastic - niesprężyste)
σa = σf + σr (f - fissin - rozszczepione, r - radiatire capture -
uchwyt radiacyjny)
σt = σe + σi + σf + σr
Mikroskopowy przekrój czynny
Σt = Σe + Σi + Σf + Σr
Makroskopowy przekrój czynny
Średnia droga swobodna λ[cm] - jest to odległość jaką przebywa neutron pomiędzy kolejnymi zderzeniami.
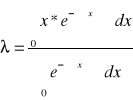
Σx - makroskopowy przekrój czynny
e-x = Ix/I0 - prawdopodobieństwo przebycia przez neutron drogi x bez udziału w reakcji jąder; względnie liczba padających neutronów którym udało się przebyć drogę x bez udziału w reakcji jądrowej.
Własność relaksacji λe
λs=1/Σs
λa=1/Σa
λt=1/Σ t = 1/(Σs+Σa) = 1/[(1/λs)+ (1/λa)] = λs*λa/(λs+λa)
Strumień neutronów - suma dróg przebytych przez neutrony w 1 cm3 w czasie 1 s.
Φ = nV [n/cm3]
Liczba zderzeń pojedynczego neutronu w 1 cm3/s
n(1) = V/λ
Liczba neutronów w 1 cm3/s
N(n) = nV/λ = nVΣ
Strumień neutronów jest wielkością skalarną gdyż szybkości wszystkich neutronów nie mają ustalonej wartości poruszają się w różnych kierunkach.
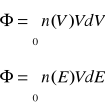
Wydajność reakcji jądrowych z neutronami
C=ΣΦ=ΣnV
C=NσnV
W funkcji prędkości neutronów są 3 rodzaje neutronów:
a) termiczne; b) rezonansowe; c) prędkie
Epitermiczne - neutrony
Mikroskopowe przekroje czynne.
Neutron |
Mikroskop. przekr. czynne |
Jądro |
||
|
|
U235 [b] |
U238 [b] |
U naturalny |
termiczny (0,0253 eV) |
σe σi σt σr |
6,0 - 582 112 |
8,0 - 0 2,71 |
8,0 - 4,16 3,47 |
Prędki (1 MeV) |
σe σi σt σr |
3,9 1,4 1,2 0,093 |
3,9 1,6 0,18 0,14 |
5 1,6 0,26 0,14 |
Neutrony w procesie rozszczepiania są neutronami prędkimi.
Zderzenie pojedynczego neutronu z jądrem:
W układnie laboratoryjnym obserwator jest obok, a w układzie środka masy obserwator porusza się w centrum (środku) masy.
Prędkość początkowa neutronu w układzie lab. - V0
Układ L (przed zderzeniem) Układ C (przed zderzeniem)
Chcemy zmierzyć stosunek energii przed i po zderzeniu
![]()
SPOWALNIANIE NEUTRONÓW
W układzie L neutron zderzy się z jądrem pod kątem ϑ
(Vn2L)2= (Vn2C)2+ (VCL)2 - 2(VN2C* VCL)*cos(180-Φ)
(Vn2L)2=(Vn1L)2[M2/(m+M2)]+ (Vn1L)2[m2/(m+M2)]-
-2(Vn1L)[m*M/(m+M2)]* cos(180-Φ)
(Vn2L)2=(Vn1L)2*[M2+m2+2MmcosΦ/(M+m)2]
En2/En1=(Vn2L)2/(Vn1L)2=A2+1+2AcosΦ/(A+1)2
1).neutron zderzył się prostopadle ze ścianą Φ=π
-zderzenie centralne, zachodzi tu max. zmiana energii.
En2/En1=A+1-2A/(A+1)2=(A-1/A+1)2
Ta strata max energii jest określona jako α
(En2/En1)min=(A-1/A+1)2=α
α- jest funkcją masy atomowej jądra, z którą neutron się zderza.
En2 min=αEn1
En1- En2/ En1=1-α
2).muśnięcie neutronu o jądro czyli φ=0
En2/En1=A2+1+2A/(A+1)2=(A+1/A+1)2=1
Energia po zderzeniu jest równa energii przed zderzeniem.
Nie ma straty energii.
En2/En1=1+α/2 + 1-α/2cosΦ
Obliczanie cosΘ na podstawie cosΦ
cosΘ=1+AcosΦ/√(1+A2+2AcosΦ)
Jeżeli znamy energię przed i po zderzeniu
cosΘ=(A+1)/2 √( En2/En1)-[(A-1/2)√ (En1/En2)
Obliczanie w ujęciu statystycznym
Statystyczne ujęcie spowalniania neutronów opiera się na prawie rozpraszania. Okazuje się, że zderzenia w układzie c
Izotropowe-wszystkie kąty zderzeń są w równym stopniu prawdopodobne-zderzenie kulisto-symetryczne.
CosΦ są jednocześnie prawdopodobne.
W układzie L średnia wartość kąta Θ:
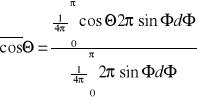
___
cosΘ=2/3A 2πsinΦdΦ - jednostkowy kąt bryłowy
___
Im większe A tym mniejszy cosΘ
W układzie L dla bardzo ciężkich jąder (dla dużych wartości A) rozpraszanie jest praktycznie izotropowe. W technologii reaktorowej ważną rolę odgrywa średnia strata energii przypadająca na jedno zdarzenie sprężyste.
Średni dekrement logarytmiczny energii
![]()
Prawdopodobieństwo, że neutron o energii początkowej E1n będzie miał energię po zderzeniu.
PdE = dE/(En1 - αEn1) = dE/[En1(1 - α)]
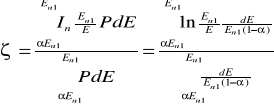
dla mianownika = 1
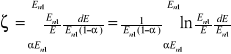
Nowa zmienna x=E/En1
dx=dE/dEn1
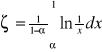
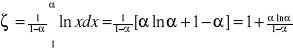
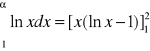
![]()
![]()
![]()
![]()
Zależność na ζ staje się niejednoznaczne dla A=1 i dla A=∞. Wartość ζ można obliczyć metodą obliczania granic dla A=1 ζ=1
W zderzeniach czołowych z jądrem atomu wodoru neutron może sam stracić energię dla AႥ ၺႥ
-liczba spowalniania od neutronu prędkiego do termicznego
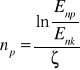
p - początkowa
k - końcowa
Pierwiastek |
Symbol chemiczny |
A |
ၺ |
nP |
Wodór |
H |
1 |
1 |
18 |
Deufer |
D |
2 |
0,725 |
25 |
Hel |
Ha |
4 |
0,425 |
44 |
Lit |
Li |
7 |
0,260 |
67 |
Beryl |
Be |
9 |
0,208 |
84 |
Węgiel |
C |
12 |
0,158 |
114 |
Tlen |
O |
16 |
0,120 |
150 |
Aluminium |
Al. |
27 |
0,074 |
246 |
Żelazo |
Fe |
36 |
0,038 |
472 |
Cyrkon |
Zr |
91 |
0,021 |
866 |
Uran |
U |
238 |
0,004 |
4480 |
ၺ nie jest wystarczającym kryterium spowalniania
Zdolność spowalniania:
ZM=ၺၓS(f)
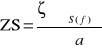
Dobry moderator powinien posiadać duże ၺ i ၓS oraz małe ၓa.
Właściwości materiałów moderatorów.
Moderator |
Gęstość |
N |
ၳS |
ၳa |
ZM=ၺၓS |
|
H2O |
1 |
0,03344 |
44 |
0,66 |
1,53 |
60 |
D2O |
1,1 |
0,03132 |
16 |
0,0026 |
0,37 |
5600 |
Be |
1,85 |
0,12357 |
6 |
0,009 |
0,176 |
125 |
BeO |
2,69 |
0,063 |
9,8 |
0,009 |
0,125 |
170 |
grafit |
1,8 |
0,09030 |
4,8 |
0,0045 |
0,064 |
190 |
Najlepsza jest ciężka woda powstająca z wody morskiej. Na uranie naturalnym można zbudować moderator z ciężkiej wody lub grafitu. Wzbogacony uran i woda mogą być moderatorem i chłodziwem.
Neutrony termiczne właściwości
-równanie termiczne ze środowiskiem
podlegają one rozkładowi Maxwella-Ballzmana
![]()
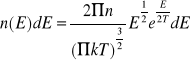
n-liczba neutronów
nV-liczba neutronów w jednej objętości, których prędkości znajdują się w przedziale
T-temperatura bezwzględna
Neutrony te można scharakteryzować :
a)najbardziej prawdopodobna prędkość neutronów
![]()
VP=13,8*105ზep [cm/s]
Vp=1,28*104ზT
Dla 20Ⴐ
Vp=2200 m/s
b)najbardziej prawdopodobna energia potencjalna
eP=1/2(mv2)=kT
c)średnia prędkość
![]()
d)średnia energia kinetyczna
![]()
e)średnia kwadratowa prędkość
![]()
Zależność VP od temperatury
Temperatura |
VP [m/s] |
eP [eV] |
|
CႰ |
KႰ |
|
|
0 |
273,15 |
2120 |
0,0235 |
20 |
293,15 |
2200 |
0,0253 |
727 |
1000 |
4060 |
0,0861 |
Gdy neutron spowolni się to następuje zjawisko dyfuzji - gdy neutron jest termiczny. Dyfuzja neutronu - polega na znajdywaniu rozkładu przestrzennego w reaktorze. Znalezienie metody przybliżenia dyfuzyjnego :
-neutrony są monoenergetyczne
-rozkład w układzie L jest izotropowy
Przeliczamy średnią drogę rozproszenia na średnią drogę transportu.
![]()
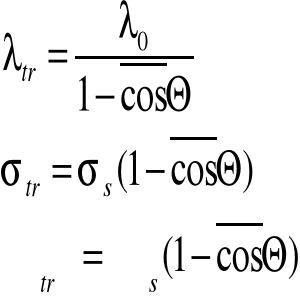
Teoria dyfuzji opiera się na prawie Ficka :
-dyfuzja masy
-dyfuzja ciepła
-dyfuzja ładunku elektrycznego
-dyfuzja momentu pędu
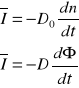
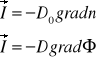
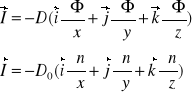
![]()
![]()
![]()
![]()
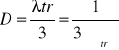
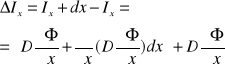
![]()
![]()
![]()
Ta zmiana prądu
![]()
![]()
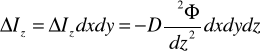
![]()
![]()
![]()
![]()
Bilans neutronów
-ucieczka - pochłanianie+źródło=Ⴖn/Ⴖt
![]()
Dla metody dwugrupowej
-prędkie
![]()
-termiczne
![]()
Kwadrat długości spowolnienia
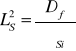
Kwadrat długości dyfuzji
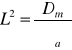
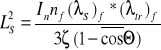
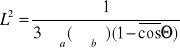
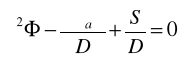
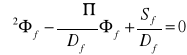
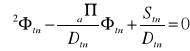
Średnia długość migracji M2=LS2+L2
ၥ - fast fission factor - współczynnik rozszczepień na neutronów prędkich
PP - prawdopodobieństwo uniknięcia ucieczki przez neutrony prędkie
P - prawdopodobieństwo uniknięcia pochłonięcia rezonansowego neutronu
1-p - prawdopodobieństwo wychwytu rezonansowego
Ptn - prawdopodobieństwo uniknięcia ucieczki przez neutron termiczny
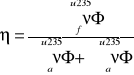
f-współczynnik wykorzystania termicznego
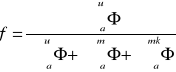
uran moderator materiał
konstrukcyjny
Keth- ef.wspól.mnożenia
![]()
Wzór czterech czynników (dla nieskończenie dużego reaktora)
KႥ=ၥpၺၨ
Dბ2၆-ၓa၆+S=0
a) Dtბ2၆f-ၓSl၆f+Sf=0
b) Dthბ2၆th-ၓa၆th+Sth=0
Metoda jednogrupowa
S=kႥၓa၆
Dბ2၆-ၓa၆+S=0
Dბ2၆-ၓa၆+kႥၓa၆=0
Dბ2၆+(kႥ-1)ၓa၆=0
Dბ2၆+[(kႥ-1)/D]ၓa၆=0
D/ၓs=L2
ბ2၆+[(kႥ-1)/L2]၆=0
Parametr geometryczny I parametr materiałowy
ბ2၆+B2၆=0
B2=[(kႥ-1)/L2]
L2B2=kႥ-1
1+ L2B2=kႥ
Warunek krytyczności reaktora w metodzie jednogrupowej
[(kႥ)/1+L2+B2]=1
Metoda jednogrupowa zmodyfikowana
[(kႥ)/1+M2+B2]=1
M2=L02+L2
Źródła neutronów
S=kႥၓa၆
Sf=ၺၨၓa၆th
Sth=ၥpၓSl၆f
Źródłem neutronów termicznych są spowolnione neutrony prędkie
Dfბ2၆f-ၓSl၆f+Sf=0 /:Df
Dthბ2၆th-ၓa၆th+Sth=0 /:Dth
ბ2၆f-[(ၓSl၆f)/Df]+[(fၨၓa၆th)/Df]=0
ბ2၆th-[(ၓa၆th)/Dth]+[(ၥPၓSl၆f)/Dth]=0
Chcemy uzyskać układ równań falowych
B2၆f=[(fၨၓa၆th)/Df]-[(ၓSl၆f)/Df)]
B2၆th=[(ၥPၓSl၆f)/Dth]-[(ၓa၆th)/Dth)]
B2၆f=[(fၨၓa၆th)/Df]-[ ၆f/LS2]
B2၆th=[(ၥPၓSl၆f)/Dth]-[(၆th)/ L2)]
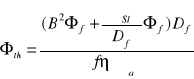
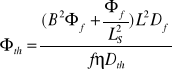
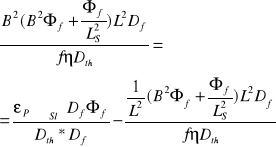
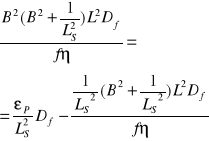
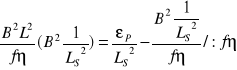
![]()
![]()
![]()
![]()
![]()
warunek krytyczności dla metody dwugrupowej
![]()
Metoda biegu Fermiego
Warunek krytyczności reaktora
![]()
Rozwiązanie równań reaktora dla różnych geometrii
1)dla kuli
![]()
2)dla walca
![]()
3)dla walca nieskończonego
![]()
4)dla prostopadłościanu
![]()
5)dla ściany nieskończonej
![]()
Ad 1 dla kuli:
1)r=0 ၆=၆0
2)r=R ၆=၆R
3)r=Re ၆=0
Re=R+ၬe
Ix=၆/4+[(ၬTRd၆)/6dx]
Ⴖ၆/Ⴖx=၆r/ၬe
၆R/4=[(ၬTR*၆R)/6ၬe]
ၬe=2/3ၬTR
ၬe=0,71ၬTR
Ⴖ2၆/Ⴖr2+[(2Ⴖ၆/rႶr)]+R2၆=0
U=၆r
၆=U/r
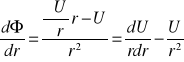
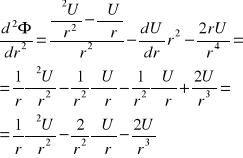
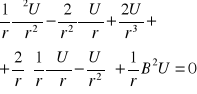
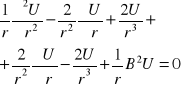
![]()
![]()
U=cosBr+esinBr
၆=(A/r)cosBr+(e/r)sinBr {(A/r)cosBr Ⴅ}
၆=(e/r)sinBr
r=Re ; ၆=0
0=(e/Re)sinBRe
BRe=0 ; BRe=ၐ ; BRe=kၐ
Pierwsze rozwiązanie jest zerowe
B=ၐ/Re ; B2=(ၐ/Re)2
၆=(e/r)sin(ၐ/Re)r
![]()
![]()
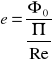
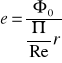
PRZEMIANA ENERGII CIEPLNEJ W ENERGIĘ MECHANICZNĄ
Entalpia jest stała gdy procesy są bez zmian.
Wymiarem jest s[kJ/kgk]
Obieg Carnota składa się z 2 izotermii i 2 izotrop
၄Q1 - powierzchnie 3'-3-4-1-2-2'-3'
၄Q2 - powierzchnie 3'-3-2-2'-3'
၄Q1-၄Q2=၄L
Obiekt ten będzie miał największą sprawność wtedy gdy nie będzie w nim strat.
၄LMAX=၄Q1-၄Q2
Strat nie będzie gdy
ၓs=၄s1-၄s2=0
Przyrost entalpii = 0
၄s1=၄s2
၄s1=၄Q1/TG
၄s2=၄Q2/TG
၄LMAX=၄Q1-၄s2Td
၄LMAX=၄Q1-၄s1Td
၄LMAX=၄Q1-၄Q2/TG
၄LMAX=၄Q1-၄Q1*(TG/Td)
Sprawność
ၨ=၄LMAX/၄Q1=1-(Td/TG) - wzór ten w praktyce nie jest wykorzystywany
3-3a pompowanie wody
3a-4 podgrzewanie wody w kotle
4-5 odparowanie wody
5-1 podgrzewanie pary
1-2 rozprężanie pary w turbinie
2-3 oddawanie ciepła (skroplenie w kondensatorze)
W praktyce stosuje się wykres i(s)
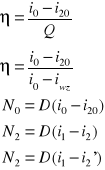
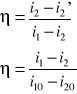
ၨi - sprawność wewnętrzna turbiny
ၨr - sprawność termodynamiczna rurociągu
ၨelektrowni =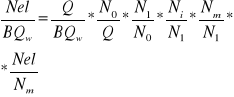
BQw - energia chemiczna paliwa dostarczonego do kotła
Sprawność kotła
![]()
Sprawność teoretyczna obiegu
![]()
Sprawność rurociągu
![]()
Sprawność wewnętrzna turbiny
![]()
Sprawność turbiny
![]()
Sprawność generatora
![]()
ηel=ηkηTηrηiηmηg
ηi obwodu=ηTηrηi
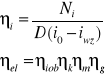
Metody podwyższania ηT
regeneracyjne podgrzewanie wody zasilającej
międzystopniowe przegrzewanie pary
Bilans dla turbiny:
Di1=Dik'+Ni
D(i1- ik)=Nel/[(ηmηg)]
Nel =[kW]
i1=[kJ/kg]
i'k=[kJ/kg]
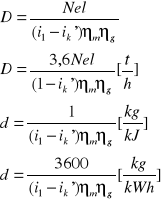
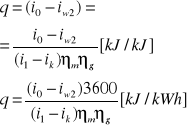
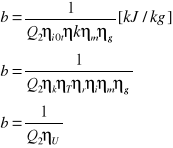
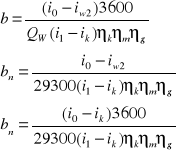
Ad.a Ad.a) część pary nie idzie do kondensatora
Di1=Duik'+Dkik'+Ni
Dk=Dk -Du
Di1=Duik'+Dkik'+(Nel/ηmηg)
D(i1-ik)-Du(iu'-ik')-[(Nel)/(ηmηg)]
Du=αuD
D(i1-ik)-αuD(iu'-ik')-[(Nel)/(ηmηg)]
D[(i1-ik')-αuD(iu'-ik')-[(Nel)/(ηmηg)]
i1-ik=Mk iu'-ik'=HkHu
D{(i1-ik')[1-αu(iu'-ik')/(i1-ik)]}=Nel/(ηmηg)
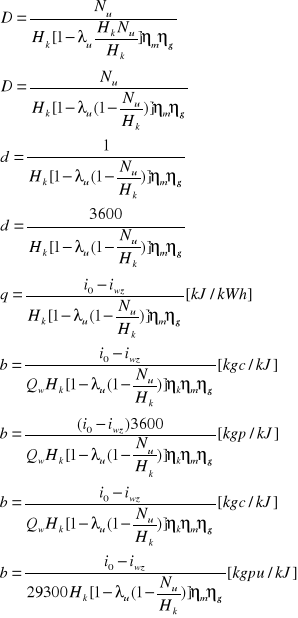
Hu1=i1-iu'1
Hu2=i1-iu'2
Hun-1=i1-iun-1
Hun=i1-i'u1
Hk=i1-ik'
Du1/D=λu1 ; Du2/D=λu2
Dun-1/D=λun-1 ; Dun/D=λun
Dk/D=λuk
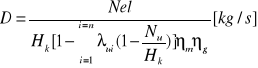
Ad.b) para po wykonaniu pracy w części wysokopojemnej
Di1+Di3=Di2'+Diu'+N0/ηmηg
D= [(i1-i2')+( i3-iu')]=N0/ηmηg
D= Nel/[(i1-i2')+( i3-iu')]=N0/ηmηg
D= Nel[(i1-i2')+( i3-iu')]ηmηg
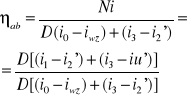
|
a |
b |
Ilość w Polsce |
TK50 |
+ |
- |
15 |
TK120 |
+ |
+ |
24 |
TK200 |
+ |
+ |
62 |
TK360 |
+ |
+ |
16 |
TK500 |
+ |
+ |
2 |
…………UKŁADY CIEPLNE ELEKTROCIEPŁOWNI
1)Układ z turbiną upustową - kondensacyjną
N0
N
H
t
N
1T1/2 2T1/2 3T1/2
Rdzeń reaktora
1 2 3
90
140
60 (Fe, Cu)
[MeV] Ew/A
A
5
1 Ew/A = f(A)
10
dx
Ix
I0
0,1 eV
1000 eV
0,1 MeV
10 MeV
termiczne
rezonansowe
prędkie
zderzenia
sprężyste
zderzenia sprężyste i niesprężyste
σa
σa>σs
σs
σa>>σs
σt ≈ σs
ϑ
Φ
Vn2C
180°- Φ
Vn2L
Vn2C , V0 , Vn2L
n(V)
Vp
Zmiana anizotropii na izotropowość
Z teorii transportu
Ix+dx
Iy+dy
Ix+dx
Iy
Ix
dx
dx
dz
dy
Iz+dz
N
u238
Nၥ
NၥPf(1-p)
N*ၥ-Pf
NၥPfp
NၥPf(1-Ptn)
NၥPfpPtn
NၥPfpPtn(1-f)
NၥPfpPtnf
NၥPfpPtnfၨ
NၥP1PfpPtnf(1-ၨ)
Nၥ(1-Df)
czas
En
C
B
A
၆R
၆0
ၬe
3S1
3S2
3,4 - sprzężenie
4,1 - izotermy
1,2 - izotopy
၄S1
1
2
3
4
Tg
Ty
၄S2
2
1
ၓ
i0
Iw2
i1
~
3a
3
5
3
Punkt
Ⴗ krytyczny
Para nasycona
Para przegrzana
4
3a
2
1
s
T
s
T
2
3
3a
4
5
1
3
i1-i2
ၨr=-------
i1-i3
i0
t0
t1
i20
i2'
P2
I2'
P0
s
i
MK=i1-iu'
MK=i1-ik'
MK
MK
MK
i1'
i1
iu'
iu
iK'
iK'
ၓ
~
Dc
Du1
Du2
Dun-1
Dun
c
In'
I3
ၓ
i0
Iw2
~
i1
i2
rozpr.
rozpr.
przegrz.
Wyszukiwarka