Ćwiczenie 25

Temat: Wyznaczanie stosunku C_P do C_V dla powietrza i dwutlenku węgla metodą akustyczną.

Wprowadzenie teoretyczne

1. Powstawanie i własności fal dźwiękowych.

2. Równanie różniczkowe fali płaskiej i jego rozwiązanie. Wyprowadzenie wzoru na prędkość dźwięku w gazie.

3. Fale stojące.

4. Kinetyczno-molekularna teoria ciepła właściwego gazu.

5. Zasada ekwipartycji energii (Maxwell).

6. Maxwell'owski rozkład prędkości.

7. Prędkość średnia kwadratowa drobin gazu.

8. Prawa gazowe.

Powstawanie i własności fal dźwiękowych

Fale dźwiękowe są podłużnymi falami mechanicznymi. Mogą one rozchodzić się w ciałach stałych, cieczach i gazach. Materialne cząstki ośrodka, w którym rozchodzi się fala, drgają wzdłuż prostej pokrywającej się z kierunkiem propagacji tej fali. Częstotliwość fal dźwiękowych, słyszalnych dla ucha ludzkiego, rozciąga się od około 20 Hz do 20 000 Hz. Fale słyszalne powstają w wyniku drgań strun, słupów powietrza, płyt i membran. Wszystkie te elementy drgające na przemian zgęszczają i rozrzedzają otaczające je powietrze.

Wyprowadzenie wzoru na prędkość dźwięku w gazie

parametr ściśliwości :

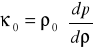
, gdzie

W przypadku gdy ośrodkiem jest gaz, np. powietrze:

Fale stojące

Fale podłużne biegnące w rurze odbijają się od jej końców. Interferencja pomiędzy falami biegnącymi w przeciwnych kierunkach prowadzi do wytworzenia się fali stojącej podłużnej.

Kinetyczno-molekularna teoria ciepła właściwego gazu

Energia wewnętrzna gazu doskonałego jest proporcjonalna do temperatury w skali Kelvina i zależy wyłącznie od tej temperatury:

,

gdzie N - liczba cząstek,

k - stała Boltzmana,

T - temperatura.

Wzór ten jest prawdziwy tylko dla gazów jednoatomowych. Ciepłem właściwym substancji nazywamy ciepło, które trzeba dostarczyć do jednostki masy tej substancji, aby spowodować jednostkową zmianę temperatury.

Założenia teorii kinetyczno-molekularnej:

1. Gaz składa się z cząsteczek, które można traktować jako punkty materialne.

2. Cząsteczki poruszają się chaotycznie i podlegają zasadom dynamiki Newtona.

3. Całkowita liczba cząsteczek jest bardzo duża.

4. Objętość cząsteczek jest tak małą częścią objętości zajmowanej przez gaz, że można ją pominąć.

5. Poza momentem zderzenia na cząsteczki nie działają żadne siły.

6. Zderzenia są sprężyste, a czas ich trwania można pominąć.

Zasada ekwipartycji energii (Maxwell)

Całkowita energia układu składającego się z wielkiej liczby cząsteczek, z których każda jest obiektem mającym strukturę wewnętrzną, składa się z kinetycznej energii ruchu postępowego, z kinetycznej energii rotacji, z kinetycznej energii drgań atomów tworzących cząsteczkę oraz z energii potencjalnej drgań atomów. Na podstawie mechaniki statystycznej można wykazać, że gdy liczba punktów materialnych jest bardzo duża i obowiązuje mechanika newtonowska, wówczas wszystkie te wyrazy mają taką samą wartość średnią i ta średnia wartość zależy wyłącznie od temperatury. Jest to zasada ekwipartycji energii. Każdy z takich niezależnych sposobów absorbcji energii nazywany jest stopniem swobody.

Maxwell'owski rozkład prędkości

Clerk Maxwell pierwszy rozwiązał zagadnienie najbardziej prawdopodobnego rozkładu prędkości wielkiej liczby cząsteczek gazu. Jego prawo rozkładu prędkości cząsteczek, dla próbki gazu zawierającej N cząstek ma postać:

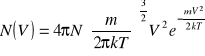
W tym równaniu N(V)dV jest liczbą cząsteczek w próbce gazu mających prędkości zawarte między V a V+ dV. T jest temperaturą bezwzględną, k stałą Boltzmana, m masa cząsteczki. Zauważmy, że dla dowolnego gazu rozkład prędkości zależy tylko od temperatury. Całkowitą liczbę cząsteczek w próbce N znajdujemy całkując liczby odpowiadające każdemu różniczkowemu przedziałowi prędkości od 0 do ∞, czyli

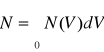
Prędkość średnia kwadratowa drobin gazu

gdzie p - ciśnienie gazu, ρ - gęstość gazu, - średni kwadrat prędkości.

Prawa gazowe

- Przemiana izotermiczna. Prawo Boyle'a-Mariotte'a : (T = const)

- Przemiana izobaryczna. Prawo Gay-Lussaca : (p = const)

- Przemiana izochoryczna. Prawo Charlesa : (V = const)

- Przemiana adiabatyczna. Wzór Poissona : (ΔQ = 0),

gdzie p - ciśnienie,

V - objętość,

T - temperatura,

C_P - ciepło właściwe przy stałym ciśnieniu

C_V - ciepło właściwe przy stałej objętości

ΔQ - wymiana ciepła z otoczeniem.

Jeżeli cząsteczka jest obdarzona i stopniami swobody, to jej średnia energia kinetyczna:

W gazie doskonałym nie ma sił wzajemnego oddziaływania między cząsteczkami, a zatem wzajemna energia potencjalna cząsteczek jest równa zero. Dlatego energia wewnętrzna 1 mola gazu doskonałego równa się sumie energii kinetycznych N_A cząsteczek:

Molowe ciepła właściwe C_P i C_V dla gazu doskonałego łatwo można wyznaczyć z równań:

i

Wobec tego

=>

=> ,

gdzie V - prędkość dźwięku,

M - masa cząsteczkowa,

R - stała gazowa,

T - temperatura bezwzględna gazu,

i - liczba stopni swobody molekuły.

---