Wydział: Inżynierii Środowiska	Dzień/godzina Środa / 14:15 - 17:00			Nr zespołu: 4
		Data: 3.III.2004
Nazwisko i Imię	Ocena z przygotowania:		Ocena ze sprawozdania:		Ocena:
Piotr Owczarczyk Jarosław Maślany Marek Paukszto
Prowadzący: Roszko		Podpis prowadzącego:

Badanie odbicia światła od powierzchni diElektryków.

I. Cel ćwiczenia.

Celem ćwiczenia jest określenie wartości natężenia światła odbitego od powierzchni dielektryków dla różnych kątów padania a szczególności wyznaczenie wartości kąta Brewstera i kąta granicznego całkowitego wewnętrznego odbicia oraz na podstawie ich znajomości określenie współczynnika załamania szkła. Celem ćwiczenia jest również sprawdzenie prawa Malusa. Do wykonania ćwiczenia potrzebne są: źródło światła, dwa polaryzatory, stolik goniometryczny, płytki szklane, fotodetektor z miernikiem fotoprądu.

II. Podstawa teoretyczna.

Podstawowymi wiadomościami potrzebnymi do wykonania ćwiczenia jest znajomość definicji fali oraz polaryzacji.

Fale

Fale są to przemieszczające się w przestrzeni zaburzenia wielkości fizycznych. Światło również jest falą, przy czym wielkościami, które ulegają zmianie są natężenie pól elektrycznego i magnetycznego. Najprostszym do opisu rodzajem takiej fali elektromagnetycznej jest zaburzenie okresowe o częstości  nazywane falą monochromatyczną. Natężenie pola elektrycznego dla fali monochromatycznej w dowolnym punkcie przestrzeni zmienia się w czasie proporcjonalnie do funkcji cos(t) i oscylacje te przesuwają się w przestrzeni ze stałą prędkością v. Wektor natężenia pola elektrycznego E monochromatycznej fali elektromagnetycznej opisywany jest wzorem:

E₀ - amplituda natężenia pola elektrycznego,

(tkx) - fazą fali

k= /v - liczbą falową.

Natężenie pola elektrycznego, ze względu na szybkość zmian, jest nie możliwe do pomierzenia. Dlatego Wielkością mierzalną jest natężenie światła, określające średnią wartość energii fali elektromagnetycznej padającej na detektor. Natężenie światła jest liczbowo proporcjonalne do kwadratu amplitudy natężenia pola elektrycznego.

Polaryzacja światła.

Jeżeli kierunki drgań wektora natężenia pola elektrycznego i magnetycznego zmieniają się w sposób przypadkowy, to światło nie jest spolaryzowane. Dla światła spolaryzowanego kierunek wektorów natężenia pola jest stały lub zmienia się w sposób ściśle określony. Zjawisko polaryzacji występuje tylko w przypadku fal poprzecznych, a taką jest właśnie fala świetlna. Wyróżniamy polaryzację liniową, kołową, eliptyczną. Natężenie światła przechodzącego przez polaryzator wynosi:

I = I₀cos²θ - prawo Malusa

I₀ - natężenie światła spolaryzowanego

θ - kąt między osią analizatora, a kierunkiem padającego światła

Odbicie i załamanie fali w dialektrykach.

Dialektyki to takie ośrodki, w których nie ma swobodnie poruszających się ładunków, a pole elektryczne zewnętrze rozsuwa ładunki ujemne i dodatnie tworząc dipole elektryczne. Na skutek nakładania się fali pierwotnej i wtórnej (wytworzonej przez dipole elektryczne cząstek ośrodka pobudzonych do drgań) prędkość rozchodzenia się światła w dielektrykach jest mniejsza od prędkości światła w próżni. Przy przejściu z jednego ośrodka do drugiego fala świetlna ulega załamaniu i pojawia się dodatkowo fala odbita. Związany z tym jest współczynnik załamania światła danego ośrodka:

C - prędkość światła w próżni

V - prędkość w badanym ośrodku

Światło przechodzące z jednego ośrodka do drugiego o innym współczynniku załamania ulega częściowemu odbiciu i załamaniu. Nie dzieję się to jednak w sposób dowolny. Zachodzi tu zależność, w której kąt padania równa się kątowi odbicia fali. Z kolei zależności pomiędzy kątem padania a załamania określa prawo Snelliusa, czyli prawo załamania światła:

Kąt graniczny i kąt Brewstera

Katem Brewstera nazywamy taki kąt pomiędzy promieniami odbitymi i załamanymi, który wynosi 90°. Dokładniej kąt Brewstera to kąt, dla którego nie ma fali odbitej w polaryzacji  (polaryzacji, dla której wektor natężenia pola elektrycznego leży w płaszczyźnie padania). Odpowiadający kątowi Brewstera _B kąt załamania wynosi  =90^O - _B, czyli po wstawieniu do prawa załamania otrzymuje się:

Odbicie światła na granicy dwóch różnych ośrodków występuje zawsze, oprócz przypadku zjawiska Brewstera. Przechodzenie światła do drugiego ośrodka i obserwowany przy tym efekt załamania może się natomiast odbywać tylko w pewnym zakresie kątów padania i tu pojawia się kąt graniczny, dla którego fala załamana porusza się wzdłuż granicy rozdzielającej oba ośrodki, tzn.  =90°, co po wstawieniu do wzoru Snelliusa prowadzi do wyniku:

Z tego można wywnioskować, że kąt graniczny występuje, gdy fala pada z ośrodka o większym współczynniku załamania na ośrodek o mniejszym współczynniku załamania (n₁/n₂>1).

III. Schemat

IV. Prawo Malusa

[°]	0 ±1	5 ±1	10 ±1	15 ±1	20 ±1	25 ±1	30 ±1	35 ±1	40 ±1	45 ±1	50 ±1	55 ±1	60 ±1	65 ±1	70 ±1	75 ±1	80 ±1	85 ±1	90 ±1
mA	17,5	16,5	15,5	15,3	14,5	13,5	12,5	11	9,75	8	6,75	5,5	4	3	2	1,5	1	1	1,25
[°]	95 ±1	100 ±1	105 ±1	110 ±1	115 ±1	120 ±1	125 ±1	130 ±1	135 ±1	140 ±1	145 ±1	150 ±1	155 ±1	160 ±1	165 ±1	170 ±1	175 ±1	180 ±1
mA	1,5	2,5	3,25	4,5	5,75	7	8,25	10	11,3	12,3	13,5	14	15	15,8	16,3	16,5	16,8	17,5

Odczytując z wykresu:

I_max1 = 17,5 mA dla α = 180°

I_½max1 = 8,75 mA dla α = 127°

Obróciliśmy polaryzator o kąt 53°

I_max2 = 17,5 mA dla α = 0°

I_½max2 = 8,75mA dla α = 47°

Obróciliśmy polaryzator o kąt 47°

Z obliczeń teoretycznych:

I = I₀cos²θ

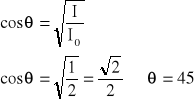
V. Wykresy polaryzacji π i γ

Polaryzacja	kąt	25° ±1	30° ±1	35° ±1	40° ±1	45° ±1	50° ±1	56° ±1	60° ±1	65° ±1	70° ±1	75° ±1	80° ±1	85° ±1	90° ±1
π	I[mA]	0,4	0,5	0,2	0,15	0,1	0,05	0,02	0,07	0,3	0,5	0,9	1,5	2	2,9
γ	I[mA]	0,2	0,3	0,35	0,4	0,5	0,6	0,8	1,1	1,7	2	2,2	2,4	2,7	3

VI. Obliczenia

Współczynnik załamania światła w szkle:

Znając kąt Brewstera:

Domyślając się z wykresu, mniej więcej gdzie znajduje się kąt Brewstera:

Na podstawie obserwacji doświadczenia oraz wykonanego wykresu dla polaryzacji π Brewstera mieści się w przedziale α є (50°,60°).

Dla α = 50° n₂ = tgαn₁ n₁ = 1 więc n₂ = 1,19

Dla α = 60° n₂ = tgαn₁ n₁ = 1 więc n₂ = 1,73

Czyli n₂ є (1,19; 1,73). Średni współczynnik załamania wychodzi, więc n₂ = 1,46.

Dokładnie analizując wykres i pomiary:

Na podstawie pomiarów i wykonanego wykresu obliczyliśmy że kąt Brewstera wynosi 55° ± 1°. Obliczamy współczynnik załamania światła dla szkła:

n₁ - współczynnik załamania światła dla powietrza n₁ = 1

n₂ - współczynnik załamania światła dla szkła

Obliczony współczynnik wynosi: n₂ = tgα_B = 1,43

Ze wzoru na różniczkę zupełną obliczamy błąd w wyznaczaniu współczynnika załamania światła:

Dane: Δα = 1° = 0,0167

Więc wynik ostateczny wynosi: n2 = 1,43 ± 0,05

W rzeczywistości współczynnik załamania światła w szkle wynosi 1,4.

Znając kąt graniczny całkowitego wewnętrznego odbicia:

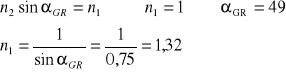
VII. Wnioski

W ćwiczeniu wyznaczyliśmy dwoma innymi sposobami współczynnik załamani światła w szkle. Oba wyniki nieznacznie różnią się między sobą i są porównywalne z analogicznymi wartościami zamieszczonych w tablicach. Drugą częścią ćwiczenia było sprawdzenie prawa Malusa: I = I₀cos²θ. Kąt θ jest kątem, o jaki trzeba obrócić polaryzator, aby wartość natężenia światła spadła o połowę. Wynika z tego, że:
. Uzyskana przez nas wartość 47° jest wartością zbliżoną do wynikającej z prawa Malusa, a więc można powiedzieć, że zgodną z tym prawem. Niewielki błąd, jakiego się dopuściliśmy wynikł z niedokładności naszych pomiarów oraz z niedokładnym odczytywaniem wartości z miernika fotoprądu, który zmylony światłem białym (lamki, światło górne) podawał inne od prawdy wartości. Poza tym światło lasera docierające do fotoelementu nie było skupione na małej powierzchni, utrudniało to wyznaczenie badanego natężenia światła. Oba czynniki wpłynęły na dokładność pomiaru i obarczone były błędem.

- 1 -

---