Politechnika Łódzka

Filia w Bielsku-Białej

Wydział Fizyki Technicznej

Informatyki i Matematyki Stosowanej

Semestr II rok 1998/99

ĆWICZENIE NR 15

WYZNACZANIE PRĘDKOŚCI DZWIĘKU W POWIETRZU I CIAŁACH STAŁYCH

Paweł Bartoszek

Sebastian Górka

Piotr Handzlik

1. CZĘŚĆ TEORETYCZNA

• FALA

Przez falę w ośrodku stałym, ciekłym czy gazowym rozumiemy rozchodzenie się zaburzeń ośrodka wywołanych lokalnie. Rozchodzeniu się fal w ośrodku towarzyszy transport energii. Jeśli źródło fali wywołuje ruch harmoniczny cząstek ośrodka, mówimy o fali harmonicznej.

Równanie fali harmonicznej ma postać:

A - amplituda wychylenia cząstek ośrodka, T - okres drgań cząstek ośrodka [s],

- oznacza częstość kołową, v - prędkość rozchodzenia się fali [m/s].

ν - częstość [1/s],

Graficznym przedstawieniem równania fali zarówno w funkcji czasu przy ustalonym x,

jak i w funkcji x przy ustalonej chwili t jest sinusoida jak na rysunku poniżej.

y(t)

t

T

y(x)

x

λ

Powyższe równanie fali dotyczy fali płaskiej (występuje tylko jedna współrzędna miejsca - x)

Oznacza to, że czoło fali przemieszcza się w dodatnim kierunku osi OX dla znaku `-`

i ujemnym dla znaku `+'. Dla zadanej wartości x, np. x = x₁ wychylenia wszystkich punktów ośrodka leżących na płaszczyźnie x = x₁ są takie same. Mówimy, że płaszczyzna x = x₁ jest płaszczyzną stałej fazy ruchu (czoło fali), przez fazę zaś rozumiemy argument

funkcji cos, a więc :

• INTERFERENCJA FAL

Jeżeli w ośrodku rozchodzi się kilka fal, które np. rozchodzą się w wzdłuż osi OX, to fale te oddziaływają ze sobą w złożony sposób. Gdy źródło każdej z fal wytwarza falę w krótkim przedziale czasu i gdy czasy rozpoczęcia emisji fal są przypadkowe, wówczas otrzymany ciąg fal jest niespójny i mówimy, że mamy do czynienia z superpozycją fal. Przykład niespójnego ciągu fal przedstawiono na rysunku poniżej.

y(t)

¾ Tω

½ Tω

ωt

Niespójność polega na tym, że przy złożeniu poszczególnych fal występują skokowe, różne zmiany fazy, np.: pomiędzy 1 i 2 jest ¼ ωT, zaś pomiędzy 2 i 3 jest ½ ωT. Jeśli przesunięcia

w fazie dla wszystkich fal są takie same, to ciąg fal nazywamy spójnym. Oddziaływanie fal niespójnych nazywamy superpozycją fal, natomiast oddziaływanie fal spójnych nazywamy interferencją.

• FALE STOJĄCE

Równania dwóch fal płaskich biegnących w przeciwnych kierunkach mają postać:

Amplitudy obu fal są takie same, takie same są również częstotliwości kołowe drgań.

Złożenie obu fal daje wyrażenie:

Pierwsza część tego równania opisuje amplitudę fali. Amplituda ma wartość zerową jeśli:

, n = 1,2,3, ...

oznacza to, że w miejscach
cząstki ośrodka znajdują się w spoczynku.

Miejsca te nazywamy węzłami fali. Amplituda fali ma wartość maksymalną gdy:

tzn. dla

Miejsca maksymalnej amplitudy fali nazywamy strzałkami.

Fala stojąca może powstać jeśli fala padająca ulega odbiciu i fala odbita interferuje z falą padającą. Odbicie fali od ośrodka gęstszego następuje ze zmianą fazy o π, zaś odbicie od ośrodka rzadszego następuje bez zmiany fazy.

y(x)

λ/2

x

x = λ

x = λ/4 x = λ/2

2. PRZEBIEG DOŚWIADCZENIA I OBLICZENIA

• Pomiar prędkości fali dzwiękowej metodą Quinckiego

Do pomiaru prędkości dźwięku w różnych ośrodkach wykorzystano metodę rezonansu mającego miejsce wtedy gdy częstotliwość drgań źródła wzbudzającego drgania pokrywa się z jedną z częstotliwości drgań własnych wzbudzanego układu.

Do pomiarów w powietrzu zastosowano układ Quinckiego. Wykorzystano tutaj rezonans akustyczny zachodzący pomiędzy drgającym kamertonem a drganiami słupa powietrza nad woda w rurze. Zmierzono odległość h pomiędzy dwoma położeniami poziomu cieczy dla których słychać w słuchawce wzmocnienia dźwięku.

Prędkość fali wyznaczamy wtedy ze wzoru:

gdzie: h₁ , h₂ - wysokości słupa powietrza dla których słyszalne były wzmocnienia,

ν_k - częstość drgań własnych kamertonu.

Samo doświadczenie polegało na wzbudzeniu kamertonu do drgań i podnoszeniu poziomu cieczy w rurze (poprzez naczynia połączone) oraz na równoczesnym nasłuchiwaniu wzmocnienia dzwięku.

Obliczenia i pomiary

TAB.1

h 1	h2	νk	h	v	Δv
m	m	Hz	m	m/s	m/s
0,220	0,605	435	0,385	334,95	5,22
0,215	0,600	435	0,385	334,95	5,22

Błąd pomiaru: Δh = Δh₁ = Δh₂ =0,003 m Poniżej przykładowe obliczenia:

=2*h=0,770
=334,95 m/s

• Pomiar prędkości fali dzwiękowej w prętach metalowych

(na przykładzie aluminium i miedzi)

Do pomiarów prędkości fali w prętach wykorzystano rurę Kundta, w której zachodzi rezonans między drganiami podłużnymi w pręcie wykonanym z badanego materiału i drganiami słupa powietrza w rurze ograniczonego płytką kończącą pręt i zakończeniem przysłony. Długości fali w powietrzu i pręcie wyznaczamy z zależności:

gdzie: n - ilość połówek fali stojącej w słupie powietrza o długości L,

l - długość badanego pręta.

Prędkość fali wyznaczamy ze wzoru:

Prędkość v₁ zależy od gęstości materiału p i modułu Younga E:

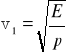
Doświadczenie polega na umocowaniu pręta w rurze z wysypanymi opiłkami korka. Po wywołaniu drgań podłużnych pręta za pomocą sukna z kalafonią powstaje rezonans sygnalizowany charakterystycznym ułożeniem się opiłek korka.

Obliczenia i pomiary

TAB.2

Nazwa pręta	l	Δl	L	ΔL	n	v 1	Δv 1	E	ΔE
	m	M	m	M		m/s	m/s	N/m^2	N/m^2
miedziany	0,923	0,005	0,085	0,01	11	3,63716*10^3
aluminiowy	0,933	0,005	0,063	0,01	15	4,96045*10^3

Długość Rury=0,945 m

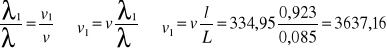
Przykładowe obliczenia dla miedzi:

=

* * *

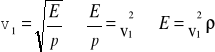
• Prędkość dźwięku w :

-powietrzu v = 339 ± 8,7

-powietrzu v = 343 ± 8,7

-aluminium v₁ = 4956,9 ± 238

-miedzi v₁ = 3712,8 ± 138

• Moduł Younga dla :

-aluminium E = 6,68 * 10¹⁰ ± 1,62 * 10¹⁰

-miedzi E = 12,3 * 10¹⁰ ± 9,14 * 10⁹

• WZORY UŻYWANE DO OBLICZEŃ :

3. WNIOSKI KOŃCOWE

Największy wpływ na dokładność pomiarów miały:

• dokładność odczytu wysokości wzmocnienia fali w układzie Quinckiego wywołana określoną czułością ucha ludzkiego,

• dokładność pomiaru długości prętów używanych w drugiej części ćwiczenia wynikająca

z błędu paralaksy odczytującego,

• stopień dokładności subiektywnego oszacowania maksimów fali stojącej w rurze Kundta oraz stopień dokładności pomiaru odległości pomiędzy nimi.

Pośredni wpływ na dokładność obliczeń miały też oszacowane niedokładności Δl oraz ΔL.

Jak widać z dokonanych obliczeń, prędkość dźwięku w powietrzu, jest zgodna z wielkością tablicowa ( = 343
) w granicach założonego błędu. Natomiast prędkości dźwięku w badanych prętach odbiegają od wielkości tablicowych ( aluminium v = 6420
, miedź v = 5100
).Uzyskane wyniki świadczą , o zbyt optymistycznie oszacowanym błędzie ΔL i bardzo dużej niedokładności metody wyznaczania prędkości fali w prętach. Wyznaczone wartości modułu Younga są zgodne z wielkościami tablicowymi w granicach podanych błędów ( aluminium E = 7,05 *10¹⁰
, miedź E = 10,5 - 13,0 *10¹⁰
).

Dla rezonansu, znając λ i v materiału i powietrza

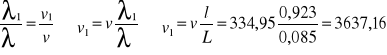
ρ aluminium =2,699 g/

ρ miedzi =8,96 g/

---