Mariusz SZTABIŃSKI

A.O.R sem.VIII

Ćwiczenie 6

Dyskretne przekształcenie Fouriera - DFT i szybkie przekształcenie Fouriera FFT.

1. Dyskretne przekształcenie Fouriera - DFT.

x[n]={1,2,3,4,5,0,0,0} n=0,1...,7

y[n]= x[n+2]

Z powyższych wykresów możemy stwierdzić ,że dyskretne widmo amplitudowe ciągów x[n] i y[n]

jest takie samo .Charakterystyki fazowe ,rzeczywiste ,urojone są zupełnie inne wartości. Przesunięcie

ciągu powoduje, że widmo amplitudowe nie ulega zmianie.

FOLD (obrót kołowy) - powoduje wyznaczenie x[-n], t.zn. obracamy ciąg x[n] , tworzymy jego przedłużenie . okresowe , wykorzystujemy próbki z przedziału 0 < n < N-1.

SELF-CONVOULUTION - powoduje wyznaczenie x[n] x[n] (splot kołowy w dziedzinie „n”)

Splotowi kołowemu w dziedzinie „n” odpowiada mnożenie transformat po stronie transformaty DFT

x[n] x[n] = X[k]
X[k]

SELF-PRODUCT - wyznacza x² [n]

Mnożenie w dziedzinie „n” odpowiada splotowi

x[n] x[n] =
X[k]*Y[k]

MODULATION - wyznacza ciąg : y[n]= x[n] cos[2
n
]

Przyjmujemy, że m=2 . Ciąg y[n] powstał przez wymnożenie kolejnych próbek x[n] przez 1,0,-1,0.

2. Szybkie przekształcenie Fouriera.

1. cos(0.2
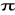
   n)+cos(0.22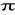
   n)+cos(0.6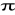
   n) o dł. N=25,50,75,100.

Okno prostokątne ma najmniejszą rozdzielczość ,ponieważ listek główny jego widma jest najwęższy. Inne okna wymagają większej długości N, przy czym zwiększeniu N musi towarzyszyć większa liczba próbek sygnału i nie można tego osiągnąć przez uzupełnianie zerami.

Okno Boxcar 680

Hamming 760

Von Hann 780

Bartlett 760 dla padded length = 2000

Blackman 830

Powyższa zestawienie przedstawia dł. okna pozwalającą wykryć wszystkie trzy cosinusoidy w widmie FFT.

b) cos(2
t)

Ustawiając padded length=10 możemy zaobserwować tylko dwa prążki o wartości 0.5 dla

częstotliwości 1 kHz. Przy zwiększeniu padded length i zwiększeniu liczby próbek sygnału obserwujemy dodatkowe składowe częstotliwościowe (fałszywe) - jest to przeciek widma.

Przecieku widma można uniknąć, gdy signal length, paddad length,samp rate będą takie same lub gdy

przy szybkości próbkowania 10 Hz, paddaed length i signal length będą wielokrotnościami 10.

c) cos(18
t)

dla signal length i padded length=10, obserwujemy widmo amplitudowe syg. o częstotliwości

1 Hz ,a nie 9Hz (jak powinno być), jest to skutek nakładania się widma. Efekt ten jest widoczny dla

szybkości próbkowania 10 Hz. By uniknąć nakładania się widma należy dobrać odpowiednia wartość częstotliwości próbkowania zgodnie z twierdzeniem o próbkowaniu.

d) Stosując różne okna do analizy sygnałów można uzyskać lepszą rozdzielczość wyokienkowanego widma poprzez zwiększenie liczby próbek.

---