PKT MAT Ciało o znikomych rozmiarach, czasie jego ruchu pomija się zmiany położenia wywołane przez obrót. CIAŁO DOSK SZTYW Ciało stałe, którego 2 dowolne pkt nie zmieniają wzajemnie odległości pod wpływem przyłożonych sił. CIAŁO SWOBOD Ciało swobodne to ciało sztywne mogące poruszać się w przestrzeni. PRZESTRZEN Położenie pkt może być zdef przez podanie 3 dł mierzonych od danego pkt odniesienia w 3 danych kier. CZAS Wlk określająca czas trwania danego zdarzenia. SIŁA Oddziaływanie jednego ciała na drugie. Wywierana bezpośrednio w wyniku kontaktu ciał lub na odległość. Siły zew to siły wywierane na pkt danego układu wywołane działaniem pkt innego układu. Siły wew to siły oddziaływania między pkt mat danego układu. Siły czynne to siły, które wywołują lub starają się wywołać ruch danego ciała. Siły bierne to siły, które wyrażają działanie więzów. WLK SKALAR Wlk skalarne określa się przez podanie ich wartości. WLK WEKTOROWE Wlki wektorowe określa się przez podanie wartości, kierunku i zwrotu. WEKTOR Wektor jest skierowanym odc prostym. Wektor oznaczamy:
,
,
. Dł odc określa moduł wektora (wartość), strzałka określa zwrot wektora, kierunek wektora jest określany przez kierunek odc. Wektorem przeciwnym jest wektor
(wektor o tym samym kierunku, module i przeciwnym zwrocie) DWÓJKA ZEROWA Dwójka zerowa to suma wektora i wektora przeciwnego równa 0. I PRAWO NEWTONA Jeżeli siła wypadkowa działająca na pkt jest równa 0, to pkt ten pozostaje w spoczynku (jeżeli był w spoczynku przed przyłożeniem sił) lub porusza się ze stałą prędkością po linii prostej (jeżeli początkowo był w ruchu) II PRAWO NEWTONA Jeżeli siła wypadkowa działająca na pkt nie jest równa 0, to pkt ten będzie poruszał się z przyspieszeniem proporcjonalnym do wartości tej siły w kierunku tej siły.
III PRAWO NEWTONA Siły wzajemnego oddziaływania między ciałami znajdującymi się w kontakcie mają te same wartości, kierunek działania i przeciwny zwrot. ST SWOBODY

St swobody to możliwość wykonania ruchu niezależnego od innych ruchów. Pkt mat ma na płaszczyźnie 2, a w przestrzeni 3 st swobody. Ciało sztywne ma na płaszczyźnie 3, a w przestrzeni 6 st swobody. WIĘZY

Więzy to warunki ograniczające ruch ciała, w statyce tę funkcję pełnią podpory. RODZAJE PDP

Pdp o znamy kierunku reakcji: pdp gładka, pdp przegubowa przesuwna, cięgno, nieważkie pręty przegubowe. Pdp o nieznanym kierunku reakcji: pdp szorstkie, pdp przegubowa stała, utwierdzenie. ILOCZYN SKALAR 2 WEKTORÓW Iloczynem skalarnym 2 wektorów jest skalar (liczba) o wartości iloczynu modułów mnożonych wektorów i cos kąta zawartego między nimi.
ILOCZYN WEKTOROWY 2 WEKTORÓW Iloczynem wektorowym 2 wektorów jest wektor prostopadły do płaszczyzny utworzonej przez mnożone wektory o module równym iloczynowi modułów tych wektorów przez sin kąta zawartego między nimi.
,
Zwrot wektora dla prostokątnego ukł współrzędnych określa reguła 3 palców prawej dłoni. Iloczyn wektorowy wektorów równoległych jest równy 0. Mnożenie wektorowe wektorów jest nie przemienne. SKRĘTNIKI Skrętnikiem nazywamy ukł 2 wektorów gł wektora sił i wektora gł mom leżących na jednej prostej (wektory leżące na jednej prostej to wektory kolinearne). Prosta, na której leżą gł wektor siły i mom skrętnika nosi nazwę osi centralnej. RÓWNOWAGA SIŁ Z UWZGLĘDNIENIEM TARCIA NP. CIAŁO NA RÓWNI POCHYŁEJ Siła tarcia jest siła stat do pow 2 ciał w kontakcie i przeciwdziałających ruchowi tych ciał względem siebie. Rozróżniamy 2 typy tarcia: tarcie suche (tarcie Culomba), tarcie płynne występujące pomiędzy warstwami płynu poruszającymi się z różnymi prędkościami. Dla ciała pozostającego spoczynku siła tarcia jest mniejsza bądź równa sile tarcia. Gdy siła tarcia osiąga swa maksymalną wartość to mówimy o tarciu całkowicie rozwiniętym.
Ciało znajduje się w równowadze statycznej a warunek analityczny równowagi jest następujący:
,
,
,
,
,
Ciało znajdujące się na równi pochyłej pozostaje w spoczynku, jeżeli kąt nachylenia równi α jest mniejszy od kąta tarcia ρ.
RÓW RUCHU PKT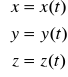
RÓW TORU PKT Poruszający się pkt opisuje w przestrzeni linię, która jest miejscem geometrycznym jego położeń stąd też podane wyżej równania są nazywane także równaniami parametrycznymi toru pkt gdzie parametrem jest czas. Jeżeli z tych równań wyłączymy czas to otrzymamy równanie toru w postaci
. Jeżeli torem ruchu tego pkt jest linia prosta to ruch tego pkt nazywamy prostoliniowym, w odróżnieniu od ruchu krzywoliniowego, którego torem może być dowolna krzywa. RÓW DROGI PKT Jeżeli tor poruszającego się pkt jest znany, to położenie tego pkt można przedstawić określając współrzędną S mierzoną wzdłuż tego toru od pewnego nieruchomego pkt O. Współrzędną S równą długości łuku OA nazywamy drogą pkt A, gdy punkt porusza się po torze, współrzędna S jest funkcją czasu
PRZYSPIESZENIE ŚR PKT Pkt porusza się po torze krzywoliniowym, a jego prędkość zmienia swą wartość. Przyspieszenie śr to stosunek przyrostu wektora prędkości do czasu, w którym ten przyrost nastąpił:
. Wektor przyspieszenia śr ma ten sam kierunek i zwrot jak wektor
PRZYSPIESZENIE CHWILOWE PKT Przyspieszenie chwilowe określamy w następujący sposób:
,
. Wektor przyspieszenia jest równy I pochodnej wektora prędkości lub II pochodnej promienia wektora względem czasu. Jego kierunek i zwrot wynika z kierunków i zwrotów wektorów przyspieszenia normalnego i stycznego. PRZYSPIESZENIE CORIOLISA Równa się podwójnemu iloczynowi wektorowemu, wektora prędkości kątowej w ruchu uniesienia i wektora liniowej prędkości względnej.
. RUCH WZGLĘDNY Ruchy jednych ciał względem drugich także ruchomych nazywamy ruchami względnymi. Ruch każdego ciała może być rozpatrywany jako wielokrotnie względny. RUCH UNOSZENIA Ruchem unoszenia nazywamy ruch układu, względem, którego rozpatrujemy ruch względny. PRZYSPIESZENIE BEZWZGLĘDNE Przyspieszenie bezwzględne w ruchu złożonym pkt jest równe sumie geometrycznej przyspieszenia względnego, przyspieszenia unoszenia i przyspieszenia Coriolisa.
. Jeżeli ruch względny i ruch unoszenia są ruchami krzywoliniowymi, to w ogólnym przypadku każde z tych przyspieszeń ma składową normalną i styczną. RUCH PŁASKI BRYŁY Ruch płaski bryły to taki w trakcie, którego odległość pkt bryły od danej nieruchomej płaszczyzny zwanej płaszczyzną kierującą pozostają jednakowe. Ruch płaski bryły można, więc sprowadzić do ruchu figury będącej rzutem bryły na płaszczyznę kierującą.
,
. Ruch płaski można traktować jako złożenie ruchu postępowego w płaszczyźnie o,x,y i ruchu obrotowego względem osi AZ równoległej do osi OZ. WYZNACZANIE PRĘDKOŚCI PKT BRYŁ W RUCHU PŁASKIM W każdej chwili czasu prędkości pkt bryły są takie, jakby bryła obracała się wokół pewnej osi prostopadłej do płaszczyzny ruchu bryły. Oś tą można nazwać chwilową osią obrotu, a pkt jej przecięcia z płaszczyzną ruchu bryły to chwilowy środek obrotu
,
ZASADA D'ALEMBERTA Z II zasady Newtona wynika następujące równanie
. Jeżeli podstawimy następujący związek
to otrzymamy
. Równanie to opisuje zasadę d'Alemberta, która mówi, że w czasie ruchu pkt mat siły rzeczywiste działające na pkt równoważą się w każdej chwili z odpowiednimi siłami bezwładności. Siła
nosi nazwę siły bezwładności lub d'Alemberta. Równanie wynikające z tej zasady ma formalnie postać równania równowagi. PRACA Rozważa się pkt przemieszczający się z położenia A określonego wektorem
do sąsiedniego położenia A' określonego wektorem
. Jeżeli na pkt działa siła
to praca tej siły odpowiadająca przemieszczaniu
jest definiowana następująca wielkość skalarna
. Praca jest iloczynem skalarnym wektora
i wektora przemieszczenia
. Znajdując kąt α między wektorami
i
, na podstawie definicji iloczynu skalarnego możemy napisać, że:
. Długość wektora
jest różnicą drogi ds. wartość pracy elementarnej może być wyrażana jako
. Praca jako wlk skalarna ma swą wlk i zwrot. Jeśli kąt α jest kątem ostrym to dL ma wartość dodatnią, jeżeli kąt α jest kątem rozwartym to dL ma wartość ujemną. Jeżeli kąt α jest równy 90^o to dL jest równe 0. ENERGIA KINETYCZNA Rozpatruje się ruch pkt o masie m, na który działa siła F, do położenia A₁ pkt przebył drogę s₁ i ma prędkość V₁, w położeniu A₂ jego droga wynosi s₂, a prędkość V₂.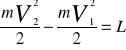
Wielkość skalarną równa połowie iloczynu masy pkt i kwadratem jego prędkości nazywamy energią kinetyczną.

PRAWO RÓWNOŚCI ENERGII KINETYCZNEJ I PRACY Przyrost energii kinetycznej pkt mat w skończonym przedziale czasu równy jest sumie prac, jakie wykonały siły działające na ten pkt funkcji drogi s. ENERGIA POTENCJALNA Praca siły ciężkości jest równa iloczynowi tej siły i przemieszczenia pionowego ∆y. Praca jest dodatnia, jeżeli ∆y<0, czyli wtedy, gdy ciało porusza się w dół. Pracę siły prędkości można przedstawić jako następującą różnice
. Praca ta nie zależy od drogi, a jedynie od początkowej i końcowej wartości funkcji mgy. Funkcję tę nazywamy energią potencjalną:
PRAWO ZACHOWANIA ENERGII MECHANICZNEJ Gdy pkt mat porusza się w zachowawczym polu sił to suma jego energii kinetycznej i energii potencjalnej zwana energią mechaniczną jest wielkością stałą

PKT MAT Ciało o znikomych rozmiarach, czasie jego ruchu pomija się zmiany położenia wywołane przez obrót. CIAŁO DOSK SZTYW Ciało stałe, którego 2 dowolne pkt nie zmieniają wzajemnie odległości pod wpływem przyłożonych sił. CIAŁO SWOBOD Ciało swobodne to ciało sztywne mogące poruszać się w przestrzeni. PRZESTRZEN Położenie pkt może być zdef przez podanie 3 dł mierzonych od danego pkt odniesienia w 3 danych kier. CZAS Wlk określająca czas trwania danego zdarzenia. SIŁA Oddziaływanie jednego ciała na drugie. Wywierana bezpośrednio w wyniku kontaktu ciał lub na odległość. Siły zew to siły wywierane na pkt danego układu wywołane działaniem pkt innego układu. Siły wew to siły oddziaływania między pkt mat danego układu. Siły czynne to siły, które wywołują lub starają się wywołać ruch danego ciała. Siły bierne to siły, które wyrażają działanie więzów. WLK SKALAR Wlk skalarne określa się przez podanie ich wartości. WLK WEKTOROWE Wlki wektorowe określa się przez podanie wartości, kierunku i zwrotu. WEKTOR Wektor jest skierowanym odc prostym. Wektor oznaczamy:
,
,
. Dł odc określa moduł wektora (wartość), strzałka określa zwrot wektora, kierunek wektora jest określany przez kierunek odc. Wektorem przeciwnym jest wektor
(wektor o tym samym kierunku, module i przeciwnym zwrocie) DWÓJKA ZEROWA Dwójka zerowa to suma wektora i wektora przeciwnego równa 0. I PRAWO NEWTONA Jeżeli siła wypadkowa działająca na pkt jest równa 0, to pkt ten pozostaje w spoczynku (jeżeli był w spoczynku przed przyłożeniem sił) lub porusza się ze stałą prędkością po linii prostej (jeżeli początkowo był w ruchu) II PRAWO NEWTONA Jeżeli siła wypadkowa działająca na pkt nie jest równa 0, to pkt ten będzie poruszał się z przyspieszeniem proporcjonalnym do wartości tej siły w kierunku tej siły.
III PRAWO NEWTONA Siły wzajemnego oddziaływania między ciałami znajdującymi się w kontakcie mają te same wartości, kierunek działania i przeciwny zwrot. ST SWOBODY

St swobody to możliwość wykonania ruchu niezależnego od innych ruchów. Pkt mat ma na płaszczyźnie 2, a w przestrzeni 3 st swobody. Ciało sztywne ma na płaszczyźnie 3, a w przestrzeni 6 st swobody. WIĘZY

Więzy to warunki ograniczające ruch ciała, w statyce tę funkcję pełnią podpory. RODZAJE PDP

Pdp o znamy kierunku reakcji: pdp gładka, pdp przegubowa przesuwna, cięgno, nieważkie pręty przegubowe. Pdp o nieznanym kierunku reakcji: pdp szorstkie, pdp przegubowa stała, utwierdzenie. ILOCZYN SKALAR 2 WEKTORÓW Iloczynem skalarnym 2 wektorów jest skalar (liczba) o wartości iloczynu modułów mnożonych wektorów i cos kąta zawartego między nimi.
ILOCZYN WEKTOROWY 2 WEKTORÓW Iloczynem wektorowym 2 wektorów jest wektor prostopadły do płaszczyzny utworzonej przez mnożone wektory o module równym iloczynowi modułów tych wektorów przez sin kąta zawartego między nimi.
,
Zwrot wektora dla prostokątnego ukł współrzędnych określa reguła 3 palców prawej dłoni. Iloczyn wektorowy wektorów równoległych jest równy 0. Mnożenie wektorowe wektorów jest nie przemienne. SKRĘTNIKI Skrętnikiem nazywamy ukł 2 wektorów gł wektora sił i wektora gł mom leżących na jednej prostej (wektory leżące na jednej prostej to wektory kolinearne). Prosta, na której leżą gł wektor siły i mom skrętnika nosi nazwę osi centralnej. RÓWNOWAGA SIŁ Z UWZGLĘDNIENIEM TARCIA NP. CIAŁO NA RÓWNI POCHYŁEJ Siła tarcia jest siła stat do pow 2 ciał w kontakcie i przeciwdziałających ruchowi tych ciał względem siebie. Rozróżniamy 2 typy tarcia: tarcie suche (tarcie Culomba), tarcie płynne występujące pomiędzy warstwami płynu poruszającymi się z różnymi prędkościami. Dla ciała pozostającego spoczynku siła tarcia jest mniejsza bądź równa sile tarcia. Gdy siła tarcia osiąga swa maksymalną wartość to mówimy o tarciu całkowicie rozwiniętym.
Ciało znajduje się w równowadze statycznej a warunek analityczny równowagi jest następujący:
,
,
,
,
,
Ciało znajdujące się na równi pochyłej pozostaje w spoczynku, jeżeli kąt nachylenia równi α jest mniejszy od kąta tarcia ρ.
RÓW RUCHU PKT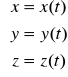
RÓW TORU PKT Poruszający się pkt opisuje w przestrzeni linię, która jest miejscem geometrycznym jego położeń stąd też podane wyżej równania są nazywane także równaniami parametrycznymi toru pkt gdzie parametrem jest czas. Jeżeli z tych równań wyłączymy czas to otrzymamy równanie toru w postaci
. Jeżeli torem ruchu tego pkt jest linia prosta to ruch tego pkt nazywamy prostoliniowym, w odróżnieniu od ruchu krzywoliniowego, którego torem może być dowolna krzywa. RÓW DROGI PKT Jeżeli tor poruszającego się pkt jest znany, to położenie tego pkt można przedstawić określając współrzędną S mierzoną wzdłuż tego toru od pewnego nieruchomego pkt O. Współrzędną S równą długości łuku OA nazywamy drogą pkt A, gdy punkt porusza się po torze, współrzędna S jest funkcją czasu
PRZYSPIESZENIE ŚR PKT Pkt porusza się po torze krzywoliniowym, a jego prędkość zmienia swą wartość. Przyspieszenie śr to stosunek przyrostu wektora prędkości do czasu, w którym ten przyrost nastąpił:
. Wektor przyspieszenia śr ma ten sam kierunek i zwrot jak wektor
PRZYSPIESZENIE CHWILOWE PKT Przyspieszenie chwilowe określamy w następujący sposób:
,
. Wektor przyspieszenia jest równy I pochodnej wektora prędkości lub II pochodnej promienia wektora względem czasu. Jego kierunek i zwrot wynika z kierunków i zwrotów wektorów przyspieszenia normalnego i stycznego. PRZYSPIESZENIE CORIOLISA Równa się podwójnemu iloczynowi wektorowemu, wektora prędkości kątowej w ruchu uniesienia i wektora liniowej prędkości względnej.
. RUCH WZGLĘDNY Ruchy jednych ciał względem drugich także ruchomych nazywamy ruchami względnymi. Ruch każdego ciała może być rozpatrywany jako wielokrotnie względny. RUCH UNOSZENIA Ruchem unoszenia nazywamy ruch układu, względem, którego rozpatrujemy ruch względny. PRZYSPIESZENIE BEZWZGLĘDNE Przyspieszenie bezwzględne w ruchu złożonym pkt jest równe sumie geometrycznej przyspieszenia względnego, przyspieszenia unoszenia i przyspieszenia Coriolisa.
. Jeżeli ruch względny i ruch unoszenia są ruchami krzywoliniowymi, to w ogólnym przypadku każde z tych przyspieszeń ma składową normalną i styczną. RUCH PŁASKI BRYŁY Ruch płaski bryły to taki w trakcie, którego odległość pkt bryły od danej nieruchomej płaszczyzny zwanej płaszczyzną kierującą pozostają jednakowe. Ruch płaski bryły można, więc sprowadzić do ruchu figury będącej rzutem bryły na płaszczyznę kierującą.
,
. Ruch płaski można traktować jako złożenie ruchu postępowego w płaszczyźnie o,x,y i ruchu obrotowego względem osi AZ równoległej do osi OZ. WYZNACZANIE PRĘDKOŚCI PKT BRYŁ W RUCHU PŁASKIM W każdej chwili czasu prędkości pkt bryły są takie, jakby bryła obracała się wokół pewnej osi prostopadłej do płaszczyzny ruchu bryły. Oś tą można nazwać chwilową osią obrotu, a pkt jej przecięcia z płaszczyzną ruchu bryły to chwilowy środek obrotu
,
ZASADA D'ALEMBERTA Z II zasady Newtona wynika następujące równanie
. Jeżeli podstawimy następujący związek
to otrzymamy
. Równanie to opisuje zasadę d'Alemberta, która mówi, że w czasie ruchu pkt mat siły rzeczywiste działające na pkt równoważą się w każdej chwili z odpowiednimi siłami bezwładności. Siła
nosi nazwę siły bezwładności lub d'Alemberta. Równanie wynikające z tej zasady ma formalnie postać równania równowagi. PRACA Rozważa się pkt przemieszczający się z położenia A określonego wektorem
do sąsiedniego położenia A' określonego wektorem
. Jeżeli na pkt działa siła
to praca tej siły odpowiadająca przemieszczaniu
jest definiowana następująca wielkość skalarna
. Praca jest iloczynem skalarnym wektora
i wektora przemieszczenia
. Znajdując kąt α między wektorami
i
, na podstawie definicji iloczynu skalarnego możemy napisać, że:
. Długość wektora
jest różnicą drogi ds. wartość pracy elementarnej może być wyrażana jako
. Praca jako wlk skalarna ma swą wlk i zwrot. Jeśli kąt α jest kątem ostrym to dL ma wartość dodatnią, jeżeli kąt α jest kątem rozwartym to dL ma wartość ujemną. Jeżeli kąt α jest równy 90^o to dL jest równe 0. ENERGIA KINETYCZNA Rozpatruje się ruch pkt o masie m, na który działa siła F, do położenia A₁ pkt przebył drogę s₁ i ma prędkość V₁, w położeniu A₂ jego droga wynosi s₂, a prędkość V₂.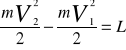
Wielkość skalarną równa połowie iloczynu masy pkt i kwadratem jego prędkości nazywamy energią kinetyczną.

PRAWO RÓWNOŚCI ENERGII KINETYCZNEJ I PRACY Przyrost energii kinetycznej pkt mat w skończonym przedziale czasu równy jest sumie prac, jakie wykonały siły działające na ten pkt funkcji drogi s. ENERGIA POTENCJALNA Praca siły ciężkości jest równa iloczynowi tej siły i przemieszczenia pionowego ∆y. Praca jest dodatnia, jeżeli ∆y<0, czyli wtedy, gdy ciało porusza się w dół. Pracę siły prędkości można przedstawić jako następującą różnice
. Praca ta nie zależy od drogi, a jedynie od początkowej i końcowej wartości funkcji mgy. Funkcję tę nazywamy energią potencjalną:
PRAWO ZACHOWANIA ENERGII MECHANICZNEJ Gdy pkt mat porusza się w zachowawczym polu sił to suma jego energii kinetycznej i energii potencjalnej zwana energią mechaniczną jest wielkością stałą

PKT MAT Ciało o znikomych rozmiarach, czasie jego ruchu pomija się zmiany położenia wywołane przez obrót. CIAŁO DOSK SZTYW Ciało stałe, którego 2 dowolne pkt nie zmieniają wzajemnie odległości pod wpływem przyłożonych sił. CIAŁO SWOBOD Ciało swobodne to ciało sztywne mogące poruszać się w przestrzeni. PRZESTRZEN Położenie pkt może być zdef przez podanie 3 dł mierzonych od danego pkt odniesienia w 3 danych kier. CZAS Wlk określająca czas trwania danego zdarzenia. SIŁA Oddziaływanie jednego ciała na drugie. Wywierana bezpośrednio w wyniku kontaktu ciał lub na odległość. Siły zew to siły wywierane na pkt danego układu wywołane działaniem pkt innego układu. Siły wew to siły oddziaływania między pkt mat danego układu. Siły czynne to siły, które wywołują lub starają się wywołać ruch danego ciała. Siły bierne to siły, które wyrażają działanie więzów. WLK SKALAR Wlk skalarne określa się przez podanie ich wartości. WLK WEKTOROWE Wlki wektorowe określa się przez podanie wartości, kierunku i zwrotu. WEKTOR Wektor jest skierowanym odc prostym. Wektor oznaczamy:
,
,
. Dł odc określa moduł wektora (wartość), strzałka określa zwrot wektora, kierunek wektora jest określany przez kierunek odc. Wektorem przeciwnym jest wektor
(wektor o tym samym kierunku, module i przeciwnym zwrocie) DWÓJKA ZEROWA Dwójka zerowa to suma wektora i wektora przeciwnego równa 0. I PRAWO NEWTONA Jeżeli siła wypadkowa działająca na pkt jest równa 0, to pkt ten pozostaje w spoczynku (jeżeli był w spoczynku przed przyłożeniem sił) lub porusza się ze stałą prędkością po linii prostej (jeżeli początkowo był w ruchu) II PRAWO NEWTONA Jeżeli siła wypadkowa działająca na pkt nie jest równa 0, to pkt ten będzie poruszał się z przyspieszeniem proporcjonalnym do wartości tej siły w kierunku tej siły.
III PRAWO NEWTONA Siły wzajemnego oddziaływania między ciałami znajdującymi się w kontakcie mają te same wartości, kierunek działania i przeciwny zwrot. ST SWOBODY

St swobody to możliwość wykonania ruchu niezależnego od innych ruchów. Pkt mat ma na płaszczyźnie 2, a w przestrzeni 3 st swobody. Ciało sztywne ma na płaszczyźnie 3, a w przestrzeni 6 st swobody. WIĘZY

Więzy to warunki ograniczające ruch ciała, w statyce tę funkcję pełnią podpory. RODZAJE PDP

Pdp o znamy kierunku reakcji: pdp gładka, pdp przegubowa przesuwna, cięgno, nieważkie pręty przegubowe. Pdp o nieznanym kierunku reakcji: pdp szorstkie, pdp przegubowa stała, utwierdzenie. ILOCZYN SKALAR 2 WEKTORÓW Iloczynem skalarnym 2 wektorów jest skalar (liczba) o wartości iloczynu modułów mnożonych wektorów i cos kąta zawartego między nimi.
ILOCZYN WEKTOROWY 2 WEKTORÓW Iloczynem wektorowym 2 wektorów jest wektor prostopadły do płaszczyzny utworzonej przez mnożone wektory o module równym iloczynowi modułów tych wektorów przez sin kąta zawartego między nimi.
,
Zwrot wektora dla prostokątnego ukł współrzędnych określa reguła 3 palców prawej dłoni. Iloczyn wektorowy wektorów równoległych jest równy 0. Mnożenie wektorowe wektorów jest nie przemienne. SKRĘTNIKI Skrętnikiem nazywamy ukł 2 wektorów gł wektora sił i wektora gł mom leżących na jednej prostej (wektory leżące na jednej prostej to wektory kolinearne). Prosta, na której leżą gł wektor siły i mom skrętnika nosi nazwę osi centralnej. RÓWNOWAGA SIŁ Z UWZGLĘDNIENIEM TARCIA NP. CIAŁO NA RÓWNI POCHYŁEJ Siła tarcia jest siła stat do pow 2 ciał w kontakcie i przeciwdziałających ruchowi tych ciał względem siebie. Rozróżniamy 2 typy tarcia: tarcie suche (tarcie Culomba), tarcie płynne występujące pomiędzy warstwami płynu poruszającymi się z różnymi prędkościami. Dla ciała pozostającego spoczynku siła tarcia jest mniejsza bądź równa sile tarcia. Gdy siła tarcia osiąga swa maksymalną wartość to mówimy o tarciu całkowicie rozwiniętym.
Ciało znajduje się w równowadze statycznej a warunek analityczny równowagi jest następujący:
,
,
,
,
,
Ciało znajdujące się na równi pochyłej pozostaje w spoczynku, jeżeli kąt nachylenia równi α jest mniejszy od kąta tarcia ρ.
RÓW RUCHU PKT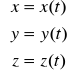
RÓW TORU PKT Poruszający się pkt opisuje w przestrzeni linię, która jest miejscem geometrycznym jego położeń stąd też podane wyżej równania są nazywane także równaniami parametrycznymi toru pkt gdzie parametrem jest czas. Jeżeli z tych równań wyłączymy czas to otrzymamy równanie toru w postaci
. Jeżeli torem ruchu tego pkt jest linia prosta to ruch tego pkt nazywamy prostoliniowym, w odróżnieniu od ruchu krzywoliniowego, którego torem może być dowolna krzywa. RÓW DROGI PKT Jeżeli tor poruszającego się pkt jest znany, to położenie tego pkt można przedstawić określając współrzędną S mierzoną wzdłuż tego toru od pewnego nieruchomego pkt O. Współrzędną S równą długości łuku OA nazywamy drogą pkt A, gdy punkt porusza się po torze, współrzędna S jest funkcją czasu
PRZYSPIESZENIE ŚR PKT Pkt porusza się po torze krzywoliniowym, a jego prędkość zmienia swą wartość. Przyspieszenie śr to stosunek przyrostu wektora prędkości do czasu, w którym ten przyrost nastąpił:
. Wektor przyspieszenia śr ma ten sam kierunek i zwrot jak wektor
PRZYSPIESZENIE CHWILOWE PKT Przyspieszenie chwilowe określamy w następujący sposób:
,
. Wektor przyspieszenia jest równy I pochodnej wektora prędkości lub II pochodnej promienia wektora względem czasu. Jego kierunek i zwrot wynika z kierunków i zwrotów wektorów przyspieszenia normalnego i stycznego. PRZYSPIESZENIE CORIOLISA Równa się podwójnemu iloczynowi wektorowemu, wektora prędkości kątowej w ruchu uniesienia i wektora liniowej prędkości względnej.
. RUCH WZGLĘDNY Ruchy jednych ciał względem drugich także ruchomych nazywamy ruchami względnymi. Ruch każdego ciała może być rozpatrywany jako wielokrotnie względny. RUCH UNOSZENIA Ruchem unoszenia nazywamy ruch układu, względem, którego rozpatrujemy ruch względny. PRZYSPIESZENIE BEZWZGLĘDNE Przyspieszenie bezwzględne w ruchu złożonym pkt jest równe sumie geometrycznej przyspieszenia względnego, przyspieszenia unoszenia i przyspieszenia Coriolisa.
. Jeżeli ruch względny i ruch unoszenia są ruchami krzywoliniowymi, to w ogólnym przypadku każde z tych przyspieszeń ma składową normalną i styczną. RUCH PŁASKI BRYŁY Ruch płaski bryły to taki w trakcie, którego odległość pkt bryły od danej nieruchomej płaszczyzny zwanej płaszczyzną kierującą pozostają jednakowe. Ruch płaski bryły można, więc sprowadzić do ruchu figury będącej rzutem bryły na płaszczyznę kierującą.
,
. Ruch płaski można traktować jako złożenie ruchu postępowego w płaszczyźnie o,x,y i ruchu obrotowego względem osi AZ równoległej do osi OZ. WYZNACZANIE PRĘDKOŚCI PKT BRYŁ W RUCHU PŁASKIM W każdej chwili czasu prędkości pkt bryły są takie, jakby bryła obracała się wokół pewnej osi prostopadłej do płaszczyzny ruchu bryły. Oś tą można nazwać chwilową osią obrotu, a pkt jej przecięcia z płaszczyzną ruchu bryły to chwilowy środek obrotu
,
ZASADA D'ALEMBERTA Z II zasady Newtona wynika następujące równanie
. Jeżeli podstawimy następujący związek
to otrzymamy
. Równanie to opisuje zasadę d'Alemberta, która mówi, że w czasie ruchu pkt mat siły rzeczywiste działające na pkt równoważą się w każdej chwili z odpowiednimi siłami bezwładności. Siła
nosi nazwę siły bezwładności lub d'Alemberta. Równanie wynikające z tej zasady ma formalnie postać równania równowagi. PRACA Rozważa się pkt przemieszczający się z położenia A określonego wektorem
do sąsiedniego położenia A' określonego wektorem
. Jeżeli na pkt działa siła
to praca tej siły odpowiadająca przemieszczaniu
jest definiowana następująca wielkość skalarna
. Praca jest iloczynem skalarnym wektora
i wektora przemieszczenia
. Znajdując kąt α między wektorami
i
, na podstawie definicji iloczynu skalarnego możemy napisać, że:
. Długość wektora
jest różnicą drogi ds. wartość pracy elementarnej może być wyrażana jako
. Praca jako wlk skalarna ma swą wlk i zwrot. Jeśli kąt α jest kątem ostrym to dL ma wartość dodatnią, jeżeli kąt α jest kątem rozwartym to dL ma wartość ujemną. Jeżeli kąt α jest równy 90^o to dL jest równe 0. ENERGIA KINETYCZNA Rozpatruje się ruch pkt o masie m, na który działa siła F, do położenia A₁ pkt przebył drogę s₁ i ma prędkość V₁, w położeniu A₂ jego droga wynosi s₂, a prędkość V₂.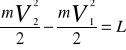
Wielkość skalarną równa połowie iloczynu masy pkt i kwadratem jego prędkości nazywamy energią kinetyczną.

PRAWO RÓWNOŚCI ENERGII KINETYCZNEJ I PRACY Przyrost energii kinetycznej pkt mat w skończonym przedziale czasu równy jest sumie prac, jakie wykonały siły działające na ten pkt funkcji drogi s. ENERGIA POTENCJALNA Praca siły ciężkości jest równa iloczynowi tej siły i przemieszczenia pionowego ∆y. Praca jest dodatnia, jeżeli ∆y<0, czyli wtedy, gdy ciało porusza się w dół. Pracę siły prędkości można przedstawić jako następującą różnice
. Praca ta nie zależy od drogi, a jedynie od początkowej i końcowej wartości funkcji mgy. Funkcję tę nazywamy energią potencjalną:
PRAWO ZACHOWANIA ENERGII MECHANICZNEJ Gdy pkt mat porusza się w zachowawczym polu sił to suma jego energii kinetycznej i energii potencjalnej zwana energią mechaniczną jest wielkością stałą

---