POLITECHNIKA LUBELSKA w LUBLINIE
LABORATORIUM PODSTAW ELEKTROTECHNIKI		Ćwicz. nr 13
TEMAT: Synteza dwójników pasywnych		DATA: 1997.01.
WYKONAŁ: WIESŁAW RYCERZ	GRUPA: ED 3.6	OCENA:

Część teoretyczna:

Problem syntezy dwójnika liniowego pasywnego polega na wyznaczeniu modelu strukturalnego, łącznie z wartościami elementów, odpowiadającego zadanej funkcji F(s). O ile w zagadnieniu analizy danemu dwójnikowi można przyporządkować tylko jedną funkcję immitancji Z(s) lub Y(s), to w zagadnieniu syntezy danej funkcji immitancji odpowiada jeden szereg różnych modeli.

Aby dana funkcja F(s) mogła być realizowana w sensie modelu fizycznego, musi być funkcją wymierną rzeczywistą dodatnią. Niech funkcja F(s), zwana też immitancją lub funkcją przejścia, dana będzie w postaci ilorazu dwóch funkcji rzeczywistych wymiernych o współczynnikach a_k i b_k dodatnich:

Funkcja ta jest wymierną rzeczywistą dodatnią i może być zrealizowana przez model fizyczny gdy spełnia następujące warunki:

Wszystkie współczynniki wielomianów są rzeczywiste i dodatnie.

Bieguny i zera leżą w lewej półpłaszczyźnie lub na osi urojonej a residua w tych biegunach są dodatnie.

Bieguny i zera leżące na osi urojonej są pojedyncze łącznie z punktem s=∞, a residua w tych biegunach są dodatnie.

Stopień licznika i mianownika różnią się co najwyżej o jeden.

Część rzeczywista na osi urojonej spełnia warunek Re F(jw)>0

Warunki te nie uwzględniają możliwości technicznych realizowania układów RLC ze względu na ograniczoną wartość tych elementów.

Jest szereg metod pozwalających na realizację funkcji F(s) spełniających warunki funkcji wymiernej rzeczywistej dodatniej. Wszystkie metody polegają na rozkładzie wielomianów określających daną funkcję i z jego postaci wyciągnięcia wniosków o strukturze odpowiadającego jej modelu.

W przypadku syntezy dwójników liniowych pasywnych istnieją dwie podstawowe metody syntezy:

metoda Fostera, polegająca na kolejnym wydzielaniu biegunów i zer oraz rozkładzie danej immitancji na ułamki proste i przyporządkowaniu tym ułamkom elementarnych obwodów RL, RC, LC oraz RLC,

metoda Cauera, bazująca na rozwinięciu zadanej immitancji w ułamek łańcuchowy i w konsekwencji przyporządkowaniu mu układu drabinkowego elementów.

wykonanie ćwiczenia

Dla zadanych przez prowadzącego ćwiczenia wartości współczynników a_k i b_k dokonujemy syntezy dwójnika z wykorzystaniem programu komputerowego synteza.pas.

Współczynniki wielomianów N(s) i M.(s) wynosiły odpowiednio:

a₃=7,5 b₃=1 R₁=7,5 W R₂=8,2 W C₁=33,7 mF

a₂=0,22 10⁶ b₂=12,2 10³

a₁=0,36 10⁹ b₁=731,7

a₀=21,7 10⁶ b₀=0

a) Wyniki obliczeń w postaci charakterystyki amplitudowej i fazowej:

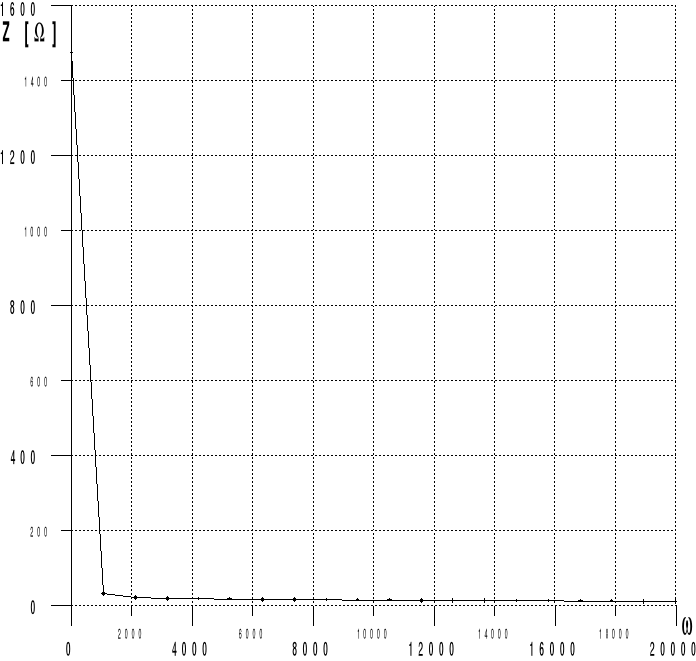
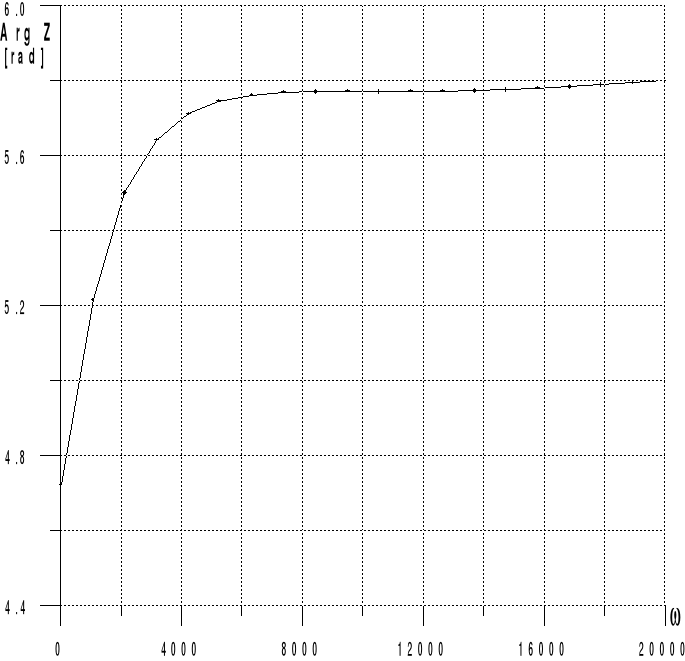
2. Wyznaczenie charakterystyki amplitudowej i fazowej (Z(jw)=f₁(w), argZ argZ(jw)=f₂(w)) dla zadanego dwójnika pasywnego.

Rys. Zadany dwójnik pasywny.

Rys. Układ do badania charakterystyk amplitudowych i fazowych dwójnika pasywnego.

W oparciu o dane elementy: R₁=7,5 W R₂=8,2 W C₁=33,7 mF C₂=10 mF L=0,45 H

stosując metodę Fostera z wykorzystaniem programu komputerowego otrzymujemy charakterystyki odpowiednio amplitudową i fazową:

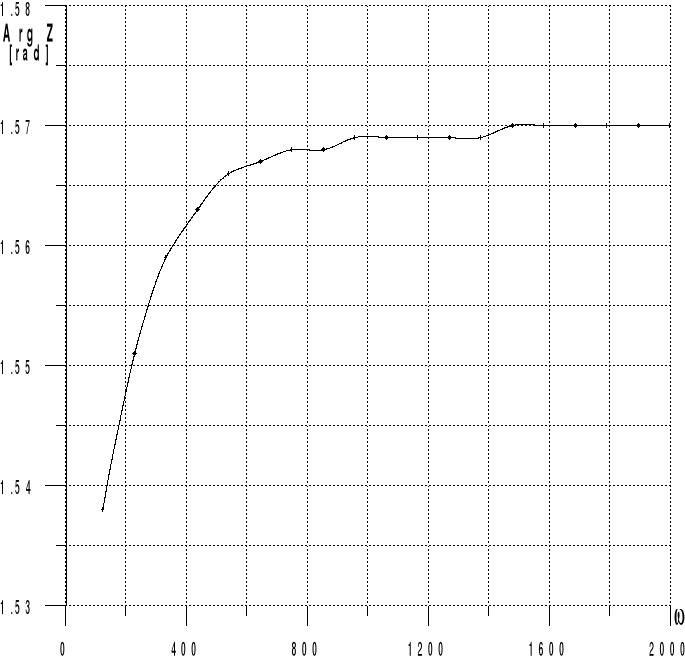
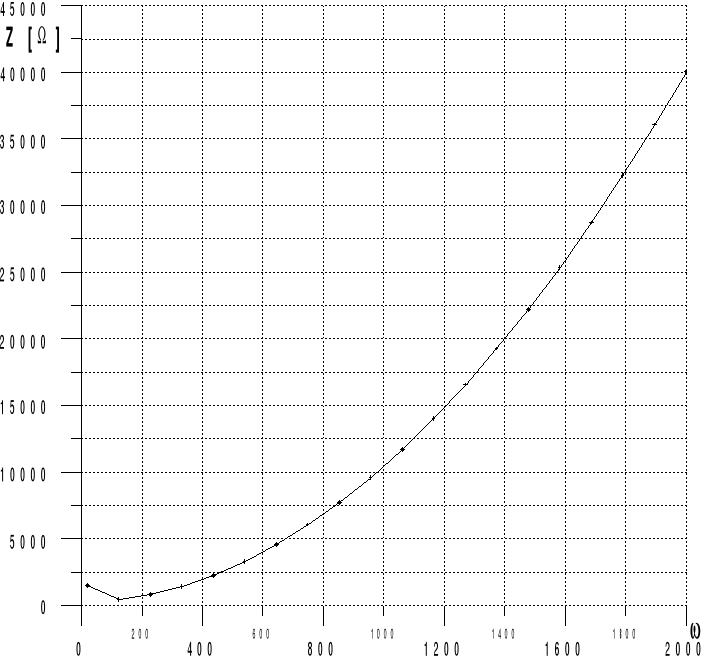
Tabela

f	U	I	P.	cos f	f	f	f teoret	Z	Zteoret
[Hz]	[V]	[A]	[W]	-	[°]	[rad]	[rad]	[W]	[W]

50	10	0,079	0,5	0,6329	50.734	0,885488	1,559	114,63	126,5
100	10	0,1	1	1	0	0	1,566	53,941	100
200	10	0,12	1,25	1,04166	-----------	------------	1,568	27,788	83,3
300	10	0,13	1,5	1,15384	-----------	------------	1,569	20,841	76,92
400	10	0,15	1,5	1	0	0	1,569	20,378	66,66
500	10	0,16	1,75	1,09375	-----------	------------	1,569	22,366	62,5
600	10	0,165	1.75	1,0606	-----------	------------	1,569	25,472	60,6
800	10	0,172	2	1,16279	-----------	------------	1,569	32,75	58,13
1000	10	0,23	1,75	0,76086	40,4590	0,706144	1,569	39,87	43.47
1500	10	0,162	1,3	0,802469	36,6334	0.639374	1,570	59,161	61.73
2000	10	0,09	0,09	1	0	0	1,570	83,364	111.1

Wnioski i spostrzeżenia:

Znaczne rożnice między amplitudami impedancji obliczonymi teoretycznie (za pomocą programów liczących), a wyznaczonymi z pomiarów wynikają przede wszystkim z niedokładności odczytu z przyrządów pomiarowych (m.in. dlatego, że watomierz był przystosowany do pomiarów w zakresie częstotliwości 20-200 Hz, a także błąd odczytu wynikający z małych wartości mocy w obwodzie do których nie był przystosowany W).

---