Zestaw 7

1. Obliczyć pochodną rzędu n funkcji:

a)
b)
c)
d)
e)

2. Wypowiedzieć twierdzenie Rolle'a. Wykazać, że między pierwiastkami funkcji
znajduje się pierwiastek jej pochodnej. Wyjaśnić to na rysunku.

3. Czy twierdzenie Rolle'a można zastosować do funkcji

w przedziale
? Wyjaśnić to na rysunku.

4. Korzystając z twierdzenia de l'Hospitala obliczyć granice:

a)
b)
c)
d)

e)
f)
g)

h)
i)
j)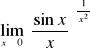
k)

5. Wypowiedzieć twierdzenie Lagrange'a. Znaleźć punkt w przedziale (-1, 3), w którym styczna do paraboli y = x² jest równoległa do cięciwy, łączącej punkty A(-1, 1), B(3, 9). Pokazać to na rysunku.

6. Narysować łuk AB linii
w przedziale
. Dlaczego łuk ten nie ma stycznej równoległej do cięciwy AB? Które z założeń twierdzenia Lagrange'a nie są tutaj spełnione?

7. Wyznaczyć przedziały monotoniczności i ekstrema funkcji:

a)
b)

c)
d)
e)
f)

g)
h)
i)