Pracownia Zakładu Fizyki Technicznej Politechniki Lubelskiej
Nazwisko i imię studenta Grzegorz Duda
|
Symbol grupy ED. 3.5 |
||||||
Data wyk. Ćwiczenia
1996-10-22 |
Symbol ćwiczenia
5.1 , 5.2
|
Temat zadania Statyczny charakter rozpadu promieniotwórczego. Rozkład Gaussa i Poissona. |
|||||
|
ZALICZENIE |
|
|
Ocena |
Data |
Podpis |
|
Podstawy teoretyczne.
Jeżeli będziemy mierzyć natężenie promieniowania jądrowego, to wartości pomiarów będą losowo rozrzucone w pewnym przedziale, tworząc zbiór wartości zmiennej losowej. Powodem tego jest statystyczny charakter procesu rozpadu promieniotwórczego oraz statystyczny charakter zjawisk związanych z detekcją promieniowania jądrowego. Funkcję podającą prawdopodobieństwo występowania zmiennej losowej w danym przedziale nazywamy funkcją rozkładu.
W tym ćwiczeniu doświadczalnie sprawdzany jest rozkład Poissona oraz rozkład Gaussa.
Rozkład Poissona stosuje się dla małych wartości zmiennej losowej. Gdy wartość średnia zmiennej losowej jest większa od 10 to krzywą rozkładu Poissona można przybliżyć krzywą rozkładu Gaussa.
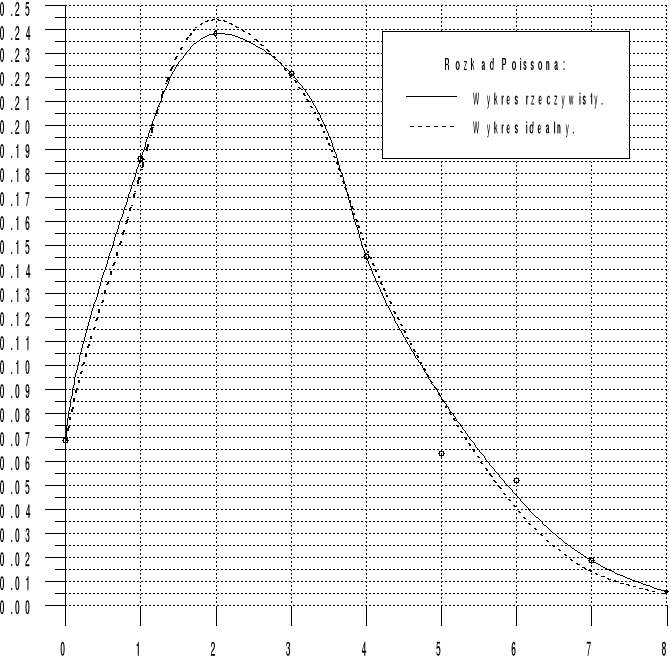
Rozkład Poissona:
Rozkład Gaussa (normalny ) zmiennej losowej nazywamy rozkład o funkcji gęstości prawdopodobieństwa określonej równaniem
Wykonanie ćwiczenia:
1. Rozkład Poissona.
Tabela pomiarowa do rozkładu Poissona.
Lp. |
Wynik pomiaru |
N-ilość zliczeń |
Xsr |
mn |
m. |
y = m.-m0 |
|
0 |
37 |
2,713222 |
0,068901 |
0,066323 |
-0,002579 |
|
1 |
100 |
2,713222 |
0,18622 |
0,179948 |
-0,006271 |
|
2 |
128 |
2,713222 |
0,238361 |
0,24412 |
0,00576 |
|
3 |
119 |
2,713222 |
0,221601 |
0,220784 |
-0,000818 |
|
4 |
78 |
2,713222 |
0,145251 |
0,149759 |
0,00451 |
|
5 |
34 |
2,713222 |
0,063315 |
0,081266 |
0,01795 |
|
6 |
28 |
2,713222 |
0,052142 |
0,036749 |
-0,015393 |
|
7 |
10 |
2,713222 |
0,018622 |
0,014244 |
-0,004378 |
|
8 |
3 |
2,713222 |
0,005587 |
0,004831 |
-0,000756 |
2. Rozkład Gaussa.
Tabela pomiarowa do rozkładu Gaussa.
Lp. |
Wynik pomiaru |
N |
mN |
XSR |
σ |
PX |
Z |
gZ |
|
11 |
1 |
0,001427 |
15,03226 |
2,489081 |
0,052618 |
-1,61998 |
0,10741 |
|
12 |
1 |
0,001427 |
15,03226 |
2,489081 |
0,11157 |
-1,21822 |
0,189954 |
|
13 |
4 |
0,005706 |
15,03226 |
2,489081 |
0,207116 |
-0,81647 |
0,285861 |
|
14 |
3 |
0,00428 |
15,03226 |
2,489081 |
0,339176 |
-0,41471 |
0,366069 |
|
15 |
6 |
0,008559 |
15,03226 |
2,489081 |
0,49483 |
-0,01296 |
0,398909 |
|
16 |
13 |
0,018545 |
15,03226 |
2,489081 |
0,651286 |
0,388795 |
0,369901 |
|
17 |
19 |
0,027104 |
15,03226 |
2,489081 |
0,785397 |
0,790549 |
0,291877 |
|
18 |
22 |
0,031384 |
15,03226 |
2,489081 |
0,883429 |
1,192304 |
0,195982 |
|
19 |
33 |
0,047076 |
15,03226 |
2,489081 |
0,944539 |
1,594059 |
0,111978 |
|
20 |
45 |
0,064194 |
15,03226 |
2,489081 |
0,977023 |
1,995813 |
0,054444 |
|
21 |
35 |
0,049929 |
15,03226 |
2,489081 |
0,991748 |
2,397568 |
0,022526 |
|
22 |
49 |
0,0699 |
15,03226 |
2,489081 |
0,997439 |
2,799323 |
0,00793 |
|
23 |
51 |
0,072753 |
15,03226 |
2,489081 |
0,999315 |
3,201077 |
0,002376 |
|
24 |
57 |
0,081312 |
15,03226 |
2,489081 |
0,999843 |
3,602832 |
0,000606 |
|
25 |
63 |
0,089872 |
15,03226 |
2,489081 |
0,999969 |
4,004587 |
0,000131 |
|
26 |
55 |
0,078459 |
15,03226 |
2,489081 |
0,999995 |
4,406341 |
2,43E-05 |
|
27 |
47 |
0,067047 |
15,03226 |
2,489081 |
0,999999 |
4,808096 |
3,81E-06 |
|
28 |
38 |
0,054208 |
15,03226 |
2,489081 |
1 |
5,209851 |
5,09E-07 |
|
29 |
30 |
0,042796 |
15,03226 |
2,489081 |
1 |
5,611605 |
5,79E-08 |
|
30 |
36 |
0,051355 |
15,03226 |
2,489081 |
1 |
6,01336 |
5,61E-09 |
|
31 |
19 |
0,027104 |
15,03226 |
2,489081 |
1 |
6,415115 |
4,62E-10 |
|
32 |
19 |
0,027104 |
15,03226 |
2,489081 |
1 |
6,816869 |
3,24E-11 |
|
33 |
17 |
0,024251 |
15,03226 |
2,489081 |
1 |
7,218624 |
1,93E-12 |
|
34 |
14 |
0,019971 |
15,03226 |
2,489081 |
1 |
7,620379 |
9,8E-14 |
|
35 |
10 |
0,014265 |
15,03226 |
2,489081 |
1 |
8,022133 |
4,23E-15 |
|
36 |
5 |
0,007133 |
15,03226 |
2,489081 |
1 |
8,423888 |
1,56E-16 |
|
37 |
6 |
0,008559 |
15,03226 |
2,489081 |
1 |
8,825643 |
4,86E-18 |
|
38 |
3 |
0,00428 |
15,03226 |
2,489081 |
1 |
9,227397 |
1,29E-19 |
Wykres do rozkładu Gaussa:
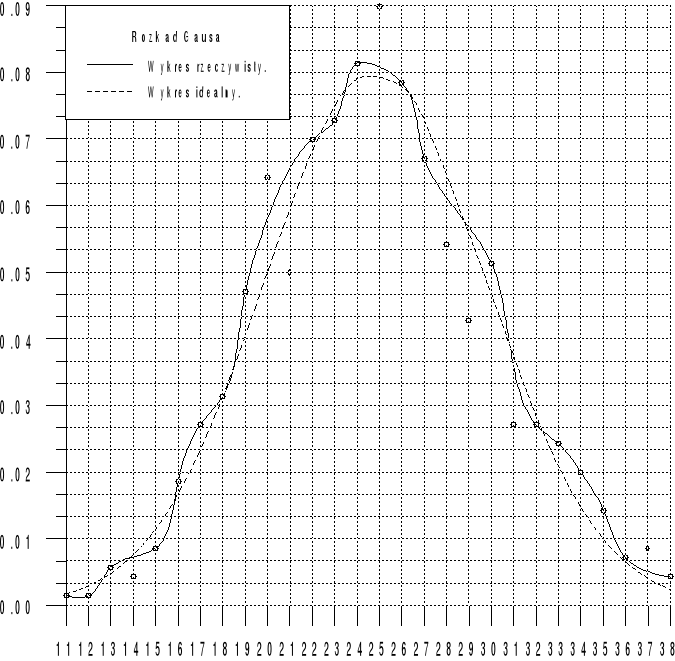
Wnioski i spostrzeżenia:
Ze względu na duże „postrzępienie” wykresu spowodowane niedokładnością pomiarów na wykresach zostały odosobnione punkty, które wpływały niekorzystnie na jego przebieg, i tak w rozkładzie Poissona zostały nieuwzględnione następujące liczby: 5 , 6 ; natomiast w rozkładzie Gaussa: 14 , 20 , 21 , 25 , 28 , 29 , 31 , 37. Usunięcie tych współrzędnych znacznie poprawiło wygląd ogólny wykresów i zmniejszyło różnicę pomiędzy nimi a wykresem idealnym.
Rozkład Poissona wyznaczony doświadczalnie bardzo ładnie pokrywa się z rozkładem wyznaczonym doświadczalnie. Parametry równania regresji świadczą o tym że równania prawie się pokrywają, a współczynnik korelacji Pearsona równy 0,9953295 świadczy o bardzo silnej zależności pomiędzy tymi rozkładami.
Dla rozkładu Gaussa wykres rozkładu rzeczywistego jest krzywą nieregularną ogólnie kształtem pokrywającą się z rozkładem idealnym. Współczynnik korelacji równy 0,97729229 jest już nieco gorszy niż w poprzednim przypadku, ale też bardzo bliski jedynce, co świadczy o bardzo silnej zależności pomiędzy rozkładami teoretycznym a rzeczywistym, co potwierdza słuszność rozkładu idealnego.
Wyszukiwarka
Podobne podstrony:
L3FIZ ~1 2, Pracownia Zak˙adu Fizyki Technicznej Politechniki Lubelskiej
L3FIZ ~1 2, Pracownia Zak˙adu Fizyki Technicznej Politechniki Lubelskiej
L3FIZ 32, Pracownia Zak˙adu Fizyki Technicznej Politechniki Lubelskiej
L3FIZ 62, Pracownia Zak˙adu Fizyki Technicznej Politechniki Lubelskiej
Wyznaczanie współczynnika osłabienia oraz energii maksymal(2), Pracownia Zak˙adu Fizyki Technicznej
ATOM2 ~1, Pracownia Zak˙adu Fizyki Technicznej Politechniki Lubelskiej
E2 1mix, Pracownia Zak˙adu Fizyki Technicznej Politechniki Lubelskiej_
Wyznaczanie wspó czynnika lepko ci cieczy metod Ostwalda, Pracownia Zak˙adu Fizyki Technicznej Polit
J9.1-1, Pracownia Zak˙adu Fizyki Technicznej Politechniki Lubelskiej
14.1 b, Pracownia Zak˙adu Fizyki Technicznej Politechniki Lubelskiej
6.2 a, Pracownia Zak˙adu Fizyki Technicznej Politechniki Lubelskiej
BAZADA~1, Pracownia Zak˙adu Fizyki Technicznej Politechniki Lubelskiej
OPT3 2~1, Pracownia Zak˙adu Fizyki Technicznej Politechniki Lubelskiej
O 3 2 , Pracownia Zak˙adu Fizyki Technicznej Politechniki Lubelskiej
Wyznaczanie napięcia zapłonu i gaśnięcia lamp y jarzeniowej, Pracownia Zak˙adu Fizyki Technicznej P
więcej podobnych podstron