Klasyczne doświadczenia Reynoldsa

1

download: http://www.mech.pk.edu.pl/~m52/pdf/[8_opis].pdf

Ćwiczenie 8

KLASYCZNE DOŚWIADCZENIA REYNOLDSA

8.1. Wprowadzenie

W 1883 r. Osborne Reynolds przeprowadził doświadczenie, które wykazało, że model

płynu doskonałego, opisanego równaniami Eulera odbiega znacznie od praw rządzących

przepływem lepkiego płynu rzeczywistego. Odmienność cech fizycznych zmusza do

odrzucenia metod, które stosowano w dynamice cieczy doskonałej. Chcąc określić

jakościowo podstawowe różnice pomiędzy ruchem cieczy doskonałej a ruchem cieczy lepkiej

rozpatrzymy ustalony przepływ cieczy przez prostoosiowy przewód o stałym przekroju

poprzecznym. Zarówno równania Eulera, jak również wywodzące się z nich równanie

Bernoulliego nie rozwiązują zagadnienia dla cieczy lepkiej, zgodnie z wynikami badań

doświadczalnych. Równania Eulera dopuszczają możliwość dowolnego, aczkolwiek ciągłego

rozkładu prędkości, podczas gdy doświadczalnie stwierdza się zawsze spadek prędkości od

osi przewodu ku ścianom. Spadek ten ma przy tym wyraźnie określony charakter,

wyróżniający się zawsze zerową wartością prędkości na ścianach. Z równania Bernoulliego

wynika, iż wzdłuż przewodu nie ma strat energii, podczas gdy przy przepływie cieczy lepkiej

dyssypacja energii jest wyraźna i mierzalna. Wymienione różnice powodują nieprzydatność

metod dynamiki cieczy doskonałej do opisu ruchu cieczy lepkiej. Należy podkreślić, że często

identyfikowano składowe prędkości ruchu w równaniach Eulera - ze składowymi prędkości

przynależnymi do ruchu głównego polegającego na dostrzegalnym, a zatem dającym się

mierzyć przemieszczaniu się cząstek cieczy w kierunku ruchu. W rzeczywistości do tej

prędkości dołącza się dodatkowa prędkość, będąca wynikiem niedostrzegalnych drobnych

ruchów pobocznych. Ruchy te przy przepływach uwarstwionych, odbywających się

z niewielkimi prędkościami, są ruchami molekularnymi, stanowiącymi istotę ciepła

i wywołującymi dyfuzję pędu z elementów poruszających się szybciej ku elementom

poruszającym się wolniej. Po przejściu ruchu uwarstwionego w ruch burzliwy do ruchów

molekularnych dołączają się molarne pulsacje o wielkiej częstotliwości, stanowiące istotę

burzliwości.

2

Klasyczne doświadczenia Reynoldsa

download: http://www.mech.pk.edu.pl/~m52/pdf/[8_opis].pdf

8.2. Doświadczenie Reynoldsa

Warunki powstawania ruchu burzliwego określił doświadczalnie Reynolds, obserwując

zjawisko przepływu wody przez rurki szklane, po wprowadzeniu w masę poruszającej się

wody cienkiej strugi cieczy zabarwionej o tej samej gęstości.

Przy dostatecznie małej średniej prędkości przepływu cienka struga zabarwionej cieczy

przedstawia się w postaci linii prostej, równoległej do osi rury. Ten ruch strugi barwnika

świadczy o uwarstwionym charakterze ruchu, stąd też wywodzi się nazwa ruch uwarstwiony.

Często ruch uwarstwiony nazywa się ruchem laminarnym. Jeżeli średnia prędkość

przepływu przekroczy pewną krytyczną wartość liczbową, struga zabarwiona doznaje

gwałtownych wahań i rozmazuje się w całej objętości cieczy. Zjawisko to było dowodem, iż

ruch cieczy po przekroczeniu prędkości krytycznej przeszedł w całej rurze w ruch burzliwy,

nazywany również turbulentnym.

Ruch burzliwy charakteryzuje się ruchami pobocznymi, które spowodowały rozmazanie

barwnika w całym obszarze płynącej cieczy. Przy przejściu ruchu laminarnego w ruch

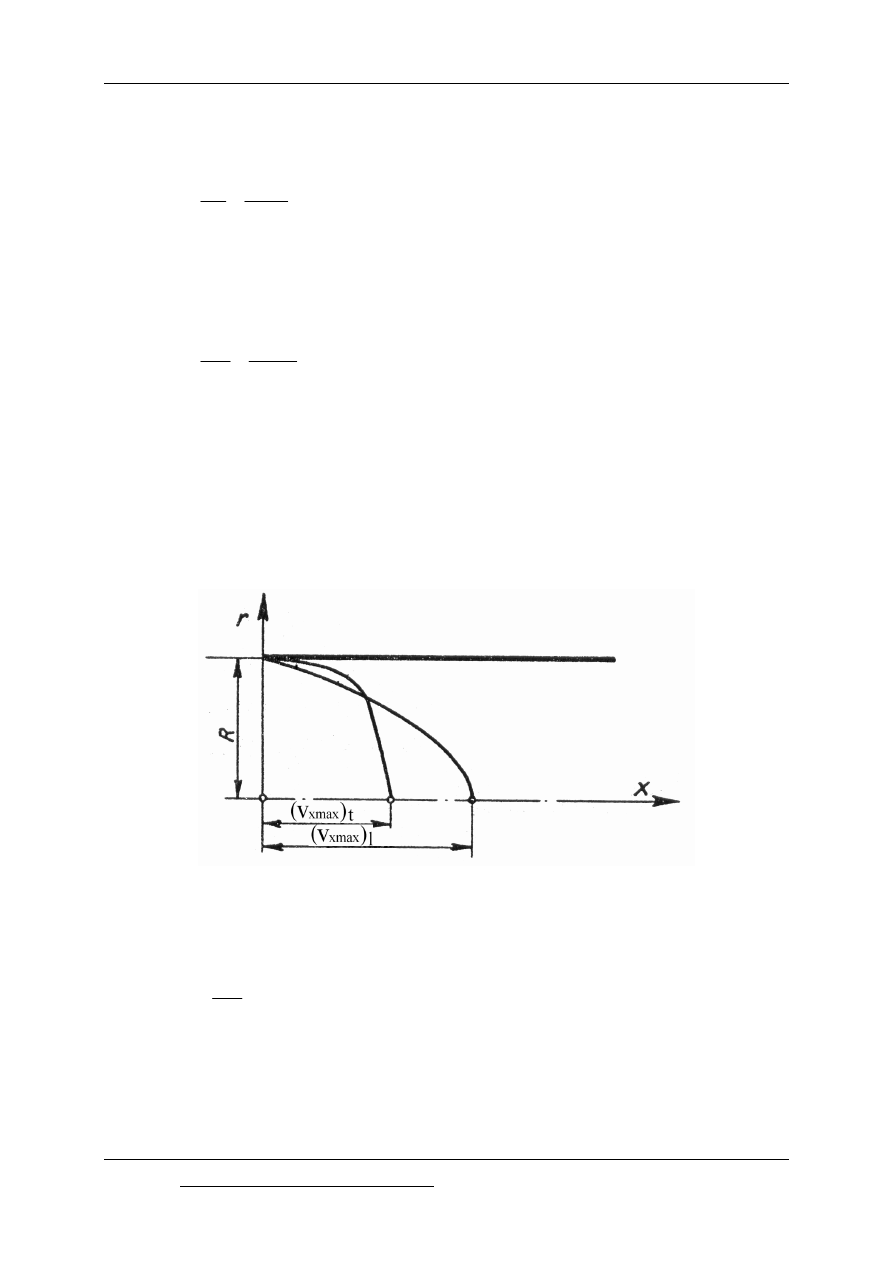
turbulentny zmienia się rozkład prędkości w przekroju poprzecznym przewodu, co pokazano

na rys. 8.2.

Doświadczenia Reynoldsa wykazały, że wartość liczbowa prędkości krytycznej v

k

jest

wprost proporcjonalna od kinematycznego współczynnika lepkości cieczy

η

, a odwrotnie

proporcjonalna do średnicy przewodu d:

k

k

v

Re

d

ν

=

(8.1)

przy czym bezwymiarowy współczynnik proporcjonalności zmieniał swą wartość

w granicach: Re = 2000

÷

2400.

Rys. 8.1. Obserwacja Reynoldsa: a) przepływ laminarny, b) przejściowa forma przepływu, c)
przepływ turbulentny

a)

b)

c)

Klasyczne doświadczenia Reynoldsa

3

download: http://www.mech.pk.edu.pl/~m52/pdf/[8_opis].pdf

Z teorii podobieństwa hydrodynamicznego wiadomo, że liczba Reynoldsa jest

zdefiniowana stosunkiem sił bezwładności do sił lepkości w płynie, co prowadzi do wzoru:

v l

v l

Re

⋅

⋅ ⋅ρ

=

=

ν

η

(8.2)

gdzie:

l - jest wymiarem liniowym, charakteryzującym dany przepływ.

Dla przewodu o przekroju kołowym liczbę Reynoldsa oblicza się ze wzoru:

v d

v d

Re

⋅

⋅ ⋅ρ

=

=

ν

η

(8.3)

gdzie:

v - średnia prędkość przepływu,

d - średnica wewnętrzna przewodu,

ν

- kinematyczny współczynnik lepkości,

η

- dynamiczny współczynnik lepkości,

ρ

- gęstość płynu.

Rys. 8.2. Rozkład prędkości przy ruchu laminarnym i turbulentnym

Z nowszych badań wiadomo, że tzw. dolna albo niższa krytyczna wartość liczby

Reynoldsa dla przewodów o przekroju kołowym wynosi:

1

k

v d

Re

2320

⋅

=

=

ν

(8.4)

Istnieje również druga wartość liczby Reynoldsa, nazwana górną albo wyższą

wartością krytyczną liczby, Reynoldsa, którą zazwyczaj przyjmuje się równą:

2

k

Re

50000

=

(8.5)

4

Klasyczne doświadczenia Reynoldsa

download: http://www.mech.pk.edu.pl/~m52/pdf/[8_opis].pdf

Na podstawie wyników szeregu badań doświadczalnych można stwierdzić, że:

1) dla liczb Re < 2320 jedyną stateczną formą ruchu płynu lepkiego jest przepływ laminarny,

2) przy wartościach liczb Reynoldsa zawartych w przedziale 2320 < Re < 50000 możliwe

jest istnienie zarówno ruchu laminarnego, jak również burzliwego. W tym przedziale

wartości Re ruch laminarny jest niestatateczny. Charakter ruchu jest uzależniony od

szeregu przyczyn dodatkowych, np. drgania przewodu, kształtu wejścia do przewodu

(ostre krawędzie) wysokości nierówności ścian (chropowatość ścian przewodu),

3) dla przepływów, w których Re > 50000 jedyną formą ruchu jest ruch burzliwy.

Wobec faktów wymienionych w kpt. 2 w obliczeniach za granicę przejścia ruchu

laminarnego w burzliwy przyjmować będziemy - dla przewodów kołowych – Re

k1

= 2320.

Poniżej podano orientacyjne wartości krytycznych liczb Re

k

dla przepływów przez:

a) przewód o przekroju trójkątnym Re

k

= 1800

÷

2000,

b) przewód o przekroju prostokątnym Re

k

= 2000,

c) szczelinę pierścieniową Re

k

= 1100,

d) zawory (w zależności od konstrukcji zaworu) Re

k

= 20

÷

500,

e) kryzę normalną do pomiaru natężenia przepływu Re

k

= 200.

Mechanizm powstawania burzliwości w czasie przepływu cieczy lepkiej przez

prostoosiowy przewód kołowy jest obecnie dokładnie zbadany [1]. Stan ruchu cieczy lepkiej,

zwany ruchem burzliwym, może występować w trzech zasadniczo różnych postaciach. Gdy

średnia prędkość przepływu przekroczy wartość graniczną, powstają w bezpośrednim

sąsiedztwie ścian drobne zaburzenia obejmujące warstewkę przyścienną, która zaczyna

ulegać drobnym okresowym drganiom stanowiącym istotę burzliwości, podczas gdy rdzenna

część cieczy porusza się nadal ruchem laminarnym. Tę pierwszą fazę burzliwości nazywamy

burzliwym stanem zaczątkowym. W miarę jak zwiększa się średnia prędkość przepływu,

wzrasta grubość burzliwej warstwy przyściennej, a maleją wymiary rdzenia poruszającego się

ruchem laminarnym. Gdy średnia prędkość przepływu osiągnie tzw. wartość krytyczną v

k

,

wymiary laminarnego rdzenia maleją do zera i ruch burzliwy ogarnia całą masę płynącej

cieczy. Ten graniczny stan ruchu nazwano stanem w pełni burzliwym. Po przekroczeniu

krytycznej wartości liczby Reynoldsa Re

k

obserwujemy zjawisko odwrotne od

zapoczątkowanego stanu burzliwego, a mianowicie część rdzenna ciekłej masy porusza się

ruchem burzliwym, a cząstki zawarte w cienkiej warstwie przyściennej poruszają się ruchem

laminarnym. Ten stan ruchu, nazywany burzliwym stanem końcowym, spotyka się najczęściej

w technicznie ważnych zjawiskach przepływu cieczy przez przewody.

Klasyczne doświadczenia Reynoldsa

5

download: http://www.mech.pk.edu.pl/~m52/pdf/[8_opis].pdf

8.3. Przebieg ćwiczenia

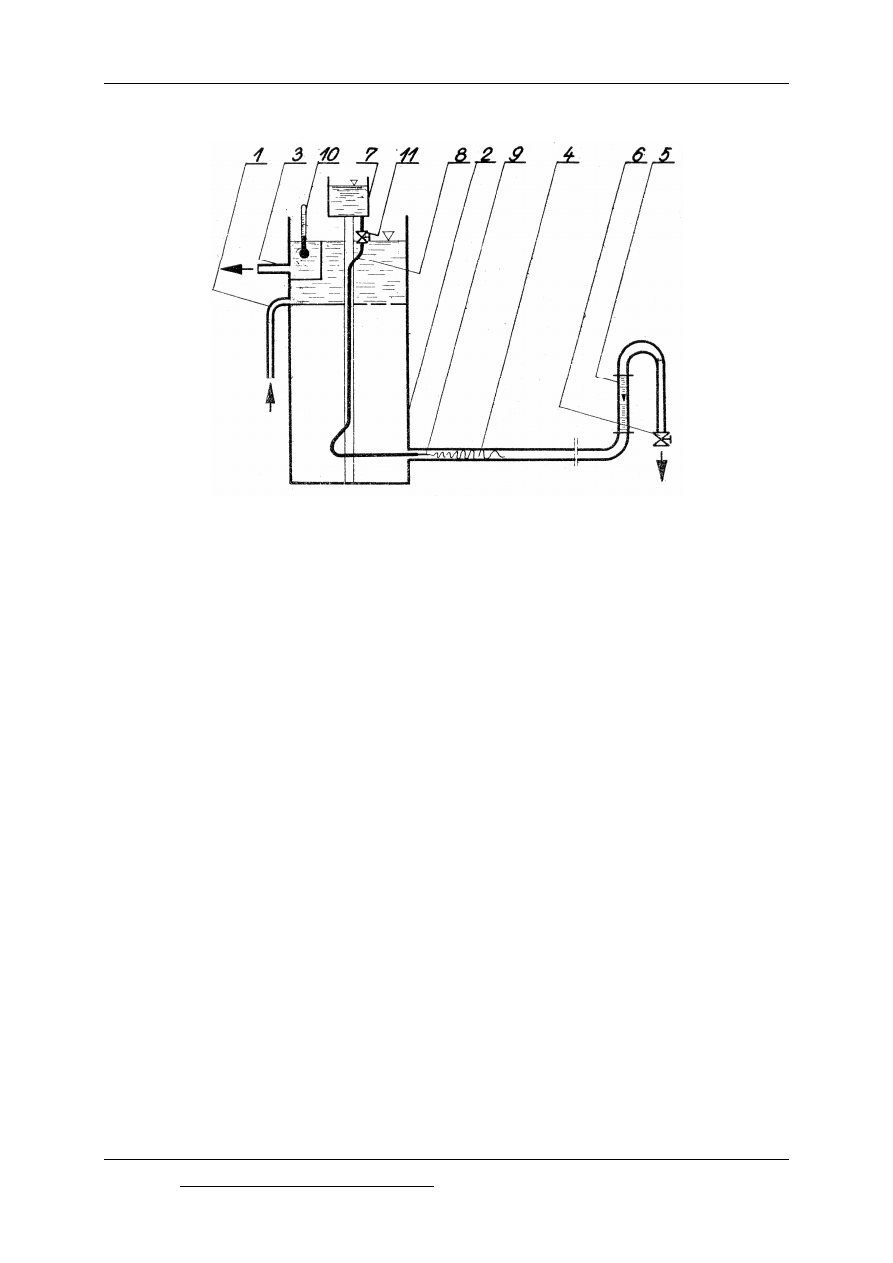
Rys. 8.3. Schemat stanowiska pomiarowego

Woda z sieci wodociągowej jest doprowadzana przewodem (1) do zbiornika (2).

Nadmiar wody jest odprowadzany przez przelew przewodem (3). Ze zbiornika woda spływa

rurą (4) przez rotametr (5) i zawór (6) do zlewu. W celu uwidocznienia charakteru przepływu

do rury (4) doprowadza się barwnik ze zbiornika (7) przez przewód (8) i igłę (9). Termometr

(10) służy do określenia temperatury wody w czasie pomiaru.

Po napełnieniu zbiornika (2) należy odkręcić zawory (6) i (11) w celu doprowadzenia

barwnika, regulując przepływ zaworem (6) szukamy takiego wydatku, przy którym następuje

przejście od ruchu uwarstwionego do burzliwego. Na rotametrze odczytujemy natężenie

przepływu wody. Obliczamy średnią prędkość przepływu wody w rurze (4). Dla odczytanej

temperatury wody szukamy kinematycznego współczynnika lepkości w tablicach. Obliczamy

liczbę Reynoldsa ze wzoru (8.3).

8.4. Literatura

[1] Troskolański A. T.: Hydromechanika. WNT, Warszawa 1967, ss. 246 -259.

[2] Prosnak W. J.: Mechanika płynów. PWN, Warszawa 1970, ss. 536 - 540.

[3] Bukowski J.: Mechanika płynów. FWN, Warszawa 1970.

[4] Wysocki J.: Mechanika płynów. PWN, Warszawa 1967, ss. 245 - 247.

[5] Daily J. W., Harleman D. B. P.: Fluid Dynamics. A.W.P.C.I.R. Massachusetts, USA 1966,

ss. 170 - 173.