1.

Podać definicję tłumienia krytycznego oraz
warunek, z którego się go wyznacza.

Współczynnik tłumienia krytycznego to taka wartość współczynnika tłumieni, po
przekroczeniu której ruch jest aperiodyczny.
Warunek – zerowanie się delty równania charakterystycznego:

km

c

mk

c

k

cr

mr

kr

2

,

0

4

,

0

2

2

=

=

−

=

∆

=

+

+

2.

Podać definicje:

a.

głównych osi bezwładności,

b.

głównych centralnych osi bezwładności.

a) Główne osie bezwładności to osie wyznaczone przez kierunki główne tensora
bezwładności.
b) Główne centralne osie bezwładności to główne osie bezwładności wyznaczone
przez kierunki główne tensora bezwładności zestawionego w środku ciężkości
bryły.

3.

Podać własności głównych osi bezwładności. 1.

Każdy sztywny układ materialny ma co najmniej trzy osie bezwładności:

−

dokładnie trzy, gdy wszystkie wartości własne są różne,

−

jedną i płaszczyznę osi, gdy dwie wartości własne są jednakowe,

−

całą przestrzeń, gdy wszystkie wartości własne są jednakowe.

2.

Tensor bezwładności w układzie głównych osi bezwładności ma postać
diagonalną (momenty dewiacji względem płaszczyzn wyznaczonych przez
główne osie bezwładności maja wartość 0).

3.

Momenty bezwładności z przekątnej głównej przyjmują wartości ekstremalne.

4.

Jeśli układ materialny posiada oś symetrii to ta oś pokrywa się z jedną
z głównych osi bezwładności

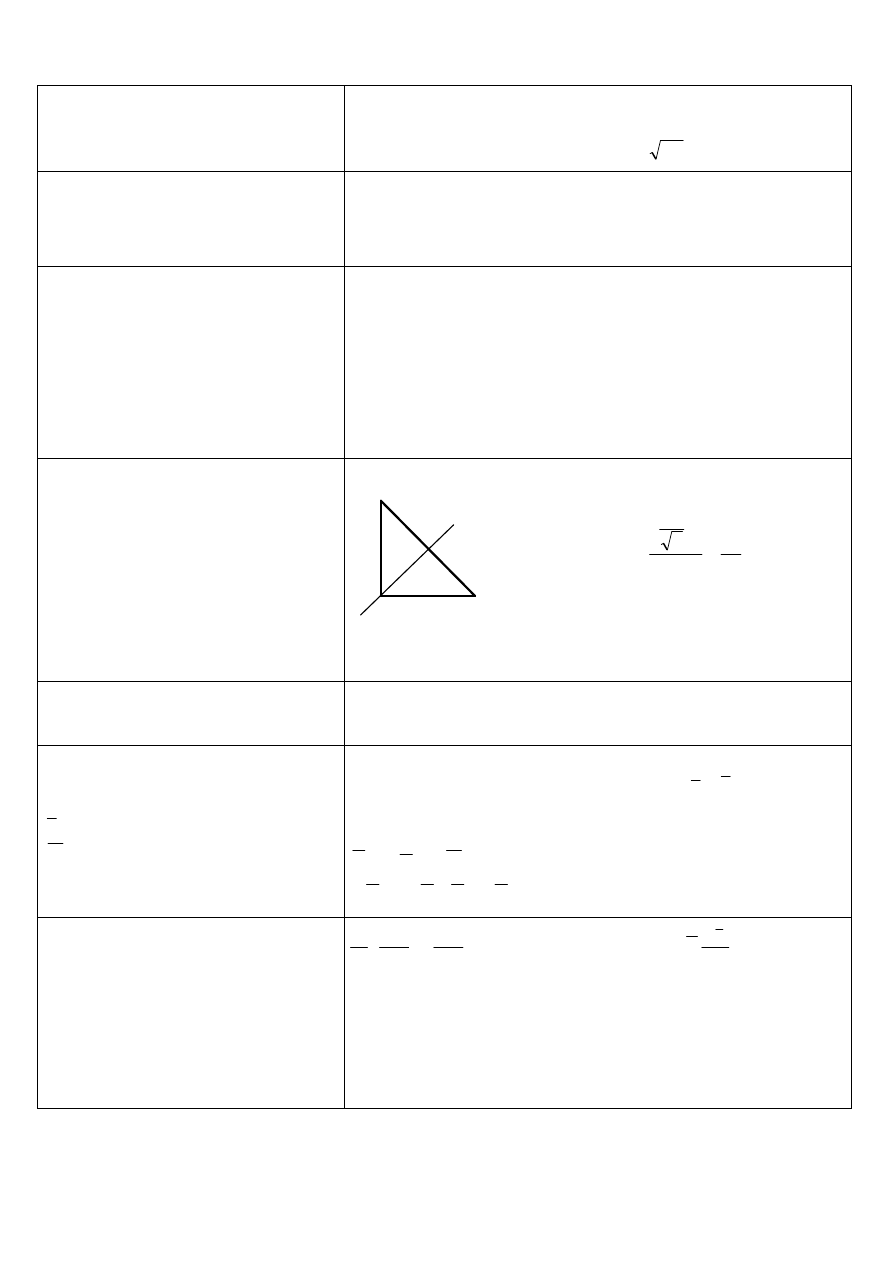
4.

Względem jakiej prostej przechodzącej przez
ś

rodek masy trójkąta materialnego

przedstawionego na rysunku moment
bezwładności jest maksymalny i ile wynosi?

24

12

2

2

4

4

a

a

I

l

=













=

5.

Przy jakim założeniu o punkcie A obowiązuje
zasada krętu?

Punkt A jest punktem stałym lub środkiem masy.

6.

Czy znajomość zredukowanego układu sił
w środku masy pozwala przewidzieć ruch
ciała sztywnego? Odpowiedź uzasadnić.

S

- suma układu sił,

M

- moment układu sił względem

środka masy,

Tak. Ten fakt wynika z postaci równań bryły sztywnej:











=

=

=

→

=

z

y

x

S

z

m

S

y

m

S

x

m

S

p

&

&

&

&

&

&

&

( )

( )

( )

(

)

(

)

(

)











=

−

+

=

−

+

=

−

+

→









×

+

=

=

=

•

•

ς

ξ

η

η

ξ

ς

ς

η

ς

ξ

ξ

ς

η

η

ξ

η

ς

ς

η

ξ

ξ

ω

ω

ω

ω

ω

ω

ω

ω

ω

ω

ω

ω

ω

ω

M

I

I

I

M

I

I

I

M

I

I

I

J

J

J

M

J

K

&

&

&

&

&

7.

Napisać równanie Lagrange’a II rodzaju oraz
podać znaczenie użytych symboli.

m

i

q

r

F

Q

n

j

Q

q

E

q

E

dt

d

i

j

i

i

j

j

j

k

j

k

,

...

,

2

,

1

,

...

,

2

,

1

=

∂

∂

=

=

=

∂

∂

−















∂

∂

∑

&

E

k

– energia kinetyczna układu,

j

q

– współrzędna uogólniona,

j

Q

– siła uogólniona,

n – liczba stopni swobody,

m – liczba punktów przyłożenia siły.

a

a

l

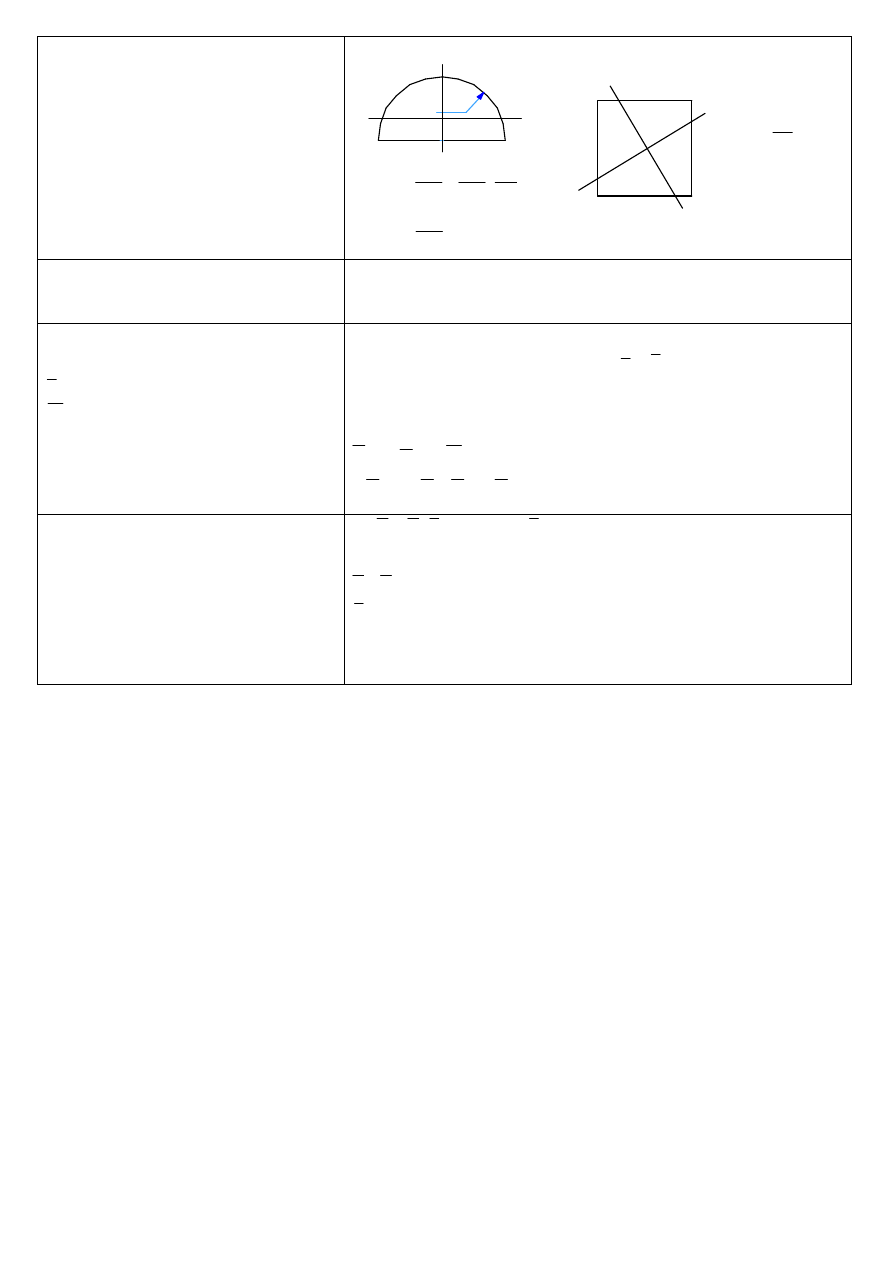
1.

W odniesieniu do przedstawionych obszarów
materialnych podać:
a.

ile głównych centralnych osi bezwładności
mają te obszary?

b.

ile wynoszą główne centralne momenty
bezwładności tych obszarów?

a) Dwie główne centralne a) ∞ wiele głównych centralnych osi bezwładności
osie bezwładności (każda oś przechodząca przez środek masy)

b)

12

4

a

I

yc

=

b)

π

π

π

3

4

2

8

2

4

r

r

r

I

xc

⋅

−

=

8

4

r

I

yc

π

=

2.

Podać twierdzenie o pędzie układu.

Pęd układu materialnego jest równy pędowi środka masy tego układu

3.

Napisać równania ruchu swobodnej bryły
sztywnej wraz z objaśnieniami użytych
symboli.

S

- suma układu sił,

M

- moment układu sił względem

środka masy,

ς

η

ξ

,

,

- gł. centralne osie bezwładności,

ς

η

ξ

I

I

I

,

,

- gł. centralne momenty bezwł.

Równanie ruchu postępowego środka masy:











=

=

=

→

=

z

y

x

S

z

m

S

y

m

S

x

m

S

p

&

&

&

&

&

&

&

Równanie ruchu obrotowego wokół osi przechodzącej przez środek masy:

( )

( )

( )

(

)

(

)

(

)











=

−

+

=

−

+

=

−

+

→









×

+

=

=

=

•

•

ς

ξ

η

η

ξ

ς

ς

η

ς

ξ

ξ

ς

η

η

ξ

η

ς

ς

η

ξ

ξ

ω

ω

ω

ω

ω

ω

ω

ω

ω

ω

ω

ω

ω

ω

M

I

I

I

M

I

I

I

M

I

I

I

J

J

J

M

J

K

&

&

&

&

&

4.

Napisać równanie wynikające z zasady
d’Alemberta (zasada prac wirtualnych układu
sił czynnych i bezwładności) wraz
założeniami o więzach. Podać znaczenie
użytych symboli.

(

)

...

,

2

,

1

0

=

∀

=

+

∑

i

B

F

si

i

si

i

i

δ

δ

Więzy: geometryczne, stacjonarne, dwustronne i gładkie.

i

i

B

F ,

– siły czynne i bezwładności

si

δ

– przemieszczenia wirtualne

r

a

a