
UNIWERSYTET ZIELONOGÓRSKI
WYDZIAŁ INŻYNIERII LĄDOWEJ I ŚRODOWISKA
INSTYTUT BUDOWNICTWA
Ć
WICZENIE PROJEKTOWE Z MECHANIKI BUDOWLI
Wykonał Piotr Kramski
Rok akademicki 2006 / 2007

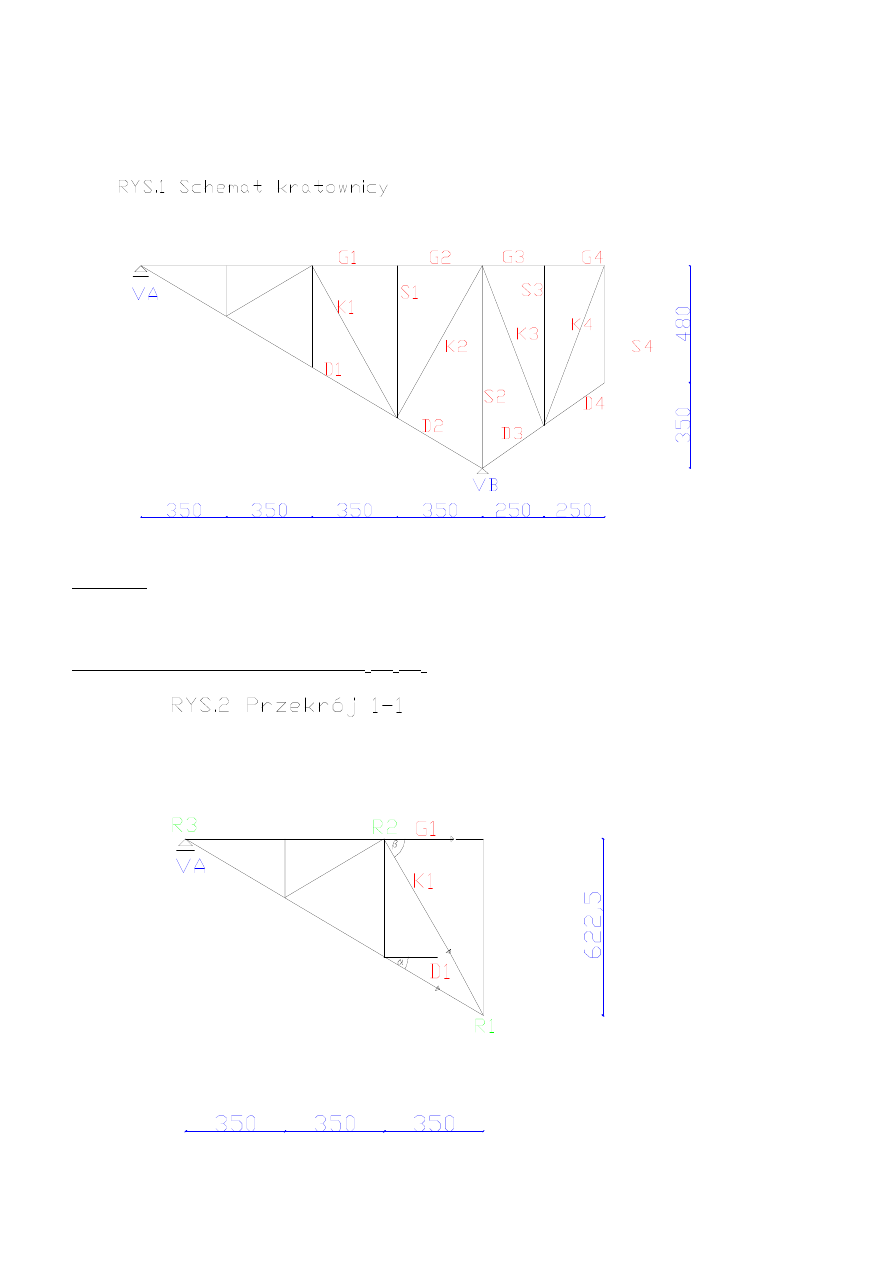
ZADANIE 1

a = 2,5 m
b = 3,5 m
c = 4,8 m
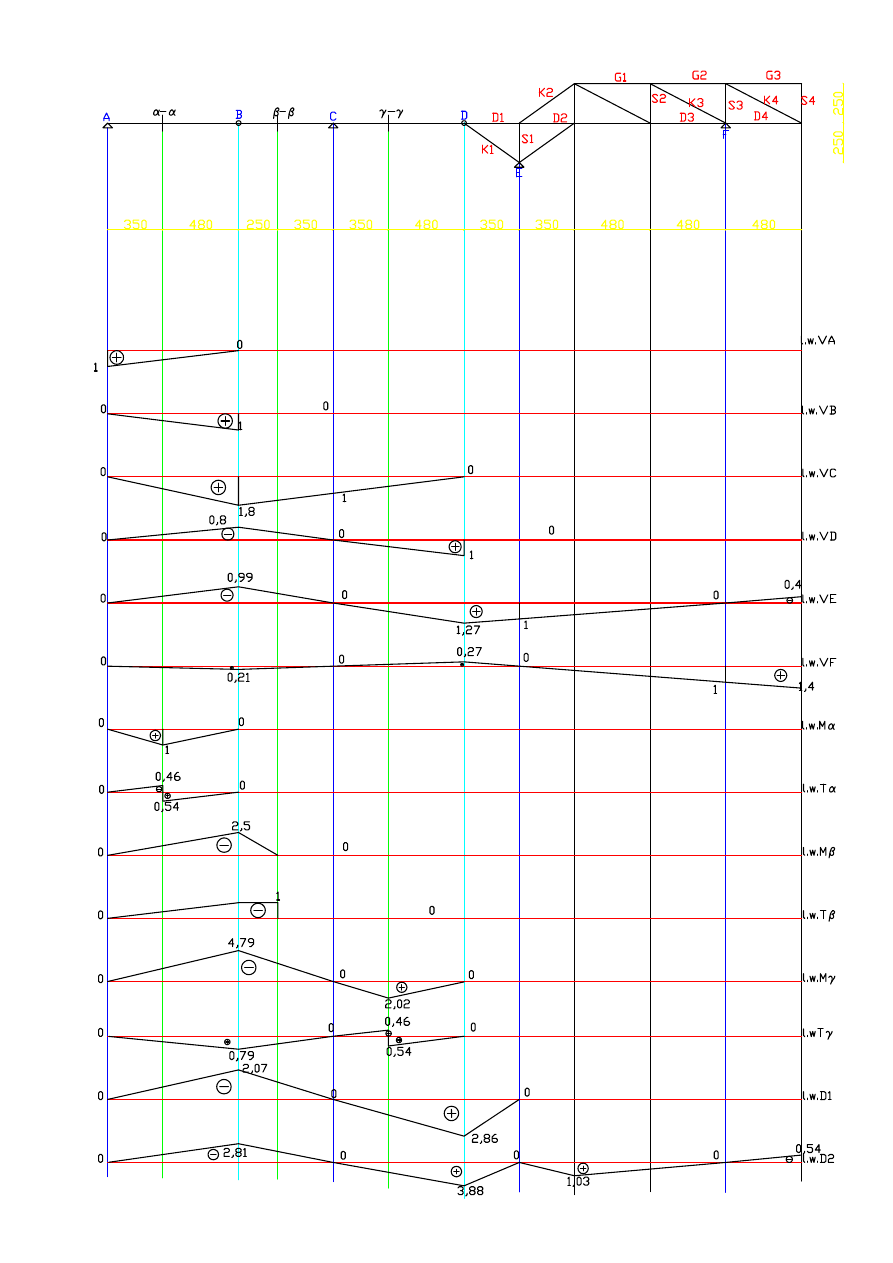
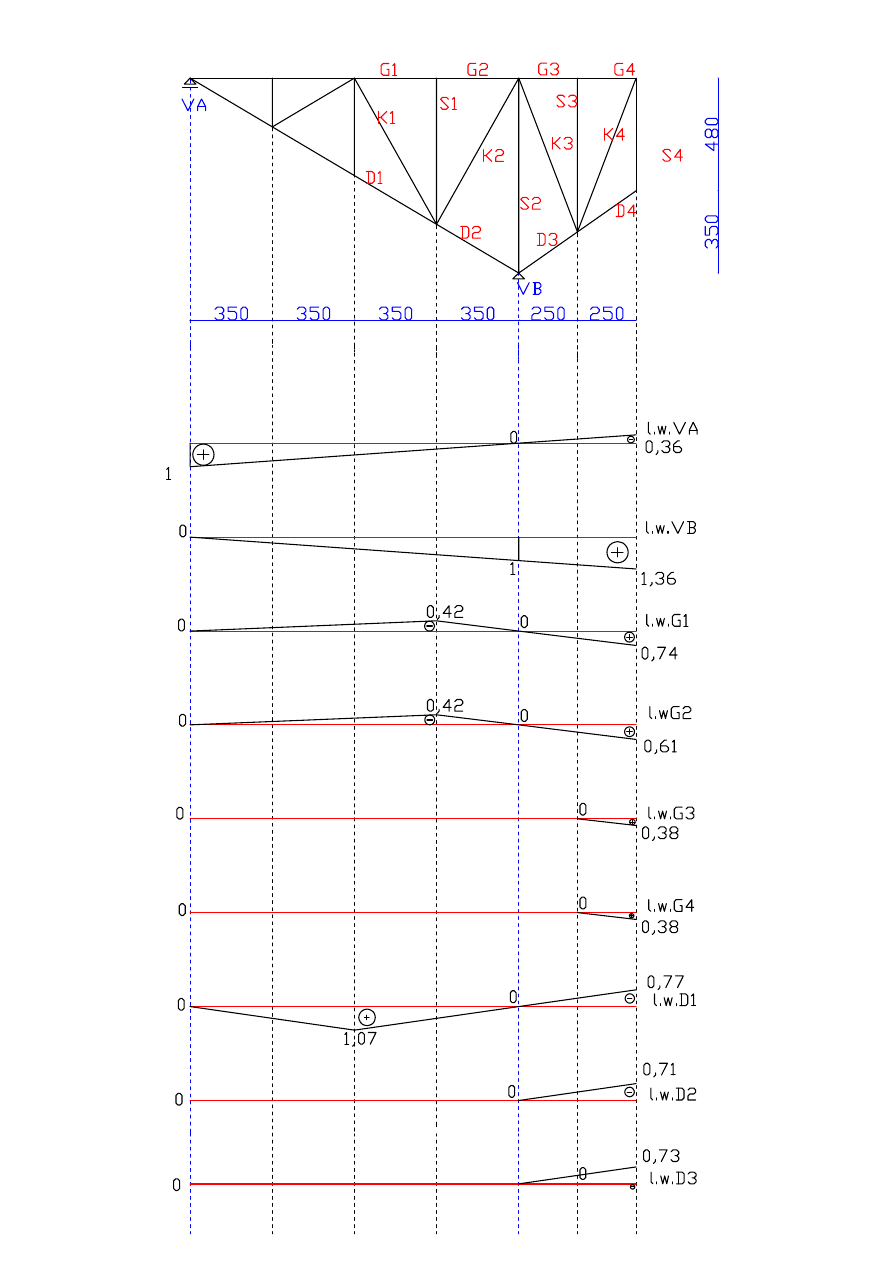
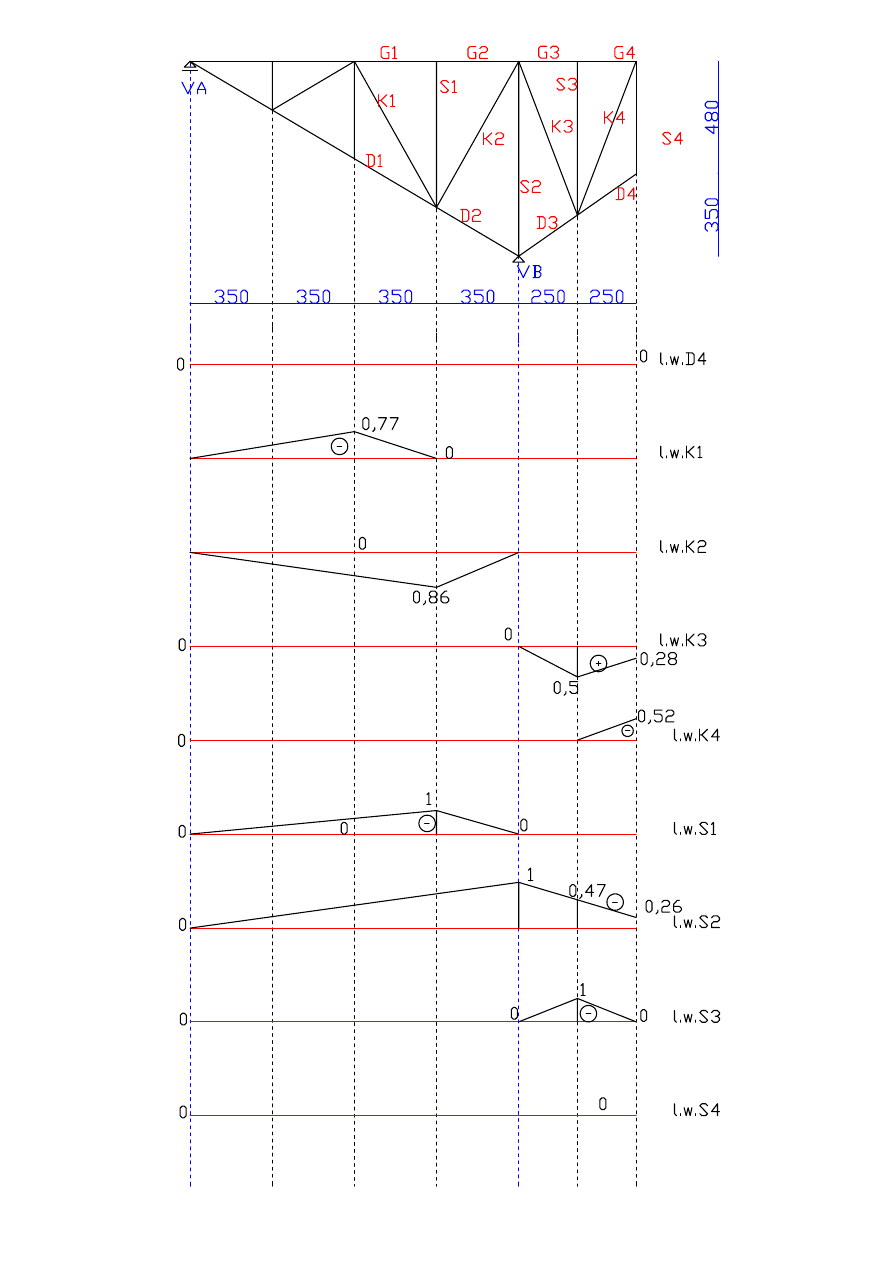
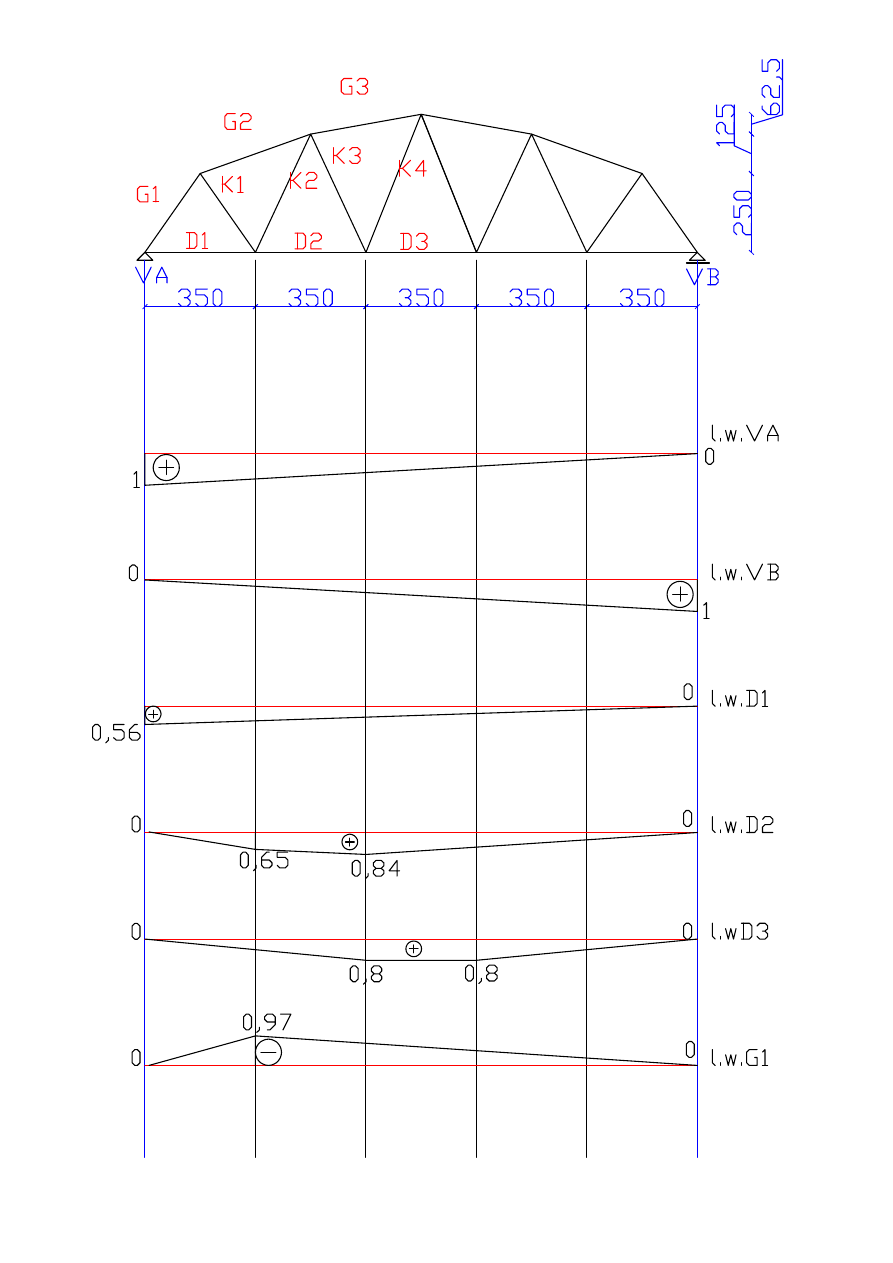
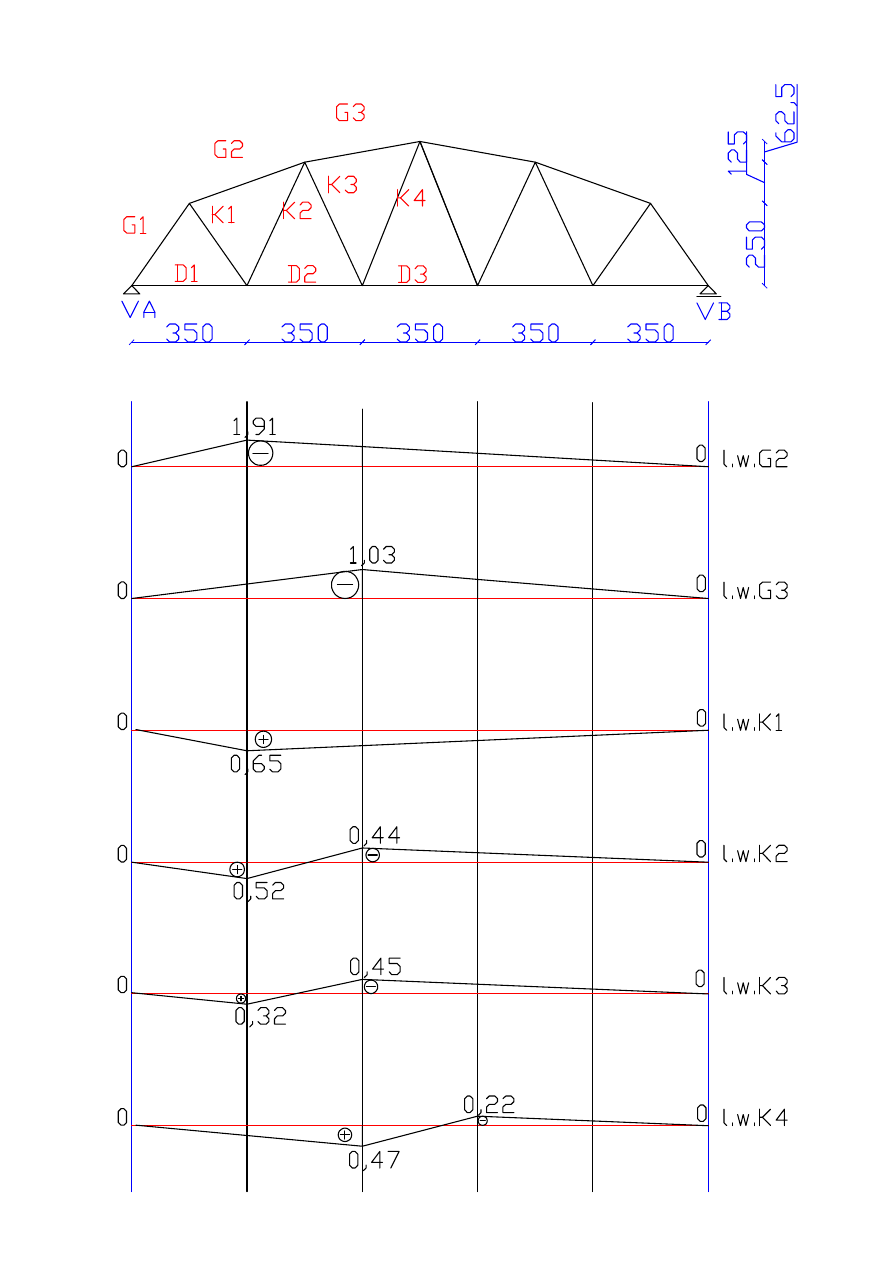
Wykresy :
- linii wpływu V
A
- linii wpływu V
B
- linii wpływu V
C
- linii wpływu V
D
- linii wpływu V
E
- linii wpływu V
F
- linii wpływu M
α
- linii wpływu T
α
- linii wpływu M
β
- linii wpływu T
β
- linii wpływu M
γ
- linii wpływu T
γ
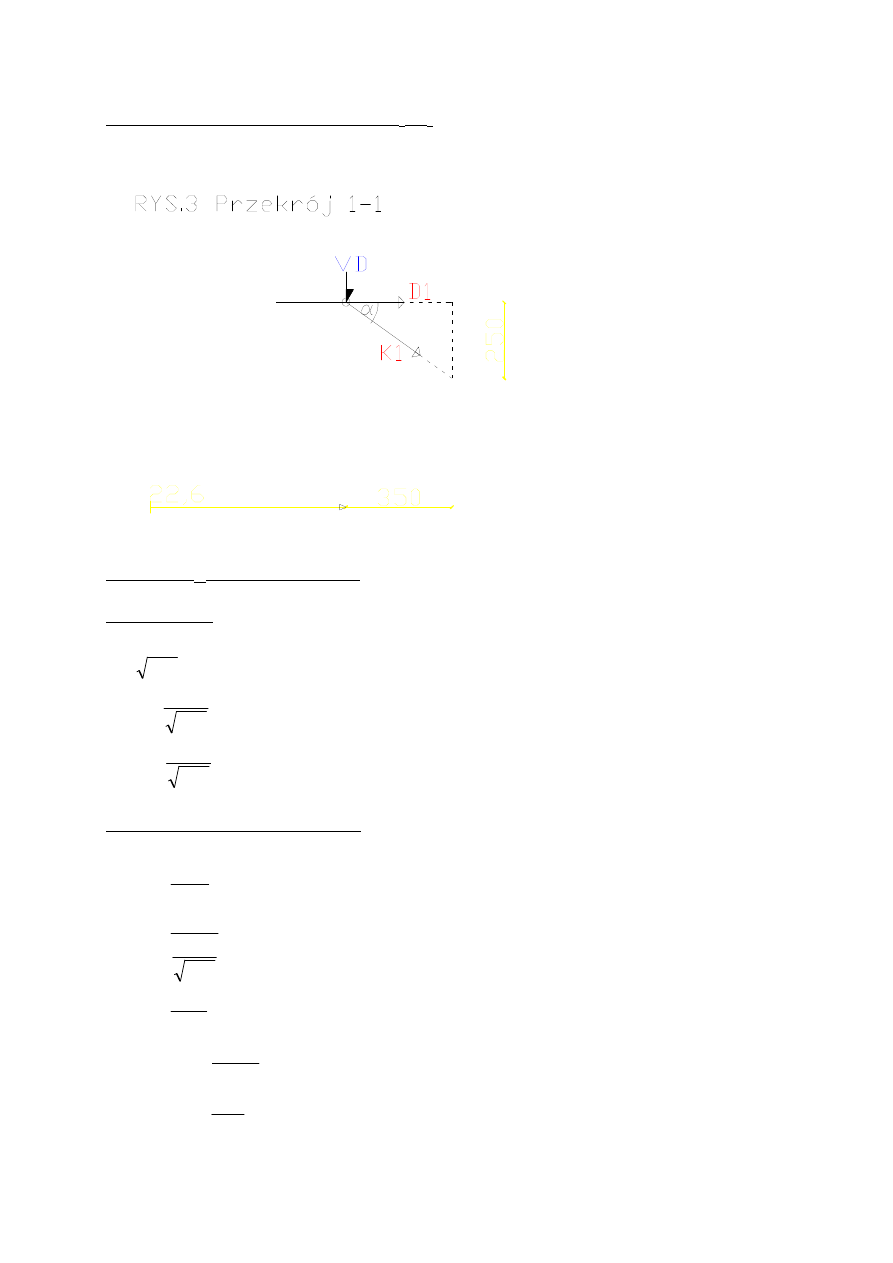
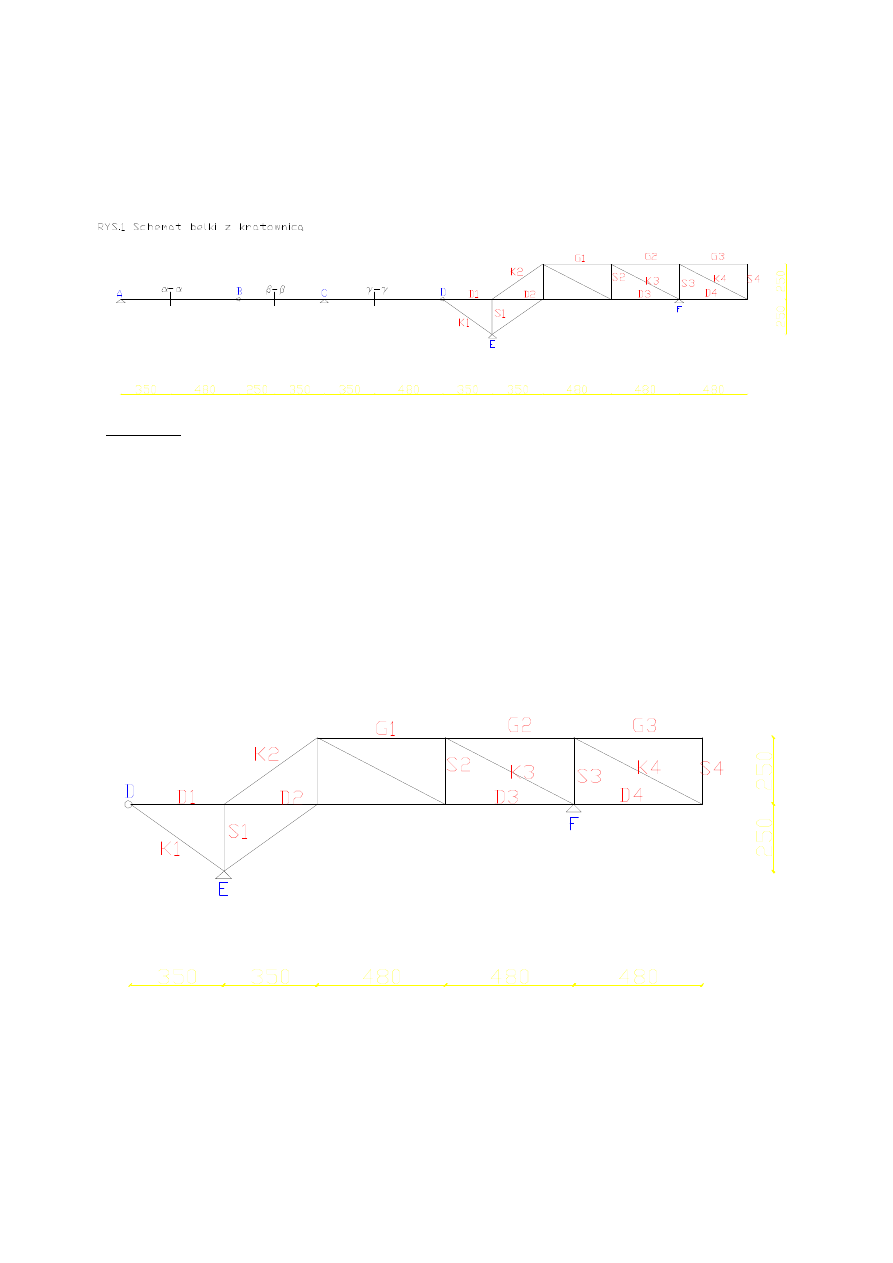
Wykonuje cięcie Rittera, aby obliczyć D
1
, K
1
Obliczam K
1
z równowagi więzów
obliczam kąt α
5
,
18
5
,
3
cos
5
,
18
5
,
2
sin
5
,
18
5
,
3
5
,
2
2
2
2
=
=
=
=
+
α
α
c
c
Gdy siła znajduje się poza więzłem
0
58
,
0
0
)
1
,
26
(
72
,
0
58
,
0
42
,
0
)
8
,
17
(
58
,
0
5
,
18
5
,
2
sin
0
sin
1
1
1
1
1
1
=
−
=
−
=
−
=
−
=
−
=
−
=
=
⋅
+
K
K
V
K
V
K
V
K
K
V
D
D
D
D
α
α
Gdy siła znajduje się w węźle
45
,
3
58
,
0
1
1
)
6
,
22
(
58
,
0
1
5
,
18
5
,
2
sin
0
sin
1
1
1
1
1
−
=
−
−
=
−
−
=
−
−
=
−
=
=
+
⋅
+
K
V
K
P
V
K
V
K
P
K
V
D
D
D
D
α
α
Obliczam D
1
z równowagi więzów
Gdy siła znajduje się poza węzłem
0
)
1
,
26
(
58
,
0
81
,
0
72
,
0
)
8
,
17
(
81
,
0
5
,
18
5
,
3
5
,
18
5
,
3
cos
0
cos
1
1
1
1
1
1
1
1
1
1
1
1
=
=
⋅
=
⋅
−
=
⋅
−
=
⋅
−
=
⋅
−
=
=
⋅
+
D
D
K
D
K
D
K
D
K
D
K
D
α
α
Gdy siła znajduje się w węźle
86
,
2
81
,
0
45
,
3
)
6
,
22
(
81
,
0
5
,
18
5
,
3
5
,
18
5
,
3
cos
0
cos
1
1
1
1
1
1
1
1
1
1
1
=
⋅
=
⋅
−
=
⋅
−
=
⋅
−
=
⋅
−
=
=
⋅
+
D
K
D
K
D
K
D
K
D
K
D
α
α
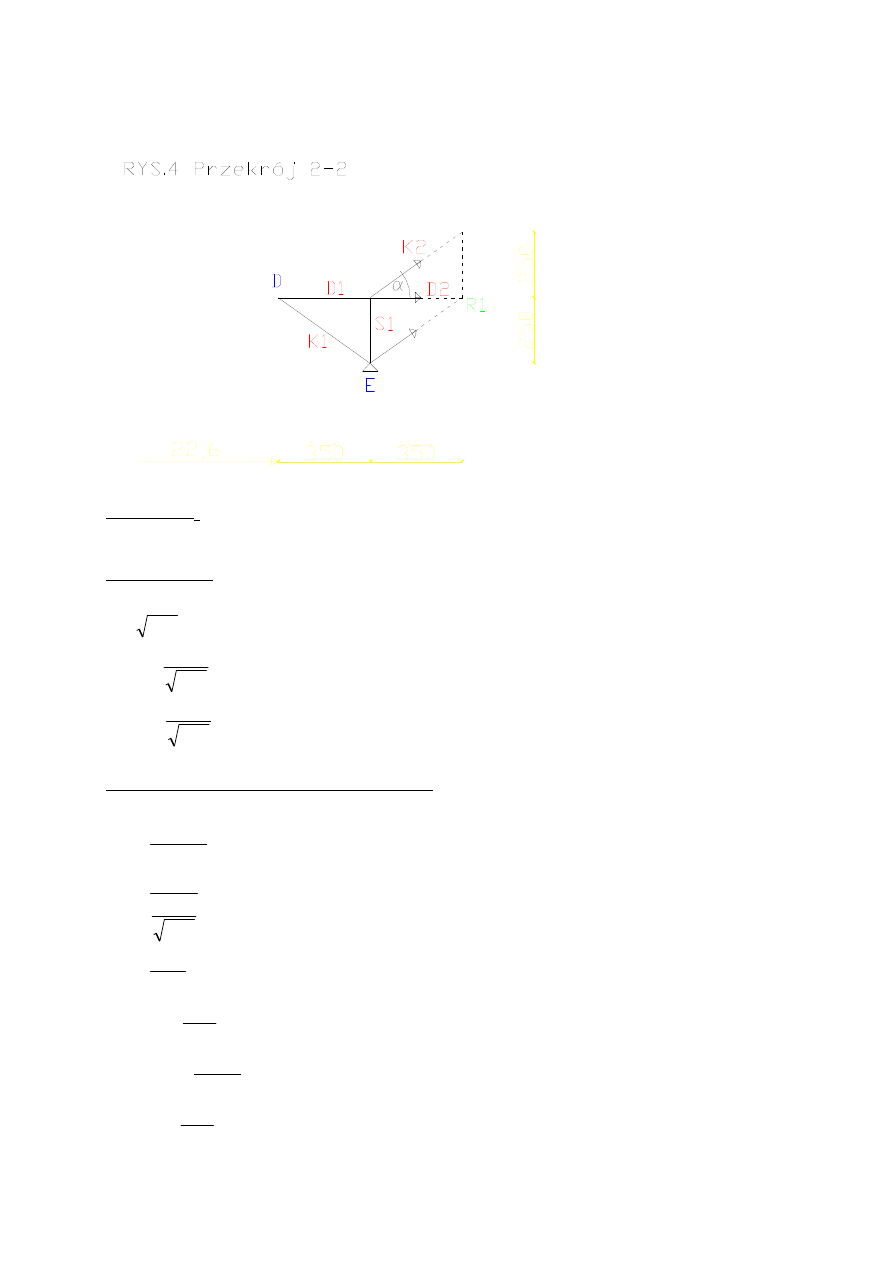
Obliczam K
2
pkt R = R
1
obliczam kąt α
5
,
18
5
,
3
cos
5
,
18
5
,
2
sin
5
,
18
5
,
3
5
,
2
2
2
2
=
=
=
=
+
α
α
c
c
Gdy siła znajduje się po prawej stronie cięcia
69
,
0
58
,
0
4
,
0
)
44
(
27
,
1
58
,
0
74
,
0
)
6
,
29
(
71
,
1
58
,
0
99
,
0
)
3
,
8
(
58
,
0
5
,
18
5
,
2
sin
0
sin
2
2
2
2
2
2
2
=
=
−
=
−
=
=
=
−
=
−
=
⋅
⋅
−
=
=
⋅
⋅
+
⋅
K
K
K
V
K
V
K
b
b
V
K
b
K
b
V
E
E
E
E
α
α
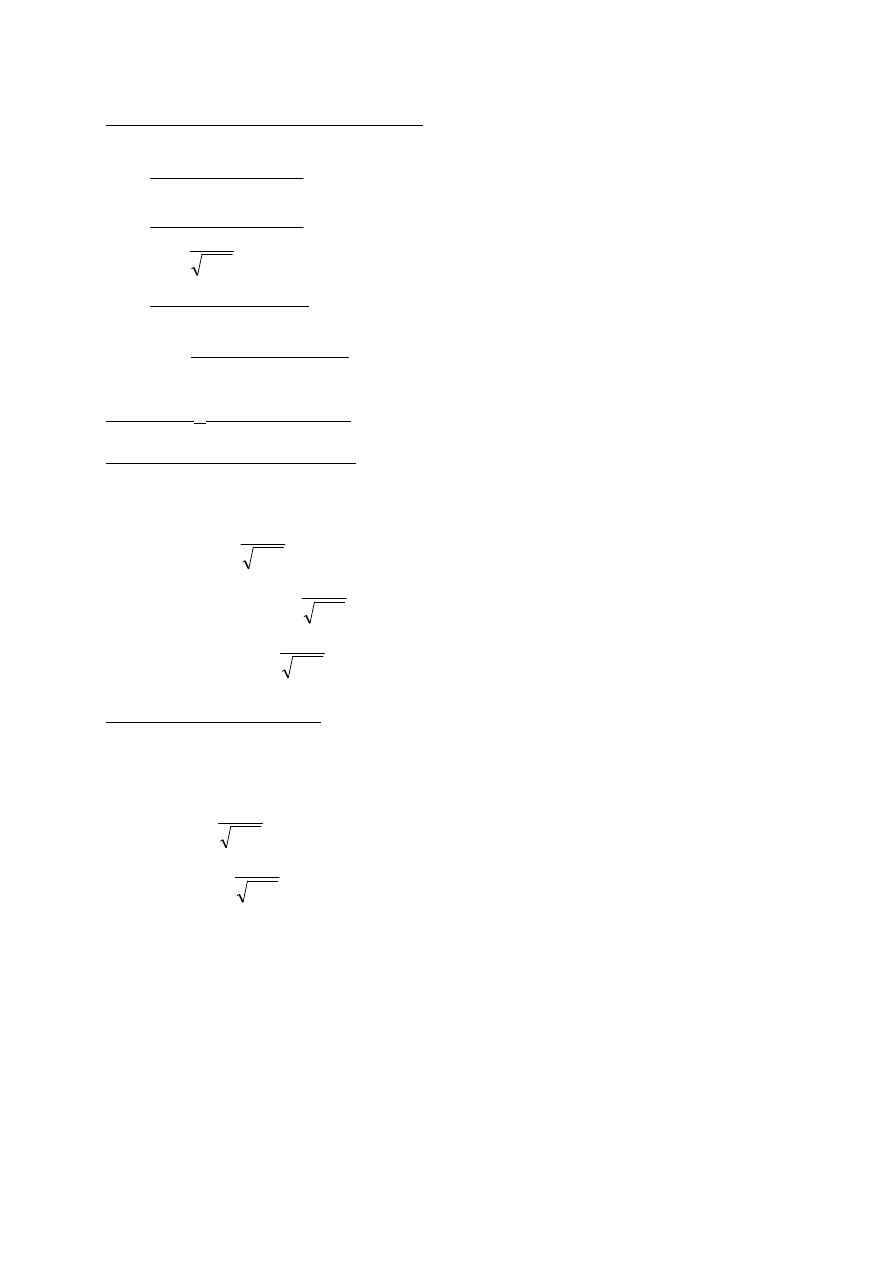
Gdy siła znajduje się po lewej stronie cięcia
0
03
,
2
)
1
,
26
6
,
29
(
5
,
3
1
)
1
,
26
(
03
,
2
)
6
,
29
(
1
5
,
3
5
,
3
5
,
18
5
,
2
)
6
,
29
(
sin
)
6
,
29
(
0
)
6
,
29
(
sin
2
2
2
2
2
=
−
+
⋅
−
=
−
+
⋅
−
=
⋅
−
+
⋅
−
=
⋅
−
+
⋅
−
=
=
−
−
⋅
⋅
+
⋅
K
x
V
K
x
P
b
V
K
b
x
P
b
V
K
x
P
b
K
b
V
E
E
E
E
α
α
Obliczam D
2
z równowagi więzła
Gdy siła znajduje się poza węzłem
03
,
1
5
,
18
5
,
3
27
,
1
0
)
6
,
29
(
88
,
3
5
,
18
5
,
3
26
,
1
86
,
2
)
6
,
22
(
5
,
18
5
,
3
cos
0
cos
2
2
2
1
2
2
1
2
1
2
2
=
⋅
+
=
=
⋅
+
=
⋅
−
=
⋅
−
=
=
−
⋅
+
D
D
K
D
D
K
D
D
D
K
D
α
α
Gdy siła znajduje się w węźle
0
5
,
18
5
,
3
0
0
)
1
,
26
(
5
,
18
5
,
3
cos
0
cos
2
2
1
2
2
1
2
1
2
2
=
⋅
+
=
⋅
−
=
⋅
−
=
=
−
⋅
+
D
K
D
D
K
D
D
D
K
D
α
α
Obliczam G
1
pkt R = R
2
Gdy siła znajduje się po prawej stronie cięcia
33
,
1
)
4
,
0
(
5
,
2
3
,
8
)
44
(
33
,
1
4
,
0
5
,
2
3
,
8
)
4
,
34
(
5
,
2
3
,
8
)
(
0
)
(
1
1
1
1
1
=
−
⋅
−
=
−
=
⋅
−
=
⋅
−
=
+
⋅
−
=
=
⋅
+
+
⋅
G
G
V
G
a
b
c
V
G
a
G
b
c
V
E
E
E
Gdy siła znajduje się po lewej stronie cięcia
54
,
0
5
,
2
)
6
,
29
4
,
34
(
1
3
,
8
74
,
0
)
6
,
29
(
5
,
2
)
4
,
34
(
1
3
,
8
)
3
,
34
(
)
(
0
)
3
,
34
(
)
(
1
1
1
1
−
=
−
+
⋅
−
=
−
+
⋅
−
=
−
+
+
⋅
−
=
=
−
−
⋅
+
+
⋅
G
x
V
G
a
x
P
b
c
V
G
x
P
a
G
b
c
V
E
E
E
Obliczam G
2
pkt R = R
3
Gdy siła znajduje się po prawej stronie cięcia
1
,
2
)
4
,
0
(
5
,
2
1
,
13
)
44
(
0
0
5
,
2
1
,
13
)
2
,
39
(
5
,
2
1
,
13
)
2
(
0
)
2
(
2
2
2
2
2
=
−
⋅
−
=
=
⋅
−
=
⋅
−
=
+
⋅
−
=
=
⋅
+
+
⋅
G
G
V
G
a
b
c
V
G
a
G
b
c
V
E
E
E
Gdy siła znajduje się po lewej stronie cięcia
0
5
,
2
)
4
,
34
2
,
39
(
1
1
,
13
4
,
0
)
4
,
34
(
5
,
2
)
2
,
39
(
1
1
,
13
)
9
,
38
(
)
2
(
0
)
9
,
38
(
)
2
(
2
2
2
2
=
−
+
⋅
−
=
−
+
⋅
−
=
−
+
+
⋅
−
=
=
−
−
⋅
+
+
⋅
G
x
V
G
a
x
P
b
c
V
G
x
P
a
G
b
c
V
E
E
E

Obliczam D
3
pkt R = R
4
Gdy siła znajduje się po prawej stronie cięcia
33
,
1
)
4
,
0
(
5
,
2
3
,
8
)
44
(
0
0
5
,
2
3
,
8
)
2
,
39
(
5
,
2
3
,
8
)
(
0
)
(
3
3
3
3
3
−
=
−
⋅
=
=
⋅
=
⋅
=
+
⋅
=
=
⋅
−
+
⋅
D
D
V
D
a
b
c
V
D
a
D
b
c
V
E
E
E
Gdy siła znajduje się po lewej stronie cięcia
33
,
1
5
,
2
)
4
,
34
4
,
34
(
1
3
,
8
4
,
0
)
4
,
34
(
5
,
2
)
4
,
34
(
1
3
,
8
)
3
,
34
(
)
(
0
)
3
,
34
(
)
(
3
3
3
3
=
−
+
⋅
=
−
+
⋅
=
−
+
+
⋅
=
=
−
−
⋅
−
+
⋅
D
x
V
D
a
x
P
b
c
V
D
x
P
a
D
b
c
V
E
E
E
Obliczam K
3
pkt R = R
5
obliczam kąt α
29
,
29
8
,
4
cos
29
,
29
5
,
2
sin
29
,
29
8
,
4
5
,
2
2
2
2
=
=
=
=
+
β
β
c
c
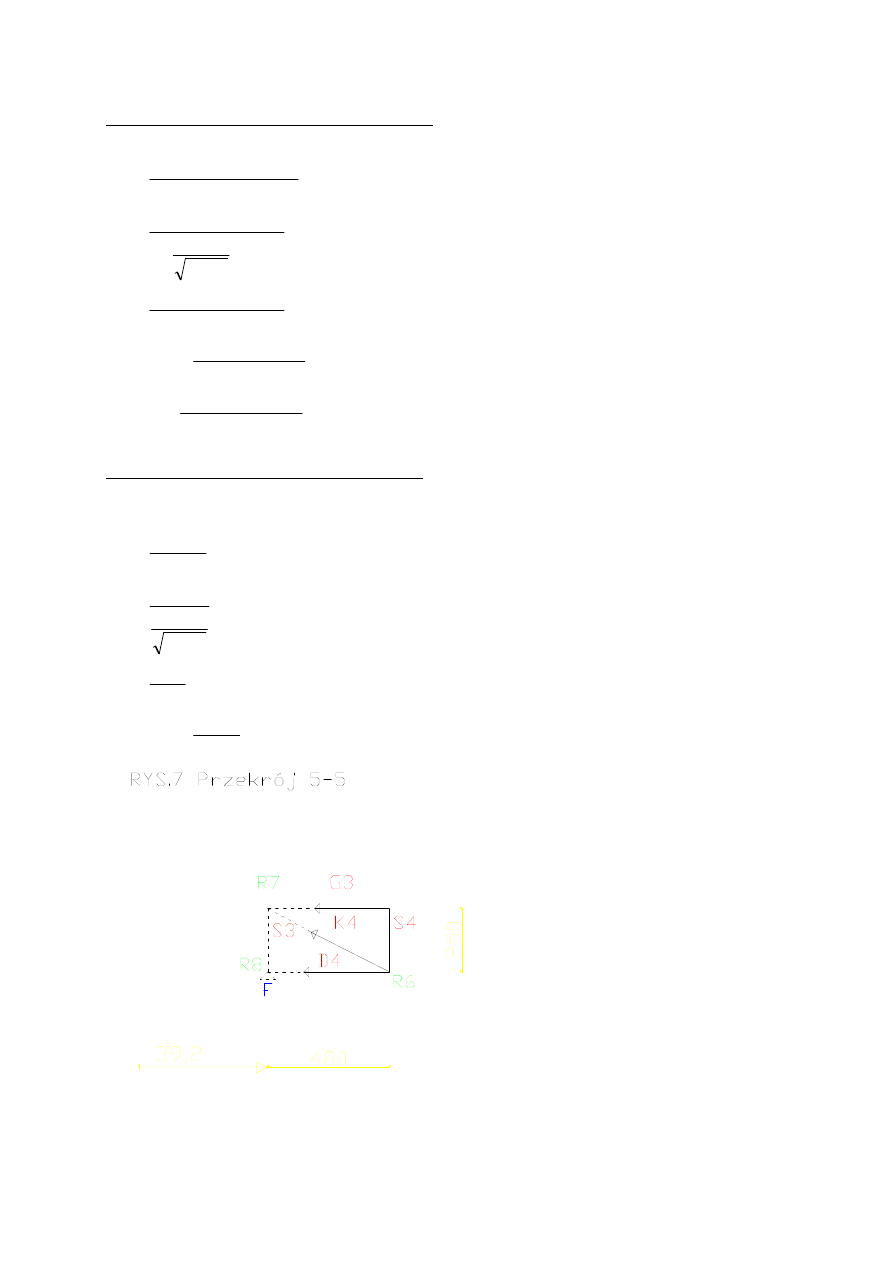
Gdy siła znajduje się po prawej stronie cięcia
87
,
0
22
,
2
5
,
2
1
,
2
3
,
8
4
,
0
)
44
(
0
22
,
2
5
,
2
0
3
,
8
0
)
2
,
39
(
22
,
2
5
,
2
3
,
8
5
,
2
29
,
29
8
,
4
5
,
2
3
,
8
cos
)
(
0
cos
)
(
3
3
2
3
2
3
2
3
2
3
−
=
⋅
−
⋅
=
=
⋅
−
⋅
−
=
⋅
−
⋅
−
=
⋅
⋅
−
⋅
−
=
⋅
⋅
−
+
⋅
−
=
=
⋅
+
⋅
⋅
+
+
⋅
K
K
G
V
K
G
V
K
a
a
G
c
b
V
K
a
G
a
K
c
b
V
E
E
E
E
β
β
Gdy siła znajduje się po lewej stronie cięcia
41
,
1
46
,
0
65
,
0
)
4
,
34
(
46
,
0
29
,
29
5
,
2
sin
0
sin
3
3
3
3
3
−
=
−
=
−
=
−
=
⋅
⋅
−
=
=
⋅
⋅
−
⋅
−
K
V
K
V
K
c
c
V
K
c
K
c
V
F
F
F
F
β
β
Obliczam G
3
pkt R = R
6
Gdy siła znajduje się po prawej stronie cięcia
0
5
,
2
)
44
44
(
1
)
44
(
3
)
44
(
1
)
44
(
0
)
44
(
3
3
3
3
=
−
−
=
−
−
=
−
−
=
=
−
−
⋅
−
G
x
G
a
x
P
G
x
P
a
G
Gdy siła znajduje się po lewej stronie cięcia
0
)
2
,
39
(
0
0
3
3
3
=
=
=
⋅
−
G
G
a
G
Obliczam D
4
pkt R = R
7
Gdy siła znajduje się po prawej stronie cięcia
92
,
1
5
,
2
)
2
,
39
44
(
1
)
44
(
5
,
2
)
2
,
39
(
1
)
2
,
39
(
0
)
2
,
39
(
4
4
4
4
−
=
−
−
=
−
−
=
−
−
=
=
−
+
⋅
D
x
D
a
x
P
D
x
P
a
D
Gdy siła znajduje się po lewej stronie cięcia
0
)
2
,
39
(
0
0
4
4
4
=
=
=
⋅
D
D
a
D
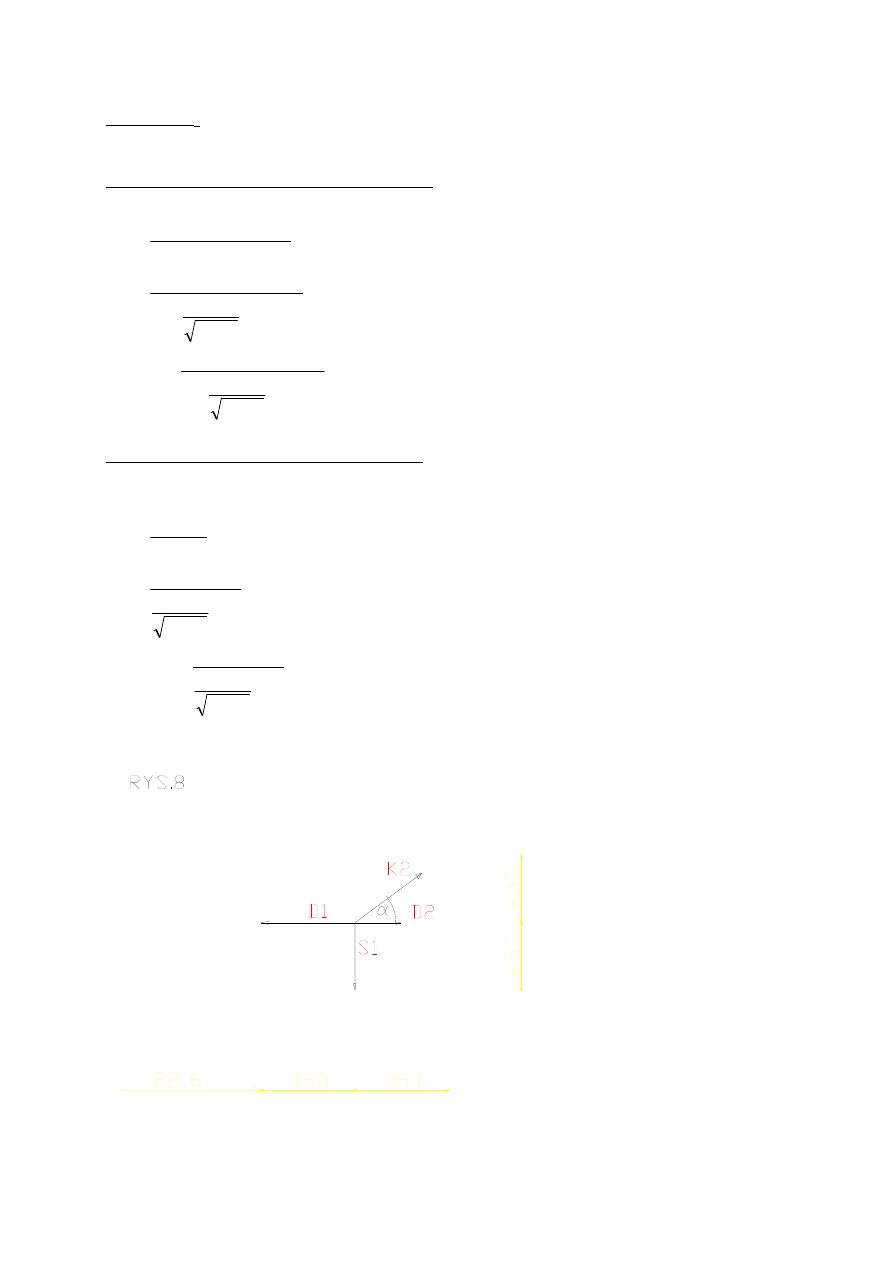
Obliczam K
4
pkt R = R
8
Gdy siła znajduje się po prawej stronie cięcia
16
,
2
8
,
4
29
,
29
5
,
2
5
,
2
0
)
2
,
39
44
(
1
)
44
(
8
,
4
29
,
29
5
,
2
5
,
2
)
2
,
39
(
sin
)
2
,
39
(
0
)
2
,
39
(
sin
4
3
4
3
4
3
4
=
⋅
⋅
−
−
=
⋅
⋅
−
−
=
⋅
⋅
−
−
=
=
⋅
−
−
+
⋅
⋅
−
K
G
x
P
K
c
a
G
x
P
K
a
G
x
P
c
K
β
β
Gdy siła znajduje się po lewej stronie cięcia
0
8
,
4
29
,
29
5
,
2
5
,
2
0
)
9
,
38
(
8
,
4
29
,
29
5
,
2
5
,
2
sin
0
sin
4
3
4
3
4
3
4
=
⋅
⋅
−
=
⋅
⋅
−
=
⋅
⋅
−
=
=
⋅
−
⋅
⋅
−
K
G
K
c
a
G
K
a
G
c
K
β
β

Obliczam S
1
z równowagi więzów
∑
=
0
Y
P
Gdy siła znajduje się poza więzłem
73
,
0
)
6
,
29
(
0
)
1
,
26
(
73
,
0
)
6
,
22
(
5
,
18
5
,
2
sin
0
sin
1
1
1
2
1
2
1
2
1
−
=
=
=
⋅
=
⋅
=
=
⋅
−
S
S
S
K
S
K
S
K
S
α
α
Gdy siła znajduje się w węźle
1
)
1
,
26
(
1
5
,
18
5
,
2
sin
0
sin
1
2
1
2
1
2
1
−
=
−
⋅
=
−
⋅
=
=
+
⋅
−
S
K
S
P
K
S
P
K
S
α
α
Obliczam S
2
z równowagi więzów
∑
=
0
Y
P
Gdy siła znajduje się poza więzłem
0
)
2
,
39
(
58
,
0
)
6
,
29
(
29
,
29
5
,
2
sin
0
sin
2
2
2
2
2
2
2
2
=
−
=
⋅
−
=
⋅
−
=
=
⋅
+
S
S
K
S
K
S
K
S
β
β
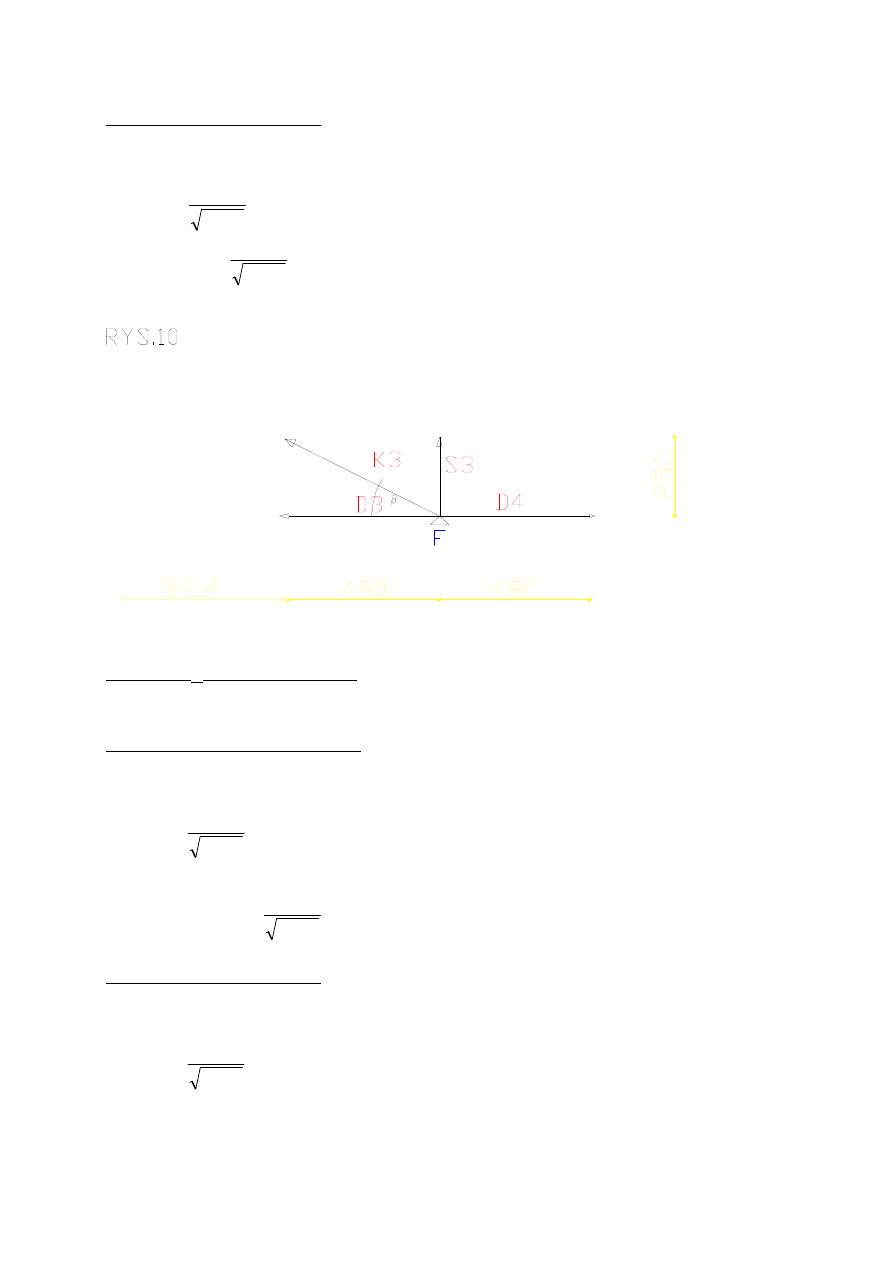
Gdy siła znajduje się w węźle
74
,
0
1
29
,
29
5
,
2
55
,
0
)
4
,
34
(
1
29
,
29
5
,
2
sin
0
sin
2
2
2
2
2
2
2
−
=
−
⋅
=
−
⋅
−
=
−
⋅
−
=
=
+
⋅
+
S
K
S
P
K
S
P
K
S
α
α
Obliczam S
3
z równowagi więzów
∑
=
0
Y
P
Gdy siła znajduje się poza więzłem
07
,
1
29
,
29
5
,
2
71
,
0
4
,
1
)
44
(
0
)
4
,
34
(
29
,
29
5
,
2
sin
0
sin
3
3
3
3
3
3
3
3
−
=
⋅
+
−
=
=
−
⋅
−
=
−
⋅
−
=
=
+
⋅
+
S
S
V
K
S
V
K
S
V
K
S
F
F
F
β
β
Gdy siła znajduje się w węźle
0
)
2
,
39
(
1
29
,
29
5
,
2
sin
0
sin
3
3
3
3
3
3
3
=
−
⋅
−
=
−
+
⋅
−
=
=
+
−
⋅
+
+
S
V
K
S
V
P
K
S
V
P
K
S
F
F
F
β
β
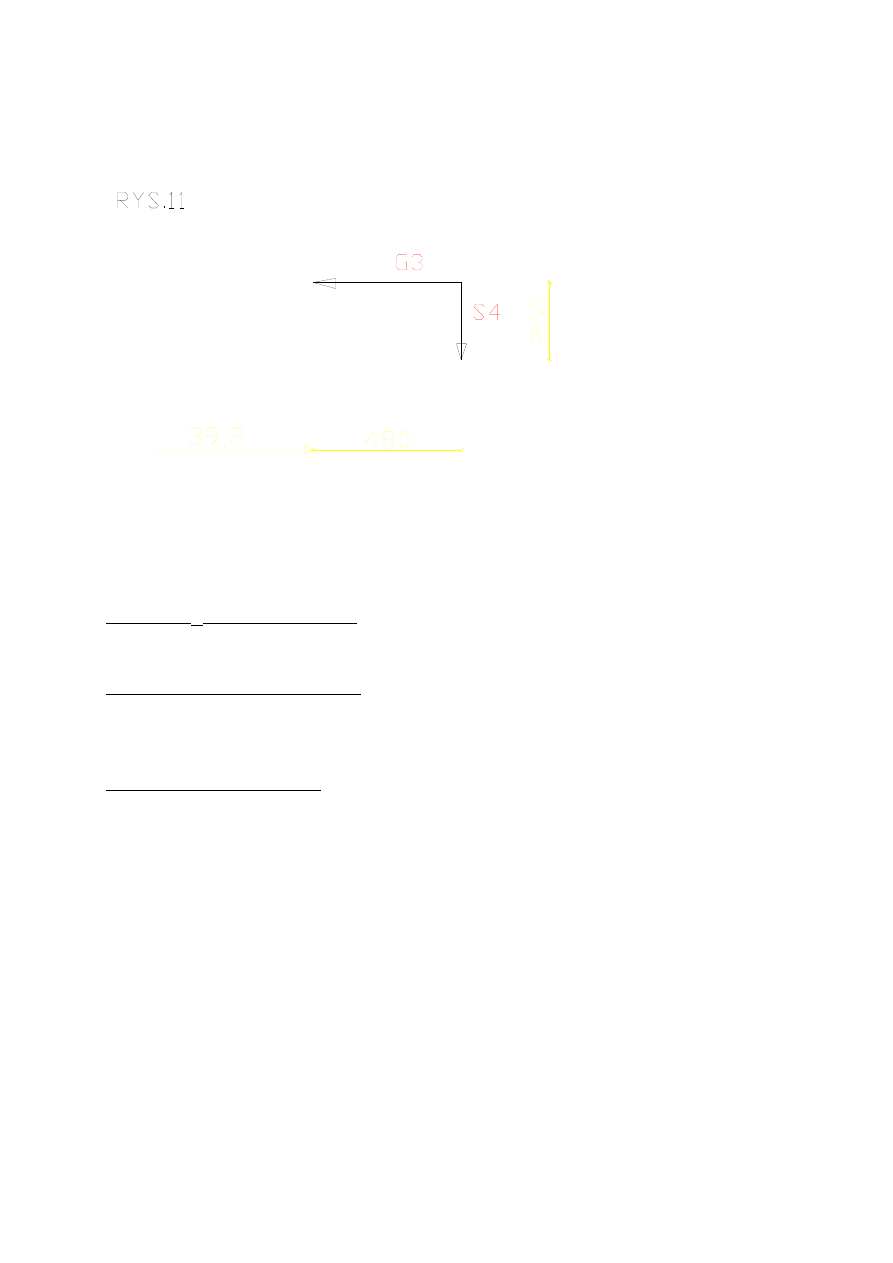
Obliczam S
4
z równowagi więzów
∑
=
0
Y
P
Gdy siła znajduje się poza więzłem
0
)
44
(
0
3
4
=
=
S
S
Gdy siła znajduje się w węźle
0
)
2
,
39
(
0
4
4
=
=
S
S

ZADANIE 2
a = 2,5 m
b = 3,5 m
c = 4,8 m
Wykresy :
- linii wpływu V
A
- linii wpływu V
B
Wykonuje cięcie Rittera, aby obliczyć G
1
, D
1
, K
1
Obliczam G
1
0 < x < 3b
0 < x < 10,5 m
pkt R = R
1
Obliczam wysokość punktu R
1
225
,
6
5
,
3
3
5
,
3
4
8
,
4
5
,
3
3
4
=
⋅
=
⋅
+
=
+
x
x
b
x
b
c
b
Gdy siła znajduje się po lewej stronie cięcia
(
)
(
)
(
)
( )
(
)
( )
(
)
125
,
1
225
,
6
7
5
,
10
1
5
,
10
5
,
0
7
0
225
,
6
0
5
,
10
1
5
,
10
1
0
225
,
6
5
,
10
5
,
10
225
,
6
3
3
0
225
,
6
3
3
1
1
1
1
1
−
=
−
+
⋅
−
=
=
−
+
⋅
−
=
−
+
⋅
−
=
−
+
⋅
−
=
=
⋅
+
−
−
⋅
G
G
x
P
V
G
x
b
P
b
V
G
G
x
b
P
b
V
A
A
A
Gdy siła znajduje się po prawej stronie cięci
( )
( )
( )
61
,
0
225
,
6
5
,
10
)
36
,
0
(
19
0
225
,
6
5
,
10
0
14
422
,
0
225
,
6
5
,
10
25
,
0
5
,
10
225
,
6
5
,
10
225
,
6
3
0
225
,
6
3
1
1
1
1
1
1
=
⋅
−
−
=
=
⋅
−
=
−
=
⋅
−
=
⋅
−
=
⋅
−
=
=
⋅
+
⋅
G
G
G
V
G
b
V
G
G
b
V
A
A
A
Obliczam D
1
0 < x < 2b
0 < x < 7m
pkt R = R
2

Obliczam kąt α
67
,
19
5
,
3
cos
67
,
19
725
,
2
sin
67
,
19
725
,
2
5
,
3
2
2
2
=
=
=
=
+
α
α
c
c
0bliczam wysokość punktu D
1
15
,
4
5
,
3
2
5
,
3
4
8
,
4
5
,
3
2
4
=
⋅
=
⋅
+
=
+
x
x
b
x
b
c
b
Gdy siła znajduje się po lewej stronie cięcia
(
)
(
)
(
)
( )
(
)
( )
(
)
07
,
1
15
,
4
67
,
19
5
,
3
7
7
1
7
5
,
0
7
0
15
,
4
67
,
19
5
,
3
0
7
1
7
1
0
15
,
4
67
,
19
5
,
3
7
7
15
,
4
cos
2
2
0
15
,
4
cos
2
2
1
1
1
1
1
=
⋅
−
−
⋅
=
=
⋅
−
−
⋅
=
⋅
−
−
⋅
=
⋅
−
−
⋅
=
=
⋅
⋅
−
−
−
⋅
D
D
x
P
V
D
x
b
P
b
V
D
D
x
b
P
b
V
A
A
A
α
α
Gdy siła znajduje się po prawej stronie cięci
( )
( )
( )
77
,
0
15
,
4
67
,
19
5
,
3
7
36
,
0
19
0
15
,
4
67
,
19
5
,
3
7
0
14
53
,
0
15
,
4
67
,
19
5
,
3
7
25
,
0
5
,
10
15
,
4
67
,
19
5
,
3
7
15
,
4
cos
2
0
15
,
4
cos
2
1
1
1
1
1
1
−
=
⋅
⋅
−
=
=
⋅
⋅
=
=
⋅
⋅
=
⋅
⋅
=
⋅
⋅
=
=
⋅
⋅
−
⋅
D
D
D
V
D
b
V
D
D
b
V
A
A
A
α
α
Obliczam K
1
0 < x < 2b
0 < x < 7m
pkt R = R
3
Obliczam kąt α
51
5
,
3
cos
51
225
,
6
sin
51
225
,
6
5
,
3
2
2
2
=
=
=
=
+
β
β
c
c
Gdy siła znajduje się po lewej stronie cięcia
( )
( )
77
,
0
51
225
,
6
7
7
1
7
0
51
225
,
6
7
0
1
0
51
225
,
6
7
2
sin
0
2
sin
1
1
1
1
1
−
=
⋅
⋅
−
=
=
⋅
⋅
−
=
⋅
⋅
−
=
⋅
⋅
−
=
=
⋅
⋅
+
⋅
K
K
x
P
K
b
x
P
K
b
K
x
P
β
β
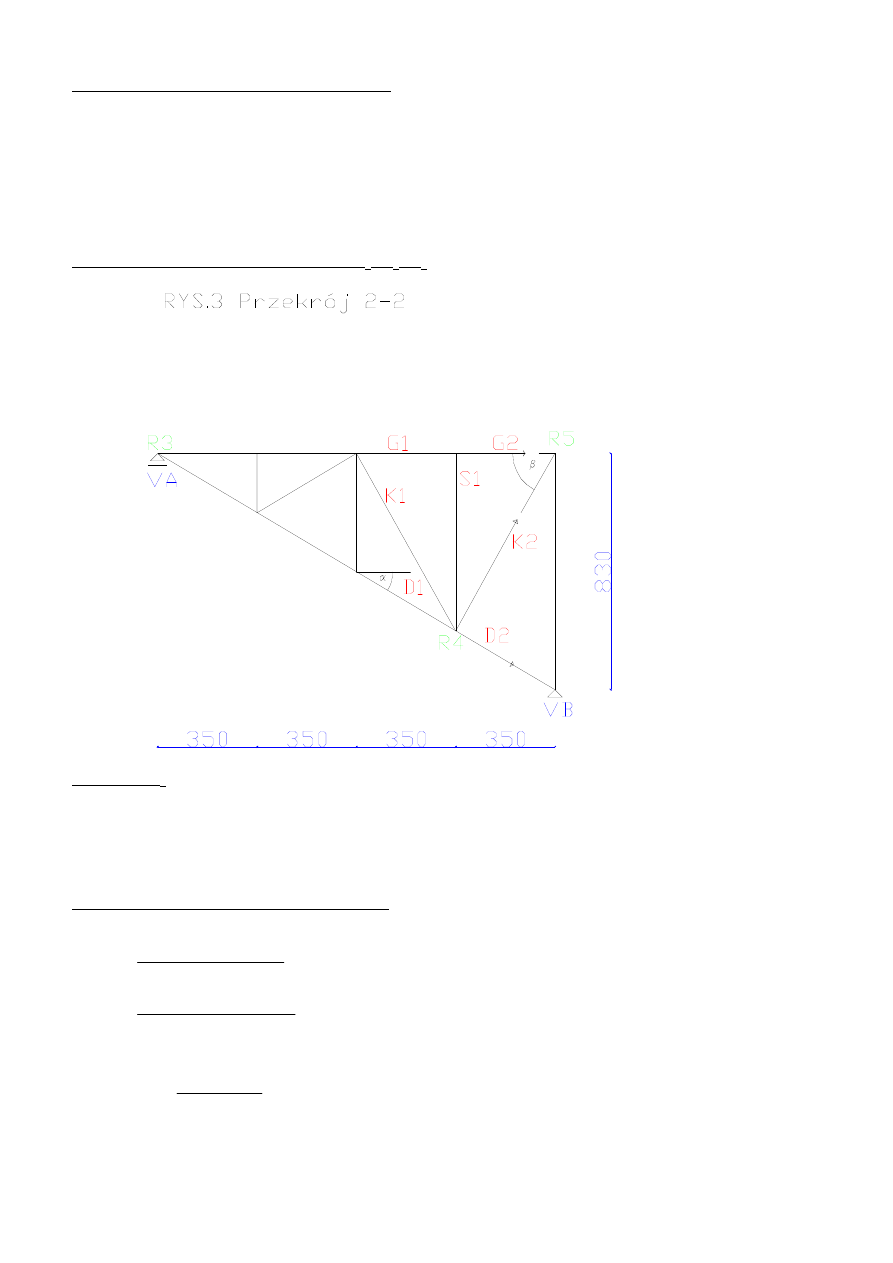
Gdy siła znajduje się po prawej stronie cięci
( )
( )
( )
0
19
0
14
0
5
,
10
0
0
2
sin
1
1
1
1
1
=
=
=
=
=
⋅
⋅
K
K
K
K
b
K
β
Wykonuje cięcie Rittera, aby obliczyć G
2
, D
2
, K
2
Obliczam G
2
0 < x < 3b
0 < x < 10,5 m
pkt R = R
1
Gdy siła znajduje się po lewej stronie cięcia
( )
( )
42
,
0
225
,
6
5
,
10
25
,
0
5
,
10
0
0
225
,
6
)
5
,
10
(
5
,
10
225
,
6
)
3
(
3
0
)
3
(
07
,
6
3
2
2
2
2
2
−
=
⋅
−
=
=
−
+
⋅
−
=
−
+
⋅
−
=
=
−
−
⋅
+
⋅
G
G
x
V
G
x
b
P
b
V
G
x
b
P
G
b
V
A
A
A

Gdy siła znajduje się po prawej stronie cięci
( )
( )
61
,
0
225
,
6
5
,
10
)
36
,
0
(
19
0
225
,
6
5
,
10
0
14
225
,
6
5
,
10
225
,
6
3
0
07
,
6
3
2
2
2
2
2
=
⋅
−
−
=
=
⋅
−
=
⋅
−
=
⋅
−
=
=
⋅
+
⋅
G
G
V
G
b
V
G
G
b
V
A
A
A
Obliczam D
2
0 < x < 4b
0 < x < 14 m
pkt R = R
4
Obliczam kąt α dla D
2
67
,
19
5
,
3
cos
67
,
19
725
,
2
sin
67
,
19
725
,
2
5
,
3
2
2
2
=
=
=
=
+
α
α
c
c
Obliczam wysokość punktu D
2
225
,
6
5
,
3
3
5
,
3
4
8
,
4
5
,
3
3
4
=
⋅
=
⋅
+
=
+
x
x
b
x
b
c
b
Gdy siła znajduje się po lewej stronie cięcia
0
06
,
7
)
5
,
10
14
(
25
,
0
14
)
5
,
10
(
0
06
,
7
)
7
14
(
5
,
0
14
)
7
(
0
06
,
7
)
0
14
(
1
14
)
0
(
06
,
7
)
14
(
14
5
,
3
67
,
19
725
,
2
225
,
6
67
,
19
5
,
3
)
14
(
14
sin
225
,
6
cos
)
4
(
4
0
)
4
(
sin
07
,
6
cos
4
2
2
2
2
2
2
2
2
=
−
−
⋅
=
=
−
−
⋅
=
=
−
−
⋅
=
−
−
⋅
=
⋅
+
⋅
−
−
⋅
=
⋅
⋅
+
⋅
−
−
⋅
=
=
−
−
⋅
⋅
−
⋅
⋅
−
⋅
D
D
D
x
P
V
D
x
P
V
D
b
x
b
P
V
b
D
x
b
P
b
D
D
V
b
A
A
A
A
α
α
α
γ
Gdy siła znajduje się po prawej stronie cięcia
( )
( )
71
,
0
06
,
7
14
36
,
0
19
0
06
,
7
14
0
14
06
,
7
14
5
,
3
67
,
19
725
,
2
225
,
6
67
,
19
5
,
3
14
sin
225
,
6
cos
4
0
sin
225
,
6
cos
4
2
2
2
2
2
2
2
−
=
⋅
−
=
=
⋅
=
⋅
=
⋅
+
⋅
⋅
=
⋅
+
⋅
⋅
=
=
⋅
⋅
−
⋅
⋅
−
⋅
D
D
V
D
V
D
b
b
V
D
b
D
D
b
V
A
A
A
A
α
α
α
α
Obliczam K
2
0 < x < 3b
0 < x < 10,5m
pkt R = R
3
Obliczam kąt α
51
5
,
3
cos
51
225
,
6
sin
51
225
,
6
5
,
3
2
2
2
=
=
=
=
+
β
β
c
c
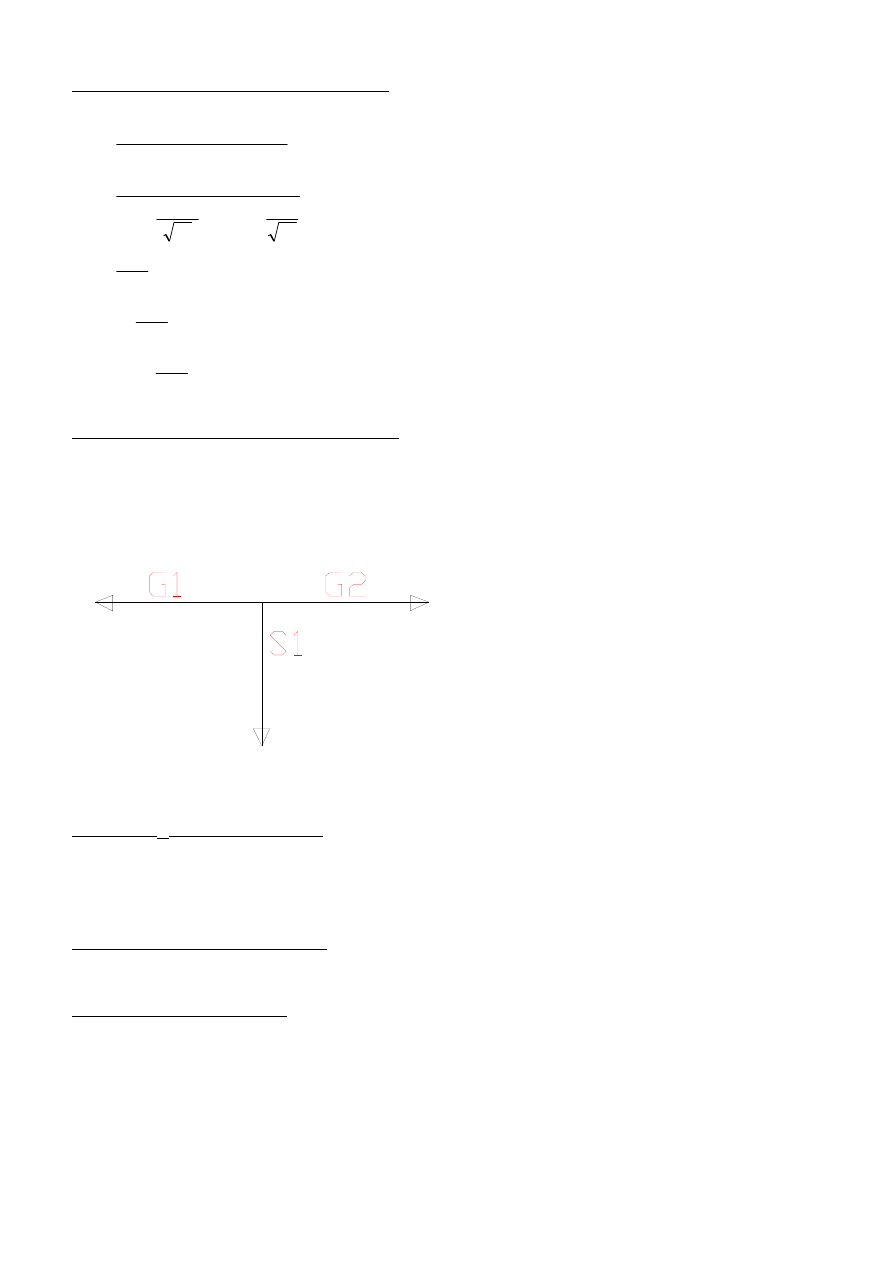
Gdy siła znajduje się po lewej stronie cięcia
( )
( )
86
,
0
2
,
12
5
,
10
0
2
,
12
0
2
,
12
51
5
,
3
225
,
6
51
225
,
6
5
,
10
225
,
6
cos
3
sin
0
225
,
6
cos
3
sin
2
2
2
2
2
2
2
=
=
=
=
=
⋅
+
⋅
⋅
=
⋅
+
⋅
⋅
=
=
⋅
⋅
−
⋅
⋅
−
⋅
x
K
x
K
x
K
x
P
K
b
x
P
K
K
b
K
x
P
β
β
β
β
Gdy siła znajduje się po prawej stronie cięcia
( )
( )
0
19
0
14
0
0
225
,
6
cos
3
sin
2
2
2
2
2
=
=
=
=
⋅
⋅
−
⋅
⋅
−
K
K
K
K
b
K
β
β
Obliczam S
1
z równowagi więzów
0 < x < 3b
0 < x < 10,5m
∑
=
0
Y
P
Gdy siła znajduje się poza więzłem
0
1
=
S
Gdy siła znajduje się w węźle
1
0
1
1
1
−
=
−
=
=
+
S
P
S
P
S
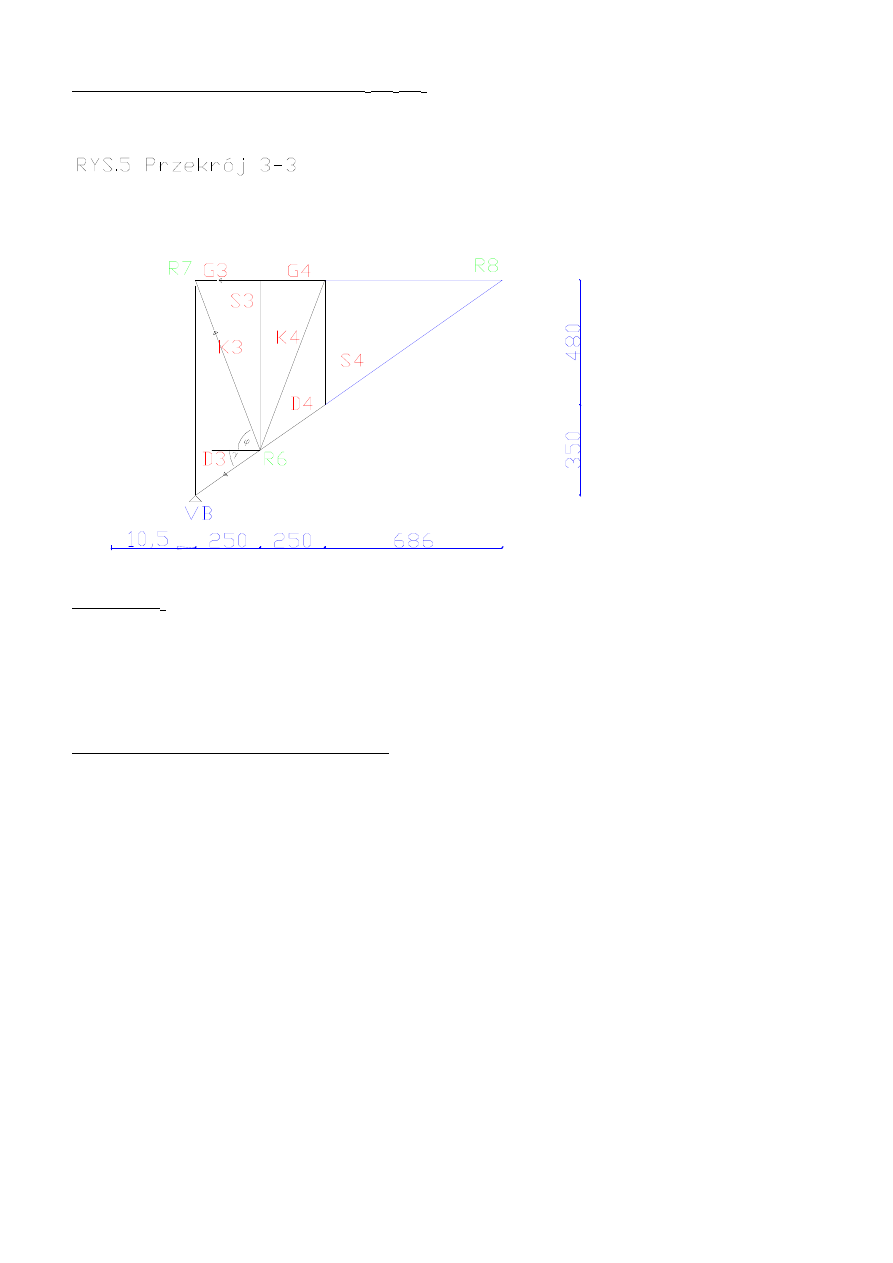
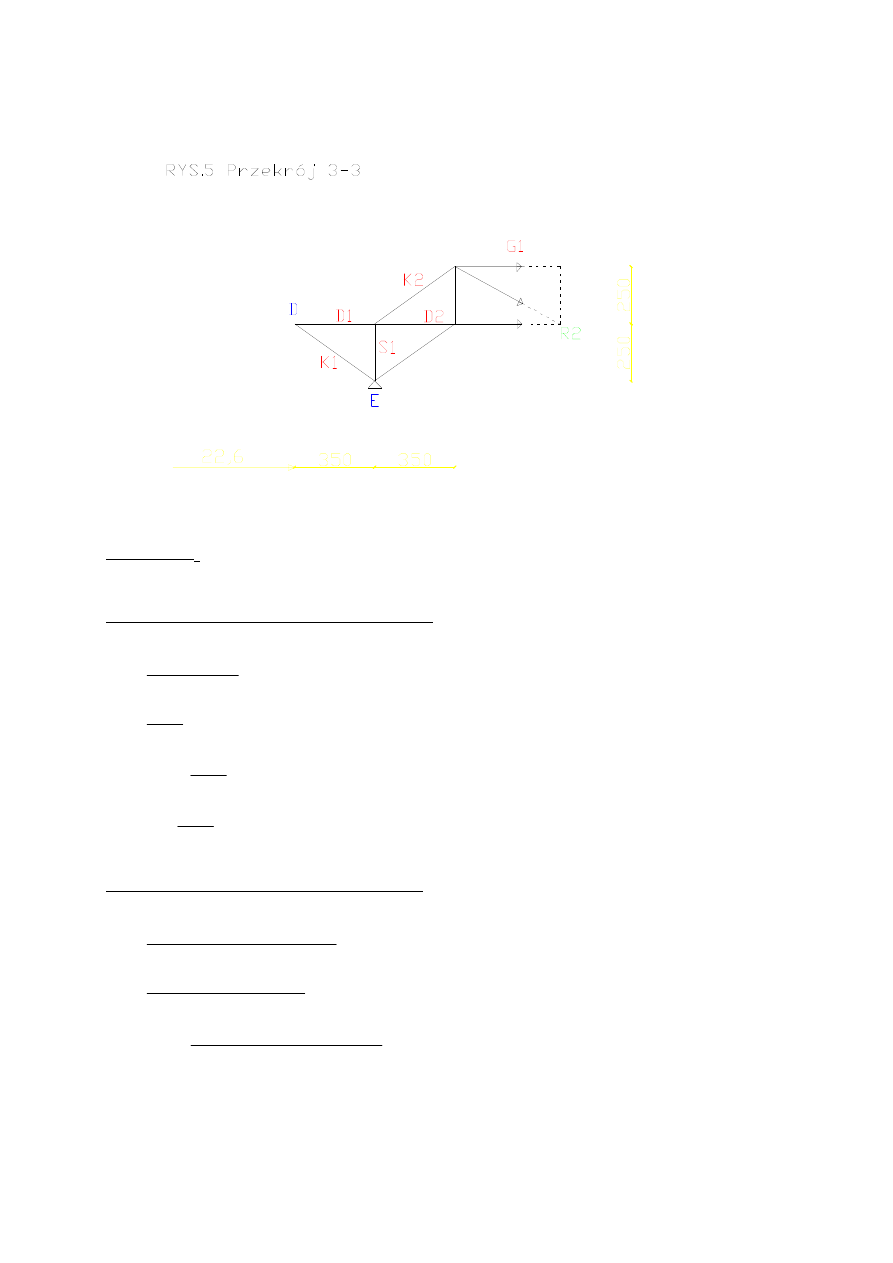
Wykonuje cięcie Rittera, aby obliczyć G
3
, D
3
, K
3
Obliczam G
3
0 < x < 4b
0 < x < 14 m
pkt R = R
6
Gdy siła znajduje się po lewej stronie cięcia
0
)
14
(
0
)
0
(
0
0
55
,
6
0
)
5
,
0
(
3
3
3
3
3
=
=
=
=
⋅
−
=
+
⋅
−
G
G
G
G
b
c
G
Gdy siła znajduje się po prawej stronie cięcia
38
,
0
55
,
6
)
5
,
16
19
(
)
19
(
0
55
,
6
)
5
,
16
5
,
16
(
)
5
,
16
(
55
,
6
)
5
,
16
(
)
5
,
0
(
)
5
,
16
(
0
)
5
,
16
(
)
5
,
0
(
3
3
3
3
3
=
−
=
=
−
=
−
=
+
−
=
=
−
+
+
⋅
−
G
G
x
G
b
c
x
P
G
x
P
b
c
G
Obliczam D
3
0 < x < 4b
0 < x < 14 m
pkt R = R
7
Obliczam kąt γ
31
,
9
5
,
2
cos
31
,
9
75
,
1
sin
31
,
9
75
,
1
5
,
2
2
2
2
=
=
=
=
+
γ
γ
c
c
Gdy siła znajduje się po lewej stronie cięcia
0
)
14
(
0
)
0
(
0
0
sin
)
5
,
0
(
cos
3
3
3
3
3
=
=
=
=
⋅
+
+
⋅
D
D
D
a
D
b
c
D
γ
γ

Gdy siła znajduje się po prawej stronie cięcia
73
,
0
8
,
6
)
14
19
(
)
19
(
37
,
0
8
,
6
)
14
5
,
16
(
)
5
,
16
(
8
,
6
)
14
(
5
,
2
31
,
9
75
,
1
55
,
6
31
,
9
5
,
2
)
14
(
sin
)
5
,
0
(
cos
)
4
(
0
)
4
(
sin
)
5
,
0
(
cos
3
3
3
3
3
3
3
−
=
−
−
=
−
=
−
−
=
−
−
=
⋅
+
⋅
−
−
=
⋅
+
+
⋅
+
−
−
=
=
+
−
+
⋅
+
+
⋅
+
D
D
x
P
D
x
P
D
a
b
c
a
b
x
P
D
a
b
x
P
a
D
b
c
D
γ
γ
γ
γ
Obliczam K
3
0 < x < 4b
0 < x < 14m
pkt R = R
8
Obliczam kąt φ
15
,
49
5
,
2
cos
15
,
49
55
,
6
sin
15
,
49
5
,
2
55
,
6
2
2
2
=
=
=
=
+
ϕ
ϕ
c
c
Obliczam odległość od końca kratownicy do R
8
86
,
6
5
86
,
11
86
,
11
3
,
8
5
,
2
75
,
1
=
−
=
=
x
x
Gdy siła znajduje się po lewej stronie cięcia
( )
( )
0
14
0
0
0
0
)
5
,
0
(
cos
)
86
,
6
(
sin
3
3
3
3
3
=
=
=
=
+
⋅
⋅
+
+
⋅
⋅
K
K
K
b
c
K
a
K
ϕ
ϕ
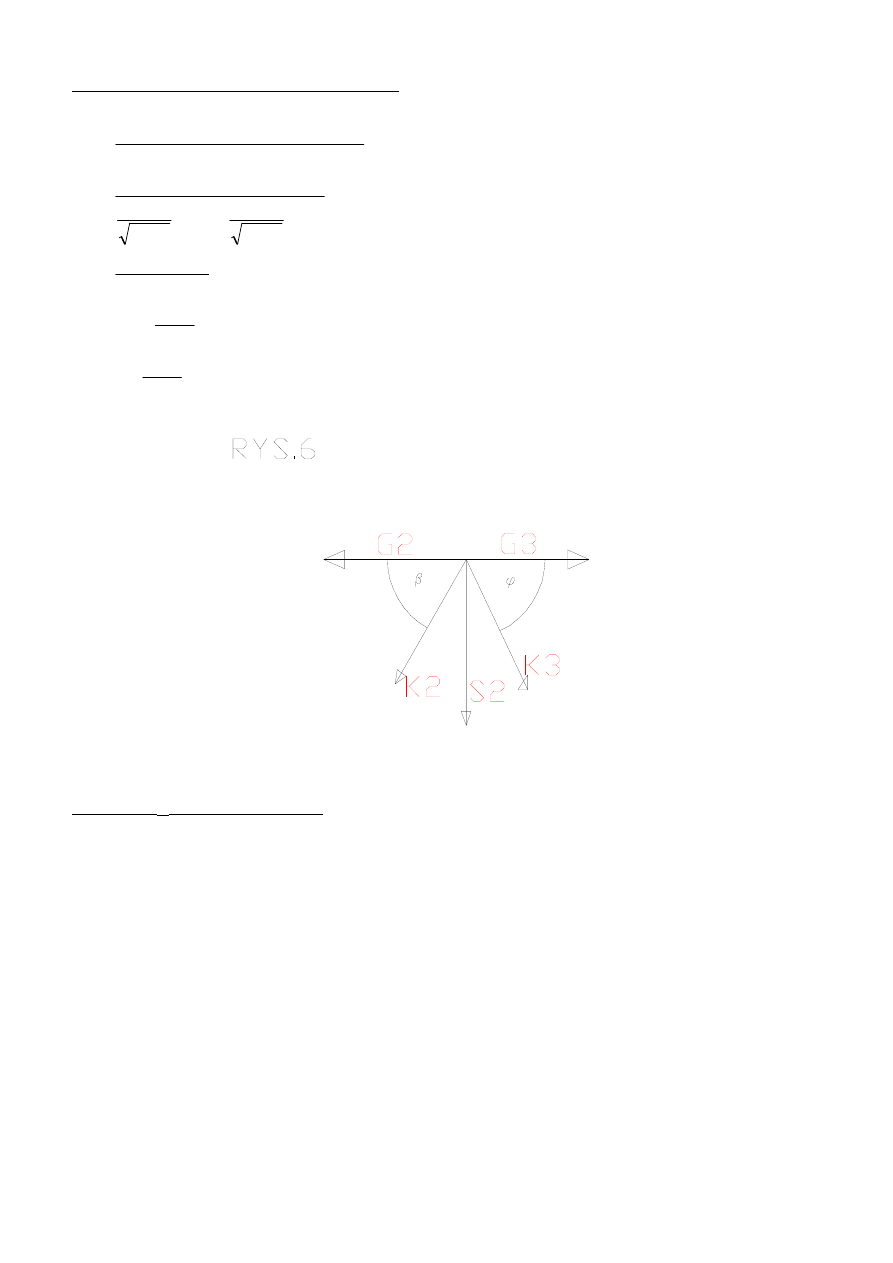
Gdy siła znajduje się po prawej stronie cięcia
( )
( )
28
,
0
79
,
11
36
,
3
19
5
,
0
79
,
11
86
,
5
5
,
16
79
,
11
)
36
,
22
(
55
,
8
15
,
49
5
,
2
36
,
9
15
,
49
55
,
6
)
36
,
22
(
)
5
,
0
(
cos
)
86
,
6
(
sin
)
36
,
22
(
0
)
36
,
22
(
)
5
,
0
(
cos
)
86
,
6
(
sin
3
3
3
3
3
3
3
=
=
=
=
−
=
⋅
+
⋅
−
=
+
⋅
+
+
⋅
−
=
=
−
−
+
⋅
⋅
+
+
⋅
⋅
K
K
x
P
K
x
P
K
b
c
a
x
P
K
x
P
b
c
K
a
K
ϕ
ϕ
ϕ
ϕ
Obliczam S
2
z równowagi więzów
0 < x < 4b
0 < x < 14m
∑
=
0
Y
P
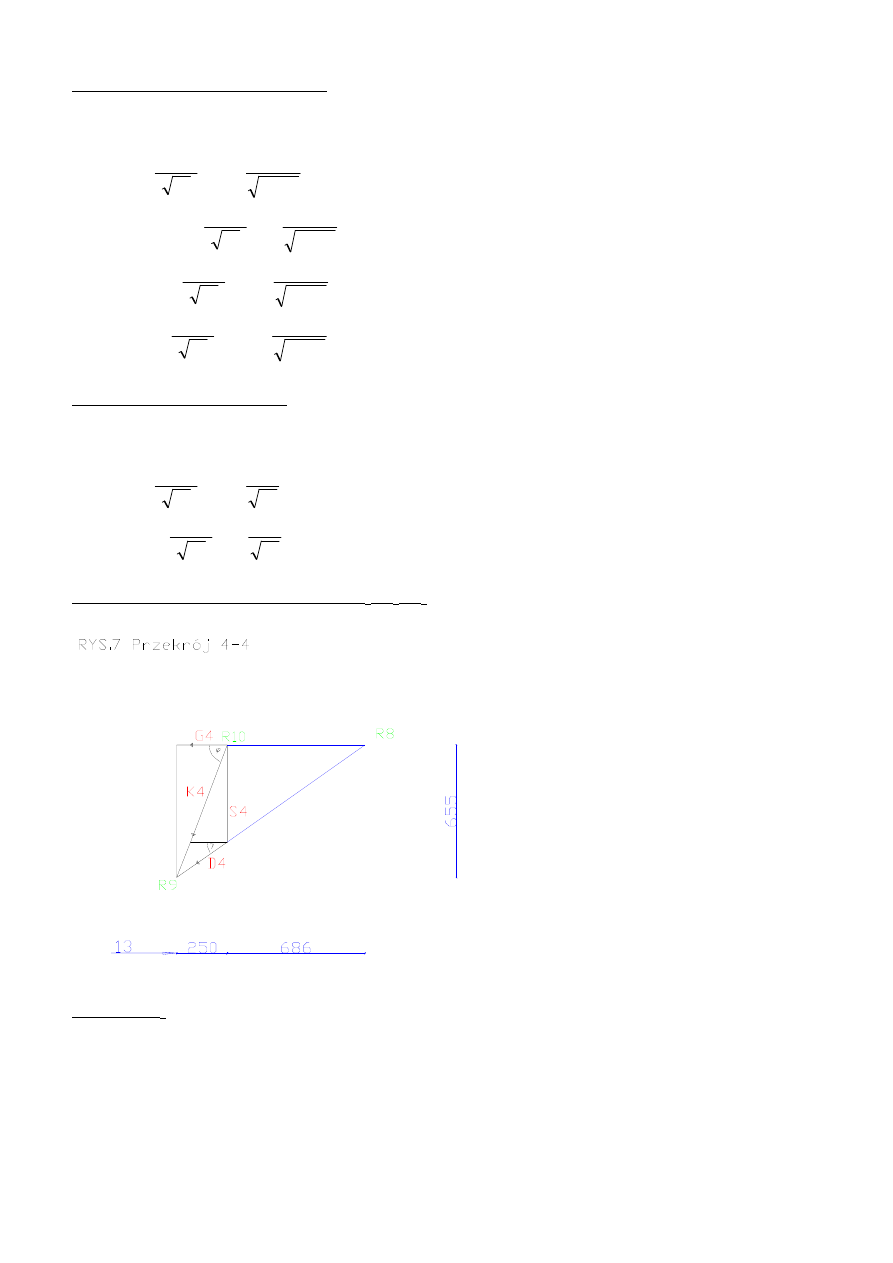
Gdy siła znajduje się poza więzłem
26
,
0
15
,
49
55
,
6
28
,
0
51
225
,
6
0
)
19
(
2
47
,
0
15
,
49
55
,
6
5
,
0
51
225
,
6
0
)
5
,
16
(
75
,
0
15
,
49
55
,
6
0
51
225
,
6
86
,
0
)
5
,
10
(
15
,
49
55
,
6
51
225
,
6
sin
sin
0
sin
sin
2
2
3
2
2
3
2
2
3
2
2
−
=
⋅
−
⋅
−
=
−
=
⋅
−
⋅
−
=
−
=
⋅
−
⋅
−
=
⋅
−
⋅
−
=
−
−
=
=
+
+
S
S
S
K
K
S
K
K
S
K
K
S
ϕ
β
ϕ
β
Gdy siła znajduje się w węźle
1
1
51
55
,
6
0
51
225
,
6
0
)
14
(
1
51
55
,
6
51
225
,
6
sin
sin
0
sin
sin
2
3
2
2
3
2
2
3
2
2
−
=
−
⋅
−
⋅
−
=
−
⋅
−
⋅
−
=
−
−
−
=
=
+
+
+
S
K
K
S
P
K
K
S
P
K
K
S
ϕ
β
ϕ
β
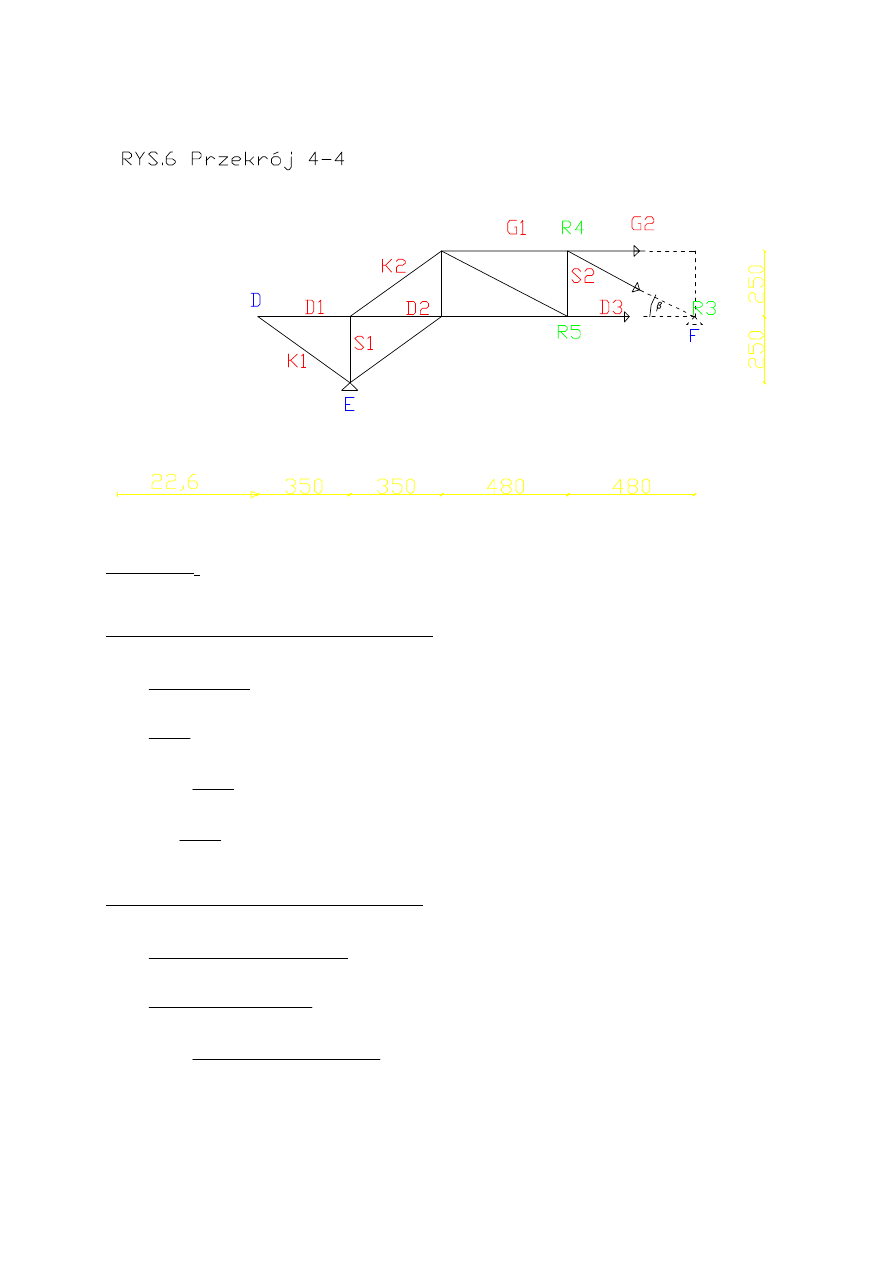
Wykonuje cięcie Rittera, aby obliczyć G
4
, D
4
, K
4
Obliczam G
4
0 < x < 4b+a
0 < x < 16,5 m
pkt R = R
9
Gdy siła znajduje się po lewej stronie cięcia
0
)
5
,
16
(
0
)
0
(
0
0
55
,
6
0
)
5
,
0
(
4
4
4
4
4
=
=
=
=
⋅
−
=
+
⋅
−
G
G
G
G
b
c
G
Gdy siła znajduje się po prawej stronie cięcia
38
,
0
55
,
6
)
5
,
16
19
(
)
19
(
55
,
6
)
5
,
16
(
0
)
5
,
16
(
55
,
6
0
)
4
(
)
5
,
0
(
4
4
4
4
=
−
=
−
=
=
−
+
⋅
−
=
+
−
+
+
⋅
−
G
x
P
G
x
P
G
a
b
x
P
b
c
G
Obliczam D
4
0 < x < 4b+a
0 < x < 16,5 m
pkt R = R
10
Obliczam kąt γ
31
,
9
5
,
2
cos
31
,
9
75
,
1
sin
31
,
9
75
,
1
5
,
2
2
2
2
=
=
=
=
+
γ
γ
c
c
Gdy siła znajduje się po lewej stronie cięcia
0
)
5
,
16
(
0
)
0
(
0
0
cos
4
4
4
4
=
=
=
=
⋅
−
D
D
D
c
D
γ
Gdy siła znajduje się po prawej stronie cięcia
0
93
,
3
)
19
19
(
)
19
(
93
,
3
)
19
(
8
,
4
31
,
9
5
,
2
)
19
(
cos
)
2
4
(
0
)
2
4
(
cos
4
4
4
4
4
=
−
=
−
=
⋅
−
=
⋅
+
−
=
=
+
−
−
⋅
−
D
x
P
D
x
P
D
c
a
b
x
P
D
a
b
x
P
c
D
γ
γ
Obliczam K
4
0 < x < 4b+a
0 < x < 16,5m
pkt R = R
8
Obliczam kąt φ
15
,
49
5
,
2
cos
15
,
49
55
,
6
sin
15
,
49
5
,
2
55
,
6
2
2
2
=
=
=
=
+
ϕ
ϕ
c
c
Obliczam odległość od końca kratownicy do R
8
86
,
6
5
86
,
11
86
,
11
3
,
8
5
,
2
75
,
1
=
−
=
=
x
x
Gdy siła znajduje się po lewej stronie cięcia
( )
( )
0
5
,
16
0
0
0
0
86
,
6
sin
4
4
4
4
=
=
=
=
⋅
⋅
−
K
K
K
K
ϕ
Gdy siła znajduje się po prawej stronie cięcia
(
)
(
)
(
)
( )
52
,
0
41
,
6
)
19
36
,
22
(
1
19
41
,
6
)
36
,
22
(
1
86
,
6
15
,
49
55
,
6
36
,
22
1
86
,
6
sin
36
,
22
0
36
,
22
86
,
6
sin
4
4
4
4
4
−
=
−
⋅
−
=
−
⋅
−
=
⋅
−
⋅
−
=
⋅
−
⋅
−
=
=
−
⋅
−
⋅
⋅
−
K
x
K
x
K
x
P
K
x
P
K
ϕ
ϕ
Obliczam S
3
z równowagi więzów
0 < x < 4b+a
0 < x < 16,5m
∑
=
0
Y
P
Gdy siła znajduje się poza więzłem
0
)
19
(
0
)
14
(
0
3
3
3
=
=
=
S
S
S
Gdy siła znajduje się w węźle
1
)
5
,
16
(
1
0
3
3
3
3
−
=
−
=
−
=
=
+
S
S
P
S
P
S
Obliczam S
4
z równowagi więzów
0 < x < 4b+2a
0 < x < 19m
∑
=
0
Y
P
Gdy siła znajduje się poza więzłem
0
15
,
49
55
,
6
0
)
17
(
15
,
49
55
,
6
sin
0
sin
4
4
4
4
4
4
4
=
⋅
=
⋅
−
=
−
=
=
+
S
K
S
K
S
K
S
ϕ
ϕ
Gdy siła znajduje się w węźle
0
1
15
,
49
55
,
6
07
,
1
)
19
(
1
15
,
49
55
,
6
sin
0
sin
4
4
4
4
4
4
4
=
−
⋅
=
−
⋅
−
=
−
−
=
=
+
+
S
K
S
P
K
S
P
K
S
ϕ
ϕ

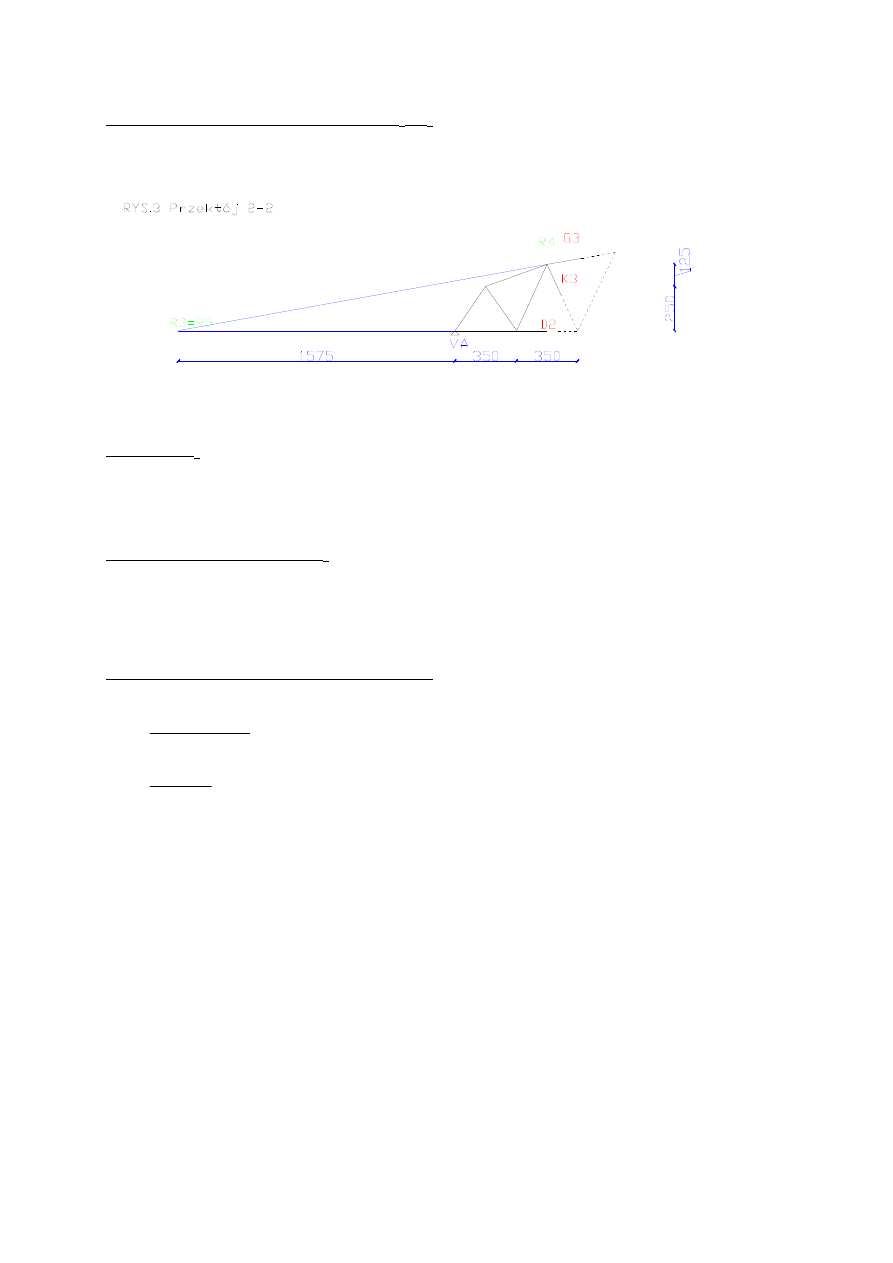
ZADANIE 3
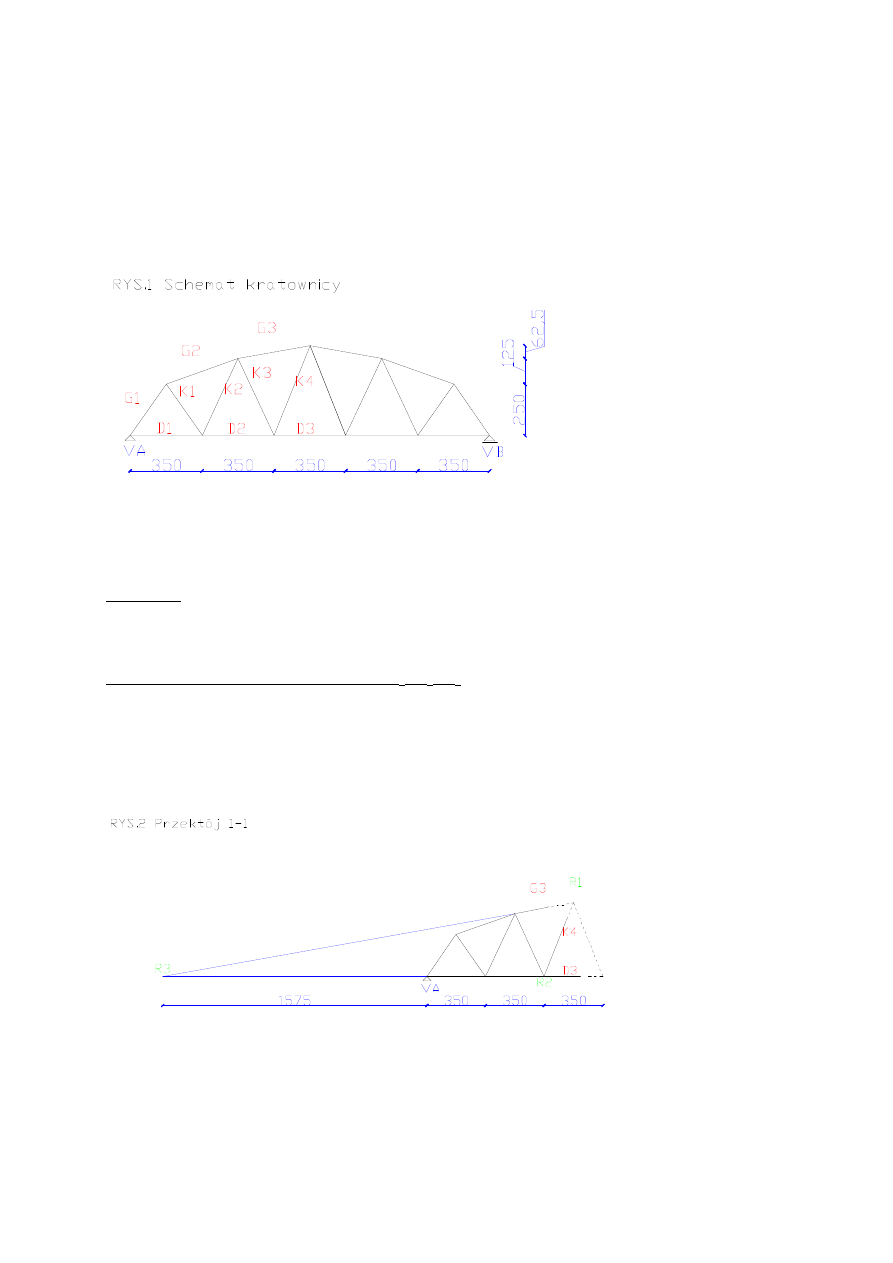
a = 2,5 m
b = 3,5 m
c = 4,8 m
Wykresy :
- linii wpływu V
A
- linii wpływu V
B
Wykonuje cięcie Rittera, aby obliczyć G
3
, D
4
, K
3

Obliczam D
3
0 < x < 2b
0 < x < 7 m
pkt R = R
1
Obliczam wysokość punktu R
1
375
,
4
5
,
2
25
,
0
5
,
2
5
,
0
5
,
2
25
,
0
5
,
0
=
=
⋅
+
⋅
+
=
+
+
x
x
x
a
a
a
Gdy siła znajduje się po prawej stronie cięcia
0
0
2
)
5
,
17
(
8
,
0
4
,
0
2
)
5
,
10
(
2
375
,
4
75
,
8
)
25
,
0
5
,
0
(
)
5
,
0
2
(
0
)
5
,
0
2
(
)
25
,
0
5
,
0
(
3
3
3
3
3
3
=
⋅
=
=
⋅
=
⋅
=
⋅
=
+
+
+
⋅
=
=
+
⋅
+
+
+
⋅
−
D
D
V
D
V
D
a
a
a
b
b
V
D
b
b
V
a
a
a
D
A
A
A
A
Gdy siła znajduje się po lewej stronie cięcia
8
,
0
375
,
4
)
7
75
,
8
(
75
,
8
6
,
0
)
7
(
0
375
,
4
)
0
75
,
8
(
75
,
8
1
)
0
(
375
,
4
)
75
,
8
(
75
,
8
)
25
,
0
5
,
0
(
)
5
,
0
2
(
)
5
,
0
2
(
0
)
5
,
0
2
(
)
5
,
0
2
(
)
25
,
0
5
,
0
(
3
3
3
3
3
=
−
−
⋅
=
=
−
−
⋅
=
−
−
⋅
=
+
+
−
+
−
+
⋅
=
=
−
+
−
+
⋅
+
+
+
⋅
−
D
D
x
P
V
D
a
a
a
x
b
b
P
b
b
V
D
x
b
b
P
b
b
V
a
a
a
D
A
A
A
Obliczam G
3
0 < x < 2b
0 < x < 7 m
pkt R = R
2
Obliczam kąt α
64
,
12
5
,
3
cos
64
,
12
625
,
0
sin
64
,
12
625
,
0
5
,
3
2
2
2
=
=
=
=
+
α
α
c
c
Gdy siła znajduje się po prawej stronie cięcia
0
06
,
4
7
0
)
5
,
17
(
69
,
0
06
,
4
7
4
,
0
)
5
,
10
(
06
,
4
7
75
,
1
64
,
12
75
,
0
75
,
3
64
,
12
5
,
3
5
,
3
2
5
,
0
sin
)
5
,
0
(
cos
2
0
5
,
0
sin
)
5
,
0
(
cos
2
3
3
3
3
3
3
3
=
⋅
−
=
−
=
⋅
−
=
⋅
−
=
⋅
+
⋅
⋅
⋅
−
=
⋅
+
+
⋅
⋅
−
=
=
⋅
⋅
+
+
⋅
⋅
+
⋅
G
G
V
G
V
G
b
a
a
b
V
G
b
G
a
a
G
b
V
A
A
A
A
α
α
α
α
Gdy siła znajduje się po lewej stronie cięcia
03
,
1
06
,
4
)
7
7
(
7
6
,
0
)
7
(
0
06
,
4
)
0
7
(
7
1
)
0
(
06
,
4
)
7
(
7
75
,
1
64
,
12
625
,
0
75
,
3
64
,
12
5
,
3
)
5
,
3
2
(
5
,
3
2
5
,
0
sin
)
5
,
0
(
cos
)
2
(
2
0
)
2
(
5
,
0
sin
)
5
,
0
(
cos
2
3
3
3
3
3
3
3
−
=
−
+
⋅
−
=
=
−
+
⋅
−
=
−
+
⋅
−
=
⋅
+
⋅
−
⋅
+
⋅
⋅
−
=
⋅
+
+
⋅
−
+
⋅
−
=
=
−
−
⋅
⋅
+
+
⋅
⋅
+
⋅
G
G
x
V
G
x
V
G
b
a
a
x
b
P
b
V
G
x
b
P
b
G
a
a
G
b
V
A
A
A
A
α
α
α
α
Obliczam K
4
0 < x < 2b
0 < x < 7 m
pkt R = R
3
Obliczam kąt β
2
,
22
75
,
1
cos
2
,
22
375
,
4
sin
2
,
22
75
,
1
375
,
4
2
2
2
=
=
=
=
+
β
β
c
c
Obliczam odległość od krawędzi kratownicy do R
3
75
,
15
75
,
8
5
,
24
)
5
,
0
2
(
5
,
24
5
,
24
375
,
4
5
,
3
625
,
0
=
−
=
+
−
=
=
b
b
x
x
Gdy siła znajduje się po prawej stronie cięcia
0
99
,
27
75
,
15
0
)
5
,
17
(
22
,
0
99
,
27
75
,
15
4
,
0
)
5
,
10
(
99
,
27
75
,
15
64
,
12
375
,
4
)
5
,
3
5
,
0
5
,
24
(
75
,
15
sin
)
5
,
0
5
,
24
(
75
,
15
0
sin
)
5
,
0
5
,
24
(
75
,
15
4
4
4
4
4
4
=
⋅
−
=
−
=
⋅
−
=
⋅
−
=
⋅
⋅
−
⋅
−
=
⋅
−
⋅
−
=
=
⋅
−
⋅
−
⋅
−
K
K
V
K
V
K
b
V
K
b
K
V
A
A
A
A
β
β
Gdy siła znajduje się po lewej stronie cięcia
47
,
0
99
,
27
)
75
,
15
7
(
75
,
15
6
,
0
)
7
(
0
99
,
27
)
75
,
15
0
(
75
,
15
1
)
0
(
99
,
27
)
75
,
15
(
75
,
15
64
,
12
375
,
4
)
5
,
3
5
,
0
5
,
24
(
)
75
,
15
(
1
75
,
15
sin
)
5
,
0
5
,
24
(
)
75
,
15
(
75
,
15
0
)
75
,
15
(
sin
)
5
,
0
5
,
24
(
75
,
15
4
4
4
4
4
4
=
+
+
⋅
−
=
=
+
+
⋅
−
=
+
+
⋅
−
=
⋅
⋅
−
+
+
⋅
−
=
⋅
−
+
+
⋅
−
=
=
+
+
⋅
−
⋅
−
⋅
−
K
K
x
V
K
x
V
K
b
x
P
V
K
x
P
b
K
V
A
A
A
A
β
β
Wykonuje cięcie Rittera, aby obliczyć D
2
, K
3
Obliczam D
2
0 < x < b+0,5b
0 < x < 5,25 m
pkt R = R
4
Obliczam wysokość punktu R
1
75
,
3
5
,
2
5
,
0
5
,
2
5
,
0
=
=
⋅
+
=
+
x
x
x
a
a
Gdy siła znajduje się po prawej stronie cięcia
0
0
4
,
1
)
5
,
17
(
84
,
0
6
,
0
4
,
1
)
7
(
4
,
1
75
,
3
25
,
5
)
5
,
0
(
)
5
,
0
(
0
)
5
,
0
(
)
5
,
0
(
2
2
2
2
2
2
=
⋅
=
=
⋅
=
⋅
=
⋅
=
+
+
⋅
=
=
+
⋅
+
+
⋅
−
D
D
V
D
V
D
a
a
b
b
V
D
b
b
V
a
a
D
A
A
A
A
Gdy siła znajduje się po lewej stronie cięcia
65
,
0
75
,
3
)
5
,
3
25
,
5
(
1
25
,
5
8
,
0
)
5
,
3
(
0
75
,
3
)
0
25
,
5
(
1
25
,
5
1
)
0
(
75
,
3
)
25
,
5
(
1
25
,
5
)
5
,
0
(
)
5
,
0
(
)
5
,
0
(
0
)
5
,
0
(
)
5
,
0
(
)
5
,
0
(
2
2
2
2
2
=
−
−
⋅
=
=
−
−
⋅
=
−
−
⋅
=
+
−
+
−
+
⋅
=
=
−
+
−
+
⋅
+
+
⋅
−
D
D
x
V
D
a
a
x
b
b
P
b
b
V
D
x
b
b
P
b
b
V
a
a
D
A
A
A
Obliczam K
3
0 < x < b+0,5b
0 < x < 5,25 m
pkt R = R
5
Obliczam kąt γ
12
,
17
75
,
1
cos
12
,
17
75
,
3
sin
12
,
17
75
,
1
75
,
3
2
2
2
=
=
=
=
+
γ
γ
c
c
Obliczam odległość od krawędzi kratownicy do R
5
75
,
15
75
,
8
5
,
24
)
5
,
0
2
(
5
,
24
5
,
24
375
,
4
5
,
3
625
,
0
=
−
=
+
−
=
=
b
b
x
x
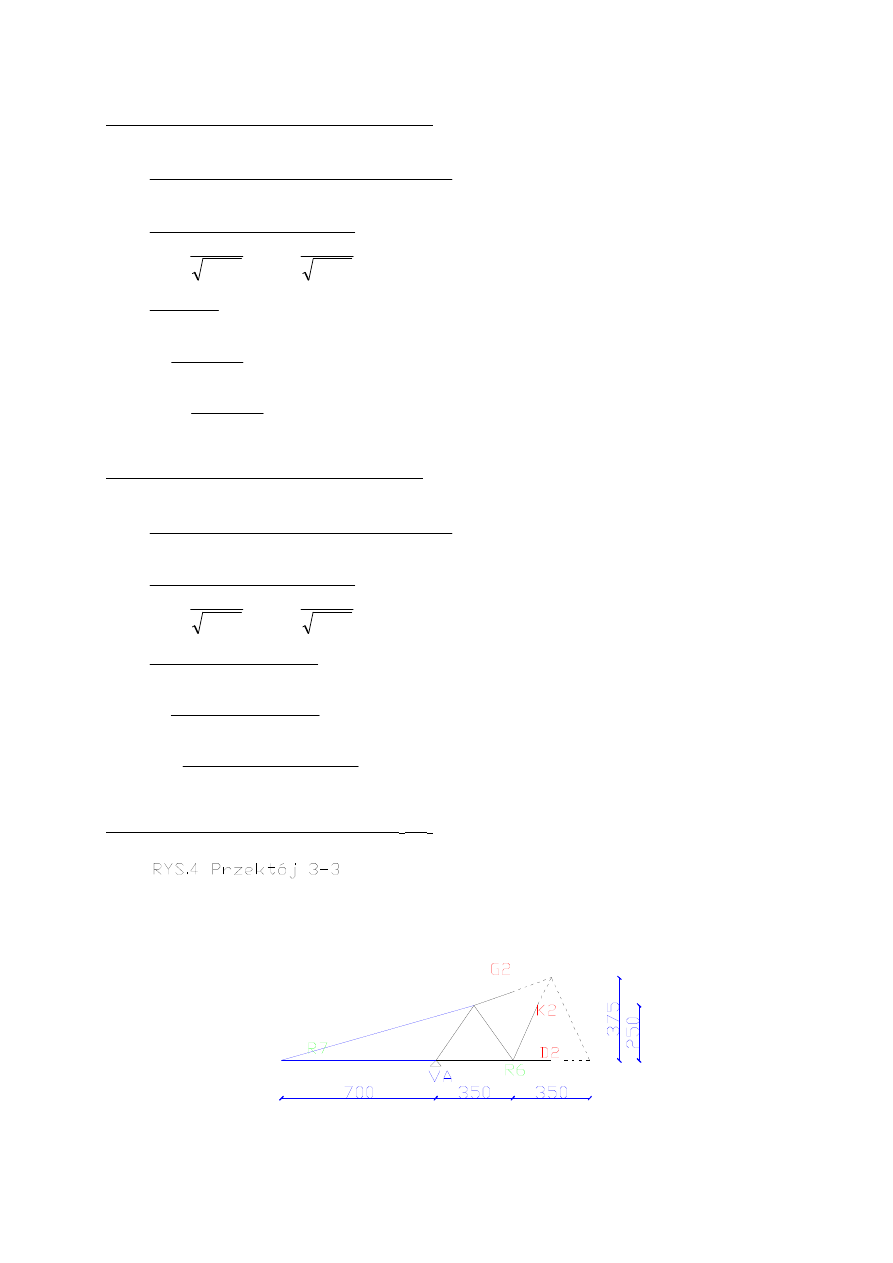
Gdy siła znajduje się po prawej stronie cięcia
0
07
,
21
75
,
15
0
)
5
,
17
(
45
,
0
07
,
21
75
,
15
6
,
0
)
7
(
07
,
21
75
,
15
12
,
17
75
,
1
75
,
3
12
,
17
75
,
3
5
,
21
75
,
15
cos
)
5
,
0
(
sin
)
75
,
15
5
,
0
(
75
,
15
0
cos
)
5
,
0
(
sin
)
75
,
15
5
,
0
(
75
,
15
3
3
3
3
3
3
3
=
⋅
−
=
=
⋅
=
⋅
=
⋅
+
⋅
⋅
=
⋅
+
+
⋅
+
+
⋅
=
=
⋅
+
⋅
+
⋅
+
+
⋅
+
⋅
−
K
K
V
K
V
K
a
a
b
b
V
K
a
a
K
b
b
K
V
A
A
A
A
γ
γ
γ
γ
Gdy siła znajduje się po lewej stronie cięcia
32
,
0
07
,
21
)
75
,
15
5
,
3
(
75
,
15
8
,
0
)
5
,
3
(
0
07
,
21
)
75
,
15
0
(
75
,
15
1
)
0
(
07
,
21
)
75
,
15
(
1
75
,
15
12
,
17
75
,
1
75
,
3
12
,
17
75
,
3
5
,
21
)
75
,
15
(
75
,
15
cos
)
5
,
0
(
sin
)
75
,
15
5
,
0
(
)
75
,
15
(
75
,
15
0
)
75
,
15
(
cos
)
5
,
0
(
sin
)
75
,
15
5
,
0
(
75
,
15
3
3
3
3
3
3
3
−
=
+
−
⋅
=
=
+
−
⋅
=
+
−
⋅
=
⋅
+
⋅
+
−
⋅
=
⋅
+
+
⋅
+
+
+
−
⋅
=
=
+
+
⋅
+
⋅
+
⋅
+
+
⋅
+
⋅
−
K
K
x
V
K
x
P
V
K
a
a
b
b
x
P
V
K
x
P
a
a
K
b
b
K
V
A
A
A
A
γ
γ
γ
γ
Wykonuje cięcie Rittera, aby obliczyć G
2
, K
2

Obliczam G
2
0 < x < b
0 < x < 3,5 m
pkt R = R
6
Obliczam kąt φ
81
,
13
5
,
3
cos
81
,
13
25
,
1
sin
81
,
13
25
,
1
5
,
3
2
2
2
=
=
=
=
+
ϕ
ϕ
c
c
Gdy siła znajduje się po prawej stronie cięcia
0
94
,
2
7
0
)
5
,
17
(
43
,
1
94
,
2
7
6
,
0
)
7
(
94
,
2
5
,
3
75
,
1
81
,
13
25
,
1
5
,
2
81
,
13
5
,
3
5
,
3
5
,
0
sin
cos
0
5
,
0
sin
cos
2
2
2
2
2
2
2
=
⋅
−
=
−
=
⋅
−
=
⋅
−
=
⋅
+
⋅
⋅
−
=
⋅
+
⋅
⋅
−
=
=
⋅
⋅
+
⋅
⋅
+
⋅
G
G
V
G
V
G
b
a
b
V
G
b
G
a
G
b
V
A
A
A
A
ϕ
ϕ
ϕ
ϕ
Gdy siła znajduje się po lewej stronie cięcia
91
,
1
94
,
2
)
5
,
3
5
,
3
(
7
8
,
0
)
5
,
3
(
0
94
,
2
)
0
5
,
3
(
7
1
)
0
(
94
,
2
)
5
,
3
(
5
,
3
75
,
1
81
,
13
25
,
1
5
,
2
81
,
13
5
,
3
)
5
,
3
(
1
5
,
3
5
,
0
sin
cos
)
(
0
)
(
5
,
0
sin
cos
2
2
2
2
2
2
2
−
=
−
+
⋅
−
=
=
−
+
⋅
−
=
−
+
⋅
−
=
⋅
+
⋅
−
+
⋅
−
=
⋅
+
⋅
−
+
⋅
−
=
=
−
−
⋅
⋅
+
⋅
⋅
+
⋅
G
G
x
V
G
x
V
G
b
a
x
b
P
b
V
G
x
b
P
b
G
a
G
b
V
A
A
A
A
ϕ
ϕ
ϕ
ϕ
Obliczam K
2
0 < x < b
0 < x < 3,5 m
pkt R = R
7
Obliczam kąt γ
12
,
17
75
,
1
cos
12
,
17
75
,
3
sin
12
,
17
75
,
1
75
,
3
2
2
2
=
=
=
=
+
γ
γ
c
c
Obliczam odległość od krawędzi kratownicy do R
7
7
5
,
3
5
,
10
5
,
10
5
,
10
75
,
3
5
,
3
25
,
1
=
−
=
−
=
=
b
x
x
Gdy siła znajduje się po prawej stronie cięcia
0
52
,
9
7
0
)
5
,
17
(
44
,
0
52
,
9
7
6
,
0
)
7
(
52
,
9
7
12
,
17
75
,
3
5
,
10
7
sin
)
7
(
7
0
sin
)
7
(
7
2
2
2
2
2
2
=
⋅
−
=
−
=
⋅
−
=
⋅
−
=
⋅
⋅
−
=
⋅
+
⋅
−
=
=
⋅
+
⋅
−
⋅
−
K
K
V
K
V
K
b
V
K
b
K
V
A
A
A
A
γ
γ

Gdy siła znajduje się po lewej stronie cięcia
52
,
0
52
,
9
)
7
5
,
3
(
7
8
,
0
)
5
,
3
(
0
52
,
9
)
7
0
(
7
1
)
0
(
52
,
9
)
7
(
7
12
,
17
75
,
3
5
,
10
)
7
(
1
7
sin
)
7
(
)
7
(
7
0
)
7
(
sin
)
7
(
7
2
2
2
2
2
2
=
+
+
⋅
−
=
=
+
+
⋅
−
=
+
+
⋅
−
=
⋅
+
+
⋅
−
=
⋅
+
+
+
⋅
−
=
=
+
+
⋅
+
⋅
−
⋅
−
K
K
x
V
K
x
V
K
b
x
P
V
K
x
P
b
K
V
A
A
A
A
γ
γ
Wykonuje cięcie Rittera, aby obliczyć D
1
, K
1
Obliczam D
1
0 < x < b
0 < x < 3,5 m
pkt R = R
8
Gdy siła znajduje się po prawej stronie cięcia
0
0
5
,
2
75
,
1
)
5
,
17
(
56
,
0
8
,
0
5
,
2
75
,
1
)
5
,
3
(
5
,
2
75
,
1
5
,
2
5
.
3
5
,
0
5
,
0
0
5
,
0
1
1
1
1
1
1
=
⋅
=
=
⋅
=
⋅
=
⋅
⋅
=
⋅
=
=
⋅
+
⋅
−
D
D
V
D
V
D
a
b
V
D
b
V
a
D
A
A
A
A
Gdy siła znajduje się po lewej stronie cięcia
7
,
0
5
,
2
0
1
75
,
1
)
0
(
5
,
2
75
,
1
5
,
2
1
5
.
3
5
,
0
5
,
0
0
5
,
0
1
1
1
1
1
=
−
⋅
=
−
⋅
=
⋅
−
⋅
⋅
=
−
⋅
=
=
−
⋅
+
⋅
−
D
x
V
D
x
V
D
a
Px
b
V
D
Px
b
V
a
D
A
A
A
A
Obliczam K
1
0 < x < b
0 < x < 3,5 m
pkt R = R
7
Obliczam kąt ω
31
,
9
75
,
1
cos
31
,
9
5
,
2
sin
31
,
9
75
,
1
5
,
2
2
2
2
=
=
=
=
+
ω
ω
c
c
Obliczam odległość od krawędzi kratownicy do R
7
7
5
,
3
5
,
10
5
,
10
5
,
10
75
,
3
5
,
3
25
,
1
=
−
=
−
=
=
b
x
x
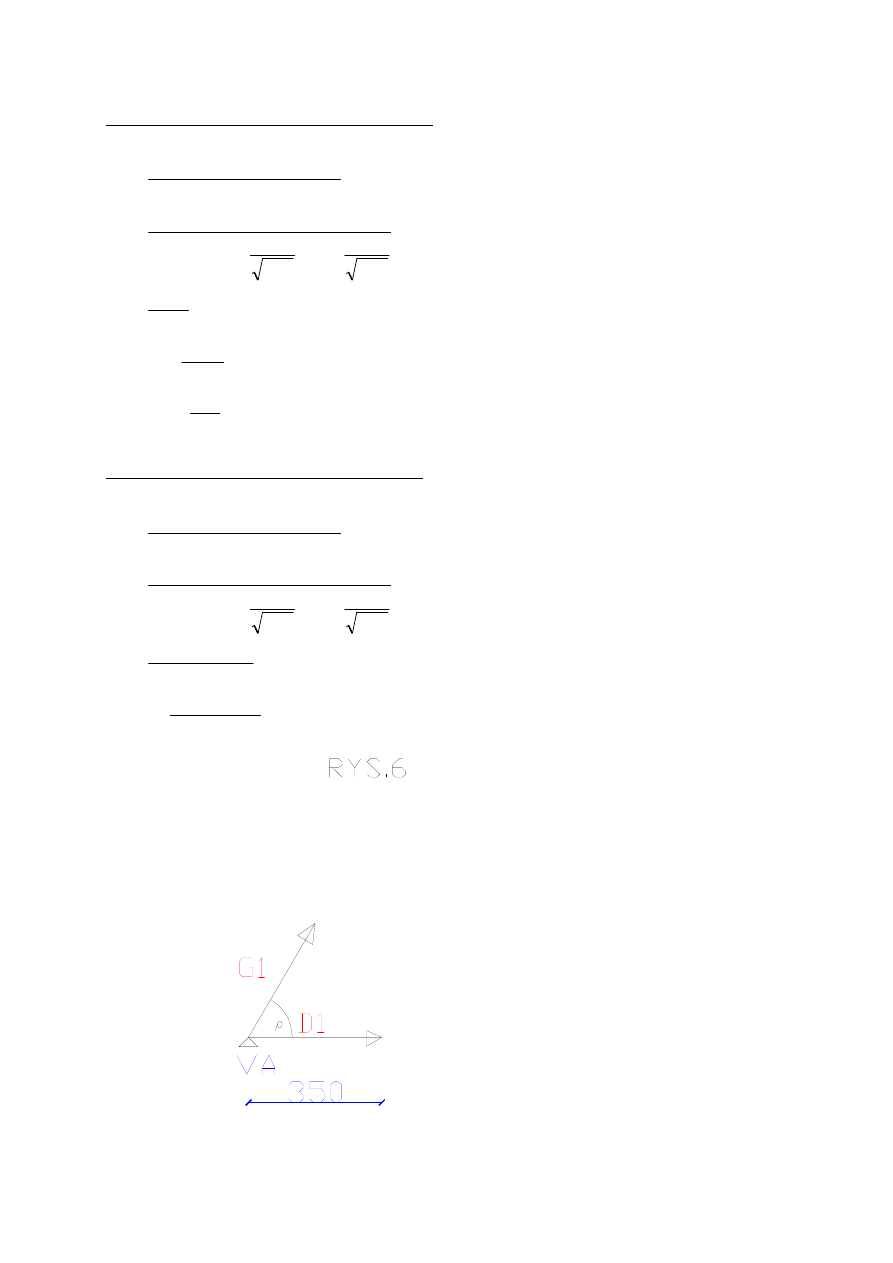
Gdy siła znajduje się po prawej stronie cięcia
0
6
,
8
7
0
)
5
,
17
(
65
,
0
6
,
8
7
8
,
0
)
5
,
3
(
6
,
8
7
31
,
9
75
,
1
5
,
2
31
,
9
5
,
2
)
7
5
,
3
5
,
0
(
7
cos
sin
)
7
5
,
0
(
7
0
cos
sin
)
7
5
,
0
(
7
1
1
1
1
1
1
1
=
⋅
=
=
⋅
=
⋅
=
⋅
+
⋅
+
⋅
⋅
=
⋅
+
⋅
+
⋅
=
=
⋅
⋅
+
⋅
+
⋅
+
⋅
−
K
K
V
K
V
K
a
b
V
K
a
K
b
K
V
A
A
A
A
ω
ω
ω
ω
Gdy siła znajduje się po lewej stronie cięcia
0
6
,
8
)
7
0
(
7
1
)
0
(
6
,
8
)
7
(
7
31
,
9
75
,
1
5
,
2
31
,
9
5
,
2
)
7
5
,
3
5
,
0
(
)
7
(
1
7
cos
sin
)
7
5
,
0
(
)
7
(
7
0
)
7
(
cos
sin
)
7
5
,
0
(
7
1
1
1
1
1
1
=
+
−
⋅
=
+
−
⋅
=
⋅
+
⋅
+
⋅
+
−
⋅
=
⋅
+
⋅
+
+
−
⋅
=
=
+
+
⋅
⋅
+
⋅
+
⋅
+
⋅
−
K
x
V
K
x
V
K
a
b
x
P
V
K
x
P
a
K
b
K
V
A
A
A
A
ω
ω
ω
ω
Obliczam G
1
z równowagi węzła
Obliczam kąt ω
31
,
9
75
,
1
cos
31
,
9
5
,
2
sin
31
,
9
75
,
1
5
,
2
2
2
2
=
=
=
=
+
ω
ω
c
c
∑
=
0
Y
P
Gdy siła znajduje się poza węzłem
0
82
,
0
0
)
5
,
17
(
73
,
0
82
,
0
6
,
0
)
7
(
97
,
0
82
,
0
8
,
0
)
5
,
3
(
82
,
0
31
,
9
5
,
2
sin
0
sin
1
1
1
1
1
1
1
=
−
=
−
=
−
=
−
=
−
=
−
=
−
=
−
=
=
⋅
+
G
G
G
V
G
V
G
V
G
G
V
A
A
A
A
ω
ω
Gdy siła znajduje się w węźle
0
82
,
0
1
1
)
0
(
82
,
0
1
31
,
9
5
,
2
1
sin
0
sin
1
1
1
1
1
=
+
−
=
+
−
=
+
−
=
+
−
=
=
−
⋅
+
G
V
G
V
G
P
V
G
P
G
V
A
A
A
A
ω
ω

ZADANIE 4
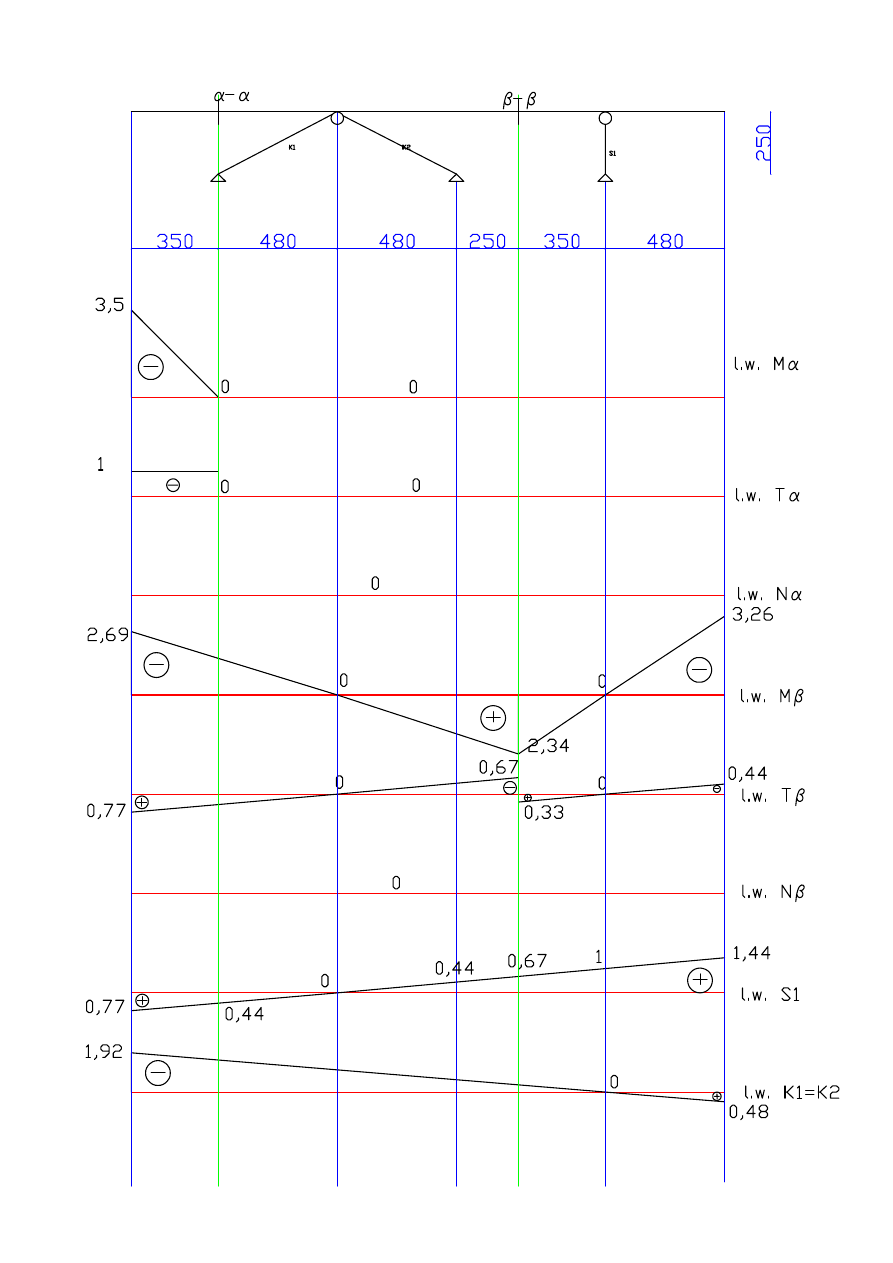
a = 2,5 m
b = 3,5 m
c = 4,8 m
Wykresy :
- linii wpływu M
α
- linii wpływu T
α
- linii wpływu N
α
- linii wpływu M
β
- linii wpływu T
β
- linii wpływu N
β
Obliczam przekrój α-α
0<x<b
0<x<3,5 m
Gdy siła jest po prawej
0
0
=
=
∑
−
M
M
α
α
0
0
=
=
∑
T
P
Y
0
0
=
=
∑
N
P
X
Gdy siła jest po lewej
0
)
5
,
3
(
5
,
3
)
0
(
)
5
,
3
(
1
)
(
0
)
(
0
=
−
=
−
−
=
−
−
=
=
−
−
−
=
∑
−
M
M
x
M
x
b
P
M
x
b
P
M
M
α
α
1
0
0
−
=
−
=
=
+
=
∑
T
P
T
P
T
P
Y
0
0
=
=
∑
N
P
X
Obliczam przekrój β- β

a+b+2c<x<a+2b+3c
15,6<x<23,9 m
Gdy siła jest po prawej
34
,
2
)
67
,
0
(
5
,
3
)
6
,
15
(
69
,
2
77
,
0
5
,
3
)
0
(
5
,
3
0
0
1
1
1
=
−
⋅
−
=
−
=
⋅
−
=
⋅
−
=
⋅
−
=
=
⋅
+
=
∑
−
M
M
S
M
b
S
M
b
S
M
M
β
β
67
,
0
)
6
,
15
(
77
,
0
)
0
(
0
0
1
1
−
=
=
=
=
−
=
∑
T
T
S
T
S
T
P
Y
0
0
=
=
∑
N
P
X
Gdy siła jest po lewej
26
,
3
)
6
,
15
9
,
23
(
1
5
,
3
44
,
1
)
9
,
23
(
34
,
2
)
6
,
15
6
,
15
(
1
5
,
3
67
,
0
)
6
,
15
(
)
6
,
15
(
1
5
,
3
)
2
(
0
)
2
(
0
1
1
1
−
=
−
−
⋅
=
=
−
−
⋅
=
−
−
⋅
−
=
+
+
−
−
⋅
−
=
=
⋅
+
+
+
−
+
=
∑
−
M
M
x
S
M
c
b
a
x
P
b
S
M
b
S
c
b
a
x
P
M
M
β
β
44
,
0
)
44
,
1
(
1
)
9
.
23
(
33
,
0
)
67
,
0
(
1
)
6
,
15
(
1
0
0
1
1
1
−
=
−
+
=
=
−
+
=
+
=
+
=
=
−
−
=
∑
T
T
S
T
S
P
T
P
S
T
P
Y
0
0
=
=
∑
N
P
X
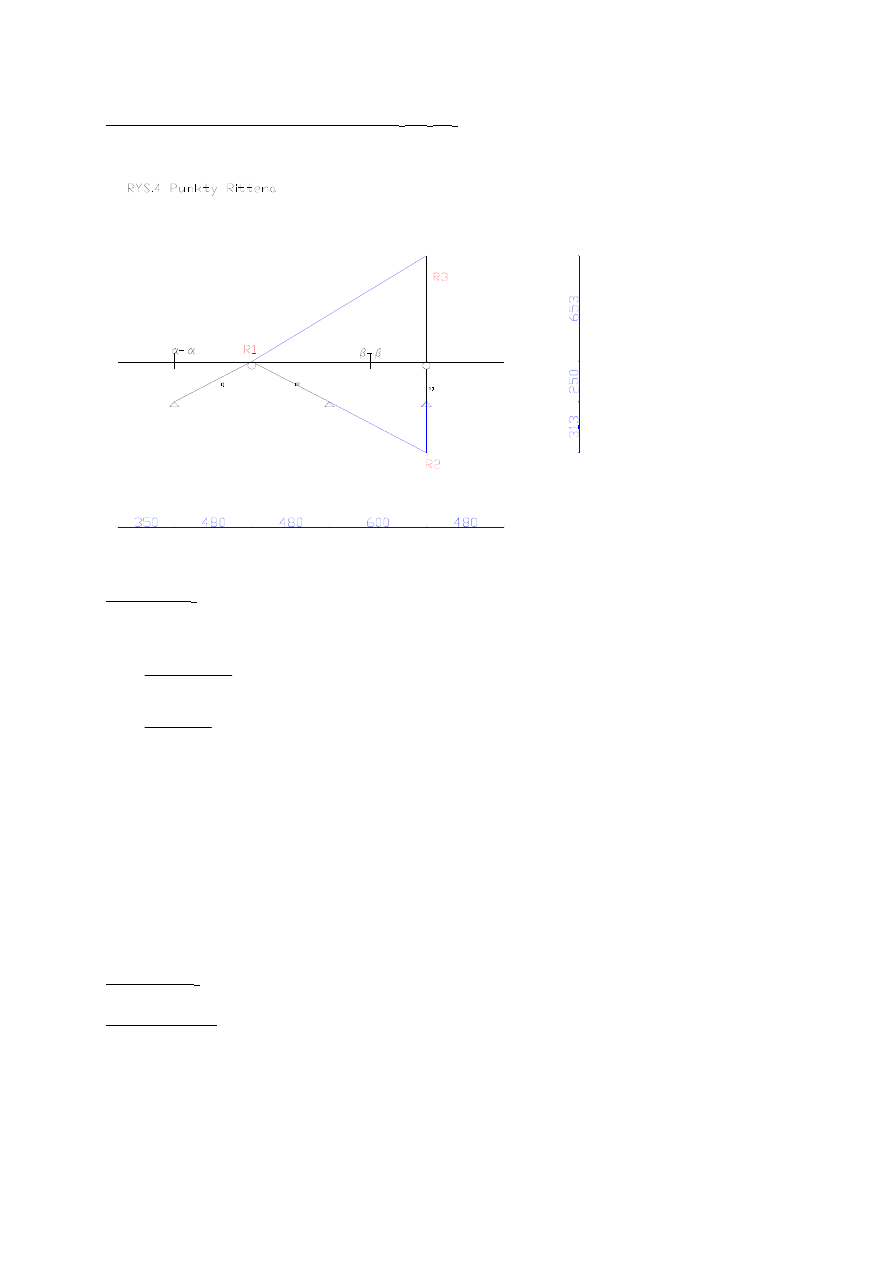
Wykonuje cięcie Rittera, aby obliczyć K
1
, K
2
, S
1
Obliczam S
1
pkt R = R
1
44
,
1
)
9
,
23
(
1
)
1
,
19
(
67
,
0
)
6
,
15
(
44
,
0
)
1
,
13
(
0
)
3
,
8
(
44
,
0
)
5
,
3
(
77
,
0
)
0
(
8
,
10
)
3
,
8
(
1
)
(
)
(
0
)
(
)
(
1
1
1
1
1
1
1
1
1
1
−
=
−
=
−
=
−
=
=
=
=
−
=
+
+
−
+
=
=
−
+
−
+
+
⋅
S
S
S
S
S
S
S
x
S
b
a
c
x
c
b
P
S
x
c
b
P
b
a
c
S
Obliczam K
1
pkt R = R
3
Obliczam kąt α
29
,
29
8
,
4
cos
29
,
29
5
,
2
sin
29
,
29
5
,
2
8
,
4
2
2
2
=
=
=
=
+
α
α
c
c
Obliczam odległość do R
3
13
,
3
5
,
2
62
,
5
62
,
5
8
,
10
8
,
4
5
,
2
=
−
=
=
x
x
48
,
0
)
9
,
23
(
0
)
1
,
19
(
35
,
0
)
6
,
15
(
6
,
0
)
1
,
13
(
08
,
1
)
3
,
8
(
56
,
1
)
5
,
3
(
92
,
1
)
0
(
97
,
9
)
1
,
19
(
62
,
5
29
,
29
8
,
4
)
8
,
4
5
,
3
5
,
2
(
29
,
29
5
,
2
)
8
,
4
2
5
.
3
2
5
,
2
(
24
,
7
cos
)
(
sin
)
2
2
(
0
)
2
2
(
24
,
7
cos
)
(
sin
1
1
1
1
1
1
1
1
1
1
1
1
=
=
−
=
−
=
−
=
−
=
−
=
−
−
=
⋅
+
+
+
⋅
−
⋅
+
⋅
+
−
=
⋅
+
+
+
⋅
−
+
+
−
=
=
−
+
+
−
⋅
⋅
−
+
+
⋅
⋅
−
K
K
K
K
K
K
K
x
K
x
P
K
c
b
a
x
c
b
a
P
K
x
c
b
a
P
K
c
b
a
K
α
α
α
α
Obliczam K
2
z sumy na X wynika, że linie wpływu K są takie same
1
2
2
1
0
0
K
K
K
K
P
X
=
=
+
−
=
∑
Wyszukiwarka
Podobne podstrony:
Mechanika budowli wyznaczenie linii wpływu
11 Wyznaczanie linii wplywu belek ciaglych a, Do˙wiadczenie1
wykl mechanika budowli 11 linie wplywu belki ciaglej
Wyznaczanie odksztalcen w belkach zginanych, BUDOWNICTWO, INŻ, semestr 4, Mechanika budowli, Mechani
Wyznaczenie odksztace w belkach zginanych, BUDOWNICTWO, INŻ, semestr 4, Mechanika budowli, Mechanika
Mechanika Budowli - Linie wpływu, BUDOWNICTWO, Mechanika budowli
Mechanika Budowli II - Laboratorium (rok III), Wyznaczenie odkształceń w belkach zginanych, Politech
Mechanika Budowli II - Laboratorium (rok III), Wyznaczenie odkształceń w belkach zginanych, Politech
Zadanie projektowe linie wpływu ukł stat niewyznaczalnych, Zadanie Projektowe z Mechaniki Budowli
Mechanika Budowli - Linie wpływu, BUDOWNICTWO, INŻ, semestr 4, Mechanika budowli, Mechanika Budowli
Wyznaczenie srodka zginania (1), BUDOWNICTWO, INŻ, semestr 4, Mechanika budowli, Mechanika Budowli 2
Mechanika Budowli I (rok II), Mechanika Budowli - Linie wpływu, Politechnika Gdańska
więcej podobnych podstron