1

Regresja nieliniowa. Aproksymacja

krzywych dla potrzeb geodezyjnych

i in

ż

ynierskich

Wykonawca:

Grzegorz Kruczek

Grupa

ć

wiczeniowa 1

Rok akademicki 2015/2016

Numeryczne algorytmy in

ż

ynierskie

2

Spis tre

ś

ci

Tok post

ę

powania........................................................................................................3

Wykresy........................................................................................................................5
Próba skonstruowania bardziej adekwatnego modelu.................................................8
Wybór modelu..............................................................................................................9

3

Tok post

ę

powania:

1. Okre

ś

lenie długo

ś

ci wektora opracowania:

len=1001

2. Zdefiniowanie warto

ś

ci na osi x:

x=seq(0,10,by=0.01) - zakres od 0 do 10, warto

ść

co 0.01

3. Przypisanie warto

ś

ciom na osi x argumentów:

y=sin(3*x)+rnorm(len,0,0.04) - do funkcji sin(3x) wprowadzony zostaje szum losowy

4. Utworzenie ramki danych:

ds=data.frame(x=x,y=y)

5. Utworzenie wykresu obrazuj

ą

cego dane:

plot(y~x)

6. Zaznaczenie na wykresie funkcji modelowej y=sin(3x) (ci

ą

głej i pozbawionej

szumów losowych):

s=seq(0,10,by=0.01)
lines(s,sin(3*s),lty=2,col="red")

7. Wpasowanie iteracyjne metod

ą

nls:

m=nls(y~I(sin(liczba*s)),data=ds,start=list(liczba=3),trace=T)
1.546485 : 3
1.546046 : 2.999836
1.546046 : 2.999836 - ostateczny wynik otrzymano w drugiej iteracji; ró

ż

ni si

ę

on

nieznacznie od zało

ż

onej funkcji modelowej.

8. Podsumowanie procesu iteracyjnego:

summary(m)

Formula: y ~ I(sin(liczba * s))

Parameters:
Estimate Std. Error t value Pr(>|t|)
liczba 2.9998362 0.0003071 9767 <2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 0.03932 on 1000 degrees of freedom

4

Number of iterations to convergence: 2
Achieved convergence tolerance: 3.397e-08

9. Narysowanie linii wygenerowanego modelu:

lines(s,predict(m,list(x=s),lty=1,col="blue"))

10. Oszacowanie jako

ś

ci wpasowania:

a) wyznaczenie parametru residual sum of squares (RSS)

RSS.p=sum(residuals(m)^2)
[1] 1.546046

b) wyznaczenie parametru total sum of squares (TSS):

TSS=sum((y-mean(y))^2)
[1] 502.6502

c) okre

ś

lenie jako

ś

ci modelu wygenerowanego na podstawie wpasowania metod

ą

nls:

1-(RSS.p/TSS)
[1] 0.9969242 - wysoka jako

ść

modelu

d) okre

ś

lenie jako

ś

ci znanej funkcji (jako

ść

zale

ż

na od szumu):

1-sum(sin(3*x)-y)^2/TSS
[1] 0.9901581 - wysoka jako

ść

funkcji

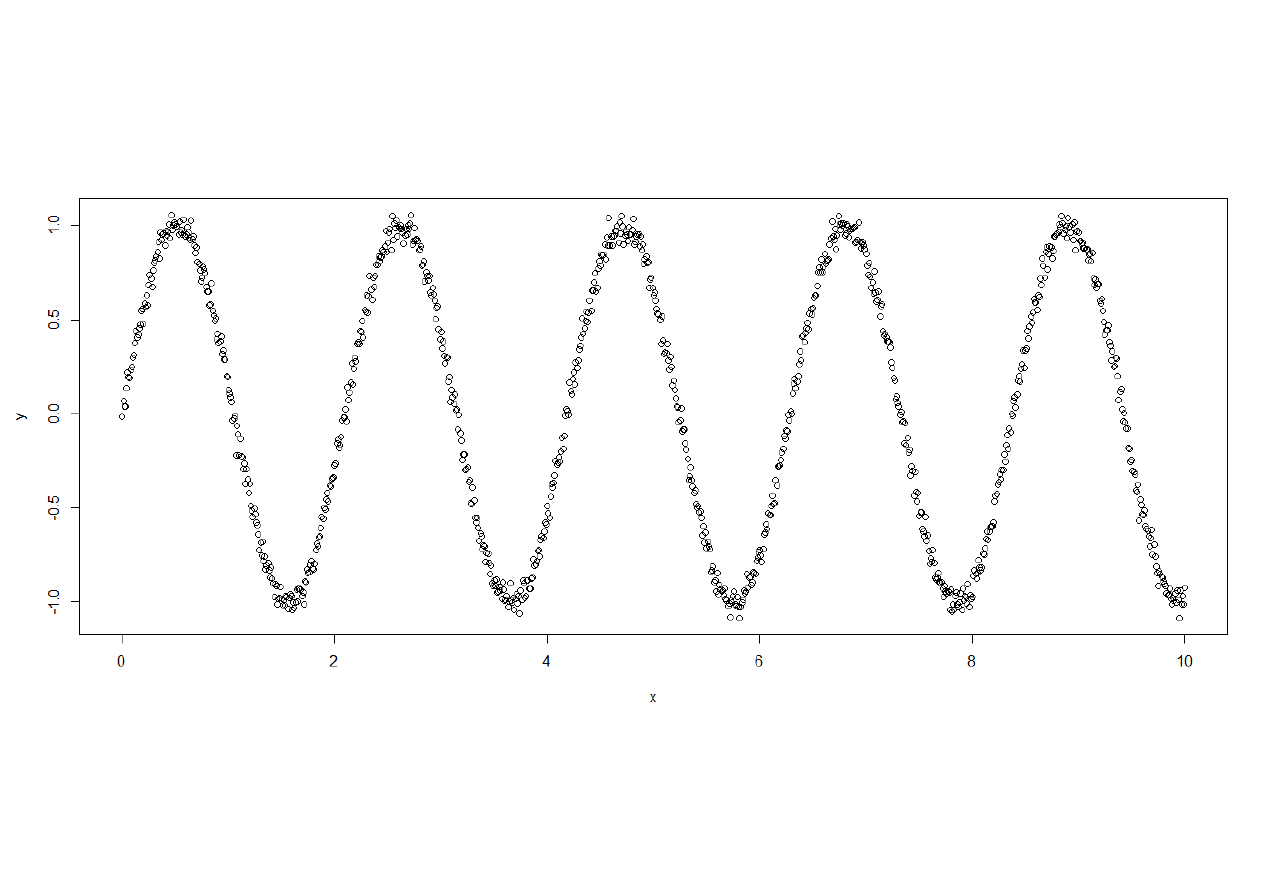
5

Wykresy

Wykres danych

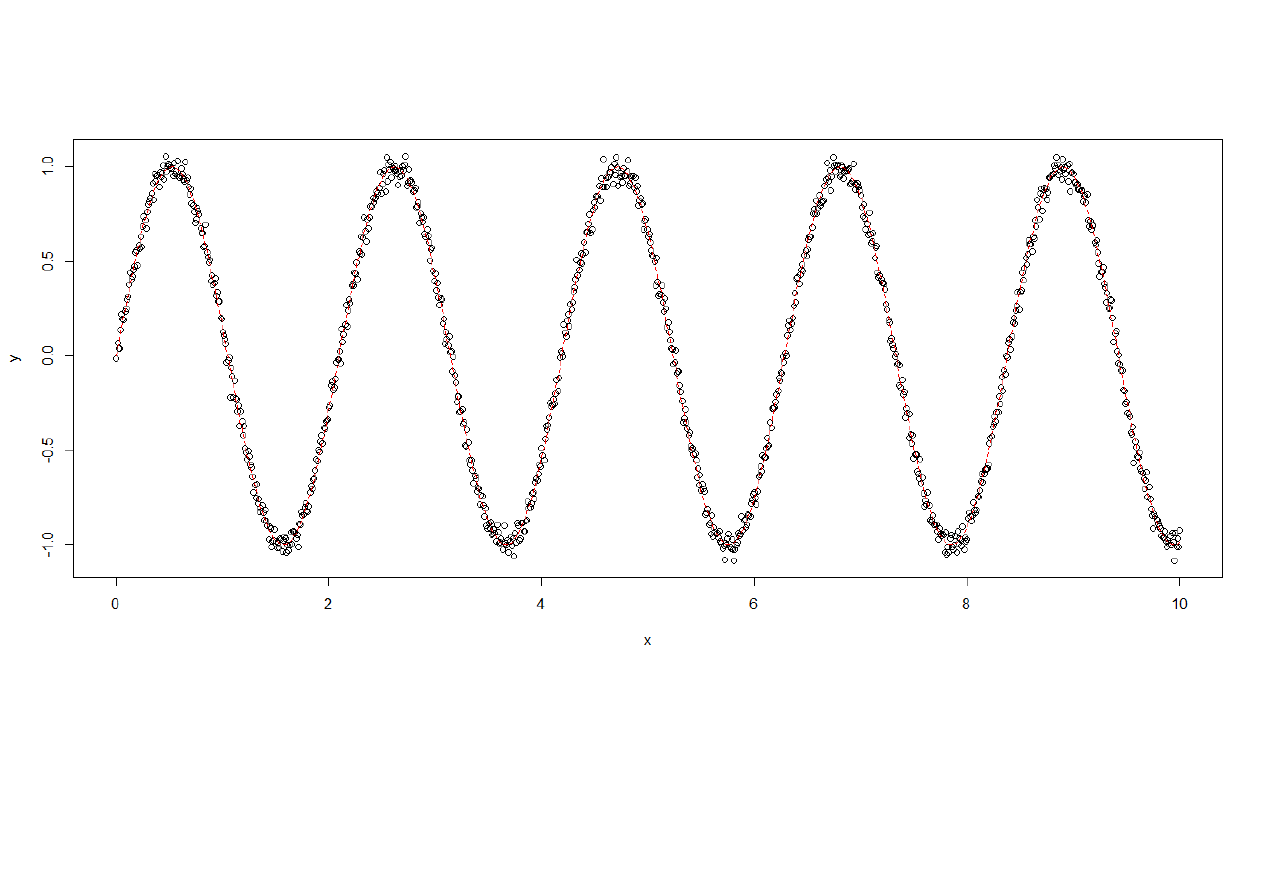
6

Wykres danych z zaznaczon

ą

funkcj

ą

modelow

ą

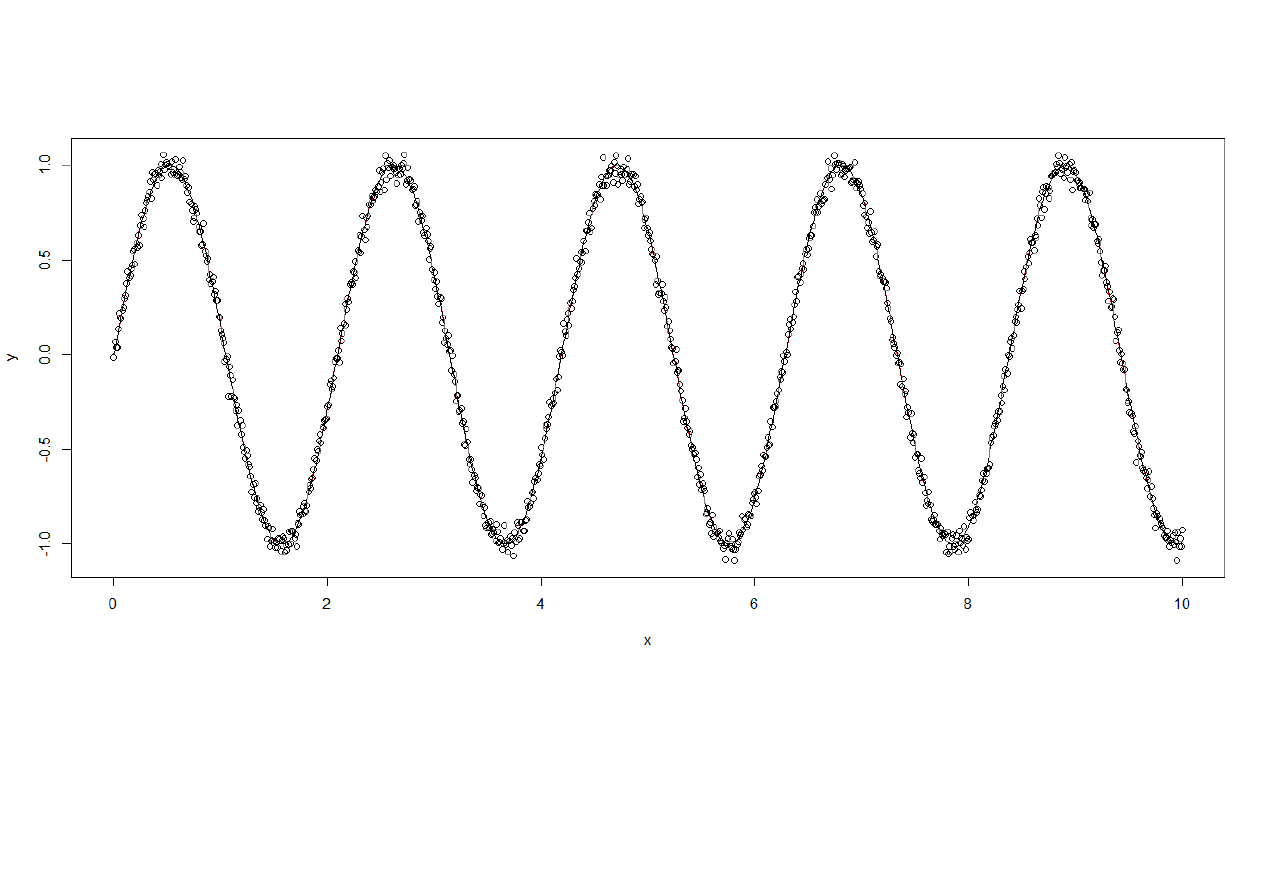
7

Wykres danych z zaznaczon

ą

linia wygenerowanego modelu

Wygenerowany model ma bardzo podobny przebieg do funkcji modelowej. Obydwie linie niemal si

ę

pokrywaj

ą

.

8

Próba skonstruowania bardziej

adekwatnego modelu

1. Wpasowanie iteracyjne metoda nls zmodyfikowanej funkcji:

sinus=function(x,w,b)
{sin(w*x)+b}
m.2=nls(y~sinus(x,w,b),data=ds,start=list(w=3,b=0),trace=T)

1.546485 : 3 0
1.540819 : 2.99978915 -0.00229316
1.540819 : 2.999788838 -0.002293284 - w wyniku dwóch iteracji wyznaczone
zostały parametry funkcji y=sin(wx)+b

2. podsumowanie procesu iteracyjnego:

summary(m.2)

Formula: y ~ sinus(x, w, b)

Parameters:
Estimate Std. Error t value Pr(>|t|)
w 2.9997888 0.0003078 9744.968 <2e-16 ***
b -0.0022933 0.0012456 -1.841 0.0659 .
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 0.03927 on 999 degrees of freedom

Number of iterations to convergence: 2
Achieved convergence tolerance: 8.99e-08

3. Oszacowanie jako

ś

ci wpasowania:

a) wyznaczenie parametru residual sum of squares (RSS)

RSS.pb=sum(residuals(m.2)^2)
[1] 1.540819

b) wyznaczenie parametru total sum of squares (TSS):

TSS=sum((y-mean(y))^2)
[1] 502.6502

c) okre

ś

lenie jako

ś

ci modelu wygenerowanego na podstawie wpasowania metod

ą

nls:

1-(RSS.pb/TSS)
[1] 0.9969346 - wysoka jako

ść

modelu

9

Wybór modelu

anova(m.2,m)

Analysis of Variance Table

Model 1: y ~ sinus(x, w, b)
Model 2: y ~ I(sin(liczba * s))
Res.Df Res.Sum Sq Df Sum Sq F value Pr(>F)
1 999 1.5408
2 1000 1.5460 -1 -0.0052277 3.3894 0.65911 .
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Otrzymany wynik analizy wskazuje,

ż

e lepszym rozwi

ą

zaniem b

ę

dzie przyj

ę

cie

modelu 1.