
max
2
2
1
1
→
+
+
+
n
n
x
c
x
c
x
c
...
0
,
,
2
1
2
2
1
1
1
1
2
12
1
11
≥
≤
+
+
+
≤
+
+
+
n
m
n
mn
m
m
n
n
x
x
x
b
x
a
x
a
x
a
b
x
a
x
a
x
a
...
...
...
...
...
...
...
...
...
...
...
Rozwi
Rozwi
ą
ą
zanie algorytmu SIMPLEKS
zanie algorytmu SIMPLEKS
metod
metod
ą
ą
rachunku macierzowego
rachunku macierzowego
Zagadnienie programowania liniowego w ogólnej postaci:

0
max
≥
≤
→
x
b
Ax
cx
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
=
mn
m
m
n
a
a
a
a
a
a
A
...
...
...
...
...
...
2
1
1
12
11
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
=
n
x
x
x
x
...
2
1
gdzie:
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
=
m
b
b
b
...
1
[
]
n
c
c
c
...
1
=
Zagadnienie programowania liniowego w postaci macierzowej:
c
b
x
b
z
j
c
j
-z
j
c
A
I
0
c
b
A
– jest macierzą współczynników występujących po lewej stronie
warunków ograniczających
b
– jest wektorem wyrazów wolnych warunków ograniczających
c
– jest wektorem wierszowym współczynników funkcji celu (zdefiniowanej
po wprowadzeniu zmiennych bilansujących)
x
b
– jest wektorem zmiennych bazowych
c
b
– jest wektorem kolumnowym współczynników funkcji celu dla zmiennych
bazowych
I
– jest macierzą jednostkową o wymiarach (
m x m) –
macierz
ą
współczynników
przy zmiennych występujących w pierwszej bazie
0
– jest wektorem zer
Postać pierwszej tablicy simpleksowej w postaci ogólnej
wartość zmiennych
bazowych
wartość funkcji celu
zmienne
bazowe
rozwiązanie
A
B
l
1
−
1
−
l
B
b
B
l
1
−
A
B
c
b
T
b
1
−
1
−
b
T
b
B
c
b
B
c
b
T
b
1
−
A
B
c
c
b
T
b
1
−
−
1
−
−
b
T
b
B
c
j
j
z
c
−
j
z
bl
x
bl
c
c
l
B
Macierz jest macierz współczynników ograniczających stojących przy aktualnych
(w
l
-tej iteracji) zmiennych bazowych
Postać tablicy simpleksowej po
l
-tej iteracji:
zmienne
bazowe
rozwiązanie
A
V
l
l
V
b
V
l
A
V
c
l
T
b
l
T
b
V
c
b
V
c
l
T
b
A
V
c
c
l
T
b
−
l
T
b
V
c
−
j
j
z
c
−
j
z
bl
x
bl
c
c
l
l
V
B
=
−1
Macierz jest macierzą odwrotną współczynników ograniczających
stojących przy aktualnych zmiennych bazowych ( w
l
-tej iteracji )
l
V

Rozwiązać zagadnienie programowania liniowego w postaci kanonicznej:
max
3
2
)
,
,
,
,
(
2
1
5
4
3
2
1
→
+
=
x
x
x
x
x
x
x
f
0
,
,
,
,
16
4
8
2
14
2
2
5
4
3
2
1
5
1
4
2
1
3
2
1
≥
=
+
=
+
+
=
+
+
x
x
x
x
x
x
x
x
x
x
x
x
x
[
]
c
0
0
0
3
2
=
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
=
1
0
0
0
4
0
1
0
2
1
0
0
1
2
2
A
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
=
16
8
14
b
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
=
5
4
3
2
1
x
x
x
x
x
x

Rozwiązać zagadnienie programowania liniowego w postaci kanonicznej:
max
3
2
)
,
,
,
,
(
2
1
5
4
3
2
1
→
+
=
x
x
x
x
x
x
x
f
0
,
,
,
,
16
4
8
2
14
2
2
5
4
3
2
1
5
1
4
2
1
3
2
1
≥
=
+
=
+
+
=
+
+
x
x
x
x
x
x
x
x
x
x
x
x
x
[
]
c
0
0
0
3
2
=
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
=
1
0
0
0
4
0
1
0
2
1
0
0
1
2
2
A
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
=
16
8
14
b
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
=
5
4
3
2
1
x
x
x
x
x
x
Wartości
c
j
– z
j
nazywamy
wskaźnikiem optymalności
(kryterium simpleks)
cx →max
2
3
0
0
0
Baza
c
B
x
1
x
2
x
3
x
4
x
5
x
3
0
2
2
1
0
0
14
x
4
0
1
2
0
1
0
8
x
5
0
4
0
0
0
1
16
z
j
0
0
0
0
0
0
c
j
- z
j
2
3
0
0
0
0
b
Tablica simpleks w pierwszej postaci bazowej
cx →max
2
3
0
0
0
Baza
c
B
x
1
x
2
x
3
x
4
x
5
x
3
0
2
2
1
0
0
14
x
4
0
1
2
0
1
0
8
x
5
0
4
0
0
0
1
16
z
j
0
0
0
0
0
0
c
j
- z
j
2
3
0
0
0
0
b
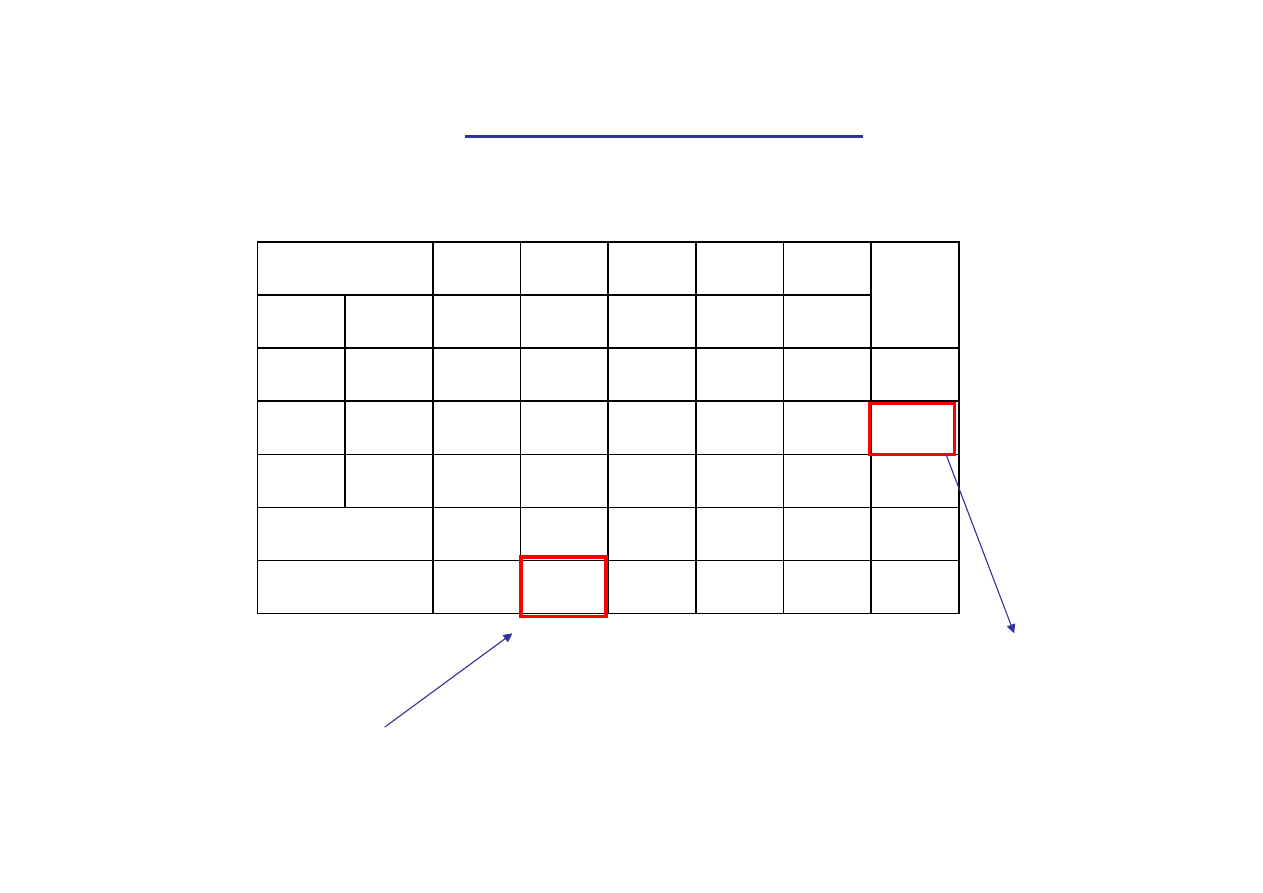
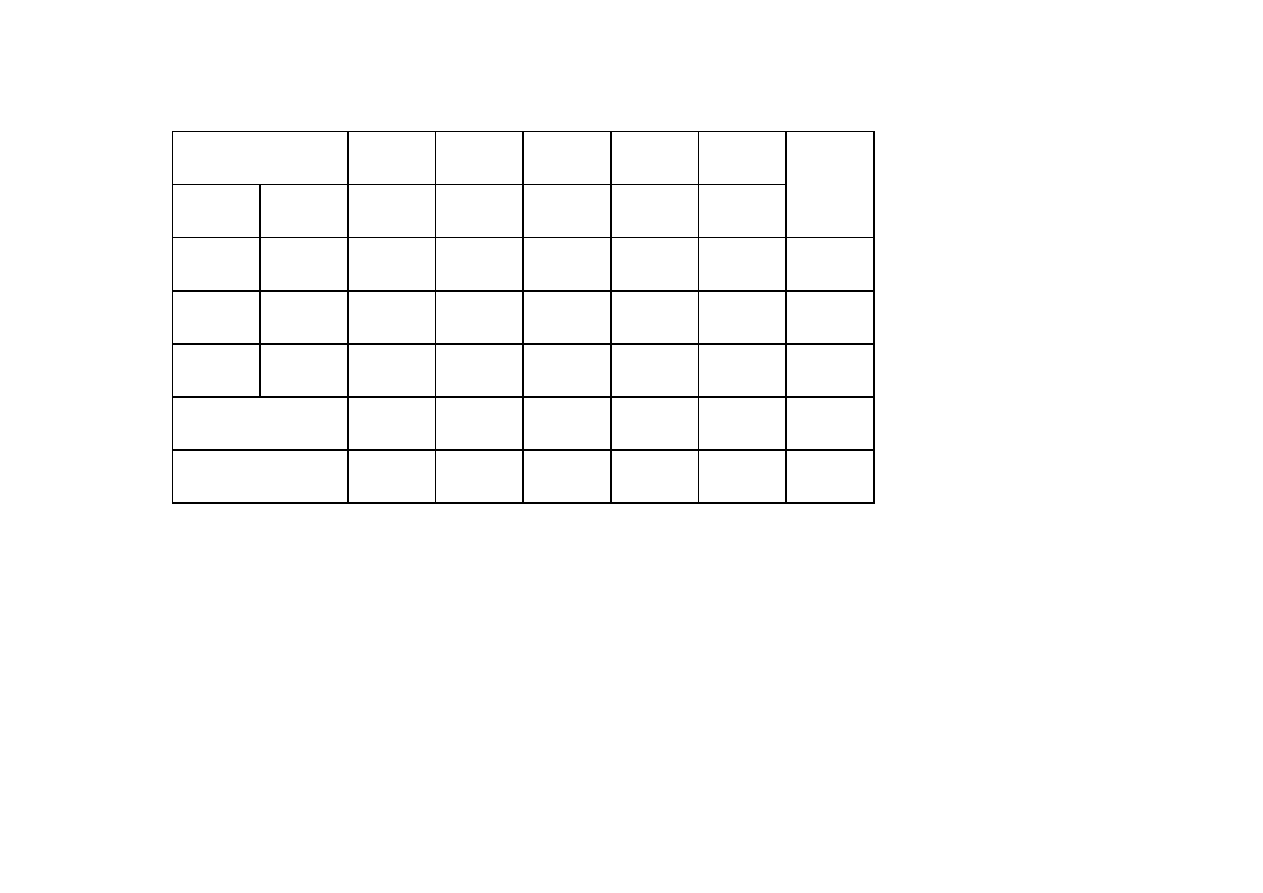
Tablica simpleks w pierwszej postaci bazowej
kryterium wejścia
kryterium wyjścia
cx →max
2
3
0
0
0
Baza
c
B
x
1
x
2
x
3
x
4
x
5
z
j
c
j
- z
j
b
cx →max
2
3
0
0
0
Baza
c
B
x
1
x
2
x
3
x
4
x
5
x
3
x
2
x
5
z
j
c
j
- z
j
b
Tablica simpleksowa w trakcie II iteracji
cx →max
2
3
0
0
0
Baza
c
B
x
1
x
2
x
3
x
4
x
5
x
3
0
x
2
3
x
5
0
z
j
c
j
- z
j
b
Tablica simpleksowa w trakcie II iteracji
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
=
1
0
0
0
2
0
0
2
1
2
B
x
3
x
2
x
5
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
−
=
1
0
0
0
5
,
0
0
0
1
1
2
V
cx →max
2
3
0
0
0
Baza
c
B
x
1
x
2
x
3
x
4
x
5
x
3
0
1
-1
0
x
2
3
0
0,5
0
x
5
0
0
0
1
z
j
c
j
- z
j
b
Tablica simpleksowa w trakcie II iteracji
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
=
1
0
0
0
2
0
0
2
1
2
B
x
3
x
2
x
4
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
−
=
1
0
0
0
5
,
0
0
0
1
1
2
V
cx →max
2
3
0
0
0
Baz
a
c
B
x
1
x
2
x
3
x
4
x
5
x
3
0
1
-1
0
x
2
3
0
0,5
0
x
5
0
0
0
1
z
j
c
j
- z
j
b
Tablica simpleksowa w trakcie II iteracji
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
=
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
⋅
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
−
=
⋅
0
4
1
5
,
0
0
1
0
2
4
1
2
2
1
0
0
0
5
,
0
0
0
1
1
A
V
s
cx →max
2
3
0
0
0
Baz
a
c
B
x
1
x
2
x
3
x
4
x
5
x
3
0
1
0
1
-1
0
x
2
3
0,5
1
0
0,5
0
x
5
0
4
0
0
0
1
z
j
c
j
- z
j
b
Tablica simpleksowa w trakcie II iteracji
cx →max
2
3
0
0
0
Baz
a
c
B
x
1
x
2
x
3
x
4
x
5
x
3
0
1
0
1
-1
0
x
2
3
0,5
1
0
0,5
0
x
5
0
4
0
0
0
1
z
j
c
j
- z
j
b
Tablica simpleksowa w trakcie II iteracji
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
=
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
⋅
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
−
=
⋅
16
4
6
16
8
14
1
0
0
0
5
,
0
0
0
1
1
2
b
V
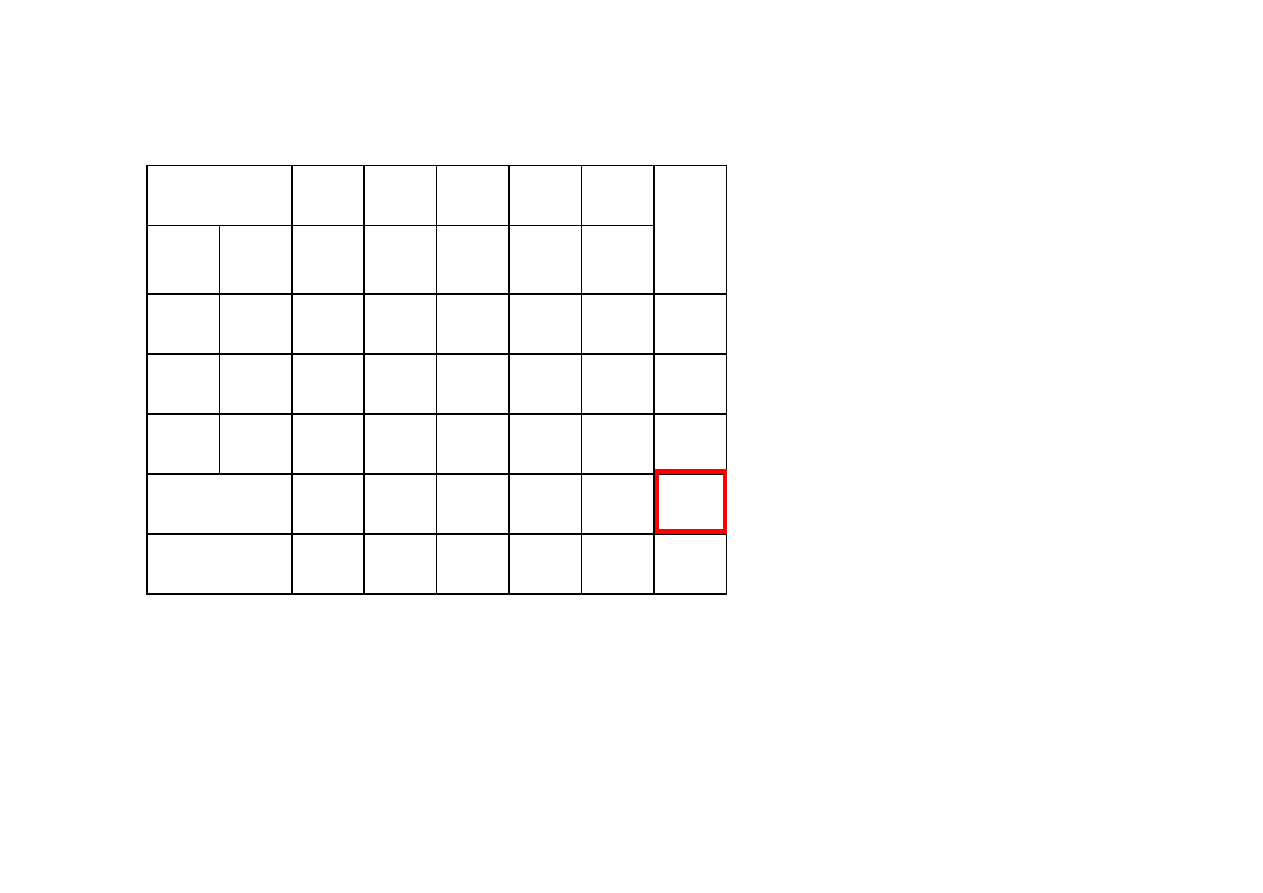
cx →max
2
3
0
0
0
Baz
a
c
B
x
1
x
2
x
3
x
4
x
5
x
3
0
1
0
1
-1
0
6
x
2
3
0,5
1
0
0,5
0
4
x
5
0
4
0
0
0
1
16
z
j
c
j
- z
j
b
Tablica simpleksowa w trakcie II iteracji
12
0
3
0
16
4
6
2
2
=
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
⋅
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
=
⋅
⋅
b
V
c
B
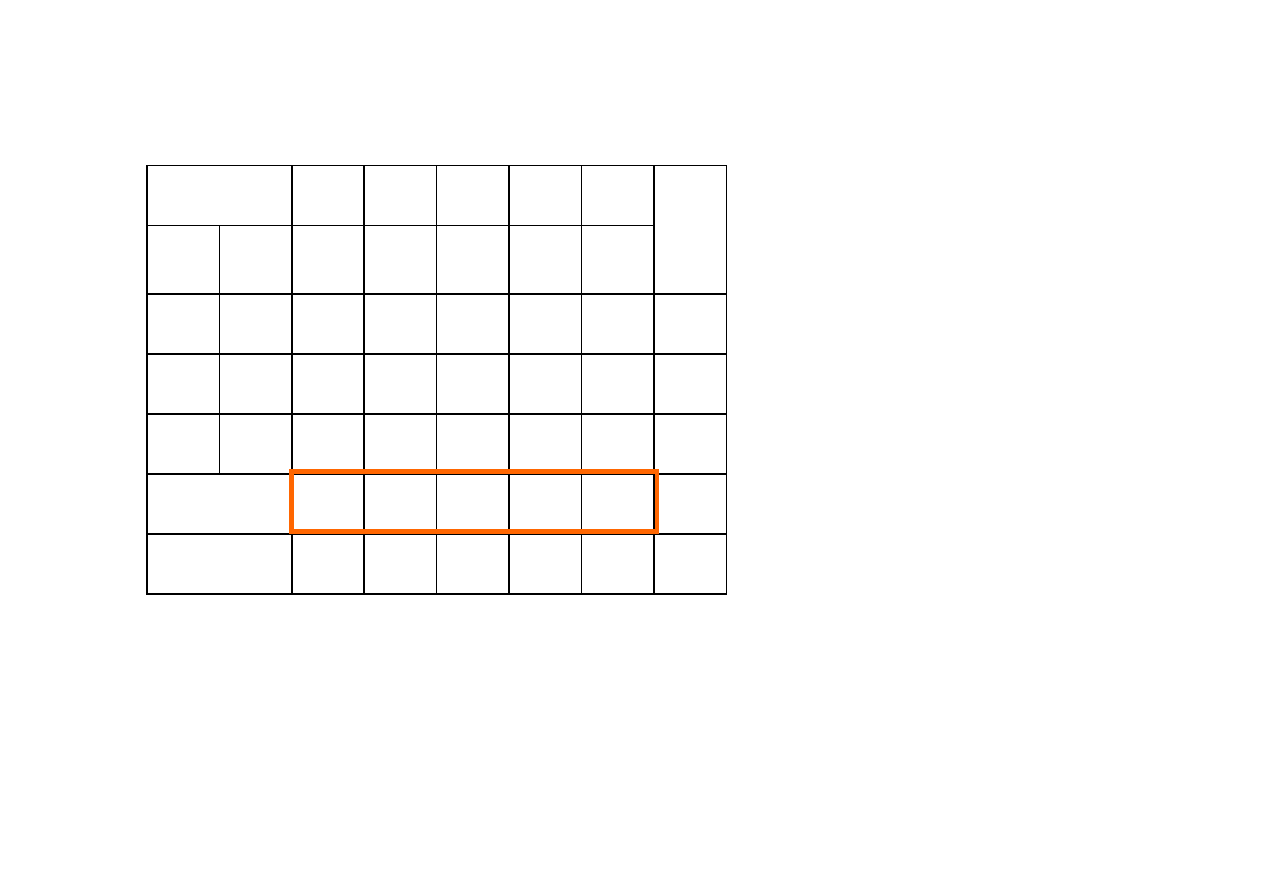
cx →max
2
3
0
0
0
Baz
a
c
B
x
1
x
2
x
3
x
4
x
5
x
3
0
1
0
1
-1
0
6
x
2
3
0,5
1
0
0,5
0
4
x
5
0
4
0
0
0
1
16
z
j
12
c
j
- z
j
b
Tablica simpleksowa w trakcie II iteracji
[
]
0
0
0
3
5
,
1
0
4
5
,
0
3
0
1
0
3
0
2
2
=
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
⋅
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
=
⋅
⋅
A
V
c
B
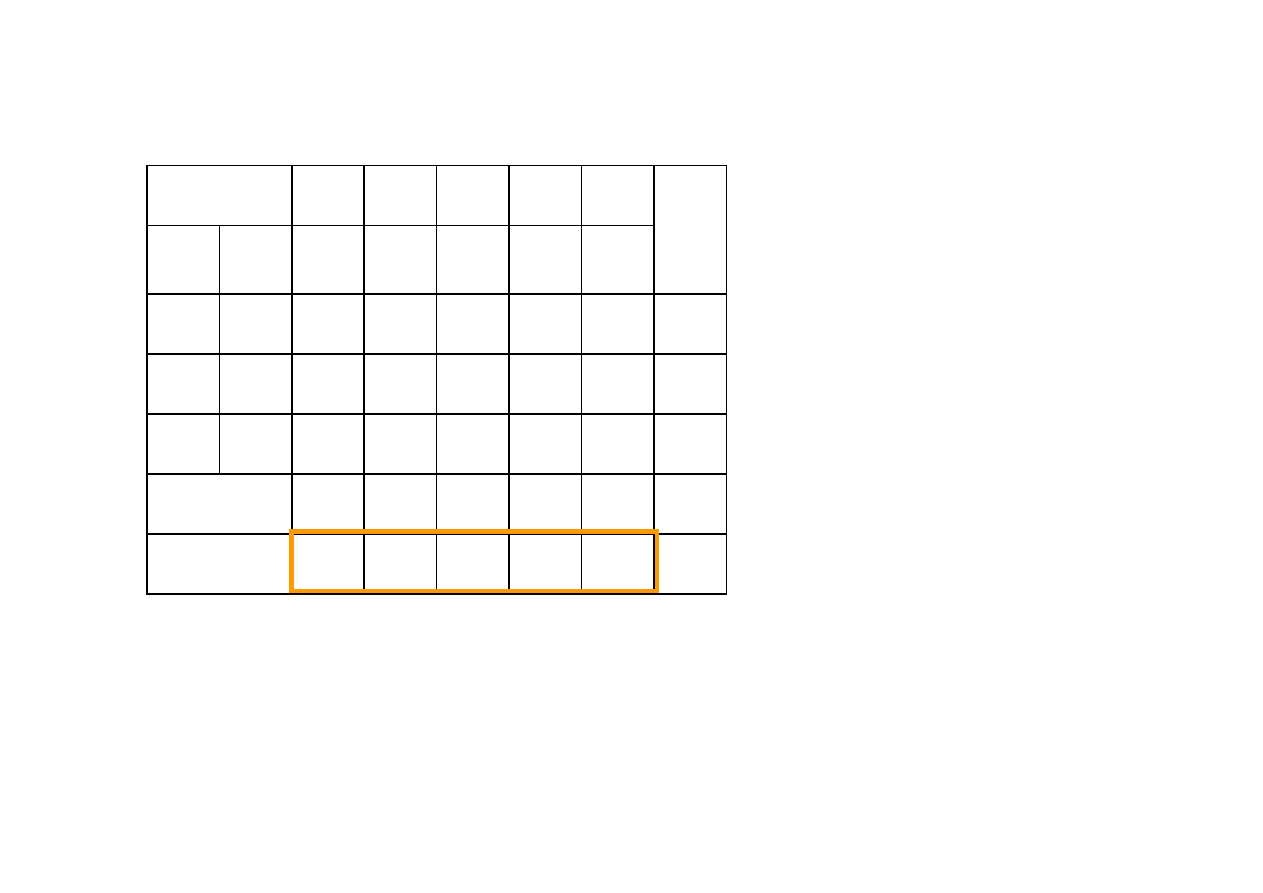
cx →max
2
3
0
0
0
Baz
a
c
B
x
1
x
2
x
3
x
4
x
5
x
3
0
1
0
1
-1
0
6
x
2
3
0,5
1
0
0,5
0
4
x
5
0
4
0
0
0
1
16
z
j
1,5
3
0
1,5
0
12
c
j
- z
j
b
Tablica simpleksowa w trakcie II iteracji
[
] [
]
[
]
0
5
,
1
0
0
5
,
0
0
0
0
3
5
,
1
0
5
,
1
0
3
2
2
2
−
=
=
−
=
⋅
⋅
−
A
V
c
c
B

cx →max
2
3
0
0
0
Baz
a
c
B
x
1
x
2
x
3
x
4
x
5
x
3
0
1
0
1
-1
0
6
x
2
3
0,5
1
0
0,5
0
4
x
5
0
4
0
0
0
1
16
z
j
1,5
3
0
1,5
0
12
c
j
- z
j
0,5
0
0
-1,5
0
b
Tablica simpleksowa po II iteracji
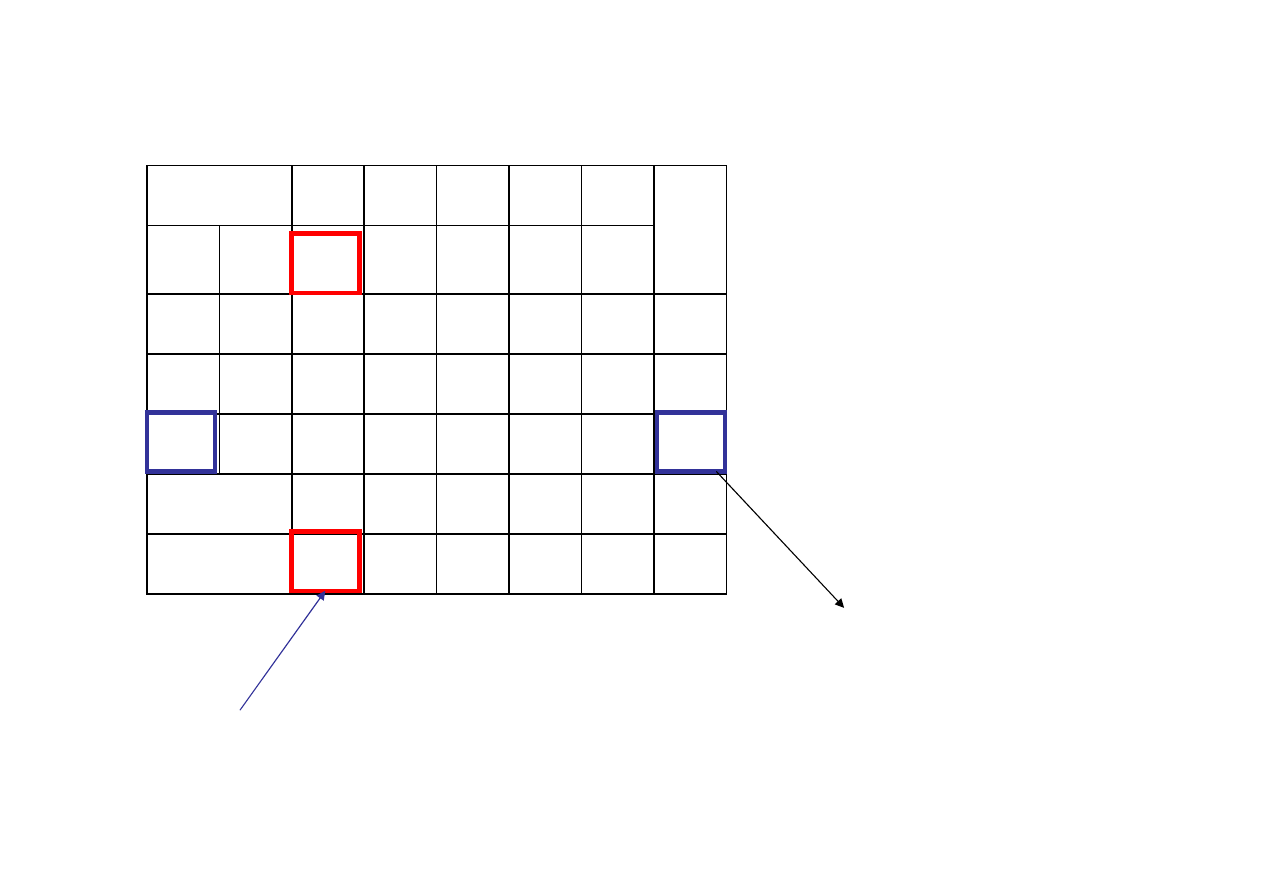
cx →max
2
3
0
0
0
Baz
a
c
B
x
1
x
2
x
3
x
4
x
5
x
3
0
1
0
1
-1
0
6
x
2
3
0,5
1
0
0,5
0
4
x
5
0
4
0
0
0
1
16
z
j
1,5
3
0
1,5
0
12
c
j
- z
j
0,5
0
0
-1,5
0
b
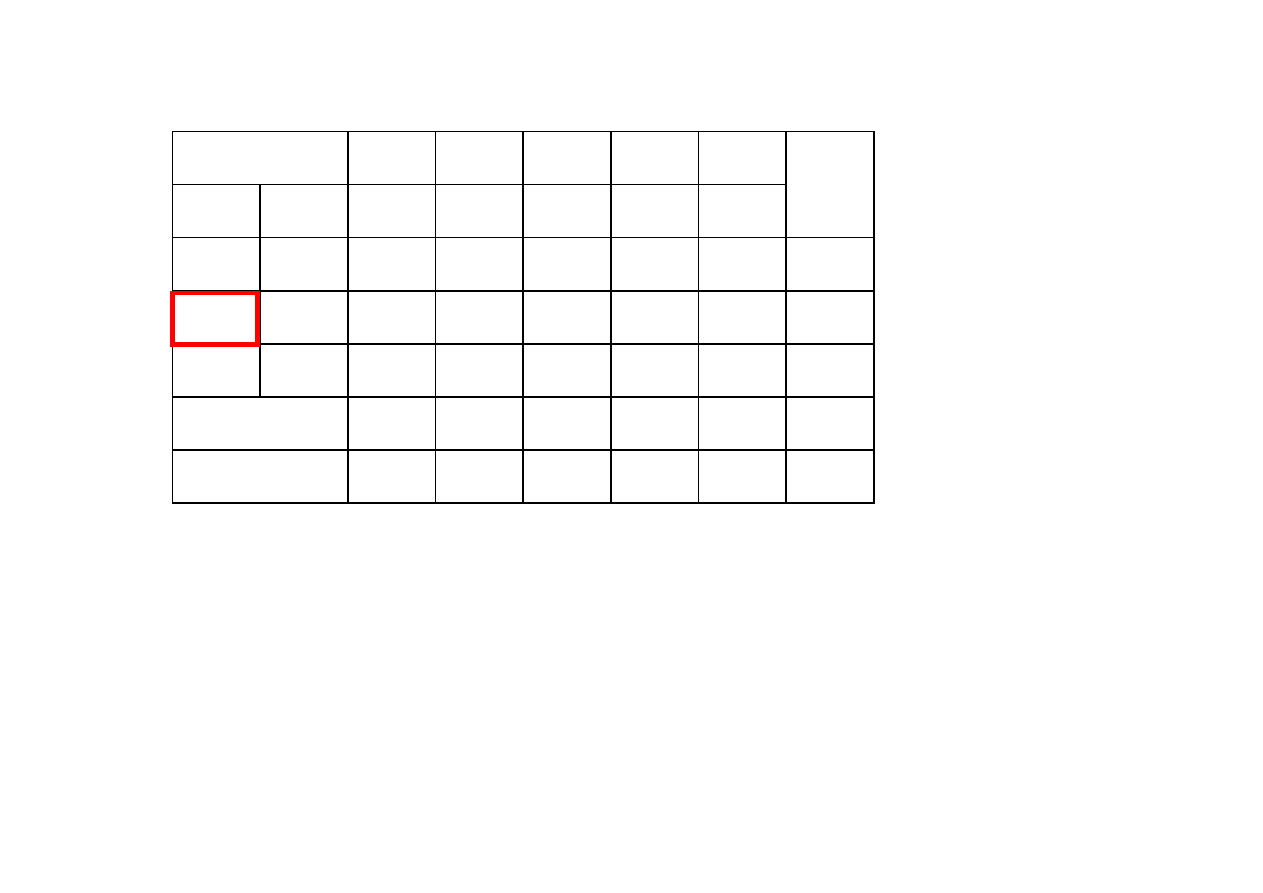
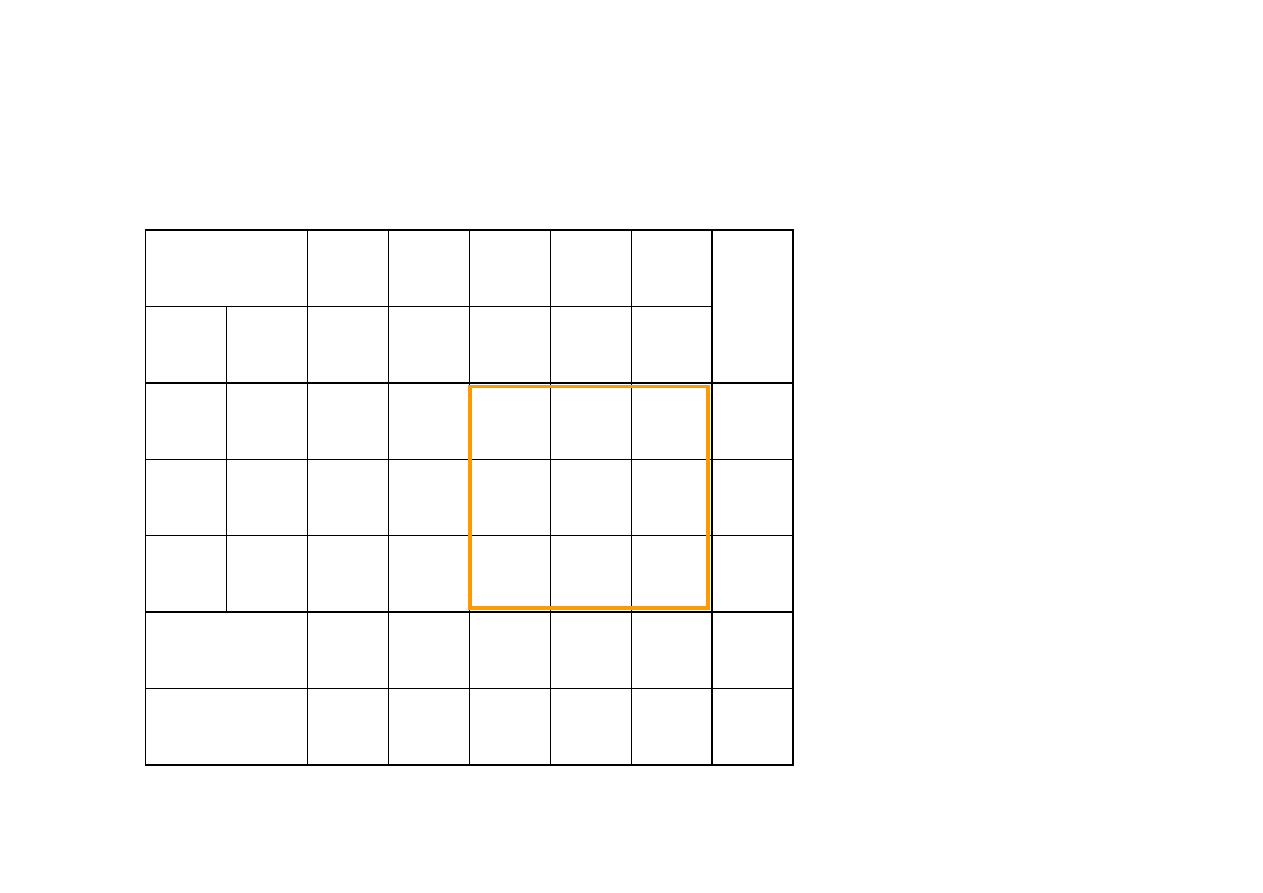
Tablica simpleksowa w trakcie II iteracji
kryterium wejścia
kryterium wyjścia
cx →max
2
3
0
0
0
Baz
a
c
B
x
1
x
2
x
3
x
4
x
5
x
3
0
x
2
3
x
1
2
z
j
c
j
- z
j
b
Tablica simpleksowa w trakcie III iteracji
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
=
4
0
0
1
2
0
2
2
1
3
B
x
3
x
2
x
1
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
−
−
−
=
25
,
0
0
0
13
,
0
5
,
0
0
25
,
0
1
1
3
V
cx →max
2
3
0
0
0
Baza
c
B
x
1
x
2
x
3
x
4
x
5
x
3
0
1
-1
-0,25
x
2
3
0
0,5
-0,13
x
1
2
0
0
0,25
z
j
c
j
- z
j
b
Tablica simpleksowa w trakcie III iteracji
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
=
4
0
0
1
2
0
2
2
1
3
B
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
−
−
−
=
25
,
0
0
0
13
,
0
5
,
0
0
25
,
0
1
1
3
V
x
3
x
2
x
1
cx →max
2
3
0
0
0
Baza
c
B
x
1
x
2
x
3
x
4
x
5
x
3
0
1
-1
-0,25
x
2
3
0
0,5
-0,13
x
1
2
0
0
0,25
z
j
c
j
- z
j
b
Tablica simpleksowa w trakcie III iteracji
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
=
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
⋅
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
−
−
−
=
⋅
1
0
0
1
0
0
0
4
2
1
2
2
25
,
0
0
0
13
,
0
5
,
0
0
25
,
0
1
1
3
A
V
cx →max
2
3
0
0
0
Baza
c
B
x
1
x
2
x
3
x
4
x
5
x
3
0
0
0
1
-1
-0,25
x
2
3
1
0
0
0,5
-0,13
x
1
2
0
1
0
0
0,25
z
j
c
j
- z
j
b
Tablica simpleksowa w trakcie III iteracji
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
=
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
⋅
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
−
−
−
=
⋅
4
2
2
16
8
14
25
,
0
0
0
13
,
0
5
,
0
0
25
,
0
1
1
3
b
V
cx →max
2
3
0
0
0
Baza
c
B
x
1
x
2
x
3
x
4
x
5
x
3
0
0
0
1
-1
-0,25
2
x
2
3
1
0
0
0,5
-0,13
2
x
1
2
0
1
0
0
0,25
4
z
j
14
c
j
- z
j
b
Tablica simpleksowa w trakcie III iteracji
14
2
2
=
⋅
⋅
b
V
c
B

cx →max
2
3
0
0
0
Baza
c
B
x
1
x
2
x
3
x
4
x
5
x
3
0
0
0
1
-1
-0,25
2
x
2
3
1
0
0
0,5
-0,13
2
x
1
2
0
1
0
0
0,25
4
z
j
3
2
0
1,5
0,13
14
c
j
- z
j
0
0
0
-1,5
-0,13
b
Tablica simpleksowa w trakcie III iteracji
Kryterium simpleks
(wartości nieujemne)
Wartość funkcji
kryterium
Wartości zmiennych
decyzyjnych
Spe
ł
niaj
ą
ce warunek
maksymalizacji FC
Wyszukiwarka
Podobne podstrony:
więcej podobnych podstron