
A Model of Robust Positions in Social Networks
Forthcoming: American Journal of Sociology
Matthew S. Bothner, University of Chicago
Edward Bishop Smith, University of Michigan
Harrison C. White, Columbia University
Word Count (including notes): 15,838
*
We have benefited from the advice of Peter Bearman, Ron Breiger, Ron Burt, Tim Conley, James Evans, John Levi
Martin, Mark Mizruchi, and John Padgett, as well as seminar participants at the University of Chicago, Columbia
University, the Tuck School of Business, and the Yale School of Management. Financial support from the University
of Chicago Booth School of Business and from the Ewing Marion Kauffman Foundation is gratefully acknowledged.
We thank Val Burris for generously making data available on the sociology PhD exchange network. Correspondence
may be directed to Matt Bothner at mbothner@chicagobooth.edu

2
A Model of Robust Positions in Social Networks
Abstract:
What are features of robust rather than fragile social positions? This article introduces a network
model that pictures occupants of robust positions as recipients of diversified support from durably
located others, and portrays occupants of fragile positions as dependents on tenuously situated
others. The model extends Herfindahl’s index of concentration by bringing in the recursivity of
Bonacich’s (1987) method. Using Newcomb’s panel study of status-conferring flows among
members of a college fraternity, we find empirical support for the contention that fragility reduces
future growth in status. Extensions of the model both to input-output networks among industries
in the U.S. economy and to hiring networks among academic departments are presented.
Implications for future research are discussed.

3
What are features of robust rather than fragile social positions? Various approaches have
long equated robust positions with diversification, and fragile, vulnerable ones with
concentration. For instance, the early treatments of Emerson (1962) and Blau (1964) pictured
occupants of fragile positions as those who depend primarily on just one other entity in a social
network. Since then, many investigations have discussed both the hazards of relying on a single
source and the advantages that result from ties to a wide range of others. Examples of this theme
appear in the core tenets of resource dependency theory (Pfeffer and Salancik 1978), ecological
conceptions of niche width as a shelter from environmental change (Hannan and Freeman 1989;
Peli 1997), and network-theoretic accounts of the social structures that sustain malleability and
preserve options in complex games (Padgett and Ansell 1993). It is thus well understood that the
range of an actor’s ties in a network is an important determinant of the robustness of its position.
We develop a conception of robustness and fragility that builds on these earlier lines of
research but also departs from them in an important respect. While harnessing notions of
diversification and concentration, we also draw on the concepts of “decoupling” and “coupling”
developed in White’s (2008) theory of identity and control to allow for mutual influence among
social actors’ identities and networks. We use the term decoupling to refer to clean breaks and
sharp distinctions between social actors, as when consumers’ perceptions of an industry are
unaffected by the practices of its overseas suppliers. Conversely, by coupling we refer to close
connections that yield consequences beyond those of mere contact, as when an executive’s style
of leadership spills over and colors others’ opinions of her direct reports (White 2008; cf. White
2002, pp. 200-220). In our view, to be coupled with another actor is not simply to have contact,
exchange, or a social tie with that actor. It is also to be intertwined with that actor’s identity and
network.
Goffman’s (1968, pp. 30, 47) account of stigmatization and its diffusion offers acute
examples of this intertwining. According to his view, “the loyal spouse of the mental patient, the
daughter of the ex-con, the parent of the cripple, the friend of the blind, the family of the

4
hangman, are all obliged to share some of the discredit of the stigmatized person to whom they
are related [and] persons who acquire a degree of stigma in this way can themselves have
connections who acquire a little of the disease twice-removed. … The issue is that in certain
circumstances the social identity of those an individual is with can be used as a source of
information concerning his own social identity, the assumption being that he is what the others
are.” Thus, as long as social ties are detectable by third parties, in networks of intangible flows—
like the ones Goffman (1968) described, or the more familiar flows of recognition and esteem
among scientists described by Merton (1968)—coupling equates to the influence of another’s
identity on one’s own. And in networks of tangible flows, such as goods and services moving
among production markets, coupling occurs when the position of a given market is affected by
the exchange patterns of contiguous markets.
We contend that a conceptualization of robustness—or fragility, its theoretical
complement—must take into account concentration and coupling. We define the occupant of a
fragile position as one who is both highly dependent on and closely coupled with others who are
themselves tenuously located in social structure. An example of a fragilely positioned nonprofit
is one whose support comes exclusively from an unpopular politician (Hannan 1998:149-50). An
example of a fragilely positioned company is one whose footing resides solely in a precariously
undiversified market (cf. White 2002:246-7). We view fragility as dependency on dependents,
and robustness as diversification across the diversified.
Consistent with this view, in what follows, we develop a network model of fragility and
robustness that jointly takes concentration and coupling into account. We then illustrate its
applicability in three empirical settings: our primary setting is Newcomb’s (1961) study of a
college fraternity, where we examine the effect of fragility on growth and decline in status; next,
in an extension that permits us to examine our model’s implications in a network of flows
unrelated to social status, we assess the effect of fragility on the performance of industries tracked
by the U.S. Department of Commerce’s Bureau of Economic Analysis (Moyer et al. 2004); we

5
then return to status-related themes by investigating the effect of fragility on academic
departments’ prestige, using Burris’s (2004) data on the sociology PhD exchange network.
Our aims, which are theoretical as well as methodological, integrate several streams of
earlier research. We move toward our primary theoretical aim—to bring into focus the status-
eroding effects of fragility in social systems—by drawing from Abbott’s (2001) etiology of
status, Weber’s (1978) discussion of types of charisma, and Whyte’s (1993) ethnography of a
North Boston street gang. We work toward our methodological objective—to construct a general
measure of fragility of positions in networks—by drawing on Herfindahl’s measure of
concentration and melding it with the underlying mathematics of Bonacich’s (1987) measure of
status.
Theoretical Antecedents
Our starting point is Abbott’s (2001) observation that an individual’s status may turn
more significantly on the range of his or her current options than on a history of affiliations with
high-status institutions. According to this view, “it should not be assumed that the ultimate elite
career is one that hooks together all the perfect elite trajectories... The most elite individual may
be that person who maintains the largest number of possible future trajectories that s/he could
jump onto” (Abbott 2001, p. 247).
This insight carries several interrelated implications. One is that, although many
sociologists have long viewed status largely as the product of stable traits (Berger et al. 1977),
status may instead rise and fall in response to shifts in the durability of an actor’s location in
social structure. Another implication is that much of the growth and decline in status we observe
in social life may well have their most fundamental antecedents in audience members’ taste for
robustness and distaste for fragility. Abbott’s claim points directly to the appealing theoretical
possibility that possession of durable social support invites prestige-conferring reactions, whereas
occupants of fragile social positions are seen as illegitimate and therefore attract responses from

6
others that attenuate their social standing. We believe that deference accruing to durably situated
actors, as well as disdain for those in fragile roles (evident in diatribes like “he’s only hanging on
by a thread—cut him loose”) should figure centrally in our portrayals of status-based processes.
Cases of fragility’s corrosive effects also appear as far back as Weber’s (1978)
comparison of two distinct types of charismatic leaders. The first (most familiar) type of
charismatic leader is the extraordinary figure whose military exploits, intellectual powers, or
miraculous works elicit the deference of a broad community of followers. This individual,
standing on a wide base of support, inhabits what for us is a robust position. Conversely, for
Weber, the second type is the person whom the first type eventually (with age) consecrates as his
or her successor. The second type’s social standing therefore rests perniciously on the
sponsorship of the original charismatic leader. Unlike the “pure” charisma of the predecessor,
mere “hereditary charisma” or “lineage charisma” (Weber 1978, pp. 248, 1135-41) marks the
successor’s role—a role not nearly as legitimate as that of the first type. This second type is
fragilely situated, having been chosen by the original, now deceased leader, and frequently
evokes suspicion and conflict among prospective followers—those whose allegiance the first type
garnered with relative ease. Weber’s distinction is important because it brings into focus the
unfavorable perceptions that encircle and damage occupants of fragile social roles. With fragility
often come reactions that erode legitimacy, such as Quakers’ epithetical descriptions of
successors as “hirelings” (Weber 1978, p. 249).
Whyte’s ([1943] 1993) celebrated ethnography of Boston’s North End, especially his
analysis of the Nortons street gang, offers further examples. In particular, two components of
Whyte’s qualitative account—his description of the Nortons’ bowling match and its competitive
aftermath, and his portrayal of the realignment of the gang after its leader fell from grace—neatly
illustrate two main pieces of our argument: that fragility invites status-reducing penalties, and that
an actor is increasingly fragile when the sources of that actor’s social support are themselves
vulnerable. We draw on this case in detail because of its depth and relevance.

7
We begin by turning in figure 1 to Whyte’s (1993, p. 13) original hand-drawn sociogram
of the Nortons. Of the thirteen depicted, three are most relevant for our theory: Doc, the gang’s
leader, Alec at the bottom, and, most significantly, Long John, who while enjoying a moderate
level of prestige nonetheless stood on fragile social ground. With weak ties to most Nortons,
Long John’s social support was strongly concentrated in his relations with Doc, Danny, and
Mike. According to Whyte (1993, p. 12), “Long John was in an anomalous position … his
friendship with the three top men gave him a superior standing. As Doc explained: ‘It’s because
we’ve always catered to Long John. When we go somewhere, we ask Long John to go with us.
We come up to him and slap him on the back. We give him so much attention that the rest of the
fellows have to respect him.’ Nevertheless, he had little authority over the followers.”
The social consequences of Long John’s fragility within the structure of the gang were
most visible as Alec (positioned at the bottom of the sociogram in figure 1) singled out Long John
for one-on-one competition after a high-stakes intragang bowling match (Whyte 1993, pp. 20-24).
In the intragang match, individuals’ bowling scores ended up being virtually identical to their
locations in the status ordering. According to Whyte, it was normative for high-status gang
members to heckle their lower-status rivals, but not vice versa, and so there was a tendency for
each contestant to bowl in accordance with his status.
Nevertheless, the apparent equilibration of status and athletic performance was not left
unchallenged, particularly by Alec. In an effort to recover, Alec targeted Long John, daring him
to one-on-one bowling contests and beating him repeatedly. Additionally, “when bowling was
resumed in the fall, Long John became Alec’s favorite opponent, and for some time Alec nearly
always came out ahead. He gloated. Long John explained: ‘He seems to have the Indian sign on
me’” (p. 22). Summarizing Alec’s attack, Whyte drew the following conclusion, which nicely
illustrates the status-corrosive reactions occupants of fragile roles tend to elicit: “It is significant
that, in making his challenge, Alec selected Long John instead of Doc, Danny, or Mike. It was
not that Long John’s bowling ability was uncertain. His average was about the same as that of

8
Doc or Danny and better than that of Mike. As a member of the top group but not a leader in his
own right, it was his social position that was vulnerable” (p. 22). Alec persistently trounced Long
John in the bowling alleys, before Doc intervened and shored up Long John’s confidence.
In the future, Doc was not nearly as able to prop up Long John, however. And this fact
takes us to our second point—namely, that an individual’s position becomes more fragile if that
individual’s source of social support becomes less robust. Doc’s fall—and, due to their coupling
in the network, Long John’s heightened fragility—resulted from his failed foray into the North
End’s political ambit.
In his summary of Long John’s dilemma, Whyte (1993, p. 45) highlighted a central
component of the model of fragility we develop, specifically that the fragility of an actor’s
position is exacerbated when that actor’s source of social support—in this case, Danny, Mike, and
especially Doc—grows more vulnerable: “Long John divided his time between Spongi’s and the
Norton Street corner. The realignment left him in a vulnerable position. There were two groups
that hung around Spongi’s “joint”: the inner circle and the hangers-on. Spongi included his
brother, Danny, Doc, and two others in the inner circle. When he went for “coffee-ands,” for a
drive, or to the movies, he would invite them to accompany him. He did not include Long John in
his invitations, so Long John was excluded from the inner circle. Without the support of Doc,
Danny, and Mike, he had no standing among the boys who remained on Norton Street, and he did
The Nortons grew disillusioned with Doc and underwent sharp social-
structural changes after the summer of 1938 (Whyte 1993, pp. 42-51). Although there were
several exits, entries, and shifts in stayers’ positions, the most jugular realignments, particularly
for Long John, followed Doc’s repositioning. When Doc’s position became less robust—Doc
had lost much of the support of the Nortons and had grown dependent on Spongi, a new player,
not included in figure 1—Long John became nearly an isolate.
1
Although this second point concerns our conceptualization, rather than the expected consequences, of fragility, it does
imply a corollary prediction—namely, that Alec would have been even more likely to challenge Long John in the
bowling alleys had the social positions occupied by Long John’s supporters grown less robust.

9
not know where to go.”
Measurement
The distinctiveness of social positions resembling the one occupied by Long John brings
us to a more formal description of our measurement of fragility and robustness. We start with the
Herfindahl index to account for concentration and then bring in the recursivity of Bonacich’s
(1987) method to account for coupling.
The Herfindahl index has long been used to assess industry concentration, where it is
written as the sum of firms’ squared market shares (Schmalensee 1989, pp. 966-7; McLean and
Padgett 1997). It has also been used to quantify religious homogeneity within a geographical area
(Ellison et al. 1997). We take it as our point of departure for measuring fragility because it aptly
captures the degree to which one node in the network depends on a narrow base of alters rather
than facing diversification across others. More specifically, if we consider a hypothetical
relational matrix
X
, where
ij
x
=
X
,
0
ii
x
=
, and
ij
x
denotes the flow of respect
(endorsements, recognition, esteem, deference, liking, support, precedence, or honor) directed
from individual
j
to
i
, then we can express the Herfindahl index for members of the social
network summarized by
X
very simply as:
1
n
i
ij
j
H
d
−
=
∑
(1)
where the important transformation is from
X
to
D
as follows:
2
1
/
n
ij
ij
ij
j
d
x
x
−
=
∑
.
(2)
When applied to relational matrices like
X
, the Herfindahl index thus involves these
straightforward steps: divide each entry through by its row sum, square the resulting proportions,

10
and then collect the row sums for the new matrix of squared proportions. If
i
H
equals one,
i
then receives all of his or her respect or social support from just one other actor in the network.
Under this scenario,
i
is completely dependent. If, by contrast, the index for a given actor equals
(
)
1/
1
n
−
, that actor is then minimally dependent, and his or her position is consequently far less
fragile. The Herfindahl index captures the concentration of sources of incoming flows and
therefore serves as a constructive baseline for measuring the fragility of social positions.
Used by itself, however, the Herfindahl index has limitations. When applied to a given
social network, it considers only the distribution of an actor’s immediate ties, making no
allowance for the identities and networks of that actor’s contacts to exert influence. The use of
Herfindahl’s measure thus assumes complete decoupling by construction because it contains no
provision for network spillovers. Although full decoupling—that is, the complete absence of
network spillovers—may accurately describe some social structures, it likely mischaracterizes
most networks of interest to sociologists. Consequently, to build coupling into our measure of
fragility, we turn to a salient feature of Bonacich’s (1987) status measure, whose structure we
now summarize as the backcloth of our approach.
Using again a hypothetical relational matrix
X
as our reference point, Bonacich
(1987:1172-75) recursively defines the status of
i
as:
( )
(
)
α,β
α+β
i
j
ij
j
S
S x
=
∑
(3)
where
ij
x
again denotes the respect
j
directs to
i
,
j
S
is the status of
j
,
α
is a scaling constant,
and
β
is a parameter allowing for the incorporation of White’s (1992) notion of coupling in
networks (cf. Bonacich 1987: 1174). The intuition underlying the measure hinges on
β
. When
β
equals zero,
'
i s
status is just the sum of the flows of respect directed to
i
from the other actors

11
in the network—
'
i s
row sum in
X
adjusted by the scaling constant
α
, in other words. As
β
rises, flows of respect carry greater force when they emanate from higher-status actors. To the
extent that
β
exceeds zero, the status of
j
affects the status of
i
through
'
j s
respect for
i
.
Used widely in empirical research, and increasingly in formal models (Hannan et al. 2003;
Ballester et al. 2004; Bothner et al. 2010), Bonacich’s (1987) measure thus has the particularly
appealing feature of permitting the researcher to operationalize status as a state enjoyed by those
who are highly regarded by highly-regarded others. That is, it folds into the computation of an
actor’s status score an added boost insofar as that actor receives respect (endorsements,
recognition, esteem, deference, liking, support, precedence, or honor) from those who themselves
receive respect (see also Abbott 1981). It is therefore sensitive to the identity or source—not just
the count or intensity—of the endorsements an actor receives.
Using this feature of Bonacich’s (1987) approach in the context of measuring fragility is
straightforward. To do so, we shift attention from totals (Bonacich’s row sums, collected from
X
) to dispersions (Herfindahl’s summed squared proportions, taken from
D
), while allowing for
coupling in the network. More specifically, we express our measure of fragility as follows, where
i
F
represents the fragility of actor
i
:
( )
(
)
,
+
i
j
ij
j
F
d
a b
a bF
=
∑
(4)
The core elements in equation (4) are
ij
d
and
b
. Recall that, in discussing Herfindahl’s index,
we set
2
1
/
n
ij
ij
ij
j
d
x
x
−
=
∑
in equation (2), so that
ij
d
was the squared proportion of
'
j s
respect
for
i
. Summarizing Bonacich’s measure, we also stressed the salience of the
β
parameter,
underscoring its affinity with the notion of coupling. The parameter
b
in equation (4) for
fragility is the analog of
β
for status in (3), and
a
like
α
is a scaling constant. Since
j
F

12
denotes the fragility of actor
j
,
b
determines the extent to which the fragility of
j
shapes the
fragility of
.
i
A high value of
b
, which corresponds to coupling in the social structure, is
consistent with connected actors’ identities and networks mattering discernibly. According to
equation (4), an actor is fragile to the extent that a large proportion of his or her respect comes
from those who are themselves dependent.
To view coupling among fragility levels from another vantage point, we rewrite equation
(4) as an infinite sum, where
ij
d
is an entry in the matrix
D
:
( )
k
1
k=0
,
k
a b
a
b
∞
+
=
∑
F
D
1
(5)
For equation (5) to converge,
1
b
λ
−
<
must hold, where
λ
equals the largest normed eigenvalue
of
D
.
b
Given this constraint, we write the relationship between and
λ
as follows, where
c
denotes a coupling coefficient.
1
c
b
λ
−
= ⋅
(6)
Thus, for
c
0
=
, full decoupling is taken to characterize the relevant network, and fragility
therefore correlates perfectly with the Herfindahl index. Under
c
0
=
, in other words, fragility
reduces to concentration. Conversely, as
c
1
→
, each actor’s fragility score
i
F
is increasingly
affected by the fragility score
j
F
of those on whom
i
depends.
The substantive interpretation of
c
will of course vary across different kinds of networks.
When analyzing a network through which intangible resources circulate, such as the Nortons
street gang, a researcher would likely select a high value of
c
when the members of the network
attach significance to instances in which individuals are “propped up” by others who are in turn
2
The solution (readily computed with standard packages) to equation (5) in matrix form is
( )
(
)
1
,
a b
b
a
−
=
−
I
D
D1
F
, where
I
is an identity matrix (cf. Bonacich 1987, eq. 4).

13
weakly positioned. Stated more generally,
c
0
accommodates settings where actors’
identities seep out and affect one another. A promotion tournament—for instance, one
comprising junior executives racing one another for a senior position—also fits this image.
There, gossip likely mars contestants whose strongest endorsements issue from the most weakly
positioned vice chairmen. Consequently, just as the parameter
β
for status “can be thought of as
a radius” inside of which the analyst chooses to evaluate the status formation process (Bonacich
1987, p. 1174), the coupling coefficient
c
from equation (6) could correspond to the weight
applied to contiguous actors’ identities when quantifying fragility.
Conversely, in a network through which tangible resources flow, such as the network of
loans and business opportunities tying together the Florentine families trenchantly analyzed by
Padgett and Ansell (1993), one would choose a large value of
c
when measuring fragility insofar
as economic shocks reverberate over long distances through the chains of the network. Under
such conditions, assuming that the goal for families is economic and political survival, it would
be especially risky for a given family to depend appreciably on a small set of counterparts whose
own alliances are sparse. Therefore, for networks of tangible flows, the coupling coefficient
c
from (6) could correspond to the weight given to adjacent actors’ economic networks.
With these descriptions in place, we can now express robustness as the complement of
fragility. That is, the occupant of a robust position is one who is not dependent on dependents,
but is anchored solidly in multiple nodes that are in turn durable constituents of the network. We
define robustness by linearly transforming (5) as follows.
3
Although it may be more accurate to refer to our measure as “structural robustness” or “relational robustness” to
distinguish it from the separate ideational component of robustness (see Moody and White’s [2003, esp. p. 104]
discussion), we have opted for the simplest label. In addition, we choose the scaling constant
a
so that the sum of
squared fragility scores equals the number of actors in the matrix (cf. Bonacich 1987, p. 1173). We could also of
course substitute in place of 1 , as the minuend, a column vector of constants equal to the largest fragility score plus
the smallest fragility score, in order to linearly convert fragility scores into robustness scores. Using the max plus the
min has the benefit of making the robustness distribution a mirror image of the fragility distribution, with the same
endpoints and variance.

14
( )
k
1
k=0
,
k
a b
a
b
∞
+
= −
∑
R
1
D
1
(7)
Positions and Dynamics in Newcomb’s Fraternity
We turn to data from Newcomb’s (1961) panel study of a college fraternity to pursue two
main objectives: Our first aim is to depict simply and visually the distinctive features of our
measure of fragility introduced in equation (4); our second aim is to empirically test our
theoretical proposition that fragility is status-eroding. Newcomb’s study tracked 17 male college
students who were recruited to live expense-free for a semester-long period in a fraternity-style
house. Each week, for fifteen weeks, the students were required to rank one another from 1 to 16
according to likeability or “favorableness of feeling.” Newcomb and his colleagues utilized the
resulting data to draw inferences about friendship formation in small groups. The data, which can
be represented as a series of interpersonal networks, have since been used in several studies
(White, Boorman, and Breiger 1976; Doreian et al. 1996; Gould 2002; Moody, McFarland, and
Bender-deMoll 2005) and are useful for the present study for at least four reasons.
First, as a small-scale social structure, Newcomb’s fraternity serves as a particularly
transparent site for bringing relief to differences between fragile and robust social positions in
cross-section (consistent with our first aim). Second, it allows us to compute time-varying levels
of fragility and status (keeping with our second aim). The regularly collected “favorabless of
feeling” appraisals convert easily into asymmetric matrices suitable for the construction of time-
changing status and fragility scores. With them, we can assess the impact of fragility on future
adjustments in status, net of the current level of status, allowing us to assess our expectation that
fragility induces status decline. Third, Newcomb’s data allow us to disentangle the effects of
fragility on status growth and decline from those of individuals’ time-constant characteristics.
Fourth, participants in the experiment did not know one another before its inception, because they
were transfer students. This feature of the research design permits us to focus exclusively on

15
dynamics that occur within, rather than starting before, the semester-long window. Before
turning to dynamic models, we begin by visualizing differences in the social positions of
fraternity members in the first week of the study.
Cross-sectional differences in social positions . Our starting point is an examination of
the first of fifteen 17-by-17 weekly relational matrices
t
X
that summarize the social structure of
the fraternity. Cell
ijt
x
of
t
X
equals 16 if, in week
t
, individual
j
gave
i
a ranking of 1 in
terms of likeability, and equals 1 if
j
gave
i
a ranking of 16. Reverse-coding thus transforms
the initial rankings into positive flows from columns to the rows of
t
X
. For example, according
to the first weekly relational matrix
1
X
depicted in table 1, individual 2 gave individual 3 the
least favorable possible ranking, while individual 4 dispensed to individual 2 the most favorable
ranking attainable. To each of the fifteen weekly matrices, we applied Bonacich’s (1987) status
measure, setting
β
equal to ¾ of the inverse of the largest normed eigenvalue of
t
X
(Podolny
2005). Using this approach, a high-status individual is the target of favorable sentiments from
others who are themselves favorably appraised. We also used
( )
,
a b
F
from equation (5) to
compute individuals’ time-varying fragility scores. Because peer monitoring in close living
quarters likely made fraternity members intensely aware of the nature of one another’s social ties,
we chose to assign to the coupling coefficient
c
its maximum possible value of
.99
.
Using the relational matrix
1
X
in table 1, the plot of status against fragility in figure 2
offers a portrayal of individuals’ social positions in week 1 of the study. The most apparent
feature of figure 2 is of course that more fragilely positioned individuals filled subordinate status
4
However, in panel models that supplement those we subsequently discuss, we also explored results using five distinct
levels of c —in particular,
{
}
c
0, .25, .5, .75, .99
∈
. We took this approach to evaluate our assertion that coupling is a
central component of fragility, while also assessing our anticipation of a negative effect of fraternity members’ fragility
levels.

16
positions in the network. In figure 2, individual 17 inhabits an especially high-status and robust
position, unlike individual 8, who is low in status and highly fragile.
More interesting is the fact
that some fraternity members, such as 13 and 16, are near status-equivalents, but differ
considerably in the fragility of their positions. That is, individuals 13 and 16 offer an example of
how actors may enjoy equivalent amounts of recognition from esteemed others, while one
depends disproportionately on just a few sponsors (as did Long John, going back to figure 1),
while another stands on a much wider base of support (as did Nutsy—Long John’s close
counterpart in figure 1). More generally, differences in fragility among status-equals is not unlike
a case of two towers of equal height that nevertheless stand on markedly dissimilar foundations.
We further explore differences in social foundations in figures 3 and 4—where we depict the
positions of individuals 13 and 16, respectively—to highlight distinctive features of our
approach.
The raw data in
1
X
offer a valuable initial vantage point. An inspection of rows 13 and
16 of table 1 gets quickly to the main analytical difference between status and fragility. Very
simply, the measurement of status begins with computing row sums, whereas the measurement of
fragility starts with calculating dispersions. It is for this reason that status and fragility are
analytically distinct summary statistics conveying unique information about actors’ social
positions. Corresponding to the comparable heights of individuals 13 and 16 on the vertical axis
5
Although our panel models predict the growth (rather than level) of future status as a function of current fragility net
of current status, we also simulated versions of Newcomb’s week 1 matrix to ensure that far weaker cross-sectional
correlations between status and fragility are plausible. Using these alternative matrices (again with seventeen nodes,
each ranking each other from 1 to 16 followed by reverse-coding), we not only observed correlations that were virtually
at zero, we also viewed individuals who were much more sharply positioned on the off-diagonal than 13 and 16 in
figure 2—and who offer leads for future research on fragility and status. More specifically, our simulations (not
reported, but available on request) brought relief to “drones” (that is, individuals receiving lukewarm support from
many, while lighting up no one) as inhabitants of low-status, low-fragility roles, while also highlighting “polarizers” as
occupants of high-status, high-fragility roles. We believe that a promising line of future research would involve
investigating contextual conditions that give rise to particularly low correlations between fragility and status. One such
context may be deeply contested settings where factions emerge and where polarizers deploy drones as their trusted
between-group emissaries.
6
An alternative, though broadly related, theoretical approach is brought forward in Mizruchi et al.’s (1986)
disaggregation of status scores into derived (generated by alters) and reflected (generated by ego) components.
Although their concept of derived status bears some resemblance to our concept of fragility, our approach differs from
theirs in that we construct a separate measure rather than present a decomposition of status.

17
in figure 2, 13’s row sum equals 120 and 16’s row sum is nearly identical—equaling 127. In
contrast, we see a discernible difference in the extent to which 13 and 16 face concentrated social
support: Individual 13’s incoming flows are noticeably lumpy—given 13’s relatively high
dependence on individuals 1 and 6—whereas flows directed at individual 16 are more “even.”
The greater fragility of individual 13’s position relative to that of individual 16 is also
apparent in a comparison of pictures of ego-networks we present in figures 3 and 4. Summarized
very briefly, figures 3 and 4 jointly convey that individual 13 is heavily dependent on particularly
fragile alters—specifically, individuals 8, 1, and 6—while individual 16 faces comparatively
distributed social support and is far less dependent on the most fragilely positioned alters in the
network. We chose line-widths to reflect relative levels of dependence and selected smaller
(larger) circles for the fragilely (robustly) situated alters in the focal individual’s ego-network.
Summarized in greater detail, figures 3 and 4 result from applying the two-step
transformation introduced in equation (2) to the relational matrix
1
X
in table 1. That is, we made
1
X
row-stochastic and then squared the resulting proportions, thereby converting
1
X
to
1
D
. We
collected fragility scores by applying
( )
,
a b
F
from equation (5) to
1
D
for all members of the
fraternity in week 1—precisely the scores arrayed along the horizontal axis in figure 2. Placing
individual 13 at the center of figure 3, we then arranged all other fraternity members clockwise
along its outer edge—in increasing order of 13’s level of dependence on each alter. More
specifically, we extracted and sorted individual 13’s row in
1
D
, arrayed 13’s alters accordingly,
and made the thickness of the connecting lines proportional to entries in row 13 in
1
D
. We then
embedded individual 13’s alters in circles whose radii are a decreasing function of fragility.
7
Code for generating figures 3 and 4 is available on request. We made line thickness a linear function of entries in
Consistent with figure 2, individual 17 resides in the largest circle, while individual 8’s circle is
1
D
and for added emphasis nonlinearly transformed alters’ fragility levels when selecting the radii of their surrounding
circles.

18
the smallest. We took exactly the same steps when constructing figure 4. Viewed together,
figures 3 and 4 are important because they highlight salient structural differences in the positions
of individuals occupying nearly the same level of status computed by Bonacich’s (1987) method.
In addition, figures 3 and 4 reflect our conception of fragility as a function of dependency
(captured by line-thickness) on dependents (summarized by alters’ circle-sizes).
Status growth and decline. Consistent with the observations of Abbott (2001), Weber
(1978), and Whyte (1993), we expect an individual to face status decline as that individual’s
social position becomes increasingly fragile. In particular, the mechanism we envision is one
where fraternity members develop negative impressions about—and thus rank less favorably—
those whose social footings are narrow and slippery. Although the precise mechanisms linking
fragility to outcomes will of course vary across empirical sites, we believe the one just proposed
is accurate for a network of young college students who are groping for a place in their world and
likely to esteem those who have secured durable standing.
We began our investigation of status dynamics by taking a sequence-analytic approach
(Abbott 1995; Abbott and Tsay 2000), which allows us to examine typical paths through the
status distribution. We proceeded by collecting the time series of status scores, across weeks 1
through 15, for all seventeen individuals in the study, and created a 17-by-17 matrix of pairwise
distances in these time series. In this matrix, cell
( )
,
i j
was large to the extent that
'
i s
fifteen-
week movement through the status distribution differed substantially from
'
j s
. We then grouped
individual trajectories into clusters using standard model-based clustering techniques (Banfield
and Raftery 1993). Three clusters emerged with roughly equal numbers of individuals allocated to
each. By averaging the fragility and status scores of all individuals in a cluster, we were able to
generate a characteristic trajectory for each cluster through the status and fragility state spaces
over time.

19
Figure 5 highlights these movements. The left-hand plot illustrates how a typical
individual’s level of fragility might vary across time for each cluster. The right-hand plot, by
contrast, shows week-to-week movements in status. Clusters are represented in each plot by a
marker: closed boxes (individuals 4, 5, 9, 14, 17), open boxes (3, 10, 15, 16), and circles (1, 2, 6,
7, 8, 11, 12, 13). Viewed together the plots indicate an association between fragility and status
decline. For example, the cluster showing the lowest fragility (closed boxes) maintains the
highest average level of status across the 15-week semester. Conversely, the cluster marked by
highest fragility in the left-hand plot (open squares) also drops most precipitously in status in the
right-hand plot.
We also estimated panel models predicting growth in status that take the form:
,
1
1
,
1
φ
i
it
it
it
i t
t
i t
S
S
S
F
µ
ρ
τ
ε
+
+
+
−
=
+
+ +
+
(8)
where
it
S
and
it
F
denote the status and fragility scores,
1,...,17
i
=
and
1,...,14
t
=
. With lagged
status included on the right-hand side, equation (8) models dynamics of adjustment as a function
of time-changing levels of fragility.
We enter fixed effects represented by
i
µ
to absorb invariant, subject-specific propensities
to fill fragile positions. These sweep out fraternity members’ levels of prior educational
attainment, charisma, intrinsic likeability, social skill (Leifer 1988), and all other stable traits that
plausibly channel sorting into fragile social positions (cf. Gould 2002, pp. 1143-4). Using a
fixed-effects specification thus eliminates all between-person variation, so that the coefficients
reflect within-person effects of fragility on growth in status. Additionally, as denoted by the
indicators
1
t
τ
+
, we adjust for all types of overall temporal heterogeneity, such as aggregate levels
of reciprocity and transitivity, the eigenvalue from which fragility is computed, and all other
global properties of the network (Doreian et al. 1996; Moody, McFarland, and Bender-deMoll

20
2005). Since
1
t
τ
+
enter jointly with
i
µ
, the effect of age is also fully accounted for. Correlations
and descriptive statistics for variables in our analyses are included in table 2.
Table 3 presents six models predicting future status growth in Newcomb’s fraternity. We
present one-tailed tests for all continuous covariates given the clarity of our expectations about
the directions of the effects. We also present standardized regression coefficients because of their
usefulness in conveying effect magnitudes in models containing network-related covariates.
Model 1 contains just lagged status and fixed effects for individuals and periods as a baseline.
Inspection of the individual fixed effects (not reported to conserve space) confirms that variation
in fraternity members’ average levels of status growth is clearly pronounced, reinforcing the
merits of the within-estimator. Consistent with our expectations about the importance of
coupling, we find in model 2 that the effect of fragility (as Herfindahl’s measure, where complete
decoupling is assumed) is indiscernibly different from zero.
In model 3 we enter
|
0
it c
F
=
and
|
.99
it c
F
=
jointly. Whereas
|
0
it c
F
=
reduces to the
Herfindahl index,
|
.99
it c
F
=
assumes coupling, with adjacent individuals’ positions influencing the
fragility of a given individual’s position in social structure. In model 3, the coefficient on
|
0
it c
F
=
stays insignificant, whereas
|
.99
it c
F
=
exerts a discernibly negative effect. Through regressing
status growth on
|
0
it c
F
=
and
|
.99
it c
F
=
jointly, the estimate on
|
.99
it c
F
=
reflects the variation that is
orthogonal to
|
0
it c
F
=
. Thus, the persistence of the effect of
|
.99
it c
F
=
, where coupling is taken into
account, offers preliminary evidence to suggest that, at least in the present empirical setting,
network spillovers may matter more than immediate dependencies. In particular, this result is
consistent with the notion that identities of actors’ contacts matter more than concentration levels
of ego-networks. When estimating other models (available upon request), with
c
equal to .25, .5,
and .75, we also found that fragility is significant only at the highest possible level of coupling,
8
We report within-person correlations because our estimator focuses only on within-person variance.

21
c
.99
=
. This set of outcomes is important, because it suggests that taking coupling into account
is a necessary part of understanding the link between positional fragility and dynamics of
prestige. Model 4 confirms that the negative effect of fragility measured with coupling stays
significant when its counterpart is excluded from the set of covariates.
In models 5 and 6, we take two additional steps to assess further our main finding that
fragility negatively affects status growth, before turning to an application of our fragility measure
in a network of economic flows unrelated to status. First, we guard against the possibility that
behavioral correlates of fragility fuel the effect we observe. It is easy to imagine that (at least
some) occupants of fragile roles tend to act sycophantically, whereas occupants of robust
positions are more prone to feather displays and, in general, carry themselves with considerable
aplomb—much to their advantage, especially in a fraternity-style setting. We have argued,
building on prior sociological theory, that fragility undermines legitimacy and is therefore status-
eroding, whereas robustness solidifies legitimacy and is consequently status-enhancing. We
nonetheless address the counterpossibility that locations on an axis marked by fragility and
robustness are in fact undetectable by others in a network, making them by definition
inconsequential, in a direct sense, for processes of growth and decline in status. If this alternative
view is descriptive, then an easily tracked, behavioral correlate of fragility, such as sycophantic
conduct (cf. Burt 1976:104-9) may well fuel the effect we observe. Although the fixed effects
i
µ
absorb time-constant intrinsic propensities to behave subserviently, conduct of this type may have
a time-changing component as well.
We constructed a weighted asymmetry measure to proxy individuals’ shifting
propensities to act obsequiously by working from the premise that a focal actor is sycophantic to
the degree that he sends out more positive affect in a given exchange than he receives. Our
measure thus captures imbalances in the flows that mark a chosen actor’s set of implicit trades, so
that the individual meting out lots of favorable rankings to those who send back unfavorable

22
rankings gets a large value. Using our reverse-coded weekly relational matrices
t
X
, a fraternity
member’s time-varying propensity for sycophantic behavior is measured as follows:
(
)
2
16
1
2
ijt
jit
it
ijt
j
x
x
A
σ
=
−
=
⋅
∑
(9)
where the indicator
ijt
σ
equals 1 if
j
gave
i
a less favorable ranking than
i
gave
j
, -1
otherwise. We expect
it
A
to diminish future growth in status. Correspondingly, when we enter
it
A
in model 5 we observe a strong negative effect, and also find that fragility remains discernibly
negative. Having accounted fraternity members’ time-varying levels of asymmetric exchange,
we can conclude with greater confidence that fragilely situated individuals face status-related
penalties because of the unique features of the positions they occupy.
Second, we evaluate our primary result further by ensuring that the pattern of results does
not hinge on any particular subject’s series. We do so both because of the relatively small size of
Newcomb’s panel, and due to the fact that one member of the fraternity persistently garnered
poor ratings. White, Boorman, and Breiger (1976, p. 759) drew attention to “a scapegoat …
(man 10), who received one of the bottom three choices of each of the other 16 persons.”
Correspondingly, the intercept for the tenth individual is strongly and conspicuously negative
across all models in table 4. We therefore estimated a version of model 5 omitting the tenth
individual.
9
We also estimated a version of our final model with status scores computed with
Results of this approach appear in model 6. Our effect of interest stays strongly
negative (-2.43 t-test for fragility), leading us to conclude that the scapegoat does not
disproportionately configure the effects we observe. To assess the findings more generally, we
β = 0 , rather than the standard ¾
multiplier, to ensure that our results did not hinge on a particular choice of beta. Although this is in our view a
theoretically less attractive way to proceed (here, status is measured just as counts of reverse-coded rankings, rather
than weighting by evaluators’ status), the effect of fragility measured at c
.99
=
was still discernible with a coefficient
of -.209 and -2.03 t-test.

23
also estimated sixteen other versions of model 5 in which we omitted each of the other subjects of
the study in turn. Without exception, across these sixteen alternative specifications, we found
evidence of a negative effect of fragility, whose impact was always significant at the .05 level of
confidence.
Fragility and Robustness of Industries in the U.S. Economy
We have thus far primarily discussed the fragility and robustness of positions in networks
of intangible flows, such as flows of esteem, recognition, and respect among individuals.
Although we have framed our measurement strategy as one that is valuable mainly for the
analysis of purely social systems, particularly status-based systems, we believe it to be reasonably
context-invariant (cf. White 1992, pp. 207-209) in the sense that it also applies (in connection
with different substantive mechanisms) to systems of tangible flows, such as biological,
electronic, and economic networks. For example, in a predator-prey network, a fragile population
of animals is one that preys on a vulnerable input (see Clark 1987, for the classic case of black-
footed ferrets’ near extinction because of their dependence on at-risk prairie dogs), whereas a
robust population’s food web is diversified at several layers. Or, a fragilely situated website
(Kleinberg 2007) sits at the end of a chain, getting the majority of its traffic from a site that itself
depends for traffic on one or just a few other sites. Similarly, organizations and industries are
fragile or robust as a function of their transaction patterns (cf. Hirschman 1962, pp. 98-119 on
satellite versus master industries and on linkage effects). A robustly situated industry is one
whose incumbents sell to (or buy from) a range of industries that have a diversified mix of
transaction partners.
We turn to standard input-output data for industries defined by the North American
Industrial Classification System (NAICS) to illustrate the applicability of our approach in a
10
These supplementary models are available upon request. Significance tests for fragility all exceed in absolute value
the critical value of 1.645 for a one-tailed test, ranging from -1.71 when the eighth individual is deleted
to -2.43 when the tenth individual is omitted, as discussed above.

24
network of economic flows. Like its predecessor, the U.S. Standard Industrial Classification
(SIC) system, the NAICS classifies establishments by the kind of economic activity in which they
engage, but unlike the SIC, the NAICS offers more accurate categorizations of emerging and
service industries (Yuskavage 2007). Transactions among 67 industrial categories tracked in the
input-output accounts of the Bureau of Economic Analysis (BEA) allowed us to compute annual
levels of fragility for industries from 2000 through 2005, and to assess their effects on industries’
total value added, where total value added is defined as total industry output minus total industry
input (Smith 2005). These industry categories, together with their average levels of total input,
total output, and total value added are shown in table 4. The industry ID refers to row number in
the BEA’s annual Use of Commodities by Industries matrices (Moyer et al. 2004).
To explore the association of total value added with measures of fragility in input-output
networks, we began by assembling six yearly 67-by-67 matrices
t
I
, where
t
I
ijt
=
I
and
I
0
ii
=
for all
i
.
I
ijt
Cell
records for year
t
the sales of industry
i
to industry
j
—or, stated
differently,
'
j s
input from
i
. We then used
( )
,
a b
F
from equation (5) to calculate industries’
time-changing fragility scores.
We did so in two ways in order to exploit the opportunity our data provide to detect
fragility levels in terms of both selling and buying. First, we used the matrices
t
I
to calculate sell
fragility,
,
SELL it
F
. When
,
SELL it
F
for a chosen industry is high, it is revenue-dependent on other
industries that are dependent in their selling patterns. To compute
,
SELL it
F
, we proceeded as
before, normalizing each entry in
t
I
by its row sum and then squaring each proportion in the
resulting row-stochastic matrix. That is, consistent with equation (2), we let
11
We address the possible effects of large diagonals (the amount of intracategory sales, as when automakers sell to
automakers) with a separate adjustment. Whereas our measure of fragility deals with dependency on other nodes in the
network, the adjustment we introduce captures dependency on oneself at an aggregate level.

25
2
66
1
I /
I
ijt
ijt
ijt
j
=
Θ =
∑
, where
t
ijt
= Θ
Θ
, and then applied equation (5) to
t
Θ
to calculate
,
SELL it
F
. Second, to compute buy fragility,
,
BUY it
F
, we worked with the transpose of
t
I
. We
again used the same two-step conversion process—make the matrix row-stochastic and then
square proportions—on
t
T
I
, and applied our measure
( )
,
a b
F
to the twice-transformed matrix. If
,
BUY it
F
for a given industry is high, that industry is dependent, in the procurement of its goods or
services, on other industries that are dependent in their buying patterns.
To convey a sense of the chainlike underpinnings of fragile positions in the input-output
network, in figures 6 and 7 we depict patterns for two industries that, on average, have high
fragility scores. In figure 6, we map out selling patterns contributing to a high sell fragility score
for Chemical Products, and in figure 7 we trace buying patterns leading to a high buy fragility
score for Truck Transportation.
To identify the sell-chain for Chemical Products in figure 6, we constructed the matrix
I
as the average of six annual matrices
t
I
2000 through 2005, and then computed sell fragility
scores for industries, with the coupling parameter
c
equal to
.99.
12
Two of the 67 categories—Federal General Government and State and Local General Government—necessarily have
undefined sell fragility scores because their row sums in
Chemical Products neared
the top of the distribution, with just ten industries ahead of it—for example, Farms as well as
Support Activities for Mining both had higher scores. Chemical Products was therefore ranked
considerably ahead of robustly positioned sectors—for instance, Computer and Electronic
Products and Food Services and Drinking Places—that offer inputs to a wide array of other
industries. Then, with Chemical Products as our point of departure, and using entries in the row-
t
I are zero. These sectors are of course important buyers in
the columns of
t
I , however, and so are included in the computation of fragility scores. After making the original
matrix
t
I row-stochastic and squaring each entry, the undefined entries in their rows of the resulting matrix were reset
to zeroes. We exclude both governmental categories from our panel models because we are interested primarily in
within-effects of fragility. When between or overall-effects of fragility are of interest, we suggest assigning a fragility
score of zero to actors with zero row sums in the relational matrix, and capturing the consequence of their isolate
position with a separate dummy variable.

26
stochastic version of
I
, we moved from first to third-order connections in the network, at each
remove identifying the adjacent industry on which the focal industry was most relatively
dependent for its sales. As shown by the pattern of sell dependencies in figure 6, Chemical
Products sells primarily to Plastics and Rubber Products, which sells mainly to Construction,
which in turn sells mainly to Real Estate.
Turning to the buy-chain for Truck Transportation in figure 7, we followed the same
steps just outlined, except that we worked from the transpose of
I
. Using
T
I
to calculate buy
fragility scores for industries,
I
we found that Truck Transportation ranked near the top of the
distribution, close to other input-dependent industries, such as Food Services and Drinking
places, the lion share of whose inputs come from Food and Beverage and Tobacco Products.
Using a column-stochastic version of , we then tracked the buy-dependencies evident in the
chain in figure 7. Truck Transportation buys mainly from Petroleum and Coal Products, which
buys disproportionately from Oil and Gas Extraction, which then relies principally on Rental
Leasing Services and Lessors of Intangible Assets.
To investigate associations between industries’ time-varying levels of fragility and total
value added, we turn to panel models of the form:
(
)
(
)
,
1
,
1
1
,
1
ln
ln
it
it
it
i
i t
i t
t
i t
TVA
TII
µ
ρ
τ
ε
+
+
+
+
+
+
=
+
+
+
+
F
β
θ X γ
C
(10)
where
, 1
i t
TVA
+
denotes the total value added by industry
i
in year
1
t
+
.
, 1
i t
TVA
+
equals gross
industry output in the focal year, minus total industry input in that year, which we represent by
13
Two additional categories of the original 67—Noncomparable Imports as well as Scrap, Used and Secondhand
Goods—did not receive inputs from any of the other categories and therefore had row sums equal to zero in
t
T
I
. We
also exclude them from our panel models, given that they allow no within-category variation. We include them,
however, in the columns of
t
T
I
when calculating fragility scores because of the inputs they provide.

27
, 1
i t
TII
+
. We focus on
, 1
i t
TVA
+
as an outcome because it is a transparent measure of industry
performance, capturing the extent of a given industry’s contributions to overall U.S. economic
growth (Smith 2005, p. 2). We enter
, 1
i t
TII
+
as an adjustment for industry size, given the
possibility of scale-based efficiencies. We enter logs of both measures because of the skewness
of their original distributions.
The matrix
it
F
whose coefficients are in
β
contains four versions of our fragility
measure from equation (5). Two of the four covariates in
it
F
are the fragility scores just
discussed—
,
SELL it
F
and
,
BUY it
F
—each of which was computed with the coupling parameter
c
set to its maximum value of
.99.
The other two are versions of sell fragility and buy fragility
with
c = 0
, and are therefore perfectly correlated with Herfindahl indices of concentration in
selling and buying relations, respectively. Thus, using more precise notation, the full set of
measures in
it
F
are:
, |
.99
SELL it c
F
=
,
, |
.99
BUY it c
F
=
,
, |
0
SELL it c
F
=
, and
, |
0
BUY it c
F
=
. Unlike our analysis
of Newcomb’s fraternity, where we had strong, theoretically informed expectations about both
the appropriate level of
c
in measuring fragility and the direction of its effect on status, there is
less guidance available in the existing literature for anticipating effects of these fragility scores on
industries’ annual levels of value creation.
Yet, it is possible informally to sketch reasons why we might observe a negative effect of
fragility on total value added, especially for
,
SELL it
F
when coupling in chains of sales is
accounted for. As an industry is increasingly fragile with respect to its customer base—that is, as
its customer base grows more specialized—that industry will be more susceptible to the vagaries
of its buyers. Additionally, if we consider demand for an industry’s outputs to be at least partly
random, quantity demanded will certainly at times fall beneath the threshold at which the focal
industry’s establishments can sell at a positive profit. As an industry grows more fragile, the
value it adds may shrink because its establishments are dying, laying off workers, or making

28
other costly adjustments. Just as important, it is also not hard to imagine that a long chain of
output-related dependencies (from Chemical Products to Real Estate in figure 6) is worse than a
short chain (from Chemical Products just to Plastic and Rubber Products). In a chain of
considerable length, there are multiple sites, not just a single site, at which problems (perhaps
related to being held up by powerful suppliers or other events) can surface. We believe that a
measure sensitive to such contingencies is better suited to characterizing fragility than one that
ignores them. Consequently, we anticipate that
, |
.99
SELL it c
F
=
will negatively affect future total
value added.
Moving to the matrix
it
C
in equation (10), we also enter as adjustments two realizations
of Bonacich’s measure from equation (3). As with our measurement of fragility in this empirical
setting, we again consider industries’ positions in terms of both sales and procurement. Although
for Whyte’s street gang and Newcomb’s fraternity we drew on equation (3) to measure status, in
the context of inputs and outputs tying together industries, we view it as a measure of centrality.
Although there is much evidence pointing to the positive effects of organizational status on
economic performance (Podolny 2005), the industry categories on which we rely are defined at a
sufficiently high level of aggregation that we suspect any meaningful prestige-related distinctions
among establishments are primarily within, rather than between, categories.
Consequently, we used equation (3) to compute sell centrality,
,
SELL it
C
, from
t
I
and to
compute buy centrality,
,
BUY it
C
, from
t
T
I
.
,
SELL it
C
is large for industries, such as Broadcasting
and Telecommunications, that send substantial outputs into several other sell-central industries.
Correspondingly,
,
BUY it
C
is large for industries, such as Construction, that take in substantial
inputs from a host of other buy-central industries. Thus, although we can view high sell
centrality as being analogous to the epicenter of a ripple effect, high buy centrality is not unlike a
vortex suctioning in other industries’ goods and services. We view
,
SELL it
C
and
,
BUY it
C
as

29
proxies for an industry’s importance in the economy—having to do with the scale of transaction
partners—and we therefore expect them to affect total value added positively, adjusting for total
industry input.
Shifting to
it
X
in equation (10), we include additional covariates that address two
particular features of input-output tables. First, we devised the dummy variable
it
negativeflow in
light of the small number of cases in which negative flows of dollars appeared in an industry’s
row or column of the input-output matrices. For example, in year 2000, the dollar value of the
input from Insurance to Farms was -$181.7 million. This is because the insurance industry
weathered losses as the farming industry’s claims exceeded benefits. Since we recoded negative
entries to zeros in
t
I
in order to calculate fragility and centrality scores, we include the indicator
it
negativeflow as a cautionary adjustment.
Second, because our measure of fragility concerns the nature of an actor’s ties to others in
a network, as noted previously we set the diagonal equal to zero in the matrices
t
I
. Zeros along
the diagonal is the rule rather than the exception in most analyses of social networks. Conversely,
given the broad level of aggregation at which industries are defined for input-output tables,
diagonals measuring intraindustry sales (as when computer manufacturers sell components to one
another) are frequently nonzero. We therefore enter two further adjustments:
it
intrarow , the ratio
of industry
'
i s
diagonal to its row sum in
t
I
, and
it
intracolumn , its diagonal over its column
sum in
t
I
. We use these measures to capture a focal industry’s time-varying levels of internal
exchange.
Finally, as denoted by
i
µ
and
1
t
τ
+
, we enter fixed effects for industries and for years,
respectively. Using industry-specific fixed effects
i
µ
accounts for a number of factors, including
cross-industry heterogeneity in demand, average distance from the end consumer, and other time-

30
constant traits. With year indicators
1
t
τ
+
, we adjust for various aggregate macroeconomic
fluctuations likely to influence industry performance. Correlations and descriptive statistics for
variables in our analyses are shown in table 5.
Table 6 presents results of five models predicting total value added. We begin with very
simple specifications and then proceed to models that more stringently adjust for consequential
sources of variation. Model 1 contains only total industry input and sell fragility measured with
maximal coupling. We find, keeping with our expectations, that industries that are less robustly
positioned in their selling patterns add less value. Model 1 thus offers preliminary evidence in
support of the supposition that positional robustness in an economic network elevates
performance. Turning to model 2, we observe a negative effect as well for our measure of buy
fragility.
In model 3, we move to a two-way fixed effects specification that conservatively absorbs
between-industry, as well as temporal, heterogeneity. Given this approach, the available variation
is within-industry and unrelated to aggregate-level macroeconomic factors. We observe first that
the effect of sell centrality,
,
SELL it
C
, is strongly positive, indicating that as a chosen industry sells
increasingly to other important industries, its future performance rises. Also, although the effect
of sell fragility without coupling (the equivalent of the Herfindahl index) is indiscernibly distinct
from zero, the estimate of sell fragility measured with coupling,
, |
.99
SELL it c
F
=
, retains its
significance in the presence of various adjustments. Using the estimates of model 3 together with
the descriptive statistics presented in table 5, we find that a one within-industry standard
deviation increase in sell fragility with coupling lowers future total value added by about 2%
(exp[-.2299599*.078491] = 0.98). This result is important because it suggests that occupancy of
a position implicated in chains of dependencies has performance-eroding consequences.
Although we do not at this juncture take this effect as definitive evidence of a causal relationship
because we do not exogenously vary fragility, given the conservative nature of our panel model,

31
we do believe it is an important association for consideration in future research.
We arrive at a different pattern of effects in model 4, where we turn from measures keyed
to downstream ties to those that build from ties a chosen industry has to others situated upstream
in the supply chain. Unlike model 2, which omitted industry-specific fixed effects, model 4
presents us with a pattern in which buy fragility is no longer consequential. Similarly, whereas
sell centrality mattered appreciably in model 3, its counterpart in model 4 loads poorly, given its
strong association with unobserved stable traits.
We also see in model 4 that the effect of
, |
0
BUY it c
F
=
is both strongly significant and
positive (3.03 t-test). Although this effect lacks the attractive stability of sell fragility measured
with coupling—which holds up across models, with and without industry-specific indicators—it
is still a suggestive result. In particular, it points to the importance of a discussion of the scope
conditions bracketing the generality of our approach—a discussion we pursue in our concluding
section. We underscore for now the fact that, although we have portrayed our fragility measure
as a factor conducive to declines in coveted outcomes, it is not difficult to envision settings where
just the opposite is true.
Given the distinctive features of our current empirical domain, it is not entirely surprising
that
, |
0
BUY it c
F
=
is positively associated with future value added. One plausible account follows
from the high level of aggregation in input-output data and from the fact that input markets differ,
in terms of availability of substitutes, from output markets. More precisely, there are no
substitutes in terms of suppliers, at least in the short-run, at this level of aggregation: although it
is reasonable to anticipate relatively fast changes in the mix of industries to which a focal industry
can sell—for example, telecommunications can shift from selling mainly to one market to another
quickly—it is unlikely that any given industry can significantly and speedily alter its mix of
suppliers. As an example, an instantaneous transition from rail transportation to truck
transportation as an input is implausible. Consequently, at this level of aggregation, it may be

32
desirable to draw from just one supplier industry, within which substitutes may be found, rather
than a wide range of supplier industries—all of whom, in turn, could increase their input prices.
We examine finally model 5, where all previously discussed covariates enter jointly,
together with
it
negativeflow
,
it
intrarow
, and
it
intracolumn
. Including these three additional
measures is important because input-output data differ in material ways from most sociometric
data: Input-output data present both the numerical equivalent of negative ties and nonzero
diagonal elements. When these three covariates enter in model 5, they fall just shy of
significance at a standard level and our coefficient of interest—on sell fragility with coupling—
retains its significance. Thus, in a setting that is substantively very distant from the status-based
systems of Whyte (1993) and Newcomb (1961), we find evidence to suggest that taking chains of
dependency into account is important for understanding outcomes in networks.
Prestige and Fragility in the PhD Exchange Network
Our third empirical application is a reanalysis of the data used in Burris’s (2004)
investigation of the determinants of sociology departments’ prestige and thus brings us back to
status-related themes. An advantage of revisiting Burris’s data is the opportunity they offer to
assess the effect of fragility on an important outcome now known to vary discernibly with
network centrality. Using a sample of 94 departments listed in the ASA’s 1995 Guide to
Graduate Departments of Sociology, Burris (2004) documented that, net of established measures
of research productivity, centrality in the PhD exchange network explains a disproportionate
share of the variation in departmental prestige scores.
These prestige scores were drawn from a National Research Council survey (Goldberger,
Maher, and Flattau 1995) and were “based on ratings by disciplinary peers of the ‘scholarly
quality of program faculty’ on a five-point scale ranging from ‘distinguished’ to ‘marginal’”
(Burris 2004, p. 245). The key independent variable—social capital—was measured as logged
14
We are grateful to an anonymous AJS reviewer for suggesting that we apply our measure to Burris’s (2004) data.

33
network centrality using Bonacich’s (1972) eigenvector measure on a symmetric matrix recording
the trading of scholars between departments.
( )
,
i j
Cell
of the relational matrix used to
compute social capital (and from which we calculate fragility) tallies the number of full-time
faculty members who had been hired from department
i
to
j
and from department
j
to
i
during the chosen observation window. The data for this matrix came from the ASA’s
1995 Guide. Burris’s (2004) results are interesting and important because they counter
conventional, purely productivity-based etiologies of departmental prestige by underscoring the
salience of the status-related consequences of departments’ positions in the hiring network.
Centrally located departments appear to enjoy a number of interrelated advantages, such as
recognition from other well-situated departments and a large base of well-placed researchers
poised to preserve the status of their intellectual roots (pp. 243-5).
Adjusting for the predictors entered in Burris (2004), we anticipate a negative effect of
fragility in the PhD exchange network on departmental prestige. A fragilely located department
is one that trades scholars with a limited set of departments that are similarly restricted in their
sets of exchange partners. We think that occupancy of a fragile position will negatively affect
departmental prestige for at least two reason: One plausible mechanism is that fragility operates
as a market signal of intellectual myopia; another is that occupancy of a fragile position
unwittingly elicits indifference or antagonism among those departments falling outside the
exchange-set and thus (perhaps unconsciously) negatively affects peers’ appraisals.
Consequently, we begin with model 1 in table 7, which replicates model 4 in table 4 of
Burris (2004). Detailed summaries of measures of scholarly productivity entered in model 1
appear on pp. 254-5 of the original article. Very briefly, both Article Publications and Citations
15
The correlation between Burris’s logged measure of social capital based on Bonacich (1972) and the measure
centrality based on Bonacich (1987) we use throughout the current article is .90. In addition, results are virtually
identical if we replace the former measure with the latter in our subsequent regression models. We use the former
measure in our reanalysis for sake of consistency with Burris’s original study.

34
are averages of counts across a focal department’s full-time faculty over a prior five-year
window, and Research Grants is the percentage of faculty members garnering external research
grants in the seven-year period before the NRC survey. In addition, consistent with Keith and
Babchuk (1998), Weighted Article Publications is a measure that takes into account the
heightened impact that results from publishing in the most influential journals, and Book
Publications is the mean count of books per faculty member earning reviews in Contemporary
Sociology from 1980 through 1989. Model 1 thus re-presents results showing that, on top of
influential article and book production, centrality in the hiring network is strongly associated with
favorable peer-appraisals.
Model 2 adds to model 1 our measure fragility with the coupling coefficient
c
.99
=
.
Consistent with our expectation, net of the strong positive effect of social capital, fragility in the
PhD exchange network is discernibly associated with lower ratings on the NRC scale.
Furthermore, the effect magnitude of fragility is comparable in absolute value to those of the two
consequential productivity-based predictors in the model—weighted articles and book
publications. This is most apparent in model 3, where we present standardized regression
coefficients.
According to model 3, a one standard deviation increase in a department’s fragility
effectively counterbalances an equivalent increase in either (weighted) journal or book
publishing. This result is important substantively because it indicates that a standard shift in
fragility within the doctoral hiring network matters as much as a standard shift in production. It
also suggests that, net of centrality, robustness in the network may convey openness and generate
goodwill among peers. More broadly, the effect of interest in model 3 is suggestive of a social
(rather than merit-based) process by which changes in departmental status occur over time.
16
Table A in Burris (2004, p. 262) provides descriptive statistics and correlations for all covariates included in model 1.
An extended version of this table that includes our measures of fragility is available on request.

35
Although these data are not dynamic, it is not hard to imagine departments shifting in the extent
to which they exchange provincially and consequently altering views held by their peers.
Finally, whereas in models 2 and 3 we entered only fragility with coupling set to its
maximum value, we conclude in model 4 by adding fragility with coupling set to zero. This
allows us to assess the value of our measure against that of Herfindahl’s concentration index.
Similar to the pattern of results from our analyses of Newcomb’s fraternity and of input-output
networks, the significance of
|
.99
i c
F
=
taken together with the insignificance of
|
0
i c
F
=
reinforces
the importance, on a methodological level, of incorporating coupling in the measurement of
fragility. Finally, on a substantive level, the results in model 4 are important because they point
directly to the relevance of exchange partners’ positions in the network for a given department’s
level of prestige.
Discussion and Conclusion
Our aims in this article have been both to advance our understanding of status dynamics
by bringing into focus the negative consequences of fragility and to develop a method for
arraying network positions along a continuum defined by fragility and robustness. To summarize
briefly: We framed our approach on the backdrop of prior analyses that harnessed concentration
versus diversification of social ties as salient constructs. We then brought forward the importance
of taking into account coupling among the nodes that comprise a social system. Melding
disparate approaches, we developed a measure of fragility that is attentive to the extent to which a
focal actor is propped up by those who are themselves precariously situated. Using Whyte’s
(1993) ethnography of the Nortons as an initial illustrative case, we turned to an application of
our measure in three distinct empirical settings and found similar results. In Newcomb’s panel,
we found that more fragilely situated fraternity members faced declines in status over the course
of a semester-long period. In our panel of industries, adjusting for centrality, we found in both

36
pooled cross-sectional and within-models that our measure of fragility in selling patterns lowered
industry value added. Our reanalysis of Burris’s (2004) data demonstrated that fragility in the
PhD exchange network is negatively associated with departmental prestige.
Thus, in addition to the empirical results we have presented, one of our primary
contributions has been to demonstrate that an actor’s ranking in an ordering of status (or of
centrality, in the case of industrial sectors) may be insufficient for accurately characterizing its
network position. Using the first week of Newcomb’s panel as an example, we illustrated that,
although metrics like Bonacich’s (1987) approach serve as powerful methods for detecting
prestige orderings from relational data, our measure of fragility illuminates important, and
otherwise occluded, distinctions between actors that appear status-equivalent and yet rely on very
different social footings. We believe that future analyses of the antecedents and consequences of
status will profit from looking beyond the aggregation of prestige-conferring flows to the paths
by which those flows converge on positions in social structure. When virtually all respect,
esteem, or social support emanates from a single vulnerable source, the receiver’s position is
considerably less robust.
We have also drawn attention to the importance of constructing network models that
account for extralocal processes. We found in particular that taking coupling into account in the
measurement of fragility was important for explaining variance in the outcomes we examined.
Our results indicated that attention to ego-network composition through Herfindahl’s measure
alone was insufficient. In this sense, our approach is consonant with other portrayals of processes
traveling through chains of considerable length. Examples of work in this vein include
Rapoport’s (1963) models of interaction, White’s (1970) analyses of vacancy chains, Tilly’s
(1990) discussion of immigration patterns, Abbott and Hrycak’s (1990) analyses of careers, and
Burt’s (2007) models of reputational stability as a function of closure among indirect contacts.
As Burt (2007) argues, whether or not extralocal processes matter deserves careful scrutiny and
carries central implications for research design. If causality resides entirely in the immediate

37
network—that is, if decoupling is a characteristic feature of the population—then it is
unnecessary to capture the network as a whole. Data on ego-networks alone are sufficient.
Conversely, attention to the full pattern of ties within a population becomes increasingly
necessary insofar as identity-related spillovers occur. Our approach indicates that collecting
complete network data is important, at least in some empirical contexts, for moving toward richer
portrayals of status-related processes.
Limits on generality. Before sketching implications for other lines of sociological
theory, we emphasize three conditions that restrict the generality of the perspective we have
presented. First, there are clearly institutional settings in which extralocal processes do not
matter, and where decoupling therefore defines the network. In these settings, fragility is best
measured just as a Herfindahl measure of concentration, without attention to contiguous actors’
identities and networks. Consider in this connection the two-by-two table in figure 8, whose
vertical axis extends from fragile to robust and whose horizontal axis goes from decoupling to
coupling. If in fact decoupling marks the network, then fragility should be measured in way that
is consistent with the bottom-left cell in figure 8, where A relies completely on D, but where D’s
identity and network are inconsequential for A. This quadrant is therefore quite different from its
counterpart on the bottom right, where A is fragile because of its position at the end of a chain,
and from the upper-right cell, where A is robust by virtue of its wide range of connections to
others who are diversified in their sources of social support.
The extent to which a social structure is “readable” (White 1992, pp. 106-11) contributes
significantly to the degree of coupling depicted on the horizontal axis, and thus is a factor
determining the best measurement strategy. Although many social systems allow incumbents (as
well as observers) to map out who is connected to whom and in what way—consider, as
extremes, a rank-order tournament or, less commonly, a matrix organization whose publicly
displayed organizational chart accurately reflects its informal structure—other systems are far
more opaque, even for insiders. There, the concrete patterning of social ties is fuzzy and

38
uncertain for all involved—incumbents and observers have difficulty discerning, or even
inchoately sensing, nonlocal patterns—and network spillovers are therefore rare. Consequently,
an important condition for our approach is a reasonable level of perception within the network.
Coupled identities, where spillovers occur, necessarily require opportunities for detecting or
discerning social ties.
We therefore expect extralocal ties to matter appreciably in the estimation of fragility
effects within transparent settings like investment banking, where firms’ locations in public
pecking orders are widely monitored (Podolny 1993). In such settings, we recommend
computing fragility with a large
b
weight. Conversely, for less penetrable settings that would
tend toward the left column in figure 8—such as semiconductors (Podolny, Stuart, and Hannan
1996), where consumers likely have difficulty discerning the circuitous patterns of interfirm
patenting ties—we anticipate little in the way of network spillovers and thus suspect that firms’
levels of fragility will be best calculated more restrictively—that is, with a smaller
b
weight, or
even with
b
set equal to zero.
Second, our depiction of A’s position as fragile due to chaining in the bottom right of
figure 8 leads us to reinforce the importance of examining global-network structure when
deciding whether to implement our measure. As we discuss in more technical detail in our
appendix, a central consideration in determining if our measure will yield information over and
above Herfindahl’s index is whether the structure of the global network permits chains of
reasonable length among its nodes, or is instead a tightly connected clique. Simulations
presented in our appendix show that social structures marked by longer mean path lengths allow
for greater expression of differences between our measure of fragility and one agnostic with
respect to context. We believe these simulations are important because they shed additional light
on the conditions in which the
b
weight is large in the practical sense. Although in a closely knit
cult our measure differs little from Herfindahl’s, it offers much additional information in more

39
differentiated networks that are typically the subject of sociological investigation.
Third, in empirical settings different from the status systems of Whyte (1993) and
Newcomb (1961), it is entirely plausible to expect that what we have measured as fragility in
equation (4) will exert positive effects on coveted outcomes. Consequently, in such settings,
although its algebraic form will remain unchanged, our measure will require substantive
recasting. Consistent with this possibility, Zuckerman’s (1999, 2000) work clearly demonstrates
the benefits of constructing a narrow, concentrated identity. When individuals or organizations
winnow their focus to an existing node in a way that renders their performance easier to appraise,
corresponding advantages result. There are also the possibilities that sharp focus on another node
in a network enhances trust and reduces learning costs (Uzzi 1996) and that specialized firms
both more readily respond to distinctive customer preferences (Carroll and Hannan 2000; Bothner
2003) and more effectively convey future work experiences to prospective employees (Baron
2004). More generally, there are certainly settings in which fragility is ideologically construed as
positive.
To adjudicate among ways of discussing the likely effects of our measure, we believe it is
essential as a starting point to consider differences in where concentration comes from—from ego
or from alter. Consider a case from the computer industry as an example. Dell’s choice
historically to focus exclusively on the direct sales channel is markedly different from a fraternity
brother who gets a disproportionate share of his social support from one other member of the
house—although Herfindahl’s index will be high for both. Dell’s strategy has largely proven
status-enhancing, but in Newcomb’s fraternity we found that concentration is status-eroding.
Where these cases differ importantly is not in levels of analysis, but in the provenance of
concentration and therefore in terms of control. Whereas a computer maker can deliberately
decide to specialize within a specific segment, the fraternity brother has far less discretion over
whether he receives the lion’s share of his social support from a particular peer. When this does
occur, those other than the focal individual are consequently the ones imputing (unfavorable)

40
meaning to his position.
Thus, in keeping with lines of research differing from our own, the measure of fragility
we have introduced might be recast as a measure of focus in other contexts. In such contexts,
actors receive rewards for establishing exclusive ties to those with narrow allegiances, and the
fragile-robust axis labels for the ordinate in figure 8 could therefore be replaced respectively with
focused-disordered. When the cost of forging such ties varies inversely with actors’ quality
levels, as at times they do in apprenticeship programs, for instance, equation (4) will measure
focus, rather than unwanted complexity or disorder, as a viable market signal in Spence’s (1974)
sense.
To mitigate concerns about generality, in addition to describing how to substantively
reframe our measure to accommodate different settings, we stress the pervasiveness of the social
structural conditions that are consistent with the viewpoint we have advanced: our approach
posits that actors sort into positions in a status ordering as a function of the recognition they
receive, and that the network is sufficiently transparent that they are aware of the means by which
positions in this ordering are determined—whether these positions are durably built through
diversification or exist vulnerably because of concentration. Although the conditions necessary
for our perspective do not mark all social settings, they certainly characterize many. We believe
our approach is generally applicable for theoretical and methodological reasons: both because of
the frequency with which peer monitoring and gossip make the underpinnings of social positions
transparent and because of the frequency with which network-analytic study designs collect data
on ties for whole populations.
17
Although we believe that attention to the origins of fragility—with ego or with alter—serves as a useful starting
point, it is insufficient. Like a laser steadily aimed at the wrong target, ego can of course deliberate narrow his or her
focus on the wrong audience.
18
This point also raises the issue of lineages, if actors in a system span cohorts or generations. Under this scenario,
equation (4) could measure purity of lineage, as when an artist or academic comes from the right (and narrow) line of
teachers. Purity is then a by-product of having collaborated exclusively with a master who was him or herself sharply
discriminating as a disciple. For instance, this is almost certainly the legitimating process the Apostle Paul had in mind
when, in his defense, he cited Gamaliel as his teacher (Acts 22).

41
Future directions. In addition to replicating our results in other settings, especially in those
where status in known to precede coveted outcomes, we see three particularly promising ways to
proceed further. First, although our measure of fragility operates at the level of individual nodes,
it is easy to imagine opportunities to link up with important group-level themes highlighted by
Moody, White, Harary, and colleagues in their work on structural cohesion (see, e.g., Moody and
White 2003; White and Harary 2001). Moody and White (2003) discuss robustness at the group-
level in terms of a focal group’s capacity to persist in spite of node removal and thus picture
cohesive groups as those that have “a status beyond any individual group member” (p. 112).
They also suggest that future research may benefit from focusing on the hazards of removal faced
by particular nodes. Along this line, we believe that our measure of fragility may be particularly
valuable.
Consider, as a potential empirical site, recent work in biology on metabolic and other
cellular networks (Jeong et al. 2000) that focus on individual substrates, connected by
biochemical pathways, constituting a metabolic network. In this domain, a highly fragile
substrate is one that is connected to one or a few narrowly focused alternate substrates. In
addition, not unlike many social networks, biological networks are often characterized by long-
tailed distributions where a few substrates account for much of the network connectivity.
Although this can result in stability for the network as a whole—in the sense that networks stay
largely intact in the face of random error—researchers are now interested in examining cross-
organism differences in the identities and durability of individual substrates (Jeong et al. 2000).
Arraying nodes in these and similar kinds of networks according to their fragility may be useful
for locating otherwise subaltern fault lines in global structures and thus for further understanding
group-level robustness as envisioned by Moody and White (2003).
Two additional next steps are to link notions of fragility and robustness more tightly to
etiologies of status and also to harness the approach we have developed to further pinpoint the

42
structural foundations of robust action—or action that preserves options (Leifer 1988; Padgett
and Ansell 1993). We conclude with very preliminary sketches of how theories of status and of
robust action might be extended in light of our approach.
We found in our analysis of Newcomb’s data that fraternity members enjoyed increments
in status as their positions within the social structure became more robust. This finding is
consistent with Abbott’s (2001) observation that eliteness is a by-product of possessing a wide
range of future options. We interpreted this finding on a purely structural level as evidence
consistent with the premise that audience members esteem those in robust positions. In arguing
that structure directly affects perceptions, we sought to adjust as stringently as possible for fixed
and time-changing behavioral differences in our empirical models. Nevertheless, we believe that
future work on the determinants of eliteness may benefit from examining some of the possible
behavioral concomitants of robustness. These are actions that emerge from the durability of
actors’ positions and in turn contour their levels of prestige. We refer here in particular to actions
that are permissible and sustainable exclusively for inhabitants of robust positions. Examples
include the “attractive arrogance” Merton (1968, p. 61) ascribed to elite scientists, or excessive
acts of generosity directed toward others who lack the resources to reciprocate. Through tracing
out the links among robustness, modes of conduct, and harvests of future deference, we anticipate
that our conceptions of where status comes from are likely to sharpen.
Turning in conclusion to further implications for theory, we suspect that robust positions,
as we have defined them, render robust action more sustainable. Work on robust action has
immediate precedents in Leifer’s (1991) research on chess masters. This study found that the
very best chess players are not those endowed with uncommon forecasting abilities, but rather
those who can sustain flexibility with respect to (or remain robust with respect to) opponents’
moves. More generally, robust action refers to strategic conduct that is difficult for a competitor
to interpret and that therefore keeps its practitioner from getting absorbed in an undesirable role.
For example, by acting robustly in a romantic relation, a suitor veils actual intentions and

43
therefore circumvents appearing overly committed and becoming the less powerful; or by acting
robustly in international relations, one nation wishing to conquer another nation adroitly provokes
its target to start a war and then successfully brands it as the instigator (Leifer 1988, pp. 867-9).
Correspondingly, for a political figure, this strategy equates to maneuvering in ways that are
indecipherable to opponents and therefore congenial to continued flexibility (Padgett and Ansell
1993).
We believe that attention to positional robustness may shed new light on the incidence of
robust action. Although we fully agree that social skills (Leifer 1988) and protean identities
(Padgett and Ansell 1993:1263-4) greatly facilitate robust action, we contend as well that this
strategy may be aided by durability of social position. This is because of the costs involved.
Notwithstanding its many advantages, robust action has a dark side and can be dangerous. The
cagey suitor invites accusations of insincerity and indecisiveness. Robust actors, though they
may be exquisitely patient and shrewd, open themselves to the accusation that they are slow
ciphers. Given these risks, we conclude with a disconfirmable prediction. We expect robust
action to be more likely among robustly positioned actors because of the capacity of their social
positions to absorb, much like an insurance policy, the costs of accidents as they behave
strategically.

44
Appendix: Linking Local Measurement to Global Network Structure
This appendix works toward the construction of a bridge between our egocentric
measurement of fragility and the global network structure on which the fragility of a focal node
depends. Since our model reaches beyond the ego-network through our weighting parameter
b
to reflect larger structure, we believe it is important to examine, at least preliminarily, how this
broader context conditions our measure. One way to bring into focus and better understand this
local-global link is to identify the global-level circumstances in which a large
b
weight induces a
vector of fragility scores that differs most significantly from a corresponding set of Herfindahl
indices. Consequently, returning to equation (3) in the main text, our question is the following:
Under what global-network conditions is fragility computed with
c
.99
=
least correlated with
fragility computed with
c
0
=
(i.e., with Herfindahl’s index)? Through identifying the extralocal
circumstances in which
.99
c
=
F
differs most from
0
c
=
F
, we can better appreciate when a chosen
coupling coefficient is indeed “large” in the practical sense that its application yields information
beyond a metric that is insensitive to alters’ positions in the network.
We examine the measurement-related consequences of varying global structure through
the lens of mean path length—a long-studied network-level metric. The path distance between
two nodes is the shortest number of steps between them: Two directly connected individuals have
a path distance of one; individuals capable of reaching one another by a single go-between have a
path distance of two; a pair linked most directly through five intermediaries has a path distance of
six; and so forth (see Burt 1982, pp. 25-29 for measurement; Burt 2005, pp. 32-24 for empirical
illustration). Moving from the dyadic to the global level, the mean path length—the average
shortest distance between all connected pairs—for a given social structure is an index of its
overall reachability or efficiency (Wasserman and Faust 1994). To the extent that mean path
length is low, members of the social structure can get to each other quickly. In contrast, a high
mean path length reflects the presence of long winding strands of social ties.

45
We investigate how mean path length conditions fragility scores in order to assess a
direct implication of our approach—namely, that fragility measured with a high coupling
coefficient is most likely to offer unique information in networks marked by extended chains of
dependence. We believe that pursuing this implication is important on theoretical and empirical
grounds. On a theoretical level, it begins to illuminate the contextual underpinnings of fragility
by bringing relief to global-level dynamics likely to increase variation along a fragility-robustness
axis. On an empirical level, it has the potential to alert researchers to the types of observable
social structures in which attending to context (over and above the immediate composition of the
ego-network) in the computation of fragility yields the greatest payoffs.
We proceeded by generating 1,000 simulated networks of various sizes and levels of
connectivity. Using these networks, we could then assess the effect of mean path length on our
correlation-based outcome of interest,
(
)
.99
0
,
c
c
cor
=
=
F
F
, which we refer to as cormeasures.
The square matrices from which we constructed these networks ranged in size
n
from 50 to 150
rows. To induce variation in the total number of non-zero entries across our various matrices, we
worked with an array of “cutpoints” in each matrix size-category.
More precisely, after generating a square matrix of a given size
n
from
2
n
random draws
from the standard normal distribution, we set all entries above the chosen cutpoint equal to 1,
brought other entries to zero, and constrained the main diagonal to equal zero regardless of the
value of the initial random draw. We used six cutpoints in total: 0, .5, 1, 1.5, 2, and 2.25. With
equal frequency, we applied the first four of these cutpoints to 160 matrices of size 50; we applied
all but the largest to a total of 600 matrices of sizes 75, 100, and 125; and we used all six

46
cutpoints on 240 matrices of size 150. Thus, for each size-cutpoint pair, we simulated 40 random
matrices, yielding a total of 1,000 directed non-valued networks.
We then computed cormeasures as the correlation between fragility for
c
.99
=
and
fragility for
c
0
=
, as well as mean path length, for each of these networks. Although our results
are virtually identical if we set isolates’ fragility scores equal to zero, we eliminated isolates from
our analysis both because fragility is undefined for completely disconnected nodes and because
the average path length of a network is undefined when no path exists between two nodes.
The plot shown in figure A.1 reveals a strong negative association between mean path
length and cormeasures. Thus, the greater the average shortest distance between connected pairs
in a network, the more significant the consequences of applying a large coupling coefficient. As
the non-parametric smoothing function (Friedman 1984) we have added suggests, this association
appears to stay strong until a mean path length of roughly six.
We also took steps to guard against the possibility that the association we observe is an
artifact of the number of nodes. In a simple model regressing cormeasures on mean path length
and network size, the coefficient on mean path length was -.155 (-94.56 t-test) and the coefficient
on network size was .000492 (7.19 t-test). In addition, in a second model in which our predictor
of interest enters reciprocally due to the nonlinear pattern evident in figure A.1, the coefficient on
1/(mean path length) was 1.25 (63.37 t-test) and the estimate on network size was .000421 (4.37
t-test).
We conclude by depicting specific networks created in the course of our simulations that
differ by mean path length and cormeasures. We focus on the extremes and a midpoint for sake
of illustration. In the successive sociograms shown in figure A.2, we move from simulated
networks in which our measure of fragility overlaps with standard concentration to those in which
19
Consistent with our earlier discussion of relational matrices as images of status-conferring flows among members of
a social structure, on a substantive level one might envision (in addition to any number of other interpretations of a
simulated tie) a value of 1 in a chosen cell of a given matrix as an indicator of whether the individual in that column
recognizes or acknowledges the individual in that row. Thus, a focal individual can “reach” a distant alter along a path
composed of third parties that convey recognition, drawing on one to get to another if the first intermediary dispenses
recognition to the focal individual.

47
it differs appreciably. Each network was generated from a matrix of size 100, with the full 100
included in panel 1, 92 nodes (due to the removal of 8 isolates) in panel 2, and 82 nodes in panel
3. We report for each graph its mean path length and the correlation between fragility scores with
minimal and maximal coupling. Panel 1 shows a highly connected network where nodes can
reach others almost immediately on average. For such networks, whose basic structure is perhaps
found most often in small cults, measuring fragility with a large
b
weight has little impact.
Conversely, the networks depicted in panels 2 and 3 correspond to higher mean path length and
are ones in which incorporating broader context in the measurement of fragility has discernible
consequences. These are also more similar in typology to the kinds of networks frequently of
interest to sociologists. It is also in such networks that nodes can depend highly on other nodes
that are themselves caught in chains of dependence, and thus occupy positions that differ
significantly from their more robustly positioned counterparts.

48
References
Abbott, Andrew. 1981. “Status and Status Strain in the Professions.” American Journal of
Sociology 86: 819-835.
—. 1995. “Sequence Analysis.” Annual Review of Sociology 21: 93-113.
—. 2001. Time Matters: On Theory and Method. Chicago: University of Chicago Press.
Abbott, Andrew and Alexander Hrycak. 1990. “Measuring Resemblance in Sequence Data: An
Optimal Matching Analysis of Musicians’ Careers.” American Journal of Sociology 96:
144-185.
Abbott, Andrew and Angela Tsay. 2000. “Sequence Analysis and Optimal Matching Methods in
Sociology.” Sociological Methods and Research 29: 3-33.
Ballester, Coralio, Antoni Calvó-Armengol and Yves Zenou. 2006. “Who’s Who in Networks.
Wanted: The Key Player.” Econometrica, Econometric Society 74: 1403-1417.
Baron, James N. 2004. “Employing Identities in Organizational Ecology.” Industrial and
Corporate Change 13: 3-32.
Blau, Peter. 1964. Exchange and Power in Social Life. New York: Wiley.
Berger. Joseph, M, Hamit Fisek, Robert Z. Norman, and Morris Zelditch, Jr. 1977. Status
Characteristics and Social Interactions: An Expectation States Approach. New York:
Elsevier
Bonacich, Phillip. 1987. “Power and Centrality: A Family of Measures.” American Journal of
Sociology 92:1170-1182.
Bothner, Matthew S. 2003. “Competition and Social Influence: The Diffusion of the Sixth-
Generation Processor in the Global Computer Industry.” American Journal of Sociology
108:1175-1210.
Bothner, Matthew, Richard Haynes, Wonjae Lee, and Edward Bishop Smith. 2010. “When Do
Matthew Effects Occur?” The Journal of Mathematical Sociology 34:80-114.
Burris, Val. 2004. “The Academic Caste System: Prestige Hierarchies in PhD Exchange
Networks.” American Sociological Review 69: 239-264.
Burt, Ronald S. 1976. “Positions in Networks.” Social Forces 55:93-122.
—. 1982. Toward a Structural Theory of Social Action. New York, NY: Academic Press.
—. 2005. Brokerage and Closure. New York, NY: Oxford University Press.
—. 2007. “Closure and Stability: Persistent Reputation and Enduring Relationships among
Bankers and Analysts.” in The Missing Links: Formation and Decay in Economic
Networks, edited by James Rauch: Russel Sage Foundation.
Carroll, Glenn and Michael T. Hannan. 2000. The Demography of Organizations and Industries.
Princeton, NJ: Princeton University Press.
Clark, Tim W. 1987. “Black-Footed Ferret Recovery: A Progress Report.” Conservative Biology
1: 8-11.
Doreian, Patrick, Roman Kapuscinski, David Krackhardt, and Janusz Szczypula. 1996. “A Brief
History of Balance through Time.” Journal of Mathematical Sociology 21:113-31.
Ellison, Christopher G., Jeffrey A. Burr, and Patricia L. McCall. 1997. “Religious Homogeneity
and Metropolitan Suicide Rates.” Social Forces 76:273-99.
Emerson, Richard M. 1962. “Power-Dependence Relations.” American Sociological Review
27:31-41.
Friedman, J. H. 1984. “A Variable Span Smoother.” Tech. Rep. No. 5, Laboratory for
Computational Statistics. Dept. of Statistics, Stanford University.
Goffman, Erving. 1968. Stigma. London: Penguin.
Golberger, Marvin L., Brendan A. Maher, and Pamela Ebert Flattau. 1995. Research-Doctorate
Programs in the United States: Continuity and Change. Washington, DC: National
Academy Press.

49
Gould, Roger V. 2002. “The Origins of Status Hierarchies: A Formal Theory and Empirical
Test.” American Journal of Sociology 107:1143-1178.
Hannan, Michael T. 1998. “Rethinking Age Dependence in Organizational Mortality: Logical
Formalizations.” American Journal of Sociology 104:126-164.
Hannan, Michael T. and John Freeman. 1989. Organizational Ecology. Cambridge, MA: Harvard
University Press.
Hannan, Michael T., László Pólos and Glenn R. Carroll. 2003. “The Fog of Change: Opacity and
Asperity in Organizations.” Administrative Science Quarterly 48: 399-432.
Hirschman, Albert O. 1962. The Strategy of Economic Development. New Haven: Yale
University Press.
Jeong, H. B. Tombor, R. Albert, Z. N. Oltavi, and A. L. Barabasi. 2000. “The Large-scale
Organization of Metabolic Networks.” Nature 407:651-654.
Keith, Bruce and Nicholas Babchuck. 1994. “A Longitudinal Assessment of Productivity in
Prominent Sociology Journals and Departmental Prestige.” American Sociologist 25: 4-
27.
Kleinberg, John. 2007. Cascading Behavior in Networks: Algorithmic and Economic Issues, in
“Algorithmic Game Theory.” Cambridge: Cambridge University Press.
Leifer, Eric M. 1988. “Interaction Preludes to Role Setting: Exploratory Local Action.” American
Sociological Review 53: 865-868.
—. 1991. Actors as Observers: A Theory of Skill in Social Relationships. New York: Garland.
McLean, Paul D., and John F. Padgett. 1997. “Was Florence a Perfectly Competitive Market?
Transactional Evidence from the Renaissance.” Theory and Society 26:209-244.
Merton, Robert K. 1968. “The Matthew Effect in Science.” Science 159:56-63.
Mizruchi, Mark S., Peter Mariolis, Michael Schwartz, and Beth Mintz. 1986. “Techniques for
Disaggregating Centrality Scores in Social Networks.” Sociological Methodology 16: 26-
48.
Moody, James, Daniel McFarland, and Skye Bender-deMoll. 2005. “Dynamic Network
Visualization.” American Journal of Sociology 110:1206-1241.
Moody, James, and Douglas R. White. 2003. “Social Cohesion and Embeddedness.” American
Sociological Review 68: 103-127.
Moyer, Brian C., Mark A. Planting, Mahnaz Fahim-Nader, and Sherlene K.S. Lura. 2004.
“Preview of the Comprehensive Revision of the Annual Industry Accounts.” Survey 84:
38-51.
Newcomb, Theodore M. 1961. The Acquaintance Process. New York: Holt, Rinehart & Winston.
Padgett, John F., and Christopher K. Ansell. 1993. “Robust Action and the Rise of the Medici,
1400-1434.” American Journal of Sociology 98:1259-1319.
Peli, Gabor. 1997. “The Niche Hiker’s Guide to Population Ecology: A Logical Reconstruction of
Organization Ecology’s Niche Theory.” Sociological Methodology 27:1-46.
Pfeffer, Jeffrey, and Gerald R. Salancik. 1978. The External Control of Organizations: A
Resource Dependence Perspective. New York: Harper & Row.
Podolny, Joel M. 1993. “A Status-Based Model of Market Competition.” American Journal of
Sociology 98:829-872.
—. 2005. Status Signals. Princeton, NJ: Princeton University Press.
Podolny, Joel M., Toby E. Stuart, and Michael T. Hannan. 1996. “Networks, Knowledge, and
Niches: Competition in the Worldwide Semiconductor Industry, 1984-1991.” American
Journal of Sociology 102:659-689.
Rapoport, Anatol. 1963. “Formal Games as Probing Tools for Investigating Behavior Motivated
by Trust and Suspicion.” Journal of Conflict Resolution 7:570-579.
Schmalensee, Richard. 1989. “Intra-Industry Profitability Differences in US Manufacturing 1953-
1983.” Journal of Industrial Economics 37:337-357.

50
Smith, George M. 2005. “Annual industry accounts: revised estimates for 2001-2003.” Survey of
Current Business 85: 9(35).
Spence, A. Michael. 1974. Market Signaling: Informational Transfer in Hiring and Related
Processes. Cambridge, MA: Harvard University Press.
Tilly, Charles. 1990. Coercion, Capital and European States, AD 990-1992. Cambridge, MA:
Blackwell.
Uzzi, Brian. 1996. “The Sources and Consequences of Embeddedness for the Economic
Performance of Organizations: The Network Effect.” American Sociological Review
61:674-698.
Weber, Max. 1978. Economy and Society: An Outline of Interpretive Sociology. Berkeley, CA:
University of California Press.
White, Douglas R., and Frank Harary. 2001. “The Cohesiveness of Blocks in Social Networks:
Node Connectivity and Conditional Density.” Sociological Methodology 31: 305-359.
White, Harrison C. 1970. Chains of Opportunity: System Models of Mobility in Organizations.
Cambridge, MA: Harvard University Press.
—. 2002. Markets from Networks: Socioeconomic Models of Production. Princeton, N.J.:
Princeton University Press.
— .2008. Identity and Control: How Social Formations Emerge. Princeton: Princeton University
Press. [Extension and revision of 1992 book]
White, Harrison C., Scott A. Boorman, and Ronald L. Breiger. 1976. “Social Structure from
Multiple Networks. I. Blockmodels of Roles and Positions.” American Journal of
Sociology 81:730-780.
Whyte, William F. 1993 [1943]. Street Corner Society. Chicago: University of Chicago Press.
Zuckerman, Ezra W. 1999. “The Categorical Imperative: Securities Analysts and the Illegitimacy
Discount.” American Journal of Sociology 104:1398-1438.
—. 2000. “Focusing the Corporate Product: Securities Analysts and De-Diversification.”
Administrative Science Quarterly 45:591-619.
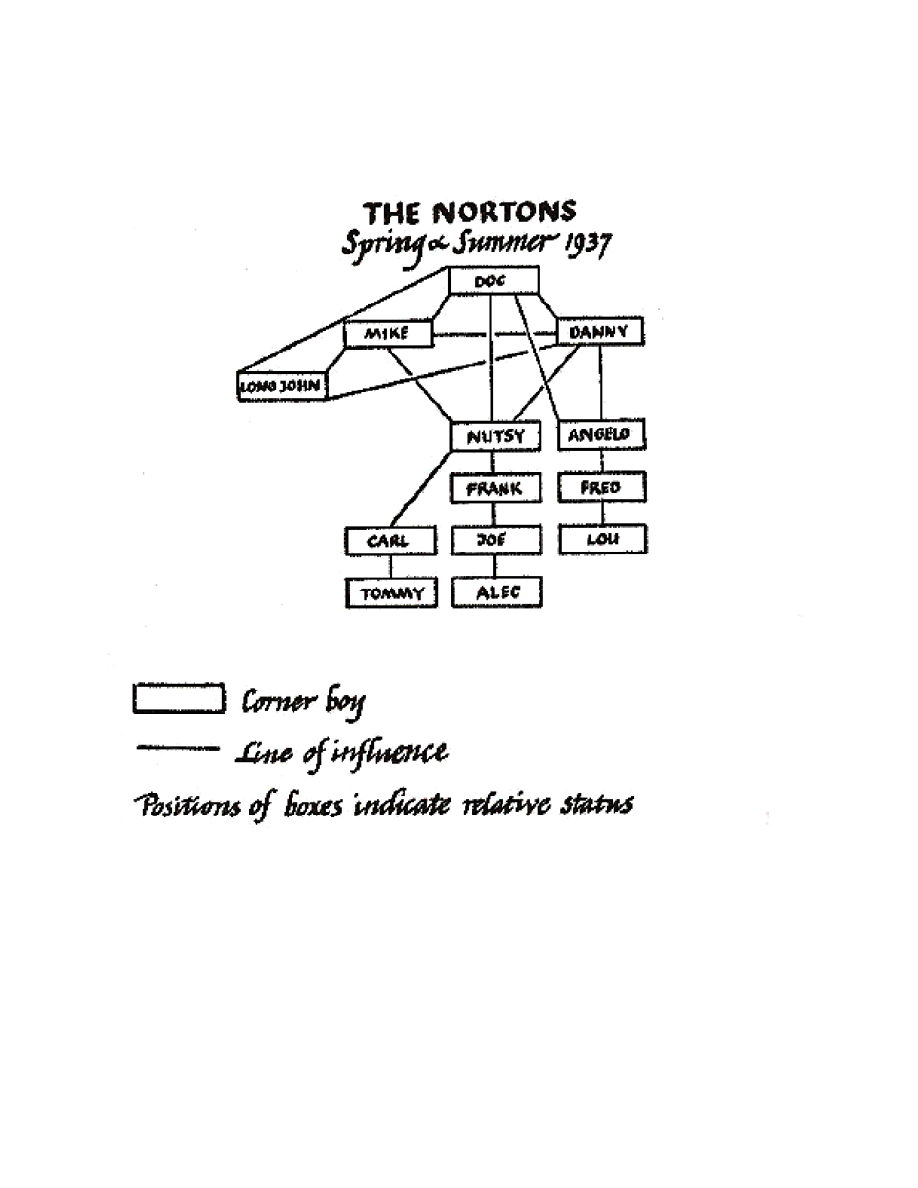
51
Figure 1 A depiction of the social structure of the Nortons street
gang, as hand-illustrated by Whyte (1993 [1943], p. 13).

52
Figure 2 Status versus fragility in week 1 of Newcomb’s study.
Status and fragility scores were computed from the relational
matrix
1
X
shown in table 1, the first of fifteen weekly matrices
t
X
used to compute network measures in our panel models. Numbers of
individuals’ rows in Newcomb’s matrices label each observation.
Dashed lines correspond to the status and fragility scores of
individuals 13 and 16.
Fragility in Newcomb's Fraternity: Week 1
S
tat
us
i
n N
ew
c
om
b'
s
F
rat
er
ni
ty
: W
eek
1
0.8
0.9
1.0
1.1
1.2
1.3
0.
6
0.
8
1.
0
1.
2
1.
4
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
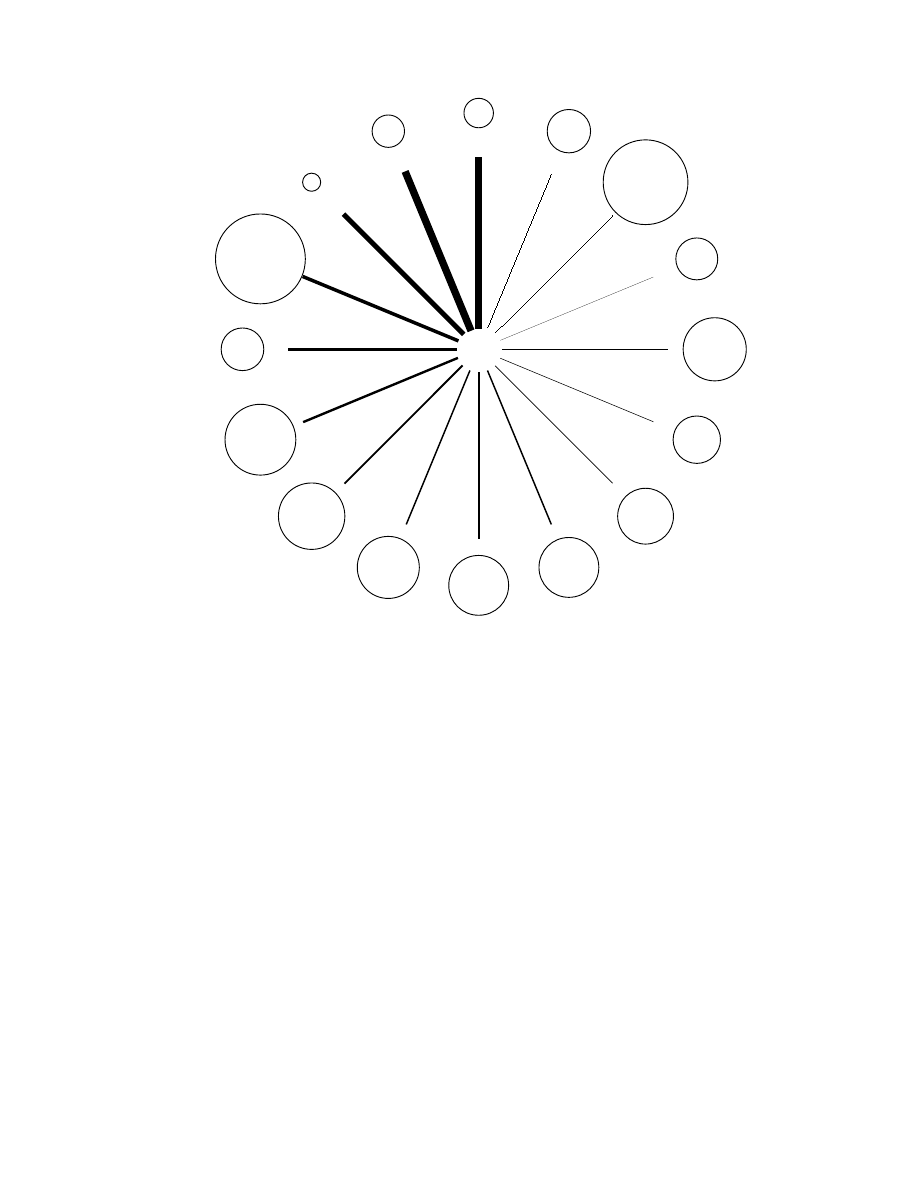
53
13
3
12
14
7
5
10
11
15
16
9
4
2
17
8
1
6
Figure 3 A portrayal of the ego-network of individual 13 in week 1
of Newcomb’s study. Individual 13’s contacts are arrayed clockwise
in increasing order of 13’s relative dependence on them. Levels of
relative dependence on each alter are proportional to line-thickness.
Radii of circles surrounding alters decrease (increase) with alters’
levels of fragility (robustness) depicted along the horizontal axis of
figure 2.
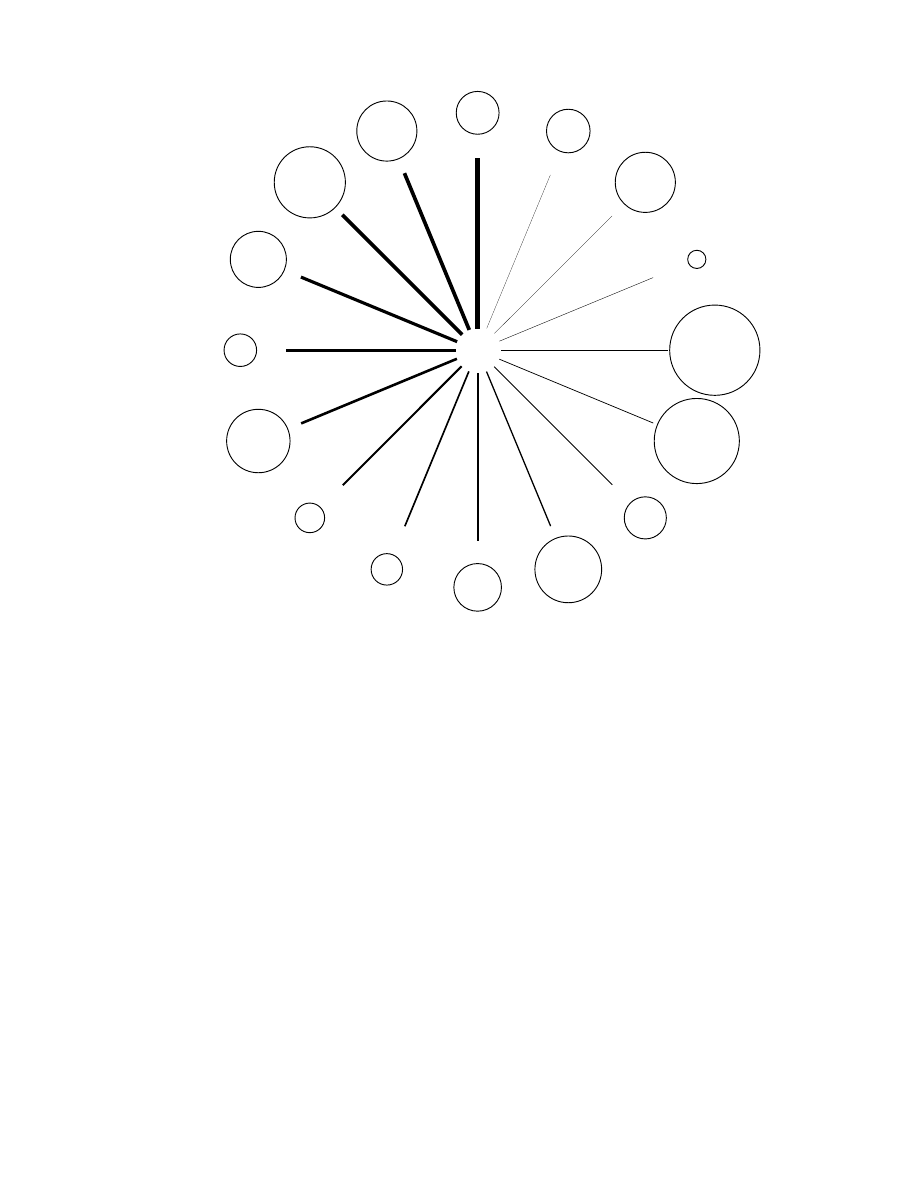
54
Figure 4 A portrayal of the ego-network of individual 16 in week 1
of Newcomb’s study. Individual 16’s contacts are arrayed clockwise
in increasing order of 16’s relative dependence on them. Levels of
relative dependence on each alter are proportional to line-thickness.
Radii of circles surrounding alters decrease (increase) with alters’
levels of fragility (robustness) depicted along the horizontal axis of
figure 2.
16
3
15
8
17
12
14
9
5
13
6
7
1
10
4
11
2
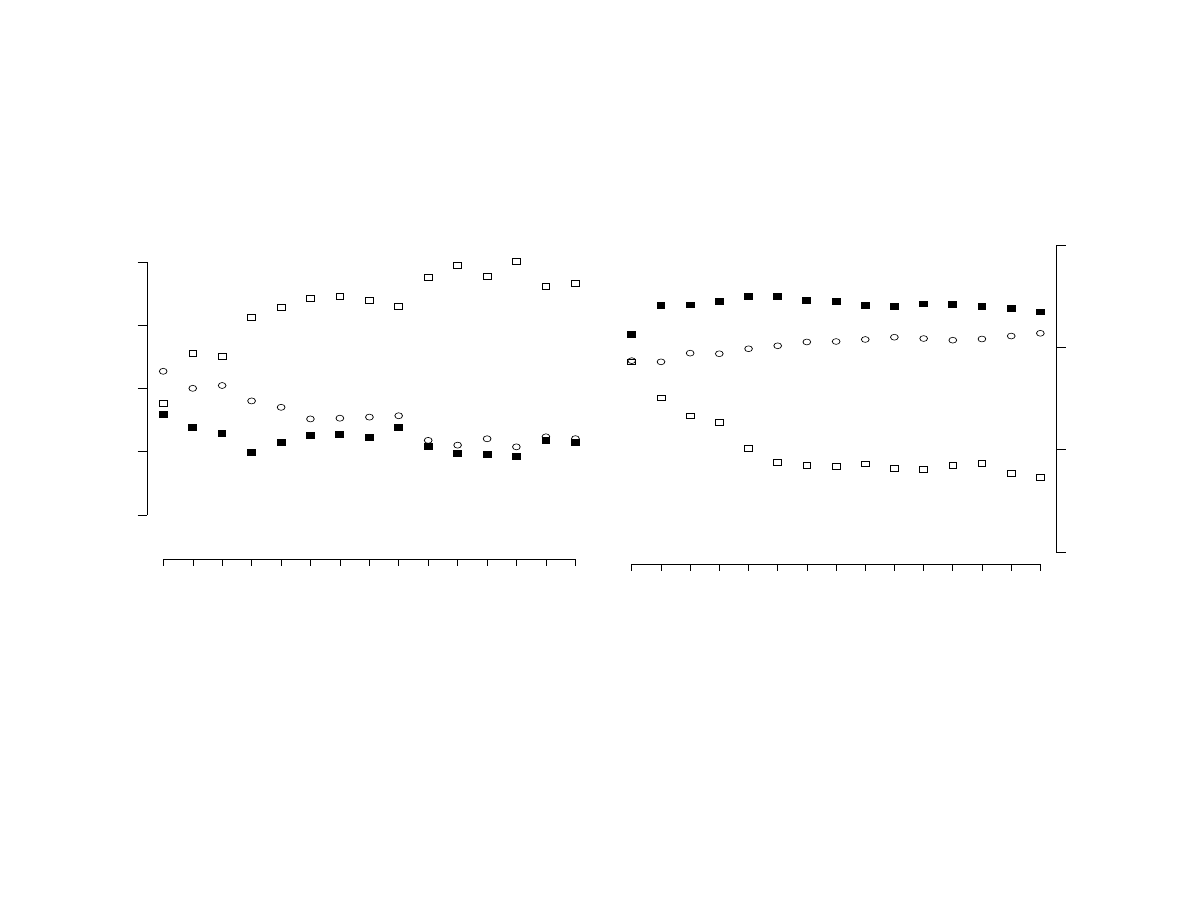
T i m e
F
ra
gilit
y
1
2
3
4
5
6
7
8
9
1 0 1 1 1 2 1 3 1 4 1 5
0.
6
0.
8
1.
0
1.
2
1.
4
T i m e
0.
0
0.
5
1.
0
1.
5
S
tat
us
1
2
3
4
5
6
7
8
9
1 0 1 1 1 2 1 3 1 4 1 5
Figure 5 Times series plots of average fragility scores (left side) and
status scores (right side) for three groups of individuals in
Newcomb’s fraternity. Groups were identified from a sequence
analysis of status trajectories: closed boxes (individuals 4, 5, 9, 14,
17), open boxes (3, 10, 15, 16), and circles (1, 2, 6, 7, 8, 11, 12, 13).
Time is measured in weeks of the study. These series suggest that
increases (decreases) in fragility over time were associated with
declines (growth) in status.
56
15
Chemical Products
16
Plastics and Rubber Products
7
Construction
45
Real Estate
Figure 6 A chain of sales-based ties leading to a high sell fragility
score for Chemical Products. Chemical Products sells primarily to
Plastics and Rubber Products, which sells mainly to Construction,
which in turn sells mainly to Real Estate. Numbers of industries’
rows in the BEA’s use matrices label each node in the chain.
57
32
Truck Transportation
14
Petroleum and Coal Products
3
Oil and Gas Extraction
46
Rental Leasing Services and
Lessors of Intangible Assets
Figure 7 A chain of procurement-based ties leading to a high buy
fragility score for Truck Transportation. Truck Transportation buys
mainly from Petroleum and Coal Products, which buys
disproportionately from Oil and Gas Extraction, which then relies
mainly on Rental Leasing Services and Lessors of Intangible Assets.
Numbers of industries’ rows in the BEA’s use matrices label each
node in the chain.
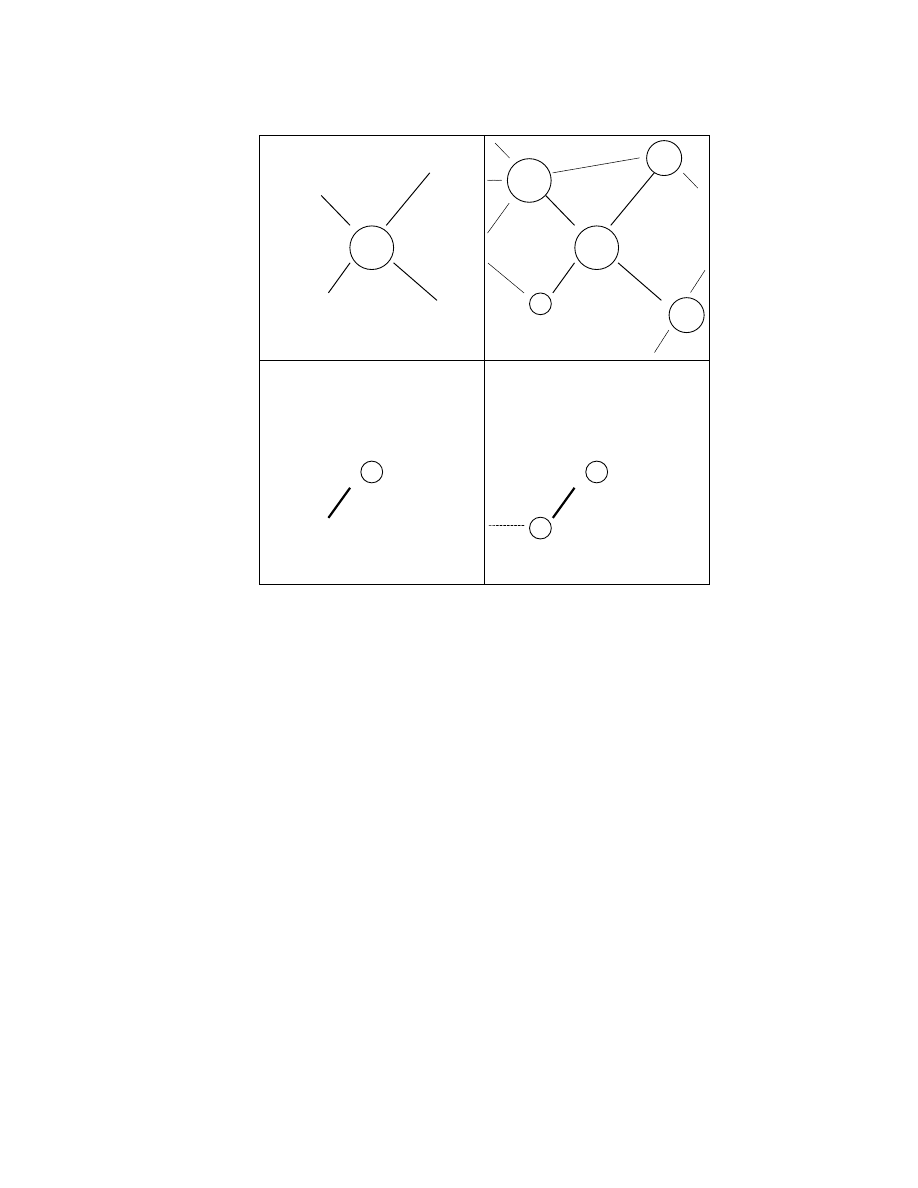
58
A
A
A
A
D
D
D
D
B
B
C
C
E
E
Decoupling
Coupling
Fragile
Robust
Figure 8 Visual representations of fragility and robustness for
decoupled and coupled networks. Solid lines denote first-order
ties of social support. Dotted lines represent second-order ties
of social support. Diameters of circles around nodes reflect
levels of robustness. Nodes are circled if their identity and
network affect the robustness of the focal actor A.
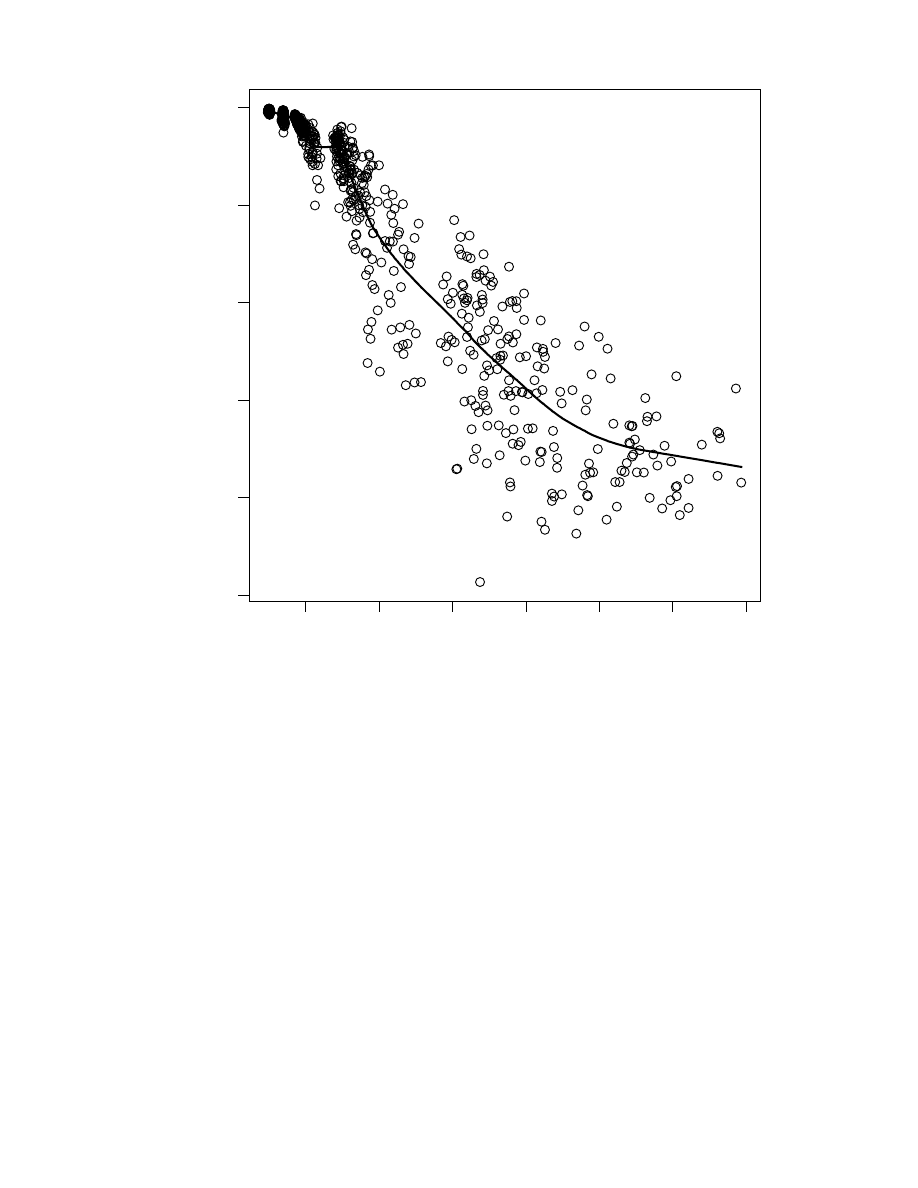
59
Figure A.1 The negative association between cormeasures—the
correlation between fragility measured with
.99
c
=
and fragility
measured with
0
c
=
—and mean path length. Outcomes for 1,000
simulated networks are depicted. A curve provided by a bivariate
smoother is included.
mean path length
c
or
m
eas
ur
e
s
2
3
4
5
6
7
8
0.
0
0.
2
0.
4
0.
6
0.
8
1.
0
60
cormeasures = .99
mean path length = 1.69
cormeasures = .52
mean path length = 4.44
cormeasures = .19
mean path length = 6.97
Figure A.2 Three networks differing in mean path length and in the
correlation between fragility measured with
.99
c
=
and fragility
measured with
0
c
=
.

61
Table 1. A relational matrix
1
X
recording likeability levels in week 1 of Newcomb’s study
[1]
[2]
[3]
[4]
[5]
[6]
[7]
[8]
[9]
[10]
[11]
[12]
[13]
[14]
[15]
[16]
[17]
[1]
0
9
4
4
3
10
2
8
11
15
5
2
16
3
1
9
8
[2]
10
0
7
16
7
4
13
9
1
1
10
6
2
12
8
6
2
[3]
5
1
0
2
6
6
6
1
9
8
13
15
1
9
13
2
7
[4]
6
16
10
0
10
14
14
10
3
3
9
11
10
11
9
14
15
[5]
7
6
9
3
0
2
1
7
4
6
11
12
13
4
16
4
13
[6]
13
5
6
13
1
0
9
16
6
13
3
3
15
8
4
1
6
[7]
4
15
8
14
5
7
0
3
13
14
8
10
5
15
6
3
12
[8]
3
3
2
1
13
15
11
0
2
7
1
4
3
1
5
5
5
[9]
2
7
11
5
12
13
8
6
0
10
14
7
4
16
11
16
14
[10]
1
4
12
10
11
1
7
14
10
0
4
13
9
14
15
8
10
[11]
14
2
15
11
15
3
12
15
16
2
0
14
11
5
14
15
9
[12]
8
11
16
8
14
12
15
12
15
9
15
0
6
10
12
11
16
[13]
16
10
1
9
4
16
3
13
8
5
7
1
0
2
7
7
11
[14]
12
8
5
6
2
5
5
2
12
4
2
9
7
0
2
10
1
[15]
9
12
13
7
9
8
4
5
5
16
6
8
14
13
0
12
3
[16]
11
14
3
12
8
9
10
4
7
11
12
5
8
6
3
0
4
[17]
15
13
14
15
16
11
16
11
14
12
16
16
12
7
10
13
0

62
Table 2. Correlations and Descriptive Statistics for Variables in the Analysis
of Newcomb’s Fraternity
[1]
[2]
[3]
[4]
[1] Status
1
[2] Fragility (c = 0)
-0.6131
1
[3] Fragility (c = .99)
-0.5670
0.9558
1
[4] Sycophant
-0.9013
0.5388
0.4617
1
Mean
0.9511
0.9813
0.9706
0
Standard Deviation
0.3095
0.1929
0.2411
12.4961
Min
0.1794
0.7822
0.7377
-27.2813
Max
1.4963
1.9030
2.1452
34.1563
Note.— Within-correlations

63
Table 3. Standardized Regression Coefficients for Fixed-Effects Models of Status Growth in Newcomb’s Fraternity
1
2
3
4
5
6
Status
-1.7583
-1.8841
-1.8630
-1.9317
-2.6064
-2.7008
(0.1406)***
(0.1798)***
(0.1790)***
(0.1722)***
(0.3641)***
(0.3941)***
Fragility (c = 0)
-0.1286
0.4359
(0.1147)
(0.3186)
Fragility (c = .99)
-0.5417
-0.1770
-0.2167
-0.3190
(0.2855)*
(0.1023)*
(0.1033)**
(0.1312)**
Sycophant
-0.6984
-0.6112
(0.3329)**
(0.3518)*
N
238
238
238
238
238
224
R
2
within
0.4321
0.4355
0.4453
0.4402
0.4520
0.4018
Standard errors in parentheses
* significant at 10%; ** significant at 5%; *** significant at 1%
Individual and time fixed effects included in each model

64
Table 4
Industry
ID
Industry Input
Industry Output
Value Added
Farms
1
140653.30
226356.90
85703.56
Forestry, fishing, and related activities
2
26545.78
52722.33
26176.55
Oil and gas extraction
3
65476.18
163180.70
97704.47
Mining, except oil and gas
4
24639.00
52866.15
28227.15
Support activities for mining
5
27785.12
50811.48
23026.37
Utilities
6
133361.30
335695.80
202334.40
Construction
7
543079.20
1085010.00
541930.80
Food and beverage and tobacco products
8
441142.70
609195.10
168052.40
Textile mills and textile product mills
9
50982.08
74036.68
23054.60
Apparel and leather and allied products
10
26584.37
45694.48
19110.12
Wood products
11
60706.13
93724.62
33018.50
Paper products
12
101460.00
152891.80
51431.83
Printing and related support activities
13
48617.33
94093.69
45476.37
Petroleum and coal products
14
227630.40
268945.50
41315.13
Chemical products
15
293146.30
464042.70
170896.30
Plastics and rubber products
16
110445.40
175049.10
64603.68
Nonmetallic mineral products
17
51249.98
98002.30
46752.32
Primary metals
18
108063.60
155912.00
47848.32
Fabricated metal products
19
137038.30
251089.20
114050.90
Machinery
20
158110.90
257307.40
99196.48
Computer and electronic products
21
253429.70
384404.20
130974.50
Electrical equipment, appliances, and components
22
58029.42
105076.70
47047.34
Motor vehicles, bodies and trailers, and parts
23
356501.60
466462.00
109960.40
Other transportation equipment
24
102267.90
168526.90
66259.02
Furniture and related products
25
42478.95
74952.20
32473.23
Miscellaneous manufacturing
26
68293.34
128761.80
60468.45
Wholesale trade
27
253107.90
912496.80
659388.90
Retail trade
28
326095.50
1030896.00
704800.90
Air transportation
29
69189.37
117946.70
48757.37
Rail transportation
30
17717.27
43247.35
25530.08
Water transportation
31
23009.57
30959.83
7950.28
Truck transportation
32
117959.80
218202.50
100242.70
Transit and ground passenger transportation
33
10787.68
26521.35
15733.67
Pipeline transportation
34
20509.60
32113.18
11603.58
Other transportation and support activities
35
30587.42
107669.30
77081.88
Warehousing and storage
36
10725.12
40223.25
29498.13
Publishing industries (includes software)
37
117607.90
234023.60
116415.70
Motion picture and sound recording industries
38
45352.96
82347.10
36994.13
Broadcasting and telecommunications
39
315438.50
588061.90
272623.30
Information and data processing services
40
53465.05
101594.70
48129.63
Federal Reserve banks, credit intermediation, and related activities
41
187492.00
580050.10
392557.90
Securities, commodity contracts, and investments
42
123229.80
281169.80
157940.00
Insurance carriers and related activities
43
235777.30
490853.30
255075.90
Funds, trusts, and other financial vehicles
44
63316.13
81845.45
18529.28
Real estate
45
416120.80
1679320.00
1263199.00
Rental and leasing services and lessors of intangible assets
46
119552.40
257450.60
137898.20
Legal services
47
58146.05
213350.30
155204.30
Miscellaneous professional, scientific and technical services
48
334861.70
790237.80
455376.10
Computer systems design and related services
49
70193.47
240492.40
170298.90
Management of companies and enterprises
50
118088.00
309771.70
191683.70
Administrative and support services
51
172480.50
457265.90
284785.30
Waste management and remediation services
52
27604.10
55652.32
28048.23
Educational services
53
60413.46
150490.00
90076.53
Ambulatory health care services
54
174752.50
545440.70
370688.20
Hospitals and nursing and residential care facilities
55
226020.40
511579.50
285559.10
Social assistance
56
41515.53
105436.40
63920.84
Performing arts, spectator sports, museums, and related activities
57
27695.32
72705.16
45009.85
Amusements, gambling, and recreation industries
58
37699.79
101712.40
64012.57
Accommodation
59
36536.68
100576.60
64039.87
Food services and drinking places
60
237611.20
462741.80
225130.60
Other services, except government
61
274611.50
600479.10
325867.50
Federal government enterprises
62
22250.10
85822.66
63572.57
State and local government enterprises
64
101491.50
175110.70
73619.20
Note.-- In millions of dollars, averaged over years 2000 through 2005. Omitted categories include: Federal general government (62),
State and local general government (65), Noncomparable imports (66), Scrap, used and secondhand goods (67)

65
Table 5. Correlations and Descriptive Statistics for Variables in the Analysis of Industry Performance
[1]
[2]
[3]
[4]
[5]
[6]
[7]
[8]
[9]
[10]
[11]
[1] ln(Total Value Added)
[2] ln(Total Industry Input)
0.6875
[3] Sell Fragility (c = .99)
-0.2625
-0.115
[4] Buy Fragility (c = .99)
0.1774
0.1063
0.0466
[5] Sell Centrality
0.1644
0.0961
-0.0028
-0.0661
[6] Buy Centrality
-0.0268
0.1121
0.1276
0.0147
0.389
[7] Sell Fragility (c = 0)
0.0512
0.0806
-0.0891
-0.2732
0.0148
-0.0268
[8] Buy Fragility (c = 0)
0.2092
0.081
0.0678
0.729
-0.0174
0.0061
-0.2988
[9] Intrarow
-0.0349
0.1066
0.0948
0.0776
0.149
0.4178
-0.1032
0.0113
[10] Intracolumn
0.1003
0.0085
-0.024
-0.0032
0.4356
0.0971
-0.1175
-0.0351
0.5209
[11] Negativeflow
-0.0768
-0.0107
0.027
0.047
-0.1613
-0.0482
0.09
-0.0082
0.0187
0.0386
Mean
11.3431
11.3445
0.31242
0.77544
0.66943
0.66276
0.68663
0.7888
0.1486
0.16088
0.04444
Standard Deviation
0.11939
0.12078
0.07849
0.12639
0.04804
0.05283
0.04811
0.09485
0.01328
0.011
0.11838
Min
8.83203
9.08469
0.0068
0.26115
0.00704
0.04558
0.13135
0.33719
0
0
0
Max
14.199
13.3905
5.86601
4.23476
4.39572
3.29411
3.57717
4.52637
0.70106
0.82611
1
Note.-- Within correlations and standard deviations

66
1
2
3
4
5
ln(Total Industry Input)
0.903
0.888
0.381
0.398
0.316
(0.035)**
(0.033)**
(0.057)**
(0.062)**
(0.064)**
Sell Fragility (c = .99)
-0.089
-0.230
-0.241
(0.035)*
(0.057)**
(0.055)**
Buy Fragility (c = .99)
-0.374
-0.011
0.007
(0.047)**
(0.053)
(0.049)
Sell Centrality
0.394
0.298
(0.094)**
(0.115)*
Buy Centrality
0.045
-0.010
(0.095)
(0.102)
Sell Fragility (c = .00)
-0.031
0.181
(0.092)
(0.094)
Buy Fragility (c = .00)
0.218
0.261
(0.072)**
(0.068)**
2002
0.023
0.024
0.016
(0.014)
(0.014)
(0.013)
2003
0.057
0.047
0.043
(0.014)**
(0.015)**
(0.014)**
2004
0.101
0.100
0.104
(0.015)**
(0.016)**
(0.016)**
2005
0.120
0.120
0.130
(0.018)**
(0.020)**
(0.020)**
Intrarow
0.084
(0.481)
Intracolumn
1.048
(0.544)
Negative Flow
-0.045
(0.036)
Constant
1.134
1.571
6.804
6.592
7.081
(0.405)**
(0.377)**
(0.631)**
(0.674)**
(0.676)**
Industry Fixed Effects
No
No
Yes
Yes
Yes
N
315
315
315
315
315
R
2
0.6836
0.7312
0.6139
0.5903
0.6648
Standard errors in parentheses
* significant at 5%; ** significant at 1% (two-tailed tests)
Note.-- All continuous covariates are lagged one year with the exception of industry input. Models 3-5 report within R2
Table 6. Models Predicting ln(Total Value Added)

67
Table 7. Models Predicting Departmental Prestige in Burris’s PhD Exchange Network
1
2
3
4
Social Capital
1.118
1.105
0.747
1.068
(0.069)**
(0.067)**
(0.045)**
(0.078)**
Fragility (c = 0)
-0.085
(0.093)
Fragility (c = .99)
-0.101
-0.093
-0.096
(0.039)*
(0.036)*
(0.039)*
Article Publications
0.072
0.067
0.070
0.064
(0.051)
(0.049)
(0.052)
(0.049)
Citations
0.005
0.005
0.026
0.005
(0.010)
(0.010)
(0.053)
(0.010)
Research Grants
-0.000
-0.001
-0.008
-0.000
(0.003)
(0.003)
(0.045)
(0.003)
Weighted Article Publications
0.180
0.176
0.112
0.165
(0.082)*
(0.079)*
(0.051)*
(0.080)*
Book Publications
0.245
0.217
0.114
0.232
(0.090)**
(0.088)*
(0.046)*
(0.089)*
Constant
-0.401
-0.294
-0.000
-0.138
(0.150)**
(0.151)
(0.034)
(0.227)
N
94
94
94
94
R
2
0.89
0.90
0.90
0.90
Standard errors in parentheses. Model 3 reports standardized regression coefficients and corresponding standard errors.
* significant at 5%; ** significant at 1%
Document Outline
- A Model of Robust Positions in Social Networks0F*
- Matthew S. Bothner, University of Chicago
- Edward Bishop Smith, University of Michigan
- Harrison C. White, Columbia University
- Word Count (including notes): 15,838
Wyszukiwarka
Podobne podstrony:
social positions in influence networks
Shan A Model of Wavefunction Collapse in Discrete Space Time
exploring the social ledger negative relationship and negative assymetry in social networks in organ
Harrison C White Status Differentiation and the Cohesion of Social Network(1)
The algorithm of solving differential equations in continuous model of tall buildings subjected to c
Zoledronic acid improves femoral head sphericity in a rat model of perthes disease
Grosser et al A social network analysis of positive and negative gossip
knowledge transfer in intraorganizational networks effects of network position and absortive capacit
Gnotobiotic mouse model of phage–bacterial host dynamics in the human gut
Interaction between ascorbic acid and gallic acid in a model of
A theoretical model of differential social attributions toward computing technology when the metapho
Harrison C White Reconstructing the Social and Behavioral Sciences(1)
JEHOVAH LIVES IN BROOKLYN JEHOVAH S WITNESSES AS A MODEL OF FUNDAMENTALISM by Richard Francis (1999
the impacct of war and financial crisis on georgian confidence in social and governmental institutio
Comments on a paper by Voas, Payne & Cohen%3A �%80%9CA model for detecting the existence of software
Dance, Shield Modelling of sound ®elds in enclosed spaces with absorbent room surfaces
Proteomics of drug resistance in C glabrata
Microstructures and stability of retained austenite in TRIP steels
więcej podobnych podstron