
44
4 DQF-COSY, Relayed-COSY, TOCSY
© Gerd Gemmecker, 1999
Double-quantum filtered COSY
The phase problem of normal COSY can be circumvented by the DQF-COSY, using the MQC term
generated by the second 90° pulse:
90°
y
→ −
I
1z
cos(
Ω
1
t
1
) cos(
π
Jt
1
)
I
1
polarization
+ 2I
1y
I
2x
cos(
Ω
Ω
1
t
1
) sin(
ππ
Jt
1
)
I
1
/ I
2
double/zero quantum coherence
+ I
1y
sin(
Ω
1
t
1
) cos(
π
Jt
1
)
I
1
in-phase
single quantum coherence
+ 2I
1z
I
2x
sin(
Ω
1
t
1
) sin(
π
Jt
1
)
I
2
anti-phase single
quantum coherence
Phase cycling can be set up to select only the DQC part at this time, which is only present in the
2I
1y
I
2x
term (leaving the cos(
Ω
1
t
1
) sin(
πJt
1
) part away for the moment):
2I
1y
I
2x
= 2
-i
/
2
(I
1
+
- I
1
-
)
1
/
2
(I
2
+
+ I
2
-
) =
-i
/
2
(I
1
+
I
2
+
+ I
1
+
I
2
-
- I
1
-
I
2
+
- I
1
-
I
2
-
)
DQC
ZQC ZQC
DQC
Only the DQC part survives (50 % loss!) and yields (after convertion back to the Cartesian basis):
-i
/
2
(I
1
+
I
2
+
- I
1
-
I
2
-
) =
-i
/
2
{
(I
1x
+ iI
1y
) (I
2x
+ iI
2y
) - (I
1x
- iI
1y
) (I
2x
- iI
2y
)
}
=
1
/
2
(2 I
1x
I
2y
+ 2 I
1y
I
2x
)
However, this magnetization is not observable, only after another 90° pulse:
90°
y
1
/
2
(-2 I
1x
I
2y
- 2 I
1y
I
2x
)
→
1
/
2
(2 I
1z
I
2y
+ 2 I
1y
I
2z
)
Since we still have the cos(
Ω
1
t
1
) sin(
πJt
1
) modulation from the t
1
time evolution, our complete
signal at the beginning of t
2
is
1
/
2
2 I
1z
I
2y
cos(
Ω
Ω
1
t
1
) sin(
ππ
Jt
1
) +
1
/
2
2 I
1y
I
2z
cos(
Ω
Ω
1
t
1
) sin(
ππ
Jt
1
) .
45
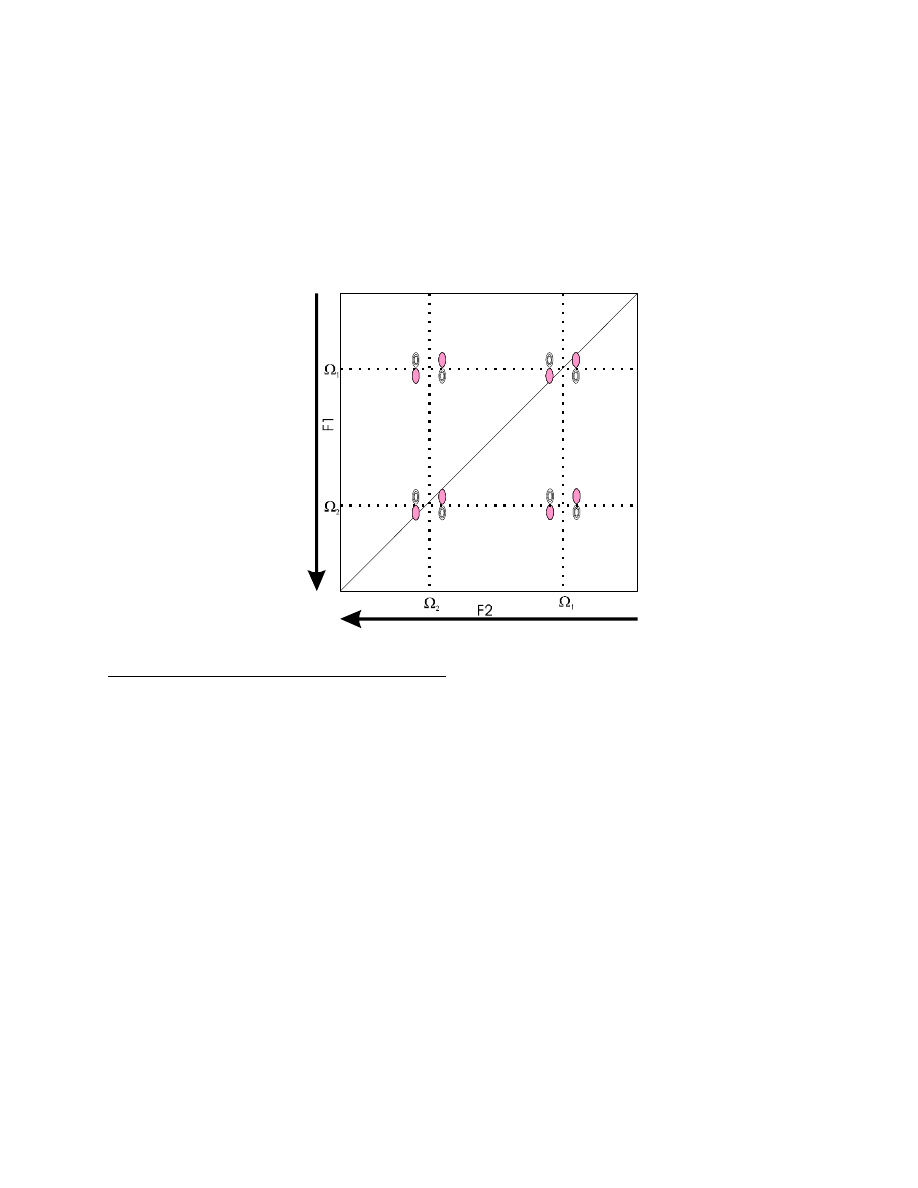
After 2D FT, this translates into two signals:
- both are antiphase signals at
Ω
1
in F1 (with identical absorptive/dispersive phase) and
- both are y antiphase signals (i.e., identical phase) in F2, the first one at
Ω
2
(cross-peak) and the
second one at
Ω
1
(diagonal peak).
Characteristics of the DQF-COSY experiment:
- the spectrum can be phase corrected to pure absorptive (although antiphase) cross- and diagonal
peaks in both dimensions
- both cross- and diagonal peaks are derived from a DQC term requiring the presence of scalar
coupling (since it can only be generated from an antiphase term with the help of another r.f.
pulse: 2I
1y
I
2z
→
2I
1y
I
2x
). Therefore, singulet signals – e.g., solvent signals like H
2
O! – should
be completely suppressed, even as diagonal signals.
Usually this suppression is not perfect (due to spectrometer instability, misset phases and pulse
lengths, too short a relaxation delay between scans etc.), and a noise ridge occurs at the frequency of
intense singulets. In addition, this solvent suppression occurs only with the phase cycling during the
acquisition of several scans with for the same t
1
increment, i.e., after digitization! To cope with the
46
limited dynamic range of NMR ADCs, additional solvent suppression has to be performed before
digitization (i.e., presaturation).
If the DQ filtering is done with pulsed field gradients (PGFs) instead of phase cycling, then this suppresses
the solvent signals before hitting the digitizer. However, inserting PGFs into the DQF-COSY sequence causes
other problems (additional delays and r.f. pulses, phase distortions, non-absorptive lineshapes, additional
50 % reduction of S/N).
With the normal COSY sequence, they result in gigantic dispersive diagonal signals obscuring most
of the 2D spectrum.
Intensity of cross- and diagonal peaks
In the basic COSY experiment, diagonal peaks develop with the cosine of the scalar coupling, while
cross-peaks arise with the sine of the coupling. Theoretically, this does not make any difference (FT
of a sine wave is identical to that of a cosine function, except for the phase of the signal). While this
is normally true for the relatively high-frequency chemical shift modulations (up to several
1000 Hz), the modulations caused by scalar coupling are of rather low frequency (max. ca. 20 Hz for
J
HH
), with a period often significantly shorter than the total acquision time.
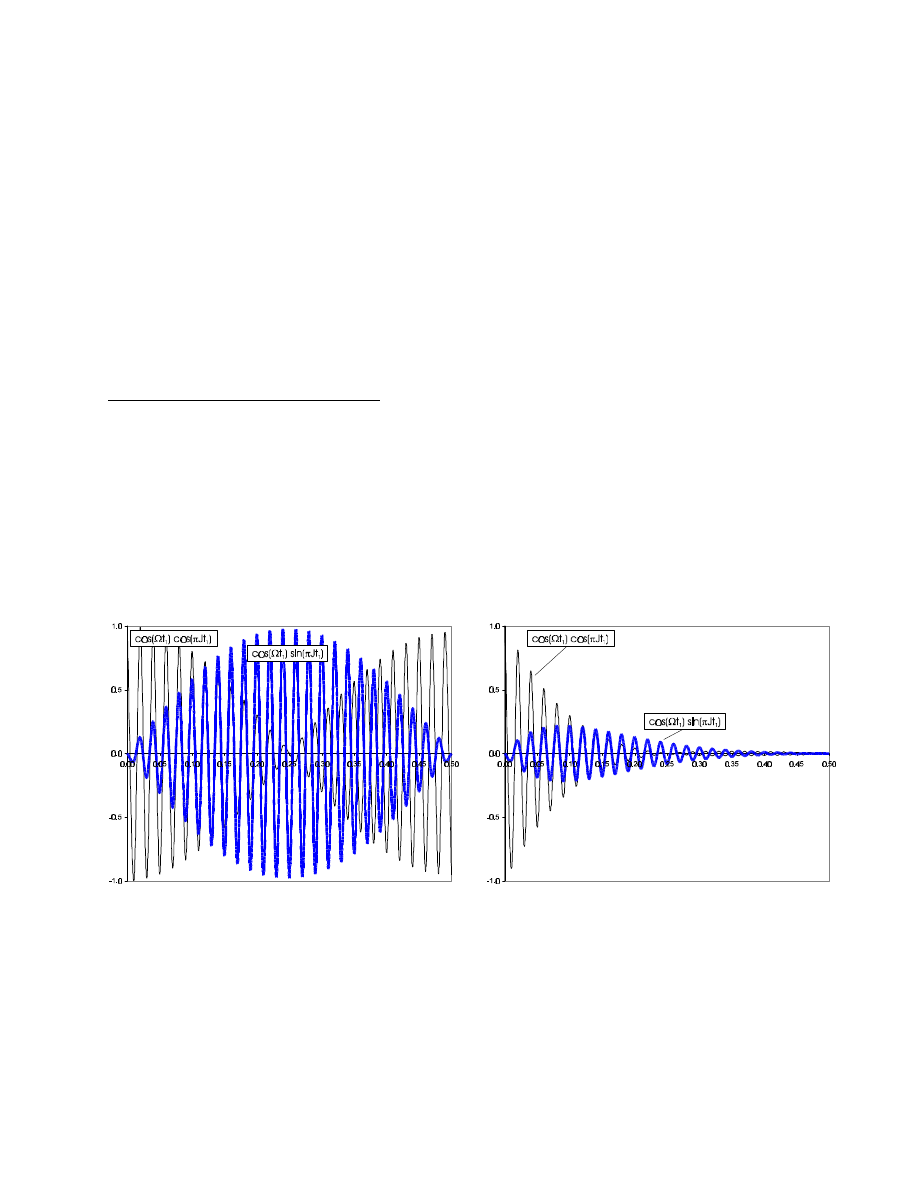
Time development of in-phase (cos
πJt
1
) and antiphase (cos
πJt
1
) terms, with
Ω
1
= 50 Hz, J = 2 Hz,
for T
2
= 10 s (left) and T
2
= 0.1 s (right).
While the total signal intensity accumulated over a complete (or even half) period is identical for
both in-phase and antiphase signals, an acquisition time much shorter than
1
/
2
J
will clearly favor the
in-phase over the antiphase signal in terms of S/N. This difference in sensitivity is further increased
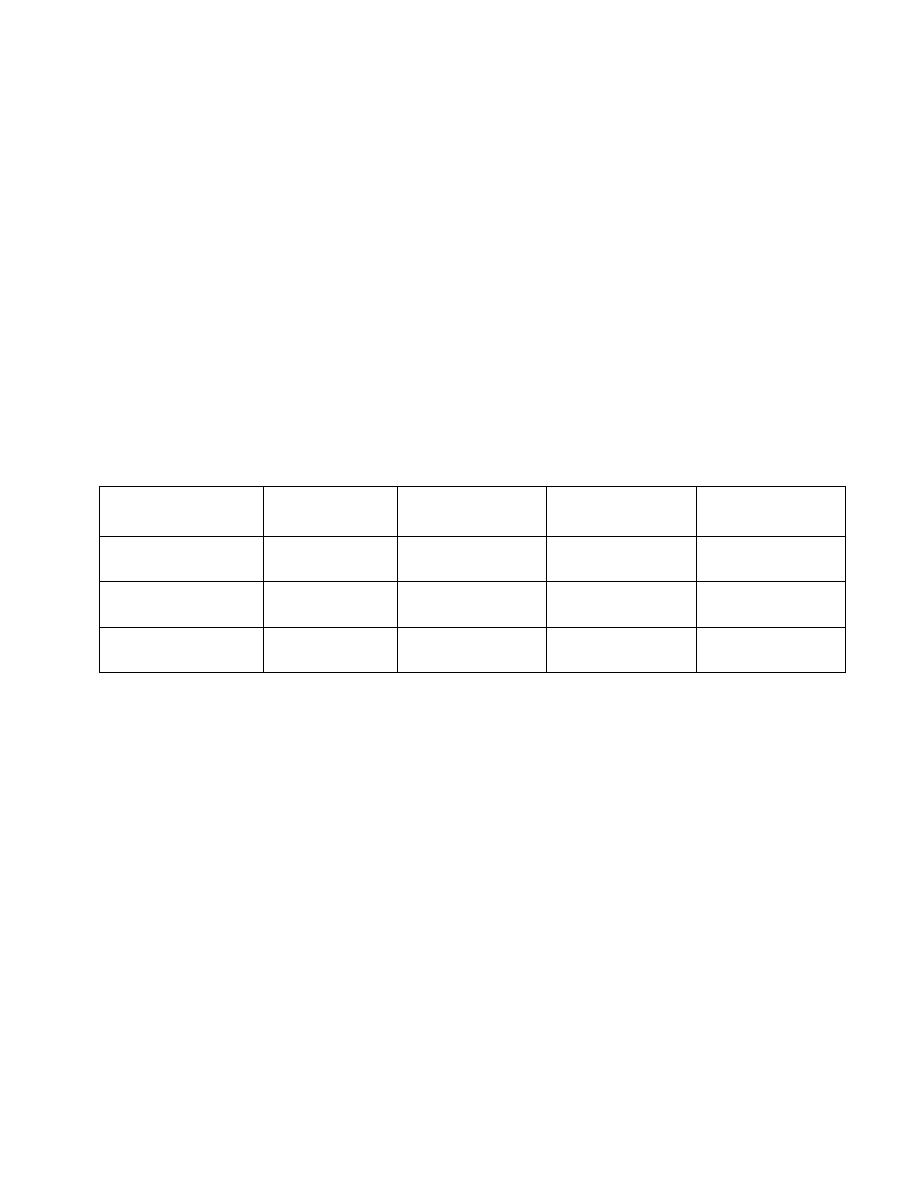
47
by fast T
2
(or T
1
) relaxation, leaving the antiphase signal not enough time to evolve into detectable
magnetization.
This phenomenon can also be explained in the frequency dimension: short acquisition times or fast
relaxation leads to broad lines, which results in mutual partial cancelation of the multiplet lines in
the case of an antiphase signal.
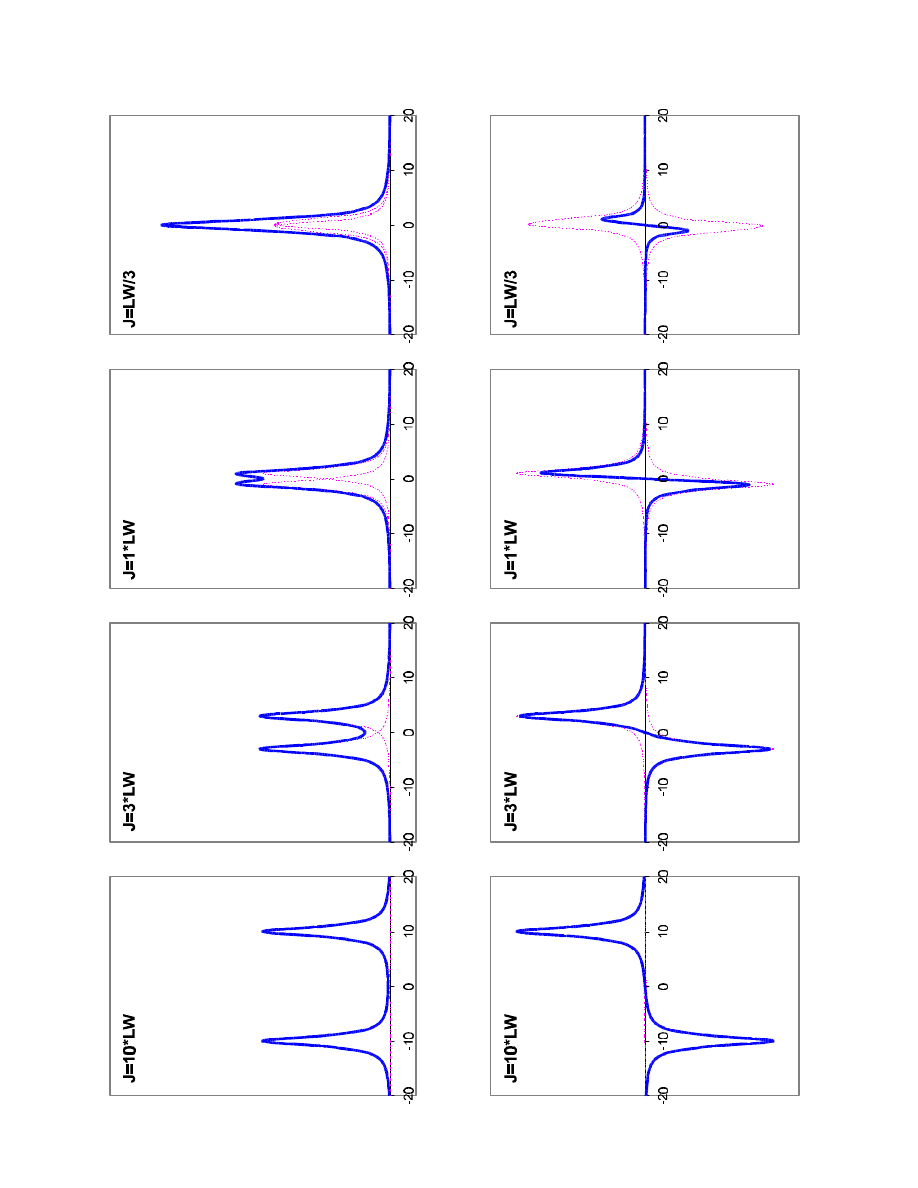
The simulation (next page) shows the dublet appearances for different ratios between coupling
constant J and linewidth (LW). The linewidths were set constant to 2 Hz (at half-height), so that the
different intensities of the dublet signal are only due to different J values.
Obviously, the apparent splitting in the spectrum can differ from the real coupling constant, if the
two dublet lines are not baseline separated: for in-phase dublets, the apparent splitting becomes
smaller, for antiphase dublets it is large than the true J value.
Ratio J/L:
10
3
1
1
/
3
True J value [Hz}
20.0
6.0
2.0
0.7
In-phase splitting
20.0
6.0
1.8
n/a
Antiphase splitting
20.0
6.0
2.2
1.3
In the basic COSY experiment the diagonal signals are in-phase and the cross-peaks antiphase, so
that signals with small J couplings and broad lines (due to short AQ or fast relaxation) will show
huge diagonal signals, but only very small or vanishing cross-peaks.
In the DQF-COSY, both types of signals stem from antiphase terms, so that both the cross- and
diagonal peak intensity depends on the size of the coupling constants.
48

49
Spins with more than one J coupling
For spins with several coupling partners, all couplings evolve simultaneously, but can be treated
sequentially with product operators (just as J coupling and chemical shift evolution).
J
12
J
13
I
1x
→
I
1x
cos(
π
J
12
t)
→
I
1x
cos(
π
J
12
t) cos(
π
J
13
t)
+ 2I
1y
I
3z
cos(
π
J
12
t) sin(
π
J
13
t)
+ 2I
1y
I
2z
sin(
π
J
12
t)
+ 2I
1y
I
2z
sin(
π
J
12
t)
cos(
π
J
13
t)
- 4I
1x
I
2z
I
3z
sin(
π
J
12
t) sin(
π
J
13
t)
The double antiphase term 4I
1y
I
2z
I
3z
develops straightforward from the I
1y
factor in 2I
1y
I
2z
,
according to the normal coupling evolution rules I
1y
→
− 2I
1x
I
3z
sin(
πJ
13
t).
When we consider the time evolution of the single antiphase terms required for coherence transfer,
such as 2I
1y
I
2z
sin(
πJ
12
t) cos(
π
J
13
t) and 2I
1y
I
3z
cos(
πJ
12
t) sin(
πJ
13
t) , we find that their
trigonometric factors (the transfer amplidute) always assume the general form
2I
1y
I
2z
sin(
πJ
12
t) cos(
π
J
13
t) cos(
π
J
14
t) cos(
π
J
15
t) …
with J
12
being called the active coupling (that is actually responsible for the cross-peak) and all other
the passive couplings.
When all J couplings are of the same size, then the maximum of these functions is not at t =
1
/
2
J
, but
at considerably shorter times, between ca.
1
/
6
J
and
1
/
4
J
(depending on the number of cosine factors
and relaxation).
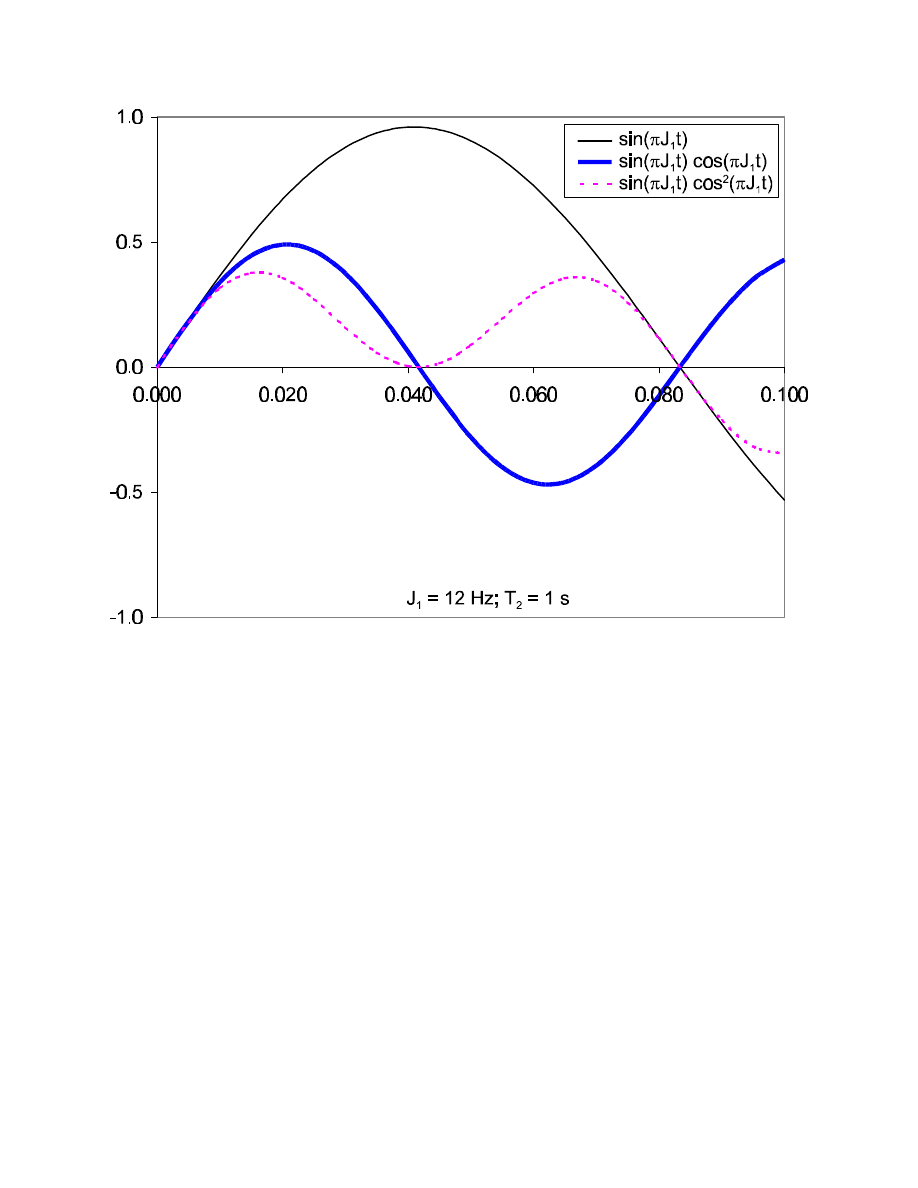
50
However, in real spin systems the size of J varies considerably, for
2, 3
J
HH
from ca. 1 Hz up to ca.
12 Hz (or even 16-18 Hz for
2
J and
3
J
trans
in olefins). The largest passive coupling determines when
the transfer function becomes zero again for the first time (e.g.,
1
/
2
J
= 35 ms for J = 14 Hz), and the
maximum of single antiphase coherence the occurs at or shortly before ca.
1
/
4
J
for this coupling
constant. With only one passive coupling constant and a very small active coupling, one could wait
till after the first zero passing to get more intensity. However, with a large number of passive
couplings of unknown size (as in most realistic cases), the only predictable maximum will occur at
20-30 Hz for most spin systems.
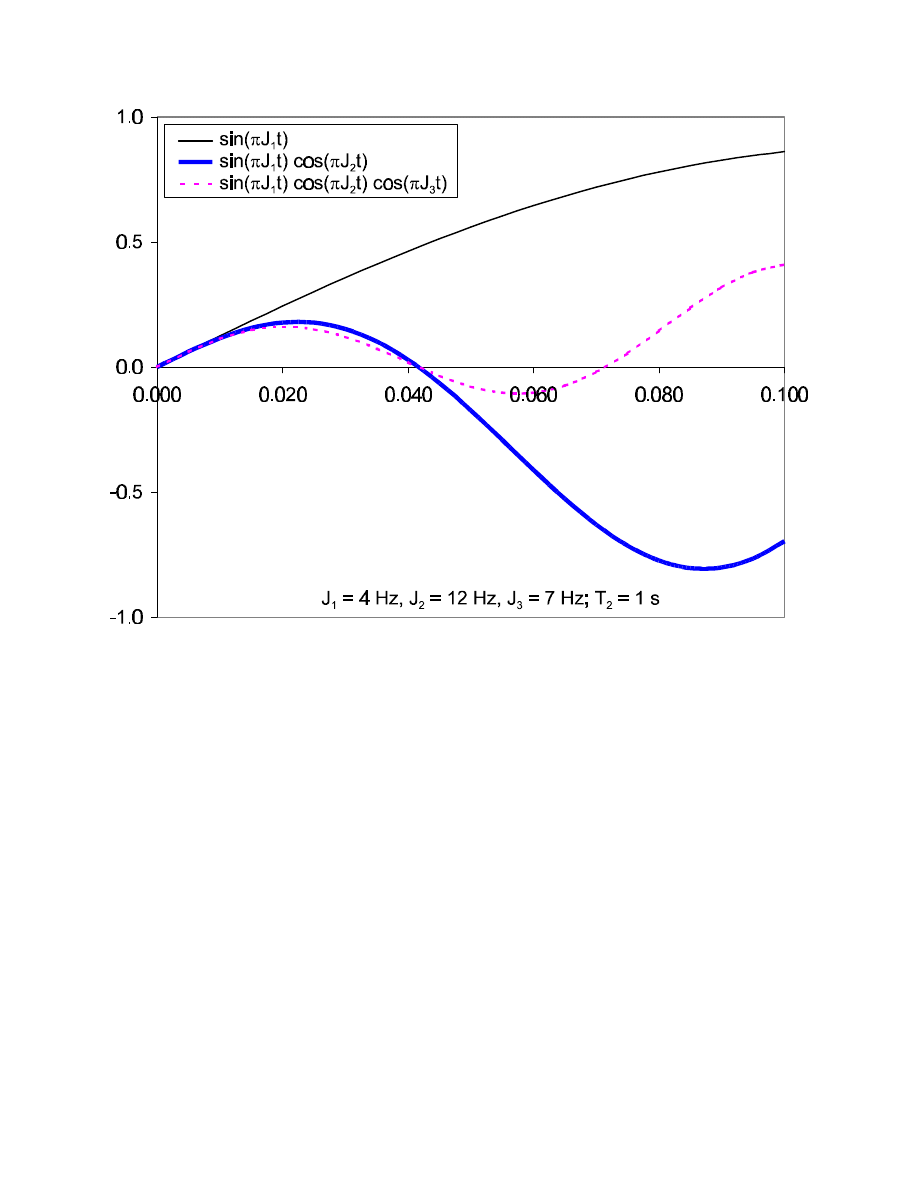
51
The same considerations as for the creation of 2I
1y
I
2z
terms out of in-phase magnetization apply to
the refocussing of these antiphase terms back to detectable in-phase coherence. In COSY
experiments, the single antiphase terms are generated during the t
1
time and (after coherence
transfer) refocus to in-phase during the acquisition time t
2
. Since both are direct and indirect
evolution times which are not set to a single value, but cover a whole range from t=0 up to the
chosen maximum values, the functions shown in the above diagrams will be sampled over this whole
range and always contain data points with good signal intensity (as well as some with zero intensity).
52
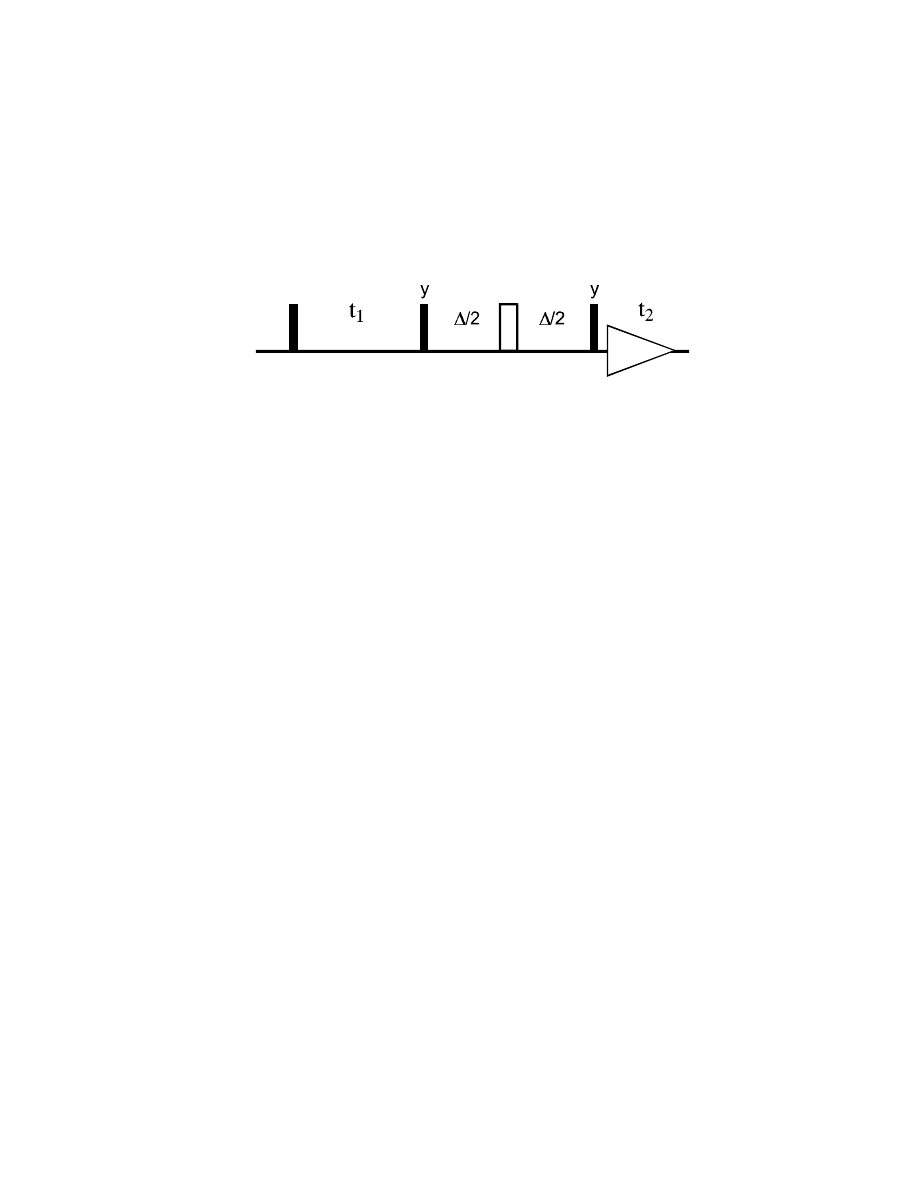
Relayed-COSY
The considerations about transfer functions become more important in experiments with fixed delay,
e.g., for coupling evolution. The simplest homonuclear experiment here is the Relayed-COSY, with
the following pulse sequence:
It allows to correlate the chemical shifts of spins that are connected by a common coupling partner,
as in the linear coupling network I
1
— I
2
— I
3
, with the coupling constants J
12 and
J
23
.
After the t
1
evolution period and the second 90° pulse we get (cf. COSY):
→ −
I
1z
cos(
Ω
1
t
1
) cos(
π
J
12
t
1
)
+ 2I
1y
I
2x
cos(
Ω
1
t
1
) sin(
π
J
12
t
1
)
+ I
1y
sin(
Ω
1
t
1
) cos(
π
J
12
t
1
)
+ 2I
1z
I
2x
sin(
Ω
1
t
1
) sin(
π
J
12
t
1
)
During the period
∆
, chemical shift evolution is refocussed (180° pulse in the center!), but J
12
coupling evolution continues:
J
12
→ −
I
1z
cos(
Ω
1
t
1
) cos(
π
J
12
t
1
)
(no coupling evolution, I
z
!)
+ 2I
1y
I
2x
cos(
Ω
1
t
1
) sin(
π
J
12
t
1
)
(no coupling evolution, MQC!)
+ I
1y
sin(
Ω
1
t
1
) cos(
π
J
12
t
1
) cos(
π
J
12
∆
)
−
2I
1x
I
2z
sin(
Ω
1
t
1
) cos(
π
J
12
t
1
) sin(
π
J
12
∆
)
(evolution of antiphase)
+ 2I
1z
I
2x
sin(
Ω
1
t
1
) sin(
π
J
12
t
1
) cos(
π
J
12
∆
)
+ I
2y
sin(
Ω
1
t
1
) sin(
π
J
12
t
1
) sin(
π
J
12
∆
)
(refocusing to in-phase)

53
The last two terms, however, are spin 2 coherence, and spin 2 has two couplings, J
12
(which we have
just considered) and J
23
, the effect of which we have to calculate now. Just as with chemical shift
and coupling, which evolve simultaneously, but can be calculated sequentially, we can here calculate
the effects of J
12
and J
23
one after the other (the order doesn't matter).
J
23
→ −
I
1z
cos(
Ω
1
t
1
) cos(
π
J
12
t
1
)
(not affected by J
23
)
−
2I
1y
I
2x
cos(
Ω
1
t
1
) sin(
π
J
12
t
1
) cos(
ππ
J
23
∆∆
)
−
2I
1y
I
2y
I
3z
cos(
Ω
1
t
1
) sin(
π
J
12
t
1
) sin(
ππ
J
23
∆∆
)
+ I
1y
sin(
Ω
1
t
1
) cos(
π
J
12
t
1
) cos(
π
J
12
∆
)
(not affected by J
23
)
−
2I
1x
I
2z
sin(
Ω
1
t
1
) cos(
π
J
12
t
1
) sin(
π
J
12
∆
)
(not affected by J
23
)
+ 2I
1z
I
2x
sin(
Ω
1
t
1
) sin(
π
J
12
t
1
) cos(
π
J
12
∆
) cos(
ππ
J
23
∆∆
)
+ 4I
1z
I
2y
I
3z
sin(
Ω
1
t
1
) sin(
π
J
12
t
1
) cos(
π
J
12
∆
) sin(
ππ
J
23
∆∆
)
+ I
2y
sin(
Ω
1
t
1
) sin(
π
J
12
t
1
) sin(
π
J
12
∆
) cos(
ππ
J
23
∆∆
)
−
2I
2x
I
3z
sin(
Ω
1
t
1
) sin(
π
J
12
t
1
) sin(
π
J
12
∆
) sin(
ππ
J
23
∆∆
)
From the evolution of the second coupling, J
23
, we get a double antiphase term 4I
1z
I
2y
I
3z
(J
23
does not refocus the original 2I
1z
I
2x
antiphase of spin 2 relativ to spin 1!) and another term 2I
2x
I
3z
,
which is spin 2 antiphase coherence with respect to spin 3.
The third 90° pulse has to be performed with the same phase setting as the second (i.e., either both
from x or both from y)! After this 90° pulse, we get the folowing terms at the beginning of t
2
:
90°
y
→ −
I
1x
cos(
Ω
1
t
1
) cos(
π
J
12
t
1
)
spin 1 in-phase
−
2I
1y
I
2z
cos(
Ω
1
t
1
) sin(
π
J
12
t
1
) cos(
π
J
23
∆
)
spin 1 antiphase
−
2I
1y
I
2y
I
3x
cos(
Ω
1
t
1
) sin(
π
J
12
t
1
) sin(
π
J
23
∆
)
MQC
+ I
1y
sin(
Ω
1
t
1
) cos(
π
J
12
t
1
) cos(
π
J
12
∆
)
spin 1 in-phase
+
2I
1z
I
2x
sin(
Ω
1
t
1
) cos(
π
J
12
t
1
) sin(
π
J
12
∆
)
spin 2 antiphase
54
−
2I
1x
I
2z
sin(
Ω
1
t
1
) sin(
π
J
12
t
1
) cos(
π
J
12
∆
) cos(
π
J
23
∆
)
spin 1 antiphase
+ 4I
1x
I
2y
I
3x
sin(
Ω
1
t
1
) sin(
π
J
12
t
1
) cos(
π
J
12
∆
) sin(
π
J
23
∆
)
MQC
+ I
2y
sin(
Ω
1
t
1
) sin(
π
J
12
t
1
) sin(
π
J
12
∆
) cos(
π
J
23
∆
)
spin 2 in-phase
++
2I
2z
I
3x
sin(
Ω
Ω
1
t
1
) sin(
ππ
J
12
t
1
) sin(
ππ
J
12
∆∆
) sin(
ππ
J
23
∆∆
)
spin 3 antiphase
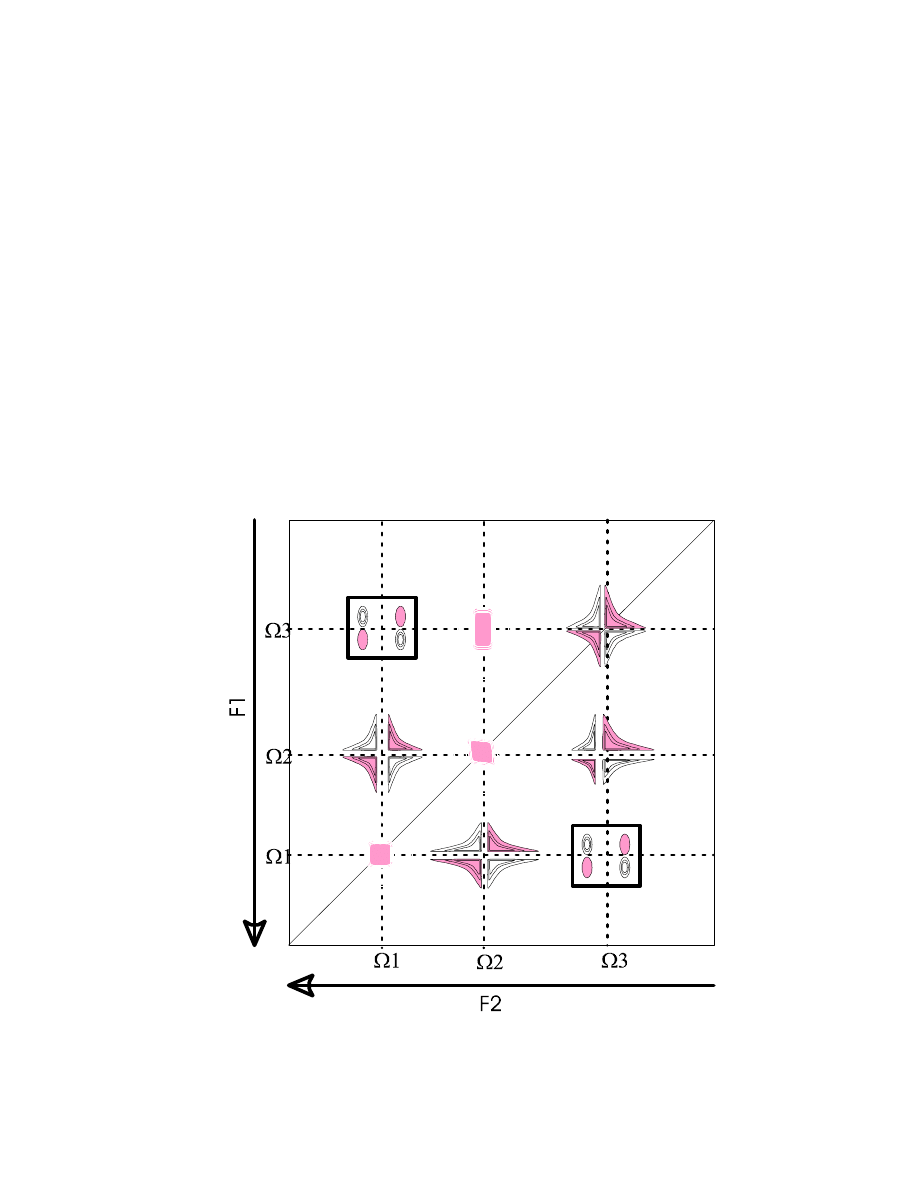
From the observable terms during t
2
now, we get three types of peaks, all labeled with
Ω
1
in F1:
- diagonal peaks at
Ω
1
in F2 (mixture of terms with different phases)
- COSY peaks at
Ω
2
in F2 (mixture of terms with different phases)
- Relayed peaks at
Ω
Ω
3
in F2 (pure antiphase in both dimensions)
Relayed-COSY spectrum, only the Relayed peaks (in boxes) show pure (anti-) phase behaviour
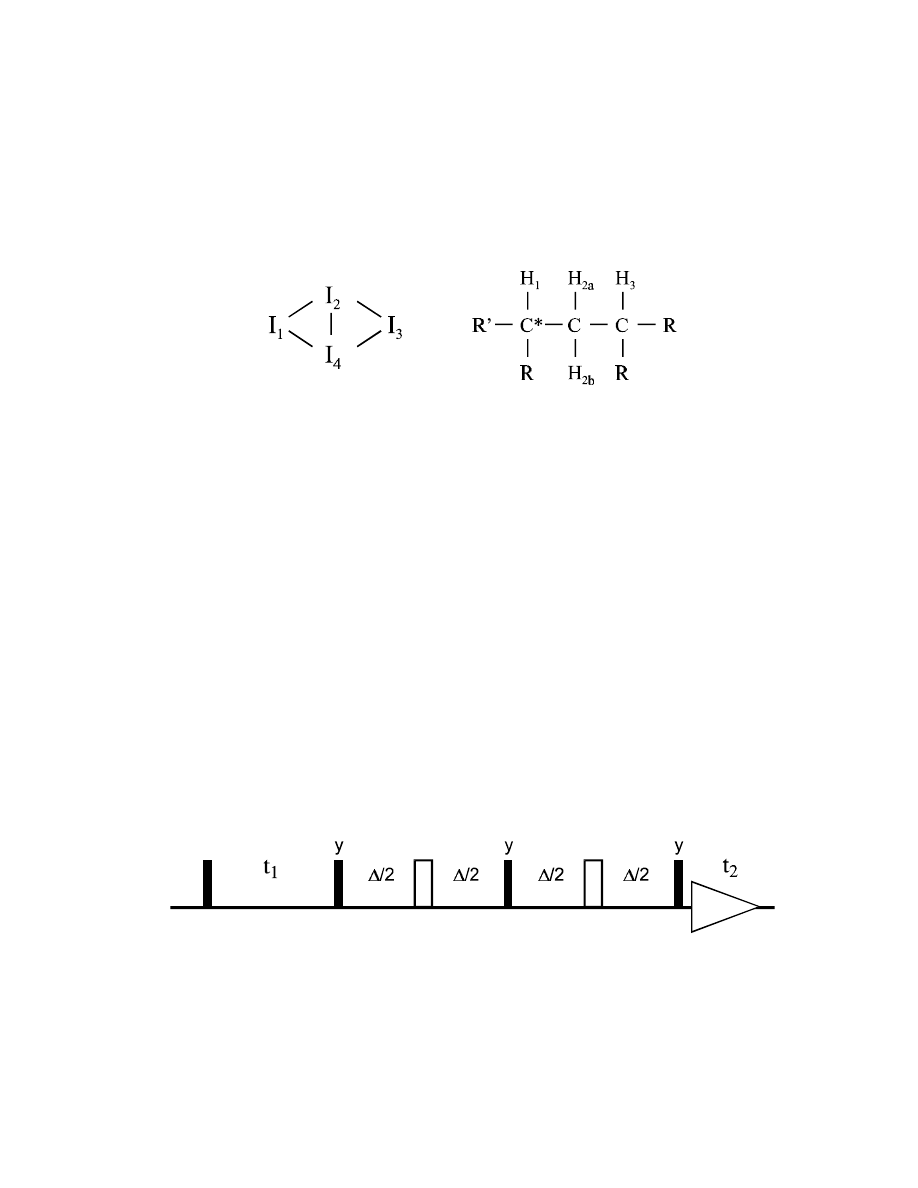
55
For the interesting Relayed peak, the transfer amplitude part from the fixed delay
∆
is
sin(
πJ
12
∆) sin(πJ
23
∆) , which would be at a maximum for
∆
=
1
/
2
J
(for J
12
= J
23
).
However, if there are more couplings to the relais spin 2, e.g., in a spin system topology
then the transfer function, for going from 2I
1z
I
2x
at the beginning of
∆
to – 2I
2x
I
3z
at its end
(and 2I
2z
I
3x
after the final 90° pulse) would be
sin(
πJ
12
∆) sin(πJ
23
∆) cos(πJ
24
∆)
and, because of the cosine factor, it would be zero at
1
/
(2J
24
)
. Therefore, the delay
∆
should be set to
no more than 20-30 ms to avoid losing some Relayed peaks due to large passive couplings.
The Relayed-COSY can be easily extended to a Double-Relayed-COSY experiment, just by adding
another delay
∆
and another 90° pulse, to perform transfers I
1
→
I
2
→
I
3
→
I
4
:
However, like in the simple Relayed-COSY, the phases of most of the peaks cannot be corrected to
pure absorption, and the sensitivity decreases further, due to the inefficient transfers and the
increasing length of the pulse sequence. Today, the Relayed experiments have been widely replaced
by the TOCSY experiment.
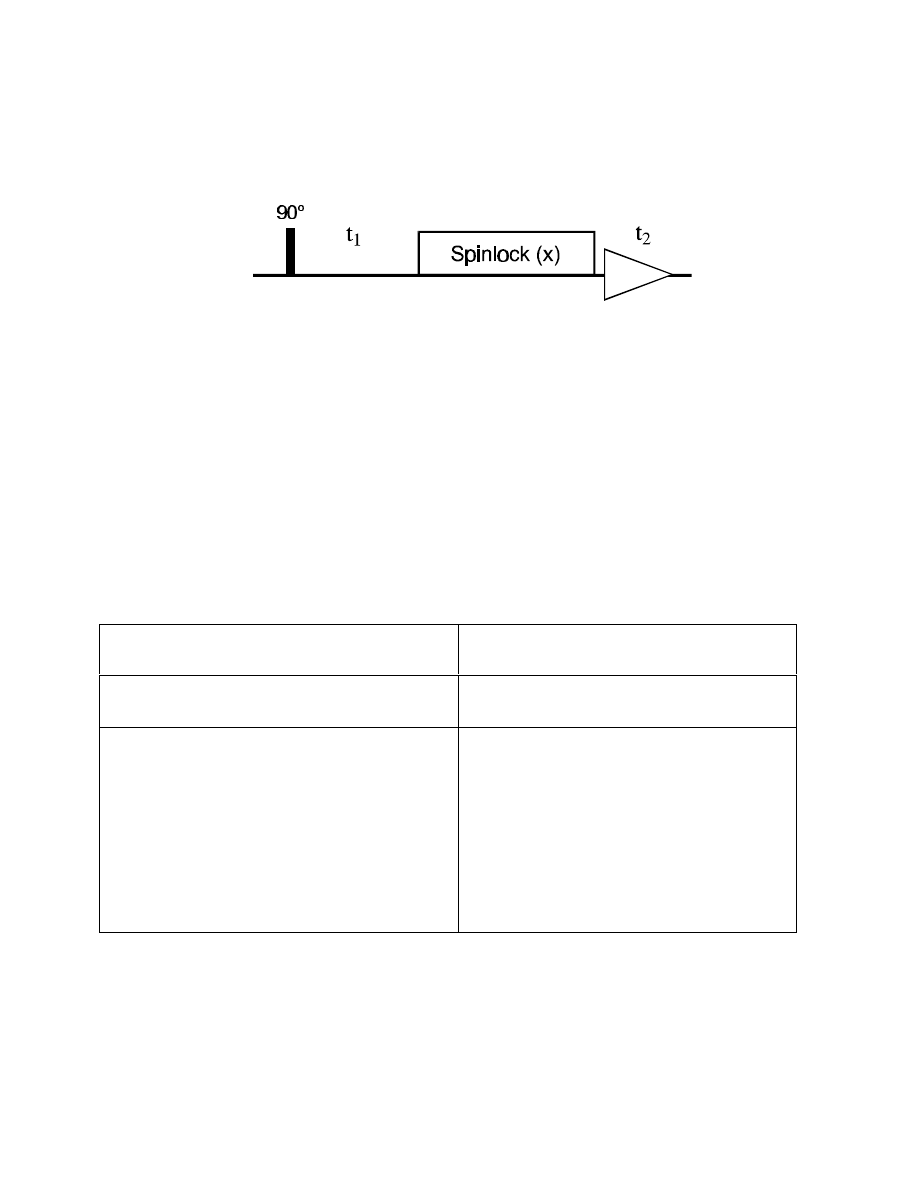
56
TOCSY / HOHAHA
The TOCSY / HOHAHA experiment does also create a multi-transfer step
1
H,
1
H correlation:
It starts like any other 2D experiment so far, with a 90° pulse creating transverse magnetization
(coherence) which then evolves during an incremented t
1
period to yield the indirect F1 dimension
after 2D FT. Between the two evolution times t
1
and t
2
for the two
1
H dimensions, a mixing step has
to perform the coherence transfer. While this is done with simple 90° pulses in all COSY type
experiments, the TOCSY has a "black box" spinlock period instead.
What happens during this time cannot really be understood in terms of vector models or even the
product operators, because it relies on strong coupling. The term strong coupling applies to J
coupled systems where the coupling actually dominates the spectrum:
weak coupling
strong coupling
J <<
∆
Ω
J >>
∆
Ω
all signals occur at their proper individual
chemical shift frequencies (dominating effect),
but are split into multiplets with equally
intense lines (small perturbation from J
coupling)
J coupling no more "minor disturbance", but
dominating: coherences of spins are
"coupled" together; instead of individual
resonance frequencies of individual spins,
combination lines occur which cannot be
assigned to just a single spin anymore
Under strong coupling conditions, chemical shift differences between different spins become
negligible, and in the energy level diagram for a two spin system the two states
αβ
and
βα
become
identical in energy. Instead of transitions of single spins, the coherences now involve transitions of
combinations of spins:
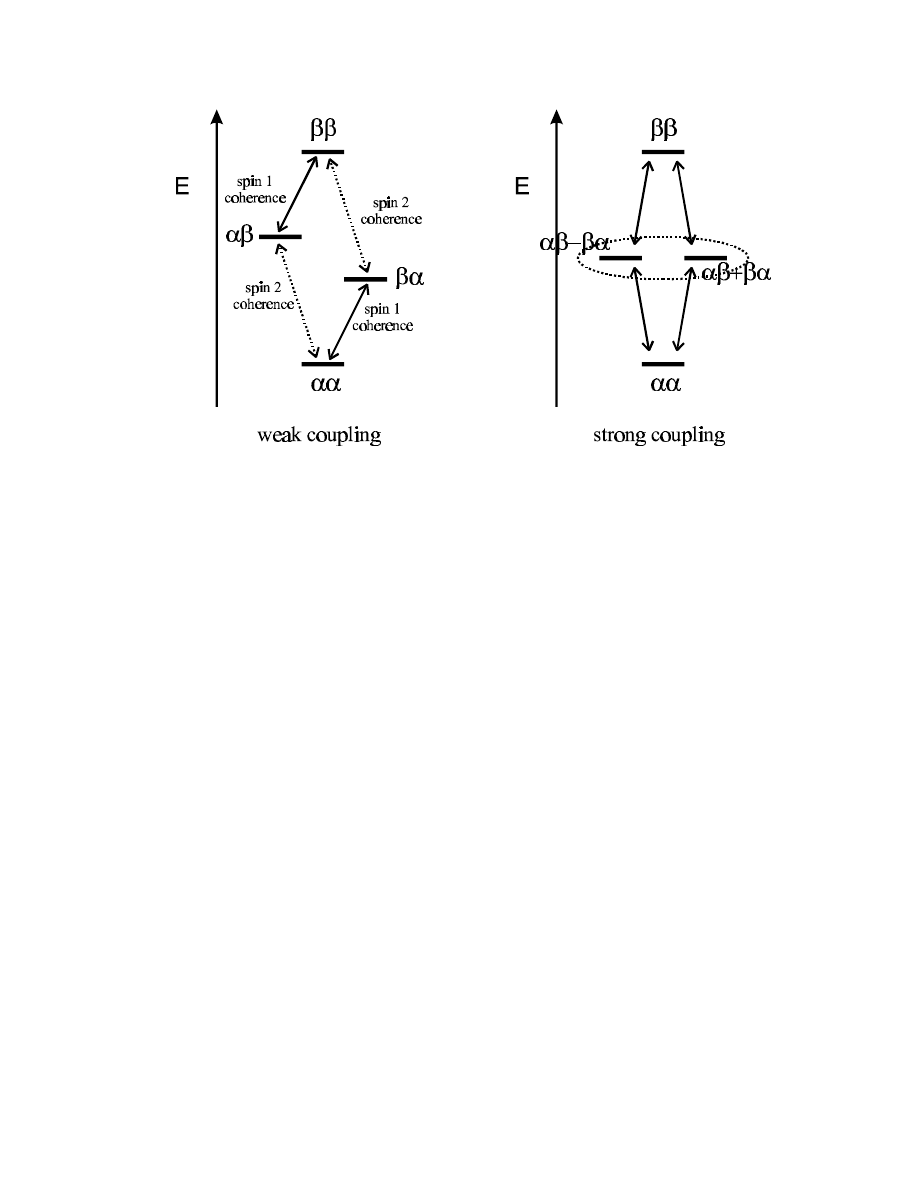
57
Under these conditions, a coherence / transition of one spin is actually in resonance with a coherence
of its coupling partner(s) (all with the same frequency / chemical shift), and will oscillate back and
forth between all coupled spins, like two (or more) coupled resonant oscillators (e.g., pendulums).
For a two-spin system, the evolution of strong coupling can be described as follows:
strong J
I
1x
→
0.5 I
1x
{1 + cos(2
π
J
12
τ
)}
+
0.5 I
2x
{1 – cos(2
π
J
12
τ
)}
+
(I
1y
I
2z
– I
1z
I
2y
) sin(2
π
J
12
τ
)
So during the TOCSY spinlock, in-phase coherence of a spin is transferred directly into in-phase
coherence of its coupling partner, and back, in an oscillatory way. The frequency of this oscillation
is directly proportional to the coupling constant between the two spins, and complete transfer occurs
(for the first time) at t =
1
/
2J
(see following diagramm).
As shown, another oscillatory component consists of "zero-quantum coherence" with respect to the
spinlock axis, of the form (I
1y
I
2z
– I
1z
I
2y
) , i.e., dispersive antiphase coherence of spins 1 and 2.
This term is the reason for the (usually rather small) dispersive contributions to the mainly in-phase
absorptive TOCSY cross-peaks.
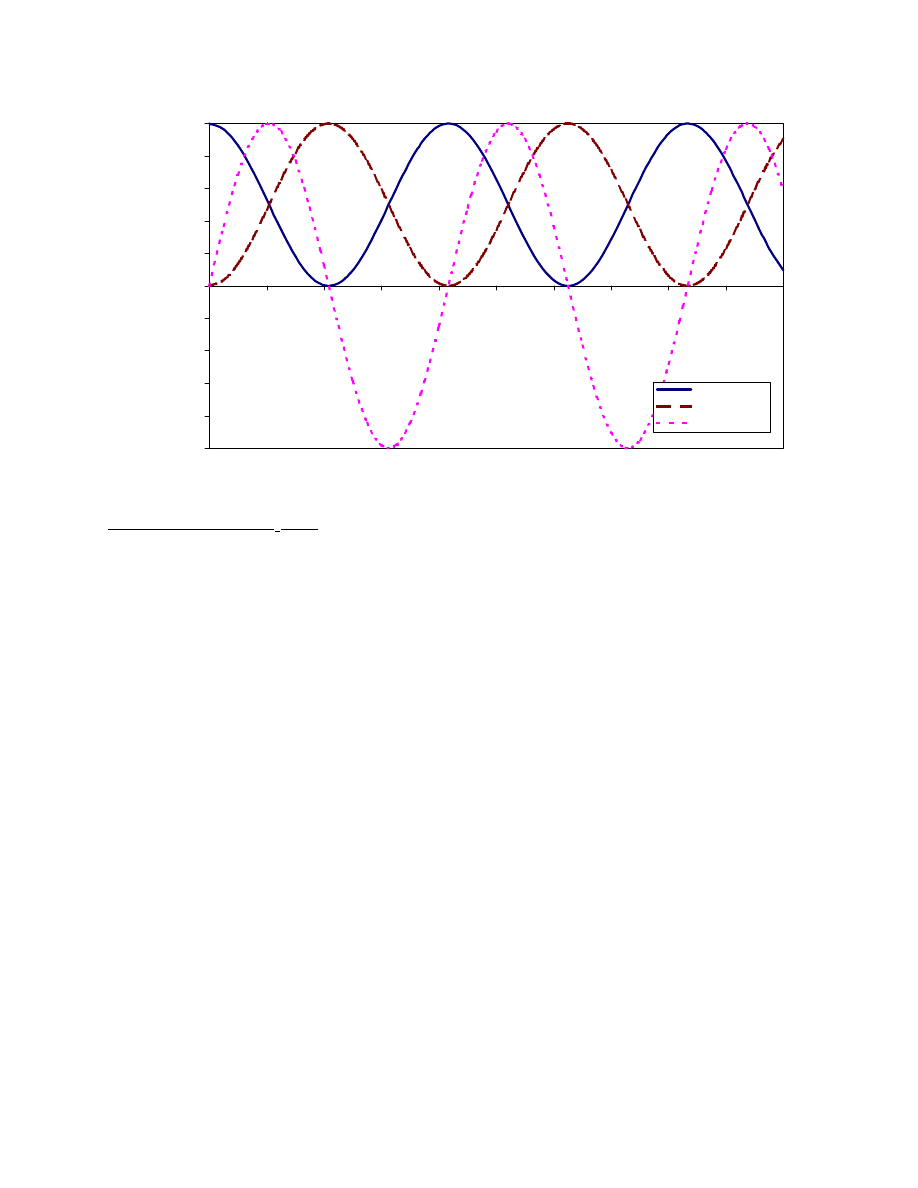
58
-1,00
-0,80
-0,60
-0,40
-0,20
0,00
0,20
0,40
0,60
0,80
1,00
0
20
40
60
80
100
120
140
160
180
200
t [ms]
Intensity
I1x
I2x
I1yI2z – I1zI2y
Locking spins with a B
1
field
The spinlock needed for converting a weakly coupled into a strongly coupled spin system consists
essentially of a continuing r.f. irradiation, e.g., in the x direction. Its field strength has to be much
stronger than the z component corresponding to the chemical shifts of the spins. These chemical
shifts usually cover a range of a few kHz (= precession frequency of the spins relativ to the
transmitter / receiver reference frequency). If the r.f. field strength is higher, then B
1
will dominate
and the spins will start to precess about the B
1
(i.e., x ) axis instead of the z axis: the magnetization
components aligned along the x axis (i.e., I
x
) are frozen / spinlocked there, and no more chemical
shift evolution occurs in the xy plane. With all chemical shifts reduced to zero, their differences also
vanish, and the strong coupling condition J >>
∆
Ω
is fulfilled.
In praxi, the high power transmitters (ca. 50 W for
1
H, ca. 200 W for heteronuclei) can usually
generate field strengths of ca. 20-40 kHz, but only for a few hundred microseconds. Then the
spectrometer usually turns itself of automatically (thankfully), to prevent damage to the amplifiers or
the transmitting coils in the probe. Instead of just turning the transmitter on (CW mode), TOCSY
spinlocks are therefore performed with composite pulse trains, consisting of a repetitive series of
pulses with defined pulse lengths and phases. These spinlock sequences allow to effectively spinlock
spins within a wide range of chemical shifts, with reasonable transmitter powers of a few kHz. Some
often used sequences are, e.g., MLEV-17, WALTZ16, DIPSI-2.
59
There are two different classes of spinlocks: isotropic and anisotropic. Isotropic spinlocks (like
WALTZ or MLEV16) allow transfer of all magnetization components:
I
1x
→
→
I
2x
/
I
1y
→
→
I
2y
/ I
1z
→
→
I
2z
At the end of the t
1
period in the TOCSY experiment, however, there are absorptive and dispersive
magnetization components (as a result of chemical shift and J coupling evolution, cf. COSY). All
these contribute to the TOCSY crosspeaks in the case of an isotropic spinlock, creating large
dispersive contributions.
Therefore, nowadays usually only anisotropic spinlock sequences are employed for TOCSY
experiments (MLEV-17, DIPSI), which can transfer only one transverse component (e.g., I
x
) and the
z component:
I
1x
→
→
I
2x
/
I
1y
////
→
→
I
2y
/ I
1z
→
→
I
2z
This anisotropic TOCSY version was initially named the homonuclear H
ARTMANN
-H
AHN
experiment,
HOHAHA (today the terms TOCSY and HOHAHA are mostly used as synonyms). It leads to almost
absorptive cross-peaks (at least in the 2D plots, as long as one does not look at rows or columns, or a
1D TOCSY spectrum).
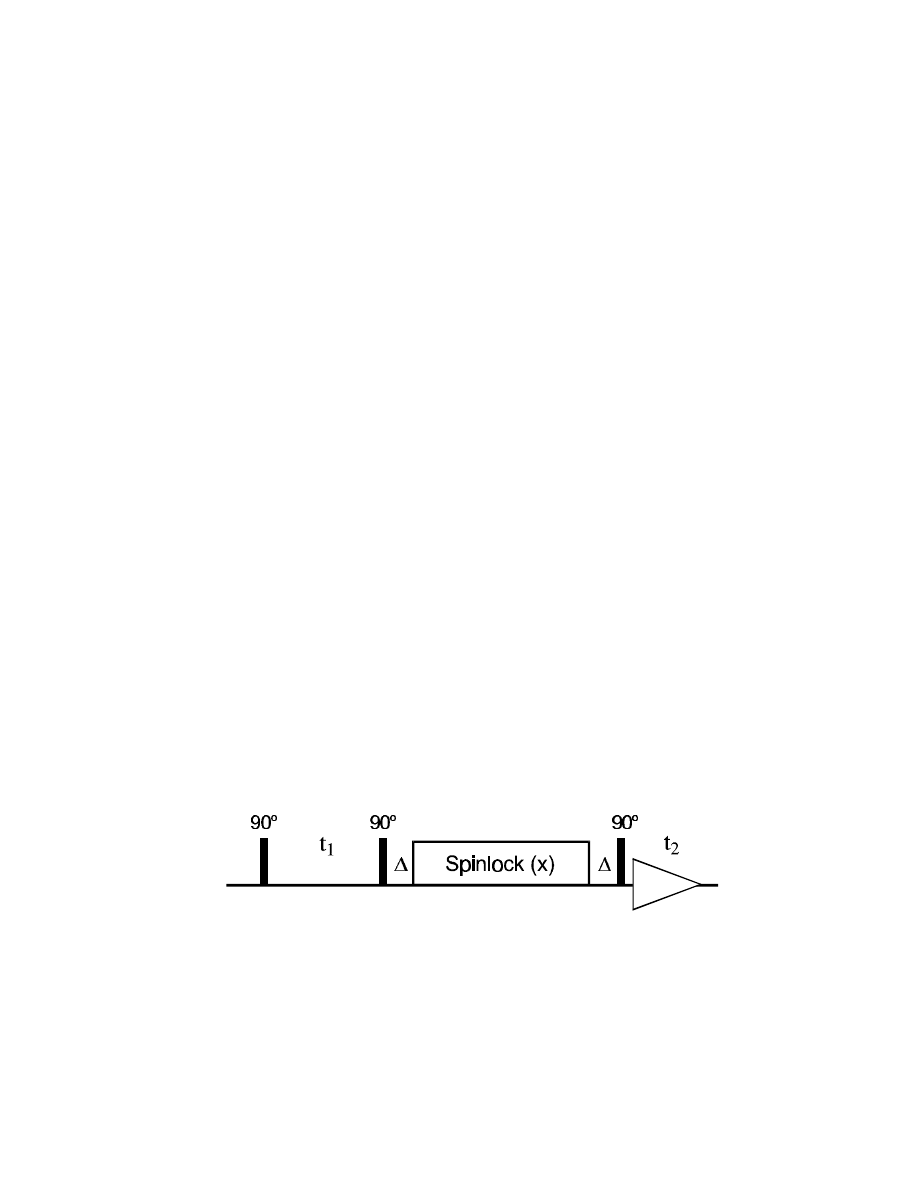
For really pure absorptive phases, a z-filtered TOCSY has to be performed:
Here, all magnetization components except for I
z
are destroyed during the
∆
delays. This can be
achieved in different ways:
- by waiting. For larger molecules with T
1
>> T
2
, the z components will relax only slowly (with
T
1
), while all transverse components will decay fast (with T
2
).

60
- since the difference between T
1
and T
2
is usually not large enough for good suppression, the
effect can be enhanced by greatly increasing the B
0
field inhomogeneities for a short time during
∆
. This is done either with homospoil pulses (i.e., DC pulses on the z shim coils) or – with much
better performance – with pulsed field gradients (PFGs) from specifically designed z gradient
coils directly in the NMR probe.
- in additon, one can also vary the
∆
delays and then add scans acquired with different delay
lengths. This does not affect the z components, but all transverse magnetization terms will evolve
chemical shifts during
∆
. With many different
∆
settings, their positions will be always at
different positions somewhere in the xy plane and cancel after coaddition. This requires,
however, a large enough variation of
∆
(at least over 10-20 ms), so that even the slowly rotating
zero-quantum coherences can go around at least once (they evolve only with the difference of the
chemical shifts of the two coupling protons). Also the coaddition of as many different
∆
settings
as possible (at least 6-8) is needed for good cancelation, thus increasing the minimum
experiment time considerably, since the
∆
variation has to be done on top of the phase cycling.
The additional 90° pulses at the end of t
1
and beginning of t
2
are needed to convert transverse
components into I
z
and then back to detectable magnetization again:
90°
SL
90°
→ →
I
1x
cos
Ω
1
t
1
→
I
1z
cos
Ω
1
t
1
→
I
2z
cos
Ω
1
t
1
→
I
2x
cos
Ω
1
t
1
Since all other magnetization components containing any transverse terms are quickly dephased
during the
∆
periods, the resulting spectrum shows pure in-phase absorptive lineshapes, for both the
cross-peaks and diagonal peaks.
Τ
1ρ
Relaxation
During the spinlock period, relaxation occurs according to a different mechanism, with a time
constant T
1
ρ
which is neither T
1
nor T
2
, but somewhere in between. This means that in cases with
T
2
>> T
1
(slow tumbling limit) T
1
ρ
is longer than T
2
(which is active, e.g., during the Relayed-
COSY mixing sequence). Due to this and the in-phase nature of its cross-peaks, TOCSY can still be
used for molecules up to ca. 10-20 kDa.
Wyszukiwarka
Podobne podstrony:
cosy cottage
Sciągi, sin, sin(x+y)= sinx cosy+siny cosx
Inne materiały, mat-funkcje trygonometryczne2, sn(x+y)=sinx cosy + cosx siny
więcej podobnych podstron