T1 

Techniki Obliczeniowe i Symulacyjne
Interpolacja, estymacja średniokwadratowa, optymalizacja 

dr inż. Tomasz Zieliński 

2010.03.01

 

Ćwiczenie 1 (1 pkt) 

Interpolacja. W poniższej tabeli przedstawiono wyniki pomiaru temperatury (N=4): 

LP 

1 2 3 4 

Godzina x

1

=5:00

x

2

=6:00

x

3

=8:00

x

4

=11:00 

Temperatura [

o

C] y

1

=1 y

2

=2 y

3

=7 y

4

=15 

Załóżmy, że wielomian interpolujący funkcję z tablicy ma postać: 

( )

1

0

1

1

N

N

y x

a

a x

a

x

−

−

=

+

+K

                                                 (1) 

Dla N punktów pomiarowych mamy N równań: 

( )

,

1,

,

i

i

y x

y

i

N

=

= K

 

które możemy zapisać razem w postaci macierzowej: 

1

1

1

1

1

1

2

2

2

1

1

0

1

1

1

N

N

N

N

N

N

N

a

y

x

x

y

x

x

a

a

y

x

x

−

−

−

−

⎡

⎤ ⎡

⎤ ⎡

⎤

⎢

⎥ ⎢

⎥ ⎢

⎥

⎢

⎥ ⎢

⎥ ⎢

⎥

=

⎢

⎥ ⎢

⎥ ⎢

⎥

⎢

⎥ ⎢

⎥ ⎢

⎥

⎣

⎦ ⎣

⎦

⎣

⎦

T

L

M

L

M

M

M

L M

L

14442444

3

                                              (2) 

Rozwiąż równanie (2) jedną z metod z Lab2 (czyli oblicz a), a następnie skorzystaj z (1) aby obliczyć 
poszukiwaną temperaturę yz dla interesującej nas godziny xz=9:30. Zwróć uwagę, że układ równań (2) 
jest źle uwarunkowany dla dużego N. Macierz T jest macierzą Vandermonde’a: 

T=vander(x); a=inv(T)*y; yz=polyval(a,xz); 

yz=vander([xz zeros(1,N-1)])*a; yz=((xz*ones(1,N)).^(N:-1:0))*a; 

Ćwiczenie 2 (2 pkt) 

Interpolacja - wielomiany interpolujące Lagrange’a i Newtona. Wyznacz analitycznie jaka była 
najbardziej prawdopodobna temperatura o godzinie 9:30 jeśli zastosujemy metodę interpolacji 

Lagrange’a oraz Newtona (sprawdź dla obu metod). Napisz ogólny program dla obu metod interpolacji, 
zakładając, że danych jest N punktów pomiarowych (x

k

, y

k

) oraz interesuje nas przybliżona wartość dla 

x

 zadanego: 

1

zadane

N

x

x

x

≤

≤

. Porównaj otrzymane wyniki z wynikiem uzyskanym w ćw. 1. 

Ćwiczenie 3 (1 pkt) 

Estymacja. Załóżmy, że mamy dyskretny układ liniowy, którego dane wyjściowe 

y

n

 są wynikiem splotu 

danych wejściowych 

x

n

 

z próbkami odpowiedzi impulsowej układu 

h

n

 (w naszym przypadku tylko dwóch, 

h

0

 i 

h

1

), do którego dodaje się szum układu (kanału transmisyjnego): 

1

0

1

1

1

0

1

1

2

1

1

1

0

0

1

0

2

0

2

2

1

2

2

2

2

1

1

2

1

3

1

3

3

2

3

3

3

2

4

4

4

3

,

,

,

x

x

y

s

x

x

y

s

x

x

y

x

x

h

s

h

y

h

s

x

x

y

s

y

x

x

h

s

h

y

h

s

x

x

y

s

x

x

y

s

x

x

⎡

⎤

⎡ ⎤

⎡ ⎤

⎡

⎤

⎡ ⎤

⎡ ⎤

⎢

⎥

⎢ ⎥

⎢ ⎥

⎡ ⎤ ⎡

⎤ ⎡ ⎤ ⎡ ⎤

⎡ ⎤

⎡ ⎤

⎢

⎥

⎢ ⎥

⎢ ⎥

⎢

⎥

⎢ ⎥

⎢ ⎥

=

+

=

+

=

+

⋅

⎢ ⎥ ⎢

⎥ ⎢ ⎥ ⎢ ⎥

⎢ ⎥

⎢ ⎥

⎢

⎥

⎢ ⎥

⎢ ⎥

⎢

⎥

⎢ ⎥

⎢ ⎥

⎣ ⎦ ⎣

⎦ ⎣ ⎦ ⎣ ⎦

⎣ ⎦

⎣ ⎦

⎢

⎥

⎢ ⎥

⎢ ⎥

⎢

⎥

⎢ ⎥

⎢ ⎥

⎣ ⎦

⎣ ⎦

⎣

⎦

⎣ ⎦

⎣ ⎦

⎣

⎦

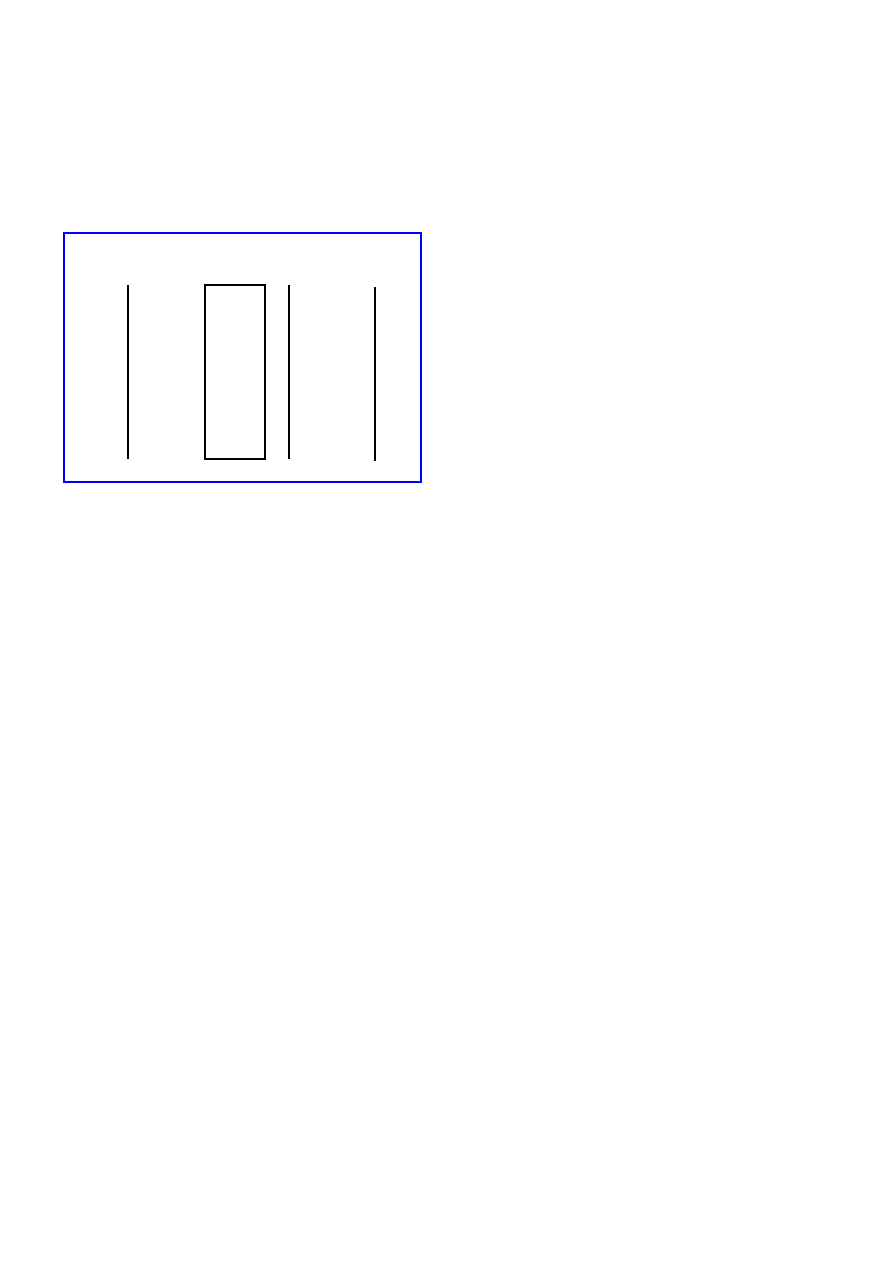
y = X h

+ s

 

(3) 

Znamy macierz 

X

 (dane wejściowe) i wektor 

y

 (dane wyjściowe). Chcemy znaleźć 

h

, dla którego 

wartość  błąd=

(

) (

)

min

T

T

=

=

s s

y - Xh

y - Xh

. Obliczamy pochodną błędu względem 

h

 i przyrównujemy 

ją do zera. Z tego równania wyznaczamy optymalną wartość 

h

. 

2 

3 

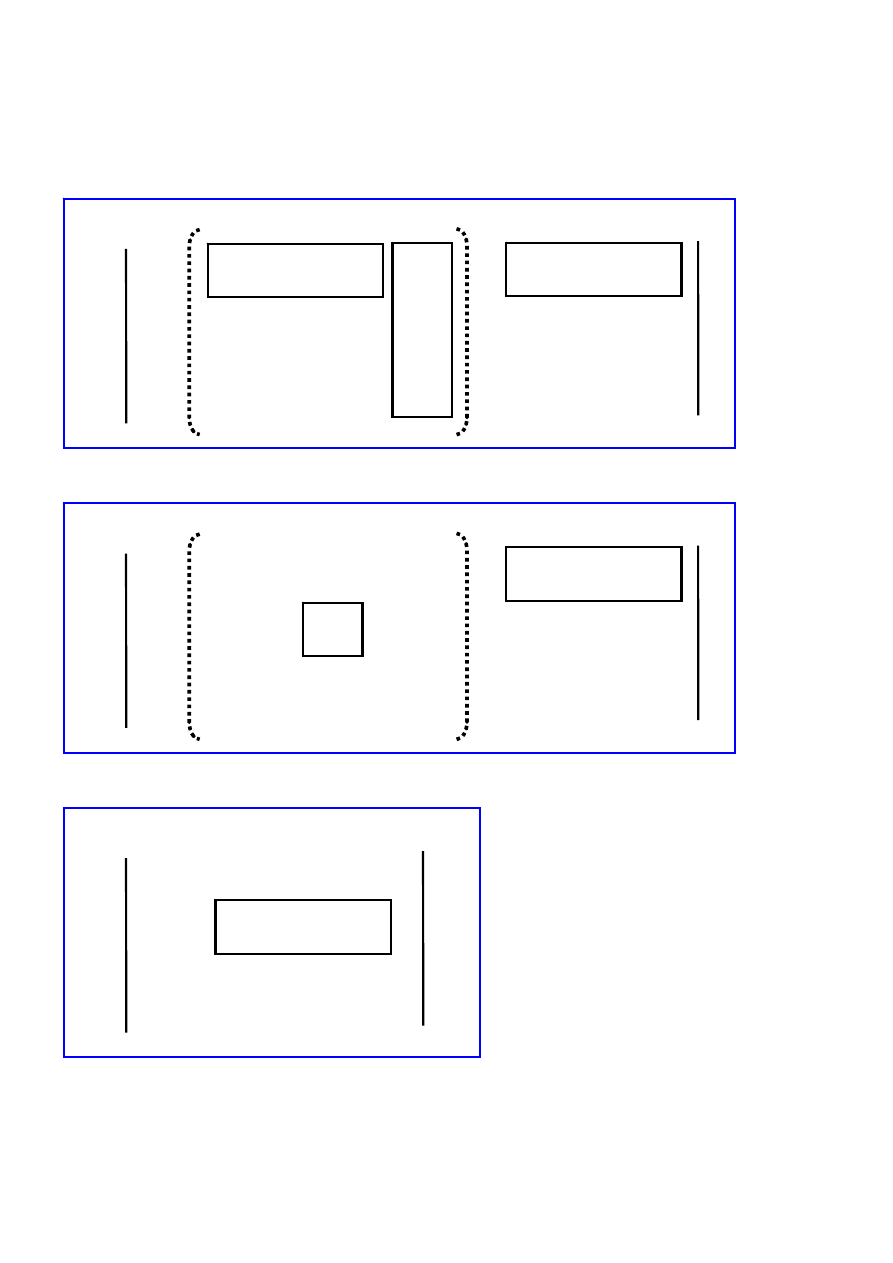
Minimum błędu kwadratowego otrzymujemy dla: 

(

)

T

T

est

-1

h

= X X

X y

                                                            (4) 

Macierz 

(

)

T

-1

X X

X

jest macierzą pseudo-odwrotną macierzy X. Ponieważ wektor 

h

 składa się z 2 liczb, 

najmniejsze wymiary macierzy 

X

 to 2×2 (układ dwóch równań z dwoma niewiadomymi). Im więcej 

przeprowadzamy pomiarów, tym macierz 

X

 ma więcej wierszy, jej macierz pseudo-odwrotna ma więcej 

kolumn i rozwiązanie 

h

est

 jest dokładniejsze. 

Przyjmij: 

M=2; h =(M:-1:1)’; 

a potem N równe kolejno 2, 3, 4, …25. Dla każdej wartości 

N

 podstaw: 

s=randn(N,1); x=rand(N+(M-1),1);

 

zbuduj macierz 

X

 i rozwiąż równanie (4). Narysuj jak się zmieniały elementy wektora 

h

est

 kiedy liczba 

punktów pomiarowych rosła. Powtórz eksperyment dla M=4. 
 

Ćwiczenie 4 (0.5 pkt) 

Zauważ, że równanie interpolacji (2) może być także przedstawione jako zadanie estymacji 
(aproksymacji) średniokwadratowej, jeśli założymy że zmierzone wartości 

y

 są zaszumione przez szum 

s

: 

1

1

1

1

1

1

1

2

2

2

2

1

1

0

1

1

1

N

N

N

N

N

N

N

N

y

a

s

x

x

y

s

x

x

a

y

a

s

x

x

−

−

−

−

⎡

⎤

⎡

⎤

⎡

⎤ ⎡ ⎤

⎢

⎥

⎢

⎥

⎢

⎥ ⎢ ⎥

⎢

⎥

⎢

⎥

⎢

⎥ ⎢ ⎥

=

+

⎢

⎥

⎢

⎥

⎢

⎥ ⎢ ⎥

⎢

⎥

⎢

⎥

⎢

⎥ ⎢ ⎥

⎣

⎦

⎣

⎦ ⎣ ⎦

⎣

⎦

X

L

M

L

M

M

M

M

L M

L

14442444

3

 

Wówczas optymalne wartości wektora 

a

, minimalizujące błąd średniokwadratowy są równe: 

(

)

T

T

est

-1

a

= X X

X y

 

Oblicz je i porównaj z poprzednio wyznaczonymi w ćw. 1 i 2. 

Ćwiczenie 5 (0.5 pkt) 

Optymalizacja. Załóżmy, że dysponujemy N=1000 próbkami sygnału 

y(n)

, który jest zaszumionym 

sygnałem 

x(t) 

o znanej postaci (

s(t)

 – szum): 

0

( )

( )

( )

cos(2

)

( )

t

y t

x t

s t

Ae

f t

s t

α

π

φ

−

=

+

=

+

+

 

Sygnał ten został spróbkowany z częstotliwością 

f

pr

 

= 1000 Hz (dt=1/fpr; t = dt*(0:N-1)). Załóżmy, 

że: 

A =4.5, f

0

 = 10 Hz, 

α = 0.5*f

0

, 

φ = 0; 

s(t) to szum gaussowski, dla którego stosunek sygnału do szumu jest równy 38 dB (s = awgn(x,38);). 

Wygeneruj sygnał 

y(t) 

oraz za pomocą funkcji Matlaba  fminsearch()  znajdź optymalne wartości 

parametrów {A, α, f

0

, φ} sygnału 

x(t)

 (minimalizujących błąd odległości punktów eksperymentalnych od 

krzywej teoretycznej: 

0

( )

cos(2

)

t

x t

Ae

f t

α

π

φ

−

=

+

 

Skorzystaj z programów cw_7.m i cw_8.m z przedmiotu MiTP-II. 

1

0

1

1

1

0

1

1

2

1

1

1

0

0

1

0

2

0

2

2

1

2

2

2

2

1

1

2

1

3

1

3

3

2

3

3

3

2

4

4

4

3

,

,

,

x

x

y

s

x

x

y

s

x

x

y

x

x

h

s

h

y

h

s

x

x

y

s

y

x

x

h

s

h

y

h

s

x

x

y

s

x

x

y

s

x

x

⎡

⎤

⎡ ⎤

⎡ ⎤

⎡

⎤

⎡ ⎤

⎡ ⎤

⎢

⎥

⎢ ⎥

⎢ ⎥

⎡ ⎤ ⎡

⎤ ⎡ ⎤ ⎡ ⎤

⎡ ⎤

⎡ ⎤

⎢

⎥

⎢ ⎥

⎢ ⎥

⎢

⎥

⎢ ⎥

⎢ ⎥

=

+

=

+

=

+

⋅

⎢ ⎥ ⎢

⎥ ⎢ ⎥ ⎢ ⎥

⎢ ⎥

⎢ ⎥

⎢

⎥

⎢ ⎥

⎢ ⎥

⎢

⎥

⎢ ⎥

⎢ ⎥

⎣ ⎦ ⎣

⎦ ⎣ ⎦ ⎣ ⎦

⎣ ⎦

⎣ ⎦

⎢

⎥

⎢ ⎥

⎢ ⎥

⎢

⎥

⎢ ⎥

⎢ ⎥

⎣ ⎦

⎣ ⎦

⎣

⎦

⎣ ⎦

⎣ ⎦

⎣

⎦

y = X h

+ s

 

 

 

 

 

X 

h 

y 

= 

+ 

s 

(

)

T

T

est

-1

h

= X X

X y

 

 
 

 

 

 

 

 

 
 

 

 

= 

(X

T

X)

-1

X

T

 

h 

= 

X

T

X 

X

T

-1

h 

 

X 

= 

X

T 

X

T

h 

-1

y 

y 

y