N-osobowe gry kooperacyjne - wartość Shapleya

Na poprzednim wykładzie mówiliśmy o dwóch rodzajach pojęcia „rozwiązania" gry

kooperacyjnej: o rdzeniu i o zbiorach stabilnych. Oba te rozwiązania odwołują się do

koncepcji dominacji albo kwestionowania pewnych podziałów przez pewne koalicje. Pojęcia

te, pomimo swojej intuicyjnej oczywistości, mają pewne wady: zachowują się w dość

nieregularny sposób, rdzeń może być zbiorem pustym, a zbiorów stabilnych może być z kolei

bardzo wiele. Tych wad nie ma inna koncepcja „rozwiązania" gry, którą zajmiemy się w tym

rozdziale. Jest nią wartość Shapleya. Wprowadzimy to pojęcie posługując się przykładem

muzyków opisanym na poprzednim wykładzie. Przypomnijmy samą tylko tabelkę tej gry –

prezentującą jej postać charakterystyczną

Koalicja

Wypłata

{Skrzypek, Pianista, Basista}

200

{ Pianista, Basista}

130

{Skrzypek,Basista}

100

{Skrzypek, Pianista}

160

{Skrzypek}

40

{ Pianista}

60

{ Basista}

0

Przypuśćmy, że trzej muzycy umówili się w jednym miejscu, na przykład na

przystanku metra o piątej po południu. Nigdy nie przyjdą na spotkanie w tym samym

momencie: ze względów losowych będą się pojawiać w jakiejś kolejności. Co więcej –

teoretycznie nie wszyscy musza się pojawić. Jeśli się dany muzyk pojawi, to jaka jest z tego

korzyść? Otóż to – ta korzyść - zależy nie tylko od tego, który to muzyk, ale też od tego w

którym momencie tworzenia koalicji się pojawi. Ową „korzyść” z przyjścia danego muzyka,

ogólnie nazywamy wkładem w koalicję. Jest sześć możliwych kolejności pojawiania się

muzyków, czyli jak mówimy - tworzenia koalicji:

{Skrzypek, Pianista, Basista}
{Skrzypek, Basista, Pianista}
{Pianista, Basista, Skrzypek}
{Pianista, Skrzypek, Basista}
{Basista, Skrzypek, Pianista}
{Basista, Pianista, Skrzypek}

Wybierzmy sobie jednego z artystów, na przykład Basistę i przeanalizujmy jego

sytuację w każdym z możliwych wymienionych wyżej przypadków. Przypuśćmy, że każdą

kolejność przyjścia interpretujemy jako proces tworzenia się zespołu w pewnej kolejności.

Interesuje nas wielkość wypłaty, jaką dany gracz — muzyk wnosi do już zastanej koalicji. W

przypadku kolejności numer l, Basista zastaje koalicję {Skrzypek, Pianista} „wartą" (jak

wynika z tabeli) 160. Po jego przyjściu wartość koalicji wzrasta do 200 dolarów, czyli o 40

dolarów. W przypadku kolejności numer 2, Basista zastaje koalicję { Skrzypek } „wartą" 40

dolarów. Po jego przyjściu wartość tej koalicji wzrasta do 100 dolarów, czyli o 60 dolarów.

Postępujemy tak dalej, na przykład dla kolejności numer 5, czy 6, Perkusista przychodzi

pierwszy i wnosi 0 dolarów, jako że sam „nie jest nic wart". Otrzymujemy w ten sposób

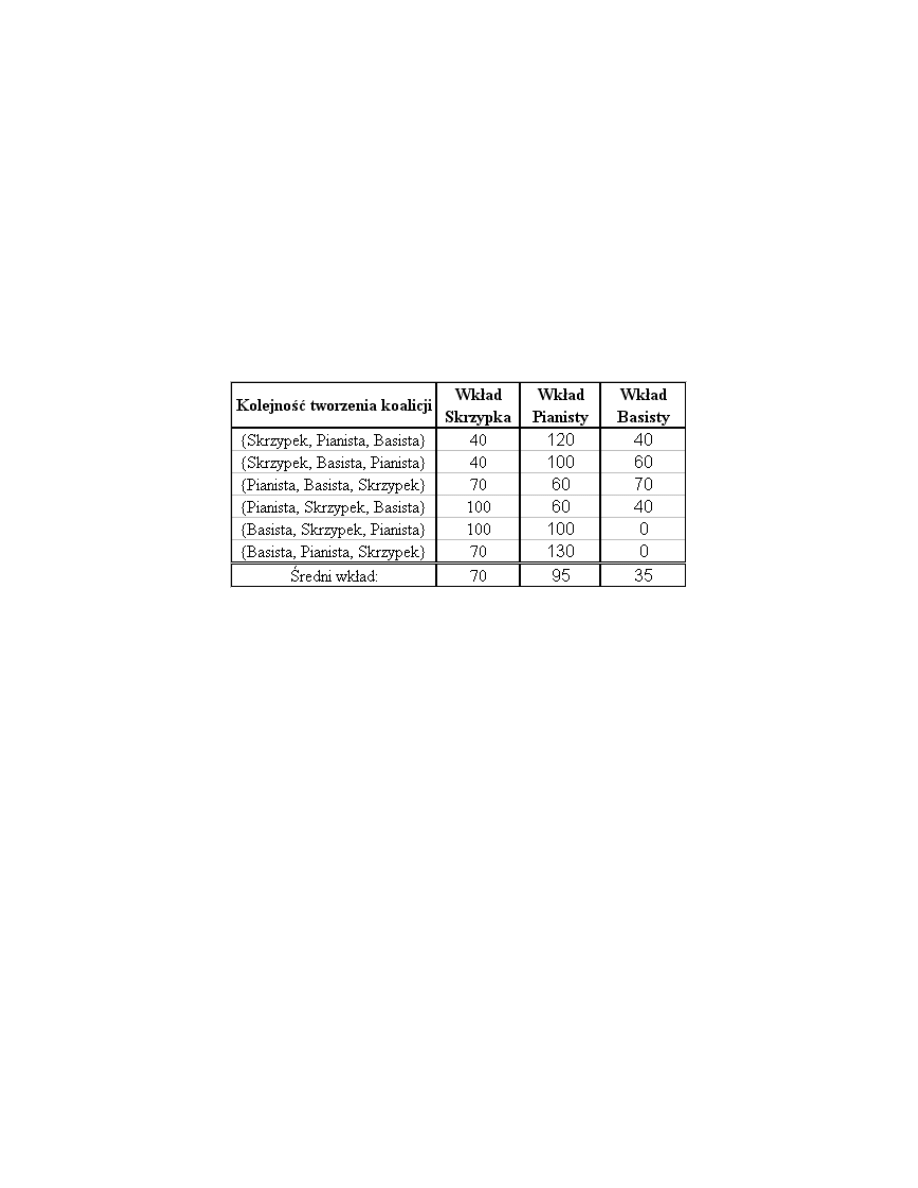
poniższą tabelę, w której wypisano wszystkie możliwe kolejności tworzenia się zespołu, a

obok — kwoty, jakie poszczególni muzycy wnoszą przychodząc w tej właśnie kolejności.

W ostatnim wierszu tej tabeli umieściliśmy średni wkład każdego z muzyków ze

względu na wszystkie możliwe kolejności tworzenia się zespołu. W ten sposób otrzymaliśmy

podział Xs == 70, Xp, = 95. Xb, = 35. Ten podział nazywa się wartością Shapleya danej gry.

Wartość Shapleya, ze względu na sposób, w jaki ją skonstruowano, można interpretować jako

ś

redni oczekiwany podział w danej grze przy rozegraniu dużej ilości partii. Zaletą wartości

Shapleya jest jej matematyczna prostota. Jest jeszcze jedna bardzo ważna rzecz: wartość

Shapleya zawsze istnieje i zawsze jest tylko jedna.

Zobaczmy jeszcze jak wygląda wartość Shapleya dla gry opisującej sytuację trzech

kolegów, Zygi, Wieśka i Mietka, a przedstawionej na poprzednim wykładzie. Postać

charakterystyczna tej gry była następująca:

Koalicja

Wypłata

{ Zyga, Wiesiek, Mietek }

100

{ Wiesiek, Mietek }

100

{ Zyga, Mietek }

100

{ Zyga, Wiesiek }

100

{ Mietek }

0

{ Zyga, }

0

{ Wiesiek }

0

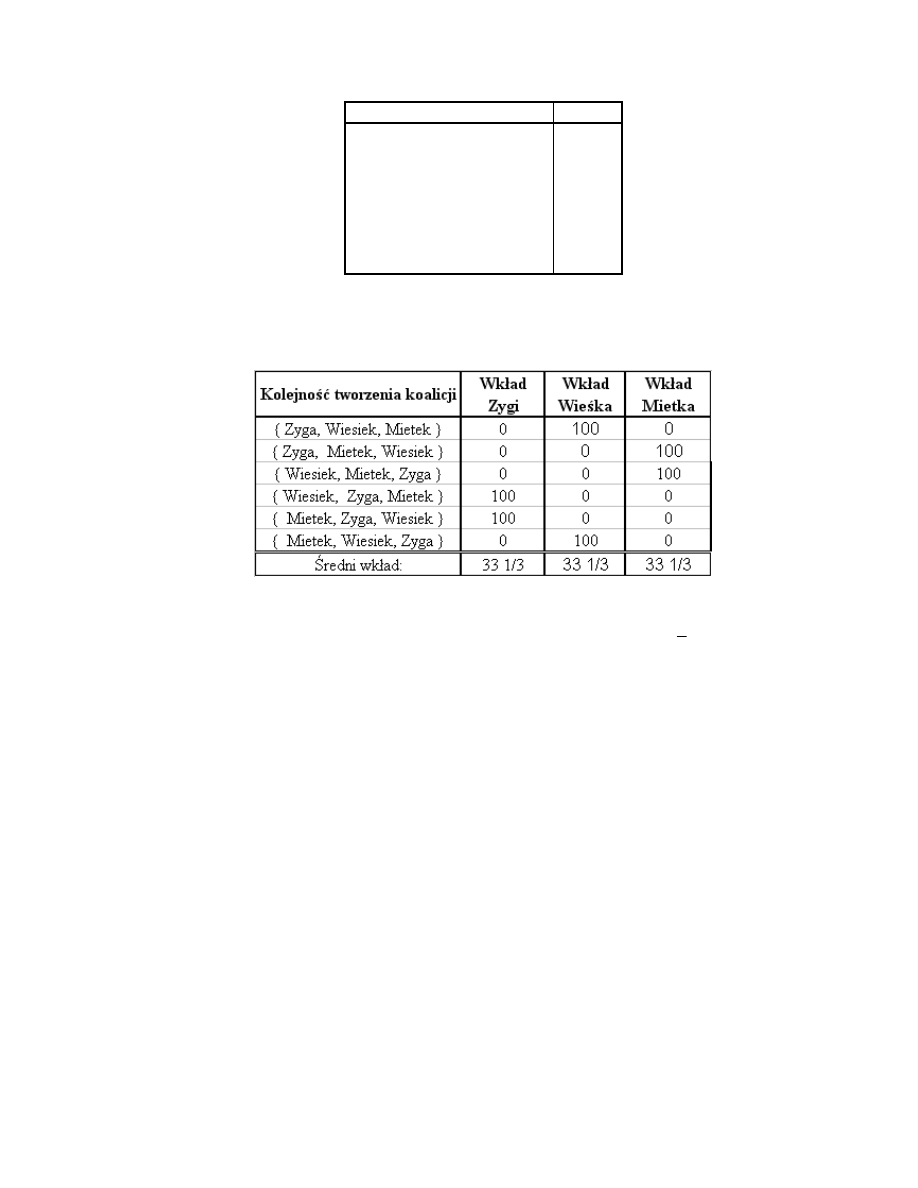
Wkłady poszczególnych graczy w różnych konfiguracjach kolejności tworzenia

koalicji przedstawia poniższa tabela:

Wartość Shapleya tej gry stanowi więc podział Xz =Xw= Xm =

3

1

33

. Otrzymany

wynik jest symetryczny, co nie jest przypadkiem. Historycznie bowiem rzecz ujmując, Lloyd

Shapley – który w latach 50 ubiegłego wieku analizował sposoby rozwiązania problemu

podziału wypłaty w koalicji - zaczął od sformułowania trzech aksjomatów, dotyczących

wartości podziału, które jego zdaniem oddają idee sprawiedliwości. Następnie wykazał, że

taka wartość istnieje i jest tylko jedna. Podał także sposób jej obliczania, był on jednak

znacznie bardziej skomplikowany niż ten, który poznali Państwo.

Wspomnianych aksjomatów nie podamy w tym miejscu, bo wykorzystują one pewne

pojęcia formalne obce Państwu, jednak powszechnie uznano je– podobnie jak aksjomaty

sprawiedliwości sformułowane przez Nasha dla gier dwuosobowych – za sensowne i

intuicyjne i raczej wszyscy się z nimi zgadzają, choć oczywiście są sytuacje, w których idee

te budzą pewne wątpliwości.

Jeden z tych aksjomatów mówi właśnie, że jeśli sytuacje graczy w grze koalicyjnej są

w pełni symetryczne, to ich wypłaty powinny być równe. A tak właśnie było w rozważanej

sytuacji trzech kolegów dźwigających skrzynie.

Wartość Shapleya bardzo szybko została zaakceptowana w teorii i praktyce jako dobra

propozycja rozwiązania problemu podziału wypłaty w koalicji. Znaleziono dla niej także inne

zastosowania. O jednym z nich powiemy w kolejnej części wykładu.

Ważone gry większości

Głosowanie na walnym zgromadzeniu akcjonariuszy spółki to również pewien

szczególny rodzaj gry kooperacyjnej. Jest to gra, której każdy uczestnik dysponuje pewną

ilością głosów zależną od jego udziałów w spółce. Sytuacja jest zatem taka: Mamy N graczy -

udziałowców. Udział i-tego gracza w firmie wyraża się liczbą w

i

, i=1,…,N. Suma wszystkich

udziałów wynosi więc

∑

=

i

i

w

W

. Do przyjęcia dowolnej uchwały potrzebna jest większość

głosów. Jest więc jakaś ustalona liczba A większa niż

2

W

. ale nie większa niż W, która

wyznacza „większość". Koalicja, która łącznie zbierze A głosów albo więcej, decyduje o

przyjęciu albo odrzuceniu uchwały. Koalicje taka nazywać będziemy koalicją nazywana

wygrywającą

Przypisujemy jej wypłatę w wysokości l. Koalicja , która nie ma większości jest

przegrywająca i przypisujemy jej wypłatę 0. Takie gry nazywamy ważonymi grami

większości.

Weźmy pod uwagę prosty przykład: czterech akcjonariuszy, których udziały wynoszą,

odpowiednio: 30, 30, 30 i 10 procent. Załóżmy, że statutowa większość potrzebna do podjęcia

jakiejś uchwały wynosi 55. Taką grę będziemy umownie oznaczać przez [30, 30, 30, 10; 55].

Umówmy się, że graczy numerujemy, a zbiory indeksów oznaczają możliwe koalicje.

Przykładowo, koalicja {l, 2, 4} składa się z akcjonariuszy numer l, 2 i 4. Stosując tę notacje

poniżej przedstawiamy tabelkę prezentującą postać charakterystyczna tej gry:

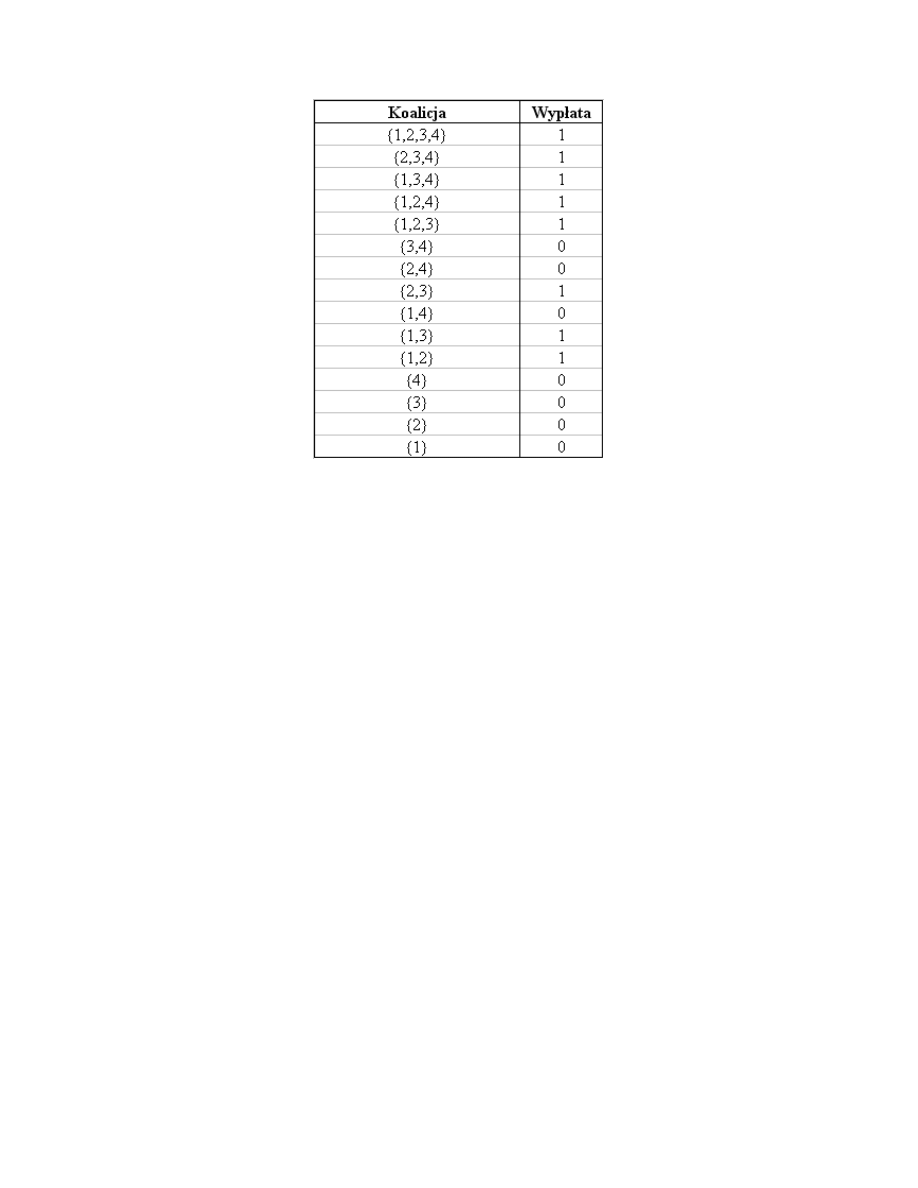
Na przykład, widzimy że koalicja {l, 2. 4} jest wygrywająca (suma udziałów

koalicjantów jest równa 70 i przekracza 55, zatem przypisujemy jej wypłatę l .

Przypomnijmy sobie obliczanie wartości Shapleya w poprzednim przykładzie.

Braliśmy tam pod uwagę wszystkie możliwe ustawienia graczy, teraz będą to 24 ustawienia

Każde takie ustawienie interpretuje się jako pewien proces tworzenia się koalicji i

przyjmuje się, że wszystkie ustawienia są równie prawdopodobne. Patrzymy następnie, dla

każdego gracza z osobna, o ile wzrosła, w każdym ustawieniu, wartość koalicji, którą ten

gracz już zastał, po jego dołączeniu się do niej. W naszym przypadku tą liczbą będzie zero:

kiedy gracz zastał koalicję przegrywającą, która pozostała nadal przegrywająca po jego

dołączeniu, albo kiedy gracz zastał już koalicję wygrywającą. Tą liczbą będzie natomiast

jeden, kiedy gracz zastał koalicję przegrywającą, która po jego dołączeniu stała się

wygrywająca; w takiej sytuacji mówimy, że ten gracz jest przy tym ustawieniu decydujący.

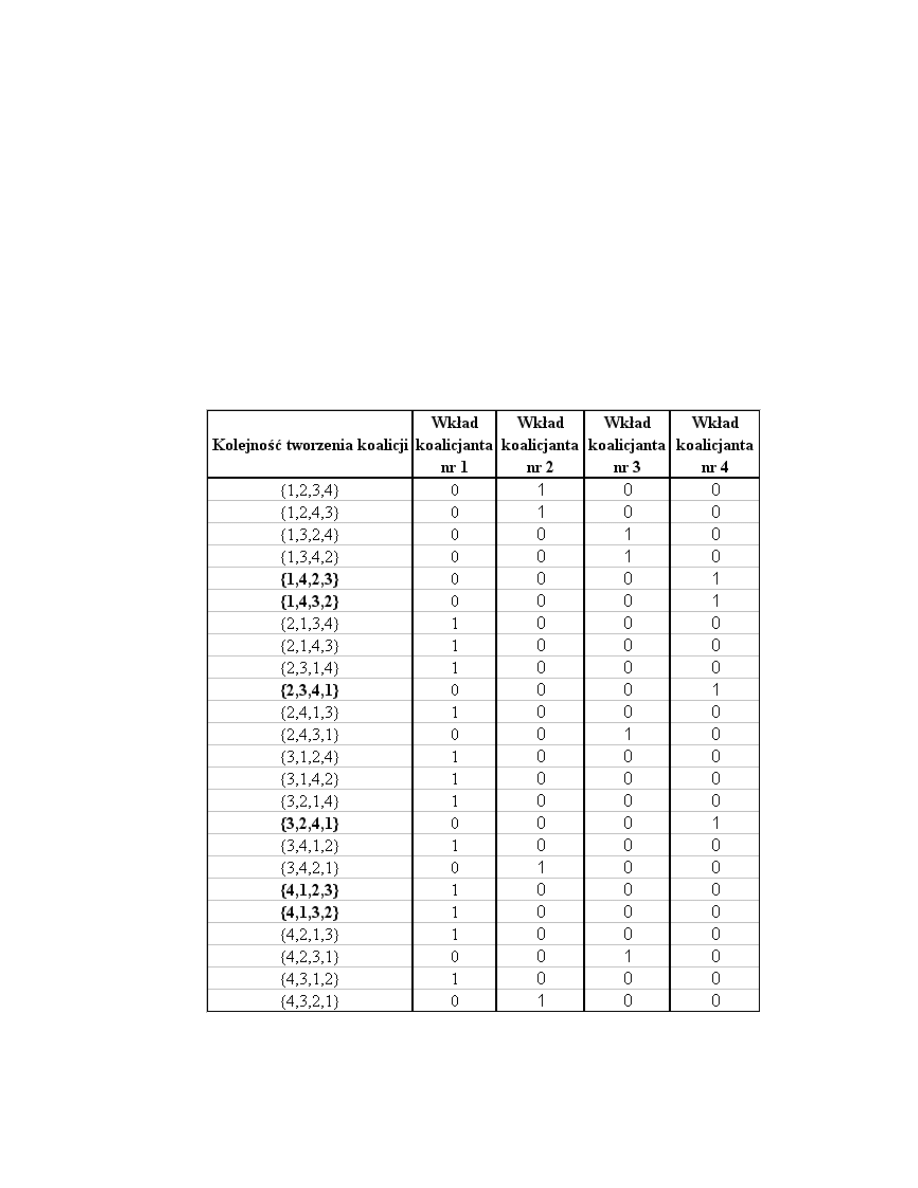
Odpowiednie ustawienia kolejności zawierania koalicji i wartość dodana przez

poszczególnych graczy przedstawione są w tabeli

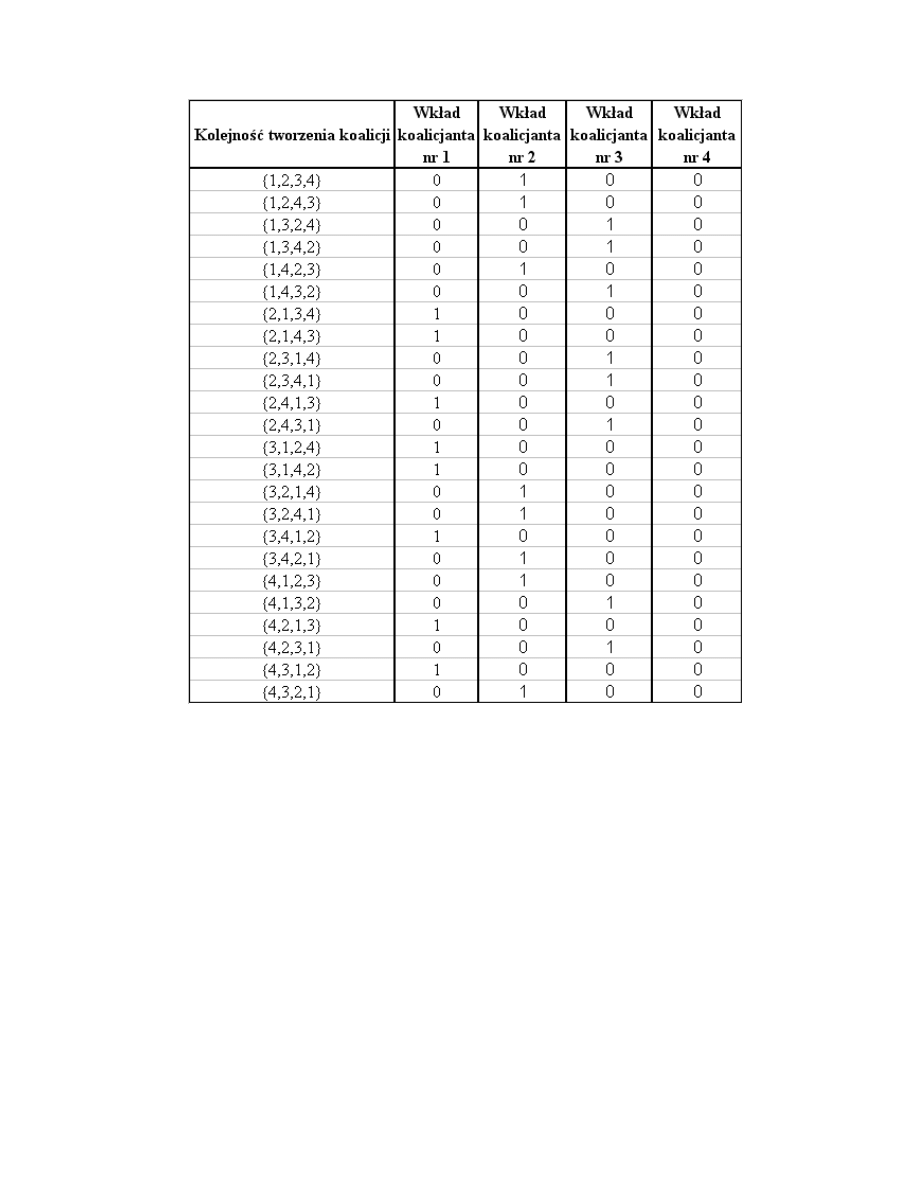
Na przykład, w pierwszym wierszu powyższej tabeli gracz drugi dodał wartość 1

pozostali po 0. Zauważmy jeszcze raz, że w tych grach zawsze tylko jeden gracz dodaje

dokładnie jeden a pozostali dokładnie zero.

Liczymy teraz „średni" wkład każdego gracza; łatwo widzimy, że trzech pierwszych

graczy po osiem razy dodawało wartość 1 , podczas gdy ostatni zawsze „wnosił” zero.

Ponieważ wszystkich możliwych kolejności zawierania koalicji jest 24 otrzymujemy

następującą wartość Shapleya gry, czyli podział X1 = X2= X3=1/3 oraz X4= 0. Wartość

Shapleya wyraża w jakimś sensie możliwości przetargowe poszczególnych graczy, ich

zdolność do tworzenia skutecznych koalicji. Sytuacja graczy l, 2 i 3 jest identyczna, więc

wartość Shapleya daje im równe udziały w wygranej. Gracz 4 jest natomiast pionkiem: jego

głos nie liczy się w żadnej sytuacji i dlatego wartość Shapleya daje mu 0. W takich

zastosowaniach jak te omawiane teraz obliczone wypłaty dla poszczególnych graczy

wynikające ze znalezionej wartości Shapleya nazywane sa indeksem siły Shapleya-Shubika.

Indeks ten mierzy wartość gracza jako potencjalnego koalicjanta – to ważne i często

wykorzystywane w analizach zastosowanie wartości Shapleya. Indeks ten został zastosowany

w takim celu po raz pierwszy w 1954 roku.

Aby zobaczyć jak ciekawe wnioski mogą wynikać z analizy indeksu siły popatrzmy jak

zmieni się wartość Shapleya, kiedy trochę zmodyfikujemy wyjściową grę. Przyjmijmy teraz,

ż

e udziały akcjonariuszy l, 2, 3 i 4 w firmie wynoszą, po odpowiednich zakupach akcji na

giełdzie, odpowiednio, 45, 30, 15 i 10. Większość wymagana do podjęcia wiążących decyzji

nadal wynosi 55. Mamy więc do czynienia z ważoną grą większości [45, 30, 15, 10; 55].

Tabela wypłat poszczególnych koalicji wygląda już teraz inaczej, konkretnie zmieniły się

wypłaty koalicji {l, 4} i {2, 3}. Oto ona

Kolejności dla których zmienili się gracze dodający wartość 1 zaznaczyliśmy w tabeli

tłustą czcionką.

Widzimy więc, że gracz numer l jest decydujący przy dwunastu ustawieniach; po

podzieleniu 12 przez 24 (liczbę wszystkich ustawień) dostajemy 1/2 podobnie robimy dla

pozostałych graczy i stwierdzamy, że wartość Shapleya dla gry otrzymanej po transferze akcji

wynosi X1 =1/2, X2=X3=X4=1/6. Otrzymany wynik jest więc zupełnie inny niż poprzednio,

może nawet trochę zaskakujący. Możliwości przetargowe graczy numer 2, 3 i 4, mających

istotnie różniące się udziały w firmie, a więc 30, 15 i 10, zostały identycznie ocenione przez

wartość Shapleya. Dzieje się tak dlatego, że identyczne są możliwości tworzenia skutecznych

koalicji przez tych akcjonariuszy. W pewnym sensie nadwyżka udziałów gracza 2 zostaje

„zmarnowana" i nie znajduje właściwego przełożenia na jego możliwości zarządzania

przedsiębiorstwem.

Podobnie ciekawych spostrzeżeń można dokonać analizując wpływ wartości progowej

A ( u nas 55) na siłę poszczególnych graczy. Może to być bardzo pouczające. Można np.

zobaczyć że na zmianie tego progu mogą zyskać „mali” gracze właśnie poprzez to, że ich siłę

zrównuje się z graczem dużo większym. Przecież w sytuacji naszego hipotetycznego walnego

zgromadzenia, gdyby próg wynosił 60, to znowu gracz 4 byłby bez znaczenia. Zatem warto

czasami dokładnie się przyjrzeć faktycznym skutkom zmian tego progu decydującego o

uznaniu decyzji za ważnie podjętą.

Teoria wartości Shapleya może równie dobrze służyć do prowadzenia analizy sytuacji

w politycznych ciałach ustawodawczych. Wtedy graczami są partie i kluby, a udziałom

odpowiada ilość głosów, jakimi te partie i kluby dysponują. Sytuacja jest jednak w tym

wypadku bardziej złożona, bo akcjonariusz z poprzednich przykładów sam decydował o

oddaniu swoich głosów (proporcjonalnych do jego udziału) za taką, czy inną opcją, natomiast

w Sejmie czy Senacie ostatecznej decyzji, jak głosować, nie podejmuje partia, ale sam poseł

czy senator.