POLITECHNIKA ŚLĄSKA

w Gliwicach

WYDZIAŁ AUTOMATYKI, ELEKTRONIKI i INFORMATYKI

Instytut Elektroniki

Zespół Inżynierii Biomedycznej

LABORATORIUM

BIOCYBERNETYKI

Sieci Kohonena

Opracował: dr inż. Jacek Kawa

Gliwice 2010,2011

1 Cel ćwiczenia.

2

1

Cel ćwiczenia.

Celem ćwiczenia jest pokazanie sposobów uczenia i funkcjonowania sieci neuronowych Kohonena (tzw. sa-

moorganizujących się map).

2

Podstawy teoretyczne

Jedną z ważniejszych cech sieci neuronowych jest zdolność do adaptacji i samoregulacji.[2]. Będące tematem

dzisiejszych zajęć sieci neuronowe Kohonena (a właściwie samoorganizujące mapy) są przykładem sieci niewy-

magających nadzoru w czasie procesu uczenia. Są również przykładem sieci rywalizacyjnych – takich, w których:

• podczas pobudzenia odpowiada tylko jeden, zwycięski neuron,

• a w czasie nauki modyfikacji ulegają wagi jedynie neuronu zwycięskiego lub również (jak w przypadku

sieci Kohonena właśnie) jego sąsiadów.

2.1

Praca sieci

Sieci Kohonena składają się z pewnej liczby neuronów (węzłów) z których każdy opisany jest przez pewien,

ustalony w wyniku uczenia wektor wag ~

w

i

. Wektor sygnałów ~

X

(j)

podanych na wejście sieci pobudza

wszystkie neurony i każdy z nich generuje pewną odpowiedź na to pobudzenie d

i

= || ~

w

i

− ~

X

j

||. Odpowiedzi

te różnią się między sobą, co sprawia, że możliwa jest rywalizacja między neuronami. Zwycięzcą rywalizacji

jest ten pojedynczy neuron, dla którego wygenerowana odpowiedź była najmniejsza (jest to określane mianem

zasady zwycięzca bierze wszystko) i to ostatecznie jego odpowiedź jest traktowana jako odpowiedź całej sieci.

Matematycznie można to przedstawić w następujący sposób.

~

w

i

=








w

1

i

w

2

i

. . .

w

n

i








~

X

(j)

=








x

(j)
1

x

(j)
2

. . .

x

(j)
n








(1)

Jeśli oba wektory są elementami tej samej przestrzeni, to można określić odległość między nimi.

d

i

( ~

X

j

) = || ~

w

i

− ~

X

(j)

||

(2)

Np. w przestrzeni Euklidesowej

d

i

( ~

X

j

) =

q

(w

1

i

− x

(j)
1

)

2

+ (w

2

i

− x

(j)
2

)

2

+ . . . + (w

n

i

− x

(j)
n

)

2

(3)

Oznacza to, że (jeśli oczywiście wagi neuronów były różne), istnieje pewien neuron k, dla którego obliczona

odległość była najmniejsza (tzn. najbliższy wektora wejściowego).

k = argmin

i

(d

i

)

(4)

Neuron ten zwycięża rywalizację a jego numer k jest przedstawiany jako odpowiedź całej sieci. Alternatyw-

nie odpowiedź sieci może zawierać informacje o wszystkich neuronach {y

i

}. W takim przypadku tylko jedna

z wartości y

i

będzie równa 1.

y

i

=

(

1

⇔ d

i

= min

z

d

z

0

w każdym innym przypadku

(5)

2.2

Interpretacja

3

Rys. 1: Przykład jednowymiarowej sieci Kohonena

2.2

Interpretacja

Założenie, że oba wektory: pobudzenia i wag, znajdują się w tej samej przestrzeni sugeruje sposób interpretacji

wyników. Sieć składa się jakby z pewnej liczby wzorcowych pobudzeń (określonych w procesie uczenia lub

narzuconych), a w czasie pracy sieci szukany jest wzorzec najbardziej podobny do podanego pobudzenia.

Np. jeśli wektor pobudzenia zawiera pewne parametry obiektu (np. wiek i wysokość), to każdy z neuronów

samoorganizującej mapy będzie sobą reprezentował pewną kombinację wieku i wysokości. Praca sieci polegać

będzie na znalezieniu tego neuronu, który będzie najbliższy równocześnie i wiekiem, i wysokością podanemu na

wejście wektorowi (pobudzeniu).

Warto przy tym zauważyć, że taki sposób rozumienia wag neuronów zastosowany do interpretacji wyników

uczenia sieci może być wykorzystany do procesu zwanego grupowaniem (co będzie tematem kolejnych zajęć).

2.3

Topologia sieci i pojęcie sąsiedztwo neuronów

Z punktu widzenia normalnej pracy sieci, jej topologia (układ) nie ma większego znaczenia: zawsze dla któregoś

neuronu odległość będzie najmniejsza, można ten neuron wykryć, a następnie analizując jego wagi zinterpretować

wynik.

Inaczej jest w przypadku procesu uczenia sieci. W procesie tym w sieciach Kohonena odstępuje się od zasady

znanej z sieci rywalizacyjnych (zwycięzca bierze wszystko) i pozwala korygować wagi nie tylko tego neuronu,

który zwyciężył rywalizację, ale również jego sąsiadów.

To, w jaki sposób zdefiniuje się owo sąsiedztwo wpływa na otrzymany w wyniku uczenia układ neuronów

– można w uproszczeniu założyć, że sąsiadujące ze sobą neurony będą miały raczej podobne, niż znacząco

różne wagi. W praktyce przyspiesza to interpretację wyników, o czym będzie można przekonać się w czasie

laboratorium

Innymi słowy definiując sieć Kohonena musimy podać w jaki sposób neurony będą wzajemnie rozlokowane

w przestrzeni oraz w jaki sposób układać będą się ich relacje z sąsiadami: które neurony nazwiemy bezpośrednimi

sąsiadami, czy sąsiedztwo będzie bezwarunkowe (konkretny neuron ~

w

i

albo jest, albo nie jest sąsiadem neuronu

~

w

j

), czy może będziemy raczej chcieli określić sąsiedztwo w bardziej złożony sposób (np. przypisując wagi).

Można to wszystko uporządkować traktując sieć jako pewien graf. Wierzchołkami tego grafu są neurony

połączone ze sobą w określony sposób gałęziami. Minimalną ilość przeskoków potrzebną, aby dostać się z neuronu

~

w

i

do ~

w

j

można wtedy wykorzystać do analitycznego zdefiniowania sąsiedztwa.

Ponieważ zwykle sieć ma charakter regularny, można wyróżnić sieci jednowymiarowe – jeden rząd neuronów

(Rys. 1), dwuwymiarowe kilka wierszy (Rys. 2), trójwymiarowe – kilka wierszy i warstw itd. Charakter połączeń

może być np. prostokątny (Rys. 2a), heksagonalny (Rys. 2b) czy wręcz losowy (rysunku oszczędzono).

Uwaga: nie należy mylić połączeń między neuronami w sieci Kohonena z drogami przekazywania (propa-

gacji) sygnałów w sieci neuronowej.

2.4

Funkcje sąsiedztwa

Bazując na liczbie przeskoków w grafie (oznaczonej tutaj przez N ) od dowolnego neuronu ~

w

i

można w sposób

analityczny zdefiniować pojęcie sąsiedztwa. W szczególności:

• brak sąsiedztwa (przydatne, gdy sieć Kohonena ma zachowywać się jak klasyczna sieć rywalizacyjna)

N ( ~

w

i

, N ) =

(

1,

N = 0

0, w przeciwnym razie

(6)

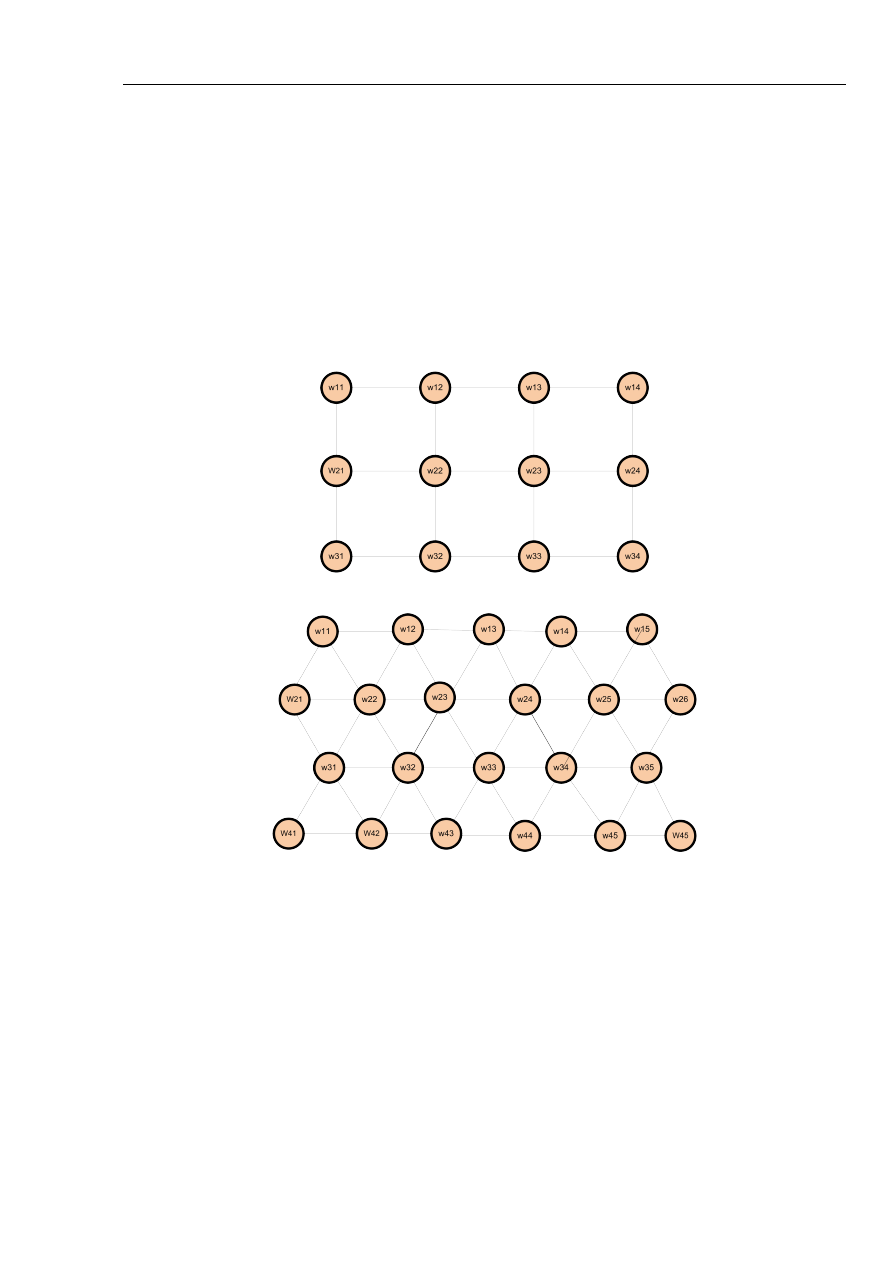
2.4

Funkcje sąsiedztwa

4

(a) układ prostokątny

(b) układ heksagonalny

Rys. 2: Przykład dwuwymiarowej sieci Kohonena

2.5

Uczenie sieci Kohonena

5

• najbliższy sąsiad (4-sąsiedztwo w sieci 2D, 6-sąsiedztwo w sieci 3D itd.)

N ( ~

w

i

, N ) =

(

1,

N ¬ 1

0, w przeciwnym razie

(7)

• sąsiedztwo gaussowskie

N ( ~

w

i

, N ) = e

−N/p

,

p ∈ R

+

(8)

itd.

2.5

Uczenie sieci Kohonena

W początkowym stanie (przed rozpoczęciem nauki) sieć Kohonena cechuje się losowymi wartościami wag przy-

pisanych poszczególnym neuronom. Wybierany jest sposób organizacji (topologia) oraz sąsiedztwo.

Następnie na wejście sieci podawany jest ciąg uczący U =< X

(1)

, X

(2)

, X

(3)

, . . . >

Każde pobudzenie ~

X

(j)

, zgodnie z zasadami pracy sieci Kohonena powoduje odpowiedź tylko jednego neuronu

k. Neuron ten jest następnie wzmacniany korzystając z zależności:

~

w

(j+1)

k

= ~

w

(j)

k

+ η

(j)

~

X

(j)

− ~

w

(j)

k

(9)

Jest to zależność znana z sieci rywalizacyjnych. Nowością jest jednak fakt, że w sieci Kohonena wzmocnieniu

ulegają również neurony sąsiadujące z neuronem zwycięskim. Matematycznie jest to modelowane włączeniem

funkcji sąsiedztwa N do powyższej formuły. Jeśli neuron ~

w

i

oddalony jest od zwycięskiego ~

w

k

o N przeskoków

~

w

(j+1)

i

= ~

w

(j)

i

+ N ( ~

w

k

, N )η

(j)

~

X

(j)

− ~

w

(j)

(10)

Jak będzie można przekonać się na laboratorium, taki sposób uczenia powoduje powstawania skupisk neu-

ronów odpowiadających skupiskom w zbiorze wektorów uczących (stąd określenie mapa).

2.6

Modyfikacje sposobu uczenia

W powyższej metodzie uczenia można wprowadzić modyfikacje, które mają wpływ na szybkość uczenia się sieci

bądź jej ostateczną postać. Jedną z istotniejszych jest zmiana rozmiaru sąsiedztwa w kolejnych epokach nauki

sieci (co zostanie przetestowane na laboratorium).

Przykładowo w początkowej fazie nauki sąsiedztwo neuronu zwycięskiego może obejmować wszystkie, bądź

prawie wszystkie pozostałe neurony, a następnie – w każdej kolejnej epoce – być redukowane aż do momentu,

w którym obejmować będzie tylko najbliższych sąsiadów.

Inna modyfikacja polega na wyłączeniu pewnych neuronów z rywalizacji, jeśli zbyt wiele razy zwyciężyły

w trakcie poprzednich etapów nauki. Pozwala to w bardziej równomierny sposób rozłożyć wagi w pewnych

obszarach mapy.

3

Sieci Kohonena w Matlabie

Projektowanie samoorganizujących (SOFM) się map w środowisku Matlab jest znacznie ułatwione dzięki zesta-

wowi dedykowanych funkcji pakietu N euralN etworks.

newsom Tworzy nową sieć typu SOFM.

% u t w o r z nowa s i e c o wymiarach 3 x 4 neurony

% p o b u d z e n i a ( j a k i w e k t o r y wag ) dwuelementowe . P i e r w s z y

% e l e m e n t t o pewna l i c z b a z p r z e d z i a l u 0 −3; a d r u g a

% z p r z e d z i a l u 1 −5.

n e t = newsom ( [ 0

3 ; 1 5 ] ,

[ 3

4 ] )

4 Program ćwiczenia

6

train Ucz sieć na podstawie danych wzorcowych

n e t = newsom ( [ 0

3 ; 1 5 ] ,

[ 3

4 ] )

[ n e t t r ] = t r a i n ( net , dane )

plotsomhits Pokazuje liczbę przyporządkowań do danych neuronów dla określonego zbioru danych

p l o t s o m h i t s ( net , dane )

plotsomplanes Pokazuje sposób rozkładu poszczególnych wag na neurony sieci

p l o t s o m p l a n e s ( n e t )

plotsomnd Pokazuje odległości między neuronami sieci

plotsomwmnd ( n e t )

sim Dodaje dane do SOFM

n e t = newsom ( [ 0

3 ; 1 5 ] ,

[ 3

4 ] )

[ n e t t r ] = t r a i n ( net , dane )

p r z y p i s a n i e = sim ( net , dana )

4

Program ćwiczenia

4.1

Część 1

1. Zgodnie ze wskazówkami prowadzącego przygotuj zbiór danych uczących i testowych. Zbiory te zawierać

będą dane o nierównomiernym rozkładzie.

2. Zaprojektuj dwuwymiarową sieć Kohonena o domyślnej topologii i rodzaju sąsiedztwa. Jakie to sąsiedztwo

i jaki jest układ sieci (doc newsom)? W ilu epokach domyślnie przeprowadzony został etap uczenia?

3. Korzystając z funkcji rysujących układ sieci sprawdź, jak wygląda układ sieci (odległości między neuronami

i ich wagi). Czy układ sieci przypomina ten ze zbioru wejściowego?

4. Wykorzystaj zbiór testujący (i uczący) do przetestowania normalnej pracy sieci. Wykorzystaj funkcję

plotsomhits do zobrazowania procesu klasyfikacji.

4.2

Część 2

1. Wygeneruj nową (niewyuczoną) sieć. Dla tych samych, co w części 1 zaobserwuj, jak przebiega proces

nauki w kolejnych epokach (spróbuj zaobserwować zmiany w strukturze sieci).

4.3

Część 3

1. Zmień topologię sieci z heksagonalnej na prostokątną. Jak zmiana ta wpłynęła na postać sieci po procesie

uczenia?

2. Wróć do układu heksagonalnego. Zmień sposób definiowania sąsiedztwa na dowolnie wybrany inny od

domyślnego. Czy obserwujesz zmiany w szybkości uczenia i ostatecznej postaci sieci?

LITERATURA

7

Literatura

[1] Paweł Badura, Wykład, 2009/2010

[2] Ryszard Tadeusiewicz, Sieci Neuronowe, Warszawa : Akademicka Oficyna Wydaw. RM, 1993.

[3] http://marcin.asia.w.interia.pl/kohonen/teoria.html