Podejmowanie optymalnych decyzji na

podstawie analizy marginalnej

Ćwiczenia 1 – Ekonomia menedżerska

mgr Krzysztof Sobczak

Katedra Ekonomii i Polityki Gospodarczej

[e-mail]

Lokalizacja centrum handlowego (1)

Pewien inwestor zajmujący się budową i sprzedażą nieruchomości planuje budowę dużego centrum
handlowego na wybrzeżu oceanu. Problem polega na tym, gdzie je zlokalizować (X). Aby ułatwić
podjęcie właściwej decyzji, zgromadzono wiele danych, które pozwoliły m.in. na opracowanie
schematycznej mapy tego regionu, pokazanej rysunku.

Główne skupiska ludności od strony zachodniej do wschodniej zostały oznaczone literami od A do H.
Ponieważ nabycie odpowiedniego terenu i uzyskanie pozwolenia na budowę nie stanowi problemu,
inwestor zakłada, że może wybudować planowany obiekt w dowolnym miejscu wzdłuż wybrzeża, na
odcinku AH.

Lokalizacja centrum handlowego (2)

•

Naturalną miarą dogodności lokalizacji jest całkowita odległość pomiędzy
centrum handlowym a wszystkimi jego potencjalnymi klientami (TTK – ang. Total
Travel Kilometres)

•

Wielkość TTK obliczamy, mnożąc odległość od centrum (punkt X) przez liczbę
dojazdów klientów z każdej miejscowości (od A do H) i sumując wynik.

•

Celem jest znalezienie optymalnej lokalizacji dla centrum handlowego.

•

Wykorzystujemy analizę marginalną (wykonujemy ruch w kierunku najbliższego
alternatywnego wariantu i sprawdzamy, czy sytuacja się poprawiła).

Tak – przesuwamy się dalej.

Nie – wracamy.

Prosty model przedsi

ę

biorstwa

Układ decyzyjny, który zamierzamy zbadać, można opisać następująco:
1. Badanie przedsiębiorstwa wytwarza jedno dobro (usługę), które

sprzedaje na jednym rynku, dążąc do osiągnięcia maksymalnego
zysku.

2. Zadanie polega na określeniu, jaką ilość dobra należy wytworzyć i

sprzedać oraz po jakiej cenie.

3. W uproszczonym modelu, od którego rozpoczynamy analizę,

zakładamy, że przedsiębiorstwo jest w stanie dokładnie przewidzieć
wpływ swoich decyzji produkcyjnych i cenowych na wielkość
utargów i kosztów.

Producent mikroprocesorów (1)

Kto?: Przedsiębiorstwo, które produkuje i sprzedaje mikroprocesory.

Problem ? jest ustalenie właściwych rozmiarów produkcji

(1 partia = 100

procesorów)

oraz poziomu ceny.

Musimy zbadać podstawą funkcję celu, która bierze pod uwagę podejmujący
decyzję menedżer.

Cel?

...

Chcąc wytwarzać mikroprocesory, przedsiębiorstwo musi mieć budynek,
urządzenia produkcyjne, materiały i pracowników. Przedsiębiorstwo ocenia, że
wytworzenie jednego mikroprocesora kosztuje

380 dol.

(koszt materiałów i

robocizny), tzn. jedna partia kosztuje

38000 dol.

Do tego należy doliczyć koszty

stałe w wysokości

100 000 dol.

Producent mikroprocesorów (2)

Równanie funkcji popytu:

Q

= 8,5 – 0,05

P

.

Odwrócone równanie popytu:

P

= …

Funkcja utargu całkowitego (

TR

) = …

Funkcja kosztów całkowitych (

TC

) = …

Zysk (

п

) = …

Producent mikroprocesorów (3)

•

Maksymalizacja zysku: Mπ=0 lub MR=MC

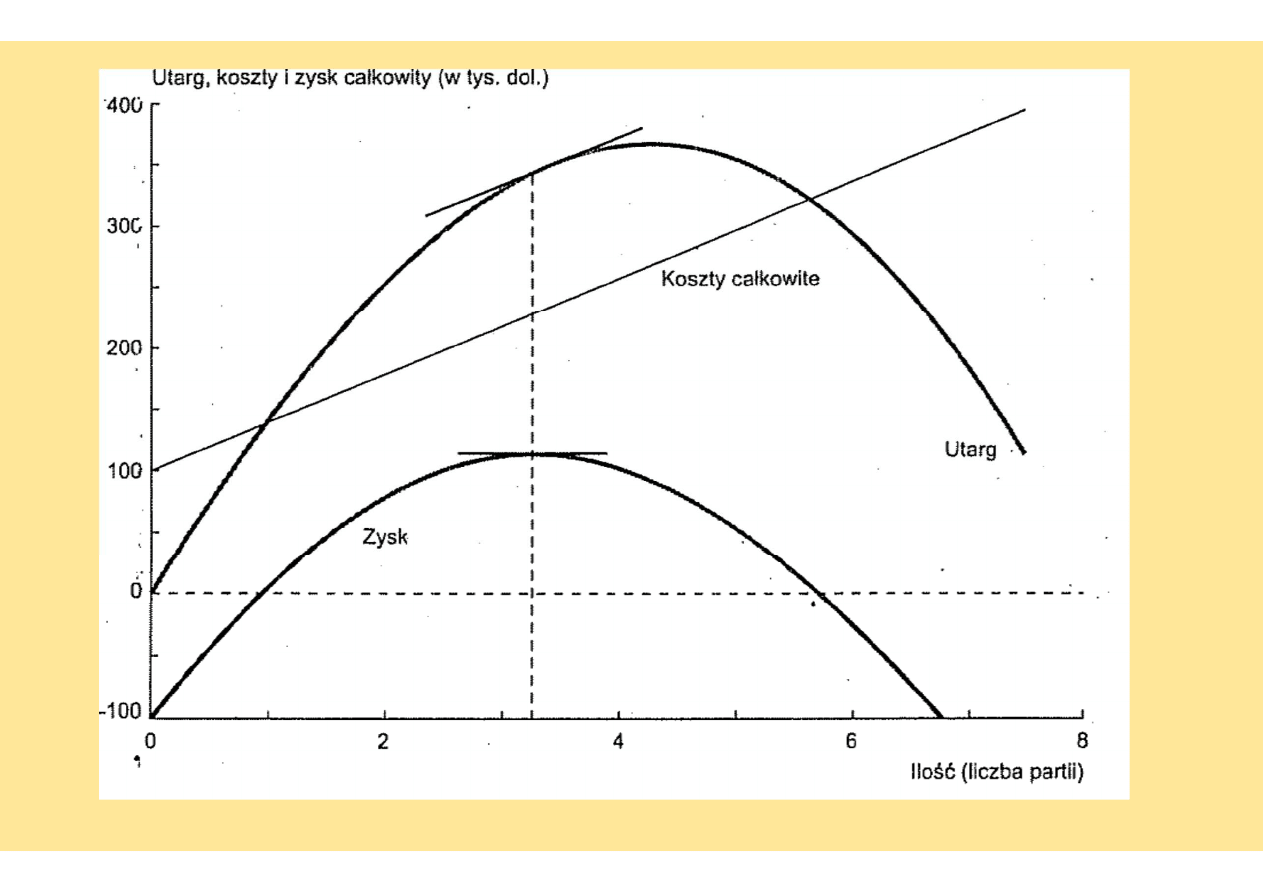
Źródło: Samuelson…2009, s. 70

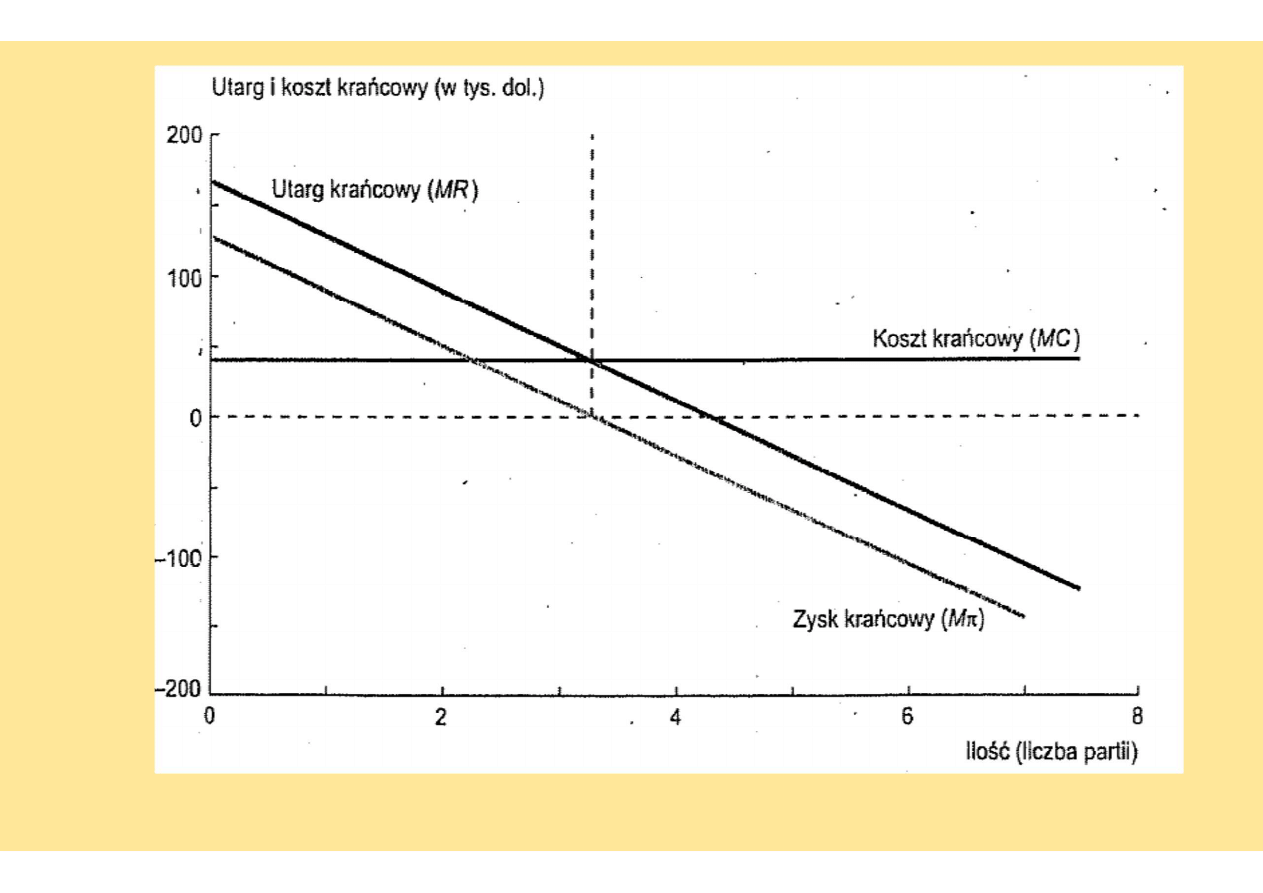
Źródło: Samuelson…2009, s. 70

Producent mikroprocesorów (4)

Analiza wrażliwości (zmiana warunków otoczenia)

1. Wzrost kosztów ogólnych z 100 000 do 112 000 dol.
2. Wzrost kosztów surowca z 38 000 do 46 000 dol. Za 1 partię

produktu.

3. Wzrost popytu: zmiana odwróconej funkcji popytu z P=170-20Q do

P = 190 – 20Q

Reguły decyzyjne

1. Podstawowym problemem decyzyjnym w przedsiębiorstwie jest

określenie wolumenu produkcji i ceny sprzedawanego dobra lub

usługi.

2. Zysk przedsiębiorstwa stanowi różnicę między przewidywanym

utargiem i kosztami. Produkcję i sprzedaż należy zwiększać, jeżeli

prowadzi to do zwiększenia sumy zysku, tzn. dopóki dodatkowy

utarg przewyższa przyrost kosztów.

3. Zmiany warunków ekonomicznych, w których działa

przedsiębiorstwo, rzutują na układ utargu krańcowego i kosztów

krańcowych, powodując w konsekwencji zmianę optymalnego

wolumenu produkcji i poziomu ceny.

Najwa

ż

niejsze ustalenia (2)

1. Podstawowymi czynnikami wyznaczającymi optymalną wielkość

produkcji i wysokość ceny w przedsiębiorstwie są

krzywe popytu i

kosztów

. Krzywą popytu można wykorzystać do

prognozowania

:

wielkości sprzedaży przy danej cenie lub poziomu ceny
zapewniającego określony wolumen sprzedaży. Mnożąc ceny przez
odpowiadające im ilości na krzywej popytu, otrzymujemy

funkcję

utargu

. Funkcja kosztów określa natomiast koszt wytworzenia

określonej ilości produktu. Zestawiając funkcję utargu z funkcją
kosztów, możemy przewidzieć

wielkość zysku

osiąganego przy

danym wolumenie produkcji.

Najwa

ż

niejsze ustalenia (3)

2. Następnym krokiem istotnym przy wyznaczaniu optymalnej decyzji

przedsiębiorstwa jest określenie utargu krańcowego i zysku

krańcowego.

•

Zyskiem krańcowym

nazywamy przyrost zysku osiągnięty dzięki sprzedaży

dodatkowej jednostki produktu.

•

Utargiem krańcowym

nazywamy przyrost utargu uzyskany ze sprzedaży

dodatkowej jednostki produktu.

•

Kosztem krańcowym

nazywamy przyrost kosztów związany z wytworzeniem

dodatkowej jednostki produkcji.

•

Zysk krańcowy

równa się różnicy między utargiem krańcowym i kosztem

krańcowym;

Mπ

,

MR

,

MC

można wyznaczyć, obliczając pierwsze pochodne

zysku, utargu i kosztów.

Najwa

ż

niejsze ustalenia (3)

3. Optymalną wielkość produkcji w przedsiębiorstwie charakteryzują
następujące, równoważne sobie warunki:

•

Mπ

=0

•

MR

=MC

Po określeniu optymalnej wielkości produkcji z równania ceny można
wyznaczyć optymalny poziom ceny, a następnie obliczyć zysk.

Dziękuję za uwagę!