Wykªad 13
Fizyka (Informatyka - EEIiA 2008/09)
06 01 2009
c
Mariusz Krasi«ski 2009
Spis tre±ci
1
1.1 Droga optyczna . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1
1.2 Soczewka . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2
1.3 Pojedyncza szczelina . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3
2 Zdolno±¢ rozdzielcza przyrz¡dów...
3
2.1 Przykªad . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4
5
3.1 Interferometr Macha-Zehndera . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
5
UWAGA! Wi¦kszo±¢ rysunków wymaga wªasnor¦cznego dopisania oznacze«! Wyliczenia zamieszczone w
ramkach stanowi¡ materiaª uzupeªniaj¡cy.
Lektura uzupeªniaj¡ca:
M. Krasi«ski, Fale rozdziaª 11 (strony 267-300) w skrypcie pt. Wst¦p do analizy matematycznej i wybranych
dziaªów zyki, red. A. Just, Wyd. Polit. ódzkiej, ód¹ 2007.
1 Interferencja
1.1 Droga optyczna
Wielko±¢
x
opt
= nx
nazywamy drog¡ optyczn¡. Jest to po prostu droga geometryczna jak¡ przebywa ±wiatªo x pomno»ona przez
wspóªczynnik zaªamania ±wiatªa n.
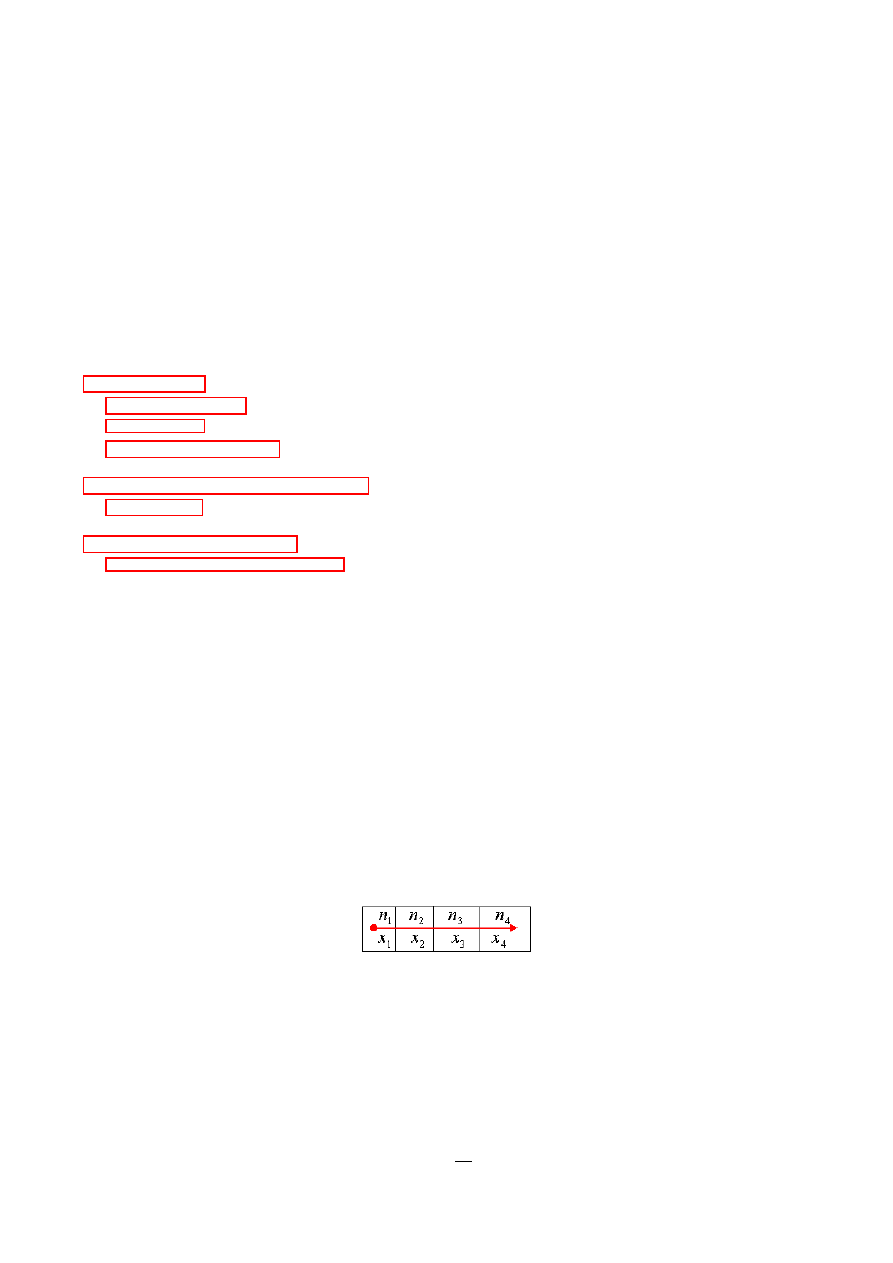
Rysunek 1: Kiedy ±wiatªo przechodzi przez kilka o±rodków......
Je±li ±wiatªo przechodzi w drodze do detektora przez kilka o±rodków to równanie dla nat¦»enia pola elektrycznego
przyjmuje posta¢
E = E
0
cos(φ) = E
0
cos
"
ωt − k
0
N
X
i=1
n
i
∆x
i
!#
gdzie
k
0
=
2π
λ
0
1
1.2 Soczewka
1 INTERFERENCJA
1.2 Soczewka
1.2.1 Dlaczego w ognisku jest jasno?
(a)
(b)
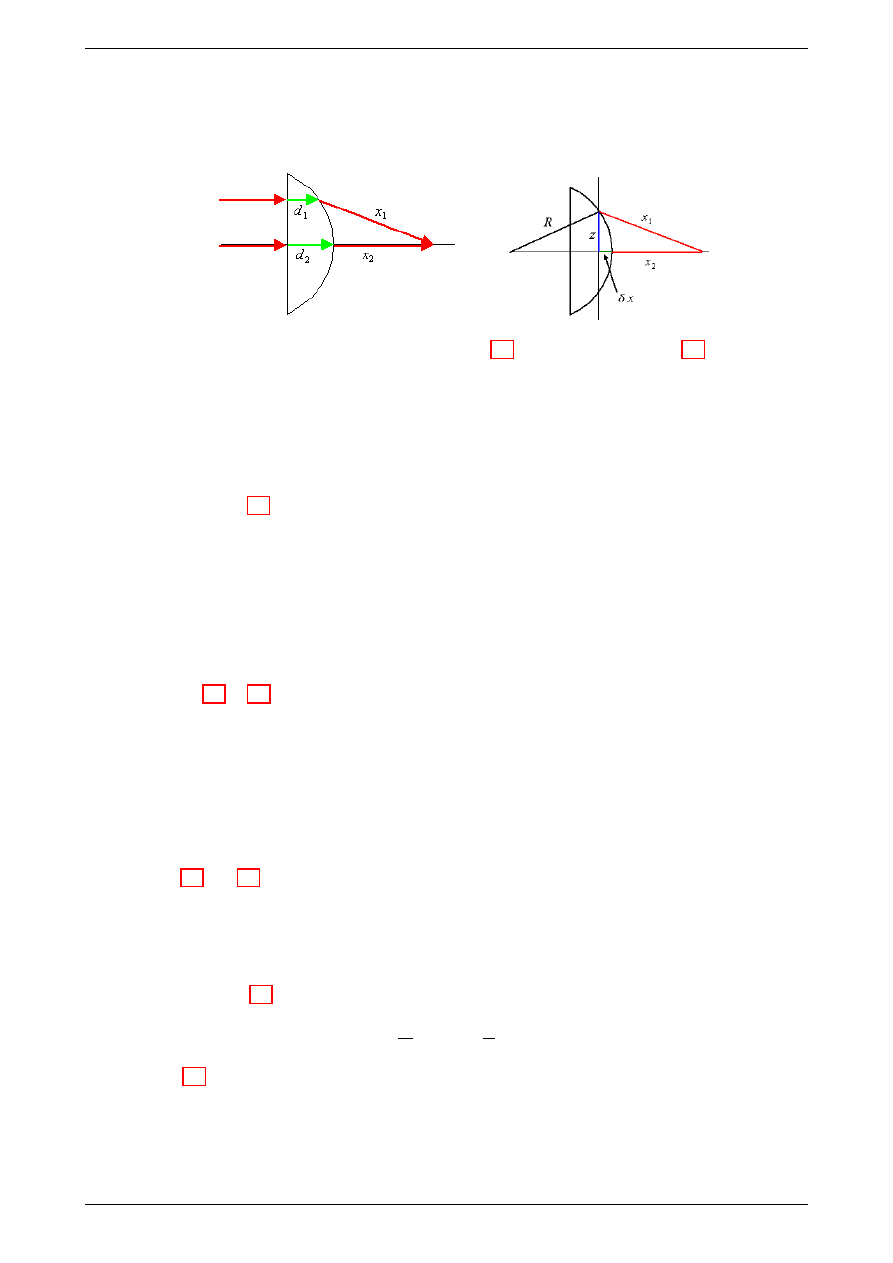
Rysunek 2: Soczewka. (a) Ilustracja do wzoru (1.1).(b) Ilustracja do wzoru (1.2).
Jaki ksztaªt musi mie¢ soczewka aby w punkcie odlegªym o x
2
od soczewki wszystkie przechodz¡ce promienie
miaªy jednakow¡ faz¦ (czyli wzmacniaªy si¦)?
Aby fazy byªy jednakowe to drogi optyczne promieni musz¡ by¢ jednakowe
x
1
+ nd
1
= x
2
+ nd
2
(1.1)
Na podstawie równania (1.1) i rysunku powy»ej mamy:
x
1
− x
2
= n(d
2
− d
1
) = nδx
(1.2)
oraz
z
2
= R
2
− (R − δx)
2
(1.3)
z
2
= x
2
1
− (x
2
+ δx)
2
(1.4)
¡cz¡c równania (1.3) i (1.4) otrzymamy
R
2
− R
2
+ 2Rδx − (δx)
2
= x
2
1
− x
2
2
− 2x
2
δx − (δx)
2
czyli
2Rδx = x
2
1
− x
2
2
− 2x
2
δx
2Rδx = (x
1
− x
2
)(x
1
+ x
2
) − 2x
2
δx
(1.5)
Podstawiaj¡c (1.2) do (1.5) i przyjmuj¡c, »e x
1
+ x
2
≈ 2x
2
otrzymamy
2Rδx = nδx2x
2
− 2x
2
δx
R = nx
2
− x
2
(1.6)
albo zapisuj¡c równanie (1.6) w inny sposób
1
x
2
= (n − 1)
1
R
(1.7)
Czy równanie (1.7) co± Ci przypomina?
c
Mariusz Krasi«ski 2009
2
1.3 Pojedyncza szczelina
2 ZDOLNO ROZDZIELCZA PRZYRZDÓW...
1.3 Pojedyncza szczelina
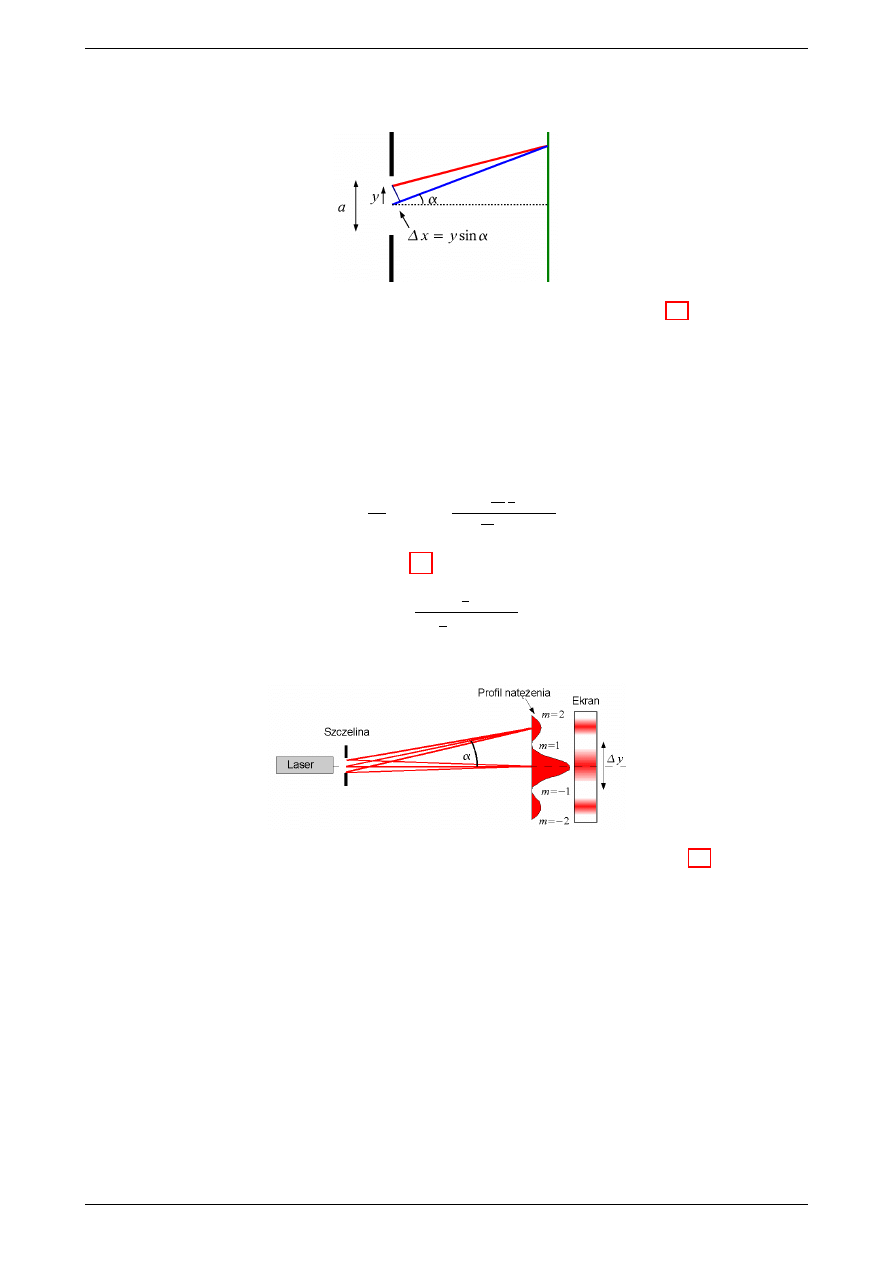
Rysunek 3: Pojedyncza szczelina. Ilustracja do wyprowadzenia wzoru (1.9)
•
Dzielimy szczelin¦ na wiele jednakowych odcinków
•
Zakªadamy, »e do ekranu jest daleko
•
czyli promienie mo»emy uwa»a¢ za równolegªe.
Nat¦»enie pola elektrycznego na ekranie (w konkretnym punkcie) liczymy sumuj¡c wkªady od poszczególnych
fragmentów szczeliny. Otrzymamy wtedy
E =
E
0
a
e
i(ωt−kx
0
)
2 sin
2π
λ
a
2
sin α
2π
λ
sin α
(1.8)
Pami¦taj¡c, »e I ∝ |E
o
|
2
otrzymamy z równania (1.8)
I = I
0
4 sin
2
π
λ
a sin α
π
λ
a sin α
2
(1.9)
Rozkªad nat¦»enia ±wiatªa na ekranie wygl¡da jak na rysunku poni»ej.
Rysunek 4: Obraz dyfrakcyjny od pojedynczej szczeliny. Ilustracja do wzoru (1.9)
Minima interferencyjne wyst¦puj¡ dla k¡tów speªniaj¡cych równanie
a sin α = mλ
2 Zdolno±¢ rozdzielcza przyrz¡dów optycznych (czyli, dlaczego teleskopy
s¡ takie du»e?)
Poni»ej zamieszczono pomocnicze obrazki. Opisy nale»y uzupeªni¢ na wykªadzie.
c
Mariusz Krasi«ski 2009
3
2.1 Przykªad
2 ZDOLNO ROZDZIELCZA PRZYRZDÓW...
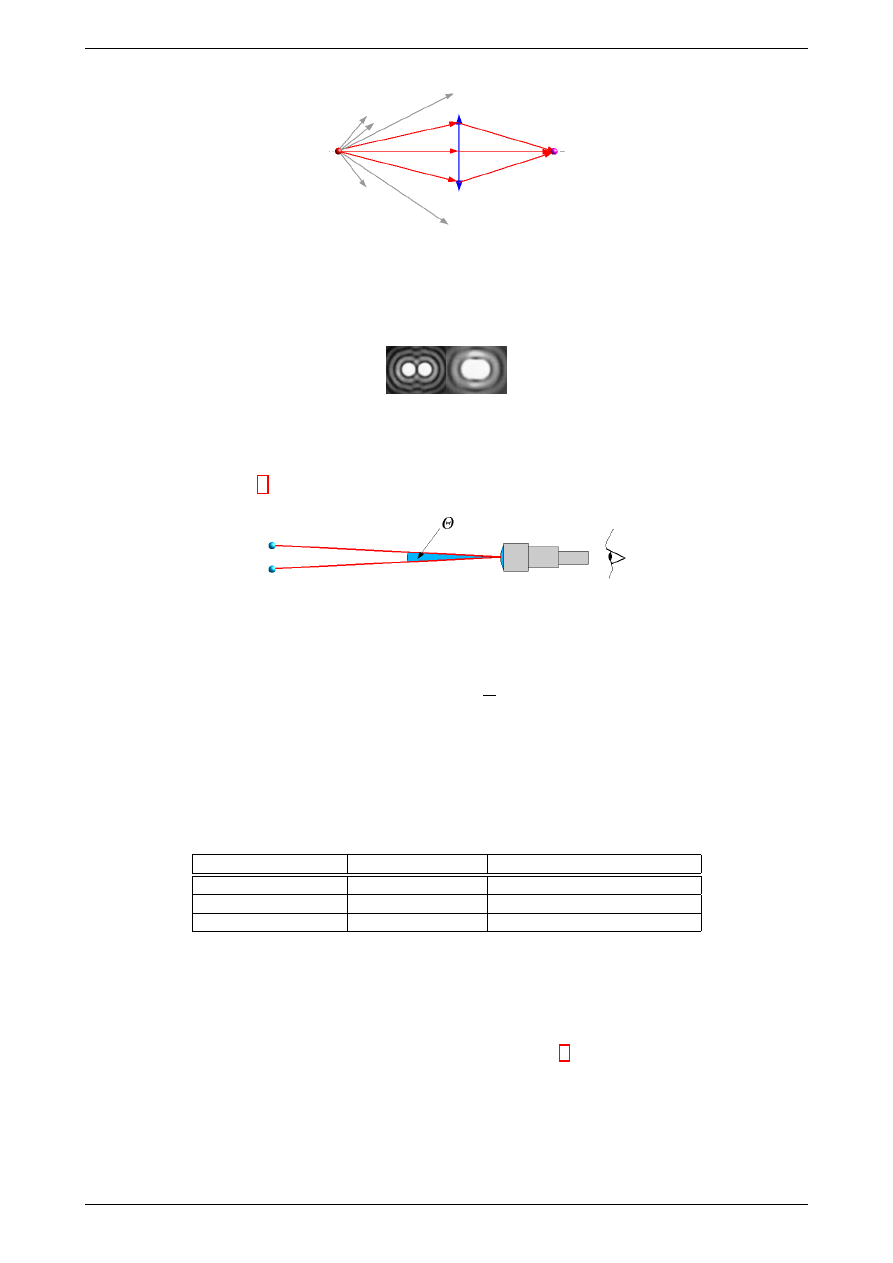
Rysunek 5: Zdolno±¢ rozdzielcza obiektywu zale»y od .................
Z powodu ograniczonej zdolno±ci rozdzielczej ukªadu optycznego dwa blisko poªo»one obiekty (punkty) nie
zawsze daj¡ si¦ rozró»ni¢
Rysunek 6: Dwa blisko poªo»one obiekty (punkty) nie zawsze daj¡ si¦ rozró»ni¢
Miar¡ zdolno±ci rozdzielczej jest minimalny k¡t Θ pod jakim widzimy dwa punktowe obiekty, które daj¡ si¦
jeszcze rozró»ni¢ (rysunek 7).
Rysunek 7: Denicja k¡ta Θ wykorzystywanego w denicji zdolno±ci rozdzielczej ukªadu optycznego.
Najcz¦±ciej przyjmuje si¦, »e zdolno±¢ rozdzielcza wynosi
sin Θ = 1, 22
λ
D
gdzie D jest ±rednic¡ wej±ciow¡ ukªadu optycznego.
2.1 Przykªad
Przyjmijmy, »e obserwujemy dwa punktowe obiekty z odlegªo±ci 100 m. Jak blisko mog¡ by¢ te punkty aby
mo»na je byªo rozró»ni¢ w przypadku ró»nych ukªadów optycznych?
Ukªad optyczny
±rednica wej±ciowa Minimalna odlegªo±¢ punktów
Oko
0,5 mm
12 cm
Lornetka
5 cm
1,2 mm
Najwi¦ksze teleskopy
10 m
0,006 mm (6 µm)
Tablica 1: Minimalna (zapewniaj¡ca optyczne rozdzielenie) odlegªo±¢ od siebie dwóch punktowych obiektów
umieszczonych w odlegªo±ci 100 m od obserwatora.
Dzi¦ki zastosowaniu ukªadu teleskopów (interferometr gwiazdowy) mo»liwe jest rozdzielenie obiektów, których
nie mo»na rozdzieli¢ klasycznym teleskopem. Poni»ej rysunek, który zostanie omówiony na wykªadzie, przed-
stawiaj¡cy zasad¦ dziaªania interferometru gwiazdowego. Opisz rysunek 8 podczas wykªadu.
c
Mariusz Krasi«ski 2009
4
3 PODSTAWY INTERFEROMETRII
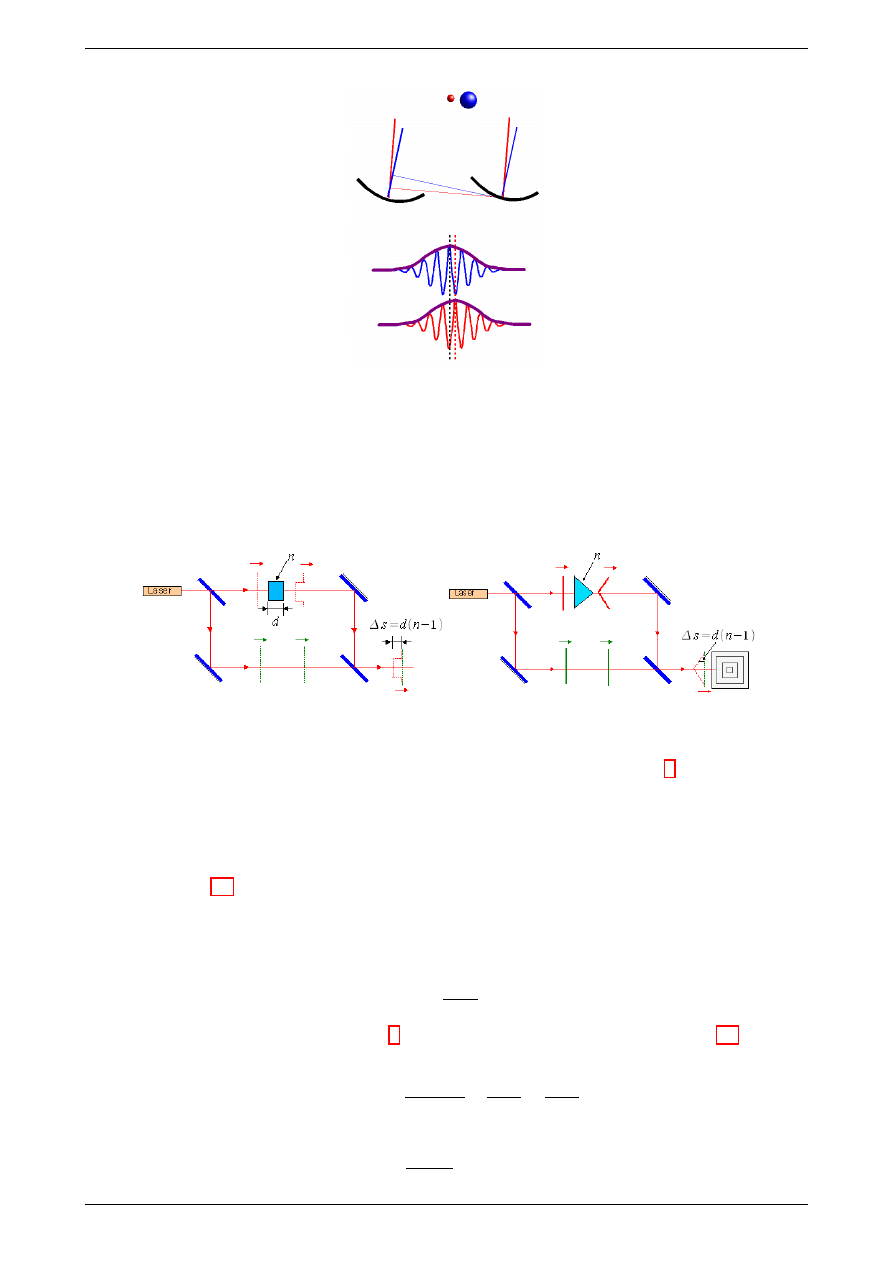
Rysunek 8: Interferometr gwiazdowy Michelsona.
3 Podstawy interferometrii
3.1 Interferometr Macha-Zehndera
Przykªady zastosowa« na wykªadzie oraz w sekcji Galeria
Rysunek 9: Interferometr Macha-Zehndera
Po przej±ciu przez o±rodek o grubo±ci d i wspóªczynniku zaªamania ±wiatªa n (rysunek 9a) czoªo fali opó¹nia
si¦ wzgl¦dem cz¦±ci czoªa fali, które przeszªy obok warstwy albo czoªa fali, która przeszªa doln¡ drog¡. Po
naªo»eniu czoªa fali, która przeszªa przez warstw¦ i czoªa fali id¡cej doln¡ drog¡ nast¡pi interferencja. Ró»nica
dróg optycznych pomi¦dzy promieniami b¦dzie
∆s = dn − d = d(n − 1)
(3.1)
Bior¡c pod uwag¦ (3.1) warunek wzmocnienia b¦dzie
d(n − 1) = N λ
(3.2)
W takim razie na obrazie interferencyjnym b¦dzie jasno (wzmocnienie) o ile grubo±¢ warstwy b¦dzie
d =
N λ
n − 1
(3.3)
Je±li grubo±¢ warstwy b¦dzie zmienna (rysunek 9b) to w miejscach gdzie grubo±¢ speªnia warunek (3.3) powstan¡
jasne pr¡»ki. Wzrost grubo±ci warstwy odpowiadaj¡cy dwóm kolejnym jasnym (albo ciemnym) pr¡»kom b¦dzie
d
N +1
− d
N
=
(N + 1)λ
n − 1
−
N λ
n − 1
=
λ
n − 1
(3.4)
Podstawiaj¡c dane dla szkªa i »óªtego ±wiatªa otrzymamy
∆d =
550
nm
1, 5 − 1
= 1100
nm
c
Mariusz Krasi«ski 2009
5

3.1 Interferometr Macha-Zehndera
3 PODSTAWY INTERFEROMETRII
Analizuj¡c zmiany jasno±ci pomi¦dzy pr¡»kami mo»na do±¢ ªatwo zmierzy¢ zmiany grubo±ci nawet do 100 razy
mniejsze czyli rz¦du 10 nm.
c
Mariusz Krasi«ski 2009
6
Document Outline
Wyszukiwarka
Podobne podstrony:
więcej podobnych podstron