
Projekt ze
statystyki
„Awarie na sieciach
wodociągowych”
Autorzy:
Dominik Szołtysik
Kamil Wieczorek

I . Niniejszy projekt powstał w ramach pracy zaliczeniowej z przedmiotu STATYSTYKA na I
semestrze studiów uzupełniających magisterskich. Celem naszego projektu było opracowanie
danych statystycznych dotyczących awarii na sieciach wodociągowych. Dane pochodzą z I półrocza
2006-go roku i zawierają następujące zmienne:
•
Rodzaj sieci na której doszło do awarii,
•
Materiał z którego wykonana jest sieć,
•
Średnica rur,
•
Data zgłoszenia awarii,
•
Data rozpoczęcia naprawy,
•
Godzina rozpoczęcia naprawy,
•
Data zakończenia awarii,
•
Godzina zakończenia awarii,
•
Czas bezuszkodzeniowej pracy,
•
Czas odnowy,
•
Nowy czas odnowy (czas zapisany dziesiętnie),
•
Czas naprawy,
•
Czas oczekiwania na naprawę,
•
Dzień tygodnia awarii.
Do wykonania mieliśmy następujące zadania:
1) Poprawić dane statystyczne - dane zawierały nieprawidłowo wyliczone czasy odnowy, czasy
naprawy i czasy oczekiwania na naprawę (dane poprawiliśmy poprzez wyliczenie różnicy
pomiędzy godziną zakończenia awarii, a godziną zgłoszenia - dla czasu odnowy i analogicznie dla
pozostałych czasów).
2) Sprawdzić częstość awarii za względu na dzień tygodnia.
3) Wykonać analizę wariancji czasu odnowy ze względu na rodzaj sieci oraz ze względu na
materiał z którego wykonana jest sieć (stal, żeliwo, ocynk), na których sieciach awarie są
najdłuższe? Czy długość trwania awarii zależy od materiału z którego wykonana jest sieć?
4) Dopasować rozkłady czasu (czas odnowy i naprawy), czy mają rozkład normalny?,
5)
Wykonać regresję ze względu na średnicę (czy ma sens?), a liczbę awarii (osobno dla każdej
sieci i w sumie).
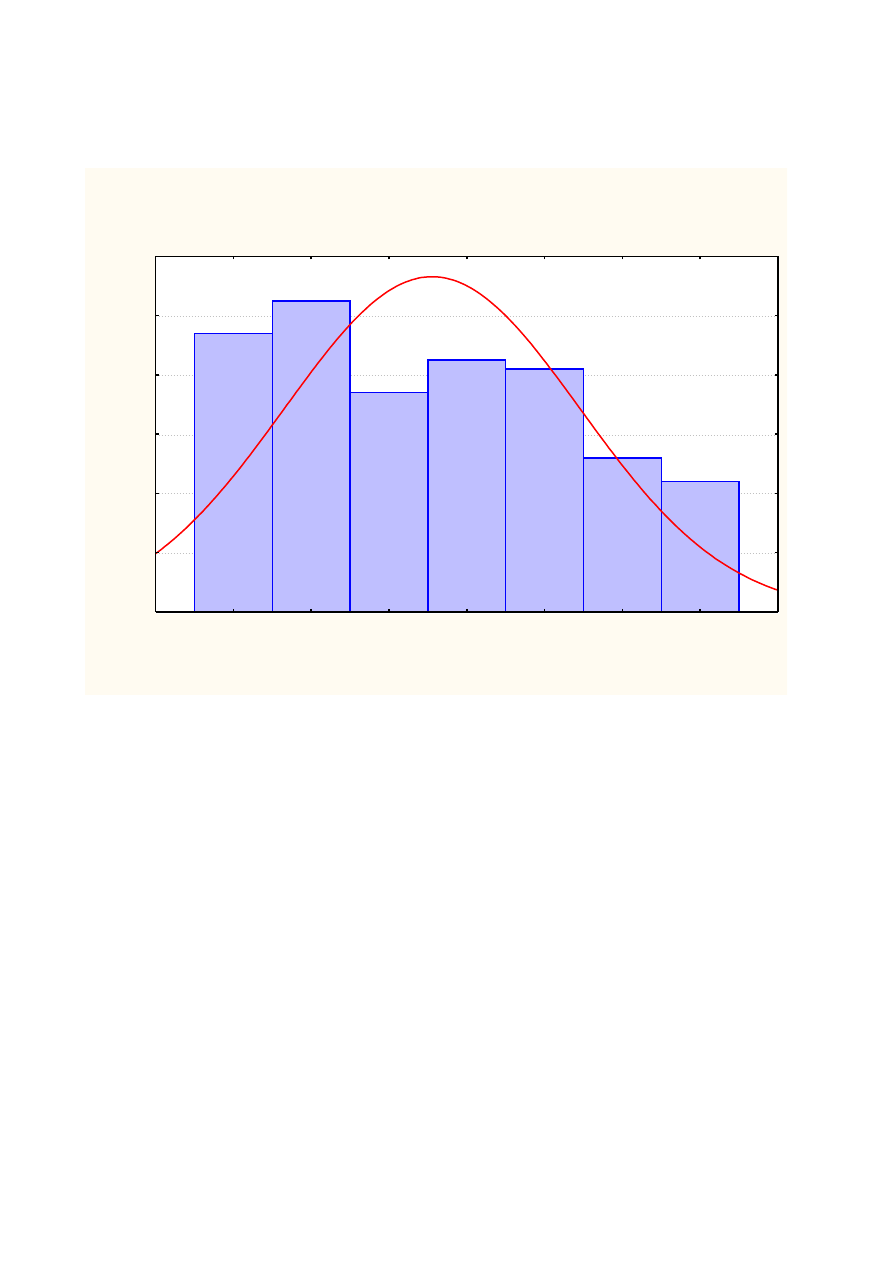
Zad.2
Analiza ilości awarii ze względu na dzień tygodnia dla wszystkich sieci:
Histogram Dzień tygodnia awarii
zbiorczy.sta 14v*536c
Dzień tygodnia awarii = 536*1*normal(x; 3,5373; 1,8901)
poniedziałek
wtorek
środa
czwartek
piątek
sobota
niedziela
Dzień tygodnia awarii
0
20
40
60
80
100
120
Li
cz
b
a
o
bs
.
z naszej analizy wynika, że najwięcej awarii zdarzyło się we wtorki (105 co stanowi 18,6%
wszystkich awarii), a najmniej w niedziele (44 tj. 8,2%).
Podsumowanie:
ilość
procentowo
poniedziałek
94
17,54 %
wtorek
105
19,59 %
środa
74
13,81 %
czwartek
85
15,86 %
piątek
82
15,30 %
sobota
52
9,70 %
niedziela
44
8,21 %
Suma
536
100 %
Jak widać ilość awarii w poszczególnych dniach tygodnia różni się. Przeprowadzimy analizę
wariancji. W tym celu stworzyliśmy nowy arkusz danych o nazwie dni_tygodnia . Arkusz zawiera 3
kolumny: data (wszystkie dni od 1.1.2006 do 30.6.2006), ilość awarii w danym dniu oraz dzień
tygodnia odpowiadający danej dacie.
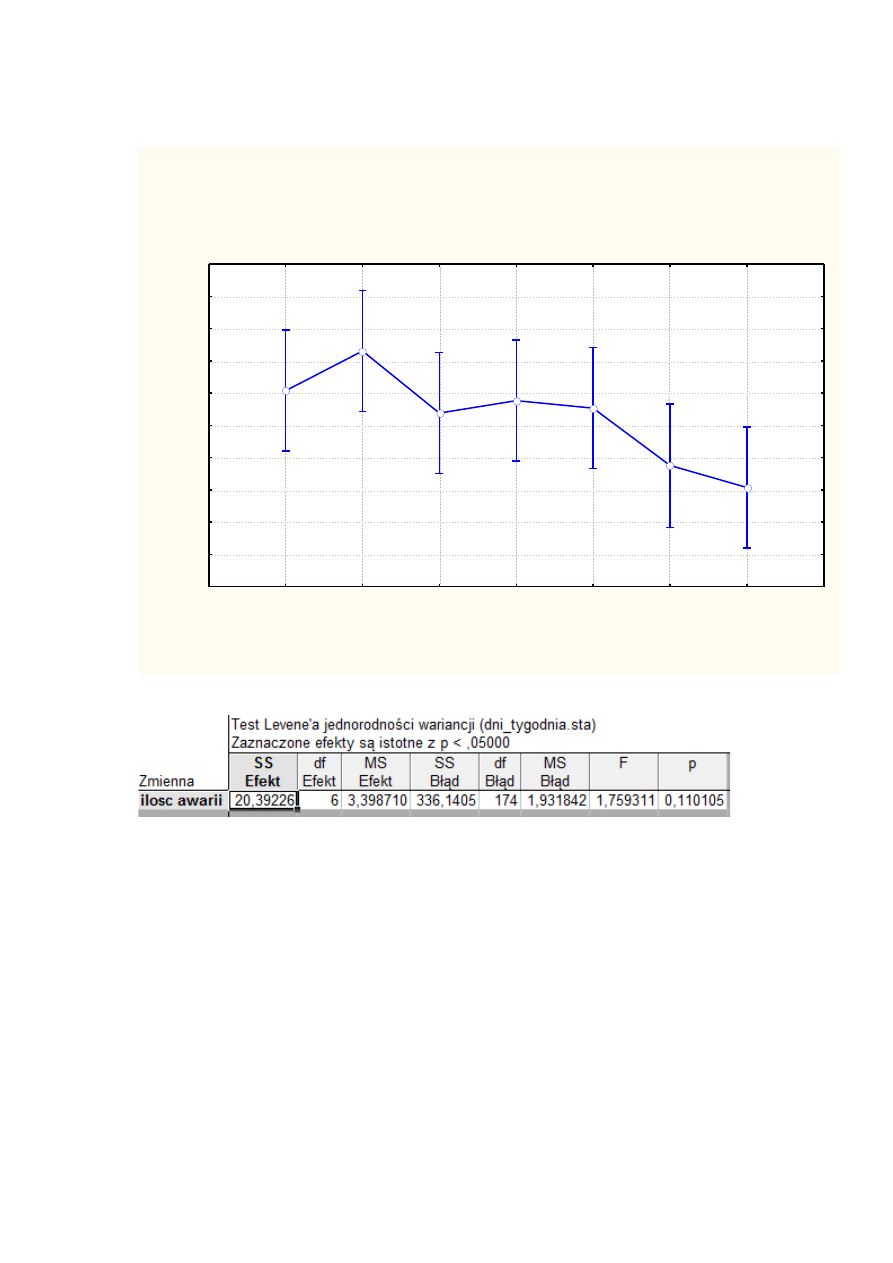
Wykres średnich w poszczególnych dniach:
dzien tygodnia; Oczekiwane średnie brzegowe
Bieżący efekt: F(6, 174)=2,2373, p=,04181
Dekompozycja efektywnych hipotez
Pionowe słupki oznaczają 0,95 przedziały ufności
poniedziałek
wtorek
środa
czwartek
piątek
sobota
niedziela
dzien tygodnia
0,0
0,5
1,0
1,5
2,0
2,5
3,0
3,5
4,0
4,5
5,0
ilo
sc
a
w
ar
ii
Wykonujemy test Leven`a. Wyniki przedstawia tabela poniżej:
Jako hipotezę H
0
przyjmujemy tezę o równości wariancji. Ponieważ w tym przypadku
wartość p jest większa od poziomu
α
= 0,05, nie mamy podstaw do odrzucenia H
0.
Tym samym
analiza nie wykazała istotnych różnic wariancji między grupami (w naszym przypadku dni
tygodnia). Przeprowadzamy dalsze rozważania.
Przeprowadzamy testy hipotezy o równości średnich w grupach (testy Post-Hoc).
Wykonujemy test Scheffego.
Wynik testu:
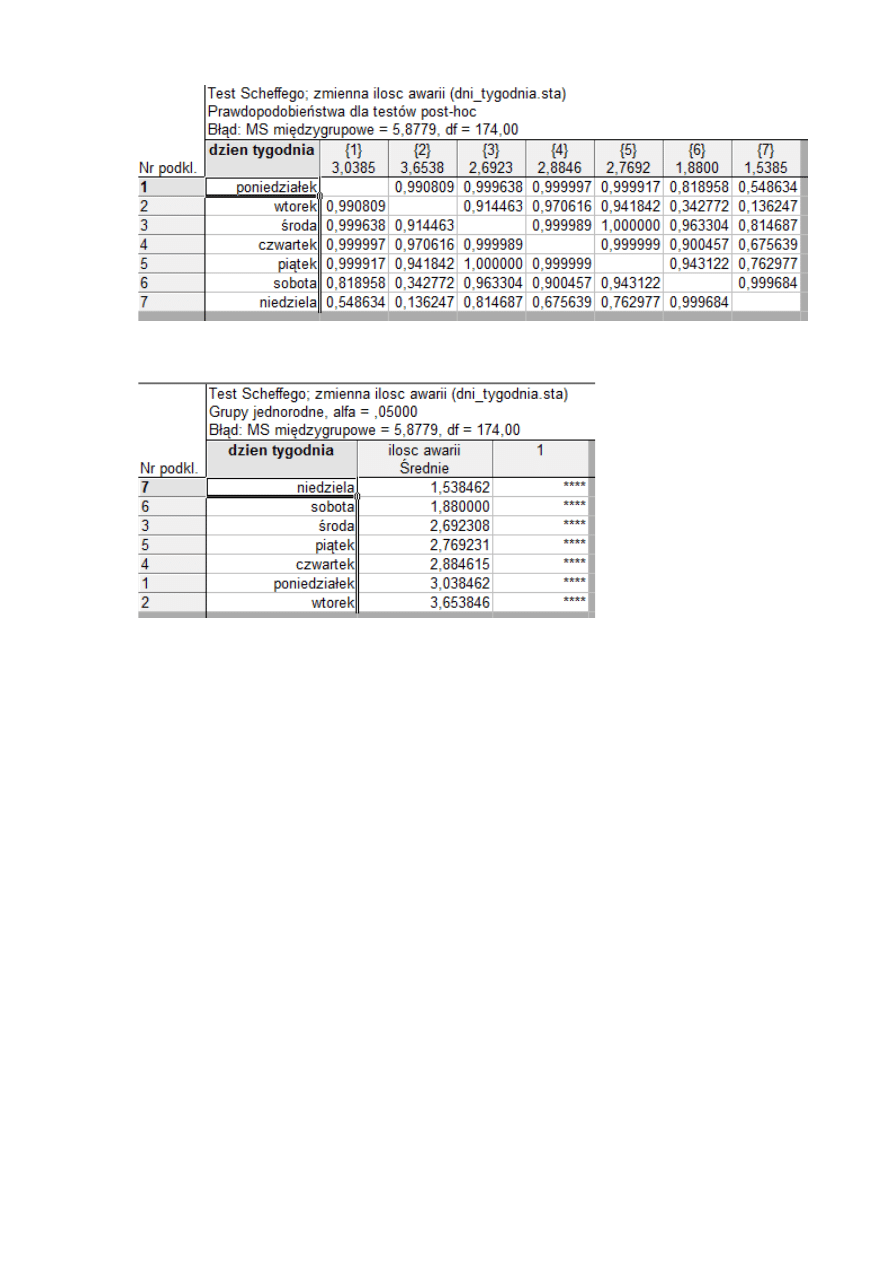
Dla lepszego zobrazowania wybieramy opcję pokazania grup jednorodnych.
Jako hipotezę H
0
przyjmujemy tezę o równości średnich ilości awarii. Wynik testu
pokazuje, że dni tworzą grupę jednorodną. Tym samym nie mamy podstaw do odrzucenia H
0
.
WNIOSEK:
Pomimo, że w okresie czasu, którego dotyczyły nasze dane obserwujemy różną ilość awarii w
zależności od dnia, test wskazuje, że dni tygodnia tworzą jedną grupę jednorodną. Nie mamy
podstaw do odrzucenia hipotezy o równości średnich ilości awarii w poszczególnych dniach
tygodnia.
•
Dane do wglądu w skoroszycie roboczym(dni_tygodnia_skoroszyt).
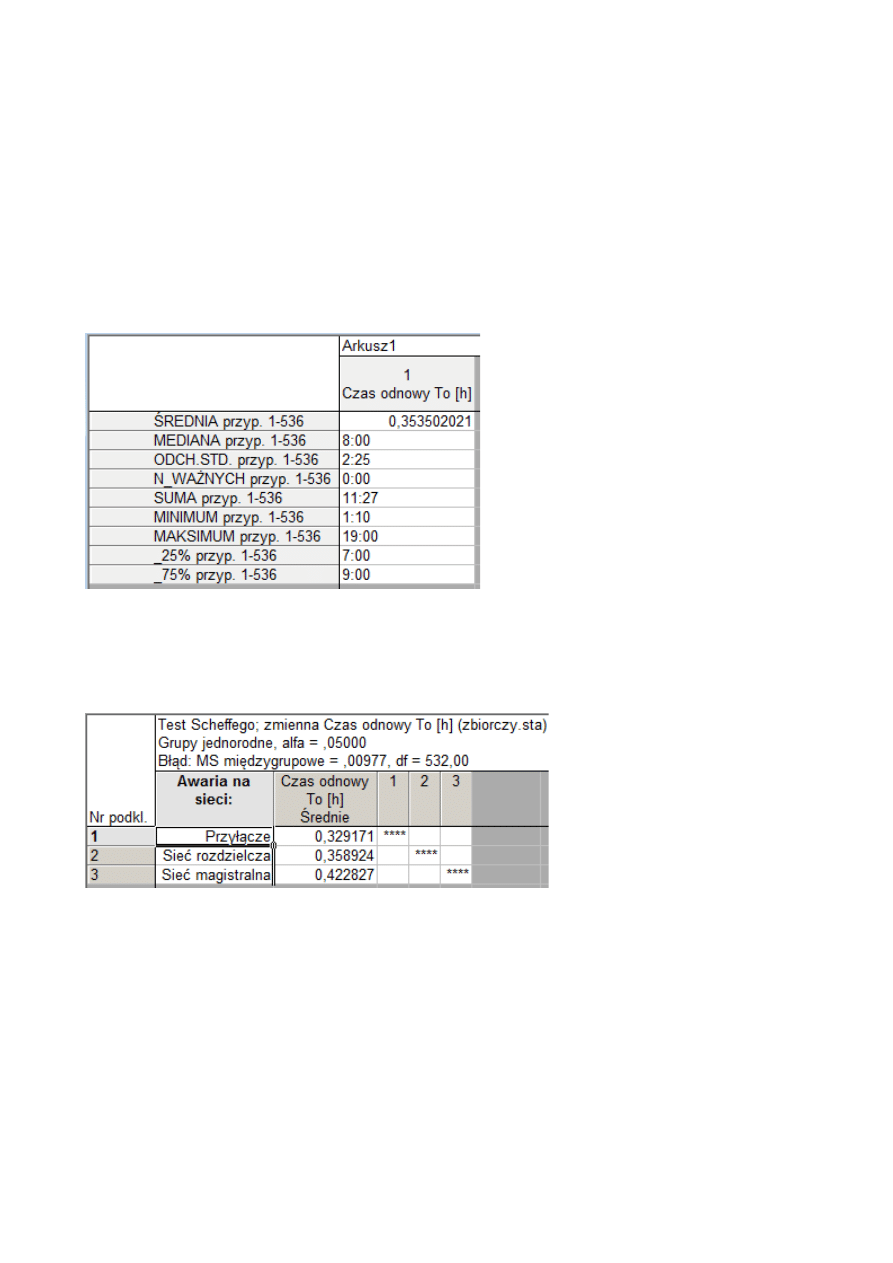
Zad.3
Wykonujemy analizę wariancji:
KOMENTARZ:
Wykonując analizę wariancji natrafiliśmy na nieoczekiwane działanie programu
STATISTICA, mianowicie wyliczone przez nas na nowo czasy odnowy były w formacie czasu
hh:ss . Okazało się, że program licząc np. średnie lub sumując tak zapisane czasy działa
nieoczekiwanie, tj. sumując czasy np. 13:00+5:00+4:00 daje 21:00, ale dodając teraz 21:00+3:00
daje wynik 0:00 i teraz dodając do tego np. 7:00 mamy 0:00+7:00=7:00. Jest to dla nas działanie
bardzo niepożądane, bo wykonując statystykę wszystkich czasów odnowy i zaznaczając opcję
wszystko otrzymujemy wynik:
jak widać wyliczenia są błędne – SUMA przyp. 1-536=11:27, a ŚREDNIA
przyp. 1-536=0,353502021.
Powyższą nieprawidłowość zauważyliśmy dopiero 2.stycznia podsumowując nasze wyniki
(naszą uwagę zwróciły bardzo małe średnie czasów odnowy w poszczególnych grupach np.
).
Konieczne okazało się zapisanie czasów odnowy w inny sposób, tj. znak „:” został zastąpiony
„ ,” , a część czasu wyrażona w minutach została zapisana dziesiętnie i tak np. czas 4:10 został
zapisany jako 4,16, a czas 9:50 jako 9,83 (komórki zostały sformatowane jako liczbowe). Czasy te
zostały zapisane jako zmienna 12 „nowy czas odnowy”. Wszystkie analizy musieliśmy
przeprowadzić na nowo.

Wykonujemy ponownie statystykę nowego czasu odnowy, by mieć pewność, że nowe dane są
poprawne:
jak widać tym razem program działa prawidłowo, tj. ŚREDNIA i SUMA są poprawne.
Przystępujemy do analizy wariancji.
•
Czas odnowy ze względu na rodzaj sieci:
Wykonujemy test Leven’a, wyniki testu przedstawia poniższa tabela
Jako hipotezę H
0
przyjmujemy tezę o równości wariancji czasów odnowy.
Ponieważ wartość p jest mniejsza od poziomu
α
= 0,05 odrzucamy hipotezę H
0
i przyjmujemy, że
wariancja zmiennej zależnej w grupach (sieciach) różni się. Przeprowadzamy testy hipotezy o
równości średnich (testy Post-Hoc).
W naszych doświadczeniach pomocny może się okazać wykres średnich w poszczególnych
grupach:
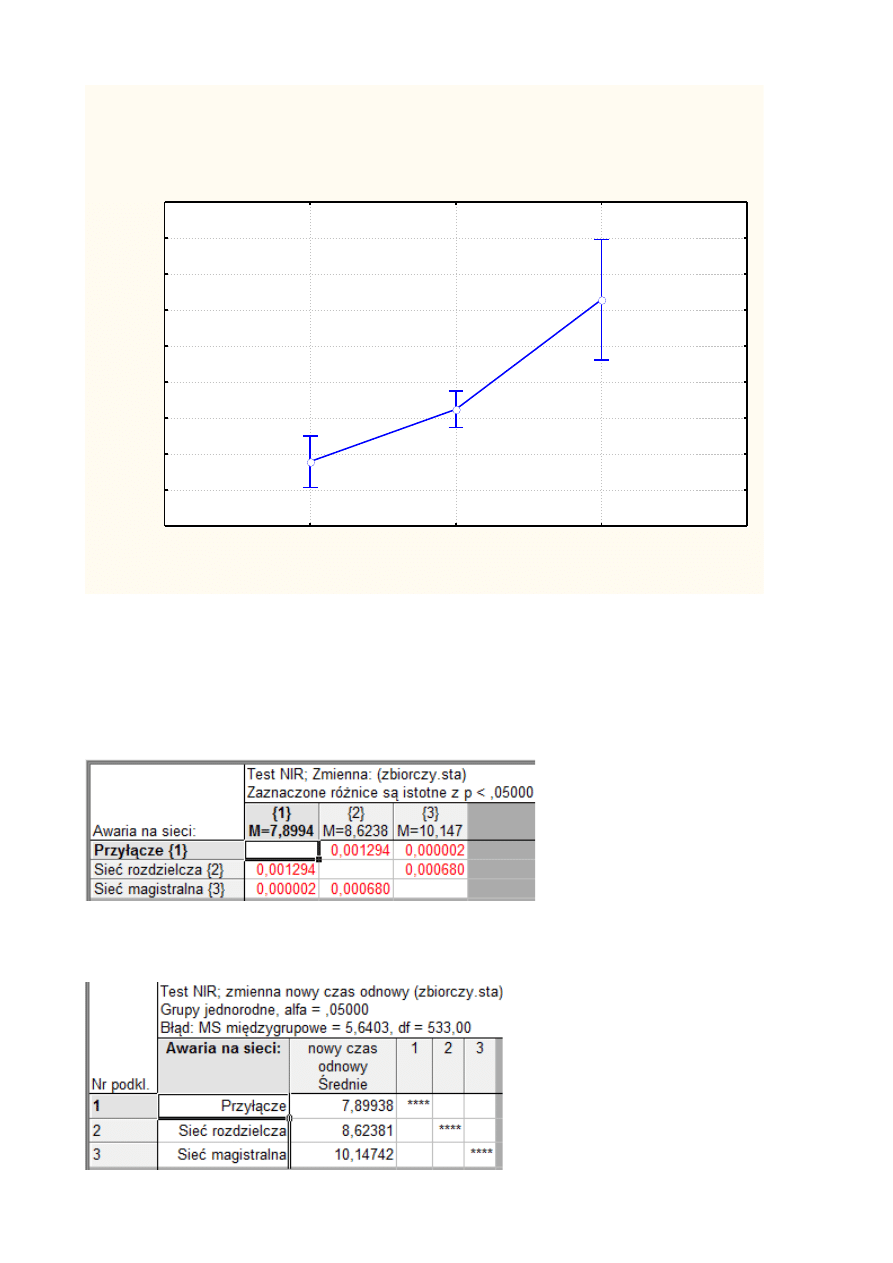
Awaria na sieci:; Oczekiwane średnie brzegowe
Bieżący efekt: F(2, 533)=13,306, p=,00000
Dekompozycja efektywnych hipotez
Pionowe słupki oznaczają 0,95 przedziały ufności
Przyłącze
Sieć rozdzielcza
Sieć magistralna
Awaria na sieci:
7,0
7,5
8,0
8,5
9,0
9,5
10,0
10,5
11,0
11,5
no
w
y
cz
as
o
dn
ow
y
Z wykresu można wywnioskować, że średnie czasy odnowy na sieciach różnią się od siebie,
jednakże widać również, że wartością najbardziej odstającą od pozostałych jest średni czas odnowy
na sieci magistralnej. Wartości dla sieci przyłącza i sieci rozdzielczej są bardziej zbliżone, w celu
wykluczenia ich jednorodności przeprowadzamy dalsze testy.
Wykonujemy test NIR Fischera. Wynik testu ilustruje poniższa tabela :
jak widać różnice między grupami są istotne. Dla lepszego zilustrowania wyniku testu zaznaczamy
również opcję pokazania grup jednorodnych (tabela poniżej).
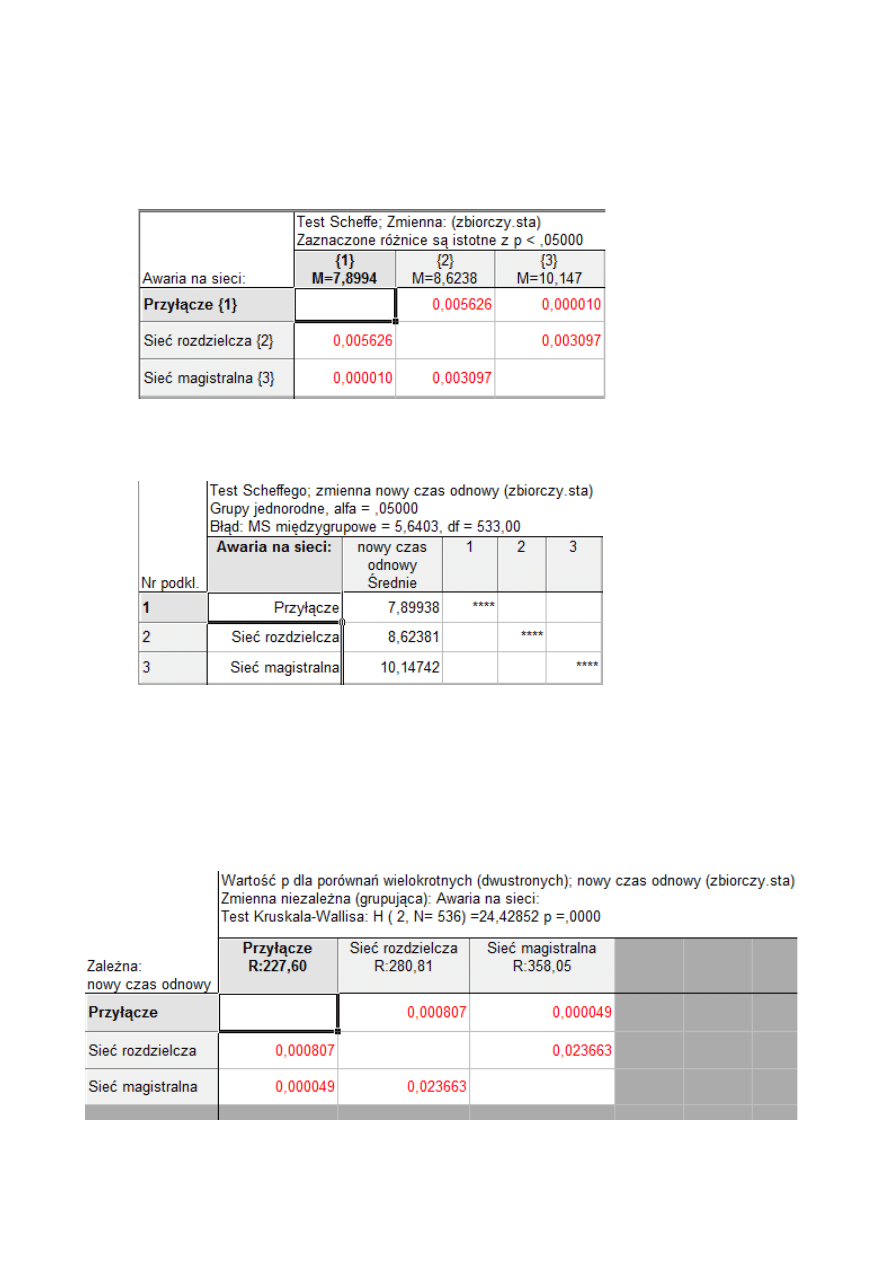
Jako hipotezę H
0
przyjmujemy tezę o równości średnich czasu odnowy. Wynik testu
pokazuje, że grupy nie są jednorodne. Tym samym odrzucamy hipotezę o równości średnich.
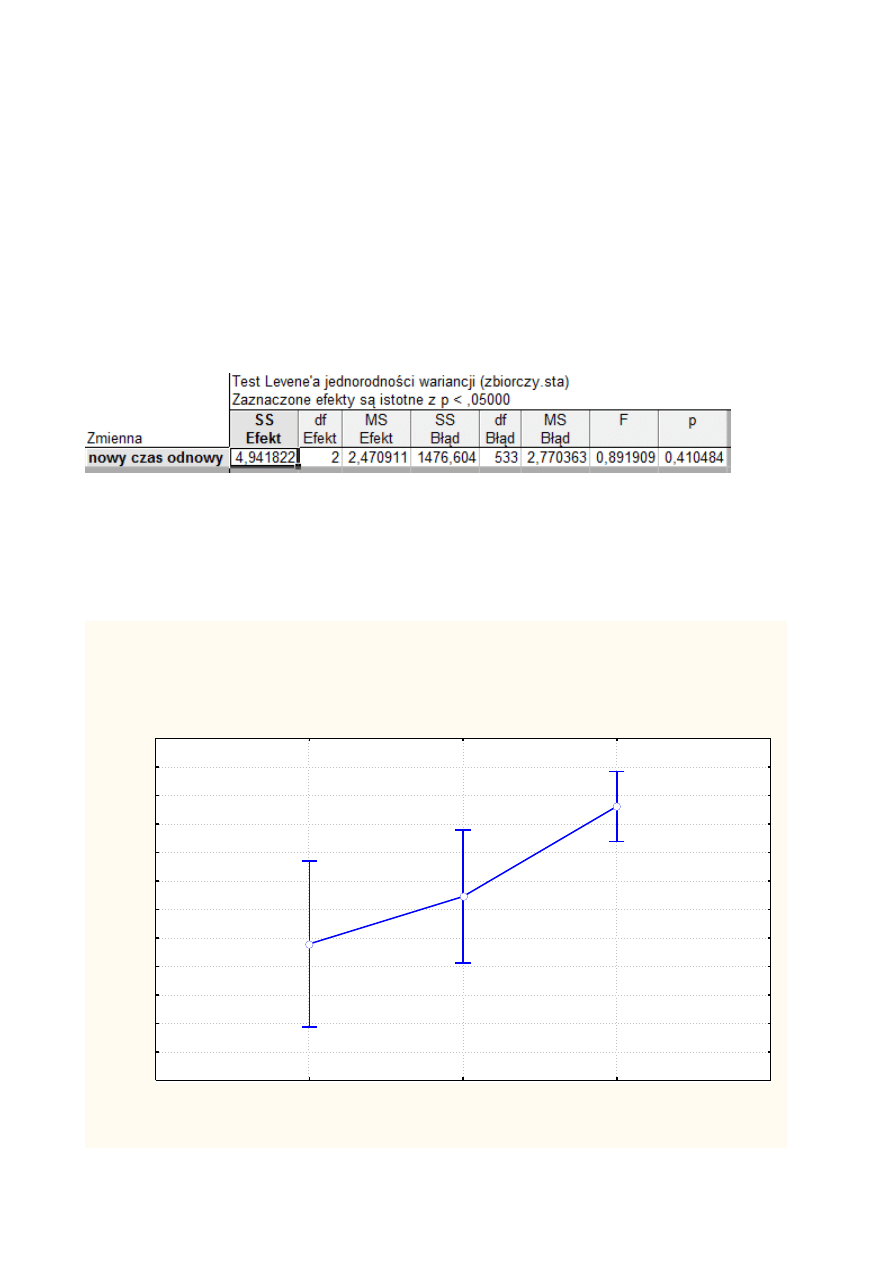
Dla porównania przeprowadzimy również test Scheffego. Wynik testu został pokazany w
poniższej tabeli:
tak samo jak w teście NIR różnice są istotne. Dla lepszego zilustrowania wyniku testu, tak jak dla
testu NIR zaznaczamy również opcję pokazania grup jednorodnych (tabela poniżej).
Jak widać wyniki testów się ze sobą pokrywają, tzn. test Schaffego również odrzucił
hipotezę o równości średnich w grupach.
Ponieważ nie jest spełnione założenie o jednorodności wariancji nasze rozważania nie są do
końca poprawne. Dla porównania wykonujemy test Kruskala-Wallisa. Wyniki testu pokazane są w
poniższych tabelach:
Jak widać wartości w tabeli wpisane zostały kolorem czerwonym, tzn. różnice są istotne i
uzyskujemy ten sam podział co w przypadku testu NIR Fischera i testu Schaffego.
WNIOSEK:
Pomimo nie spełnienia założeń o jednorodności wariancji testy dały ten sam podział na grupy
jednorodne, tzn. odrzuciliśmy hipotezy o równości średnich czasów odnowy między sieciami. Tym
samym długość czasu odnowy zależy od sieci na której doszło do awarii. Najdłuższy czas ma sieć
magistralna (można to tłumaczyć skomplikowaniem naprawy tej sieci – średnica rur jest
największa), następnie sieć rozdzielcza, a najkrótszy sieć przyłącza.
•
Dane do wglądu w skoroszycie roboczym(siec_czasodnowy_anwar).
•
Czas odnowy ze względu na materiał:
Wykonujemy test Leven’a, wyniki testu przedstawia poniższa tabela
Jako hipotezę H
0
przyjmujemy tezę o równości wariancji, ponieważ w tym przypadku
wartość p jest większa od poziomu
α
= 0,05, nie mamy podstaw do odrzucenia H
0.
Tym samym
analiza nie wykazała istotnych różnic wariancji między grupami (w naszym przypadku materiał z
którego wykonana jest sieć). Przeprowadzamy dalsze rozważania.
Wykres oczekiwanych średnich brzegowych:
Materiał; Oczekiwane średnie brzegowe
Bieżący efekt: F(2, 533)=6,1932, p=,00219
Dekompozycja efektywnych hipotez
Pionowe słupki oznaczają 0,95 przedziały ufności
stal
stal ocynkowana
żeliwo
Materiał
6,8
7,0
7,2
7,4
7,6
7,8
8,0
8,2
8,4
8,6
8,8
9,0
9,2
no
w
y
cz
as
o
dn
ow
y
Z wykresu można wywnioskować, że średnie czasy odnowy w zależności od materiału
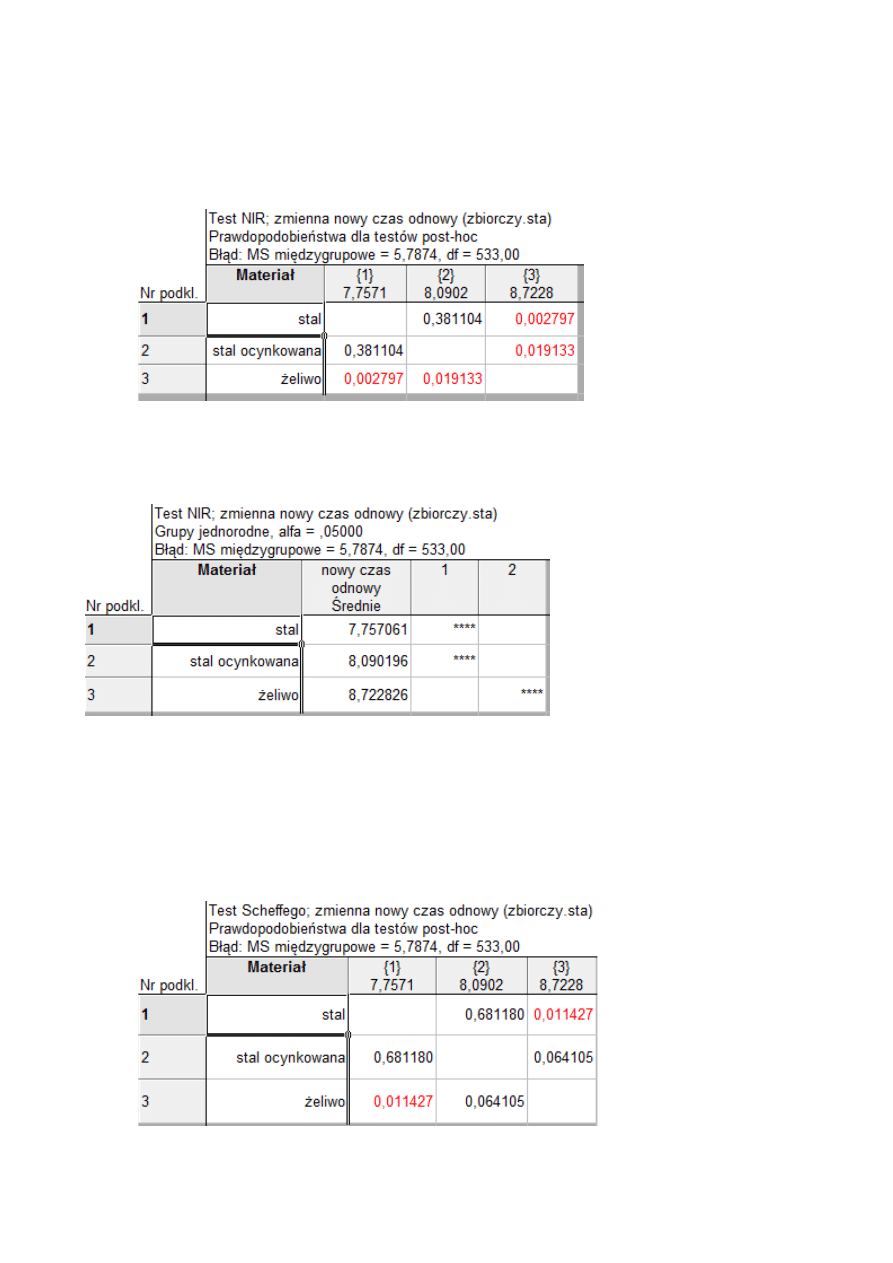
różnią się od siebie, jednakże różnice te są mniejsze niż to miało miejsce w zależności od rodzaju
sieci. Przeprowadzamy dalsze testy .
Wykonujemy test NIR Fischera. Wynik testu ilustruje poniższa tabela :
jak widać nie wszystkie różnice są istotne, stal i stal ocynkowana tworzą grupę jednorodną.
Dla lepszego zilustrowania wyniku testu zaznaczamy również opcję pokazania grup
jednorodnych (tabela poniżej).
Z testu wynika, że sieć wykonana ze stali oraz sieć wykonana ze stali ocynkowanej tworzą
grupę jednorodną, tzn. w grupie tej nie mamy podstaw do odrzucenia hipotezy H
0
, tym samym
średni czas odnowy dla tych sieci jest taki sam. Natomiast czas odnowy dla sieci wykonanej z
żeliwa jest większy i w tym przypadku odrzucamy H
0.
Dla porównania przeprowadzimy również test Scheffego. Wynik testu został pokazany w
poniższej tabeli:
jak widać w przypadku tego testu różnic istotnych jest mniej niż w teście NIR. Powstały dwie grupy
jednorodne, poniżej pokazujemy wynik testu z pokazaniem grup jednorodnych.
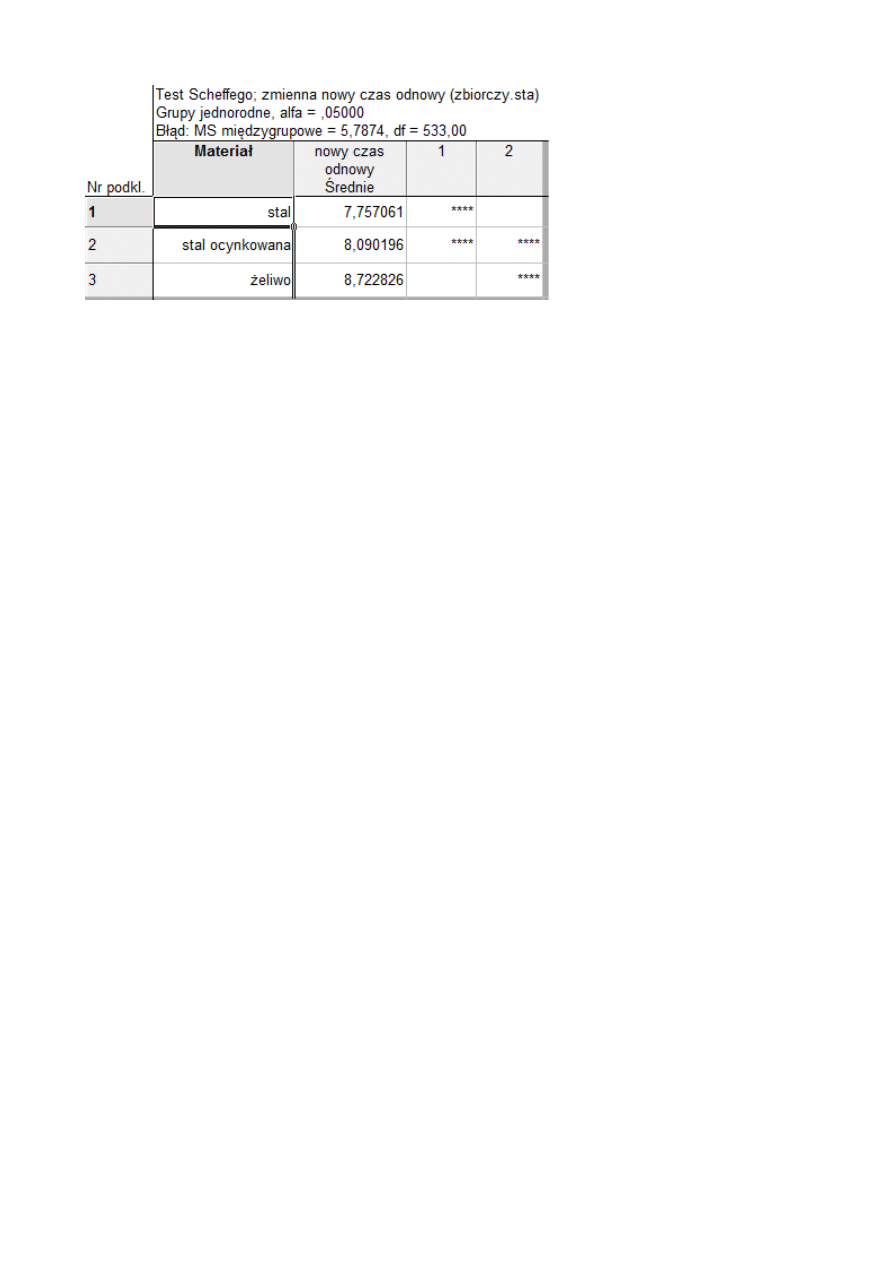
Test dał dość ciekawy podział. Zostały utworzone dwie grupy jednorodne w których nie
mamy podstaw do odrzucenia hipotezy H
0.
Jedną grupę tworzy stal i stal ocynkowana, a drugą stal
ocynkowana i żeliwo.
WNIOSEK:
Nie możemy jednoznacznie stwierdzić, czy materiał ma wpływ na czas odnowy.
•
Dane do wglądu w skoroszycie roboczym(material_czasodnowy).
Zad. 4.
Sprawdzamy czy czasy odnowy i naprawy mają rozkład normalny, oraz próbujemy
dopasować ewentualnie inne znane rozkłady.
Wyniki przedstawimy w formie tabeli:
Czas
odnowy/naprawy
Ilość przedziałów
Typ badanego rozkładu
Wartość p
O
6
Normalny
0,01
O
8
Normalny
0
O
10
Normalny
0
N
6
Normalny
0,00379
N
8
Normalny
0,0019
N
10
Normalny
0
Jako hipotezę H
0
przyjmujemy, że dane mają rozkład normalny, ponieważ wartości p są
mniejsze od poziomu
α
= 0,05, odrzucamy hipotezę H
0.
Wyniki zostały przedstawione dla testu Chi-kwadrat, natomiast badania zostały wykonane
również dla testów*: Lillieforsa, oraz Kołmogorowa-Smirnowa dając podobne wyniki tzn: nie
możemy przyjąć, że dane są w postaci normalnej.
Tak więc spróbujmy dopasować inne rozkłady:
Czas
odnowy/naprawy
Ilość przedziałów
Typ badanego rozkładu
Wartość p
O
10
Wykładniczy
0
O
10
Gamma
0
O
10
Lognormalny
0
O
10
Chi-kwadrat
0
N
10
Chi-kwadrat
0
N
10
Wykładniczy
0
N
10
Gamma
0
Dla powyższych wyników jako hipotezę zerową H
0
przyjmujemy, że dane mają rozkład
podany w tabeli(wykładniczy, gamma, lognormalny, chi-kwadrat). Wszystkie wartości parametru p
są równe 0 stąd możemy wnioskować (bo p=0 <
α
= 0,05), że dane nie są w postaci żadnego z
podanych rozkładów.
W powyższej tabeli prawdopodobieństwo p wyliczone zostało z testu chi-kwadrat, natomiast
badania zostały przeprowadzone również dla testu* Kołmogorowa-Smirnowa, gdzie wszystkie
wartości p< 0,1. Stąd test ten potwierdził tylko nasz wcześniejszy wniosek, iż nie możemy przyjąć,
że dane posiadają którykolwiek z podanych rozkładów.
WNIOSEK:
Na podstawie przeprowadzonych analiz możemy jednoznacznie stwierdzić, że dane nie mają
rozkładu normalnego, oraz nie mają również żadnego z podanych rozkładów: wykładniczy, gamma,
lognormlany, chi-kwadrat. Fakt ten wydaję się być jeszcze bardziej wiarygodny ponieważ badania
zostały wykonane na podstawie dość licznej próby (n=536 ).
•
Dane do wglądu w skoroszycie roboczym(dopasowanie rozkładu, dopasowanie rozkładu2).
Zad. 5
Regresja liniowa pomiędzy średnicą, a czasem odnowy:
Najpierw by badać regresję liniową modelu musimy sprawdzić, założenia, tak więc:
a) n>= 2 i wynosi 536(po usunięciu 502)
b) model jest liniowy co jednoznacznie pokazuje test F-Fischera
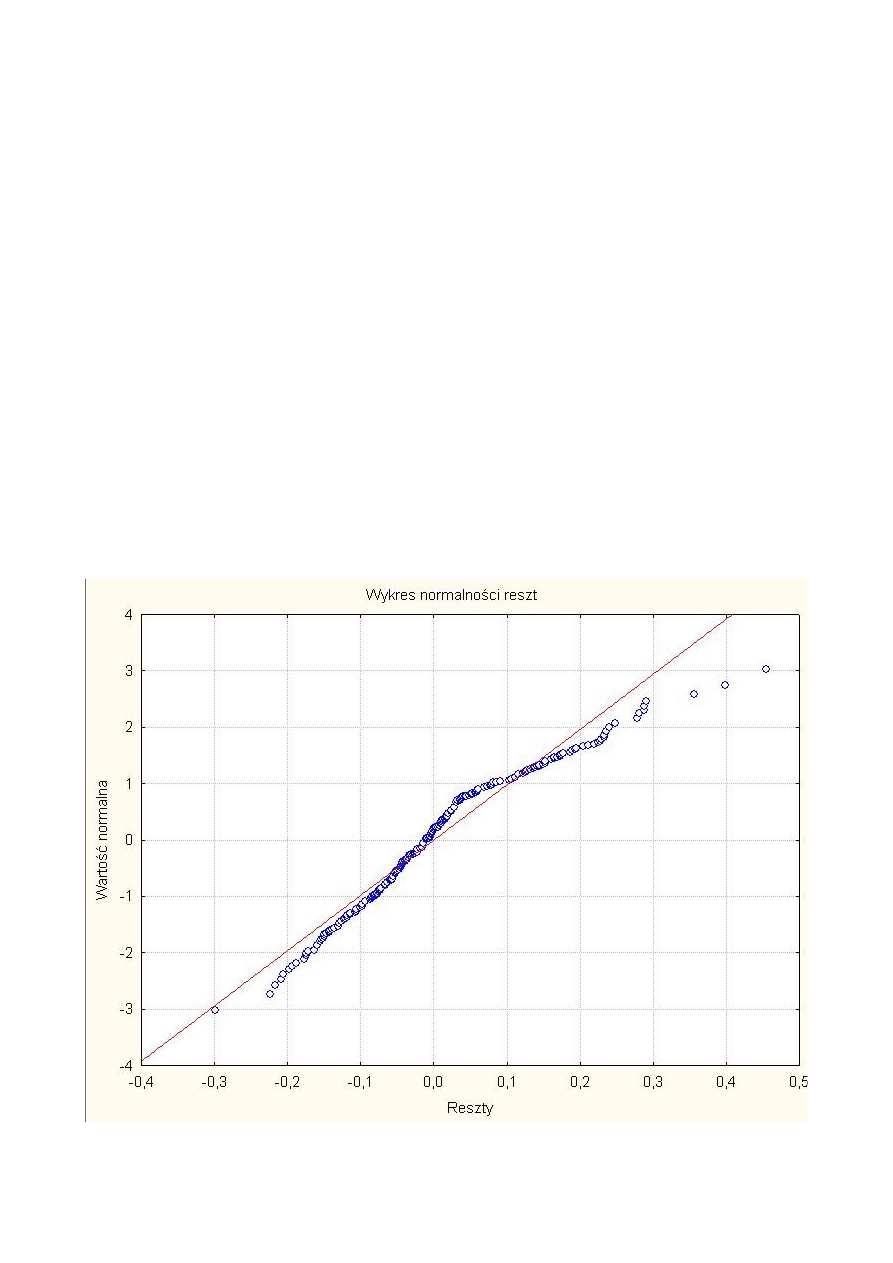
c) reszty są nieskorelowane, ale nie mają rozkładów normalnych.
Po usunięciu przypadków odstających wykres pokrywał się już niemal idealnie z linią prostą.
Po wykonaniu analizy regresji liniowej pomiędzy średnicą, a czasem odnowy na wszystkich
rodzajach sieci otrzymano prostą Y=
0,315306198589884
+
0,000194746850022978
X oraz następujące
współczynniki:
R
= 0,30; R
2
=0,09. Wszystkie otrzymane dane są istotne natomiast model wyjaśnia tylko
9% wszystkich przypadków. Natomiast gdy odstające przypadki nie zostały usunięte(założenia nie
były spełnione) współczynnik
R
2
=0,04, tak więc usunięcie odstających przypadków zwiększyło
procentowe wyjaśnienie danych poprzez model.
Regresja liniowa pomiędzy średnicą, a czasem naprawy:
Założenia:
a) n>= 2 i wynosi 536(po usunięciu 503)
b) model jest liniowy co jednoznacznie pokazuje test F-Fischera
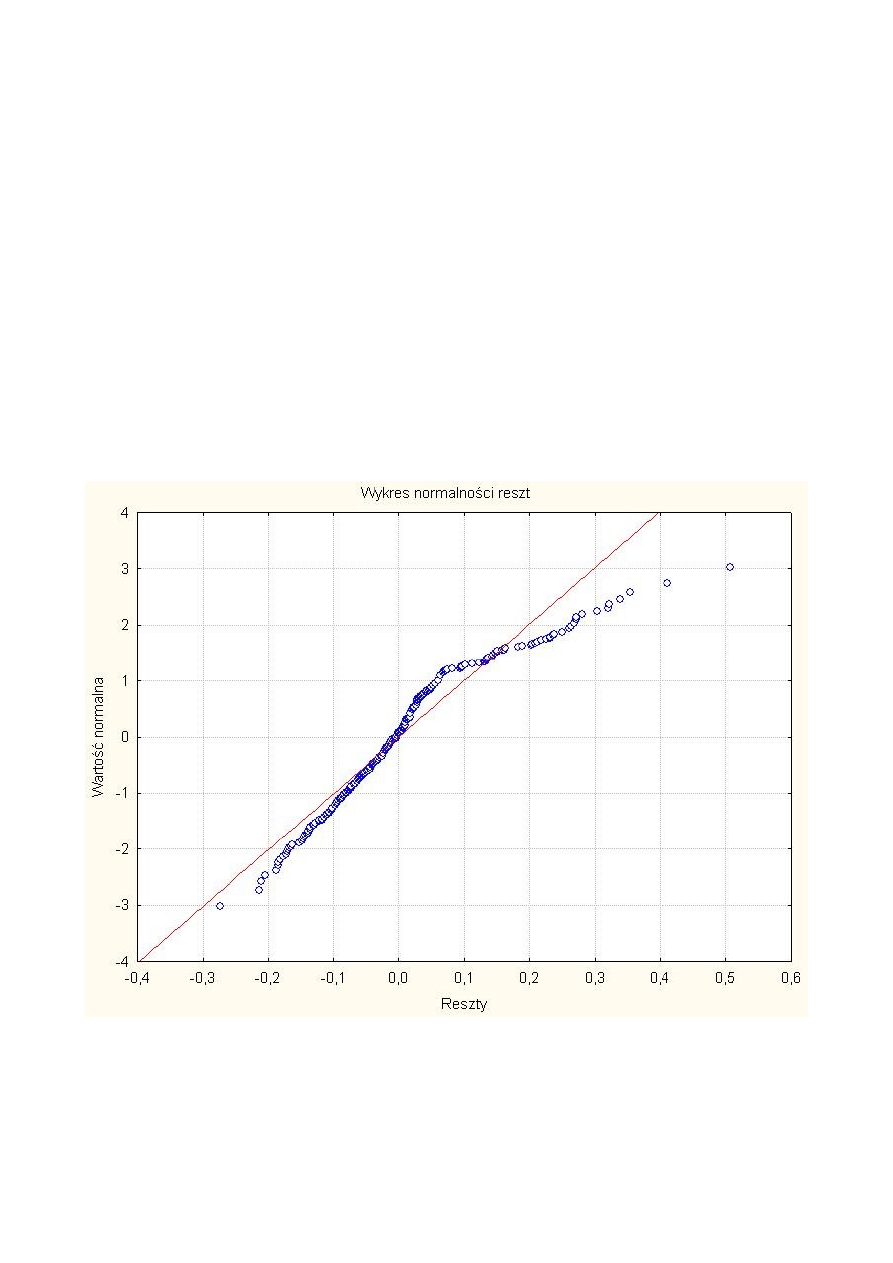
c) reszty są nieskorelowane, ale nie mają rozkładów normalnych.
Po usunięciu przypadków odstających wykres pokrywał się już niemal idealnie z linią prostą.
Po wykonaniu analizy regresji liniowej pomiędzy średnicą, a czasem naprawy na wszystkich
rodzajach sieci otrzymano prostą Y=
0,245994072353221
+
0,000142615651741813
X oraz następujące
współczynniki:
R
= 0,24;
R
2
=0,06. Wszystkie otrzymane dane są istotne natomiast model wyjaśnia tylko

6% wszystkich przypadków. W momencie gdy odstające przypadki nie zostały usunięte
współczynnik R
2
=0,04.
Regresja liniowa pomiędzy średnicą, a czasem oczekiwania na naprawę:
Założenia:
a) n>= 2 i wynosi 536(po usunięciu 503)
b) model nie jest liniowy(nawet po usunięciu odstających przypadków)
.
W związku z tym nie możemy wykonać regresji liniowej. Pomijając założenia program
wyliczył model, w którym współczynnik kierunkowy prostej regresji jest statystycznie nie istotny.
Wszelkie próby zestawienia innych danych np.: czas odnowy, naprawy, oczekiwania na
naprawę dały wyniki nie istotne statystycznie do tego nie wyjaśniały nawet 0,2% danych.
Rozpatrując regresję liniową pomiędzy średnicą, a czasem odnowy, naprawy i oczekiwania
na naprawę w wszystkich możliwych kombinacjach rozdzielonych ze względu na rodzaj sieci
(magistralna, rozdzielcza , przyłącza) możemy zauważyć, że wyniki otrzymane są bardzo do siebie
podobne. Niestety żaden z badanych przypadków nie spełnia założeń dla regresji liniowej. Modele
nie są liniowe, pomijając fakt niespełnionych założeń modele obliczone w programie statistica mają
nie istotne statystycznie współczynniki liniowe. Możemy również zauważyć pewną prawidłowość
w odstających przypadkach. Ich numery dość często się powielają, może to być spowodowane
błędnie wprowadzonymi danymi, lub z podanych informacji nie sposób stworzyć statystycznie
dobry model liniowy.
Podsumowując, wykonana regresja liniowa dla danych o awariach na sieciach
wodociągowych nie dała zadowalających wyników. Większość modeli nie spełniała założeń
potrzebnych do dalszych badań, a nawet jeśli założenia zostały spełnione to powstałe modele
wyjaśniały maksymalnie tylko 9% informacji.
Wyszukiwarka
Podobne podstrony:
więcej podobnych podstron