1

II Pracownia Fizyczna

9. Własności ośrodków dyspersyjnych.

Pomiar dyspersji materiałów za pomocą

spektrometru

I.

Zestaw przyrządów

1.

Spektrometr

2.

Lampa spektralna rtęciowa z zasilaczem

3.

Pryzmaty szklane, których własności mierzymy

II.

Cel ćwiczenia

Wyznaczenie dyspersji materiału, z jakiego wykonany jest dany pryzmat;

wyliczenie prędkości rozchodzenia się światła w materiale, w zależności od długości
fali; wyliczenie długości fali świetlnej w materiale, w zależności od długości fali
w powietrzu; zapoznanie się z budową i zasadą działania spektrometru.

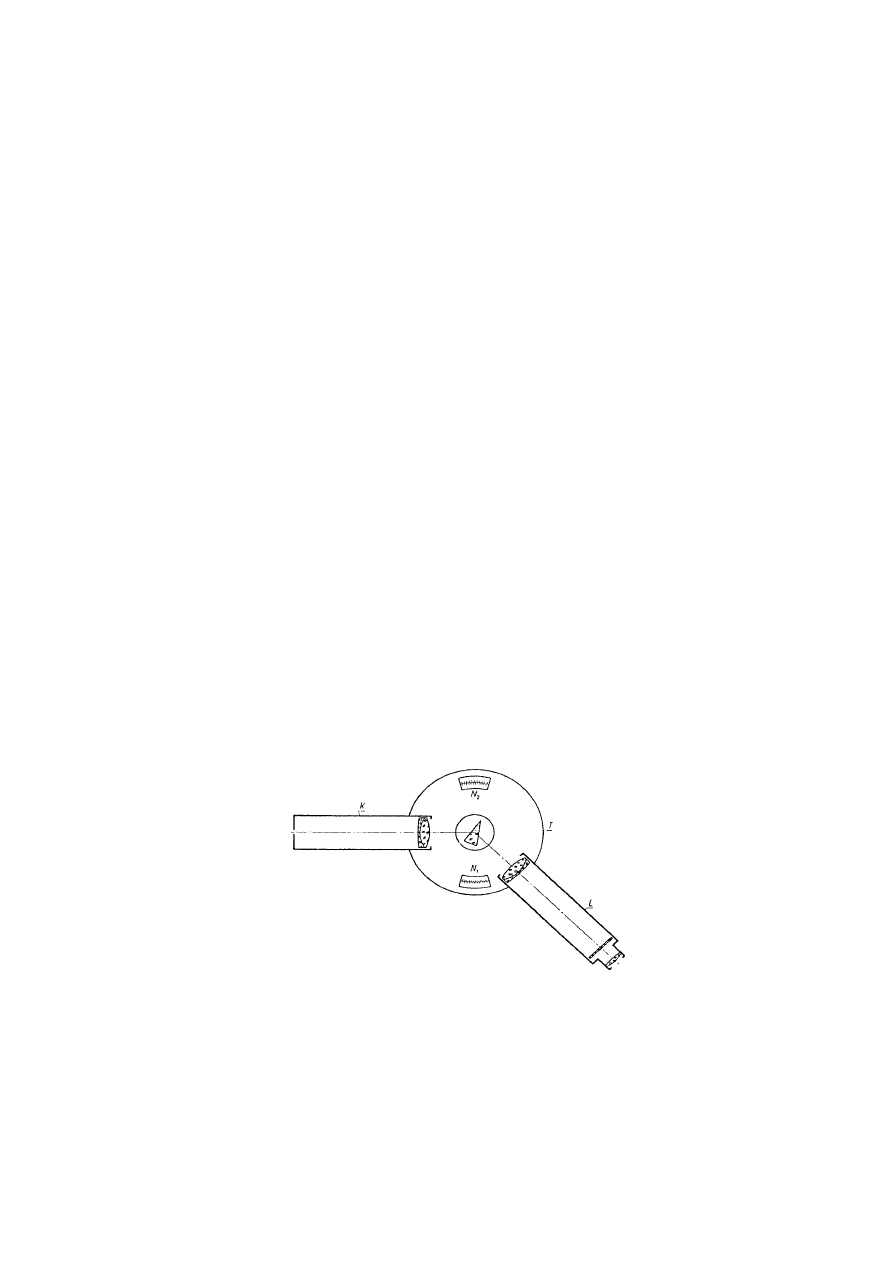
III. Schemat układu pomiarowego
Spektrometr jest przyrządem służącym do pomiaru kątów, np. pryzmatów,

kątowej odległości linii widmowych lub kąta ugięcia promieni na pryzmacie.
Zasadniczym przeznaczeniem jest jednak pomiar dyspersji materiałów.
W zależności od przeznaczenia konstruuje się spektrometry różnej budowy i różnej
dokładności. Na rysunku poniżej przedstawiona jest schematycznie budowa
spektrometru przeznaczonego do pomiarów laboratoryjnych.

Rys. 1. Schemat spektrometru

Odczytu kąta dokonuje się z jednego (dla mniej dokładnych urządzeń) lub dwóch
(dla bardziej dokładnych urządzeń) noniuszów N1 i N2, umieszczonych na kole
podziałowym T. W środku kręgu znajduje się stolik pomiarowy, który można
poziomować za pomocą śrub regulacyjnych. Oś obrotu stolika pokrywa się z osią
obrotu kręgu. Nad kręgiem umieszczona jest luneta L i kolimator

2

Rys. 2. Spektrometry: pierwszy z dwoma systemami odczytowymi (noniuszami),
drugi z jednym

Objaśnienia:

K – kolimator
L – luneta
S – stolik
Sz – szczelina kolimatora
O – okular lunety
Rk – regulacja kolimatora (na
nieskończoność: dla pierwszego = 6.75
mm, dla drugiego = 15.85 mm)
Rl – regulacja lunety (na ostry obraz
szczeliny)
Rs – śruby regulacyjne stolika
(powierzchnia stolika powinna być
prostopadła do osi obrotu stolika)
W – blokada regulacji wysokości
stolika i jego ruchu obrotowego

N – systemy odczytowe (1 i 2)
położenia lunety
Bs – blokada ruchu obrotowego –
makro stolika (dopiero po jej
zablokowaniu możliwa jest regulacja
mikro stolika, lecz razem z noniuszami)
Bl – blokada ruchu obrotowego –
makro lunety (dopiero po jej
zablokowaniu możliwa jest regulacja
mikro lunety)
Ms – regulacja mikro obrotu stolika,
lecz razem z noniuszami!
Ml – regulacja mikro obrotu lunety

3

Uwaga dla pierwszego spektrometru: Przed pomiarami, po ustawieniu noniuszów
w wygodnej do odczytu pozycji, należy dokręcić Bs i do końca wszystkich pomiarów
nie ruszać Bs i Ms.
K, w taki sposób, że ich osie celowe przechodzą nad stolikiem. W płaszczyźnie
ogniskowej obiektywu kolimatora znajduje się szczelina, której szerokość można
regulować za pomocą śruby. Szczelina jest oświetlana źródłem światła spektralnego.
Jej obraz tworzony jest przez obiektyw kolimatora w nieskończoności. Jeżeli na
stoliku pomiarowym zostanie odpowiednio umieszczony pryzmat i jeśli źródło
światła oświetlającego szczelinę nie jest monochromatyczne lecz ciągłe (białe),
wówczas w płaszczyźnie ogniskowej lunety zostanie utworzony barwny rozciągły
obraz szczeliny kolimatora. Gdy źródłem światła jest np. lampa spektralna to
w lunecie zobaczymy szereg szczelin o różnych barwach. Obrazy szczelin
odpowiadającym różnym liniom widmowym lampy, mają różne kolory.
W płaszczyźnie ogniskowej lunety znajduje się płytka z naniesionym krzyżem,
ułatwiającym dokładne nastawienie lunety na środek obrazu szczeliny – określonej
linii widmowej. Na zdjęciach przedstawiono spektrometry używane podczas
ćwiczenia.

Zasada odczytu wartości kątów za pomocą noniusza:
Systemy odczytowe zależą od producenta. Zwykle składają się z koła podziałowego
i mikroskopu lub noniusza ułatwiającego odczyt. W prostych przyrządach występuje
koło podziałowe i noniusz. Tak też są wykonane systemy w naszym ćwiczeniu. Koło
podziałowe podzielone jest na działki co 0,5

°. Z taką też dokładnością odczytujemy

skalę, którą pokazuje nam kreska zerowa noniusza. Do odczytanej wartości dodajemy
wartość odczytaną z noniusza. Sprawdzamy która kreska noniusza leży na kresce
koła podziałowego. Ponieważ noniusz ma 30 działek, więc wartość kąta odczytujemy
z dokładnością do 1 minuty kątowej.

Wyliczenie dowolnie zmierzonego kata
Pomiar dowolnego kąta

Θ, między dwoma dowolnymi ustawieniami lunety

(o położeniach A i B), jest to różnica w odczytach tych położeń. Z lunetą sprzężony
jest bowiem: albo noniusz odczytowy, albo koło podziałowe. Szukany kąt to

Θ = Θ

B

-

Θ

A

. Podane tu kąty odnoszą się do rzeczywistych wartości. Jeżeli między

dwoma położeniami występuje skok skali (0

° lub 360°), należy to uwzględnić

licząc odpowiednie dopełnienia! Powyższe wyliczenia są prawdziwe gdy
korzystamy tylko z jednego systemu odczytowego. Gdy spektrometr posiada dwa
układy odczytowe (1 i 2), korygujące błąd systematyczny mimośrodowości, należy
odczytywać na każdym systemie położenia lunety w obu ich położeniach. Mamy
więc wtedy cztery odczyty, po dwa dla każdego położenia lunety. Najpierw liczymy
kąty

Θ dla każdego systemu pomiarowego oddzielnie tzn. Θ

1

=

Θ

1B

-

Θ

1A

i

Θ

2

=

Θ

2B

-

Θ

2A

, później kąt pozbawiony błędu systematycznego

Θ = (Θ

1

+

Θ

2

)/2, co

można łatwo udowodnić.

4

Program ćwiczenia

1.

Pomiar kąta łamiącego pryzmatu

2.

Pomiar kąta minimalnego odchylenia

3.

Wyliczenie współczynników załamania

4.

Wyliczenie prędkości światła w szkle z którego wykonano pryzmat

5.

Wyliczenie długości fali światła w szkle z którego wykonano pryzmat

6.

Punkty 2-5 wykonujemy dla wybranych linii spektralnych. Wykonujemy
wykresy: współczynnika załamania, prędkości światła i długości fali światła w
szkle, w zależności od długości fali świetlnej w powietrzu.

Justowanie spektrometru
1.

Za pomocą śrub Rs wypoziomować stolik pomiarowy. Dokonujemy tego
ustawiając najpierw na stoliku specjalną płytkę w oprawce lub w ostateczności
pryzmat. Sprawdzamy czy światło wychodzące z kolimatora a odbite od płytki
lub od powierzchni pryzmatu, widoczne jest po wejściu do lunety na tej samej
wysokości. Sprawdzamy tak przynajmniej w trzech położeniach lunety: dwa
położenia gdy luneta jest ustawiona prawie prostopadle do światła
wychodzącego z kolimatora i raz dla ustawienia prawie równoległego.
Powtarzamy regulację aż do skutku.

2.

Sprawdzić czy kolimator jest ustawiony na nieskończoność, jeżeli nie, to
pokrętłem Rk ustawić go na wartość podaną w objaśnieniach, pod zdjęciami
spektrometrów. Na wyjściu kolimatora wtedy mamy wiązkę równoległą, która
po wejściu do lunety, utworzy w jej płaszczyźnie ogniskowej ostry obraz
szczeliny.

3.

Oświetlić szczelinę kolimatora za pomocą lampy spektralnej.

4.

Znaleźć ostry obraz szczeliny kolimatora przez lunetę (ewentualną korekcję
dokonujemy pokrętłem Rl),

IV. Wykonanie pomiarów

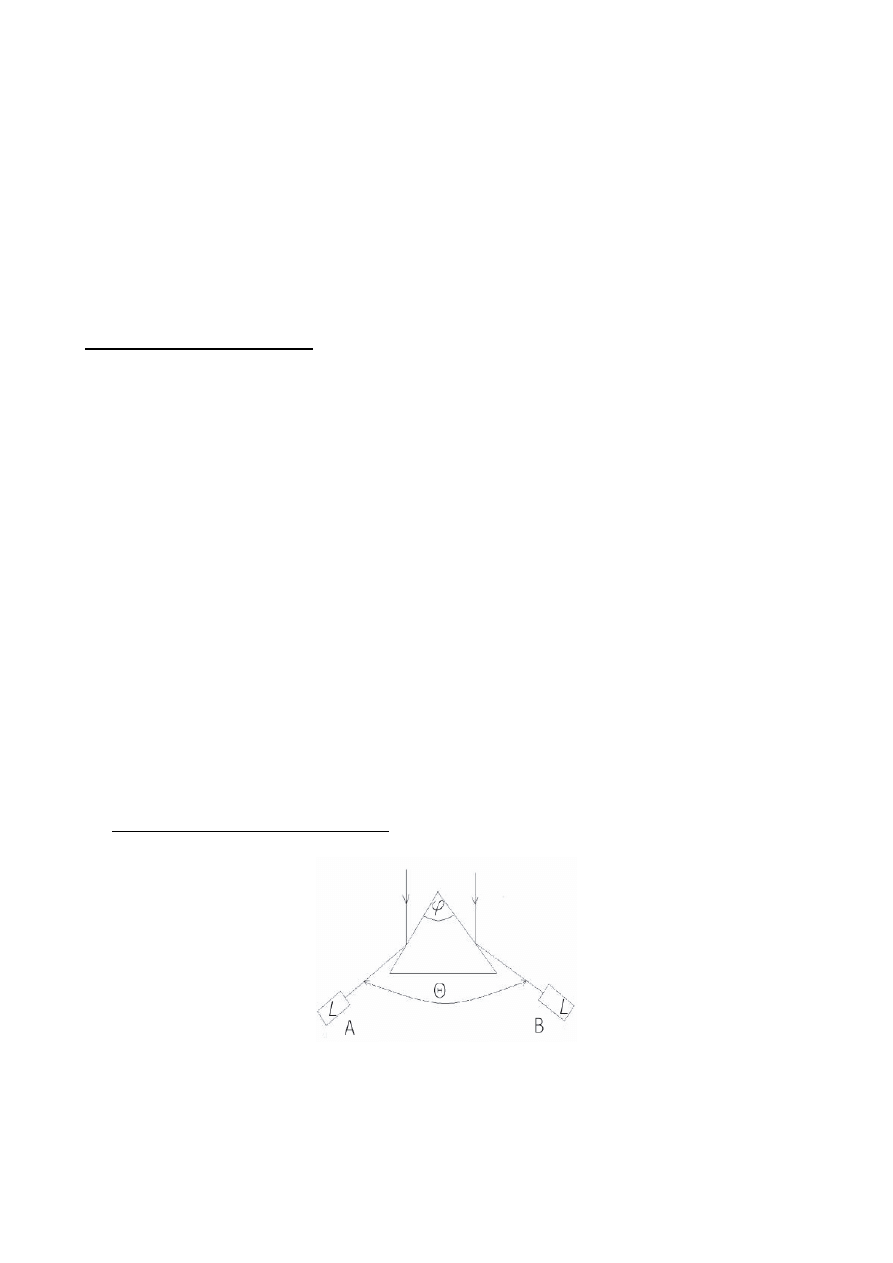
Pomiar kąta łamiącego pryzmatu

Rys. 3. Pomiar kąta łamiącego za pomocą lunety i kolimatora

Na rysunku 3 przedstawiona jest schematycznie zasada pomiaru.

1.

Na stoliku pomiarowym umieścić badany pryzmat tak by światło z kolimatora
odbijało się od dwóch jego powierzchni

5

2.

Zablokować stolik pomiarowy za pomocą blokady Bs

3.

Lunetę skierować na jedną ze ścian pryzmatu i znaleźć ostry obraz szczeliny
kolimatora

4.

Za pomocą blokady Bl zablokować obrót lunety i jedynie posługując się
mikroprzesuwem Ml lunety ustawić krzyż tak, aby jego pionowe ramię
pokrywało się ze szczeliną kolimatora i było w jego środku

5.

Dokonać odczytu położenia lunety za pomocą dwóch noniuszy odczytowych,
lub jednego jeżeli jest tylko jeden

6.

Zwalniając blokadę Bl obrócić lunetę, tak aby znaleźć obraz szczeliny
kolimatora po odbiciu od drugiej ściany pryzmatu

7.

Dokonać odczytu położenia lunety podobnie jak w powyższym podpunkcie

8.

Różnica odczytów obu położeń lunety daje wartości kątów

Θ

1

,

Θ

2

dla każdego

systemu odczytowego oddzielnie, zaś średnia arytmetyczna tych różnic daje
kąt

Θ. Dla pojedynczego systemu odczytowego Θ = Θ

1

. Kąt ten stanowi

podwójną wartość kąta łamiącego pryzmatu

ϕ. Stąd

ϕ = Θ/2

(1)

9.

Pomiary powtórzyć kilka razy w celu zminimalizowania błędów i oszacowania
niepewności pomiarowej

Pomiar kąta minimalnego odchylenia

Prowadzący zajęcia sugeruje który rodzaj pomiaru należy wybrać. Zaleca się pomiar
typowy, zaś uproszczony wybiera się gdy brak czasu.

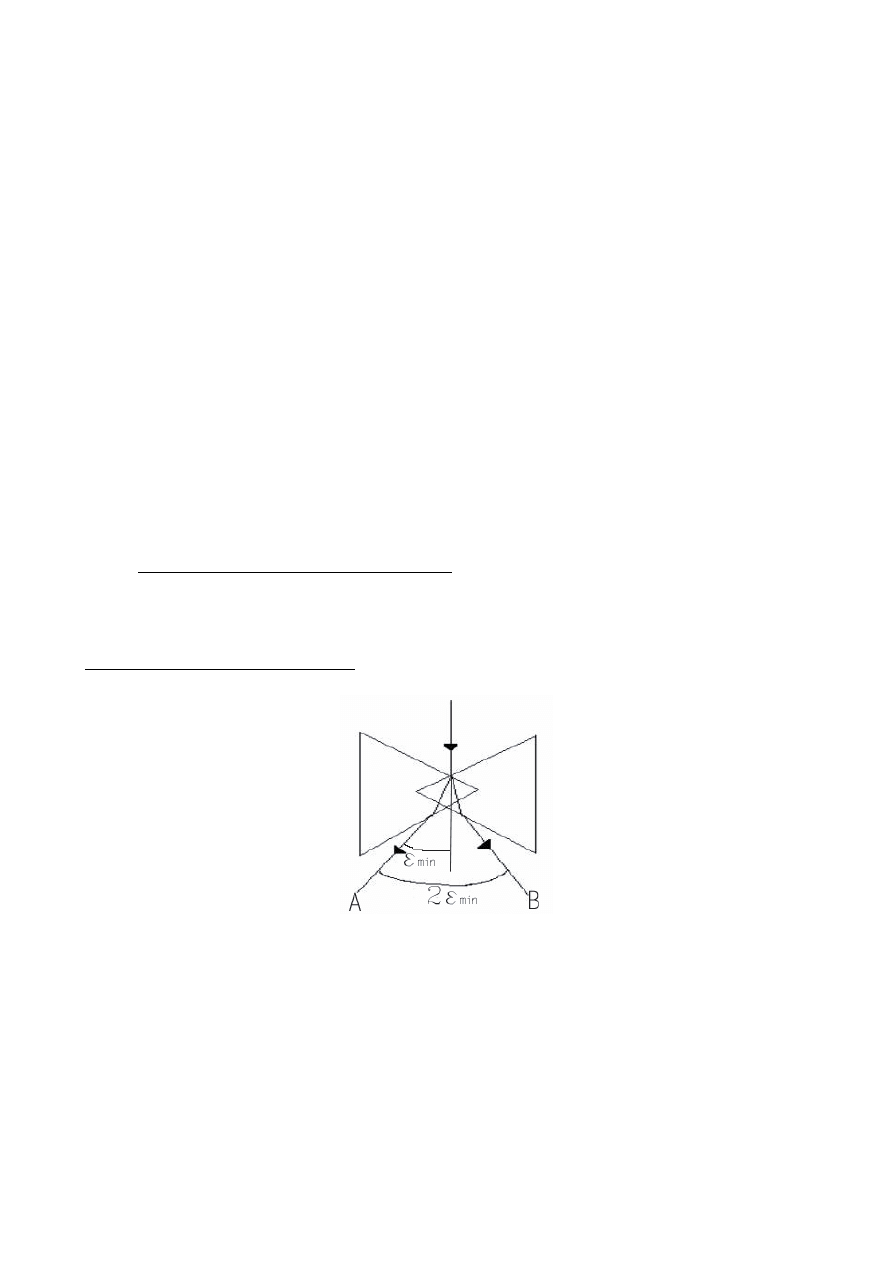
Typowy pomiar kąta odchylenia

Rys. 4. Pomiar kąta minimalnego odchylenia, przy dwóch różnych ustawieniach

pryzmatu

Kąt minimalnego odchylenia, jest to minimalny kąt, między kierunkiem na wprost

kolimatora a kierunkiem załamania światła przez pryzmat. Minimalna wartość tego
kąta zależy od ustawienia pryzmatu. Obracając stolik z pryzmatem znajdujemy jego
minimalną wartość.

6

Zasada pomiaru przedstawiona jest na rysunku 4.

1.

Szczelinę kolimatora oświetlamy lampą spektralną

2.

Na stoliku pomiarowym umieszczamy pryzmat

3.

Obracając stolik S, na którym ustawiony jest pryzmat, obserwujemy przez

lunetę przesuwający się monochromatyczny obraz szczeliny kolimatora (dla
wybranej linii widmowej)

4.

Moment, w którym obraz zatrzymuje się (znajduje się wtedy najbliżej kierunku

naprzeciw kolimatora), a następnie zaczyna przesuwać się w przeciwnym
kierunku, jest momentem, w którym pryzmat ustawiony jest na minimalne
odchylenie, dla danej linii widmowej

5.

Następnie należy sprząc lunetę z korpusem za pomocą Bl i za pomocą

mikroprzesuwu lunety Ml ustawić lunetę na jedną z linii widmowych
i dokonać odczytu za pomocą dwóch noniuszy odczytowych

6.

Opisane czynności 3-5 powtórzyć dla wszystkich wybranych linii spektralnych

7.

Czynności wyżej opisane powtórzyć także dla drugiego ustawienia pryzmatu,

przy jego symetrycznym ułożeniu

8.

Różnica odczytów przy symetrycznych ułożeniach pryzmatu daje podwójne

wartości kąta minimalnego odchylenia dla obu systemów odczytowych

ε

1min

i

ε

2min

, zaś

ε

min

= (

ε

1min

+

ε

2min

)/2. Dla pojedynczego systemu odczytowego

ε

min

=

ε

1min

.

9.

Pomiary dla różnych długości fal (dla wszystkich linii lampy spektralnej),

pozwolą wyliczyć współczynniki załamania, dla tych długości z zależności:

2

sin

)

2

sin(

min

ϕ

ε

ϕ

+

=

n

.

(2)

Uproszczony pomiar kąta odchylenia

Metoda ta, jest mniej dokładna od poprzedniej, i wykorzystywana może być przy
zmniejszonych wymaganiach na dokładność pomiaru kata minimalnego odchylenia.
Zasada pomiaru jest taka jak powyżej opisano, występują tylko dwie różnice:
1.

Zamiast punktu 7 wykonujemy pomiar położenia lunety na wprost kolimatora
gdy na stoliku nie ma pryzmatu. Powtarzamy go kilka razy i liczymy średnią.
Zastępuje ona drugie położenie lunety, takie samo dla wszystkich linii
spektralnych.

2.

Punkt 8 różni się tym, że teraz różnica obu odczytów, po przejściu światła
przez pryzmat i bez pryzmatu (luneta na wprost kolimatora), daje wartości kąta
minimalnego odchylenia

ε

min

, dla wybranych linii spektralnych.

V.

Opracowanie wyników pomiarów

1.

Wyliczyć kąt łamiący pryzmatu i określić jego niepewność pomiarową.

2.

Wyliczyć kąty minimalnego odchylenia pryzmatu, dla wszystkich linii
spektralnych i określić ich niepewności pomiarowe.

7

3.

Wyliczyć współczynniki załamania dla wszystkich linii spektralnych.

4.

Wyliczyć błąd

δn, metodą różniczki zupełnej, i wyliczyć niepewności

pomiarowe współczynnika załamania.

5.

Wyrysować dyspersję materiału n = n(

λ

p

), z jakiego został wykonany pryzmat,

identyfikując uprzednio linie widmowe używanej podczas pomiaru lampy
spektralnej.

6.

Wyliczyć prędkości rozchodzenia się światła, dla poszczególnych linii
widmowych z zależności c(

λ

p

) = c

p

/n(

λ

p

). Sporządzić wykres c(

λ

p

).

7.

Wyliczyć długości fali światła w szkle, z którego został wykonany pryzmat,
z zależności

λ(λ

p

) =

λ

p

/n(

λ

p

). Sporządzić wykres

λ(λ

p

).

8.

Wyliczyć częstotliwości drgań świetlnych (wektorów E i H), dla wybranych
linii spektralnych.

9.

Wyliczyć błędy pomiarowe wyliczonych wartości prędkości światła i długości
fal.

Kąt łamiący pryzmatu nr. ...

A

B

Θ

1A

Θ

2A

Θ

1B

Θ

2B

Θ

1

=

Θ

1B

-

Θ

1A

Θ

2

=

Θ

2B

-

Θ

2A

Θ=(Θ

1

+

Θ

2

)/2

∆Θ

ϕ=Θ/2

∆ϕ

<-śr.

Kąt minimalnego odchylenia pryzmatu nr. ...

λ

A

B

[nm]

Θ

1A

Θ

2A

Θ

1B

Θ

2B

Θ

1

=

Θ

1B

-

Θ

1A

Θ

2

=

Θ

2B

-

Θ

2A

Θ=(Θ

1

+

Θ

2

)/2

∆Θ ε

min

=

Θ/2 ∆ε

min

<-śr.

Wyliczone wielkości dla pryzmatu nr. ...

λ

p

ν

p

∆ν

p

n

∆n

c

∆c

λ

∆λ

[nm]

[1/s]

[1/s]

[m/s]

[m/s]

[nm]

[nm]

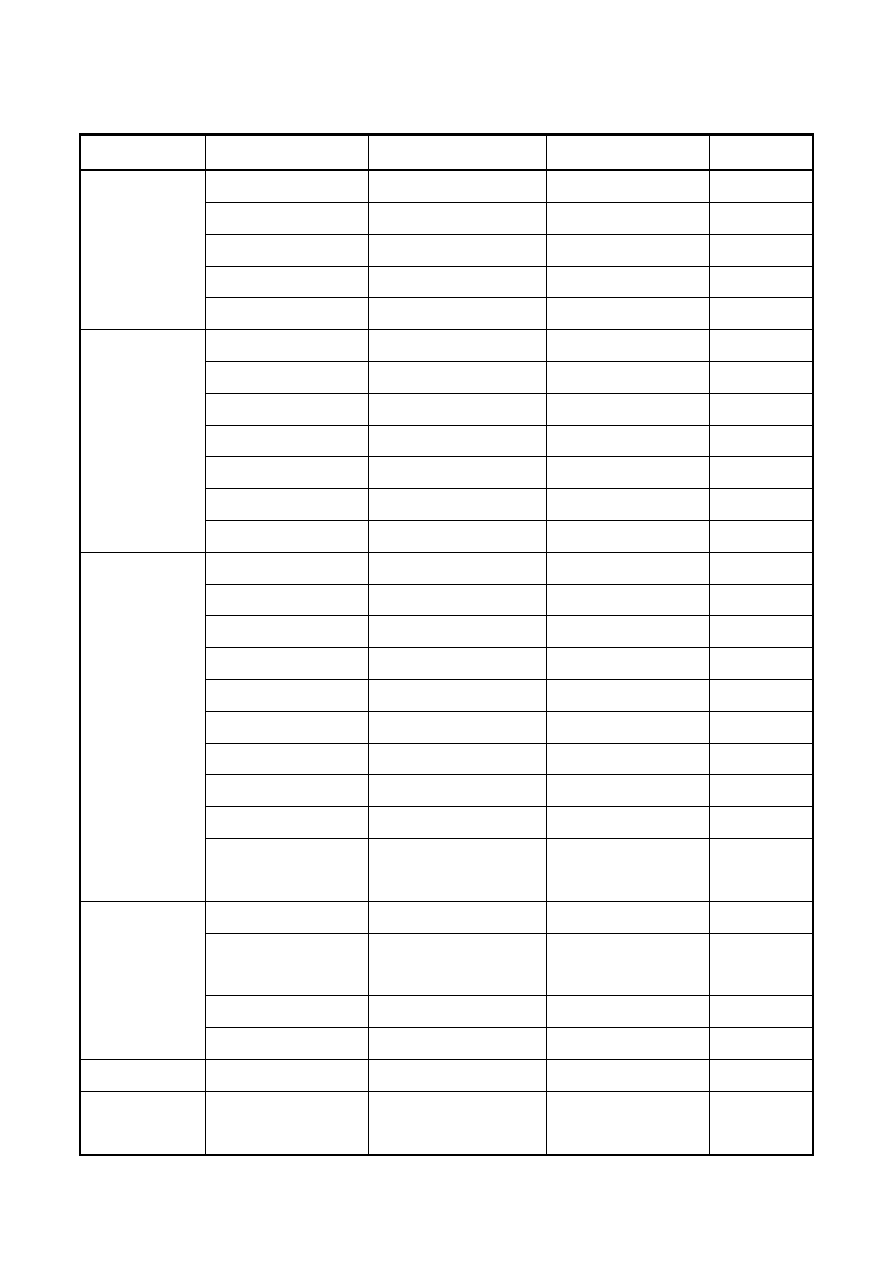
8

Tabela 1. Wybrane linie widmowe lamp spektralnych. * - linie szczególnie zalecane.

Lampa

Barwa linii Intensywność Oznaczenie

λ

p

[nm]

Czerwona

Silna

C *

656.3

niebiesko-ziel Średnia

F *

486.1

fiolet

Średnia

G’ *

434.0

Fiolet

Słaba

410.8

H

2

Fiolet

Słaba

397.O

Czerwona

Średnia

r

706.5

Czerwona

Średnia

667.8

Żółta

b. silna

d *

587.6

Zielona

Średnia

501.6

nieniesko-ziel Średnia

492.2

Niebieska

si1na

471.3

He

Fiolet

Słaba

447.1

Czerwona

Słaba

c *

690.7

Czerwona

Słaba

623.4

Żółta

b.silna dublet

579.1

Żółta

b.silna dublet

576.9

Zielona

Silna

e **

546.1

niebiesko-ziel Średnia

491.6

niebiesko-fiol Średnia

g *

435.8

Fiolet

Słaba

407.8

ciemny fio1et b. słaba

h *

404.7

Hg

b.ciemny
fiolet

b.b. słaba

i

365.0

Czerwona

b. silna

C’ **

643,8

zielono-
niebie

b. silna

508.6

Niebieska

b. silna

F’ **

480.0

Cd

Niebieska

b. silna

467.8

Na

Żółta

b.silna dublet

D *

589.3

K

czerwona
ciemna

Średnia

A’

768.2

9

UZUPEŁNIENIA

Zamieszczone tu ilustracje pozwalają lepiej zrozumieć ćwiczenie. I tak:

Na stronie 1 przedstawiono bezwzględny współczynnik załamania powietrza.

Jego niewielkie zmiany uzasadniają, przy naszych dokładnościach pomiarowych,
przyjęcie jako stałe Np.=1.000280, c

p

=2.997085

⋅10

8

[m/s], oraz

λ

p

=

λ

0

/N

p

≈λ

0

.

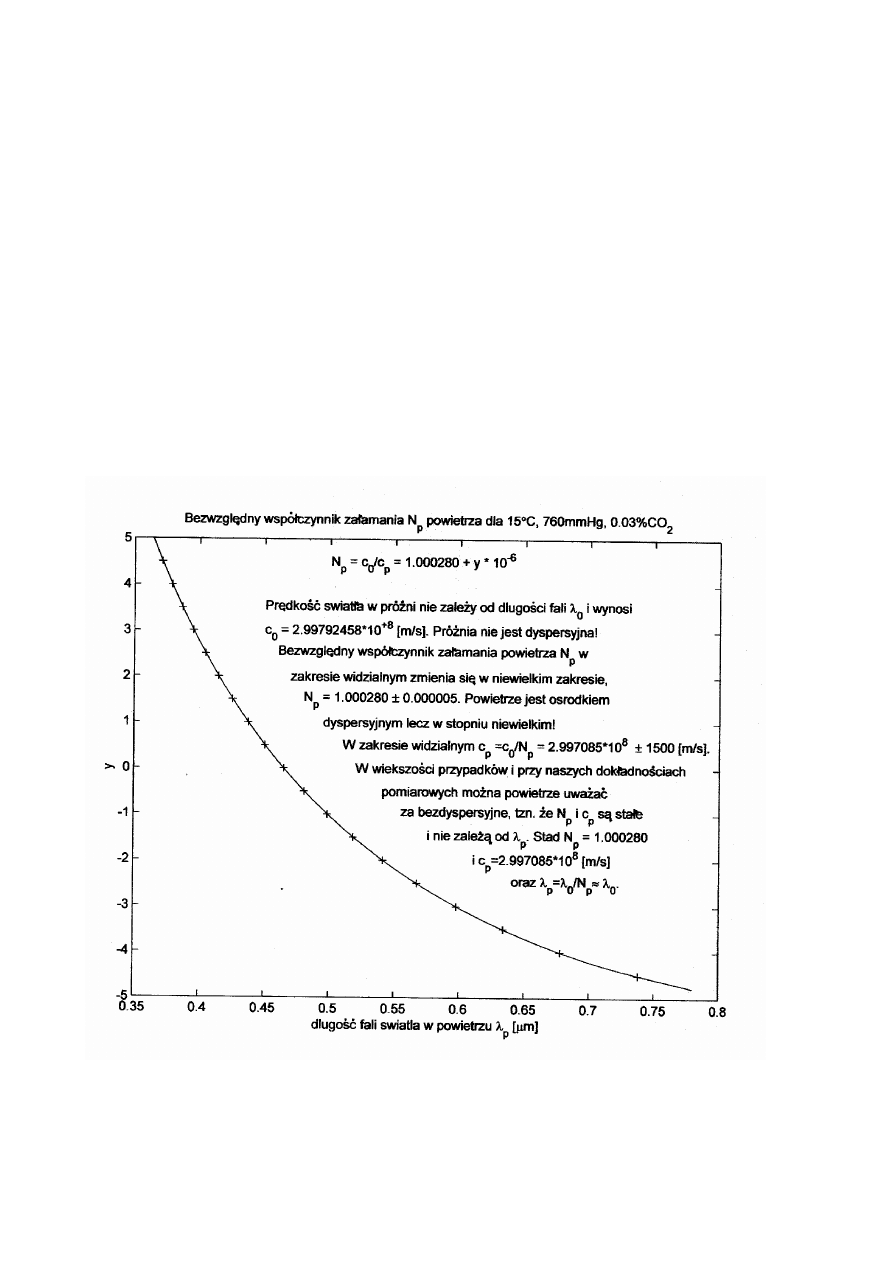
Na stronie 2 przedstawiono zmierzony spektrometrem względny współczynnik

załamania pewnego gatunku szkła, oraz wyliczoną prędkość fazową światła w tym
szkle, w zależności od długości fali.

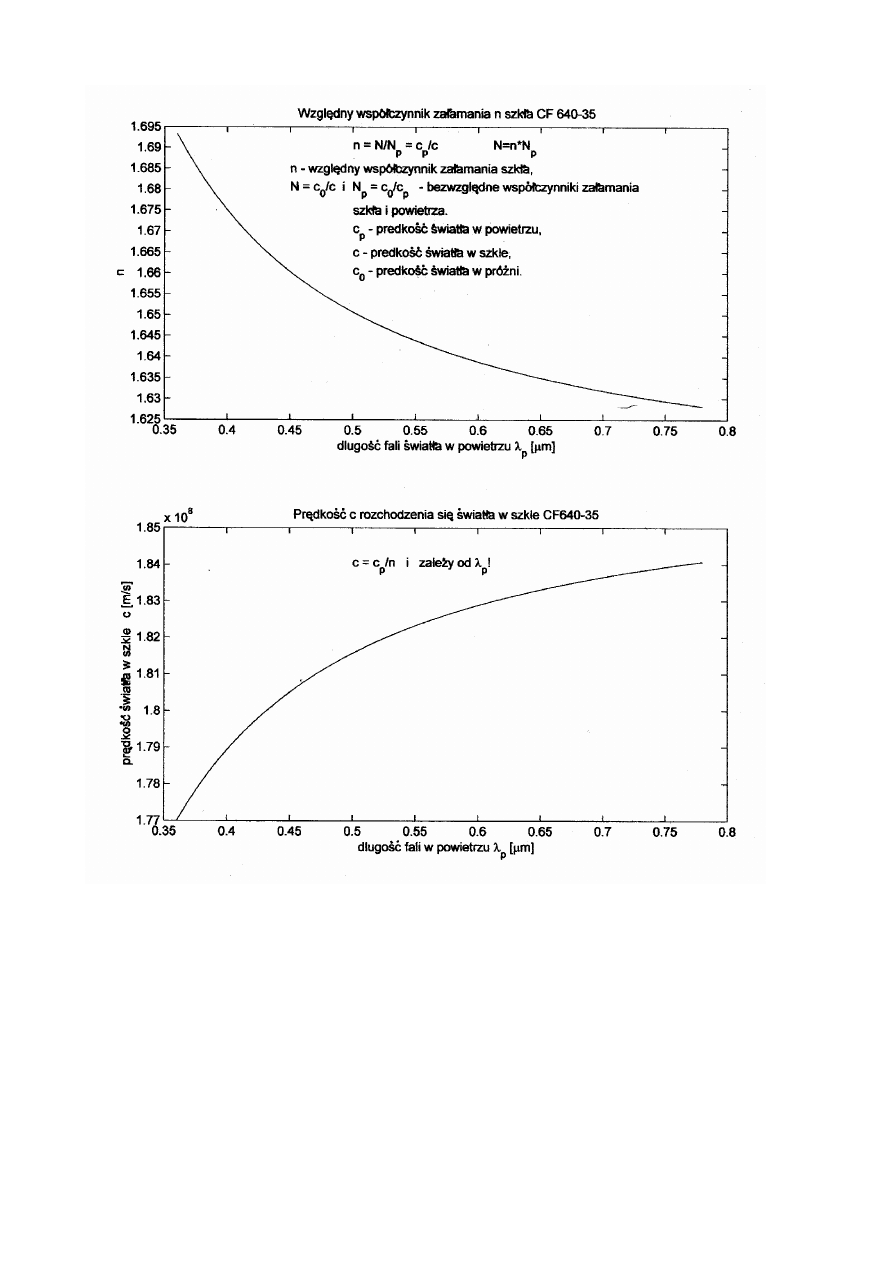
Na stronie 3 zilustrowano jak zmienia się długość fali światła przy przejściu z

powietrza do szkła, oraz jaką prędkość i długość fali ma światło w szkle.

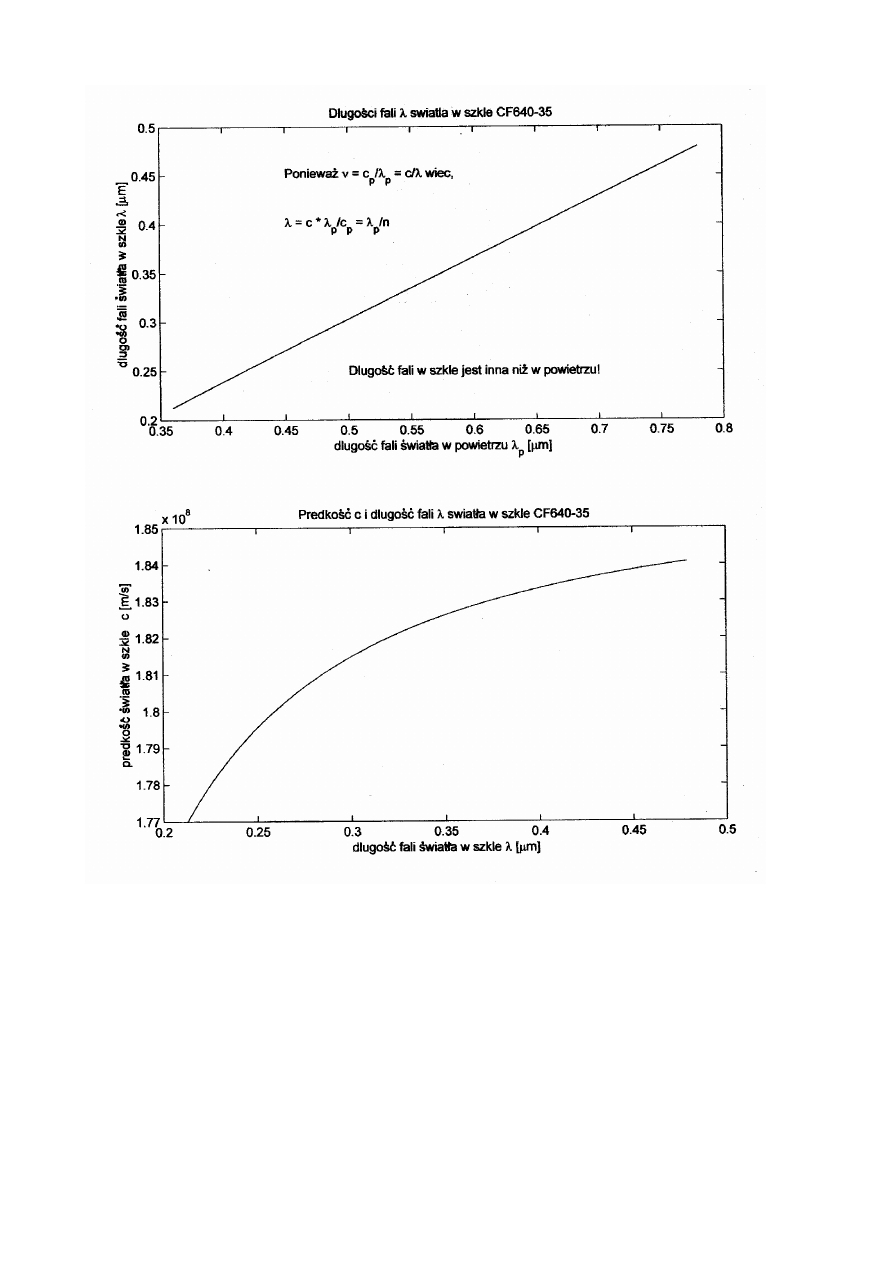
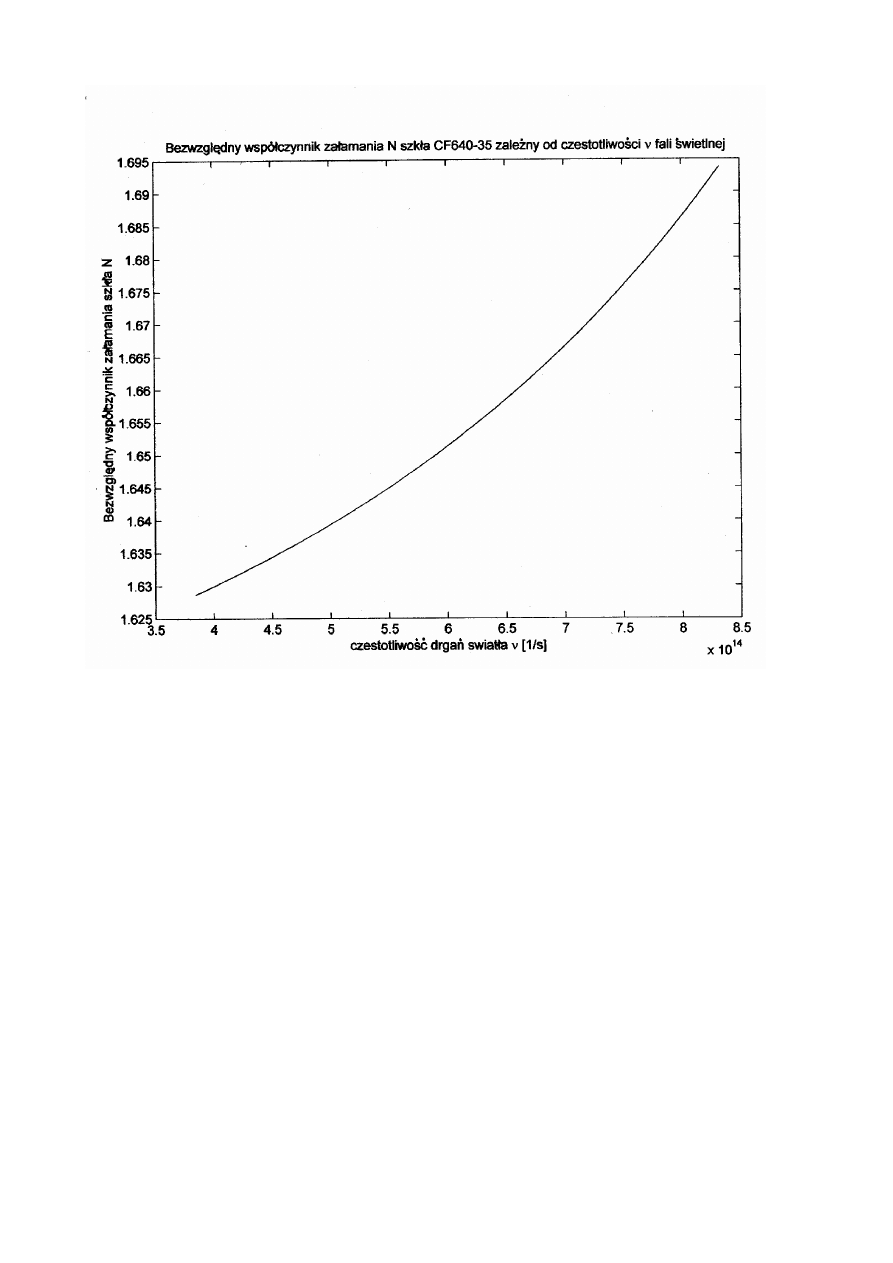
Na stronie 4 mamy wyliczony z pomiarów bezwzględny współczynnik

załamania badanego szkła w zależności od częstotliwości światła, która nie zmienia
się przy przejściu z powietrza do szkła.

10

11

12