Imię i Nazwisko ............................................................. Nr indeksu .......................

16 VI 2008

Ćwiczenia prowadzi ........................................................

Matematyka Dyskretna – Elektronika

Kolokwium nr 2. Grupa

C

Część I.

Zadania 1–12 są za 1pkt. W celu ich rozwiązania proszę podać jedynie odpowiedź, którą należy

umieścić bezpośrednio pod zadaniem.

1. Ile rozwiązań w liczbach całkowitych większych niż 3 ma równanie x

1

+ x

2

+ . . . + x

5

= 30?

10+4

4

2. Rozważmy wszystkie 3

6

pokolorowań sześcianu za pomocą 3 kolorów.

Ile spośród

tych pokolorowań przechodzi na siebie, gdy sześcian odbijamy symetrycznie względem
płaszczyzny, przechodzącej przez środki krawędzi i równoległej do podstaw?

3

5

3. Ile spośród liczb od 1 do 2100 dzieli się przez 2, 3 lub 7?

(1050 + 700 + 300) − (350 + 150 + 100) + 50 = 1500

4. Równaniem charakterystycznym pewnego równania rekurencyjnego jest r

2

+ 2 = 3r. Jak

wygląda jego rozwiązanie ogólne?

a

n

= A + B2

n

5. Znajdź funkcję tworzącą ciągu a

n

= 1 dla parzystych n > 6, a

n

= 0 dla pozostałych n.

x

6

1 − x

2

6. Dla jakich n graf K

n

jest planarny?

n ∈ {1, 2, 3, 4}

7. Wypisz podane ciągi w kolejności od najniższego rzędu do najwyższego: n!, (1, 01)

n

, n

2

oraz n log n.

n log n, n

2

, (1, 01)

n

, n!

8. Znajdź kod Prüfera dla poniższego drzewa:

557377

r

r

r

r

r

r

r

r

7

4

3

8

6

2

1

5

9. Dla jakich m i n graf K

m,n

jest hamiltonowski?

m = n > 2

10. Ile kolorów potrzeba do pokolorowania wierzchołków grafu K

4,5

, a ile do pokolorowania

krawędzi tego grafu?

2 wierzchołkowo, 5 krawędziowo

11. Narysuj drzewo o kodzie zerojedynkowym 01010010110011.

r

r

r

r

r r

r

r

12. Ile jest wszystkich grafów bez pętli, o wierzchołkach 1, 2, . . . , 8 oraz o sześciu krawędziach,

gdy dopuszczamy krawędzie wielokrotne?

6+

(

8
2

)

−1

6

=

33

6

1/2

Część II.

W zadaniach 13–15 proszę podać sposób ich rozwiązania oraz odpowiedź, które należy

umieścić bezpośrednio pod zadaniem.

13.

(3 pkt.)

Ile co najwyżej krawędzi można dodać do poniższego drzewa, aby otrzymać graf

planarny?

r r

r

r r

r

r

r

r

r

r

Odp: 27 − 10 = 17. Rozwiązanie jest analogiczne jak w grupie A.

14.

(2 pkt.)

Ile drzew spinających ma poniższy graf?

r

r

r

r

@

@

@

@

r

r

r

r

@

@

@

@

r

r

r

r

@

@

@

@

r

r

r

r

@

@

@

@

Odp: (4

2

)

4

. Rozwiązanie jest analogiczne jak w grupie A.

15.

(3 pkt.)

Znajdź funkcję tworzącą ciągu a

0

= 2, a

1

= 3, a

n+2

= a

n+1

+ 3a

n

.

f (x) =

∞

X

n=0

a

n

x

n

= 2 + 3x +

∞

X

n=2

a

n

x

n

= 2 + 3x +

∞

X

n=0

a

n+2

x

n+2

= 2 + 3x +

∞

X

n=0

(a

n+1

+ 3a

n

)x

n+2

= 2 + 3x + x

∞

X

n=0

a

n+1

x

n+1

+ 3x

2

∞

X

n=0

a

n

x

n

= 2 + 3x + x

∞

X

n=1

a

n

x

n

+ 3x

2

∞

X

n=0

a

n

x

n

= 2 + 3x + x(f (x) − 2) + 3x

2

f (x)

Skąd otrzymujemy

f (x) =

2 + x

1 − x − 3x

2

.

2/2

Imię i Nazwisko ............................................................. Nr indeksu .......................

16 VI 2008

Ćwiczenia prowadzi ........................................................

Matematyka Dyskretna – Elektronika

Kolokwium nr 2. Grupa

D

Część I.

Zadania 1–12 są za 1pkt. W ich rozwiązaniu proszę podać jedynie odpowiedź, którą należy

umieścić bezpośrednio pod zadaniem.

1. Wypisz podane funkcje w kolejności od najniższego rzędu do najwyższego: n

2

, n log n, n

n

oraz n!.

n log n, n

2

, n!, n

n

2. Ile spośród liczb od 1 do 1400 dzieli się przez 2, 5 lub 7?

(700 + 280 + 200) − (140 + 100 + 400) + 20 = 920

3. Ile kolorów potrzeba do pokolorowania wierzchołków grafu K

10

, a ile do pokolorowania

jego krawędzi?

10 wierzchołkowo, 9 krawędziowo

4. Dla jakich m graf K

m,m

nie jest planarny?

dla m

> 3

5. Znajdź kod Prüfera dla poniższego drzewa:

533525

r

r

r

r

r

r

r

r

@

@

2

7

5

8

1

6

4

3

6. Narysuj drzewo o kodzie zerojedynkowym 00101011010011.

r

r

r

r

r r

r

r

7. Rozważmy wszystkie 4

6

pokolorowań sześcianu za pomocą 4 kolorów.

Ile spośród

tych pokolorowań przechodzi na siebie, gdy sześcian odbijamy symetrycznie względem
płaszczyzny przechodzącej przez dwie przeciwległe krawędzie boczne i przekątne podstaw
sześcianu?

4

4

= 256

8. Ile rozwiązań w liczbach całkowitych większych niż 4 ma równanie x

1

+ x

2

+ . . . + x

7

= 50?

15+6

6

9. Równaniem charakterystycznym pewnego równania rekurencyjnego jest r

2

+ 4 = 4r. Jak

wygląda jego rozwiązanie ogólne?

a

n

= (A + Bn)2

n

10. Znajdź funkcję tworzącą ciągu a

n

= 3

n

dla n

> 2 oraz a

0

= a

1

= 0.

9x

2

1 − 3x

11. Ile jest wszystkich grafów zwykłych, o wierzchołkach 1, 2, . . . , 6 i siedmiu krawędziach?

(

6
2

)

7

12. Dla jakich m i n graf K

m,n

jest eulerowski?

dla m i n jednocześnie parzystych

1/2

Część II.

W zadaniach 13–15 proszę podać sposób ich rozwiązania oraz odpowiedź, które należy

umieścić bezpośrednio pod zadaniem.

13.

(3 pkt.)

Ile co najmniej krawędzi trzeba odrzucić z grafu K

7

, aby otrzymać graf planarny?

Odp:

7
2

− (3 · 7 − 6). Rozwiązanie jest analogiczne do rozwiązania w grupie B.

14.

(2 pkt.)

Ile drzew spinających ma poniższy graf?

q

q

q

q

q

q

q

q

q

q

q

q

q

q

q

Odp: (5

3

)

3

· 3. Rozwiązanie jest analogiczne do rozwiązania w grupie B.

15.

(3 pkt.)

Znajdź funkcję tworzącą ciągu a

0

= 2, a

1

= 3, a

n+2

= a

n+1

− 2a

n

.

f (x) =

∞

X

n=0

a

n

x

n

= 2 + 3x +

∞

X

n=2

a

n

x

n

= 2 + 3x +

∞

X

n=0

a

n+2

x

n+2

= 2 + 3x +

∞

X

n=0

(a

n+1

− 2a

n

)x

n+2

= 2 + 3x + x

∞

X

n=0

a

n+1

x

n+1

− 2x

2

∞

X

n=0

a

n

x

n

= 2 + 3x + x

∞

X

n=1

a

n

x

n

− 2x

2

∞

X

n=0

a

n

x

n

= 2 + 3x + x(f (x) − 2) − 2x

2

f (x)

Skąd otrzymujemy

f (x) =

2 + x

1 − x + 2x

2

.

2/2

Imię i Nazwisko ............................................................. Nr indeksu .......................

16 VI 2008

Ćwiczenia prowadzi ........................................................

Matematyka Dyskretna – Elektronika

Kolokwium nr 2. Grupa

A

Część I.

Zadania 1–12 są za 1pkt. W celu ich rozwiązania proszę podać jedynie odpowiedź, którą należy

umieścić bezpośrednio pod zadaniem.

1. Znajdź kod Prüfera dla poniższego drzewa:

588552

r

r

r

r

r

r

r

r

5

6

2

1

7

4

3

8

2. Rozważmy wszystkie 3

6

pokolorowań sześcianu za pomocą 3 kolorów. Ile spośród tych

pokolorowań przechodzi na siebie, gdy sześcian obracamy wokół pionowej osi o 90

◦

?

3

3

= 27

3. Dla jakich m i n graf K

m,n

jest hamiltonowski?

m = n > 2

4. Ile rozwiązań w liczbach całkowitych dodatnich ma równanie x

1

+ x

2

+ . . . + x

7

= 30?

23+6

6

5. Znajdź funkcję tworzącą ciągu a

n

= 3

n

dla parzystych n ≥ 2, a

n

= 0 dla pozostałych n.

9x

2

1 − 9x

2

6. Dla jakich n graf K

n

jest planarny?

n 6 4

7. Ile spośród liczb naturalnych od 1 do 420 dzieli się przez 2, 3 lub 7?

(210 + 140 + 60) − (70 + 30 + 20) + 10 = 300

8. Równaniem charakterystycznym pewnego równania rekurencyjnego jest r

2

+ r = 6. Jak

wygląda jego rozwiązanie ogólne?

a

n

= A(−3)

n

+ B2

n

9. Wypisz podane ciągi w kolejności od najniższego rzędu do najwyższego: n log n, n!, 3

n

oraz n

10

.

n log n, n

10

, 3

n

, n!

10. Ile kolorów potrzeba do pokolorowania wierzchołków grafu K

5,3

, a ile do pokolorowania

krawędzi tego grafu?

2 wierzchołkowo, 5 krawędziowo

11. Ile jest wszystkich grafów zwykłych o wierzchołkach 1, 2, . . . , 7 oraz o pięciu krawędziach?

(

7
2

)

5

12. Narysuj drzewo o kodzie zerojedynkowym 00101011010011.

r

r

r

r

r r

r

r

1/2

Część II.

W zadaniach 13–15 proszę podać sposób ich rozwiązania oraz odpowiedź, które należy

umieścić bezpośrednio pod zadaniem.

13.

(3 pkt.)

Ile co najwyżej krawędzi można dodać do poniższego drzewa, aby otrzymać graf

planarny?

r
r

r

r

r

r
r

r

r

r
r

L

L

L

L

a

a

a

a

!

!

!

!

Korzystając z nierówności dla grafów planarnych K

6 3W − 6 dla W = 11, otrzymujemy

górne oszacowanie liczby krawędzi, tzn.

K 6 3W − 6 = 3 · 11 − 6 = 27

Nastepnie z konstrukcji (na rysunku) wynika, że powyższe ograniczenie jest osiągalne. Zatem
do powyższego grafu można dorysować 27 − 10 = 17 krawędzi, nie tracąc jego planarności.

14.

(2 pkt.)

Ile drzew spinających ma poniższy graf?

r

r

r

r

r

r

r

r

r

r

r

Z tw. Cayley’a wynika, że K

5

ma 5

3

drzew spinających, a K

6

ma ich 6

4

. Każde drzewo

spinające powyższego grafu „składa się” z drzewa spinajacego grafu K

5

, drzewa spinajacego

grafu K

6

oraz krawędzi łączącej obie części. Zatem odpowiedź brzmi: 5

3

· 6

4

.

15.

(3 pkt.)

Znajdź funkcję tworzącą ciągu a

0

= 1, a

1

= 2, a

n+2

= a

n+1

+ 3a

n

.

f (x) =

∞

X

n=0

a

n

x

n

= 1 + 2x +

∞

X

n=2

a

n

x

n

= 1 + 2x +

∞

X

n=0

a

n+2

x

n+2

= 1 + 2x +

∞

X

n=0

(a

n+1

+ 3a

n

)x

n+2

= 1 + 2x + x

∞

X

n=0

a

n+1

x

n+1

+ 3x

2

∞

X

n=0

a

n

x

n

= 1 + 2x + x

∞

X

n=1

a

n

x

n

+ 3x

2

∞

X

n=0

a

n

x

n

= 1 + 2x + x(f (x) − 1) + 3x

2

f (x)

Skąd otrzymujemy

f (x) =

1 + x

1 − x − 3x

2

.

2/2

Imię i Nazwisko ............................................................. Nr indeksu .......................

16 VI 2008

Ćwiczenia prowadzi ........................................................

Matematyka Dyskretna – Elektronika

Kolokwium nr 2. Grupa

B

Część I.

Zadania 1–12 są za 1pkt. W ich rozwiązaniu proszę podać jedynie odpowiedź, którą należy

umieścić bezpośrednio pod zadaniem.

1. Wypisz podane funkcje w kolejności od najniższego rzędu do najwyższego: n

2

log n, log

2

n,

√

n oraz n!.

log

2

n,

√

n, n

2

log n, n!

2. Narysuj drzewo o kodzie zerojedynkowym 01001010110101.

r

r

r

r

r

r

r

r

3. Ile kolorów potrzeba do pokolorowania wierzchołków grafu K

8

, a ile do pokolorowania

krawędzi tego grafu?

8 wierzchołkowo, 7 krawędziowo

4. Dla jakich n graf K

3,n

jest planarny?

n ∈ {1, 2}

5. Znajdź kod Prüfera dla poniższego drzewa:

131343

r

r

r

r

r

r

r

r

@

@

4

7

3

5

8

6

2

1

6. Równaniem charakterystycznym pewnego równania rekurencyjnego jest r

2

+ 9 = 6r. Jak

wygląda jego rozwiązanie ogólne?

a

n

= (A + Bn)3

n

7. Znajdź funkcję tworzącą ciągu a

n

= 5

n

dla n ≥ 3 oraz a

0

= a

1

= a

2

= 0.

125x

3

1 − 5x

8. Ile jest wszystkich grafów bez pętli, o wierzchołkach 1, 2, . . . , 8 i pięciu krawędziach, gdy

dopuszczamy krawędzie wielokrotne?

5+

(

8
2

)

−1

5

=

32

5

9. Ile rozwiązań w liczbach całkowitych większych niż 2 ma równanie x

1

+ x

2

+ . . . + x

8

= 40?

16+7

7

10. Dla jakich m i n graf K

m,n

jest eulerowski?

dla m i n jednocześnie parzystych

11. Rozważmy wszystkie 4

6

pokolorowań sześcianu za pomocą 4 kolorów. Ile spośród tych

pokolorowań przechodzi na siebie, gdy sześcian obracamy wokół pionowej osi o 180

◦

?

4

4

= 256

12. Ile spośród liczb naturalnych od 1 do 700 dzieli się przez 2, 5 lub 7?

(350 + 140 + 100) − (70 + 50 + 20) + 10 = 460

1/2

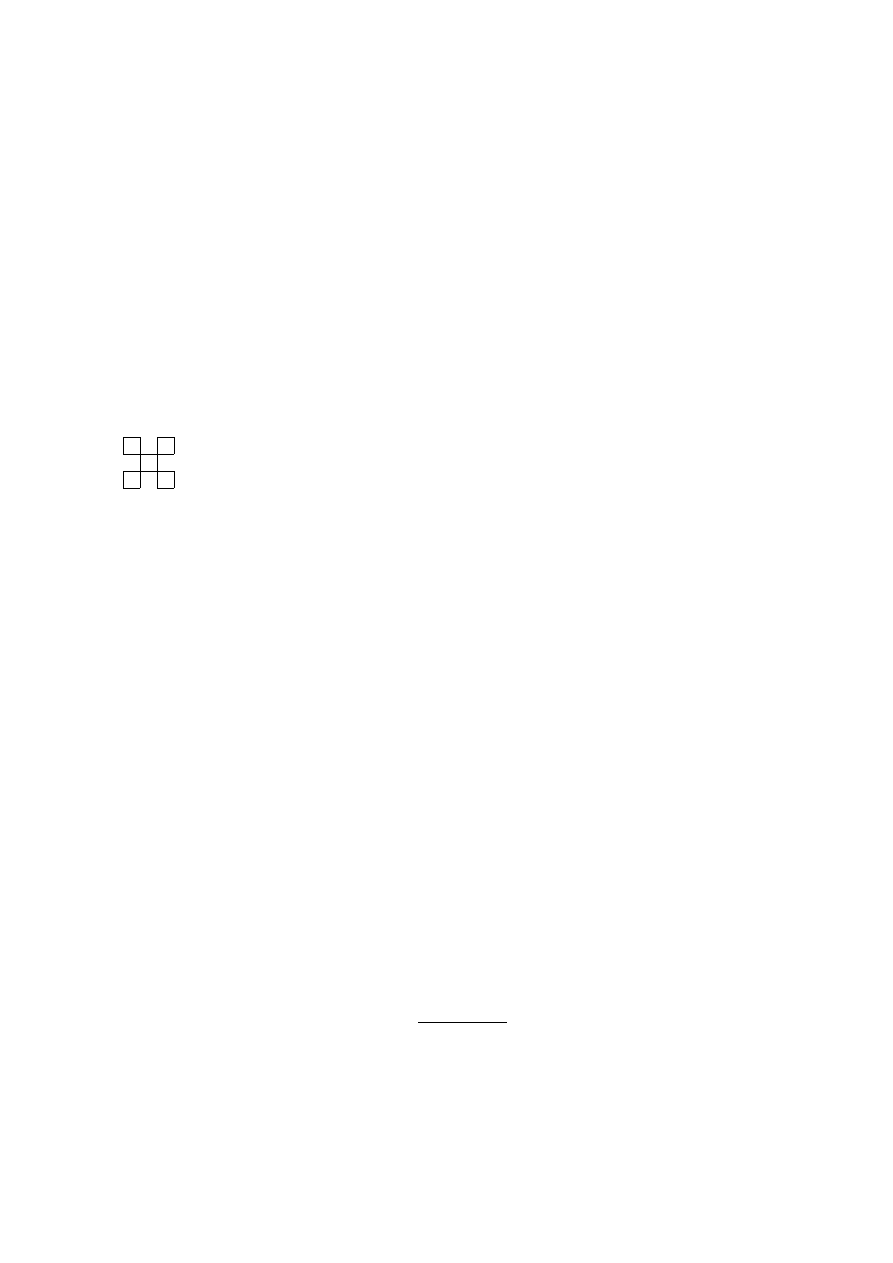
Część II.

W zadaniach 13–15 proszę podać sposób ich rozwiązania oraz odpowiedź, które należy

umieścić bezpośrednio pod zadaniem.

13.

(3 pkt.)

Ile co najmniej krawędzi trzeba odrzucić z grafu K

4,4

, aby otrzymać graf planarny?

Napoczątek zauważamy, że K

4,4

nie zawiera cyki długości 3, a zatem każdy jego podgraf

planarny nie zawiera trójkątów. Tak więc spełnia on nierówność

K 6 2W − 4 = 2 · 8 − 4 = 12

Oczywiście K

4,4

ma 16 krawędzi. Z powyższej nierówności wynika, że musimy usunąć co

najmniej 4 krawędzie. Konkretny przykład (rysunek) pokazuje, że usunięcie 4 krawędzi
wsytarcza do uzyskania grafu planarnego.

14.

(2 pkt.)

Ile drzew spinających ma poniższy graf?

r

r

r

r
@

@

r

r

r

r
@

@

r

r

r

r
@

@

r

r

r

r
@

@

Z tw. Cayley’a wynika, że K

4

ma 4

2

drzew spinających. Ponadto są 4 drzewa spinające

cyklu C

4

. Każde drzewo spinające powyższego grafu „składa się” z czterech drzew spinajacych

każdego z grafów K

4

oraz drzewa spinajacego cyklu w środku. Zatem odpowiedź brzmi: (4

2

)

4

·4.

15.

(3 pkt.)

Znajdź funkcję tworzącą ciągu a

0

= 2, a

1

= 3, a

n+2

= a

n+1

− 2a

n

.

f (x) =

∞

X

n=0

a

n

x

n

= 2 + 3x +

∞

X

n=2

a

n

x

n

= 2 + 3x +

∞

X

n=0

a

n+2

x

n+2

= 2 + 3x +

∞

X

n=0

(a

n+1

− 2a

n

)x

n+2

= 2 + 3x + x

∞

X

n=0

a

n+1

x

n+1

− 2x

2

∞

X

n=0

a

n

x

n

= 2 + 3x + x

∞

X

n=1

a

n

x

n

− 2x

2

∞

X

n=0

a

n

x

n

= 2 + 3x + x(f (x) − 2) − 2x

2

f (x)

Skąd otrzymujemy

f (x) =

2 + x

1 − x + 2x

2

.

2/2