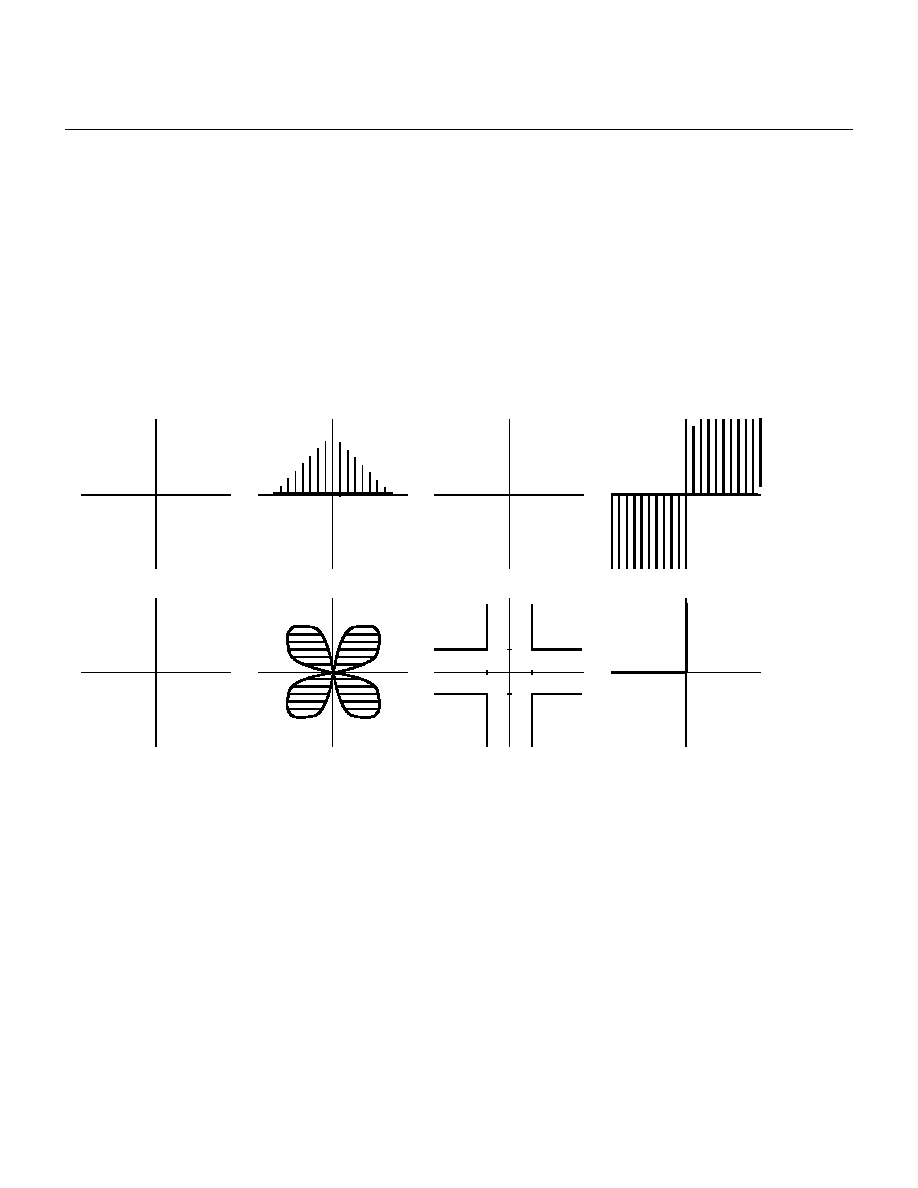
Algebra

linio

w

a

2

Lista pierwsza

Zadanie

1.1

Uzasadni¢ z denicji, »e zbiór wszystkich rzeczywistych macierzy trójk¡tnych górnych stopnia 2 wraz z dodawaniem

macierzy i mno»eniem macierzy przez liczby rzeczywiste stanowi przestrze« liniow¡.

Zadanie

1.2

Sprawdzi¢, »e podane zbiory

W

s¡ podprzestrzeniami liniowymi odpowiednich przestrzeni liniowych

V

:

a)

W

=

(2

x

,

y ;

y

+

z

)

2

R

2

:

x;

y ;

z

2

R

,

V

=

R

2

; b)

W

=

(

x;

y ;

z

;

t

)

2

R

4

:

x

,

y

=

z

,

t

,

V

=

R

4

;

c)

W

=

fp

2

R

2

[

x

] :

p

(1) =

p

0

(0)

g

,

V

=

R

[

x

];

d)

W

=

n

A

2

M

33

:

A

=

A

T

o

,

V

=

M

33

:

Zadanie

1.3

Który z narysowanych ni»ej zbiorów jest poprzestrzeni¡ liniow¡ pªaszczyzny ?

-

6

@

@

@

@

@

@

@

@

a)

y

x

-

6

@

@

@

@

,

,

,

,

1

,1

1

b)

y

x

-

6

s

c)

y

x

-

6

d)

y

x

-

6

,

,

,

,

,

,

,

,1

1

e)

y

x

-

6

f

)

y

x

-

6

g)

1

,1

1

,1

y

x

,

,

,

,

,

,

,

,

,

,

,

,

,

,

,

,

,

,

,

,

,

,

,

,

,

,

,

,

,

,

,

,

,

,

,

,

,

,

,

,

,

,

,

,

,

,

,

,

,

,

,

,

,

,

,

,

,

,

,

,

,

,

,

,

,

,

,

,

,

,

,

,

,

,

,

,

,

,

,

,

,

,

,

,

,

,

,

,

,

,

,

,

,

,

,

,

,

,

,

-

6

h)

y

x

Zadanie

1.4

Opisa¢ wszystkie podprzestrzenie liniowe przestrzeni

R

3

:

Zadanie

1.5

Okre±li¢, które z podanych zbiorów

U

;

W

;

X

;

Y

s¡ podprzestrzeniami liniowymi wskazanych przestrzeni liniowych

V

:

a)

V

=

R

2

,

U

=

f

(

x;

y

) :

jx

,

y j

¬

1

g

;

W

=

(

x;

y

) : ln

,

1

,

x

2

,

y

2

­

0

;

X

=

(

x;

y

) : 9

x

2

+ 12

xy

+ 4

y

2

= 0

;

Y

=

(

x;

y

) : 3

x

2

+ 5

xy

,

2

y

2

= 0

;

b)

V

=

R

4

,

U

=

f

(

x;

y ;

z

;

t

) : 3

jxj

= 2

jy jg

;

W

=

f

(

xy ;

y ;

x;

0) :

x;

y

2

Rg

;

X

=

(

x;

y ;

z

;

t

) :

x

2

+

z

6

= 0

;

Y

=

f

(

x;

x

+

y ;

,x;

,y

) :

x;

y

2

Rg

;

c)

V

=

R

1

,

U

=

n

(

x

n

) : lim

n!1

jx

n

j

=

1

lub lim

n!1

x

n

= 0

o

;

W

=

f

(

x

n

) : istnieje

n

0

2

N

takie, »e

x

n

= 0dla ka»dego

n

­

n

0

g

;

X

=

f

(

x

n

) : ci¡g (

x

n

) jest zbie»ny lub ograniczony

g

;

Y

=

f

(

x

n

) :

x

n+2

=

x

n

+

x

n+1

dla ka»dego

n

2

Ng

;

d)

V

=

R

[

x

],

U

=

fp

: stopie« wielomianu

p

jest równy 4

g

;

W

=

f

p

: 2

p

(

x

) =

p

(2

x

)dla ka»dego

x

2

Rg

;

X

=

fp

:

p

(0) = 0 lub

p

0

(0) = 0

g

;

Y

=

fp

: wielomian

p

jest funkcj¡ parzyst¡

g

;

1

e)

V

=

C

(

R

),

U

=

ff

: funkcja

f

jest niemalej¡ca

g

;

W

=

ff

: funkcja

f

jest ró»niczkowalna

g

;

X

=

ff

: funkcja

f

jest staªa na zbiorze

Ng

;

Y

=

ff

:

f

(

x

+

y

) =

f

(

x

)

f

(

y

)dla dowolnych

x;

y

2

Rg

;

f)

V

=

M

22

,

U

=

8

<

:

A

:

A A

T

=

2

4

0 0

0 0

3

5

9

=

;

;

W

=

f

A

: det

A

­

0

g

;

X

=

8

<

:

2

4

a

b

c

d

3

5

:

abcd

= 0

9

=

;

;

Y

=

8

<

:

2

4

a

b

c

d

3

5

:

a

+

c

=

b

9

=

;

:

Zadanie*

1.6

Uzasadni¢ bezpo±rednio z denicji przestrzeni liniowej, »e

a) istnieje tylko jeden wektor zerowy;
b) istnieje tylko jeden wektor przeciwny do ka»dego wektora;
c)

~

0

=

~

0

dla ka»dego

2

R:

Lista druga

Zadanie

2.1

Wektory (3

;

,

2

;

5), (0

;

1

;

1) przedstawi¢ na wszystkie mo»liwe sposoby jako kombinacje liniowe wektorów:

a) (3

;

,

2

;

5), (1

;

1

;

1);

b) (3

;

,

2

;

5), (1

;

1

;

1), (0

;

,

5

;

2);

c) (1

;

,

2

;

3), (1

;

0

;

1), (0

;

2

;

,

1); d) (1

;

,

2

;

3), (1

;

0

;

1), (

,

1

;

,

2

;

1)

:

Zadanie

2.2

Zbada¢ z denicji liniow¡ niezale»no±¢ podanych ukªadów wektorów w odpowiednich przestrzeniach liniowych:

a) (1

;

4)

;

(2

;

3)

;

(1

;

1)

;

(5

;

6) w przestrzeni

R

2

;

b) (1

;

,

2

;

3)

;

(1

;

0

;

1)

;

(0

;

2

;

,

1); (1

;

,

2

;

3)

;

(1

;

0

;

1)

;

(

,

1

;

,

2

;

1) w przestrzeni

R

3

;

c) 3

,

x

, 4 +

x

, 2

x

+ 3; 2

,

x

3

, 3

x

+ 2,

x

2

+

x

,

1 w przestrzeni

R

[

x

];

d) 1

;

cos

x;

cos2

x;

cos

2

x

; 1

;

x;

cos

x;

e

x

w przestrzeni

C

(

R

);

e)

2

,

1

3 0

;

1 1

2 1

;

,

1 0

1 0

;

0 2

,

2 1

w przestrzeni

M

22

;

f)

I

;

A;

A

2

dla

A

=

1

,

1

2 1

w przestrzeni

M

22

:

Zadanie

2.3

Uzasadni¢ liniow¡ zale»no±¢ podanych wektorów w odpowiednich przestrzeniach liniowych przedstawiaj¡c jeden z tych

wektorów jako kombinacj¦ liniow¡ pozostaªych:

a) (1

;

2

;

3), (2

;

3

;

4), (1

;

1

;

1) w przestrzeni

R

3

;

b)

x

4

,

x

3

+

x

2

,

x

+ 1,

x

3

+

x

2

+

x

,

x

3

,

x

2

+

x

,

x

4

+

x

3

+

x

2

+

x

+ 1 w przestrzeni

R

4

[

x

];

c) sin

x;

sin

2

,

x

;

sin

3

,

x

w przestrzeni

C

(

R

);

d) arcsin

x;

arccos

x;

1 w przestrzeni

C

([

,

1

;

1])

:

Zadanie

2.4

Wektory

~

u ;

~

v;

~

w;

~

x

s¡ liniowo niezale»ne w przestrzeni liniowej

V

:

Zbada¢ liniow¡ niezale»no±¢ wektorów:

a)

~

u

+

~

v ;

~

v

+

~

w ;

~

u

+

~

w

;

b)

~

u ;

~

u

+

~

v ;

~

u

+

~

v

+

~

w ;

~

u

+

~

v

+

~

w

+

~

x

;

c)

~

u

,

~

v

;

~

v

,

~

w;

~

w

;

d)

~

u

,

~

v

;

~

v

,

~

w;

~

w

,

~

x ;

~

x

,

~

u

;

e)

~

u

,

3

~

v

+ 5

~

w;

2

~

u

+

~

v

+ 3

~

w ;

3

~

u

+ 2

~

v

+ 4

~

w

; f) 2

~

u

+ 3

~

v

+

~

w;

~

u

+ 2

~

v

+

~

x ;

4

~

u

+ 7

~

v

+

~

w

+ 2

~

x:

2

Zadanie

2.5

Niech

V

b¦dzie przestrzeni¡ liniow¡, a

~

u

,

~

v

,

~

w

,

~

x

wektorami z tej przestrzeni. Uzasadni¢, »e je»eli wektory:

a)

~

u

,

~

v

,

~

w

s¡ liniowo zale»ne, to wektory

~

u

,

~

v

,

~

w

,

~

x

te» s¡ liniowo zale»ne;

b)

~

u;

~

v

s¡ liniowo niezale»ne, a wektory

~

u

,

~

v

,

~

w

liniowo zale»ne, to wektor

~

w

jest kombinacj¡ liniow¡ wektorów

~

u

,

~

v

;

c)

~

u

,

~

v

,

~

w

s¡ liniowo niezale»ne i wektor

~

x

nie jest kombinacj¡ liniow¡ tych wektorów, to wektory

~

u

,

~

v

,

~

w

,

~

x

s¡ liniowo

niezale»ne;

d)

~

u

,

~

v

,

~

w

s¡ liniowo niezale»ne, a wektory

~

u

,

~

v

,

~

w

,

~

x

s¡ liniowo zale»ne, to wektor

~

x

jest kombinacj¡ liniow¡ wektorów

~

u

,

~

v

,

~

w :

*Co mo»na powiedzie¢ o liniowej niezale»no±ci wektorów

~

u

+

~

v

,

~

u

+

~

w

,

~

v

,

~

w ;

je»eli wektory

~

u

,

~

v

,

~

w

s¡ liniowo zale»ne ?

Zadanie

2.6

Uzasadni¢ liniow¡ niezale»no±¢ podanych niesko«czonych ukªadów wektorów z odpowiednich przestrzeni liniowych:

a)

f

(1

;

0

;

0

;

:

:

:

)

;

(1

;

1

;

0

;

:

:

:

)

;

(1

;

1

;

1

;

:

:

:

)

;

:

:

:

g

,

R

1

;

b)

1

;

x;

x

2

;

:

:

:

,

R

[

x

];

c)

p

n

2

R

[

x

] :

p

n

(

x

) =

x

n

,

1

x

,

1 dla

x

6

= 1

;

n

2

N

,

R

[

x

];

d*)

f

1

;

cos

x;

cos2

x;

:

:

:

g

,

C

(

R

);

e*)

fe

tx

:

t

2

Rg

,

C

(

R

)

:

Zadanie

2.7

Uzasadni¢, »e dowolne trzy niewspóªpªaszczyznowe wektory w przestrzeni

R

3

s¡ liniowo niezale»ne.

Lista trzecia

Zadanie

3.1

Opisa¢ (geometrycznie lub sªownie) zbiory lin

A

dla:

a)

A

=

f

(5

;

,

1

;

4)

;

(

,

10

;

2

;

,

8)

g

R

3

;

b)

A

=

x

+ 3

;

x

(

x

+ 3)

;

x

2

(

x

+ 3)

;

x

3

(

x

+ 3)

R

[

x

];

c)

A

=

8

>

>

>

<

>

>

>

:

2

6

6

6

4

0 1 0

,

1 0 0

0 0 0

3

7

7

7

5

;

2

6

6

6

4

0 0

,

2

0 0 0

2 0 0

3

7

7

7

5

;

2

6

6

6

4

0 0 0

0 0 3

0

,

3 0

3

7

7

7

5

9

>

>

>

=

>

>

>

;

M

33

;

d*)

A

=

f

(1

;

1

;

1

;

1

;

1

:

:

:

)

;

(0

;

2

;

2

;

2

;

2

:

:

:

)

;

(0

;

0

;

3

;

3

;

3

;

:

:

:

)

;

:

:

:

g

R

1

:

Zadanie

3.2

Wyznaczy¢ generatory podanych przestrzeni liniowych:

a)

V

=

(

x;

y ;

z

)

2

R

3

: 4

x

,

y

+ 2

z

= 0

;

b)

V

=

f

(2

r

+

s

,

t;

t

,

u;

r

+ 3

s

+

u;

s

+

u;

t

,

u

) :

r

;

s;

t;

u

2

Rg

;

c)

V

=

(

x;

y ;

z

;

t

)

2

R

4

:

x

,

y

=

y

,

z

=

z

,

t

;

d)

V

=

fp

2

R

3

[

x

] :

p

(1) +

p

(2) =

p

(3) +

p

0

(0)

g

:

Zadanie

3.3

Sprawdzi¢ z denicji, czy podane zbiory wektorów s¡ bazami wskazanych przestrzeni liniowych:

a)

B

=

f

(2

;

5)

;

(3

;

1)

;

(6

;

,

7)

g

;

R

2

;

b)

B

=

f

(2

;

3

;

,

1)

;

(1

;

,

3

;

2)

g

;

R

3

;

c)

B

=

f

(1

;

,

1

;

4)

;

(3

;

0

;

1)

;

(2

;

1

;

,

2)

g

;

R

3

; d)

B

=

2

x

+ 4

;

3

x

,

x

2

;

,

2

x

2

+ 4

x

,

4

;

R

2

[

x

]

:

3

Zadanie

3.4

Wektory

~

u

,

~

v

,

~

w

tworz¡ baz¦ przestrzeni liniowej

V

. Zbada¢ z denicji, czy podane zbiory wektorów te» s¡ bazami

przestrzeni

V

:

a)

~

u

,

2

~

v

+

~

w ;

3

~

u

+

~

w ;

~

u

+ 4

~

v

,

~

w

; b)

~

u;

2

~

u

+

~

v ;

3

~

u

,

~

v

+ 4

~

w :

Zadanie

3.5

Dla jakich warto±ci parametru

p

2

R

podane zbiory wektorów stanowi¡ bazy odpowiednich przestrzeni

R

n

:

a)

B

=

f

(

p

,

2

;

,p

)

;

(3

;

2 +

p

)

g

;

R

2

;

b)

B

=

f

(1

;

3

;

p

)

;

(

p;

0

;

,p

)

;

(1

;

2

;

1)

g

;

R

3

;

c)

B

=

(1

;

1

;

1

;

1)

;

(1

;

p;

2

;

3)

;

,

1

;

p

2

;

4

;

9

;

,

1

;

p

3

;

8

;

27

;

R

4

;

d*)

B

=

f

(0

;

1

;

1

;

:

:

:

;

1)

;

(

p;

0

;

1

;

:

:

:

;

1)

;

(

p;

p;

0

;

:

:

:

;

1)

;

:

:

:

;

(

p;

p;

p;

:

:

:

;

0)

g

;

R

n

?

Zadanie

3.6

Wskaza¢ bazy i okre±li¢ wymiary podanych przestrzeni liniowych:

a)

V

=

f

(

x

+

y

+

z

;

x

,

y ;

x

,

z

;

y

,

z

) :

x;

y ;

z

2

Rg

; b)

V

=

f

(

a

+ 2

b

+

c;

3

a

,

b

+ 2

c;

5

a

+ 3

b

+ 4

c

) :

a;

b;

c

2

Rg

;

c)

V

=

(

x;

y ;

z

;

t

)

2

R

4

: 2

x

,

y

=

z

,

t

= 0

;

d)

V

=

fp

2

R

4

[

x

] :

p

(2

x

) = 4

xp

0

(

x

) +

p

(0)

g

;

e)

V

=

f

A

= [

a

ij

]

2

M

34

:

a

ij

= 0 dla

i

¬

j

g

;

f)

V

= lin

f

1

;

e

x

;

e

,x

;

sh

x;

ch

xg

;

przy czym

V

C

(

R

)

:

Zadanie

3.7

Znale¹¢ bazy podanych przestrzeni liniowych zawieraj¡ce wskazane zbiory wektorów:

a)

f

(

,

1

;

5

;

3)

g

;

R

3

;

b)

f

(1

;

0

;

1

;

,

1)

;

(2

;

3

;

,

1

;

2)

;

(3

;

3

;

2

;

1)

g

;

R

4

;

c)

2

x

,

3

;

x

3

+ 4

x

,

1

;

R

3

[

x

];

d)

x

2

+ 5

;

x

2

,

3

x;

x

4

,

2

x

3

;

R

4

[

x

];

e*)

1

;

1 +

x

2

;

1 +

x

2

+

x

4

;

1 +

x

2

+

x

4

+

x

6

;

:

:

:

;

;

R

[

x

]

:

Lista czwarta

Zadanie

4.1

Znale¹¢ z denicji wspóªrz¦dne podanych wektorów we wskazanych bazach odpowiednich przestrzeni liniowych:

a)

~

v

= (1

;

4)

2

R

2

;

B

=

f

(1

;

5)

;

(1

;

6)

g

;

b)

~

v

= (8

;

1

;

7

;

5)

2

R

4

;

B

=

f

(1

;

0

;

0

;

0)

;

(1

;

1

;

0

;

0)

;

(1

;

1

;

1

;

0)

;

(1

;

1

;

1

;

1)

g

;

c)

p

=

x

2

,

3

x

+ 3

2

R

2

[

x

]

;

B

=

x

2

+ 3

x

,

1

;

,x

2

+

x

+ 3

;

2

x

2

,

x

,

2

;

d)

A

=

2

4

3 2

1 3

3

5

2

M

22

;

B

=

8

<

:

2

4

1 0

0 0

3

5

;

2

4

4 1

0 0

3

5

;

2

4

2 2

1 3

3

5

;

2

4

,

1 0

0 1

3

5

9

=

;

:

Zadanie

4.2

Wyznaczy¢ wspóªrz¦dne wektora

~

v

w podanej bazie

B

0

pewnej przestrzeni liniowej maj¡c dane jego wspóªrz¦dne w bazie

B

:

a) [4

;

,

3]

;

B

=

n

~

b

1

;

~

b

2

o

;

B

0

=

n

2

~

b

1

,

~

b

2

;

~

b

1

+ 2

~

b

2

o

;

b) [1

;

1

;

,

2]

;

B

=

x;

x

+ 1

;

x

2

+ 1

;

B

0

=

1

;

1 +

x

2

;

x

+

x

2

;

c*) [1

;

2

:

:

:

;

n

]

;

B

=

n

~

b

1

;

~

b

2

;

:

:

:

;

~

b

n

o

,

B

0

=

n

~

b

1

,

~

b

2

;

~

b

2

,

~

b

3

;

:

:

:

;

~

b

n,1

,

~

b

n

;

~

b

n

o

:

4

Zadanie

4.3

Obliczy¢ wspóªrz¦dne wskazanych wektorów w wybranych bazach podanych przestrzeni liniowych:

a)

V

=

f

(

x

,

5

y ;

x

+

y ;

2

x

+

y ;

x

+

y

) :

x;

y

2

Rg

;

~

v

= (

,

2

;

4

;

7

;

4);

b)

V

=

(

x;

y ;

z

;

t

)

2

R

4

:

x

,

2

y

=

y

,

2

z

= 0

;

~

v

= (8

;

4

;

2

;

9);

c)

V

=

f

p

2

R

3

[

x

] :

p

(1) =

p

(0)

g

;

q

= 2

x

3

,

x

2

,

x

+ 5;

d)

V

=

fA

= [

a

ij

]

2

M

22

:

a

11

+

a

22

= 0

g

;

B

=

2

4

3 1

,

2

,

3

3

5

:

Zadanie

4.4

Zbada¢, obliczaj¡c odpowiednie wyznaczniki, czy podane zbiory wektorów s¡ bazami podanych przestrzeni liniowych:

a)

~

u

= (2

;

4

;

5)

;

~

v

= (1

;

,

1

;

1)

;

~

w

= (

,

1

;

7

;

2)

;

V

=

R

3

;

b)

p

=

x

3

+

x

2

+

x

,

1

;

q

=

x

3

+

x

2

,

x

,

1

;

r

=

x

3

,

x

2

,

x

,

1

;

s

=

x

3

+

x

2

+

x

+ 1

;

V

=

R

3

[

x

];

c)

A

=

2

4

1

,

1

0 1

3

5

;

B

=

2

4

1 0

2 1

3

5

;

C

=

2

4

1

,

1

1 3

3

5

;

D

=

2

4

0 2

3

,

2

3

5

;

V

=

M

22

:

Zadanie

4.5

Znale¹¢ takie bazy odpowiednich przestrzeni liniowych, w których wskazane wektory maj¡ podane wspóªrz¦dne:

a)

~

v

= (2

;

,

1

;

3)

2

R

3

;

[1

;

0

;

1];

b)

~

v

= (1

;

1

;

1

;

1)

2

R

4

;

V

=

(

x;

y ;

z

;

t

)

2

R

4

:

x

=

t;

x

,

3

y

+ 2

z

= 0

, [2

;

2];

c*)

~

v

= (1

;

0

;

:

:

:

;

0)

2

R

n

;

[1

;

1

;

:

:

:

;

1]

:

Zadanie

4.6

Napisa¢ macierze przej±cia z bazy

B

do bazy

B

0

odpowiedniej przestrzeni liniowej:

a)

V

=

R

3

;

B

=

f

(1

;

1

;

1)

;

(1

;

1

;

0)

;

(1

;

0

;

0)

g

,

B

0

=

f

(1

;

0

;

1)

;

(0

;

1

;

1)

;

(0

;

0

;

1)

g

;

b)

V

=

R

2

[

x

]

;

B

=

x

2

;

x;

1

;

B

0

=

3

x

2

,

x;

2

x

2

+

x

,

1

;

x

2

+ 5

x

,

6

:

Zadanie

4.7

Wykorzystuj¡c macierze przej±cia z baz standardowych odpowiednich przestrzeni liniowych do baz danych znale¹¢ wspóª-

rz¦dne podanych wektorów w tych bazach:

a)

V

=

R

2

;

~

v

= (1

;

1)

;

B

0

=

f

(4

;

1)

;

(

,

2

;

3)

g

; b)

V

=

R

3

;

~

v

= (2

;

,

4

;

7)

;

B

0

=

f

(1

;

,

2

;

3)

;

(2

;

1

;

4)

;

(

,

3

;

1

;

,

6)

g

;

c)

V

=

R

3

[

x

]

;

p

= 2

x

3

,

x

2

+ 1

;

B

0

=

2

x

3

+ 3

x

2

+ 2

x

+ 1

;

2

x

3

+

x

+ 1

;

x

2

+ 2

x

+ 1

;

2

x

2

+

x

+ 1

:

Zadanie

4.8

Wektor

~

v

ma w bazie

n

~

b

1

;

~

b

2

;

~

b

3

o

wspóªrz¦dne [0

;

1

;

,

2]

:

Stosuj¡c macierz przej±cia z bazy do bazy obliczy¢ wspóªrz¦dne

tego wektora w bazie:

a)

n

~

b

1

+

~

b

2

;

~

b

2

+

~

b

3

;

~

b

1

+

~

b

3

o

;

b)

n

2

~

b

1

+

~

b

2

,

3

~

b

3

;

3

~

b

1

+ 2

~

b

2

,

5

~

b

3

;

~

b

1

,

~

b

2

+

~

b

3

o

:

Lista pi¡ta

Zadanie

5.1

Znale¹¢ z denicji rz¦dy podanych macierzy wskazuj¡c niezerowe minory maksymalnych stopni:

5

a)

2

4

4

,

2

,

8 4

3

5

; b)

2

6

6

6

4

1 3 5

2 2 1

,

1 0 3

3

7

7

7

5

;

c)

2

6

6

6

4

2 3

,

1 1

4 2 0 5

0 4

,

2

,

3

3

7

7

7

5

;

d)

2

6

6

6

6

6

6

4

1 2 3

2 1

,

2

4 5 4

1 3 4

3

7

7

7

7

7

7

5

; e)

2

6

6

6

6

6

6

6

6

6

4

1 0 1 0 1 0 1

1 5 1 0 1 6 1

1 0 1 7 1 0 1

1 8 1 0 1 9 1

1 0 1 0 1 0 1

3

7

7

7

7

7

7

7

7

7

5

; f)

2

6

6

6

6

6

6

6

6

6

4

1 1 2 0 0

2 1

,

1 0 0

4 3 3 0 0

0 0 0 7 5

0 0 0 1 6

3

7

7

7

7

7

7

7

7

7

5

:

Zadanie

5.2

Wykonuj¡c operacje elementarne na wierszach lub kolumnach podanych macierzy obliczy¢ ich rz¦dy:

a)

2

6

6

6

4

1

,

3 2 1 2

2 1

,

1 3 1

4

,

5 3 5 6

3

7

7

7

5

; b)

2

6

6

6

4

,

2 1

,

3 1

,

5

45 15 30

,

60 75

5 3 2

,

8 7

3

7

7

7

5

; c)

2

6

6

6

6

6

6

4

3 1 6 2 1

2 1 4 2 2

3 1 3 1 3

2 1 2 1 4

3

7

7

7

7

7

7

5

;

d)

2

6

6

6

6

6

6

4

1 2 3 4

5 6 7 8

9 10 11 12

13 14 15 16

3

7

7

7

7

7

7

5

; e)

2

6

6

6

6

6

6

6

6

6

4

,

4 1 1 1 1

1

,

4 1 1 1

1 1

,

4 1 1

1 1 1

,

4 1

1 1 1 1

,

4

3

7

7

7

7

7

7

7

7

7

5

; f*)

2

6

6

6

6

6

6

6

6

6

6

6

6

4

1 1 1 0 0 0 0

3 2 2 1 0 0 0

5 3 2 2 1 0 0

5 2 1 2 1 1 0

3 1 0 1 0 1 0

1 0 0 0 0 0 1

3

7

7

7

7

7

7

7

7

7

7

7

7

5

:

Zadanie

5.3

Znale¹¢ rz¦dy podanych macierzy w zale»no±ci od parametru rzeczywistego

p

:

a)

2

6

6

6

4

1 1

p

3

p

3

2

p

2 2

3

7

7

7

5

; b)

2

6

6

6

4

1

p

2

1

,

2 7 +

p

1 2 + 2

p

,

3

,

p

3

7

7

7

5

; c)

2

6

6

6

4

p

,

1

p

,

1 1

1

1

p

2

,

1 1

p

,

1

1

p

,

1

p

,

1 1

3

7

7

7

5

;

d)

2

6

6

6

4

1 1 1

p

1 1

p

p

1

p

p

p

3

7

7

7

5

; e)

2

6

6

6

6

6

6

4

p

,p

1

,p

,

2 2

,

2 2

3

p

3

p

p

1

p

1

3

7

7

7

7

7

7

5

; f*)

2

6

6

6

6

6

6

4

p

2

4 4 4 4

p

2

2

p

4 4 4

p

2

2

p

2

jpj

4 4

p

2

2

p

2

jpj

2

p

4

3

7

7

7

7

7

7

5

:

Zadanie

5.4

Zbada¢ liniow¡ niezale»no±¢ podanych wektorów we wskazanych przestrzeniach liniowych analizuj¡c rz¦dy macierzy ich

wspóªrz¦dnych w odpowiednich bazach:

a) (56

;

94

;

16), (48

;

67

;

81), (29

;

82

;

53), (74

;

15

;

38) w przestrzeni

R

3

;

b) (1

;

0

;

1

;

1

;

1)

;

(0

;

1

;

0

;

1

;

1)

;

(0

;

0

;

1

;

0

;

1)

;

(1

;

1

;

1

;

0

;

0) w przestrzeni

R

5

;

c)

x

4

,

x

2

+

x;

x

4

+ 2

x

3

+

x

2

+ 1

;

x

3

+

x

+ 1 w przestrzeni

R

4

[

x

];

d)

2

4

1

,

1

2 3

3

5

,

2

4

3 2

1 9

3

5

,

2

4

1 1

,

1 2

3

5

,

2

4

1 0

1 3

3

5

w przestrzeni

M

22

:

Zadanie

5.5

Wektory

~

w ;

~

x;

~

y;

~

z

z przestrzeni liniowej

V

s¡ liniowo niezale»ne. Zbada¢, przy pomocy rz¦dów odpowiednich macierzy,

6

liniow¡ niezale»no±¢ podanych wektorów:

a)

~

w

,

~

x

+

~

z

,

~

w

+ 2

~

x

+

~

y

+ 3

~

z

, 4

~

x

+ 3

~

y

+

~

z

;

b) 7

~

w

+ 9

~

x

+ 12

~

y

+ 8

~

z

, 21

~

w

,

9

~

x

+ 24

~

y

+ 24

~

z

,

,

7

~

w

+ 27

~

x

,

8

~

z

.

Zadanie

5.6

Okre±li¢ wymiary i wyznaczy¢ bazy podprzestrzeni liniowych generowanych przez podane zbiory wektorów ze wskazanych

przestrzeni liniowych:

a) (2

;

1

;

1)

;

(

,

1

;

1

;

2)

;

(3

;

3

;

4)

;

(5

;

,

2

;

,

5)

;

(0

;

1

;

,

1)

;

R

3

;

b) wektory wierszowe macierzy

2

6

6

6

6

6

6

4

1

,

1 1

,

1

1 2 0 1

,

2 5

,

3 4

4

,

1 3

,

2

3

7

7

7

7

7

7

5

;

R

4

;

c)

x

3

+ 2

x

2

+

x;

x

2

,

x

+ 1

;

x

3

+

x

2

;

x

3

,

x;

2

x

2

,

1

;

R

3

[

x

];

d)

2

6

6

6

4

1 0

0 2

3 0

3

7

7

7

5

;

2

6

6

6

4

1 1

0 0

3 3

3

7

7

7

5

;

2

6

6

6

4

0 1

2 2

0 3

3

7

7

7

5

;

2

6

6

6

4

0 0

2 0

3 3

3

7

7

7

5

;

M

32

:

Zadanie

5.7

Wektory

~

w ;

~

x

;

~

y ;

~

z

z przestrzeni liniowej

V

s¡ liniowo niezale»ne. Okre±li¢ wymiarypodprzestrzeni liniowych generowanych

przez podane zbiory wektorów w zale»no±ci od parametru rzeczywistego

p

:

a) 2

p

~

w

,

2

~

x

+

p

~

y

+ 3

~

z

;

4

~

w

,

p

~

x

+ 2

~

y

+ (

p

+ 1)

~

z ;

2

~

w

,

~

x

+

~

y

+ 3

~

z

;

b)

~

x

,

~

y

+

p

~

z

;

p

~

x

,

p

2

~

y

+

~

z

;

p

2

~

x

,

p

~

y

+

p

~

z

:

Lista szósta

Zadanie

6.1

W podanych ukªadach równa« liniowych okre±li¢ (nie rozwi¡zuj¡c ich) liczby rozwi¡za« oraz liczby parametrów:

a

)

8

>

>

>

>

>

>

<

>

>

>

>

>

>

:

x

+

y

+

z

= 1

x

+ 2

y

+ 3

z

= 1

2

x

+ 3

y

+ 4

z

= 2

3

x

+ 2

y

+

z

= 3

;

b)

8

>

>

>

>

>

>

<

>

>

>

>

>

>

:

2

x

,

y

= 3

x

+

y

= 4

4

x

+ 8

y

= 11

x

+ 4

y

= 10

;

c)

8

>

>

>

>

>

>

<

>

>

>

>

>

>

:

5

x

,

3

y

,

z

= 3

2

x

+

y

,

z

= 1

3

x

,

2

y

+ 2

z

=

,

4

x

,

y

,

2

z

=

,

2

;

d)

8

>

>

>

<

>

>

>

:

x

,

y

+ 2

z

,

t

= 1

2

x

,

3

y

,

z

+

t

=

,

1

x

+ 7

y

,

t

= 4

;

e)

8

>

>

>

<

>

>

>

:

x

,

3

y

+ 2

z

= 7

x

,

t

= 2

,x

,

3

y

+ 2

z

+ 2

t

= 3

:

Zadanie

6.2

Wskaza¢ wszystkie mo»liwe zbiory niewiadomych, które mog¡ by¢ parametrami okre±laj¡cymi rozwi¡zania podanych

ukªadów równa« liniowych:

7

a)

8

>

>

>

<

>

>

>

:

x

,

y

,

z

= 1

2

x

+ 2

y

+ 4

z

= 6

3

x

+

y

+ 2

z

= 7

;

b)

8

>

>

>

<

>

>

>

:

x

+ 2

y

+ 3

z

+ 4

t

=

,

1

,x

+ 8

y

+ 11

z

+ 12

t

= 5

2

x

,

y

,

z

=

,

4

; c)

8

>

>

>

<

>

>

>

:

x

,

3

y

+

z

,

2

s

+

t

=

,

5

2

x

,

6

y

,

4

s

+

t

=

,

10

2

z

+

t

= 0

:

Zadanie

6.3

Okre±li¢ liczby rozwi¡za« podanych ukªadów równa« liniowych w zale»no±ci od parametru rzeczywistego

p

:

a)

8

<

:

(

p

+ 1)

x

+ (2

,

p

)

y

=

p

(1

,

3

p

)

x

+ (

p

,

1)

y

=

,

6

; b)

8

>

>

>

<

>

>

>

:

(

p

+ 1)

x

,

y

+

pz

= 1

(3

,

p

)

x

+ 4

y

,

pz

=

,

4

px

+ 3

y

=

,

3

;

c)

8

>

>

>

<

>

>

>

:

px

+

y

+ 2

z

= 1

x

+

py

+ 2

z

= 1

x

+

y

+ 2

pz

= 1

;

d)

8

>

>

>

>

>

>

<

>

>

>

>

>

>

:

2

x

+

py

+

pz

+

pt

= 1

2

x

+ 2

y

+

pz

+

pt

= 2

2

x

+ 2

y

+ 2

z

+

pt

= 3

2

x

+ 2

y

+ 2

z

+ 2

t

= 4

:

e)

8

>

>

>

<

>

>

>

:

x

+ (

p

,

2)

y

,

2

pz

= 4

px

+ (3

,

p

)

y

+

4

z

= 1

(1 +

p

)

x

+

y

+ 2(2

,

p

)

z

= 7

:

Zadanie*

6.4

Rozwi¡za¢ podane ukªady równa« liniowych w zale»no±ci od warto±ci rzeczywistego parametru

p

:

a)

8

>

>

>

<

>

>

>

:

px

+ 3

y

+

z

+

t

= 1

2

x

,

pz

+

t

=

,

2

7

x

+

py

,

5

z

+

pt

=

,p

; b)

8

>

>

>

>

>

>

<

>

>

>

>

>

>

:

px

+

y

+

pz

= 1

x

+

y

+

z

= 1

(2

,

p

)

x

+ (2

,

p

)

y

+

z

= 1

px

+

y

+

pz

=

p

2

:

Zadanie*

6.5

Rozwi¡za¢ podane ukªady równa« liniowych dla

n

­

2 w zale»no±ci od parametru rzeczywistego

p

:

a)

8

>

>

>

>

>

>

<

>

>

>

>

>

>

:

x

1

+

px

2

+

:

:

:

+

px

n

= 1

px

1

+

x

2

+

:

:

:

+

px

n

= 1

...

... ...

... ...

px

1

+

px

2

+

:

:

:

+

x

n

= 1

; b)

8

>

>

>

>

>

>

<

>

>

>

>

>

>

:

px

1

+

px

2

+

:

:

:

+

px

n

=

p

x

1

+

px

2

+

:

:

:

+

px

n

=

p

...

... ...

... ...

x

1

+

x

2

+

:

:

:

+

px

n

=

p

:

Zadanie

6.6

W wytwórni montuje si¦ wyroby

A;

B

;

C ;

D ;

E

z czterech typów detali

a;

b;

c;

d

. Liczby detali wchodz¡cych w skªad po-

szczególnych wyrobów podane s¡ w tabeli

A

B

C

D

E

a

1 2 0 4 1

b

2 1 4 5 1

c

1 3 3 5 4

d

1 1 2 3 1

.

a) Czy mo»na obliczy¢, ile wa»¡ wyroby

D

i

E

, je»eli wyroby

A;

B

;

C

wa»¡ odpowiednio 12, 20 i 19 dag. Poda¢ znalezione

wagi.

b) Ile wa»¡ detale

a;

b;

c

, je»eli detal

d

wa»y 4 dag ?

Lista siódma

Zadanie

7.1

Znale¹¢ wymiary i wyznaczy¢ bazy przestrzeni rozwi¡za« podanych ukªadów równa« liniowych:

8

a) 2

x

,

y

+ 5

z

+ 3

t

= 0;

b)

x

+ 2

y

= 2

x

,

y

=

x

+

z

+

t

= 0;

c)

x

+

y

=

y

+

z

=

z

+

t

=

t

+

x

;

d)

x

+

y

=

y

+

z

=

z

+

s

=

s

+

t

=

t

+

y

= 0;

e)

8

>

>

>

>

>

>

<

>

>

>

>

>

>

:

x

,

3

y

,

z

,

t

= 0

2

x

+

y

+

z

+

t

= 0

3

x

+ 2

y

,

z

= 0

6

x

+ 2

y

,

z

= 0

; f)

8

>

>

>

>

>

>

<

>

>

>

>

>

>

:

x

+ 2

y

+

z

= 0

3

x

,

y

+

t

= 0

4

x

+

y

+

z

+

t

= 0

5

x

+ 3

y

+ 2

z

+

t

= 0

:

Zadanie

7.2

Czy przestrzenie rozwi¡za« podanych ukªadów równa« liniowych s¡ generowane przez wskazane wektory, odpowied¹

uzasadni¢:

a)

8

>

>

>

<

>

>

>

:

4

x

+

y

,

z

+

s

,

2

t

= 0

x

,

y

+

z

,

s

,

3

t

= 0

3

x

,

y

+

z

,

s

,

5

t

= 0

,

~

u

= (2

;

,

4

;

1

;

1

;

2)

;

~

v

= (1

;

1

;

5

;

2

;

1);

b)

8

>

>

>

<

>

>

>

:

x

,

3

y

+

z

+

t

= 0

2

x

+

y

+

z

,

7

t

= 0

x

,

y

,

z

,

5

t

= 0

,

~

u

= (4

;

1

;

,

2

;

1);

c)

8

>

>

>

<

>

>

>

:

2

x

+ 2

y

,

z

+

s

= 0

5

x

+ 6

y

+

z

+ 2

s

+

t

= 0

8

x

+ 9

y

,

3

z

+ 4

s

,

t

= 0

,

~

u

= (

,

3

;

1

;

0

;

4

;

1)

;

~

v

= (

,

1

;

,

1

;

1

;

5

;

0)

;

~

w

= (2

;

,

2

;

1

;

1

;

,

1)

?

Zadanie

7.3

Wyznaczy¢ zbiory rozwi¡za« podanych niejednorodnych ukªadów równa« liniowych zgaduj¡c jedno z tych rozwi¡za« oraz

znajduj¡c przestrzenie rozwi¡za« odpowiadaj¡cych im ukªadów jednorodnych:

a)

8

>

>

>

<

>

>

>

:

3

x

+ 4

y

,

7

z

= 0

x

,

7

y

+ 11

z

= 5

x

,

2

y

+ 3

z

= 2

;

b)

8

>

>

>

<

>

>

>

:

6

x

+ 2

y

+ 3

z

= 2

4

x

+ 2

y

,

z

+ 3

t

= 2

10

x

+ 4

y

+ 2

z

+ 3

t

= 4

;

c)

8

<

:

x

+

y

+

z

+

t

+

u

= 5

3

x

+ 2

y

+

z

+

t

,

3

u

= 4

; d)

8

<

:

6

x

,

7

y

+

z

= 3

,

12

x

+ 14

y

,

2

z

=

,

6

:

Zadanie

7.4

Zinterpretowa¢ geometrycznie zbiory rozwi¡za« podanych ukªadów równa«: liniowych:

a)

8

>

>

>

<

>

>

>

:

4

x

,

2

y

+ 8

z

=

,

6

2

x

,

y

+ 4

z

=

,

3

,

6

x

+ 3

y

,

12

z

= 9

; b)

8

>

>

>

>

>

>

<

>

>

>

>

>

>

:

3

x

,

7

y

,

z

= 4

x

,

2

y

+ 3

z

=

,

1

x

,

3

y

,

7

z

= 6

3

x

,

6

y

+ 9

z

=

,

3

:

Zadanie*

7.5

Dla jakich warto±ci parametrów

a;

b;

c

2

R

zbiory rozwi¡za« podanych ukªadów równa« liniowych przedstawiaj¡ geome-

trycznie podane zbiory:
a)

ax

+

by

=

a

2

,

b

+

ab

ax

,

by

=

,a

2

+

b

,

ab

;

punkt, prosta, pªaszczyzna;

9

b)

(

a

+

b

)

x

+ (

a

+

b

+ 1)

y

= 2

a

+ 1

(

a

,

b

+ 1)

x

+

(

a

,

b

)

y

= 4

a

2

,

1

;

punkt, prosta, pªaszczyzna;

c)

8

<

:

x

,

ay

,

bz

=

ab

x

,

ay

+

bz

= 2

ab

x

,

ay

+

bz

= 3

ab

;

punkt, prosta, pªaszczyzna, przestrze«;

d)

8

<

:

ax

+

by

+

cz

=

ab

,ax

+

by

+

cz

=

ab

,ax

+

by

,

cz

=

bc

;

punkt, prosta, pªaszczyzna, przestrze« ?

Zadanie

7.6

Uªo»y¢ ukªady równa« liniowych o podanych zbiorach rozwi¡za«:

a) prosta w

R

3

o równaniu parametrycznym

x

= 4 +

t

,

y

= 3

,

2

t

,

z

= 5,

gdzie

t

2

R

;

b) pªaszczyzna w

R

3

o równaniu

8

>

>

>

<

>

>

>

:

x

= 1

,

s

+

t

+

u

y

= 2

,

s

+ 2

t

+ 3

u

z

= 3 +

s

+ 3

t

+ 7

u

, gdzie

s;

t;

u

2

R

;

c)

f

(1 + 2

t;

3

,

4

t;

5 + 6

t;

7

,

8

t

) :

t

2

Rg

;

d)

f

(1 +

s

,

t;

2 +

s

+

t;

3

,

s

+ 2

t;

s

+ 2

t;

2

s

,

t

) :

s;

t

2

Rg

;

e)

f

(4 + 2

s

,

t;

s

+ 3

t;

2 +

s

,

u;

4

,

s

+ 2

u

) :

s;

t;

u

2

Rg

;

f)

f

(

s

+ 2

t

,

u

+

v ;

1 +

s

+

u

,

3

v

) :

s;

t;

u;

v

2

Rg

.

Lista ósma

Zadanie

8.1

Uzasadni¢ liniowo±¢ wskazanych przeksztaªce« przestrzeni liniowych:

a)

L

:

R

3

,

!

R

2

;

L

(

x;

y ;

z

) = (

x

+

y ;

2

x

,

y

+ 3

z

);

b)

L

:

R

2

,

!

R

2

;

L

jest obrotem o k¡t

2 wokóª punktu (0

;

0);

c)

L

:

R

3

,

!

R

3

;

L

jest symetri¡ wzgl¦dem pªaszczyzny

y O z

;

d)

L

:

R

[

x

]

,

!

R

3

;

(

Lp

)(

x

) =

0

@

1

Z

0

p

(

t

)

dt;

p

0

(2)

;

p

00

(3)

1

A

dla

p

2

R

[

x

];

e)

L

:

C

(

R

)

,

!

R

2

[

x

]

;

(

Lf

)(

x

) =

x

2

f

(2) +

xf

(1) +

f

(0) dla

f

2

C

(

R

).

Zadanie

8.2

Uzasadni¢, »e podane przeksztaªcenia przestrzeni liniowych nie s¡ liniowe:

a)

L

:

R

,

!

R;

L

(

x

) = (

x

+ 1)(

x

,

1);

b)

L

:

R

2

,

!

R

2

;

L

(

x;

y

) = (3

x

+ 2

y

,

1

;

2

x

,

3

y

);

c)

L

:

R

2

,

!

R

2

;

L

jest symetri¡ wzgl¦dem prostej

x

+

y

+ 2 = 0;

d)

L

:

R

3

,

!

R

3

;

L

jest rzutem prostopadªym na pªaszczyzn¦

x

,

y

+

z

= 1;

e)

L

:

R

[

x

]

,

!

R

[

x

]

;

(

Lp

)(

x

) =

p

(

x

)

p

0

(

x

);

f)

L

:

C

(

R

)

,

!

C

(

R

)

;

(

Lf

)(

x

) =

f

(sin

x

).

Zadanie

8.3

Napisa¢ wzory wszystkich przeksztaªce« liniowych

L

:

M

22

,

!

R

.

10

Zadanie

8.4

Przeksztaªcenie liniowe

L

:

R

3

,

!

R

2

przeprowadza wektor

~

x

= (2

;

1

;

1) na wektor

~

u

= (4

;

5) oraz wektor

~

y

= (1

;

,

3

;

2)

na wektor

~

v

= (

,

6

;

1)

:

Znale¹¢ obraz wektora

~

z

= (5

;

6

;

1) w tym przeksztaªceniu. Czy przy tych danych mo»na znale¹¢

wektor

L

(4

;

1

;

5)?

Zadanie

8.5

Znale¹¢ j¡dra i obrazy podanych przeksztaªce« liniowych posªuguj¡c si¦ ich interpretacj¡ geometryczn¡. Porówna¢ uzy-

skane odpowiedzi z wynikami oblicze« algebraicznych:

a)

L

:

R

2

,

!

R

2

jest rzutem prostopadªym na prost¡

l

:

y

=

x

;

b)

L

:

R

2

,

!

R

2

jest jednokªadno±ci¡ wzgl¦dem punktu (0

;

0) w skali

k

= 2;

c)

L

:

R

3

,

!

R

3

jest symetri¡ wzgl¦dem pªaszczyzny

xO y

;

d)

L

:

R

3

,

!

R

3

jest rzutem prostopadªym na prost¡

l

:

x

=

y

,

z

= 0;

e)

L

:

R

3

,

!

R

3

jest obrotem o k¡t

6 wokóª osi

O y

.

Zadanie

8.6

Wyznaczy¢ j¡dra, obrazy oraz ich bazy podanych przeksztaªce« liniowych:

a)

L

:

R

3

,

!

R

2

;

L

(

x;

y ;

z

) = (

x

+

y ;

y

+

z

);

b)

L

:

R

3

,

!

R

4

,

L

(

x;

y ;

z

) = (2

x

,

y

+

z

;

x

+ 2

y

,

z

;

,x

+ 3

y

,

2

z

;

8

x

+

y

+

z

);

c)

L

:

R

2

[

x

]

,

!

R

2

[

x

]

;

(

Lp

)(

x

) =

,

x

2

+

x

p

(2) +

,

3

x

2

,

x

p

(1)

:

Zadanie

8.7

Poda¢ wymiary j¡der i obrazów nast¦puj¡cych przeksztaªce« liniowych:

a)

L

:

R

4

,

!

R

3

;

L

(

x;

y ;

z

;

t

) = (

x

+

y

+

z

,

t;

2

x

+

y

,

z

+

t;

y

+3

z

,

3

t

);

b)

L

:

R

5

,

!

R

3

;

L

(

x;

y ;

z

;

s;

t

) = (

x

+

y

+

z

;

y

+

z

+

s;

z

+

s

+

t

);

c)

L

:

R

4

,

!

R

4

,

L

(

x;

y ;

z

;

t

)=(

x

,

2

y

+3

z

,

4

t;

3

x

+5

z

+2

t;

x

+

y

+

z

+3

t;

5

x

,

y

+9

z

+

t

)

:

Zadanie*

8.8

Skonstruowa¢ przykªady przeksztaªce« liniowych maj¡cych podane j¡dra i obrazy:

a)

L

:

R

3

,

!

R

2

;

Ker

L

=

f

(

x;

y ;

0) :

x;

y

2

Rg

, Im

L

=

f

(

x;

y

) :

x

+

y

= 0

g

;

b)

L

:

R

3

,

!

R

2

;

Ker

L

=

f

(

x;

y ;

z

) :

x

+

y

+

z

=0

g

, Im

L

=

f

(

x;

y

) :

x

+3

y

=0

g

;

c)

L

:

R

3

,

!

R

2

;

Ker

L

= lin

f

(1

;

1

;

2)

;

(1

;

,

1

;

0)

g

, Im

L

=

f

(

x;

y

) : 2

x

= 3

y g

;

d)

L

:

R

4

,

!

R

4

;

Ker

L

= Im

L

=

(

x;

y ;

z

;

t

)

2

R

4

: 2

x

,

z

= 3

y

,

t

= 0

;

e)

L

:

R

2

[

x

]

,

!

R

2

[

x

]

;

Ker

L

= lin

f

1

,

xg

;

Im

L

= lin

1 +

x;

1 +

x

2

:

Zadanie*

8.9

Niech

X

,

Y

b¦d¡ przestrzeniami liniowymi. Uzasadni¢, »e dla dowolnych podprzestrzeni

U

,

V

odpowiednio przestrzeni

X

,

Y

speªniaj¡cych zale»no±¢ dim

U

+ dim

V

= dim

X

<

1;

istnieje przeksztaªcenie liniowe

L

:

X

,

!

Y

takie, »e

Ker

L

=

U

oraz Im

L

=

V

:

Zadanie*

8.10

Napisa¢ wzór jednego z przeksztaªce« liniowych b¦d¡cych obrotem w przestrzeni

R

3

o k¡t

wokóª prostej

x

=

at;

y

=

bt;

z

=

ct;

t

2

R;

a

2

+

b

2

+

c

2

>

0

:

11

Lista dziewi¡ta

Zadanie

9.1

Napisa¢ macierze podanych przeksztaªce« liniowych w bazach standardowych rozwa»anych przestrzeni liniowych:

a)

L

:

R

3

,

!

R

4

;

L

(

x;

y ;

z

) = (

x

+

y ;

x

+

z

;

y

,

z

;

y

+ 2

z

);

b)

L

:

R

2

,

!

R

3

;

L

(

x;

y

) = (4

x

+ 3

y ;

x

,

2

y ;

3

x

+ 5

y

);

c)

L

:

R

3

,

!

R

3

;

L

jest rzutem prostopadªym na pªaszczyzn¦

:

x

+2

y

+4

z

=0;

d)

L

:

R

3

,

!

R

3

;

L

jest obrotem o k¡t

4 wokóª osi

O x

;

e)

L

:

R

2

,

!

R

2

[

x

]

;

(

L

(

a;

b

))(

x

) = (

a

+

b

)

x

2

+ (3

a

,

b

)

x

+ 6

a:

Zadanie

9.2

Znale¹¢ z denicji macierze podanych przeksztaªce« liniowych we wskazanych bazach odpowiednich przestrzeni liniowych:

a)

L

:

R

3

,

!

R

3

;

L

(

x;

y ;

z

) = (

x

,

y ;

y

,

z

;

z

,

x

)

;

~

u

1

=

~

v

1

= (1

;

0

;

0)

;

~

u

2

=

~

v

2

= (1

;

1

;

0)

;

~

u

3

=

~

v

3

= (1

;

1

;

1);

b)

L

:

R

4

,

!

R

2

;

L

(

x;

y ;

z

;

t

) = (

x

+

y ;

z

+

t

)

;

~

u

1

= (1

;

0

;

0

;

0)

;

~

u

2

= (1

;

2

;

0

;

0)

;

~

u

3

= (1

;

2

;

3

;

0)

;

~

u

4

= (1

;

2

;

3

;

4),

~

v

1

= (1

;

0)

;

~

v

2

= (1

;

2);

c)

L

:

R

4

,

!

R

3

;

L

(

x;

y ;

z

;

t

) = (

x

+2

z

+

t;

,

2

x

+

y

,

3

z

,

5

t;

x

,

y

+

z

+4

t

)

;

~

u

1

= (1

;

0

;

0

;

0)

;

~

u

2

= (1

;

1

;

0

;

0)

;

~

u

3

= (1

;

1

;

1

;

0)

;

~

u

4

= (1

;

1

;

1

;

1)

;

~

v

1

= (0

;

0

;

1)

;

~

v

2

= (0

;

1

;

1)

;

~

v

3

= (1

;

1

;

1);

d)

L

:

R

2

,

!

R

2

;

L

jest rzutem prostopadªym na o±

O x;

~

u

1

= (1

;

2)

;

~

u

2

= (2

;

3)

;

~

v

1

= (2

;

1)

;

~

v

2

= (3

;

2);

e)

L

:

R

3

,

!

R

3

;

L

jest przeksztaªceniem identyczno±ciowym,

tj.

L

(

x;

y ;

z

) = (

x;

y ;

z

),

~

u

1

= (0

;

1

;

1)

;

~

u

2

= (1

;

0

;

1)

;

~

u

3

= (1

;

1

;

0)

;

~

v

1

= (1

;

0

;

0)

;

~

v

2

= (1

;

1

;

0)

;

~

v

3

= (1

;

1

;

1);

f)

L

:

R

1

[

x

]

,

!

R

2

[

x

]

;

(

Lp

)(

x

) =

x

2

p

0

(

x

)

;

p

1

= 2

x

+ 3

;

p

2

= 3

x

,

4

;

q

1

=

x

2

+

x;

q

2

=

x

+ 1

;

q

3

1;

g*)

L

:

R

n

[

x

]

,

!

R

n,1

[

x

]

;

(

Lp

)(

x

) =

p

0

(

x

+ 1)

;

p

0

q

0

1

;

p

k

=

q

k

=

x

k

k

! dla 1

¬

k

¬

n

,

1,

p

n

=

x

n

n

!

:

Zadanie

9.3

Macierz przeksztaªcenia liniowego

L

:

U

,

!

V

ma w bazach

f

~

u

1

;

~

u

2

g

,

f

~

v

1

,

~

v

2

,

~

v

3

g

przestrzeni liniowych

U

;

V

posta¢

A

L

=

2

4

3 2

,

1 1

2

,

4

3

5

:

Wyznaczy¢ obrazy podanych wektorów w tym przeksztaªceniu:

a)

~

u

=

,

2

~

u

1

+ 3

~

u

2

; b)

~

u

= 6

~

u

1

,

~

u

2

:

Zadanie

9.4

Dla podanych przeksztaªce« liniowych przestrzeni

R

2

,

R

3

naszkicowa¢ zbiory

D

oraz

L

(

D

) i porówna¢ ich pola (obj¦-

to±ci), je»eli:

a)

L

:

R

2

,

!

R

2

;

L

(

x;

y

) = (

,

2

x;

3

y

)

;

D

=

(

x;

y

)

2

R

2

:

jxj

+

jy j

¬

1

;

b)

L

:

R

2

,

!

R

2

;

L

(

x;

y

) = (

x

+ 2

y ;

2

x

+

y

)

;

D

= [

,

2

;

1]

[0

;

1];

c)

L

:

R

3

,

!

R

3

;

L

(

x;

y ;

z

) = (3

x;

3

y ;

,z

)

;

D

=

n

(

x;

y ;

z

)

2

R

3

:

x

2

+

y

2

¬

4

;

p

x

2

+

y

2

¬

z

¬

2

o

:

Zadanie

9.5

Rozwi¡za¢ ponownie

Zadanie

9.2

stosuj¡c tym razem wzór na zmian¦ macierzy przeksztaªcenia liniowego przy zmianie

baz wychodz¡c od baz standardowych rozwa»anych przestrzeni liniowych.

Zadanie

9.6

Napisa¢ macierze podanych przeksztaªce« liniowych

L

:

U

,

!

U

w podanych bazach przestrzeni

U

:

Wykorzysta¢ wzór

12

na zmian¦ macierzy przeksztaªcenia przy zmianie bazy:

a)

L

(

x;

y

) = (

x

+ 3

y ;

y

,

3

x

)

;

U

=

R

2

;

~

u

1

= (2

;

1)

;

~

u

2

= (

,

1

;

3);

b)

L

jest rzutem prostopadªym na pªaszczyzn¦

xO z

;

U

=

R

3

;

~

u

1

= (1

;

1

;

0)

;

~

u

2

= (2

;

3

;

2)

;

~

u

3

= (0

;

1

;

3);

c) (

Lp

)(

x

) =

x

2

p

(0) +

xp

0

(1)

;

U

=

R

2

[

x

]

;

p

1

=

x

2

+

x

+ 1

;

p

2

1,

p

3

=

x

+ 1

:

Zadanie

9.7

Przeksztaªcenie liniowe

L

:

U

,

!

V

ma w bazie

f

~

u

1

;

~

u

2

g

, przestrzeni liniowej

U

i w bazie

f

~

v

1

;

~

v

2

;

~

v

3

g

przestrzeni liniowej

V

macierz

A

=

2

4

3 0

2 1

1

,

2

3

5

:

Napisa¢ macierz

A

0

przeksztaªcenia

L

w bazach

f

3

~

u

1

+ 2

~

u

2

;

,

~

u

1

+

~

u

2

g

i

f

~

v

1

,

~

v

3

, 3

~

v

2

, 2

~

v

1

,

~

v

3

g

odpowiednio prze-

strzeni

U

i

V

.

Zadanie*

9.8

Skonstruowa¢ (o ile to mo»liwe) takie bazy odpowiednich przestrzeni liniowych, w których podane przeksztaªcenia liniowe

maj¡ wskazane macierze:

a)

L

:

R

2

,

!

R

2

;

L

(

x;

y

) = (

x;

y

)

;

A

=

2

4

3 1

2

,

1

3

5

;

b)

L

:

R

2

,

!

R

3

;

L

(

x;

y

) = (

x

+

y ;

2

x

,

y ;

x

,

3

y

)

;

A

=

2

6

6

6

4

5 5

1 0

2 3

3

7

7

7

5

;

c)

L

:

R

3

,

!

R

3

;

L

(

x;

y ;

z

) = (

x;

y ;

z

)

;

A

=

2

6

6

6

4

1 2 1

0 1 1

0 1 2

3

7

7

7

5

;

d)

L

:

R

3

,

!

R

3

;

L

(

x;

y ;

z

) = (

x;

y ;

z

)

;

A

=

2

6

6

6

4

2 1 2

,

1 1 1

0 3 4

3

7

7

7

5

:

Czy w przykªadach

a)

i

c)

bazy dziedziny i obrazu przeksztaªcenia

L

mog¡ by¢ te same ?

Lista dziesi¡ta

Zadanie

10.1

Napisa¢ macierze w bazach standardowych odpowiednich przestrzeni liniowych przeksztaªce«

L

3

L

2

L

1

oraz (

L

2

)

2

L

1

,

je»eli:

a)

L

1

:

R

3

,

!

R

2

;

L

1

(

x;

y ;

z

) = (

x

,

y

+

z

;

2

y

+

z

)

;

L

2

:

R

2

,

!

R

2

;

L

2

(

x;

y

) = (2

x

+

y ;

x

,

y

)

;

L

3

:

R

2

,

!

R

4

;

L

3

(

x;

y

) = (

x

,

y ;

y

,

x;

2

x;

2

y

);

b)

L

1

:

R

2

,

!

R

2

[

x

]

;

L

1

(

a;

b

) =

ax

2

+

bx

+

a

,

b

dla (

a;

b

)

2

R

2

;

L

2

:

R

2

[

x

]

,

!

R

2

[

x

]

;

(

L

2

p

)(

x

) =

xp

0

(

,x

) dla

p

2

R

2

[

x

]

;

L

3

:

R

2

[

x

]

,

!

R

2

;

(

L

3

p

)(

x

) = (

p

(1)

;

p

0

(2)) dla

p

2

R

2

[

x

]

:

Zadanie

10.2

Niech

J

,

K

,

L

b¦d¡ przeksztaªceniami przestrzeni

R

3

w siebie, przy czym

J

jest symetri¡ wzgl¦dem osi

O z

,

K

jest

13

symetri¡ wzgl¦dem pªaszczyzny

xO z

,

L

jest obrotem o k¡t

2 wokóª osi

O y

. Napisa¢ macierze w bazie standardowej

przestrzeni

R

3

przeksztaªce« liniowych b¦d¡cych zªo»eniami

J

,

K

i

L

we wszystkich sze±ciu mo»liwych kolejno±ciach.

Zadanie

10.3

Dla tych spo±ród podanych przeksztaªce« liniowych, które s¡ odwracalne napisa¢ macierze i wzory przeksztaªce« odwrot-

nych:

a)

L

:

R

2

,

!

R

2

;

L

(

x;

y

) = (3

x

,

2

y ;

4

x

,

3

y

);

b)

L

:

R

3

,

!

R

3

;

L

(

x;

y ;

z

) = (

y

+ 2

z

;

x

+

y

+

z

;

2

x

+ 3

y

+ 2

z

);

c)

L

:

R

2

[

x

]

,

!

R

2

[

x

]

;

(

Lp

)(

x

) =

p

(2

x

)

,

4

p

(

x

) dla

p

2

R

2

[

x

];

d)

L

:

R

3

[

x

]

,

!

R

3

[

x

]

;

(

Lp

)(

x

) =

x

3

p

0

(0) +

p

(2

x

) dla

p

2

R

3

[

x

]

:

Zadanie

10.4

Macierz przeksztaªcenia liniowego

L

:

U

,

!

U

ma w bazie

f

~

u

1

,

~

u

2

,

~

u

3

g

przestrzeni liniowej

U

posta¢

A

=

2

4

1 0 3

0 2 0

2 0

,

1

3

5

:

Znale¹¢:

a)

L

3

(

~

u

1

,

2

~

u

2

+

~

u

3

); b)

L

,1

(3

~

u

1

+

~

u

2

,

~

u

3

).

Zadanie

10.5

Znale¹¢ warto±ci i wektory wªasne podanych macierzy rzeczywistych:

a)

2

4

2

,

1

1 4

3

5

;

b)

2

4

2 1

,

3

,

2

3

5

; c)

2

4

p

3

,

1

1

p

3

3

5

;

d)

2

6

6

6

4

4 1

,

5

0

,

3 5

0 0 2

3

7

7

7

5

;

e)

2

6

6

6

4

,

3 0

,

1

0 3 0

8 0 3

3

7

7

7

5

; f)

2

6

6

6

4

0 1 0

,

4 4 0

,

2 1 2

3

7

7

7

5

; g)

2

6

6

6

4

2

,

1 1

,

2 1

,

1

2 1 3

3

7

7

7

5

; h)

2

6

6

6

6

6

6

4

2 2 2 2

0 0 0 0

3 3 3 3

2 2 2 2

3

7

7

7

7

7

7

5

:

Zadanie

10.6

Wyznaczy¢ warto±ci i wektory wªasne podanych macierzy zespolonych:

a)

2

4

1 4

,

1 1

3

5

;

b)

2

4

1

i

,i

1

3

5

; c)

2

6

6

6

4

,

3 0 10

0 1 0

,

1 0 3

3

7

7

7

5

;

d)

2

6

6

6

4

6

i

0 0

4 4 + 2

i

0

i

1 5

i

3

7

7

7

5

; e)

2

6

6

6

4

i

i

i

1 1 1

2 2 2

3

7

7

7

5

; f)

2

6

6

6

4

,i

0

,

2

0 4 0

2 0

,i

3

7

7

7

5

.

Lista jedenasta

Zadanie

11.1

Znale¹¢ warto±ci i wektory wªasne podanych liniowych przeksztaªce« rzeczywistych przestrzeni liniowych:

14

a)

L

:

R

2

,

!

R

2

;

L

(

x;

y

) = (4

x

+ 2

y ;

y

,

x

);

b)

L

:

R

2

,

!

R

2

;

L

(

x;

y

) = (2

x

+

y ;

4

y

,

x

);

c)

L

:

R

3

,

!

R

3

;

L

(

x;

y ;

z

) = (

x;

2

x

+ 2

y ;

,x

,

y

,

z

);

d)

L

:

R

3

,

!

R

3

;

L

(

x;

y ;

z

) = (3

x

,

y ;

6

x

,

2

y ;

2

x

,

y

+

z

);

e)

L

:

R

2

[

x

]

,

!

R

2

[

x

]

;

(

Lp

)(

x

) =

p

00

(

x

);

f)

L

:

R

2

[

x

]

,

!

R

2

[

x

]

;

(

Lp

)(

x

) = 2

xp

0

(

x

) +

x

2

p

(0) +

p

(2)

:

Zadanie

11.2

Dla podanych liniowych przeksztaªce« pªaszczyzny

R

2

i przestrzeni

R

3

znale¹¢ warto±ci wªasne i wektory wªasne wyko-

rzystuj¡c interpretacj¦ geometryczn¡ tych przeksztaªce«:

a) symetria na pªaszczy¹nie wzgl¦dem punktu (0

;

0);

b) rzut prostopadªy w przestrzeni na o±

O z

;

c) rzut prostopadªy w przestrzeni na prost¡

l

:

x

=

y

=

z

;

d) rzut prostopadªy w przestrzeni na pªaszczyzn¦

:

x

+

y

+

z

= 0;

e) symetria w przestrzeni wzgl¦dem pªaszczyzny

xO y

;

f) symetria w przestrzeni wzgl¦dem prostej

l

:

x

+

y

= 0

;

z

= 0

:

Sprawdzi¢ otrzymane wyniki algebraicznie.

Zadanie

11.3

Wyznaczy¢ warto±ci wªasne i wektory wªasne podanych przeksztaªce« liniowych wskazanych zespolonych przestrzeni

liniowych:

a)

L

:

C

2

,

!

C

2

;

L

(

x;

y

) = (3

x

,

y ;

10

x

,

3

y

);

b)

L

:

C

2

,

!

C

2

;

L

(

x;

y

) = ((1

,

2

i

)

x

,

5

y ;

(1 +

i

)

x

,

(1

,

3

i

)

y

);

c)

L

:

C

3

,

!

C

3

;

L

(

x;

y ;

z

) = (

z

;

3

y ;

,x

);

d)

L

:

C

3

,

!

C

3

;

L

(

x;

y ;

z

) = (

,ix

,

2

z

;

y ;

2

x

,

iz

).

Zadanie

11.4

Poda¢ wszystkie mo»liwe warto±ci wªasne przeksztaªce« liniowych speªniaj¡cych podane warunki:

a)

L

2

=

,L

; b)

L

3

=

I

.

Zadanie

11.5

Napisa¢ macierze podanych przeksztaªce« liniowych przestrzeni

R

2

lub

R

3

w bazach ich wektorów wªasnych (o ile takie

bazy istniej¡):

a)

L

(

x;

y

) = (

x

+ 4

y ;

2

x

+ 3

y

); b)

L

(

x;

y

) = (5

x

,

3

y ;

3

x

,

y

);

c)

L

(

x;

y ;

z

) = (

x

,

z

;

x

+ 2

y

+

z

;

z

,

x

);

d)

L

(

x;

y ;

z

) = (

,x

,

3

y

,

2

z

;

,x

+

y

+ 2

z

;

x

+ 3

y

+ 2

z

)

:

Zadanie

11.6

Przeksztaªcenie liniowe

L

:

R

2

,

!

R

2

przeprowadza wektory (1

;

1), (1

;

,

1) odpowiednio na wektory (1

;

1), (3

;

,

3).

Obliczy¢

L

50

(5

;

1).

Zadanie

11.7

Przeksztaªcenie liniowe

L

:

R

3

,

!

R

3

speªnia warunki

L

(0

;

1

;

1) = (0

;

1

;

1),

L

(2

;

2

;

0) = (0

;

0

;

0),

L

(1

;

0

;

0) = (

,

1

;

0

;

0).

15

Obliczy¢:

a)

L

(

x;

y ;

z

) dla (

x;

y ;

z

)

2

R

3

; b)

L

105

(2

;

3

;

6)

:

Lista dwunasta

Zadanie

12.1

Sprawdzi¢, »e podane funkcje (

q

;

q

) s¡ iloczynami skalarnymi w rozwa»anych przestrzeniach liniowych:

a) (

~

x;

~

y

) = 2

x

1

y

1

,

x

1

y

2

,

x

2

y

1

+

x

2

y

2

dla

~

x

= (

x

1

;

x

2

),

~

y

= (

y

1

;

y

2

)

2

R

2

;

b) (

~

x ;

~

y

) = [

x

1

x

2

]

2

4

4

,

1

,

1 1

3

5

2

4

y

1

y

2

3

5

dla

~

x

= (

x

1

;

x

2

),

~

y

= (

y

1

;

y

2

)

2

R

2

;

c) (

~

x;

~

y

) = [

x

1

x

2

x

3

]

2

6

6

6

4

2 0

,

1

0 1 0

,

1 0 1

3

7

7

7

5

2

6

6

6

4

y

1

y

2

y

3

3

7

7

7

5

dla

~

x

= (

x

1

;

x

2

;

x

3

)

;

~

y

= (

y

1

;

y

2

;

y

3

)

2

R

3

;

d) (

p;

q

) =

n+1

X

i=1

p

(

x

i

)

q

(

x

i

) dla

p;

q

2

R

n

[

x

], gdzie

x

1

<

x

2

<

:

:

:

<

x

n+1

;

e) (

f

;

g

) =

1

Z

,1

f

(2

x

)

g

1

2

x

dx

dla

f

;

g

2

C

([

,

1

;

1])

:

Zadanie*

12.2

Uzasadni¢ dlaczego podane funkcje (

q

;

q

) nie s¡ iloczynami skalarnymi w rozwa»anych przestrzeniach liniowych:

a) (

~

x;

~

y

) = 2

x

1

y

1

+ 3

x

1

y

2

,

x

2

y

1

+ 5

x

2

y

2

dla

~

x

= (

x

1

;

x

2

)

;

~

y

= (

y

1

;

y

2

)

2

R

2

;

b) (

~

x ;

~

y

) = [

x

1

x

2

x

3

]

2

6

6

6

4

1 2

,

1

1 4

,

1

3 8 1

3

7

7

7

5

2

6

6

6

4

y

1

y

2

y

3

3

7

7

7

5

dla

~

x

= (

x

1

;

x

2

;

x

3

)

;

~

y

= (

y

1

;

y

2

;

y

3

)

2

R

3

;

c) (

p ;

q

) =

p

(1)

q

(1)

,

p

(2)

q

(2) dla

p;

q

2

R

1

[

x

];

d) (

p;

q

) =

n

X

i=1

p

(

x

i

)

q

(

x

i

) dla

p;

q

2

R

n

[

x

], gdzie

x

1

<

x

2

<

:

:

:

<

x

n

;

e) (

f

;

g

) =

b

Z

a

jf

(

x

)

g

(

x

)

j

dx

dla

f

;

g

2

C

([

a;

b

])

:

Zadanie

12.3

W przestrzeni euklidesowej

E

4

:

a) obliczy¢ norm¦ wektora (

,

1

;

1

;

2

;

,

3);

b) zbada¢ ortogonalno±¢ wektorów (1

;

4

;

,

1

;

2), (3

;

,

1

;

2

;

,

1);

c) obliczy¢ k¡t mi¦dzy wektorami (1

;

3

;

0

;

,

1), (3

;

1

;

1

;

0);

d) opisa¢ zbiór wszystkich wektorów ortogonalnych do ka»dego z wektorów (2

;

1

;

0

;

1), (0

;

,

2

;

1

;

1) i wskaza¢ jeden wektor

z tego zbioru o normie równej 2;

e) poda¢ przykªad wektora unormowanego tworz¡cego z wektorem

(1

;

2

;

0

;

,

2) k¡t 2

3

:

Zadanie

12.4

Obliczy¢ k¡t, jaki tworz¡ wektory

p

0

=

x

+ 1 ,

q

0

=

x

,

2 w przestrzeni euklidesowej

R

2

[

x

] z podanymi iloczynami

skalarnymi:

16

a) (

p;

q

) =

p

(1)

q

(1) +

p

(2)

q

(2) +

p

(3)

q

(3);

b) (

p;

q

) =

p

(0)

q

(0) +

p

0

(0)

q

0

(0) +

p

00

(0)

q

00

(0);

c) (

p ;

q

) =

1

Z

0

p

(

x

)

q

(

x

)

dx

dla

p;

q

2

R

2

[

x

]

:

*Wskaza¢ taki iloczyn skalarny w przestrzeni

R

2

[

x

]

;

przy którym wektory

p

0

,

q

0

s¡ ortogonalne i unormowane.

Zadanie

12.5

W przestrzeni liniowej

R

[

x

] z iloczynem skalarnym okre±lonym wzorem

(

p;

q

) =

1

Z

0

p

(

x

)

q

(

x

)

dx

:

a) obliczy¢

,

x

2

;

,

1

,

j

jx

+ 1

j

j

oraz cosinus k¡ta mi¦dzy wektorami

x

+ 1,

x

,

1;

b) poda¢ przykªad wielomianu mo»liwie najni»szego stopnia ortogonalnego do ka»dego z wielomianów

x

,

1,

x

2

;

c) dobra¢ staª¡

a

tak, aby wielomiany 3

x

2

+

ax

,

1 oraz 2

x

2

+ 6

x

,

1 byªy ortogonalne.

Zadanie*

12.6

Stosuj¡c nierówno±¢ Schwarza w odpowiednich przestrzeniach euklidesowych uzasadni¢, »e zachodz¡ nierówno±ci:

a) (

ab

+

bc

+

ac

)

2

¬

,

a

2

+

b

2

+

c

2

2

dla dowolnych

a;

b;

c

2

R

;

b)

,

x

3

1

+

x

3

2

+

:

:

:

+

x

3

n

2

¬

,

x

2

1

+

x

2

2

+

:

:

:

+

x

2

n

,

x

4

1

+

x

4

2

+

:

:

:

+

x

4

n

dla dowolnych

x

1

;

x

2

;

:

:

:

;

x

n

2

R

;

c)

1

Z

0

f

(

x

)

dx

¬

0

@

1

Z

0

f

2

(

x

)

dx

1

A

1

2

¬

0

@

1

Z

0

f

4

(

x

)

dx

1

A

1

4

¬

:

:

:

dla dowolnej funkcji ci¡gªej

f

:

R

,

!

R:

Lista trzynasta

Zadanie

13.1

Sprawdzi¢, »e podane zbiory wektorów s¡ bazami ortogonalnymi lub ortonormalnymi w odpowiednich przestrzeniach eu-

klidesowych i wyznaczy¢ wspóªrz¦dne wskazanych wektorów w tych bazach:
a)

~

v

1

=

3

r

1

10

;

,

r

1

10

!

;

~

v

2

=

r

1

10

;

3

r

1

10

!

;

~

u

= (5

;

6)

2

E

2

;

b)

~

v

1

= (1

;

3

;

,

2)

;

~

v

2

= (

,

1

;

1

;

1)

;

~

v

3

= (5

;

1

;

4)

;

~

u

= (1

;

0

;

1)

2

E

3

;

c)

~

v

1

= (1

;

1

;

1

;

1)

;

~

v

2

= (3

;

,

1

;

,

1

;

,

1)

;

~

v

3

= (0

;

2

;

,

1

;

,

1),

~

v

4

= (0

;

0

;

1

;

,

1)

;

~

u

= (1

;

2

;

,

3

;

2)

2

E

4

;

d)

~

v

1

=

r

1

3

;

,

r

1

3

;

r

1

3

;

0

!

;

~

v

2

=

0

;

r

1

3

;

r

1

3

;

,

r

1

3

!

;

~

v

3

=

r

1

3

;

r

1

3

;

0

;

r

1

3

!

;

~

v

4

=

,

r

1

3

;

0

;

r

1

3

;

r

1

3

!

;

~

u

= (1

;

2

;

3

;

4)

2

E

4

;

e)

p

1

1

;

p

2

= 2

,

x;

p

3

= 6

,

3

x

,

x

2

;

q

=

x

2

+

x

+ 3 w przestrzeni

R

2

[

x

] z iloczynem skalarnym wielomianów

q

1

=

ax

2

+

bx

+

c;

q

2

=

a

1

x

2

+

b

1

x

+

c

1

okre±lonym wzorem

(

q

1

;

q

2

) =

aa

1

+ (3

a

,

b

)(3

a

1

,

b

1

) + (2

b

+

c

)(2

b

1

+

c

1

)

:

Zadanie

13.2

Uzasadni¢ ortonormalno±¢ podanych zbiorów funkcji w odpowiednich przestrzeniach euklidesowych:

17

a) 1

p

2

;

cos

x

p

;

sin

x

p

;

cos2

x

p

;

sin2

x

p

;

:

:

:

w przestrzeni

C

([0

;

2

]) z iloczynem skalarnym zdeniowanym wzorem

(

f

;

g

) =

2

Z

0

f

(

x

)

g

(

x

)

dx

;

b*)

p

0

1

;

p

n

= 1

2

n

n

!

d

n

,

x

2

,

1

n

dx

n

, gdzie

n

2

N;

w przestrzeni

R

[

x

] z iloczynem skalarnym okre±lonym wzorem

(

p;

q

) =

1

Z

,1

p

(

x

)

q

(

x

)

dx:

Zadanie

13.3

Zortogonalizowa¢ podane wektory w odpowiednch przestrzeniach euklidesowych:

a) (2

;

1

;

3)

;

(1

;

6

;

2) w przestrzeni

E

3

;

b) (1

;

0

;

0)

;

(0

;

1

;

0)

;

(0

;

0

;

1) w przestrzeni

R

3

z iloczynem skalarnym wektorów

~

x

= (

x

1

;

x

2

;

x

3

),

~

y

= (

y

1

;

y

2

;

y

3

) zdenio-

wanym wzorem

(

~

x ;

~

y

) = [

x

1

x

2

x

3

]

2

4

2

,

1 0

,

1 1 0

0 0 2

3

5

2

4

y

1

y

2

y

3

3

5

;

c) (4

;

3

;

2

;

1)

;

(4

;

3

;

2

;

0)

;

(4

;

3

;

0

;

0) w przestrzeni

E

4

;

d) (0

;

1

;

1

;

0)

;

(

,

2

;

0

;

2

;

0)

;

(3

;

1

;

1

;

1) w przestrzeni

E

4

;

e) 1

;

x

+ 1

;

jxj;

sin

x

w przestrzeni

C

([

,

1

;

1]) z iloczynem skalarnym okre±lonym wzorem

(

f

;

g

) =

1

Z

,1

f

(

x

)

g

(

x

)

dx

;

f*) (

,

1

;

1

;

0

;

0), (0

;

2

;

1

;

1), (1

;

,

3

;

1

;

,

1) w przestrzeni

E

4

(zastosowa¢ macierzow¡ metod¦ ortogonalizacji).

Zadanie

13.4

Znale¹¢ bazy ortogonalne danych przestrzeni euklidesowych zawieraj¡ce wskazane wektory:

a) (1

;

,

1

;

2) w przestrzeni

E

3

;

b) (1

;

1

;

1

;

1) w przestrzeni

E

4

;

c) (1

;

0

;

1

;

1), (0

;

1

;

1

;

,

1) w przestrzeni

E

4

;

d) (1

;

0

;

3

;

,

2), (

,

1

;

0

;

1

;

1), (5

;

0

;

1

;

4) w przestrzeni

E

4

;

e) (3

;

2

;

3

;

5) w przestrzeni

E

=

(

x;

y ;

z

;

t

)

2

E

4

:

x

+

y

=

y

+

z

=

t

;

f)

f

1

1 w przestrzeni lin

1

;

sin

x;

sin

2

x

, gdzie 0

¬

x

¬

, z iloczynem skalarnym okre±lonym wzorem

(

f

;

g

) =

Z

0

f

(

x

)

g

(

x

)

dx:

Zadanie

13.5

Wyznaczy¢ bazy ortonormalne wskazanych przestrzeni euklidesowych i znale¹¢ wspóªrz¦dne podanych wektorów w tych

bazach:

a)

E

= lin

f

(1

;

0

;

,

1

;

0)

;

(0

;

1

;

1

;

,

1)

g

,

~

u

= (3

;

1

;

2

;

1)

2

E

4

;

b)

E

= lin

f

(1

;

1

;

1

;

1)

;

(1

;

,

1

;

1

;

1)

;

(

,

1

;

1

;

1

;

,

1)

g

,

~

u

= (

,

1

;

0

;

10

;

,

1)

2

E

4

;

c)

E

=

(

x;

y ;

z

;

t

)

2

E

4

:

x

+

y

+

z

= 0

;

y

=

t

,

~

u

= (

,

1

;

3

;

,

2

;

3)

2

E

4

;

d)

E

=

f

(2

x

+

y

+ 5

z

;

y

+

z

;

2

y

,

x;

x

+ 2

z

) :

x;

y ;

z

2

Rg

,

~

u

= (6

;

4

;

7

;

1)

2

E

4

;

e)

E

=

R

2

[

x

] z iloczynem skalarnym zdeniowanym wzorem

(

p;

q

) =

p

(0)

q

(0) +

p

(1)

q

(1) +

p

(2)

q

(2),

p

0

=

x

2

+

x

+ 1;

f)

E

=

R

2

z iloczynem skalarnym wektorów

~

x

= (

x

1

;

x

2

),

~

y

= (

y

1

;

y

2

) okre±lonym wzorem

(

~

x ;

~

y

) = [

x

1

x

2

]

2 1

1 1

y

1

y

2

;

~

u

= (3

;

2);

18

g*)

E

=

M

22

z iloczynem skalarnym macierzy

A

,

B

zdeniowanym wzorem (

A;

B

) = Tr

AB

T

, gdzie symbol Tr

oznacza sum¦ wszystkich elementów z gªównej przek¡tnej macierzy,

C

=

1 5

2

,

3

.

Zadanie*

13.6

Stosuj¡c wyznacznikow¡ metod¦ ortogonalizacji uzupeªni¢ wskazane wektory do baz ortogonalnych odpowiednich prze-

strzeni euklidesowych:

a) (1

;

1

;

4) w przestrzeni

E

3

;

b) (1

;

0

;

0), (0

;

0

;

1) w przestrzeni

R

3

z baz¡ ortonormaln¡

f

(1

;

0

;

0), (1

;

1

;

0), (1

;

1

;

1)

g

;

c) (1

;

1

;

3

;

1) w przestrzeni

E

4

;

d) 1

,

x

+

x

2

+ 2

x

3

w przestrzeni

R

3

[

x

] z baz¡ ortonormaln¡

1

;

x;

x

2

;

x

3

;

e) 2

~

u

,

3

~

v

+

~

w

w przestrzeni euklidesowej

E

z baz¡ ortonormaln¡

f

~

u;

~

v ;

~

w;

~

x;

~

yg

:

Zadanie*

13.7

Uzasadni¢, »e wektory

~

x

1

,

~

x

2

,

:

:

:

,

~

x

n

tworz¡ baz¦ ortonormaln¡ przestrzeni

E

n

wtedy i tylko wtedy, gdy macierz przej±cia

P

z bazy standardowej do bazy tych wektorów speªnia warunek

P

P

T

=

I

:

Sprawdzi¢ t¦ zale»no±¢ dla baz ortonormalnych

z

Przykªadu

13.1

oraz z

Zadania

13.1.

Zadanie*

13.8

Niech

V

b¦dzie rzeczywist¡ przestrzeni¡ liniow¡ z baz¡

~

v

1

,

~

v

2

,

:

:

:

,

~

v

n

. Zdeniowa¢ w tej przestrzeni iloczyn skalarny tak,

aby byªa to baza ortonormalna.

Lista czternasta

Zadanie

14.1

Sprawdzi¢, »e podane wektory s¡ ortogonalne do wskazanych podprzestrzeni przestrzeni euklidesowych:

a)

E

0

= lin

f

(2

;

0

;

3

;

1)

;

(

,

1

;

1

;

2

;

0)

;

(1

;

1

;

0

;

1)

g

,

~

v

= (1

;

1

;

0

;

,

2)

2

E

4

;

b)

E

0

=

R

1

[

x

],

p

0

= 6

x

2

,

6

x

+ 1 w przestrzeni

R

2

[

x

] z iloczynem skalarnym okre±lonym wzorem

(

p;

q

) =

1

Z

0

p

(

x

)

q

(

x

)

dx

.

Zadanie

14.2

Znale¹¢ rzuty ortogonalne podanych wektorów na wskazane podprzestrzenie przestrzeni euklidesowych:

a)

~

u

= (3

;

,

2

;

1)

2

E

3

,

E

0

jest pªaszczyzn¡

: 2

x

,

y

+ 3

z

= 0 w

E

3

;

b)

~

u

= (3

;

1

;

2

;

0)

2

E

4

,

E

0

= lin

f

(1

;

2

;

1

;

2)

;

(0

;

1

;

1

;

1)

g

;

c)

~

u

= (0

;

1

;

1

;

1)

2

E

4

,

E

0

= lin

f

(1

;

1

;

1

;

0)

;

(0

;

1

;

0

;

2)

g

;

d)

~

u

= (1

;

0

;

0

;

0)

2

E

4

,

E

0

= lin

f

(1

;

1

;

0

;

0)

;

(0

;

1

;

2

;

0)

;

(0

;

0

;

3

;

4)

g

;

e)

~

u

= (0

;

2

;

,

1

;

3)

2

E

4

,

E

0

=

(

x;

y ;

z

;

t

)

2

E

4

:

x

+

y

+ 3

t

=

y

+

z

=

x

,

y

+

z

,

3

t

= 0

;

f)

f

=

x

,

E

0

= lin

f

1

;

cos

xg

w przestrzeni wszystkich funkcji ci¡gªych na

przedziale [0

;

2

] z iloczynem skalarnym okre±lonym wzorem

(

f

;

g

) =

2

Z

0

f

(

x

)

g

(

x

)

dx

;

g)

~

u

= (1

;

1

;

1),

E

0

= lin

f

(0

;

1

;

1)

;

(0

;

0

;

1)

g

w przestrzeni

R

3

z iloczynem skalarnym wektorów

~

x

= (

x

1

;

x

2

;

x

3

),

~

y

=

(

y

1

;

y

2

;

y

3

) okre±lonym wzorem

(

~

x;

~

y

) = 2

x

1

y

1

+

x

2

y

2

+

x

3

y

3

,

x

1

y

3

,

x

3

y

1

:

Zadanie

14.3

Wyznaczy¢ rzuty ortogonalne podanych wektorów na podprzestrzenie o wskazanych bazach ortogonalnych:

19

a)

~

u

= (2

;

1

;

3)

2

E

3

,

E

0

= lin

f

(

,

1

;

4

;

1)

g

;

b)

~

u

= (1

;

,

1

;

2

;

0)

2

E

4

,

E

0

= lin

f

(2

;

0

;

1

;

,

1)

;

(1

;

1

;

,

2

;

0)

;

(1

;

1

;

1

;

3)

g

;

c)

~

u

= (1

;

2

;

:

:

:

;

n

)

2

E

n

,

E

0

= lin

f

(1

;

0

;

:

:

:

;

0)

;

(0

;

:

:

:

;

0

;

1)

g

;

d)

p

=

x

2

,

x

,

E

0

= lin

f

1

;

2

x

,

1

g

w przestrzeni

R

[

x

] z iloczynem skalarnym okre±lonym wzorem

(

p;

q

) =

1

Z

0

p

(

x

)

q

(

x

)

dx

;

a)

f

= 1

,

cos 2

x

,

E

0

= lin

n

sin

x;

sin

2 +

x

o

w przestrzeni

C

([0

;

2

]) z iloczynem skalarnym okre±lonym wzorem

(

f

;

g

) =

2

Z

0

f

(

x

)

g

(

x

)

dx

;

f)

f

=

x

,

E

0

= lin

f

1

;

cos

x;

cos2

x;

:

:

:

;

cos

nxg

;

gdzie

n

2

N

, w przestrzeni

C

([0

;

2

]) z iloczynem skalarnym jak wy»ej;

g)

f

=

x

,

E

0

= lin

f

sin

x;

sin2

x;

:

:

:

;

sin

nxg

;

gdzie

n

2

N

, w przestrzeni

C

([0

;

2

]) z iloczynem skalarnym jak wy»ej.

Zadanie*

14.4

Metod¡ najmniejszych kwadratów znale»¢ przybli»one rozwi¡zania podanych ukªadów równa«:

a)

8

>

>

>

>

>

>

<

>

>

>

>

>

>

:

x

+

y

= 2

x

+ 2

y

= 3

x

,

y

= 0

2

x

+

y

= 1

; b)

8

>

>

>

>

>

>

<

>

>

>

>

>

>

:

x

+

y

+

z

= 0

x

,

y

+

z

= 1

x

,

y

,

z

= 1

x

+

y

,

z

= 0

:

Zadanie

14.5

Niech

~

u

,

~

v

b¦d¡ niezerowymi wektorami z przestrzeni euklidesowej

E

:

Znale¹¢ najkrótszy wektor postaci

~

u

+

t

~

v

, gdzie

t

2

R

, i wykaza¢, »e jest on ortogonalny do wektora

~

v :

Zilustrowa¢ otrzymany wynik na pªaszczy¹nie.

Zadanie*

14.6

Niech

E

b¦dzie przestrzeni¡ euklidesow¡, a

E

0

jej podprzestrzeni¡ wymiaru: a)

n

= 1; b)

n

= 2

:

Uzasadni¢, »e wektorem

z przestrzeni

E

0

;

le»¡cym najbli»ej ustalonego wekora

~

u

2

E

;

jest rzut ortogonalny wektora

~

u

na podprzestrze«

E

0

:

Zadanie*

14.7

Wykaza¢, »e k¡t

'

nachylenia prostej wychodz¡cej z pocz¡tku ukªadu wspóªrz¦dnych na pªaszczy¹nie

R

2

i maj¡cej

najmniejsze ±redniokwadratowe odchylenie od

n

zadanych punktów (

a

i

;

b

i

),

i

= 1

;

:

:

:

;

n

, jest dany wzorem

tg

'

=

a

1

b

1

+

:

:

:

+

a

n

b

n

a

1

+

:

:

:

+

a

n

:

Zadanie

14.8

Niech

~

u

,

~

v

b¦d¡ ustalonymi wektorami przestrzeni euklidesowej

E

, przy czym

~

v

6

=

~

0:

Napisa¢ wzór na rzut ortogonalny

wektora

~

u

na podprzestrze«

E

= lin

f

~

ug

:

20