
POLITECHNIKA WARSZAWSKA
Instytut Radioelektroniki WEiTI
Zakład Techniki Mikrofalowej i Radiolokacyjnej
LABORATORIUM : POLA i FALE
POLA w PROWADNICACH FALOWYCH
Ćwiczenie laboratoryjne nr 4 - sala 531
Cel ćwiczenia
Celem ćwiczenia jest zapoznanie się z podstawowymi cechami pól i fal w prowadnicach
falowych. Prowadnice falowe dzielą sie na linie z falą TEM oraz falowody.Przedmiotem obserwacji
będą fale bieżące, częściowo stojące i stojące w tych prowadnicach.Sprawdzona zostanie zależność
teoretyczna między długością fali w falowodzie a długoscią fali typu TEM. Mierzone będą parametry
takie jak długość fali i współczynnik fali stojącej. Przedmiotem pomiarów i obserwacji będą także
rozkłady pól w falowodzie prostokątnym oraz linii wspolosiowej.
Podstawowe wiadomości teoretyczne:
• Fale częściowo stojące na granicy dwóch ośrodków
Fala padająca prostopadle na granicę ośrodków
Ośrodek 1
ε
1
,
μ
1
,
σ
1
x
y
z
Ośrodek 2
ε
2
,
μ
2
,
σ
2
E
1
+
E
1
−
H
1
+
H
1
−
H
2
E
2
Fala płaska o wektorze pola
z
0
x
1
1
e
i
γ
−
+
= E
E
r
r
oraz
z
1
0
y
1
1
e
Z
i
γ
−
+
=
E
H
r
r
pada na granicę dwóch ośrodków
w płaszczyźnie z=0. Fala ta ulega częściowemu odbiciu. Współczynnik odbicia dla pola elektrycznego
zdefiniowany jest zależnością:
( )
( )
0
z
0
z
1
1
=
=
=
Γ
+
−
E
E
. Współczynnik odbicia dla pola magnetycznego jest
równy: -
Γ. Tak więc fale odbite określone są zależnościami:
z
0
x
1
1
e
i
γ
−
Γ
=
E
E
r
r
,
z
1
0
y
1
1
e
Z
i
γ
−
Γ
−
=
E
H
r
r
.
Ponieważ rozważa się granicę dwóch dielektryków, z warunków brzegowych wynika, że zarówno pole
E
1
(suma pól fali padającej i odbitej) jak i H
1
na granicy ośrodków jest ciągłe, czyli E
1
(0) = E
2
(0),
H
1
(0) = H
2
(0). Fala w ośrodku drugim określona jest zależnościami:
( )
z
0
x
2
2
e
1
i
γ
−
Γ
+
=
E
E
r
r
,
( )
z
1
0
y
2
2
e
Z
1
i
γ
−
Γ
−
=
E
H
r
r
. Stosunek pola E i H w ośrodku drugim jest oczywiście równy impedancji

dr inż. Jolanta Zborowska - Pola w prowadnicach falowych
2
falowej tego ośrodka. Tak więc zachodzi zależność:
(
)
Γ
−
Γ
+
=
1
Z
1
Z
1
2
z której można obliczyć
współczynnik odbicia :
1
2
1
2
Z
Z
Z
Z
+
−
=
Γ
Jeśli ośrodek pierwszy jest bezstratny, w ośrodku tym tworzy się fala częściowo stojąca. Wyrażenie
opisujące rozkład amplitud pola E (zbiór maksymalnych wartości pola) dany jest zależnością:
(
)
ψ
+
β
Γ
+
Γ
+
=
z
2
cos
2
1
1
2
0
1
E
E
gdzie:
ψ jest argumentem współczynnika odbicia Γ.
Wyrażenie to przyjmuje wartości ekstremalne: maksymalną gdy cos(2
β
1
z +
ψ) = 1:
(
)
Γ
+
= 1
max
1
0
E
E
,
oraz minimalną gdy cos(2
β
1
z +
ψ) = -1:
(
)
Γ
−
= 1
min
1
0
E
E
Stosunek maksymalnej wartości pola do minimalnej jest nazywany: współczynnikiem fali stojącej i
oznaczany –WFS lub
ρ.
Γ
−
Γ
+
=
=
ρ
=
1
1
WFS
min
1
max
1
E
E
Jak łatwo zauważyć jeżeli ośrodki są bezstratne |
Γ| = Γ gdy Z
2
> Z
1
i wówczas
1
2
Z
Z
WFS
=
, natomiast
gdy Z
2
< Z
1
, |
Γ| = -Γ oraz
2
1
Z
Z
WFS
=
Jak wynika z zależności opisującej rozkład amplitud pola elektrycznego, gdy również ośrodek drugi
jest ośrodkiem bezstratnym, wówczas współczynnik odbicia
Γ jest liczbą rzeczywistą i na granicy
ośrodków mamy ekstremum pola. Z zależności tej wynika również, że gdy pole elektryczne osiąga
maksimum to pole magnetyczne osiąga minimum (wspólczynnik odbicia dla pola magnetycznego jest
równy -
Γ).
W wyniku padania fali na granicę dwóch bezstratnych dielektryków w ośrodku 1 tworzy się fala
częściowo stojąca, opisana współczynnikiem fali stojącej:
WFS
Z
Z
lub
Z
Z
= =
+
−
=
>
ρ
1
1
1
1
2
2
1
Γ
Γ
Współczynnik odbicia Γ =
−
+
Z
Z
Z
Z
2
1
2
1
Rozkład fali częściowo stojącej pola E ma na granicy ośrodków maksimum, gdy
Γ > 0 oraz minimum,
gdy
Γ < 0. Jeśli np. pole E ma maksimum, to pole H ma minimum. Rozkłady amplitud pól E i H są
przesunięte o
λ/4. Współczynnik odbicia mocy równa się Γ
2
, a współczynnik transmisji mocy
T
p
= −
=
+ +
1
4
2
1
2
Γ
ρ
ρ
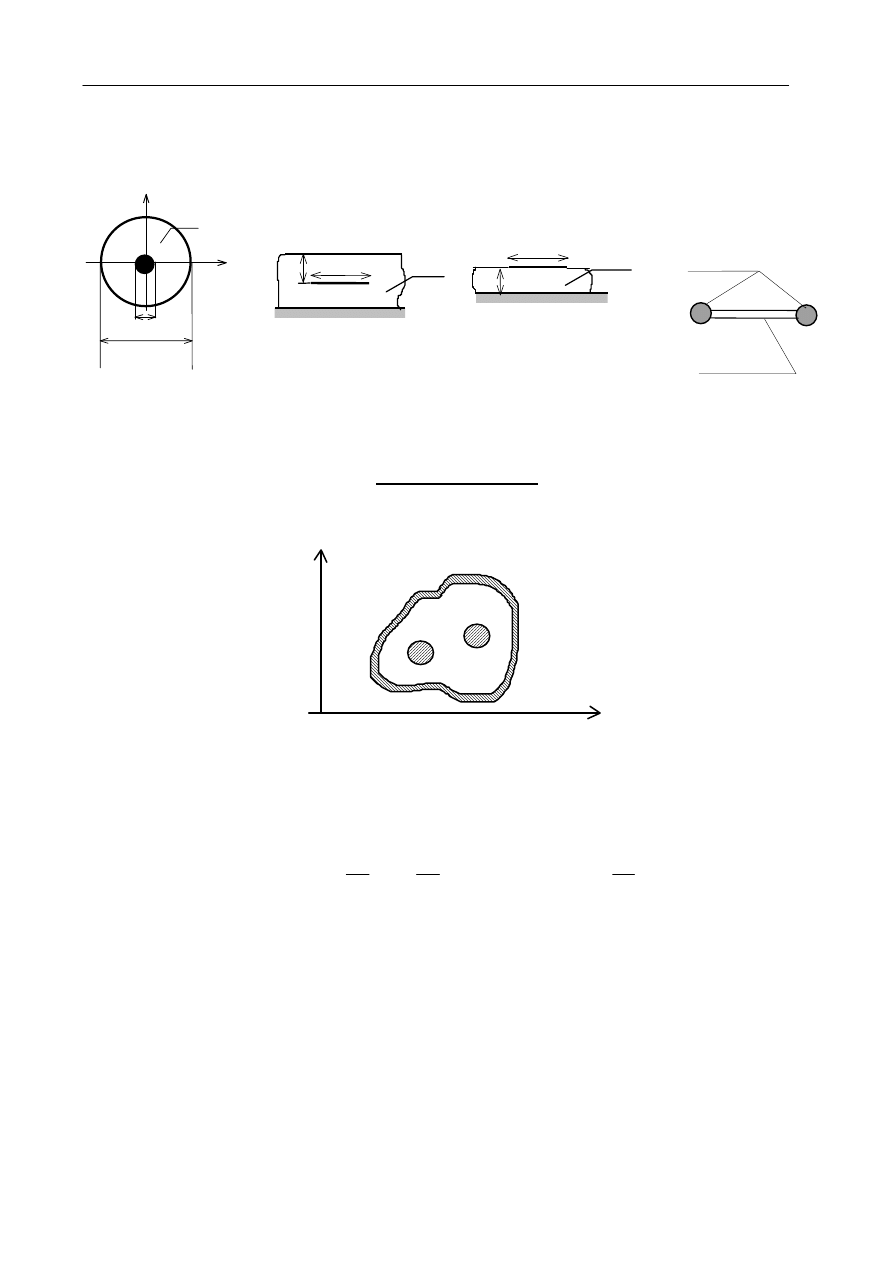
Przy padaniu fali na płaszczyznę przewodzącą następuje całkowite odbicie
(Γ = −1). W ośrodku 1
tworzy się fala stojąca (WFS
→∞). Pole E ma minimum (zero) na granicy ośrodków. Pole H ma
maksimum. Po płycie przewodzącej płynie prąd powierzchniowy o gęstości J
s
takiej - jak całkowite
pole H. Kierunek tego prądu jest prostopadły do pola H i zgodny z polem E fali padającej.
dr inż. Jolanta Zborowska - Pola w prowadnicach falowych
3
• Cechy fal w liniach TEM
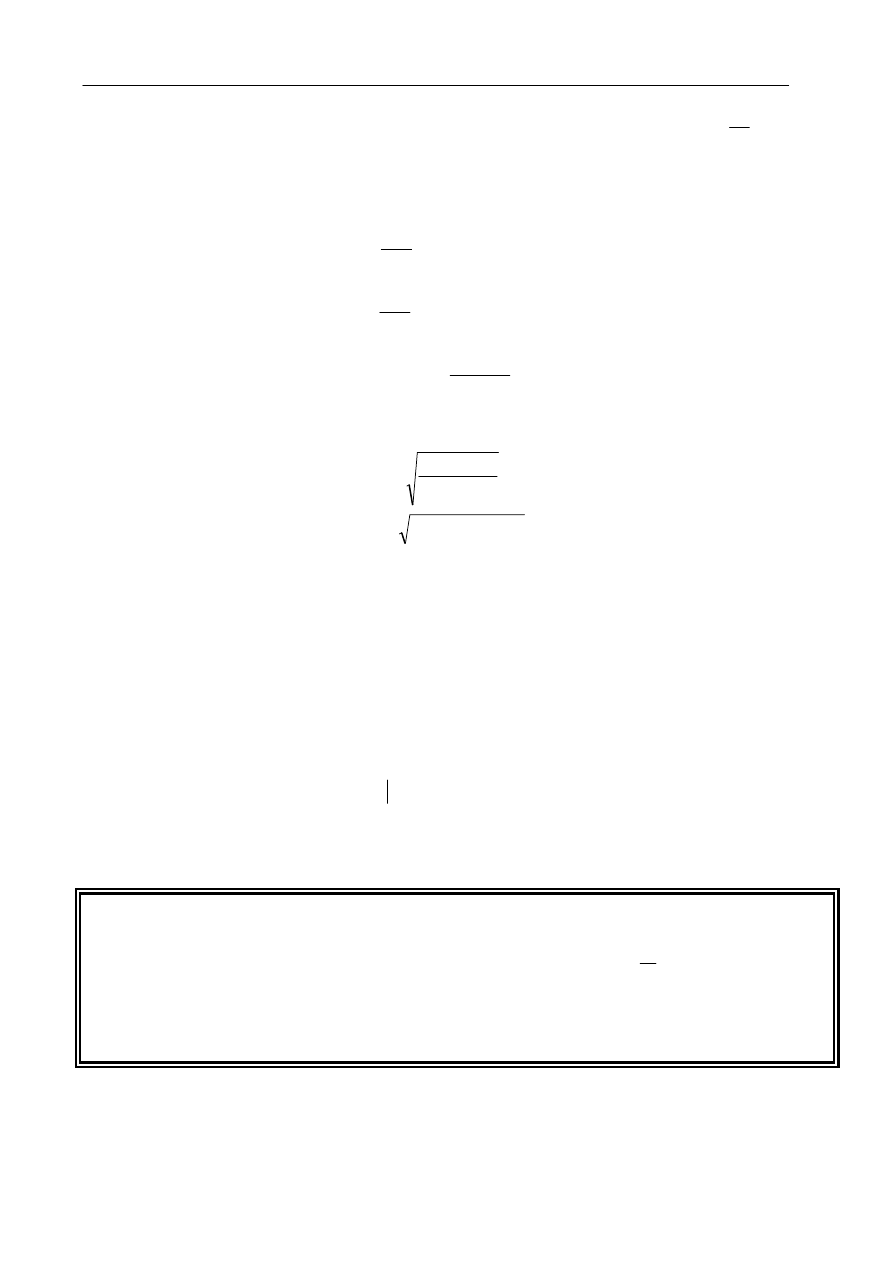
Przykłady linii TEM
a) Linia współosiowa
y
x
2b
2a
ε
w
b) Symetryczna linia
paskowa
b
b
w
ε
w
c) Niesymetryczna linia
paskowa
b
w
ε
w
d) Linia
dwuprzewodowa
Przewody
Izolacja
Fale TEM są to fale które nie mają składowych wzdłuż kierunku rozchodzenia się fali.
J
eżeli fala rozchodzi się w kierunku Oz wówczas: Ez = 0, Hz = 0
Analiza linii TEM
Prowadnicę TEM w przekroju poprzecznym pokazano na rysunku.
y
x
0
Ponieważ poszukiwane są pola, które są prostopadłe do kierunku rozchodzenia się fali, wektor nabla
dzieli się na część prostopadłą
⊥
∇
oraz wzdłużną
z
∇
:
∇ = ∇ + ∇
⊥
z
∇ =
+
⊥
r
r
i
x
i
y
x
y
∂
∂
∂
∂
∇ =
z
z
i
z
r ∂
∂
(
)
(
)
∇ + ∇ ×
=
+
⊥
⊥
⊥
z
j
r
r
H
E
σ
ω ε
(
)
∇ + ∇ ×
= −
⊥
⊥
⊥
z
j
r
r
E
H
ω μ
Po rozseparowaniu na składowe prostopadłe i wzdłużne równania Maxwella przyjmują postać:
(
)
∇ ×
=
+
⊥
⊥
z
j
r
r
H
E
σ
ω ε
∇ ×
= −
⊥
⊥
z
j
r
r
E
H
ω μ
∇ ×
=
⊥
⊥
r
H
0
∇ ×
=
⊥
⊥
r
E
0
dr inż. Jolanta Zborowska - Pola w prowadnicach falowych
4
Uzyskaliśmy rozseparowanie równań Maxwella. Równania zawierające różniczkowanie
z
∂
∂
czyli
)
(
z
∇
są takie same jak dla fali TEM w przestrzeni nieograniczonej. Wynika stąd, że stałe
γ i Z
oblicza się w przypadku linii TEM z tych samych wzorów co w przypadku przestrzeni nieograniczonej
i tak samo się te stałe wykorzystuje.
∂
∂
γ
2
2
2
0
z
r
r
E
E
⊥
⊥
−
=
∂
∂
γ
2
2
2
0
z
r
r
H
H
⊥
⊥
−
=
r
r
r
H
E
⊥
⊥
=
×
i
Z
z
f
r
r
r
E
H
⊥
⊥
=
⋅
×
Z
i
f
z
(
)
(
)
Z
j
j
j
j
f
=
+
=
+
ω μ
σ
ω ε
γ
ω μ σ
ω ε
Równania zawierające różniczkowanie względem zmiennych x i y (
∇
⊥
) mówią, że w przestrzeni
dwuwymiarowej 0xy zarówno pole
r
E
⊥
jak i pole
r
H
⊥
są bezwirowe.
Bezwirowe pole
r
E
⊥
ma więc w tej przestrzeni potencjał skalarny U(x,y):
r
E
U
= − ∇
⊥
(x, y)
Potencjał ten w przestrzeni między przewodami linii (w której nie ma ładunków) musi spełniać
równanie Laplace’a:
∇
=
⊥
2
0
U
Potencjał U(x,y) musi spełniać określone warunki brzegowe na przewodzących ściankach linii.
Ścianki te ( w płaszczyźnie 0xy są to kontury) są ekwipotencjalne, czyli warunki brzegowe mają
postać:
U
U
(x, y)
const.
na
k tym
przewodzie linii
k
−
=
=
0
Taki typ zagadnienia - rozwiązać równanie Laplace’a z zadanymi wartościami funkcji na brzegu
obszaru nazywa się zagadnieniem Dirichleta.
Rozseparowaliśmy równania Maxwella na równania wzdłuż osi Oz oraz w płaszczyźnie prostopadłej
do Oz. Pierwsze z tych równań prowadzą do równań falowych takich jak w wolnej przestrzeni. Stałe
γ
i Z (stała propagacji występująca w wyrażeniach e
z
− γ
oraz impedancja Z
E
H
=
) są takie same jak w
wolnej przestrzeni. Równania w płaszczyźnie Oxy (
┴
do osi Oz) dowodzą bezwirowości pól
r
E
i
r
H
w
przestrzeni dwuwymiarowej. Stąd
r
E
U
⊥
⊥
= − ∇
, a U da się znaleźć przez rozwiązanie równania
Laplace’a z warunkami brzegowymi (problem Dirichleta).
dr inż. Jolanta Zborowska - Pola w prowadnicach falowych
5
Algorytm obliczania pól
r
E
i
r
H
w liniach TEM
1. Znaleźć U(x,y), takie, że:
∇
=
⊥
2
0
U
(x, y)
U
U
(x, y)
na
k tym
przewodzie linii
k
−
=
0
(czyli
rozwiązać zagadnienie Dirichleta)
2. Obliczyć
(
)
γ
ω μ σ
ω ε
=
+
j
j
Z
j
j
j
=
=
+
ω μ
γ
ω μ
σ
ω ε
3.Pole E oblicza się ze wzoru :
( )
r
E
U
= − ∇
⊥
−
x, y e
e
z
j t
γ
ω
4. Pole H oblicza się ze wzoru:
r
r
r
H
E
=
×
i
Z
z
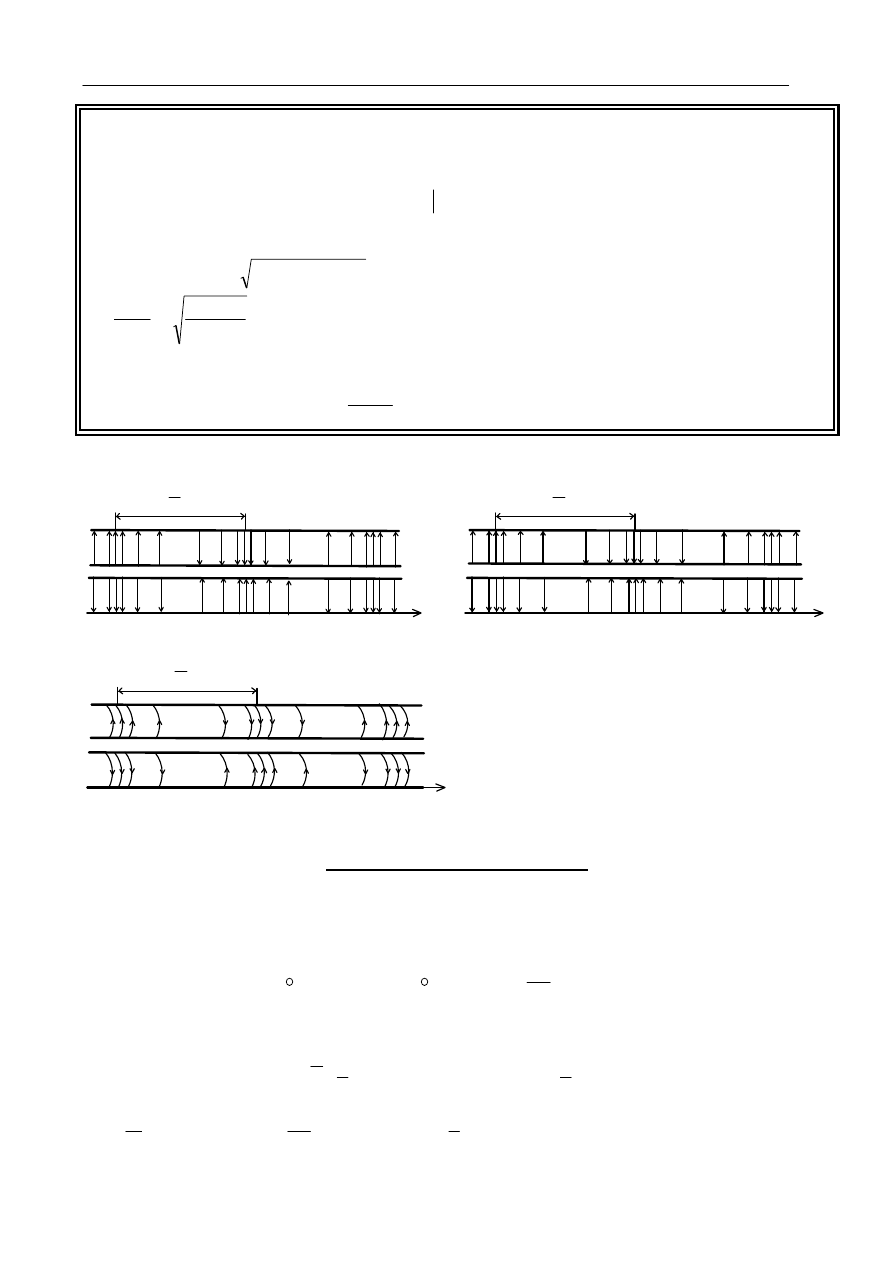
Poniżej przedstawione zostały rozkłady pól E i H wzdłuż linii współosiowej.
z
x x x x x x
x
x x x x
x
o
o
o
o
o
o
o
o
o
o
o
o
o
o o o
o
o o
o
o
o
o
o
x x x x x x x x
x x x x
x
λ
2
o
o o o
o
o o
o
o
o
o
o
x x x x x x x
x x x x
x
o
z
x x x x x x x
x x x x
x
o
o o o o
o
o o
o
o
o
o
o
x
x
x
x
x
x
x
x
x
x
x
x
x
λ
2
o
o
o o
o
o
o
o
o
o
o
o
a) fala bieżąca
b) fala stojąca
z
λ
2
o o o
o
o o
o
o o o
o
o
o o
o
o
x
x x
x
x
x x x
x
x
x x
x
x
x
x x x
x x
x
o
o o o o
o o
o
c) dla fali bieżącej - linia o stratnych ściankach
Parametry obwodowe linii TEM
U
E
A,B
A
B
d l
=
⋅
∫
r
r
∫
⋅
=
w
l
l
d
I
r
r
H
0
I
S
d
t
+
l
d
k
k
S
z
=
=
⋅⎟⎟
⎠
⎞
⎜
⎜
⎝
⎛
∂
∂
=
⋅
∑
∫∫
∫
r
r
r
r
r
D
J
H
l
gdzie:
l
w
obejmuje przewód wewnętrzny,
l
z
– obejmuje przewody linii łącznie z zewnętrznym
( )
( )
I
U
2
1
S
d
y
x,
y
x,
Re
2
1
S
0
0
⋅
=
⋅
×
=
∫∫
∗
r
r
r
H
E
P
I
U
Z
c
=
U
Q
C
1
1
=
I
L
1
φ
=

dr inż. Jolanta Zborowska - Pola w prowadnicach falowych
6
Wnioski
:
• Ponieważ pole
r
E
jest w przestrzeni dwuwymiarowej 0xy bezwirowe - wynik obliczania
napięcia między przewodami nie zależy od drogi całkowania (punkt A leży na przewodzie
wewnętrznym, punkt B - na przewodzie zewnętrznym, droga całkowania musi leżeć w płaszczyźnie
z = const)
• Z prawa przepływu wynika, że w przewodach wewnętrznym i zewnętrznym w płaszczyźnie z =
const płyną prądy o tych samych wartościach, ale w przeciwnych kierunkach
• Moc obliczona jako całka po przekroju poprzecznym z wektora Poyntinga może też być obliczona
metodami obwodowymi, za pomocą napięcia i prądu
Poniżej wyznaczone zostaną parametry obwodowe bezstratnej linii współosiowej o promieniach a, b
(a>b)
Przykładowe wyrażenia na pole elektryczne i magnetyczne w linii współosiowej:
(
)
r r
E
E
=
⋅ ⋅
−
i
b
e
j
t
z
ρ
ω
β
ρ
0
,
(
)
r r
H
E
=
⋅ ⋅
−
i
Z
b
e
j
t
z
ϕ
ω
β
ρ
0
. Można obliczyć maksymalne napięcie między
przewodami: U
E
E
=
⋅
=
∫
0
0
b
d
b ln
a
b
b
a
ρ
ρ
oraz maksymalną wartość prądu w przewodach:
I
H
l
E
l
=
⋅
=
∫
r
r
d
Z
b
0
2
π .
Następnie wyznacza się impedancję charakterystyczną linii: Z
Z
ln
a
b
c
=
=
U
I
2
π
,
pojemność jednostkową
: C
q
b
b ln
a
b
ln
a
b
1
1
0
0
2
2
=
=
=
U
E
E
ε
π
π ε
,
indukcyjność jednostkową:
L
I
H d
E
Z
b
E
Z
b ln
a
b
E
Z
b
ln
a
b
1
1
0
0
0
2
2
2
=
=
=
⋅
⋅
=
∫
φ
μ
ρ
π
μ
π
μ
π
b
a
Zauważmy, że: L
1
C
1
=
μ ε
;
L
C
Z
ln
a
b
Z
c
1
1
2
=
=
π
Jak widać w linii TEM parametry jednostkowe grają podobną rolę jak stałe materiałowe w ośrodku
nieograniczonym.
Impedancja charakterystyczna linii, prędkość rozchodzenia się fali oraz stała propagacji, dane są
zależnościami.
Z
L
C
c
1
1
=
1
1
C
L
1
v
=
γ
ω
= j
L C
1
1
Obliczmy teraz impedancję wejściową krótkiego (
Δl << λ) odcinka linii zwartego na końcu:
(
)
l
l
l
Δ
ω
=
Δ
ω
≈
Δ
β
=
1
c
c
w
L
j
v
Z
j
tg
Z
j
Z
. Jak widać krótki odcinek linii TEM zwarty na końcu
zachowuje się tak, jak skupiona indukcyjność L równa indukcyjności jednostkowej L
1
razy długość
odcinka
Δl. Podobnie, gdy rozważy się krótki odcinek linii rozwarty na końcu, widać, że zachowuje

dr inż. Jolanta Zborowska - Pola w prowadnicach falowych
7
się on jak skupiona pojemność : C = C
1
Δl. Impedancja wejściowa tego odcinka linii wynosi:
(
)
l
l
l
Δ
ω
=
Δ
ω
≈
Δ
β
=
1
c
c
w
C
j
1
j
v
Z
tg
j
Z
Z
Schemat zastępczy krótkiego odcinka linii TEM
przedstawiono obok.
Δl
L
1
Δl
C
1
Δl
Fala TEM w wolnej przestrzeni i w linii (prowadnicy) TEM
wolna przestrzeń
↔ linia TEM
ε
↔
C
1
μ
↔
L
1
Z=
=
μ
ε
E
H
↔
Z
L
C
U
I
c
=
=
1
1
v =
1
με
=
v
L C
=
1
1
1
β ω μ ε
=
=
β ω
=
L C
1
1
Zastępując
ε w wolnej przestrzeni przez C
1
w linii, i podobnie
μ przez L
1
otrzymuje się wzory
określające prędkość, stałą fazową oraz impedancję charakterystyczną linii.
• Cechy fal w falowodach
Prowadnice falowe TEM wymagały istnienia conajmniej dwóch przewodów linii. Między tymi
przewodami była różnica potencjałów - napięcie zmienne. Obecnie zajmiemy się takimi prowadnicami
falowymi, w których rozchodzenie się fal TEM nie jest możliwe. Ograniczymy się do falowodów o
przewodzących ściankach. Są to prowadnice o budowie cylindrycznej (rury wykonane z metalu -
dobrego przewodnika).
Pola E i H spełniają następujące warunki brzegowe na ściankach falowodu: Składowa styczna pola
elektrycznego, E
t
= 0, składowa normalna pola magnetycznego H
n
= 0 natomiast składowa styczna
pola magnetycznego osiąga maksimum:
∂
∂
H
t
n
= 0
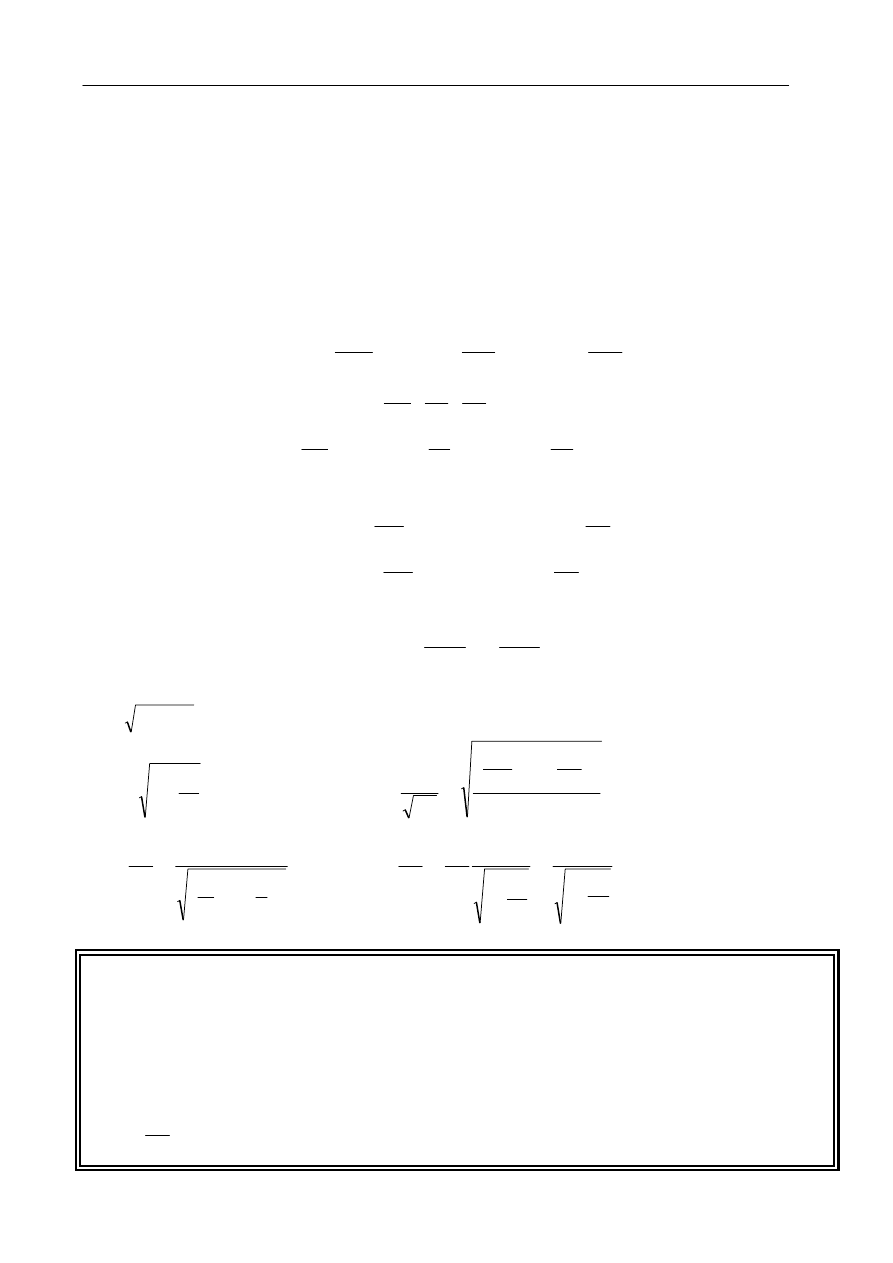
Rozpatrywany falowód prostokątny pokazany jest
na rysunku obok.
Zakłada się, że falowód jest bezstratny (ścianki
doskonale przewodzące, konduktywność
dielektryka
σ = 0). Ponadto zakłada się, że a > b.
y
x
z
a
b
Rozwiązywanie równań Maxwella w falowodzie rozpoczniemy od poszukiwania opisu pól dla
rodzajów typu E
. W tym przypadku wewnątrz falowodu istnieje niezerowa składowa E
z
, która, jako
składowa styczna, musi się zerować na ściankach falowodu. Do rozwiązania problemu zastosujemy
metodę rozdzielenia zmiennych, zapisując poszukiwaną składową E
z
jako iloczyn trzech funkcji,
dr inż. Jolanta Zborowska - Pola w prowadnicach falowych
8
zależnych kolejno od jednej spośród zmiennych niezależnych x,y,z. Po wprowadzeniu tego zapisu do
równań Helmholtza, rozseparowaniu zmiennych i uwzględnieniu warunków brzegowych otrzymuje
się rozwiązanie na funkcje X(x) oraz Y(y) w postaci funkcji sinus oraz Z(z) w postaci funkcji
wykładniczej. Pierwsze dwie z tych funkcji (sinusy) mówią o rozkładzie składowej E
z
w przekroju
poprzecznym falowodu. Ostatnia z funkcji (wykładnicza) mówi o propagacji fali wzdłuż falowodu (w
przypadku stałej
γ
z
urojonej) lub o tłumieniu fali wzdłuż osi z (w przypadku rzeczywistej wartości
γ
z
).
0
z
2
z
2
=
β
+
∇
E
E
( )
( )
( )
E
X
Y
Z
z
x
y
z
=
0
''
''
''
2
=
β
+
+
+
XYZ
Z
Y
X
Z
Y
X
Z
Y
X
X
X
Y
Y
Z
Z
''
d
d x
''
d
d y
''
d
d z
=
=
=
2
2
2
2
2
2
2
''
''
''
β
−
=
+
+
Z
Z
Y
Y
X
X
X
X
Y
Y
Z
Z
''
''
''
x
y
z
=
=
=
γ
γ
γ
2
2
2
2
2
z
2
y
2
x
β
−
=
γ
+
γ
+
γ
X
C
Y
C
=
=
x
y
sin
m
a
x
sin
n
b
y
π
π
γ
π
γ
π
x
y
j
m
a
j
n
b
=
=
Z
C
=
−
z
z z
e
γ
E
E
z
z
z z
sin
m x
a
sin
n y
b
e
=
−
0
π
π
γ
Wprowadzając nową wielkość
β
g
(graniczna stała fazowa):
2
y
2
x
2
g
γ
−
γ
−
=
β
otrzymuje się
2
2
g
z
β
−
β
=
γ
β
β
β
β
z
g
=
−
1
2
2
ω
β
μ ε
π
π
μ ε
g
g
m
a
n
b
=
=
⎛
⎝⎜
⎞
⎠⎟ +
⎛
⎝⎜
⎞
⎠⎟
2
2
λ
π
β
g
g
m
a
n
b
=
=
⎛
⎝⎜
⎞
⎠⎟ +
⎛
⎝⎜
⎞
⎠⎟
2
2
2
2
λ
π
β
π
β
β
β
λ
λ
λ
z
z
g
g
=
=
−
=
−
2
2
1
1
1
2
2
2
2
Z przeprowadzonych dotąd rozważań wynikają następujące wnioski:
• każdej parze całkowitych dodatnich liczb m, n odpowiada jeden rodzaj fali typu E. Rodzaj ten
oznaczać będziemy E
m,n
.
• liczby m = 0 lub n = 0 są wykluczone, gdyż wyprowadzony wzór daje wówczas, wbrew założeniu,
E
z
= 0. Oznacza to, że rodzaje E
m,0
lub E
0,n
nie istnieją.
• Każdy rodzaj E
m,n
ma swoją, zależną od rozmiarów falowodu (a x b) i liczb (m,n) graniczną
długość fali
λ
g
. Tej długości fali odpowiada pulsacja graniczna
ω
g
i częstotliwość graniczna
f
g
g
=
ω
π
2
. Te dwie ostatnie wielkości zależą także od parametrów ośrodka
μ, ε.
dr inż. Jolanta Zborowska - Pola w prowadnicach falowych
9
• Stała propagacji γ
z
danego rodzaju nie jest równa stałej
γ dla ośrodka nieograniczonego (w liniach
TEM
γ
z
było równe
γ dla ośrodka nieograniczonego). γ
z
zależy od częstotliwości, parametrów
ośrodka, ale też od wymiarów falowodu i liczb m,n.
• Dla fal o częstotliwości niższej od częstotliwości granicznej stała γ
z
jest rzeczywista. Fale takie nie
rozchodzą się w falowodzie (nie ma ruchu płaszczyzny stałej fazy), są wykładniczo tłumione.
Rozchodzą się tylko fale o f > f
g
.
• Najniższą wartość f
g
ma rodzaj E
11
. Jest on podstawowy wśród rodzajów E.
Znaczenie pojęcia „rodzaj podstawowy” zostanie przedstawione w dalszych rozważaniach.
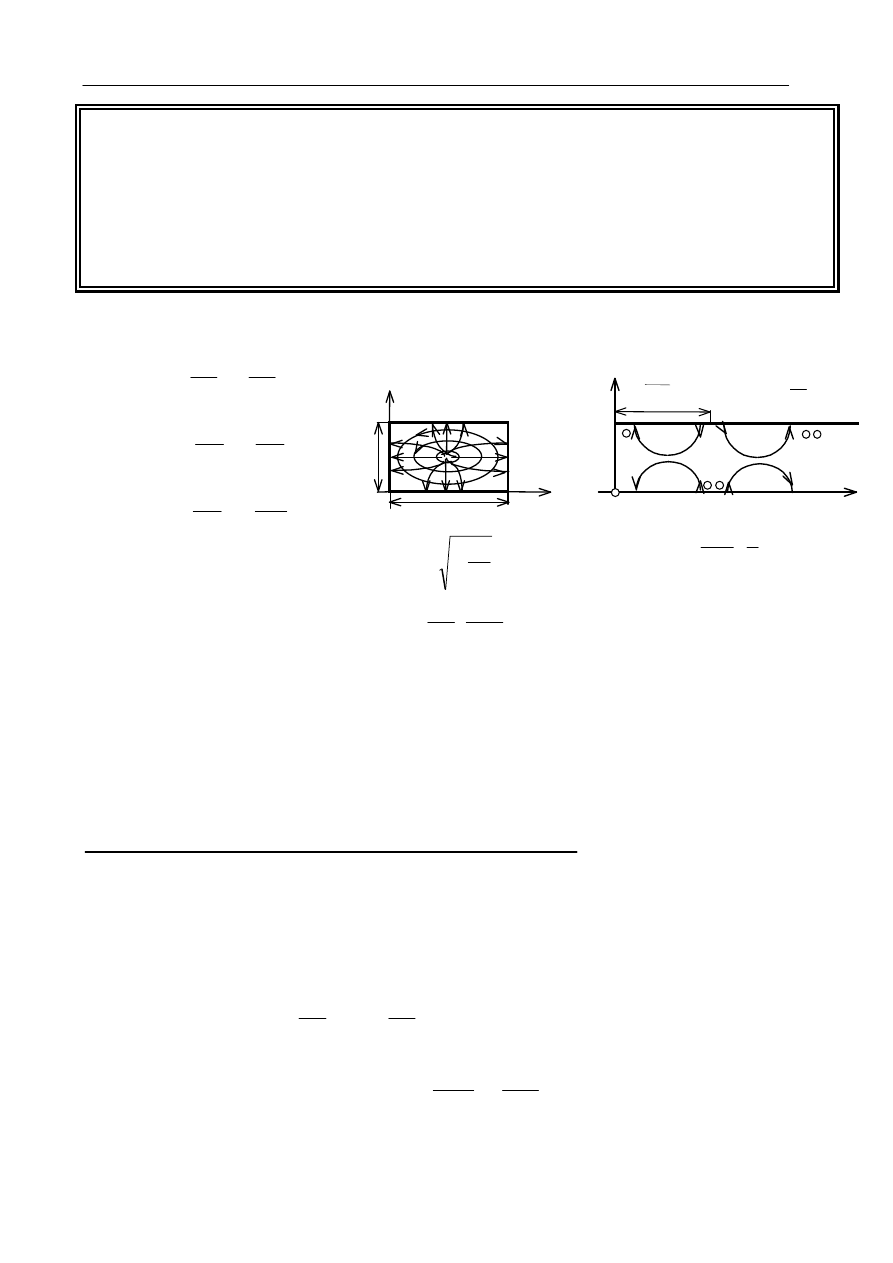
Rodzaj E11
E
E
x
x
z z
cos
x
a
sin
y
b
e
= −
−
0
π
π
γ
E
E
y
y
z z
sin
x
a
cos
y
b
e
= −
−
0
π
π
γ
E
E
z
z
z z
j
sin
x
a
sin
y
b
e
=
−
0
π
π
γ
b
a
x
y
x
y
y
x
f
2
g
2
f
Z
1
Z
Z
H
E
H
E
−
=
=
λ
λ
−
=
y
z
+
++
++
λ
z
x =
2
2
a
b
a
0
y
0
=
H
H
x
Obserwując rysunki i wzory opisujące rodzaj E
11
dochodzimy do dalszych wniosków:
• składowe poprzeczne pola E
x
, E
y
są w fazie, a składowa E
z
jest względem nich przesunięta o
π/2.
Oznacza to, że w danej płaszczyźnie z = const maksima składowych poprzecznych i E
z
są przesunięte
o ćwierć okresu, a w danej chwili czasowej t = const są one wzdłuż falowodu przesunięte o ćwierć fali.
• jeśli f < f
g
(czyli
λ > λ
g
) to impedancja falowa Z
f
jest urojona. Średni w czasie wektor Poyntinga
równa się zeru. Nie ma przenoszenia mocy wzdłuż falowodu (fala zanikająca)
• jeśli f > f
g
to Z
f
jest rzeczywiste, (Z
fE
< Z), moc fali jest przenoszona wzdłuż falowodu za pomocą
będących w fazie składowych E
x
, E
y
, H
x
, H
y
.
Poszukiwanie pól dla rodzajów typu H (H
z
≠ 0) zaczynamy podobnie jak dla pól typu E. Zakładamy,
że: H
z
= X(x) Y(y) Z(z) i staramy się zastosować metodę rozdzielenia zmiennych do równania
Helmholtza:
∇
2
H
z
+
β
2
H
z
= 0
Otrzymuje się podobne rozwiązanie jak w przypadku rodzajów E, z funkcjami trygonometrycznymi
opisującymi X(x) oraz Y(y) i z funkcją wykładniczą na Z(z). Także stałe
γ
x
,
γ
y
,
γ
z
są takie same jak
poprzednio. Jedyna różnica wynika z warunków brzegowych. H
z
jako składowa styczna osiąga teraz
maksimum na ściankach,
∂
∂
X
x
oraz
∂
∂
Y
y
na ściankach się zerują. Oznacza to, że funkcje
trygonometryczne opisujące X(x) i Y(y) muszą być kosinusami, czyli ostatecznie:
H
H
z
z
z z
cos
m x
a
cos
n y
b
e
=
−
0
π
π
γ
Z wzoru powyższego wynika, że teraz dopuszczalne są liczby m = 0 lub n = 0. Istnieją rodzaje H
m0
oraz H
0n
( nie istnieje tylko rodzaj H
00
) . Przy założeniu a > b rodzajem podstawowym wśród rodzajów
dr inż. Jolanta Zborowska - Pola w prowadnicach falowych
10
H jest H
10
. Jest on też rodzajem podstawowym w pełnym zbiorze rodzajów E i H, gdyż ma niższą
częstotliwość graniczną niż rodzaj E
11
.
W praktyce wykorzystuje się przeważnie falowody jednomodowe (jednorodzajowe), to znaczy tak
dobiera się do częstotliwości fali wymiary falowodu, aby mógł się rozchodzić tylko jeden rodzaj.
Rozchodzenie się wielu rodzajów jest szkodliwe, ponieważ każdy z nich ma inne parametry (np. inne
prędkości fal) i przesyłanie informacji za pomocą wielu rodzajów jednocześnie jest bardzo utrudnione.
Stąd duże znaczenie rodzaju podstawowego (H
10
), głównie tylko ten rodzaj jest wykorzystywany.
Pasmem pracy falowodu jest pasmo, w którym rozchodzi się tylko rodzaj podstawowy. W przypadku
falowodu prostokątnego jest to pasmo:
f
f f
gH
g H
10
01
< <
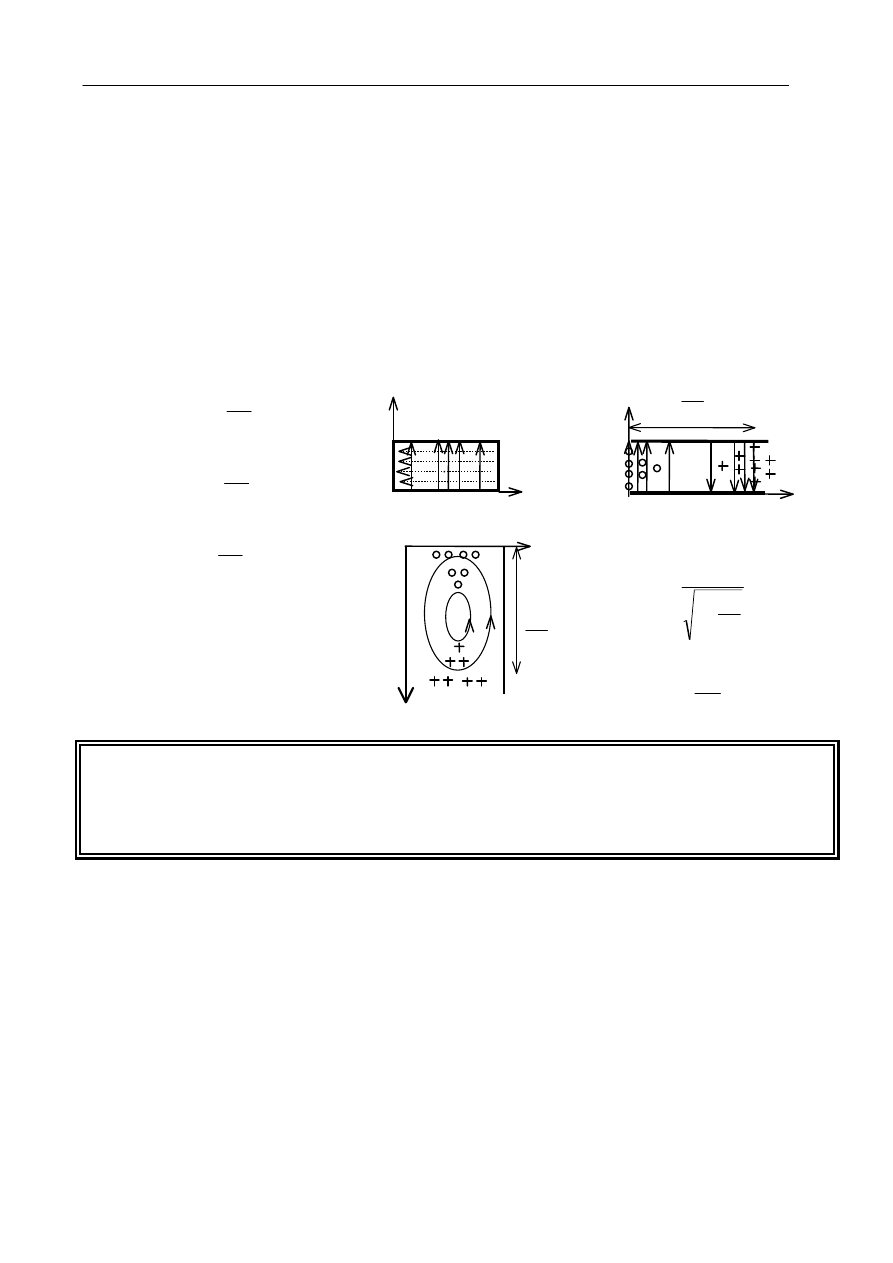
Rodzaj H10 (podstawowy)
H
H
x
x
z z
sin
x
a
e
= −
⎛
⎝⎜
⎞
⎠⎟
−
0
π
γ
H
H
z
z 0
z z
j
cos
x
a
e
=
⎛
⎝⎜
⎞
⎠⎟
−
π
γ
z
yo
y
z
e
a
x
sin
γ
−
⎟
⎠
⎞
⎜
⎝
⎛ π
= E
E
x
y
λ
z
2
y
z
λ
z
2
z
Z
Z
Z
E
H
f
g
f
y
x
=
−
= −
1
2
2
λ
λ
Rodzaj H
10
jest podstawowy w falowodzie prostokątnym, ma najniższą częstotliwość graniczną.
Poniżej
10
H
g
f
fale się nie rozchodzą. Powyżej
10
H
g
f
fale się rozchodzą, lecz przy zbyt wysokich
częstotliwościach, przekraczających
f
,f
f
g H
g E
g H
01
11
11
=
lub
20
H
g
f
są co najmniej 2 lub 3 rodzaje fal
o różnych prędkościach. Taka transmisja jest utrudniona i się jej nie stosuje.
Literatura
[1] MORAWSKI T., GWAREK W. – Pola i fale elektromagnetyczne, WNT, W-wa 1998, str. 88-95,
133-137, 149-158, 163-165, 167-174, 179-181, 189-190
[2] Wykład POLA i FALE
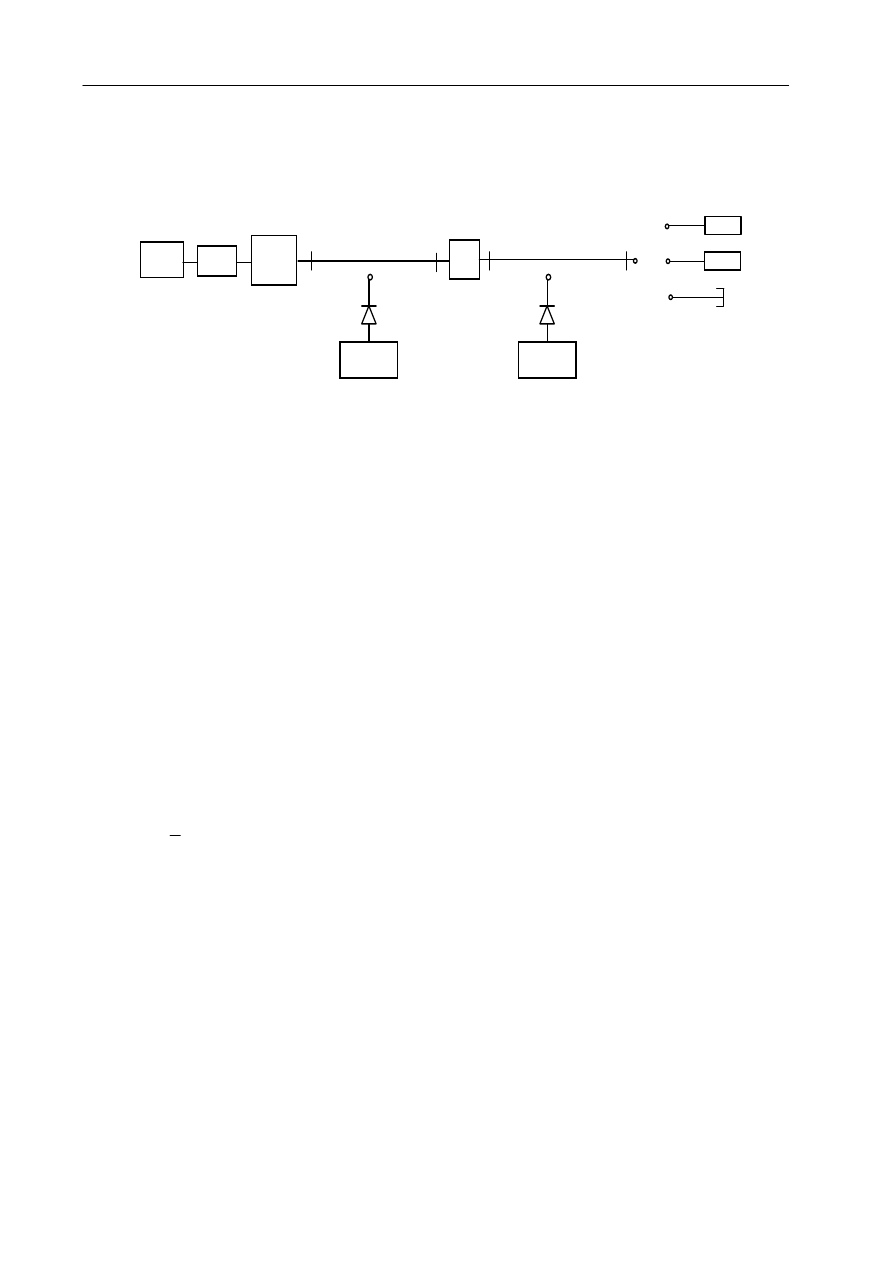
dr inż. Jolanta Zborowska - Pola w prowadnicach falowych
11
Pomiary:
1.
Linia współosiowa i falowodowa
Do obserwacji fali bieżącej, częściowo stojącej i fali stojącej oraz do pomiaru parametrów
tych fal stosuje się układ pomiarowy pokazany na rys. 1
G
D
N
Z
W
W
WLP
FLP
I
T
P
Rys. 1 Układ do pomiaru parametrów fal w linii
G - generator, I - izolator, T - tłumik regulowany, FLP - falowodowa linia pomiarowa ,
WLP - współosiowa linia pomiarowa, W - wskaźnik względnego natężenia pola elektrycznego,
P - przejście z linii falowodowej na współosiową, Zakończenia linii : D - dopasowane obciążenie, N -
niedopasowane obciążenie, Z - zwarcie
Należy zaobserwować, że:
•
w linii zakończonej obciążeniem dopasowanym jest fala bieżąca
•
w przypadku obciążenia niedopasowanego tworzy się fala częściowo stojąca
•
w przypadku zakończenia linii zwarciem tworzy się fala stojąca
Następnie należy wyznaczyć:
•
długość fali w współosiowej prowadnicy falowej
λ i porównać z długością λ0 fali obliczoną na
podstawie znajomości częstotliwości generatora
Długość fali mierzy się w prowadnicy falowej zakończonej zwarciem.
Pomiaru dokonuje się w ten sposób, że mierzy się położenia dwóch kolejnych minimów tej fali l1min ,
l2min
a następnie oblicza się długość fali ze wzoru:
λ =
−
2
2
1
(
)
min
min
l
l
Długość fali w powietrzu jest związana z częstotliwością sygnału zależnością:
f
c
0
=
λ
gdzie: c = 3 108 m/s, prędkość światła w próżni
• wyznaczyć długość fali w linii falowodowej λf (długość fali w linii falowodowej mierzy się w ten
sam sposób jak w linii współosiowej tzn. poprzez pomiar dwóch kolejnych minimów)
• porównać długość fali w falowodzie z długością fali w linii współosiowej
• znając wymiary falowodu , rodzaj pobudzonej fali oraz długość fali w wolnej przestrzeni obliczyć
długość fali w falowodzie i porównać z długością fali zmierzoną w falowodowej prowadnicy falowej
W układzie badanym boki falowodu wynoszą: a = 23mm, b = 12mm a pobudzona fala jest rodzaju
H10.
2. Rozkład pola elektrycznego w prowadnicy falowej

dr inż. Jolanta Zborowska - Pola w prowadnicach falowych
12
A.
W
układzie jak na rys. 2 wyznaczyć względny rozkład pola w linii zakończonej zwarciem.
LP
G
Z
W
Rys. 2 Układ do pomiaru rozkładu pola w
prowadnicy falowej
G - generator, LP - linia pomiarowa,
(współosiowa lub falowodowa), W - wskaźnik
względnego natężenia pola elektrycznego, Z -
zwarcie
Należy wyznaczyć:
• długość fali w prowadnicy falowej λ .
Długość fali mierzy się w prowadnicy falowej zakończonej zwarciem.
Pomiaru dokonuje się w ten sposób, że mierzy się położenia dwóch kolejnych minimów tej fali l1min ,
l2min
a następnie oblicza się długość fali ze wzoru:
λ =
−
2
2
1
(
)
min
min
l
l
• względny rozkład pola wzdłuż linii zakończonej zwarciem
Należy ustawić sondę na linii pomiarowej w maksimum pola elektrycznego oraz ustawić wskazanie
miernika W na zero decybeli. Względne pole elektryczne odpowiadające wskazaniu miernika w [dB]
wyraża się wzorem:
(
)
E
w
w
20
z z
−
=
0
10
Uwaga:
Względny rozkład pola należy wyznaczyć pomiędzy dwoma minimami
Należy odczytać położenie sondy dla następujących wartości wskazań miernika W : -1dB, -2dB, -3dB,
-6dB, -10dB, -16dB, -20dB
Względny rozkład teoretyczny dany jest zależnością
(
)
(
)
E
w
z z
sin
z z
−
=
−
0
0
2
π
λ
gdzie zo – położenie minimum fali stojącej o najmniejszej wartości zmiennej z na skali podziałki linii
pomiarowej.
Uwaga
: Pomiary i wykres teoretyczny należy umieścić na tym samym rysunku
B.
Pomiary wykonuje się w układzie jak na rys. 2, z tym, że zamiast zwarcia Z do linii
pomiarowej LP dołącza się obciążenie niedopasowane N. Należy wyznaczyć względny rozkład pola
wzdłuż linii stosując metodę opisaną w punkcie A. Po ustawieniu sondy na linii pomiarowej w
maksimum pola elektrycznego należy odczytać położenie sondy dla w = -1dB, -2dB, -3dB itd. co 1dB
oraz odczytać położenie minimum oraz wartość w w minimum fali częściowo stojącej. Narysować
wykres zależności E
w
(z) oraz obliczyć współczynnik fali stojącej.
Wyszukiwarka
Podobne podstrony:
więcej podobnych podstron