
Training
management
w h i t e p a p e r

A training
manager
could
predict the
candidate’s
course grade
by plugging
in high
school
standings
and
inventory
scores
w h i t e p a p e r
Tr a i n i n g m a n a g e m e n t
2
T
he current climate of austere budgets and shrinking manpower dictates
the training of a smaller workforce. With increasingly technical areas and
fewer training resources, the need to efficiently manage training takes on
critical importance.
Effective training management often involves scrutiny of both trainee selection
procedures and course effectiveness. In this paper, we discuss these areas as well
as some ideas for test analysis using SPSS statistical software for more effective
training management.
Selective admittance
Physical or fiscal constraints often define the number of openings in an organization’s
training courses. The effective management of training resources involves choosing:
n
Candidates who possess an aptitude for the subject/job/degree; and/or
n
Candidates who will best learn the course material; and/or
n
Candidates who will best apply training to their jobs.
When selecting training candidates, a training manager wants to select individuals
with one or more of these qualifications. But how does a manager determine qualified
candidates? Fortunately, the answers may already exist. For example, suppose the
training manager keeps student records of educational level, high school class rank, in-
ventory test score, etc. – along with the student’s final course grade. These records
could provide historical evidence of a strong association between the inventory test
score and course performance, but almost none with high school class rank. Presented
with this, it might be a good idea for the training manager to predict a candidate’s
course performance based on the inventory test score. Then, the predicted course
performance provides basis for course admittance.
The manager can summarize associations between and among data elements such
as educational level and course performance in a mathematical model. For example,
the model might be:
Predicted Final Course Grade = a*high school standing + b*inventory score
With this model, a training manager could predict the candidate’s course grade
by plugging in high school standings and inventory scores. If there were 30 candidates
for 20 course openings, selecting the top 20 candidates from a list sorted by predicted
final course grade may be an effective admittance procedure.
The way the manager builds the model (the determination of the parameters a and b,
for example) depends on the statistical procedure used, which in turn depends on the
nature of the data available. Various statistical procedures make assumptions about
the data and it is important to verify these assumptions. Many of these assumption
“checks” are graphical. Included in this paper are graphical plots the manager
can use to verify these assumptions.
You can use
statistical
techniques
to improve
training
management
w h i t e p a p e r
Tr a i n i n g m a n a g e m e n t
3
The following examples show how to use statistical techniques to improve training
management for law enforcement officers, specifically in marksmanship. But the
principles here apply to academic, as well as corporate, training.
Linear regression
Linear regression is a data modeling
procedure to use when you can assume
there is a linear relationship between
predicted information (final course
grade) and each of the predictors
(inventory test score).
For example, let’s suppose a training
manager has information on past students,
(including shooting range score, age,
gender, height and weight) and wants
to model the predicted shooting score
of incoming students. Using a graphic
called a scatterplot, the manager can
examine the relationship between two
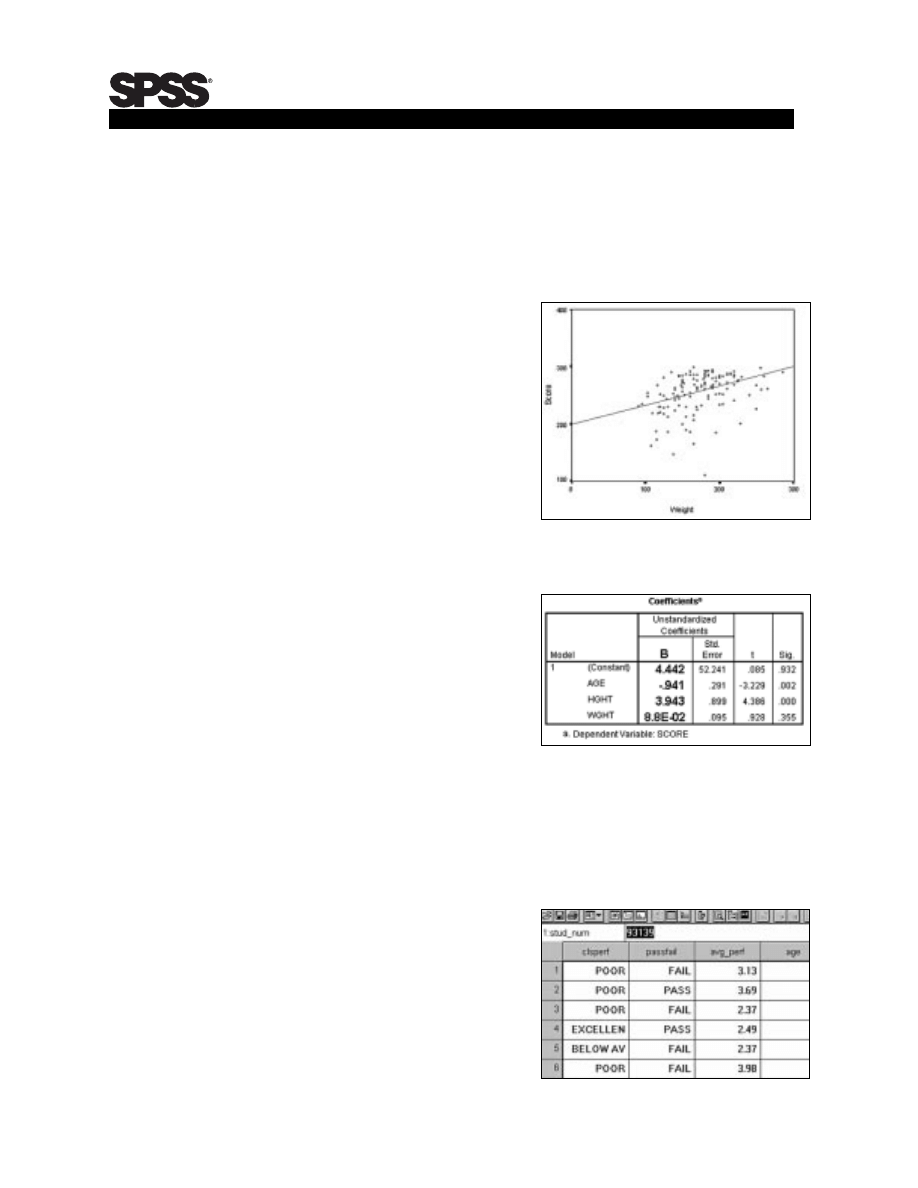
variables, for example, score and weight.
Figure 1 shows us the score tends to
increase linearly with weight. And so one
of the assumptions underlying the linear
regression procedure appears to be met.
After examining scatterplots of other
data elements, such as height and age,
the training manager ran the regression
procedure and received the output in
Table 1. The entries in column B are the
parameters of our model. The completed model is as follows:
Score = 4.442 -0.941 x Age + 3.943 x Height + 0.088 x Weight
Logistic regression
You can use logistic regression for modeling
data if the outcome you attempt to predict
has two values, for example Pass/Fail
(see Figure 2), as opposed to being a
continuous variable, such as the score
in Figure 1. Logistic regression reveals
the probability of a pass occurring rather
than a definitive prediction of pass or fail.
In addition to producing the parameters
for the logistic regression model, logistic
regression produces a classification table,
Figure 1. SPSS scatterplot of score
with weight.
Table 1. SPSS linear regression output.
Figure 2. SPSS Data Editor with a
dichotomous variable: PASSFAIL.
What makes
neural
networks
useful is
their ability
to learn
complex
patterns
and trends
in your data
w h i t e p a p e r
Tr a i n i n g m a n a g e m e n t
4
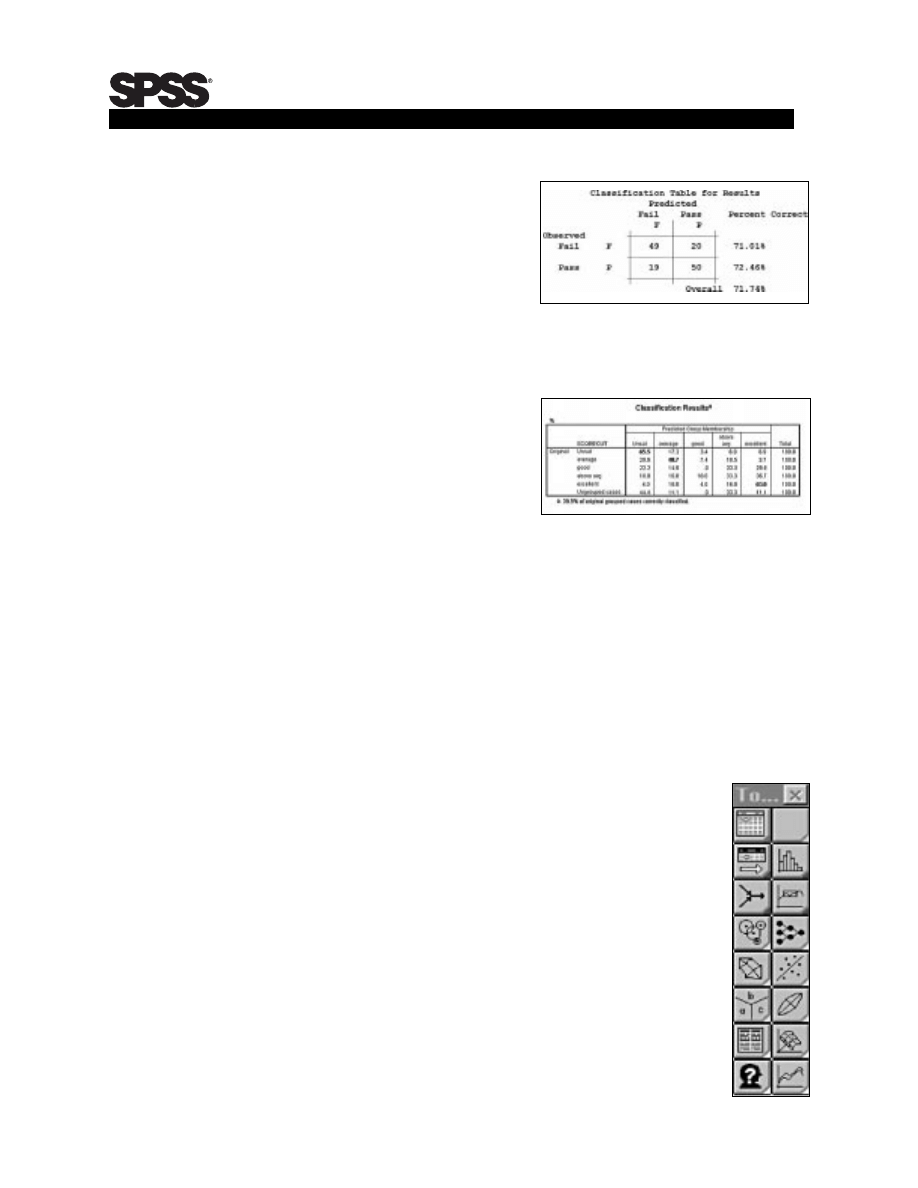
(Table 2). A training manager may
substantiate the use of a logistic regression
model by examining the number of correct
predictions made using that model. Table 2
shows candidates who failed were predicted
with 71 percent accuracy, and those who
passed with 72 percent accuracy for an
overall correct classification of 72 percent.
Discriminant analysis
To use discriminant analysis, lets suppose
an instructor had information on student
performance at the end of the training
class. And suppose it was rated on a scale
ranging from Excellent, Above Average,
Good, Average to Unsatisfactory. A
training administrator may want to
identify important criteria to classify
the candidates into five groups. The administrator could then integrate this information
into a model for predicting group membership (into one of the five groups described
above) for new candidates. To accomplish this, the administrator may choose to use
discriminant analysis. (Figure 3).
In addition to generating a model for predicting group membership, discriminant
analysis also generates a territorial map and a classification table for observed
and predicted groups.
Neural networks
In the examples above, managers had to make certain assumptions
about the data or the mathematical relationships between the
variables to use the statistical routines appropriately. However, a
training manager could have historical data that might not be
appropriate with the statistical procedures we mentioned. In this
case, the manager has another option: neural networks. For example,
many of the classical procedures mentioned assumed there were
noncategorical variables in the data model. But neural networks make
no such assumptions. At their most fundamental level, neural networks
are a new of way of analyzing your data. What makes them so useful
is their ability to learn complex patterns and trends in your data.
Building a neural networks model is easy to do in Neural Connection,
SPSS’ neural network software. To start, you drag and drop data
input icons from the tools palette (Figure 4) onto the screen. You
can also easily place output and neural algorithms and
Table 2. SPSS logistic regression
classification table.
Figure 3. SPSS classification table.
Figure 4. The SPSS Neural Connection tools palette.
Graphics
output
from Neural
Connection
includes a
plot that
indicates
model
sensitivity
to selected
inputs
w h i t e p a p e r
Tr a i n i n g m a n a g e m e n t
5
selected statistical procedures icons.
Arrows depict data flow data from input
through procedure. You can add output
to customize the model (Figure 5). Plus,
each icon has drop-down menus that
enable you to open the file within the
input icon, or format text output.
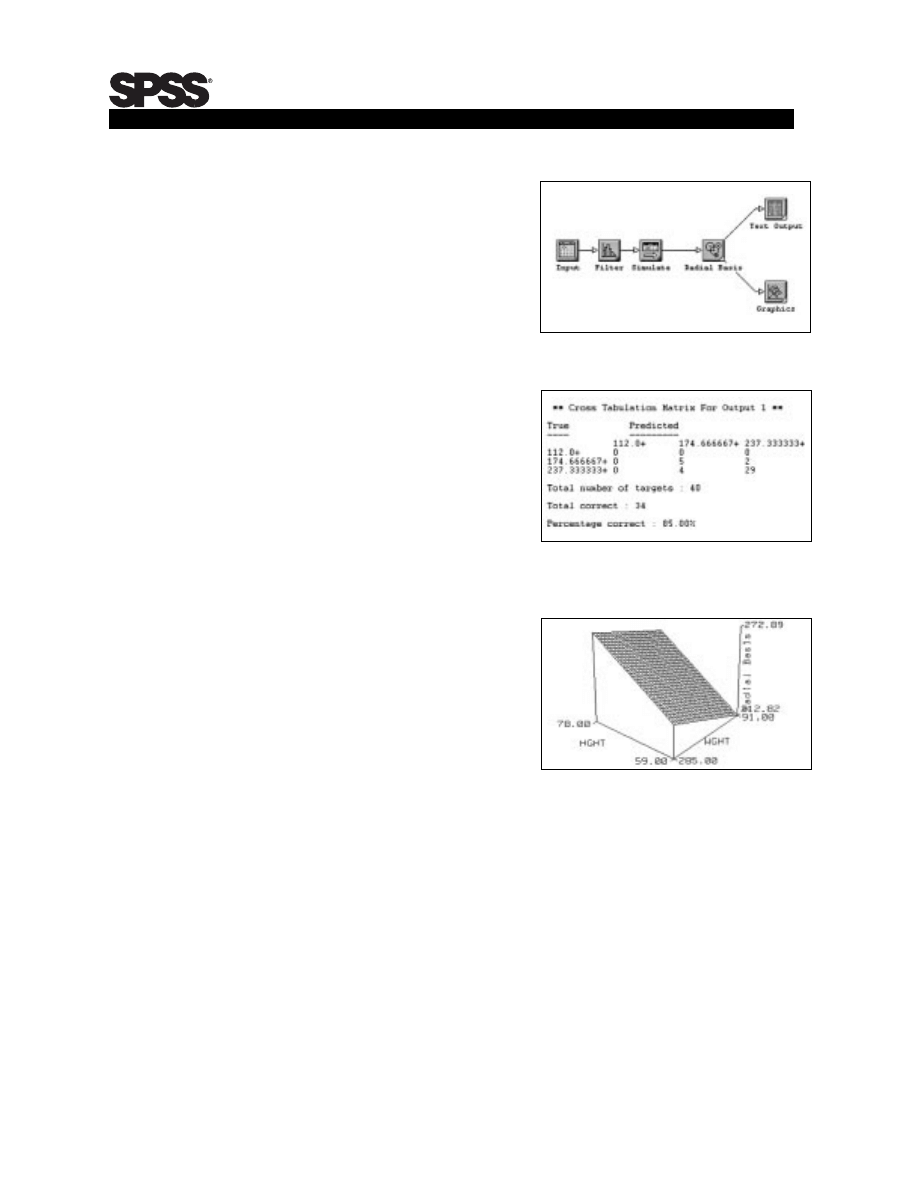
The text output from Neural Connection
features a classification table (Table 3),
which shows the percentage of correct
predictions using your generated model.
Eighty-five percent of the cases (34
of 40) were predicted correctly using
the neural networks model.
Graphics output from Neural Connection
includes a plot that indicates model
sensitivity to selected inputs. For example
in Figure 6, height and weight are plotted
against the predicted score (termed radial
basis). The plot shows the relative
contribution of these two input variables
to the predicted score. Notice the relatively
steep slope of weight vs. score for shooters
who are at or near 59 inches (near the
bottom of the contour screen). Also notice
the slope of weight vs. score is much more
gradual for those at the upper end of the
height measurements (or at the upper
end of the screen). This makes sense;
the weight of heavier shooters probably
doesn’t have much of an effect. The weight
of taller shooters probably doesn’t have a
clear advantage.
Course evaluation
Wayne Hortman, Ph.D. and chief of research and evaluation section, Instructional
Systems Design, Bureau of Prisons, uses SPSS
®
in performing course evaluations.
These courses include:
n
Basic and Advanced Financial Management Training
n
Basic and Advanced Procurement Training
n
Computer Specialty Training
n
Inventory Management Training
n
Security Officers Training
Figure 5. Neural Connection topology.
Table 3. Neural Connection classification
table.
Figure 6. Neural Connection plot for weight
(wght) and height (hght).
Coupling
these
responses
with
demographic
information
on each
student
often yields
useful
information
w h i t e p a p e r
Tr a i n i n g m a n a g e m e n t
6
Hortman performs course evaluations on three levels:
n
Level I evaluations are at the end of each course of instruction, covering student
reactions on topics such as course quality and instructor knowledge.
n
Level II evaluations measure the learning within each course by comparing scores
on precourse and postcourse tests.
n
Level III evaluations are onsite at the course graduate’s workplace, measuring the
effect course attendance has on job performance. Supervisor who have both
graduates and nongraduates reporting to them provide performance measures.
Each evaluation level measures a specific aspect of course effectiveness, employing
several graphic and statistical procedures using SPSS.
Level I
At the end of each course, course graduates
fill out a survey judging their reactions to
areas including quality of instruction,
instructor knowledge, amount and quality
of hands-on training. The responses
are ranked on a scale from 1 to 5
(1 indicates unsatisfactory and a 5
indicates outstanding). Coupling
responses with demographic information
on each student often yields useful
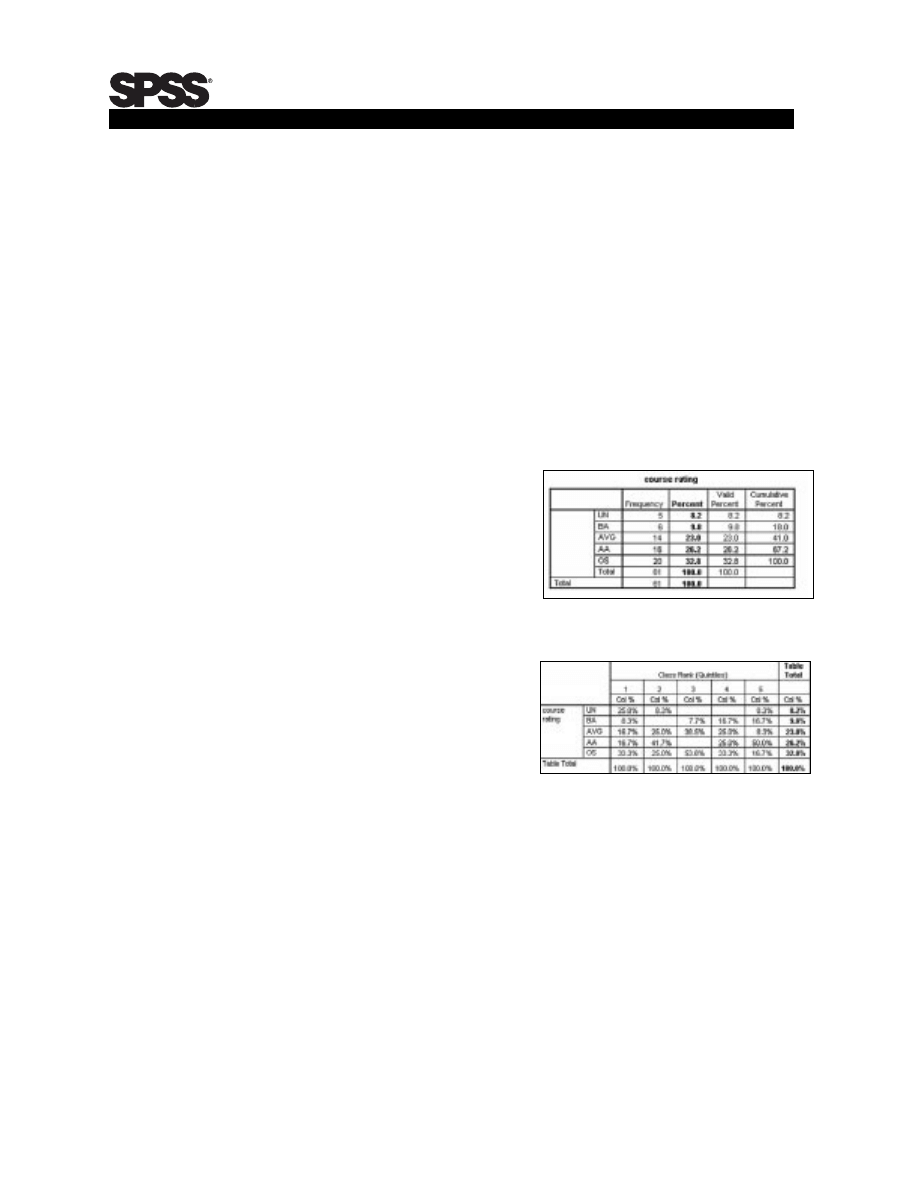
information. For example, examining
the frequency of responses on the question
concerning course rating may show the
results in Table 4.
At first glance, almost a third of the
students (32.8 percent) rated the class
outstanding, and only 8.2 percent thought
the class unsatisfactory.
If we break out the responses by class rank (where 1 corresponds to the top fifth of the
class), fully 25 percent of the top students rated the course unsatisfactory (Table 5).
This finding may require further analysis.
Level II
Level II course evaluations measure course learning (for example, if course objectives
were met). The methods used include tests on course subject material, administered
both before and after course completion. After gathering information, a manager can
use different tools – both graphical and tabular – to assess the degree of learning.
Table 4. SPSS distribution of course rating.
Table 5. SPSS distribution of course rating
(by class standing).
w h i t e p a p e r
Tr a i n i n g m a n a g e m e n t
7
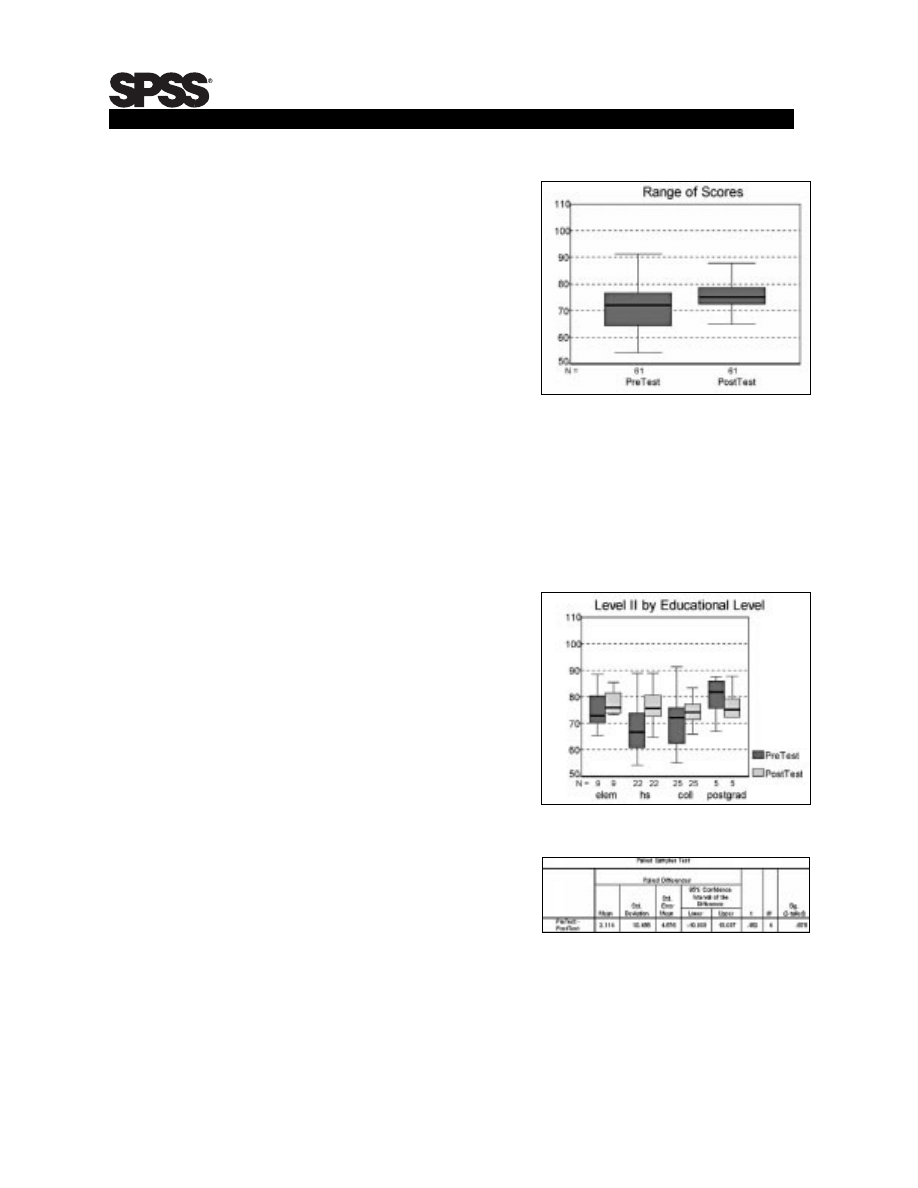
For example, the boxplot at right (Figure
7) shows the spread or distribution of
scores for the two tests.
A boxplot reveals much information.
First, each box corresponds to each
of the two sets of scores – pretest and
posttest. The heavy line within the body
of each box corresponds to the 50th
percentile, or the median score for each
group of scores. The top and bottom of
each box represent the 75th and 25th
score percentiles, respectively. The
whiskers drawn above and below each box
measure the spread of outlying scores.
This chart shows an overall improvement in scores. First, the median score has
improved (as have the 75th and 25th percentile scores). Second, the range of scores
on the posttest is smaller than on the pretest. This is evidence of a more consistent
knowledge base within the course graduates. Nevertheless, improvement might not
be as marked as the course manager wants, calling for further investigation.
Figure 8 shows another boxplot of the
scores. This time, scores are broken out
by students’ educational level. Notice the
marked improvement in scores for those
students with a high school or a college
degree. On the other hand, scores for
students with a postgraduate degree
show a downward trend. The reasons
for this aren’t evident from this chart,
and may not be cause for concern.
Also notice only five students have
postgraduate degrees (the population
sizes (N=) are printed just underneath
each boxplot). These five students may
not represent all students in this category,
and this particular showing may be
very unusual.
We can use a statistical test to judge
whether this disappointing drop in
scores for students with the postgraduate
degree is significant – or simply a result of an unfortunate/nonrepresentative sample.
The appropriate statistical test here is the paired samples t-test. Table 6 shows the
output from this test. The information we gather from running this test includes:
Once you
gather
information,
you can
use different
tools, both
graphical
and tabular,
to assess
the degree
of learning
Figure 7. SPSS boxplots of pretest and
posttest scores.
Figure 8. An SPSS boxplot of pretest and
posttest scores by educational level.
Table 6. SPSS results of paired samples t-test.
n
The mean or average difference between the pretest and posttest scores for five
students with the post graduate degree is 2.114.
n
If we repeated this same analysis 100 times (using 100 groups of five students
in 100 other iterations of this same course) 95 percent of the time we would find the
difference between pretest and posttest scores for students with postgraduate
degrees to fall within the large interval (termed the confidence interval) of -10.869
to 15.097. So there seems to be a good chance the drop in scores for this class was a
chance occurrence and not something we would expect.
Level III
Level III evaluations measure the
effect course completion might have on
graduates’ on-the-job performance. These
performance measure could be several
types, such as test scores or quantitative
assessments gathered from interviews
with graduates’ supervisors. Whatever the
measures, assessments should be gathered
from both course graduates and nongrad-
uates to determine the effect of course
completion. Again, a manager could use
from several different graphical and
statistical procedures to assess this effect.
For example, the bar chart in Figure 9
displays the differences in average performance score for the course graduates
and nongraduates in this particular assessment.
The results look promising. Yet the course manager would want to ensure this
difference is indeed significant, and not a function of the particular group of graduates
and nongraduates selected for the assessment. To do this, the manager would run a
statistical test.
Table 7 displays
descriptive statistics
on the performance
measure for the two
groups. Notice the
sample sizes are
28 and 22 for the
graduates and
nongraduates, respectively, and the means (averages) reflect what we saw in Figure 9.
Level III
evaluations
measure
the effect
course
completion
may have on
graduates’
on-the-job
performance
w h i t e p a p e r
Tr a i n i n g m a n a g e m e n t
8
Figure 9. SPSS bar chart of graduate and
nongraduate performance.
Table 7. SPSS group descriptive statistics.
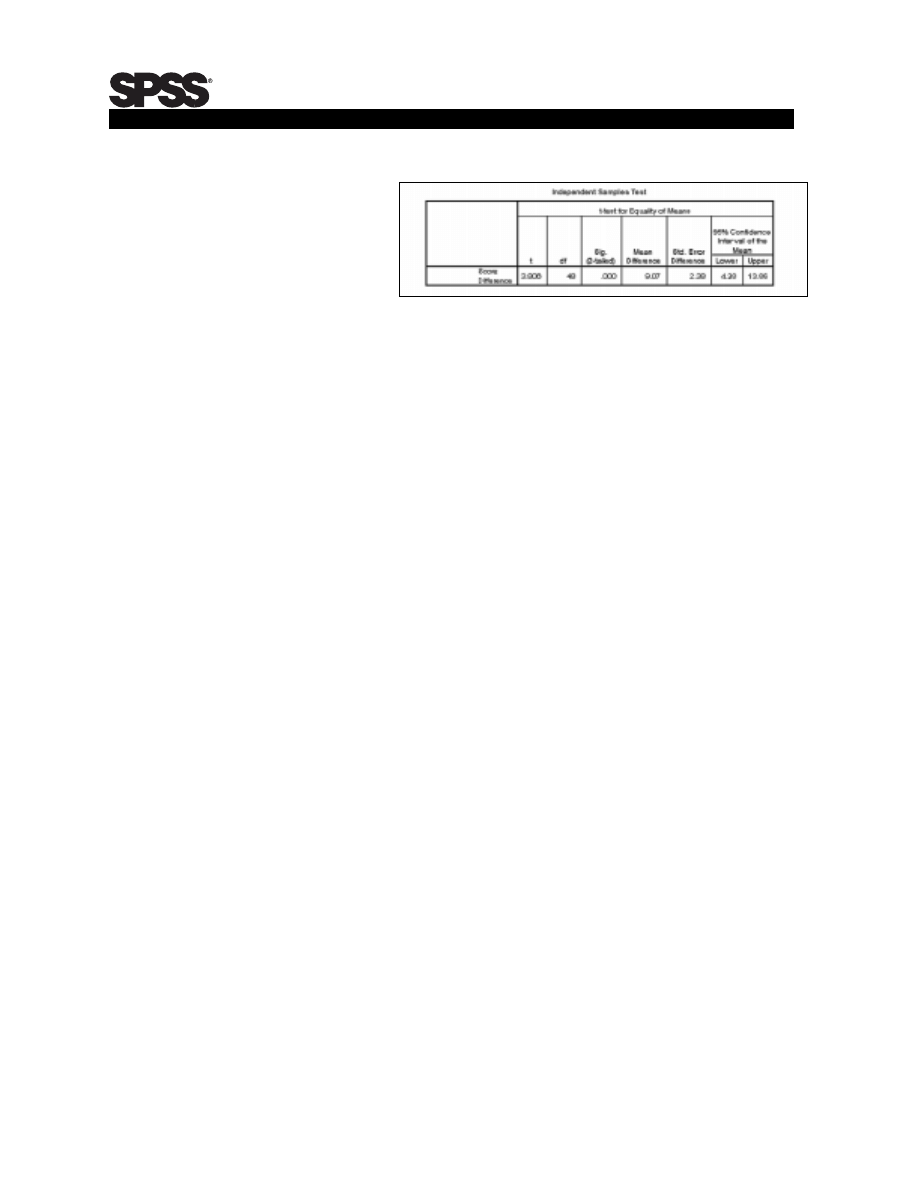
This time, notice
in Table 8 the 95
percent confidence
interval for the
mean difference.
The interval shows
the mean score
difference (9.07)
is not at all unusual. Interpretation: 95 out of 100 similar groups of subjects we could
have chosen would have shown score differences at least as great as 4.28 points. So
we can be confident course completion has a positive, significant affect on on-the-
job performance.
Course evaluation programs made possible with a statistical package such as SPSS
can assess course effectiveness from several perspectives. Ranging from the course
satisfaction look of newly graduated students to the increase in the student knowledge
base to the effect of course completion on job performance, the manager can draw
a comprehensive assessment picture.
Depending on the type and range of student data collected, course evaluations can also
be prescriptive. For example, if the before-and-after course test scores were examined
question by question, you could target the course area needing work. And, if the on-the-
job performance scores were broken down by job performance areas, you could examine
areas in which course attendance had little effect.
Test design
In Level II course evaluation, we use tests to assess the degree of learning in the
training program. We do this through a comparison of pretest and posttest scores. A
manager can use scores to make decisions about future curriculum, instructors and
training program benefits. Two test design-related issues are test reliability and test
validity. Typically, test scores reflect both true individual differences in the
characteristics being measured and the influence of chance factors, such as fatigue
or illness. A reliable test will produce consistent results when the same test is
administered at different times, or with different sets of comparable items under
various testing conditions.
In order to understand test reliability and consistency of scores, review this
example. John takes an IQ test on Monday morning and receives a score of 122.
When he takes the test again on Thursday, when he is distracted about finishing
a project before the end of the day, his score is 118. When John takes the test again
the following week, his score is 120. John’s IQ test score varies slightly depending
on his level of attention, fatigue, distraction or time of day. However, his was a reliable
test providing a stable measure of IQ, since the range of variation in his score (118 to
122) was only 4 units. Consistent test scores are critical when tests are used to measure
behavior of more than one person and then are used to rank or select/reject candidates.
Depending
on the type
and range
of student
data
collected,
course
evaluations
can also be
prescriptive
w h i t e p a p e r
Tr a i n i n g m a n a g e m e n t
9
Table 8. SPSS results of independent samples t-tests.

Test reliability
A test consists of
items or questions
classified according
to content into
scales. For example,
an aptitude test may
have a vocabulary
scale based on
vocabulary-related
items. To check if
items in a particular
scale are related,
internal test
consistency is
determined by aver-
aging correlations of
items within a test.
Consider a scale
of 15 test items,
something like
those in Table 9.
Assume those test
items were graded
and the results
entered in SPSS,
as in Table 10.
The SPSS test
reliability procedure
provides both scale
and item statistics.
Table 11 shows the
average score and
variance for the
scale if each of
the items were
excluded from the
scale one at a time.
For example, if item
five were excluded
from the scale, the average score for the scale would be 18.90 and the variance would be
11.09. The column Corrected Item-Total denotes the correlation coefficient between
the score on the individual item and the sum of scores on the remaining items.
The SPSS
reliability
procedure
provides
both scale
and item
statistics
w h i t e p a p e r
Tr a i n i n g m a n a g e m e n t
10
Table 9. An SPSS sample of test items.
Table 10. SPSS Data Editor with test items.
Table 11. SPSS partial output for scale items.

Since this test
measures a common
entity, we hope the
items are positively
correlated. But this
doesn’t seem to hold
true for all items
in this scale. For
example, item Q13 is negatively correlated with the sum of all of the other items.
Table 12 shows the overall measure of reliability amongst all test items is 0.7139
(Output labeled Cronbach’s Alpha, a measure of average inter-item correlation
which can range from 0 to 1 with 1 being perfectly reliable). Yet, in Table 10 the
Alpha jumps to 0.7545 if item Q13 is deleted from the scale. Therefore we will drop
Q13 from the scale.
Summary
Throughout this paper, we demonstrate several procedures training managers can use
to improve programs. Whether managers are ensuring the best qualified students are
admitted to training, assessing course effectiveness or examining test items for
reliability, they are using statistical procedures to reach a fundamental objective:
to monitor and create more effective, cost-efficient training programs.
w h i t e p a p e r
Tr a i n i n g m a n a g e m e n t
11
Table 12. Cronbach’s Alpha for the 15-item scale.
SPSS is a registered trademarks and the other SPSS products named are trademarks
of SPSS Inc. All other names are trademarks of their respective owners.
Printed in the U.S.A © Copyright 1998 SPSS Inc. SWPTMGT-0798M
A b o u t S P S S
To place an order or to get more information, call your nearest SPSS office or visit our
World Wide Web site at www.spss.com
C o n t a c t i n g S P S S
SPSS Inc. is a multinational software company that delivers “Statistical Product and Service
Solutions.” Offering the world’s best-selling desktop software for in-depth statistical analysis
and data mining, SPSS also leads the markets for data collection and tabulation.
Customers use SPSS products in corporate, academic and government settings for all types
of research and data analysis. The company’s primary businesses are: SPSS (for business
analysis, including market research and data mining, academic and government research);
SPSS Science for scientific research; and SPSS Quality for quality improvement.
Based in Chicago, SPSS has offices, distributors and partners worldwide. Products run
on leading computer platforms, and many are translated into Catalan, English, French,
German, Italian, Japanese, Korean, Russian, Spanish and traditional Chinese. In 1997,
the company employed nearly 800 people worldwide and generated net revenues of
approximately $110 million.
SPSS Inc.
+1.312.651.3000
Toll-free: +1.800.543.2185
SPSS Argentina srl.
+541.814.5030
SPSS Asia Pacific Pte. Ltd.
+65.245.9110
SPSS Australasia
+61.2.9954.5660
Pty. Ltd.
Toll-free: +1800.024.836
SPSS Belgium
+32.162.389.82
SPSS Benelux
+31.183.636711
SPSS Central and
+44.(0)1483.719200
Eastern Europe
SPSS Czech Republic
+420.2.24813839
SPSS East Mediterranea
+972.9.9526701
& Africa
SPSS Federal Systems
+1.703.527.6777
SPSS Finland Oy
+358.9.524.801
SPSS France SARL
+33.1.5535.2700
SPSS Germany
+49.89.4890740
SPSS Hellas SA
+30.1.7251925
SPSS Hispanoportuguesa S.L. +34.91.447.37.00
SPSS Hong Kong Ltd.
+852.2.811.9662
SPSS Ireland
+353.1.496.9007
SPSS Israel Ltd.
+972.9.9526700
SPSS Italia srl
+39.51.252573
SPSS Japan Inc.
+81.3.5466.5511
SPSS Kenya Ltd.
+254.2.577.262
SPSS Korea KIC Co., Ltd.
+82.2.3446.7651
SPSS Latin America
+1.312.494.3226
SPSS Malaysia Sdn Bhd
+60.3.704.5877
SPSS Mexico Sa de CV
+52.5.682.87.68
SPSS Middle East
+91.80.545.0582
& South Asia
SPSS Polska
+48.12.6369680
SPSS Russia
+7.095.125.0069
SPSS Scandinavia AB
+46.8.506.105.50
SPSS Schweiz AG
+41.1.266.90.30
SPSS Singapore Pte. Ltd.
+65.533.3190
SPSS South Africa
+27.11.706.7015
SPSS Taiwan
+886.2.25771100
SPSS UK Ltd.
+44.1483.719200
w h i t e p a p e r
T h e f u t u r e o f p r o g r a m e v a l u a t i o n
1 2
Wyszukiwarka
Podobne podstrony:
więcej podobnych podstron