
INSTYTUT INŻYNIERII ŚRODOWISKA
ZAKŁAD HYDROLOGII I GEOLOGII STOSOWANEJ
Laboratorium z mechaniki płynów
ĆWICZENIE NR 10
CHARAKTERYSTYKA KRYZY
2
1.
Cel ćwiczenia
Celem ćwiczenie jest poznanie zasady działania i budowy mierniczej zwężek oraz
wyznaczenie współczynnika przepływu zwężki pomiarowej.
2.
Zakres wymaganych wiadomości
•
równanie Bernoulliego,
•
zwężki pomiarowe i ich rodzaje,
•
przepływ płynu przez kryzę,
•
wielkości charakterystyczne zwężek pomiarowych.
3.
Podstawy teoretyczne
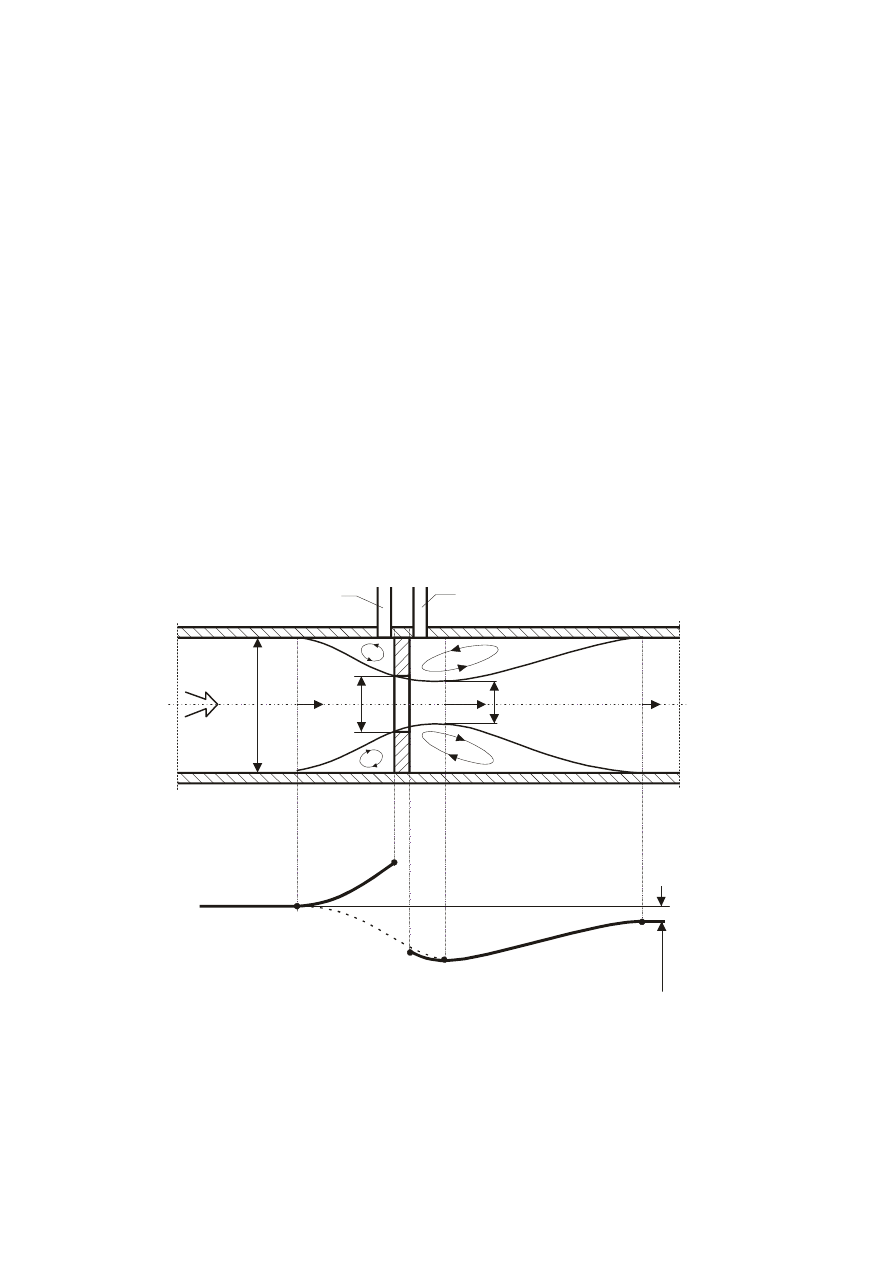
Zmianę ciśnienia podczas przepływu płynu przez kryzę przedstawia poniższy rysunek.
Rys.1. Schemat kryzy i rozkład ciśnienia przy przepływie przez kryzę
D
d
d
r
A
płyn
U
A
U
B
B
C
C
B
A
p
A
p
A
-p
C
p
B
p
C
p
1
p
1
p
2
p
2
U
C

3
Od przekroju A-A przed kryzą zauważa się już wpływ kryzy na przepływ. Struga
przepływającego płynu zwęża się, prędkość jej wzrasta. Minimum przewężenia ma struga w
przekroju B-B za kryzą wskutek bezwładności płynu. Następnie struga rozszerza się i w
dostatecznej odległości od kryzy w przekroju C-C wypełnia cały przekrój rurociągu, a
prędkość strugi jest równa prędkości płynu przed kryzą. W wyniku nieodwracalności procesu
(dyssypacji energii) strata ciśnienia strugi związana z przepływem przez kryzę jest trwała i
wynosi
C
A
p
p
−
.
Równanie Bernoulliego i prawo ciągłości strugi dla rozważanego odcinka przewodu z
kryzą wygląda następująco:
2
2
2
2
2
2
B
B
B
B
A
a
A
U
U
P
U
P
⋅
+
⋅
+
=
⋅
+
ρ
ξ
ρ
α
ρ
α
, (1)
B
B
A
A
S
U
S
U
⋅
=
⋅
,
gdzie:
B
A
α
α
,
- współczynniki Coriolisa w przekroju A-A i B-B,
ξ
- współczynnik strat na odcinku A-B odniesiony do prędkości U
B
,
B
A
S
S ,
- pola przekrojów strugi.
Stosunek pola przekrojów:
B
S
(najmniejsze pola powierzchni przekroju strugi) i
o
S (pole
otworu kryzy) nazywamy współczynnikiem kontrakcji (zwężenia):
o
B
S
S
K
=
(2)
78
,
0
60
,
0
÷
=
K
dla kryz,
0
,
1
≈
K
dla dysz.
Stosunek pola otworu kryzy do pola przewodu, zgodnie z normą PN–M-53950, nazywamy
modułem zwężki:
2
=
=
D
d
S
S
m
A
o
. (3)
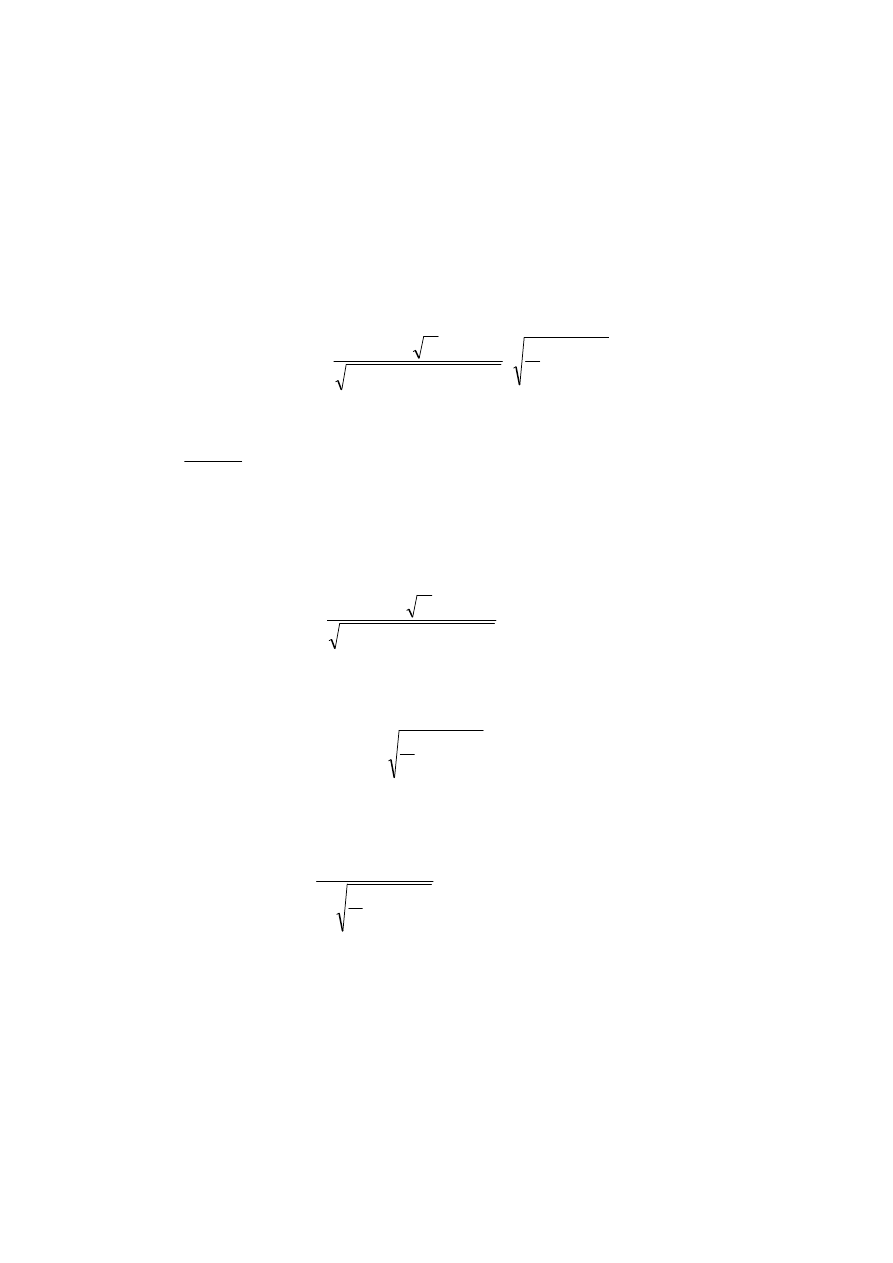
4
Podstawiając równania (2) i (3) do równania ciągłości (1) otrzymamy
B
A
U
m
K
U
⋅
⋅
=
. (4)
Przekształcając równanie Bernoulliego (1) oraz uwzględniając nie pokrywanie się punktów
odbioru ciśnienia
(
)
2
1
, p
p
z punktami
(
)
B
A
P
P ,
otrzymamy wzór na prędkość
(
)
2
1
2
2
2
p
p
m
K
K
U
A
B
B
−
⋅
⋅
⋅
−
+
=
ρ
α
ξ
α
ψ
(5)
gdzie
2
1
p
p
P
P
B
A
−
−
=
ψ
oznacza bezwymiarowy parametr.
W wzorze (5) współczynnik występujący przed pierwiastkiem z różnicy ciśnień nazywamy
współczynnikiem przepływu kryzy
2
2
m
K
K
A
B
⋅
⋅
−
+
=
α
ξ
α
ψ
α
. (6)
Strumień objętości cieczy określa więc wzór
(
)
2
1
2
p
p
S
V
o
−
⋅
⋅
=
ρ
α
&
(7)
Przekształcając powyższy wzór otrzymamy wzór na liczbę przepływu
(
)
2
1
0
2
p
p
S
V
−
=
ρ
α
&
, (8)
który może służyć do eksperymentalnego jej wyznaczenia.
Reasumując powyższe rozważania widzimy, że na współczynnik przepływu kryzy
α
mają wpływ:
- nierównomierność rozkładu prędkości w przewodzie i kryzie
(
)
B
A
α
α
,
,
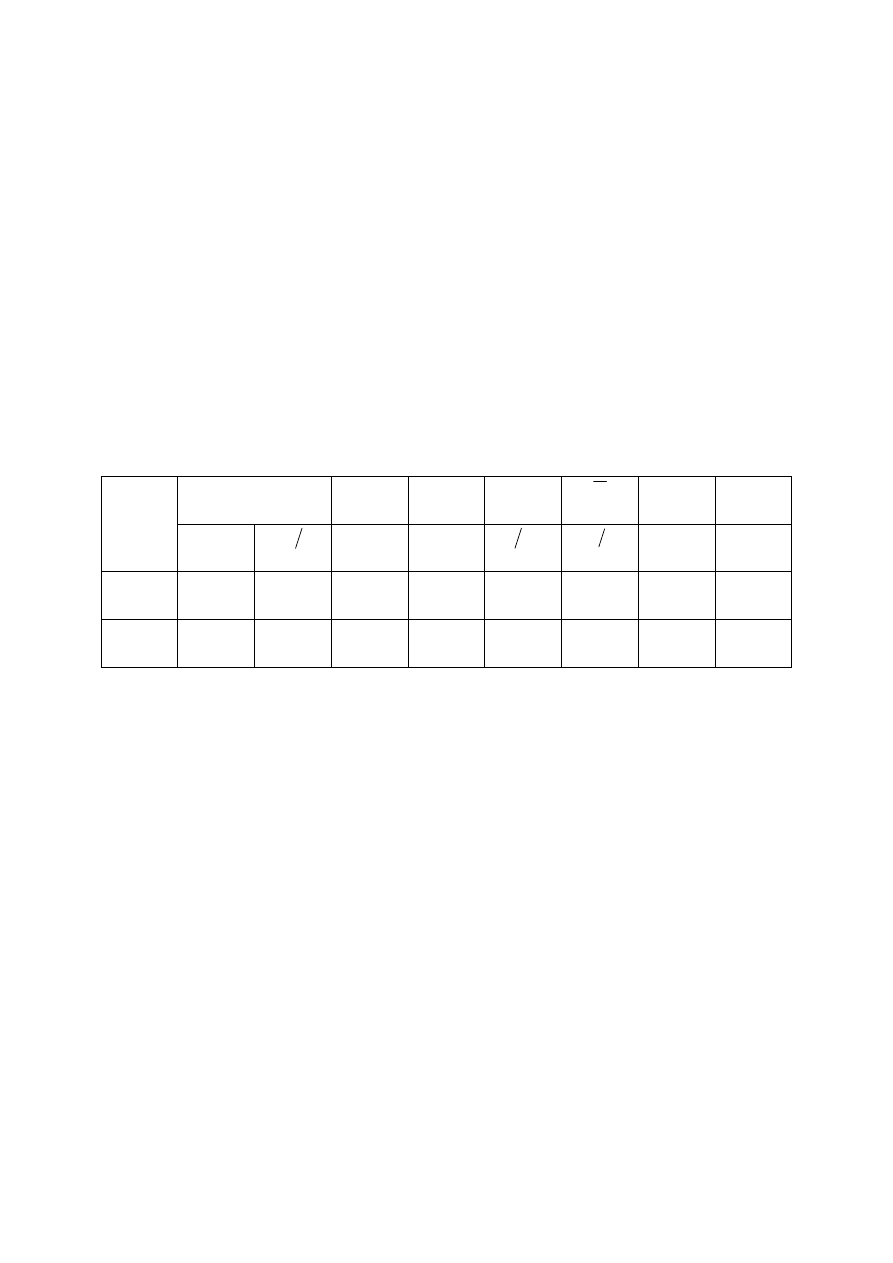
5
- stopień zwężenia strugi
(
)
K
m,
,
- strata ciśnienia
( )
ξ
,
- usytuowanie odbioru ciśnienia
( )
ψ
,
pierwsze trzy wymienione wielkości zależą od liczby Reynoldsa.
4.
Wykonanie ćwiczenia
•
naszkicować stanowisko pomiarowe,
•
naszkicować kryzę w przewodzie i spodziewany rozkład ciśnienia,
•
przeprowadzić pomiary wielkości fizycznych i wyniki umieścić w poniższej tabeli
pomiarowej:
V&
1
h
2
h
2
1
p
p
−
U
Re
α
Lp.
h
l /
s
m
3
mm
mm
2
m
N
s
m
-
-
•
wykonać wykres zależności
( )
Re
f
=
α
oraz porównać tę zależność z krzywą
(
)
m
f Re,
=
α
dla zwężek odpowiedniego typu (PN-M-53950).
5. Wnioski i dyskusja błędów
Literatura
1.
Szewczyk H. –
Mechanika płynów – ćwiczenia laboratoryjne
2.
Wereszko D. –
Pomiary podstawowych znamion termodynamicznych
3.
Bukowski J. –
Mechanika płynów
4.
PN-M-53950
Wyszukiwarka
Podobne podstrony:
więcej podobnych podstron