elements of statistical learning sol2

Elements of Statistical Learning

Solutions to the Exercises

Yu Zhang, sjtuzy@gmail.com

November 25, 2009

Exercise 2.6 Consider a regression problem with inputs x

and outputs y

and a parameterized model f

(x) to be ﬁt by least squares. Show that if

there are observations with tied or identical values of x, then the ﬁt can be
obtained from a reduced weighted least squares problem.

Proof For known heteroskedasticity (e.g., grouped data with known group
sizes), use weighted least squares (WLS) to obtain eﬃcient unbiased esti-
mates. Fig.1 explains “Observations with tied or identical values of x”. In

•

WLS.01

Figure 1: Observations with tied

the textbook, section 2.7.1 also explain this problem.

If there are multiple observation pairs x

, y

, l = 1, 2 . . . , N

at each value

of x

, the risk is limited as follows:

argmin

∑

l=1

)

− y

)

argmin

∑

)

− 2

∑

)

argmin

∑

{(f

)

− y

)

+ Constant

}

argmin

∑

{(f

)

− y

)

}

(1)

which is a weighted least squares problem.

Exercise 3.19 Show that

|| ˆβ

ridge

|| increases as its tuning parameter λ → 0.

Does the same property hold for the lasso and partial least squares esti-
mates? For the latter, consider the “tuning parameter” to be the successive
steps in the algorithm.

Proof Let λ

< λ

and β

, β

be the optimal solution. We denote the loss

function as follows

(β) =

||Y − Xβ|| + λ||β||

2
2

Then we have

(β

) + f

(β

)

≥ f

(β

) + f

(β

)

||β

2
2

+ λ

||β

2
2

≥ λ

||β

2
2

+ λ

||β

(λ

− λ

)

||β

2
2

≥ (λ

− λ

)

||β

2
2

||β

2
2

≥ ||β

2
2

|| ˆβ

ridge

|| increases as its tuning parameter λ → 0.

Similarly, in lasso case,

|| ˆβ||

increase as λ

→ 0. But this can’t guarantee

the l

-norm increase. Fig.2 is a direct view of this property.

In partial least square case, it can be shown that the PLS algorithm

is equivalent to the conjugate gradient method. This is a procedure that
iteratively computes approximate solutions of

|βA = b| by minimizing the

quadratic function

⊤

Aβ

− b

⊤

along directions that are

|A|-orthogonal (Ex.3.18). The approximate solu-

tion obtained after m steps is equal to the PLS estimator obtained after p
iterations. The canonical algorithm can be written as follows:

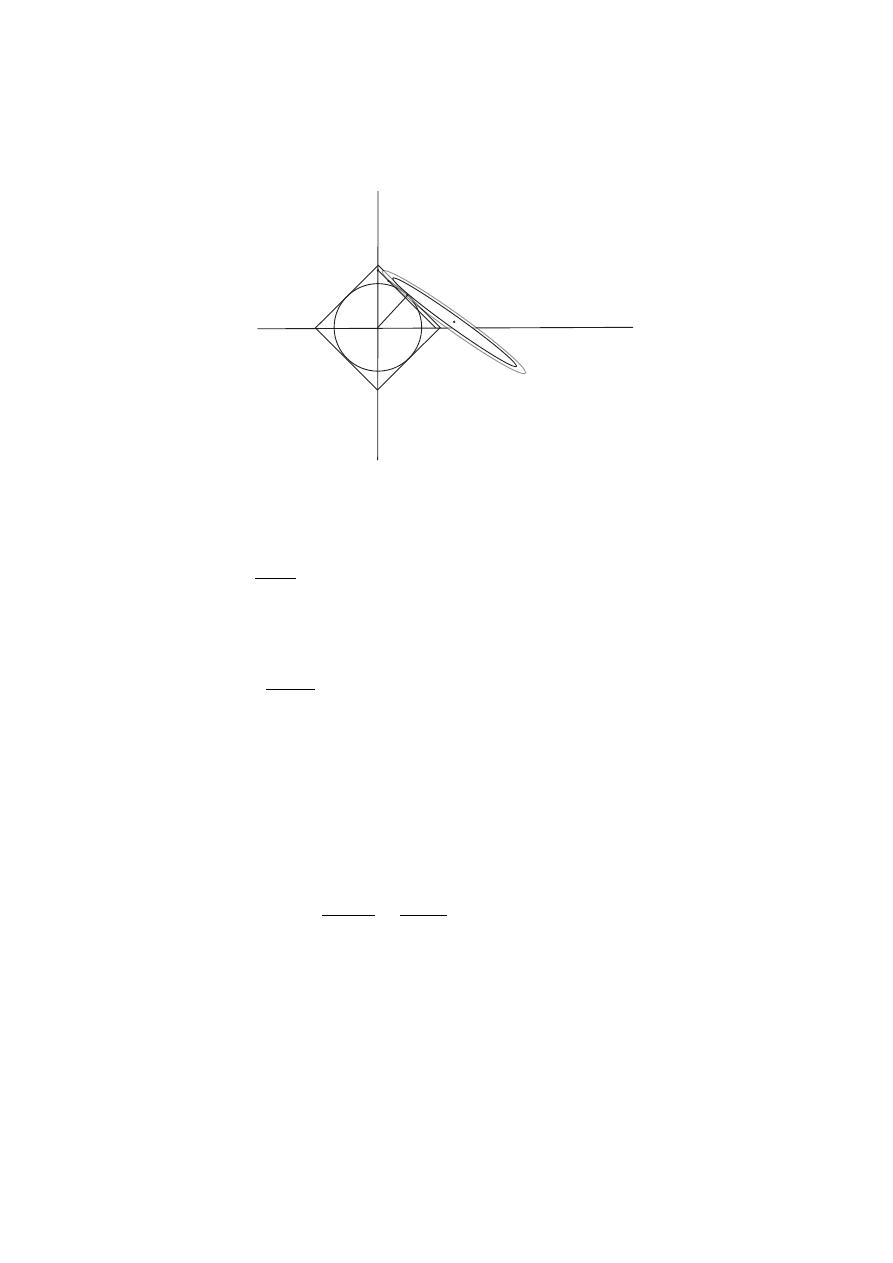
Figure 2: Lasso

1. Initialization β

= 0, d

= r

= b

− Aβ

= b

2. a

H
i

3. β

i+1

= β

+ a

4. r

i+1

= b

− Aβ

i+1

(= r

− a

)

5. b

−

i+1

H
i

6. d

i+1

= r

i+1

+ b

The squared norm of β

j+1

can be written as

||β

j+1

||x

+ 2a

2
j

||d

+ a

H
j

(2)

We need only shown that a

> 0.

∵ r

j+1

= r

j+1

+ b

j+1

and

⟨r

j+1

, d

⟩ = 0

(3)

∴ a

||r

||d

2
A

> 0(A is positive deﬁnite.)

(4)

∵ β

∑

i=0

(5)

∴ d

H
j

∑

i=0

H
j

(6)

Now we need to show that d

> 0, i

̸= j. By Step 6, we have d

∑

−1

i=0

(

∏

−1

k=i

∵ ⟨r

, r

⟩ = 0, i ̸= j

(7)

∴ b

> 0

→ d

H
j

> 0

(8)

∵ Ad

= a

−1

− r

i+1

)

(9)

∴ b

−

j+1

− r

j+1

)

||d

2
A

||r

j+1

||d

2
A

> 0

(10)

So in PLS case, the

||β||

increase with m.

Exercise 4.1 Show how to solve the generalized eigenvalue problem max a

⊤

subject to a

⊤

W a = 1 by transforming to a standard eigenvalue problem.

Proof Hence W is the the common covariance matrix, we have W is semi-
positive deﬁnite. WLOG W is positive deﬁnite, we have

W = P

(11)

Let b = P a, then the problem is

⊤

Ba = b

⊤

−1

b = b

⊤

∗

(12)

subject to a

⊤

W a = 1 = b

⊤

∗

b = 1. Now the problem transform to a

standard eigenvalue problem.

Exercise 4.2 Suppose we have features x

∈ R

, a two-class response, with

class sizes N

, N

, and the target coded as

−N/N

, N/N

(d) Show that this result holds for any (distinct) coding of the two classes.

W.L.O.G any distinct coding y

′

, y

′

. Let ˆ

β = (β, β

)

⊤

. Compute the

partial deviation of the RSS( ˆ

β) we have

∂RSS( ˆ

β)

∂β

−2

∑

i=1

− β

⊤

= 0

(13)

∂RSS( ˆ

β)

∂β

−2

∑

i=1

− β

⊤

) = 0

(14)

It yields that

⊤

∑

− ¯

⊤

∑

(15)

∑

− β

⊤

)

(16)

Than we get

⊤

∑

− ¯

⊤

∑

−

∑

⊤

(17)

′

+ N

′

−

′

+ N

′

+ N

)

(18)

′

(ˆ

− ˆµ

)

− N

′

(ˆ

− ˆµ

))

(19)

′

− y

′

)(ˆ

− ˆµ

)

(20)

Hence the proof in (c) still holds.

Exercise 4.3 Suppose we transform the original predictors X to ˆ

Y via

linear regression. In detail, let ˆ

Y = X(X

⊤

−1

⊤

Y = X ˆ

B, where Y is

the indicator response matrix. Similarly for any input x

∈ R

, we get a

transformed vector ˆ

y = ˆ

⊤

∈ R

. Show that LDA using ˆ

Y is identical to

LDA in the original space.

Proof Prof.Zhang had given the solution about this problem, but only tow
student notice this problem is tricky.

Here I give the main part of the

solution.

• First y

, . . . , y

must independent, then we have r(Σ

) = K.

• Assume that ˆ

∗K

, r( ˆ

B) = K < p, r(Σ

) = p. Note that

r( ˆ

B( ˆ

⊤

−1

⊤

) < r( ˆ

B) < r(Σ

)

. Since ˆ

B( ˆ

⊤

−1

⊤

̸= Σ

−1

when dim(Y ) < dim(X).

• This problem are equal to prove that ˆ

B( ˆ

⊤

−1

⊤

(µ

x
k

− µ

x
l

) =

−1

(µ

x
k

− µ

x
l

). Let P = Σ

B( ˆ

⊤

−1

⊤

, we have

= P

(21)

Hence P is projection matrix. Note that Y =

, y

. . . , y

} is indi-

cator response matrix, we have

x
k

⊤

∑

k=1

∑

− µ

k
i

)(x

− µ

k
i

)

⊤

/(N

− K)

− K

(

∑

k=1

∑

⊤

−

∑

k=1

x
k

(µ

x
k

)

⊤

)

− K

⊤

−

∑

k=1

⊤

)

− K

⊤

− X

⊤

Y Y

⊤

Note that

P (N

x
1

, N

x
2

. . . , N

x
K

) = P X

⊤

(22)

So we need only to shown that P X

⊤

Y = X

⊤

Y .

P X

⊤

Y = Σ

B(B

⊤

B)B

⊤

By the deﬁnition of B, we have

⊤

X(X

⊤

−1

⊤

− K

((X

⊤

X)(X

⊤

−1

⊤

− X

⊤

Y Y

⊤

X(X

⊤

−1

⊤

Y )

− K

⊤

Y (I

− Y

⊤

X(X

⊤

−1

⊤

Y )

⊤

−1

− K)(Y

⊤

X(X

⊤

−1

⊤

− X

⊤

Y Y

⊤

X)(X

⊤

−1

⊤

Y )

−1

− K)(Y

⊤

X(X

⊤

−1

⊤

Y [I

− Y

⊤

X(X

⊤

−1

⊤

Y ])

−1

Let Q = Y

⊤

X(X

⊤

−1

⊤

Y we have

⊤

(23)

− K

⊤

Y (I

− Q)

(24)

⊤

−1

− K)(Q(I − Q))

−1

(25)

Hence Q(I

− Q) is invertible matrix, we have

K = r(Q(Q

− I)) ≤ r(Q) ⇒ r(Q) = K

(26)

So Q is invertible matrix, then it yields

⊤

−1

− K)(I − Q)

−1

(27)

Combine with (16),(17),(20), we have

P X

⊤

− K

⊤

Y (I

− Q)(N − K)(I − Q)

−1

Q (28)

⊤

(29)

Since we have ˆ

B( ˆ

⊤

−1

⊤

(µ

x
k

− µ

x
l

) = Σ

−1

(µ

x
k

− µ

x
l

Wyszukiwarka

Podobne podstrony:

więcej podobnych podstron