Krzysztof ZAREMBA

1

, Andrzej PAWLAK

2

Bialystok Technical University (1), Central Institute for Labour Protection - National Research Institute (2)

Lens for luminaires with high power LED diodes

Abstract. High power LED diodes are characterized by the Lambertian luminous intensity curve, which is undesirable as far as uniform lightning for
the target surface and the glare limitation are concerned. In order to obtain the luminous intensity curve assuring uniform lightning on the target
surface, it is necessary to utilize lenses, which will dissipate the axial fraction of the luminous flux emitted by the diode. The presented luminous flux
method for designing the general shape of such a lens provides means for obtaining the target luminous intensity curve for the given luminaire.

Streszczenie. Diody LED o dużej mocy posiadają lambertowski rozsył strumienia świetlnego, który jest niekorzystny zarówno pod względem
możliwości równomiernego oświetlenia powierzchni roboczej jak i ograniczenia olśnienia. W celu osiągnięcia równomiernego oświetlenia w
ograniczonym kącie należy zastosować soczewkę, która rozproszy przyosiową część strumienia świetlnego diody LED. Zaprezentowano metodę
strumieniową projektowania kształtu soczewki zapewniającej uzyskanie założonej krzywej światłości oprawy. (Soczewki dla opraw z diodami LED
o dużej mocy)

Keywords: high power LED, luminaire, uniform illumination, lens
Słowa kluczowe: diody LED o dużej mocy, oprawa oświetleniowa, równomierne oświetlenie, soczewka

1. Introduction
Recently, we have been observing a very dynamic
evolution of LED diodes. They are used currently not only in
simple signaling devices but also find their application in
increasing number of luminaires. High power LED diodes
(1÷5 W), characterized by high luminous flux up to 150 lm
should be applied for lightning purposes. Such LED diodes
are currently available on the market [5]. However, such
high power diodes have numerous parameters which are
significantly different when compared with their low power
equivalents. All higher power diodes (3 and 5 W) have
luminous intensity curves resembling closely Lambertian
(cosine) distribution. It must be noted that such luminous
intensity distribution is highly unsuitable when it comes to its
capability to produce uniform lightning for the target work
area as well as limiting the glare effect for users. It must be
taken into consideration that high power LED diodes are
typically point light sources with luminance values ranging
from 1 Mcd/m

2

to 10 Mcd/m

2

, which is comparable with the

light bulb filament. Due to their aforementioned property,
such diodes might be used for general lightning purposes
and especially for illuminating areas with computer monitors
only when equipped with properly designed luminaires.

This work presents a synthetic method for determining

the shape of rotationally symmetrical lenses, capable of
delivering the target luminous intensity distribution for the
given luminaire. All calculations of optical and lightning
components were based on luminous flux method. The
proposed synthetic method for determining the reflector
shape is most generally saying based on comparing the
luminous flux emitted by particular elements of the said
reflector with the target flux reaching the work area. It is also
assumed that the rotationally symmetrical lens will comprise
conical elements (rectilinear in cross-section). Application of
conical elements does not contradict practical
implementation of the said reflector using a smooth profile,
since approximation precision depends only on the size of
elemental areas to be examined.

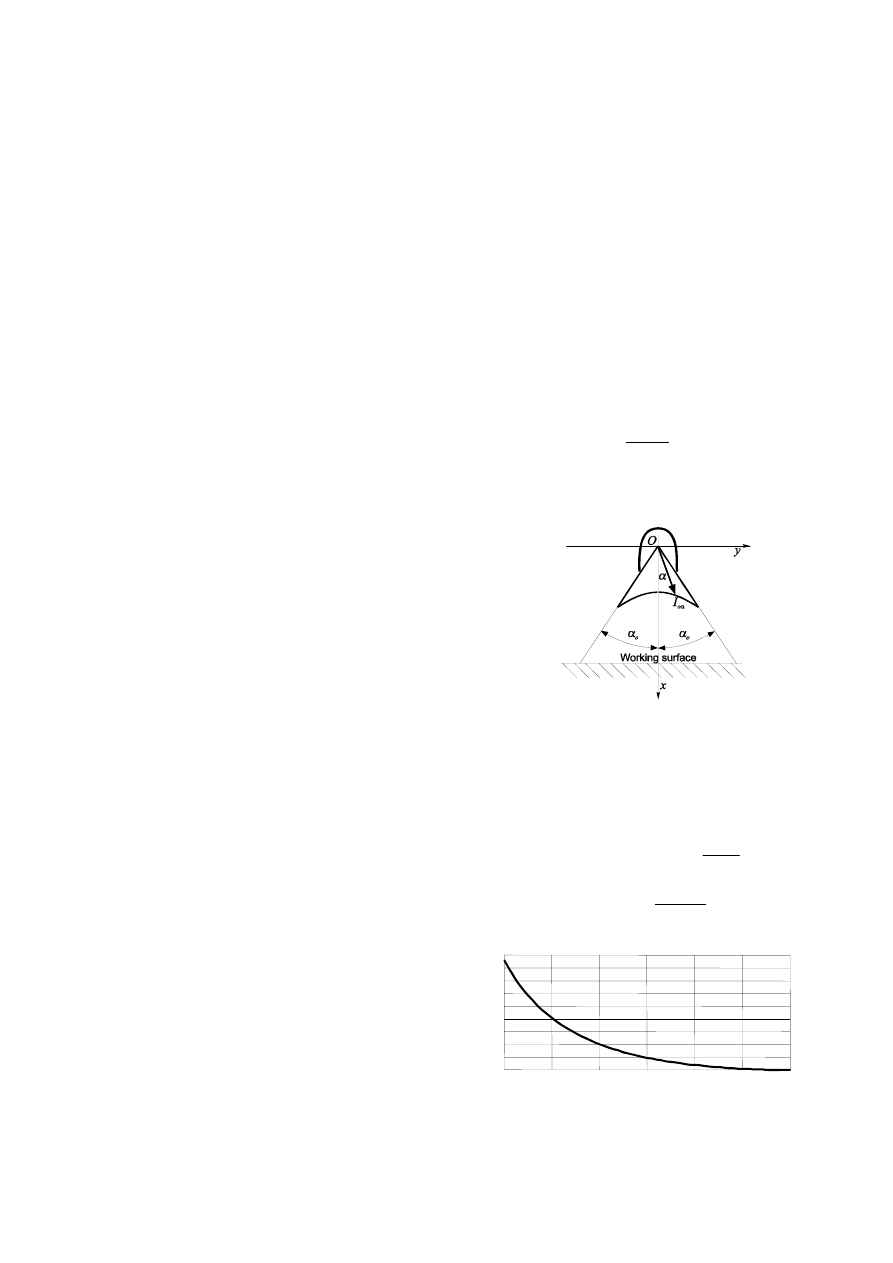
2. Luminous intensity curve for the given luminaire

The proposed method allows for determining the lens’

shape, which in the case of a light source with negligible
dimensions will realize the pre-defined luminous intensity
curve I

o

α

for the given luminaire. This work presents an

example of the estimation process through analysis of
luminous intensity curve assuring uniform lightning for a
target surface, perpendicular to the x axis of the system
(see Fig. 1). In order to obtain constant illuminance on the
target surface, it is necessary to utilize a luminaire with the

following luminous intensity curve I

o

α

:

(1)

α

α

3

0

cos

o

o

I

I

=

,

where: I

o0

– axial luminous intensity for the given luminaire

(

α

= 0

°).

Fig. 1. Geometry of the designed luminaire

The value of the axial luminous intensity I

o0

may be

estimated under the assumption that the total luminous flux

Φ

o

and luminous flux irradiation angle

α

o

for the given

luminaire are known:

(2)

o

o

o

o

o

o

o

o

I

I

d

I

d

I

o

o

α

π

Φ

α

π

α

α

α

π

α

α

π

Φ

α

α

α

2

0

2

0

0

3

0

0

tg

tg

cos

sin

2

sin

2

=

⇒

=

=

=

=

∫

∫

.

30º

40º

50º

60º

70º

80º

90º

0

100

200

300

400

500

600

700

800

900

α

o

Ι

o0

[cd/klm]

Fig. 2. Axial luminous intensity I

o0

depending on the irradiation

angle

α

o

of the luminous flux (

Φ

z

= 1000 lm)

Fig. 2 depicts a relation between the axial luminous

PRZEGLĄD ELEKTROTECHNICZNY, ISSN 0033-2097, R. 83 NR 5/2007

21

intensity I

o0

and luminous flux irradiation angle

α

o

assuming

initially, that the luminaire efficiency is estimated at 90%.
Along with the increase in the irradiation angle

α

o

value, the

axial luminous intensity I

o0

value decreases rapidly.

Axial luminous intensity I

z0

for a LED diode with the

Lambertian distribution curve I

z

α

:

(3)

α

π

α

α

cos

cos

0

z

z

z

I

I

Φ

=

=

,

where:

Φ

z

− light source luminous flux, I

z0

− axial luminous

intensity of the light source, was estimated at 318.3 cd/klm.
It is worth noting here that the luminous intensity I

z0

of the

diode is greater than the luminous intensity I

o0

of the

luminaire for irradiation angles

α

o

greater than

approximately 45°. In practical applications, luminaires with
maximum irradiation angle

α

o

estimated at approximately

55°÷65° are used for general lightning purposes. Such
luminaires may typically be realized only using lens
elements, where the axial part of the luminous flux of the
LED diode is dissipated.

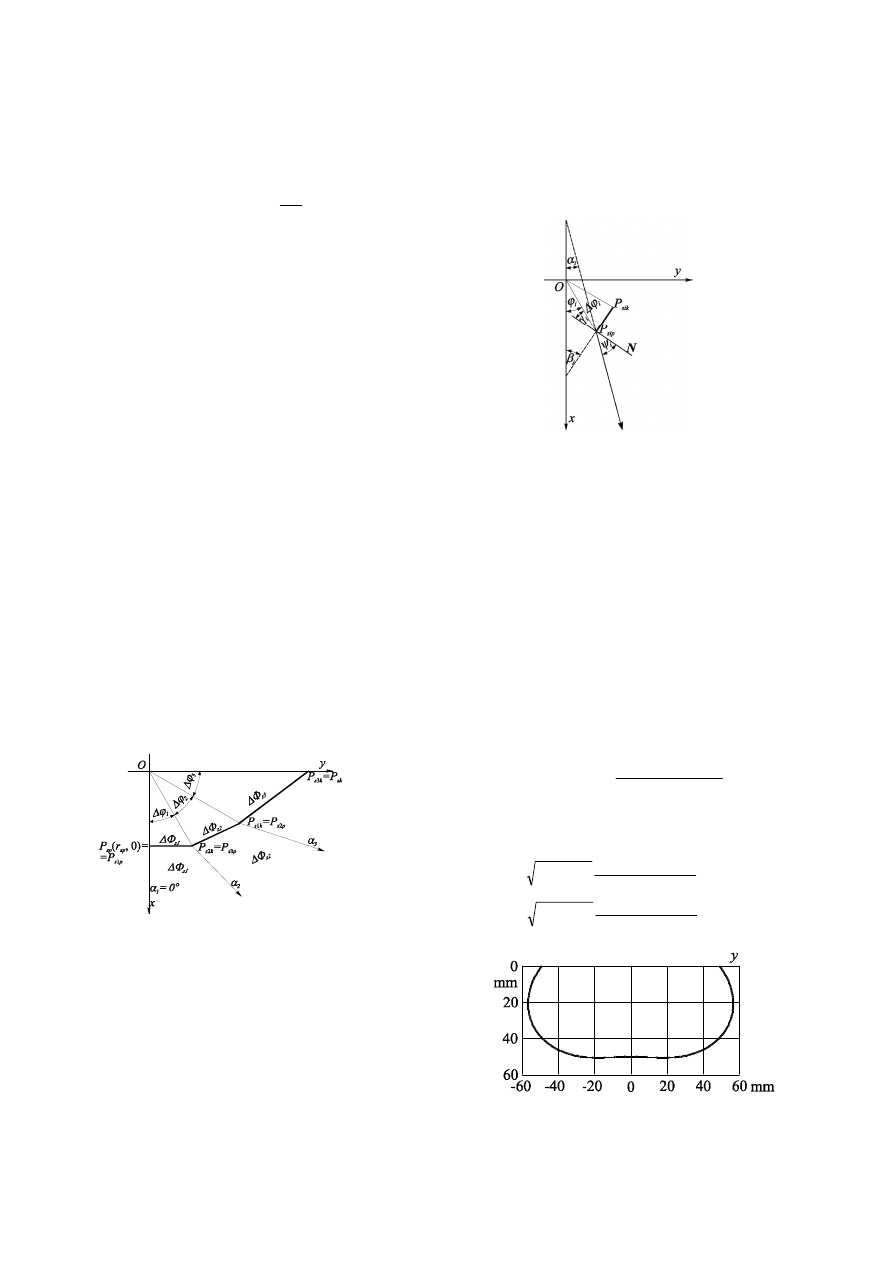
3. Algorithm for evaluating lens’ profile

The proposed method is based on an algorithm

comprising comparison between the luminous flux

ΔΦ

s

,

which ought to be emitted in the pre-defined direction by the
given luminaire (lens) with the pre-assumed luminous
intensity curve I

o

α

, and luminous flux

ΔΦ

z

emitted by the light

source towards the lens (see Fig. 3). The said lens should
be shaped in such a manner that the compared luminous
fluxes are equal, having compensated for light loss in the
lens. Additionally, it was assumed that the distance between
the diode and the external lens’ surface is a uniform optical
medium. This particular assumption results in the need to
design only the external lens’ surface shape. In practice
however, such optical systems are realized by filling in the
cavity between the external lens and diode’s surfaces using
immersion liquid with the light refractive index n

s

equal to the

lens’ material refractive index [2]. Optical elements of the
diode and lenses are typically manufactured using methyl
polymethacrylate at optical purity and material light
refractive index n

s

= 1,497.

Fig. 3. A diagram for determining lens’ profile using luminous flux
method

Estimation of the lens’ profile begins at the start point

P

sp

(r

sp

, 0), which is located on the main axis. The only

parameter, the value of which needs to be assumed for
calculation, is the initial radius-vector r

sp

. This particular

parameter defines the resulting dimensions of the given
lens. A light ray reaching the point P

sp

traverses without

direction changes (Fig. 3 –

α

1

= 0°), meaning that the first

lens’ element is perpendicular to the x axis of the rotational
symmetry of the given optical system. Light rays reaching
subsequent i

th

lens’ elements are directed towards the

α

1

angle, the value of which is determined by comparing the
luminous flux emitted by the lens of transmission coefficient

τ

and the luminous flux emitted by the luminaire with the

defined luminous intensity curve I

o

α

:

(4)

.

∫

∫

=

i

i

d

I

d

I

o

z

α

α

ϕ

ϕ

α

α

π

ϕ

ϕ

τ

π

0

0

sin

2

sin

2

In a general case, equation (4) is solved using numerical
methods.

Fig. 4. Diagram for determining parameters of the i

th

lens’ element –

refracted light rays do not cross the x axis of the optical system

Having established the value of the

Δα

i

angle, in order to

determine the location of the P

sik

point for the ending i

th

lens’

element, it is necessary to determine the value for the

β

i

angle, describing its inclination relative to the x optical
system axis (Fig. 4). Providing that the lens’ shape is under
evaluation, contrary to reflectors’ case, it is much better to
assume that the light rays will not cross the x axis of the
optical system. The values of incidence angle

γ

i

for and

refraction angle

ψ

i

for examined light rays are much smaller,

assuming that the values of

ϕ

i

and

α

i

angles are constant.

β

i

angle, describing the incidence of the lens' surface element
relative to the x optical system axis is determined based on
the following mathematical relation, derived from the
refraction theorem, holding for incidence

γ

i

and refraction

ψ

i

angles, describing a light ray reaching the i

th

lens’ element

(see Fig. 4).

(5)

i

i

s

i

i

s

i

n

n

α

ϕ

α

ϕ

β

sin

sin

cos

cos

arctan

−

−

=

.

Next, the coordinates (x

sik

, y

sik

) for the ending point P

sik

of the

i

th

lens’ element with the angular size

Δϕ

I

, are established:

(6)

(

)

(

) (

)

(

)

(

) (

)

i

i

i

i

i

i

i

sip

sip

sik

i

i

i

i

i

i

i

sip

sip

sik

y

x

y

y

x

x

ϕ

ϕ

ϕ

ϕ

β

ϕ

β

ϕ

ϕ

ϕ

ϕ

β

ϕ

β

Δ

+

Δ

+

+

+

+

=

Δ

+

Δ

+

+

+

+

=

sin

sin

sin

cos

sin

sin

2

2

2

2

.

x

Fig.

5. Calculated lens’ profile with the irradiation angle

α

o

estimated at 60°

Approximation of the lens’ surface with conical elements

PRZEGLĄD ELEKTROTECHNICZNY, ISSN 0033-2097, R. 83 NR 5/2007

22

with a constant angular size

Δϕ

i

is a most commonly applied

methods during the design process [1, 3, 4].
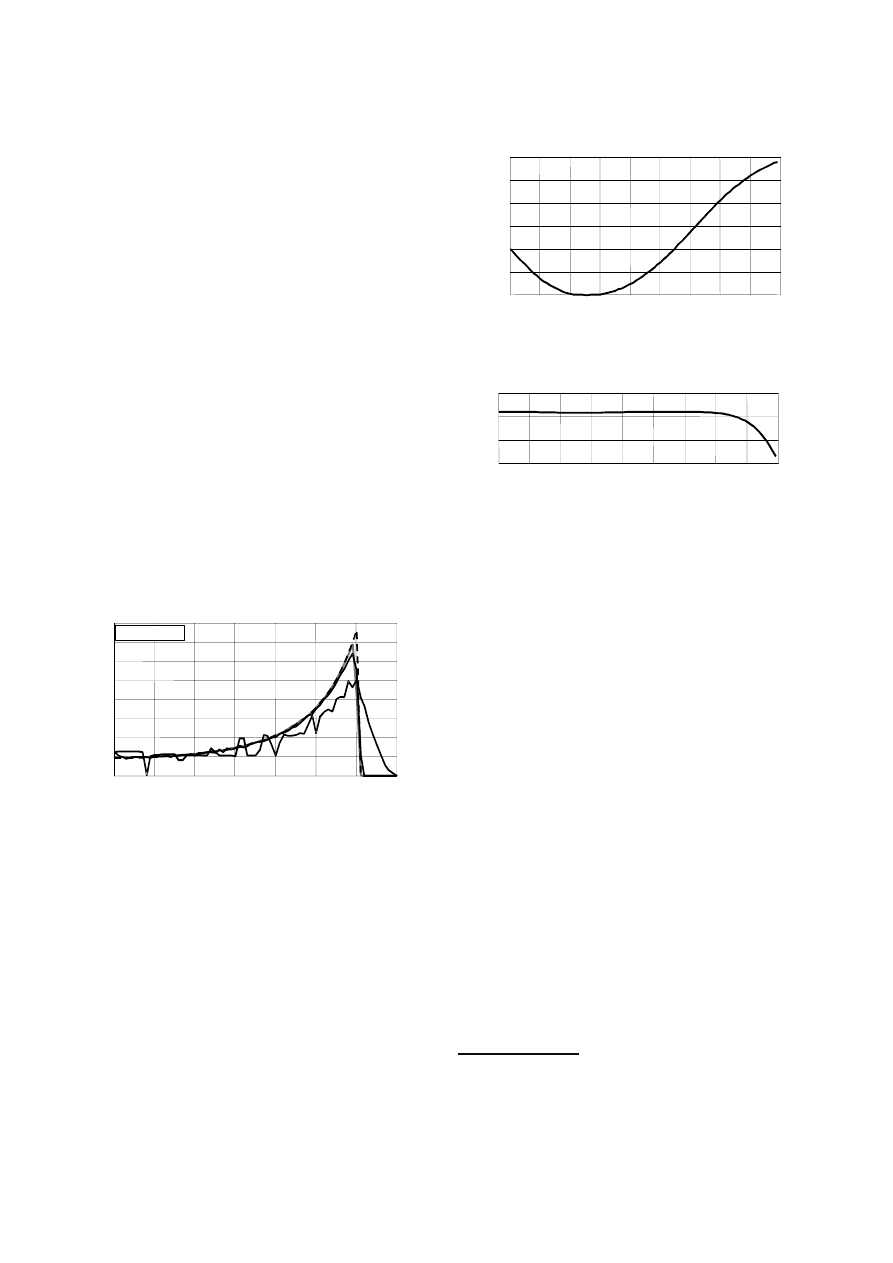
An exemplary shape of the lens calculated in
accordance with the above-presented algorithm, under the
assumption of the maximum irradiation angle value for the
luminous flux defined at

α

o

= 60° and the initial radius-vector

r

sp

= 50 mm, is presented in Fig. 5.

Precision of the proposed estimation method, under the

assumption of negligible dimensions of the light source,
depends only on the angular size

Δϕ

of the lens’ elements.

Other, currently typically applied design methods imply
angular sizes

Δϕ

most commonly defined at 5.0° [1, 3].

However, the said methods approximate the surface with
curvilinear profiles and in case of rectilinear elements, the
referred dimensions must be significantly smaller [5]. Due to
that fact, the following examination was conducted for the

Δϕ

division angle values of 5.0°; 0.5° and 0.05° (see Fig. 6).

Application of significantly smaller

Δϕ

division angle values

provides visibly better approximation of the estimated
luminous intensity curves with the pre-assumed curves. In
practice, it was observed that application of

Δϕ

division

angle value at approximately 0.5° allows for very good
approximation of the target luminous intensity curve (see
Fig. 6b). Only for very small

α

(0°÷2°) angles, the values of

the estimated luminous intensity exceeds the pre-defined
values. This particular effect stems from the applied
calculation algorithm of the luminous flux method. For small

α

angle values, the denominator contains very small values

for solid angles, resulting in significant numerical errors
occurring for these directions [5]. This fact is further
confirmed by significant decrease in the calculation errors
when the

Δϕ

angle is decreased 10 times (see Fig. 6c –

gray line).

Fig. 6. Calculated luminous intensity curves for an examined lens
for various

Δϕ

division angle values: a)

Δϕ

= 5,0°; b)

Δϕ

= 0,5°; c)

Δϕ

= 0,05° (gray line); (broken line – assumed I

o

α

4. Lens’ transmission coefficient

When designing the lens, it was initially assumed that its

transmission coefficient

τ

is uniform for all light rays.

However, the said coefficient

τ

is influenced by two effects:

luminous flux absorption and Fresnel reflection on the
border of two different optical media. Providing that the lens
is manufactured from high purity optical material, the
absorption effect might be neglected in practice, mainly due
to insignificant pathway of the light rays in the optical
medium.

Fig. 7 presents the relation between the incidence angle

γ

of light rays for the exemplary designed lens (see Fig. 5).

The incidence angles are both positive and negative,
meaning that they reach the lens’ surface from different
directions. The absolute incidence angle

γ

values do not

exceed 30° for most values of

ϕ

angle, meaning that the

transmission coefficient

τ

value (including Fresnel reflection

effect), is close to 96% (see Fig. 8). Only a very small
fraction of the luminous flux reaching the lens’ surface with
the

ϕ

angle value grater than 86% is transmitted with the

transmission coefficient

τ

value lower than 90%.

-20º

-10º

0º

10º

20º

30º

40º

0º

10º

20º

30º

40º

50º

60º

70º

80º

90º

γ

ϕ

Fig. 7. Relation between the incidence angle

γ

for the surface of the

designed lens and the

ϕ

transmission angle for light rays leaving

the light source

0,85

0,90

0,95

1,00

0º

10º

20º

30º

40º

50º

60º

70º

80º

90º

τ

ϕ

Fig. 8. Relation between the transmission coefficient

τ

for light rays

traversing the designed lens and the

ϕ

transmission angle for light

rays leaving the light source

Conclusions
High power LED diodes are characterized by the
Lambertian luminous intensity curve, which is undesirable
as far as uniform lightning for the target surface and the
glare limitation are concerned. In order to obtain the
luminous intensity curve assuring uniform lightning on the
target surface, it is necessary to utilize lenses, which will
dissipate the axial fraction of the luminous flux emitted by
the diode. The presented luminous flux method for
designing the general shape of such a lens provides means
for obtaining the target luminous intensity curve for the
given luminaire. Lens’ shape approximation using conical
elements is possible, providing that the angular size of
individual elements is sufficiently small.

0°

10°

20°

30°

40°

50°

60°

70°

0

100

200

300

400

500

600

700

800

α

I

o

α

[cd/klm]

a

a

b

b

c

c

REFERENCES

[1] D y b c z y ń s k i W.: Floodlight for illuminating a semicircular

vault, Appl. Optics , Vol. 36, No. 25, 9, 1997, 6480-6484

[2] P a r k y n W.A.: Design of illumination lenses via extrinsic

differential geometry, Illumination and Source Engineering,
Angelo V. Arecchi, Editor, Proceedings of SPIE, Vol. 3428, pp.
154-162 (1998)

[3] S c h m i d t H.J.: Luminaire design, CIE Seminar on Computer

Programs for Light and Lighting, Vienna, Austria, 5-9 October,
1992, p. 13-17

[4] Z a r e m b a K.: A Synthetic Method of Designing Rotational

Reflectors, 13

th

European Simulation Multiconference 1999,

Modelling and Simulation: A Tool for the Next Millenium,
ESM’99, Warsaw, June 1-4 1999, Poland, Vol. II, p.307-309

[5] www.lumileds.com

Acknowledgments: Financing source: The State Committee for
Scientific Research, grant number W/WE/11/06.

Autors: Krzysztof Zaremba, Ph.D. (E.Eng), Białystok Technical
University, Chair of Optical Radiation, ul. Wiejska 45D, 15-351
Białystok, Poland; phone [phone], [e-mail];
Andrzej Pawlak, M.Sc. (E.Eng.), Central Institute for Labour
Protection - National Research Institute, ul. Czerniakowska 16, 00-
701 Warszawa, Poland; phone [phone], fax [phone]-
3695, [e-mail],

PRZEGLĄD ELEKTROTECHNICZNY, ISSN 0033-2097, R. 83 NR 5/2007

23