Badanie i pomiary obwodów prądu przemiennego

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

MINISTERSTWO EDUKACJI

NARODOWEJ

Beata Organ

Badanie i pomiary obwodów prądu przemiennego

725[01].O1.03

Poradnik dla ucznia

Wydawca

Instytut Technologii Eksploatacji – Państwowy Instytut Badawczy
Radom 2007

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

Recenzenci:
dr inż. Jan Diaczuk
dr inż. Zbigniew Kobierski

Opracowanie redakcyjne:
mgr inż. Beata Organ

Konsultacja:
mgr inż. Danuta Pawełczyk

Poradnik stanowi obudowę dydaktyczną programu jednostki modułowej 725[01].O1.03
„Badanie i pomiary obwodów prądu przemiennego”, zawartego w modułowym programie
nauczania dla zawodu monter elektronik.

Wydawca

Instytut Technologii Eksploatacji – Państwowy Instytut Badawczy, Radom 2007

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

SPIS TREŚCI

1. Wprowadzenie

2. Wymagania wstępne

3. Cele kształcenia

4. Materiał nauczania

4.1. Pole elektryczne i kondensator

4.1.1. Materiał nauczania

4.1.2. Pytania sprawdzające

4.1.3. Ćwiczenia

4.1.4. Sprawdzian postępów

4.2. Pole magnetyczne i elektromagnetyczne

4.2.1. Materiał nauczania

4.2.2. Pytania sprawdzające

4.2.3. Ćwiczenia

4.2.4. Sprawdzian postępów

4.3.

Właściwości i parametry charakterystyczne dla prądu przemiennego

jednofazowego i trójfazowego

4.3.1. Materiał nauczania

4.3.2. Pytania sprawdzające

4.3.3. Ćwiczenia

4.3.4. Sprawdzian postępów

4.4. Filtry częstotliwościowe

4.4.1. Materiał nauczania

4.4.2. Pytania sprawdzające

4.4.3. Ćwiczenia

4.4.4. Sprawdzian postępów

4.5. Transformator

4.5.1. Materiał nauczania

4.5.2. Pytania sprawdzające

4.5.3. Ćwiczenia

4.5.4. Sprawdzian postępów

5. Sprawdzian osiągnięć

6. Literatura

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

1. WPROWADZENIE

Poradnik będzie Ci pomocny w przyswajaniu wiedzy z zakresu obwodów i pomiarów

prądu przemiennego, ich budowie i zastosowaniu oraz w kształtowaniu umiejętności analizy
obwodów.

W poradniku zamieszczono:

−

wymagania wstępne – wykaz umiejętności, jakie powinieneś mieć już ukształtowane,
abyś bez problemów mógł korzystać z poradnika,

−

cele kształcenia – wykaz umiejętności, jakie ukształtujesz podczas pracy z poradnikiem,

−

materiał nauczania – podstawowe wiadomości teoretyczne niezbędne do opanowania
treści jednostki modułowej,

−

zestaw pytań przydatny do sprawdzenia, czy już opanowałeś treści zawarte w rozdziałach,

−

ćwiczenia, które pomogą Ci zweryfikować wiadomości teoretyczne oraz ukształtować
umiejętności praktyczne,

−

sprawdzian postępów,

−

sprawdzian osiągnięć – przykładowy zestaw zadań i pytań. Pozytywny wynik
sprawdzianu potwierdzi, że dobrze pracowałeś podczas zajęć i że nabyłeś wiedzę
i umiejętności z zakresu tej jednostki modułowej,

−

literaturę uzupełniającą.

Z rozdziałem „Pytania sprawdzające” możesz zapoznać się:

−

przed przystąpieniem do rozdziału „Materiał nauczania” – poznając wymagania
wynikające z zawodu, a po przyswojeniu wskazanych treści, odpowiadając na te pytania
sprawdzisz stan swojej gotowości do wykonywania ćwiczeń,

−

po opanowaniu rozdziału „Materiał nauczania”, by sprawdzić stan swojej wiedzy, która
będzie Ci potrzebna do wykonywania ćwiczeń.

Kolejny etap to wykonywanie ćwiczeń, których celem jest uzupełnienie i utrwalenie
wiadomości z zakresu badania obwodów i pomiaru prądu przemiennego.

Wykonując ćwiczenia przedstawione w poradniku lub zaproponowane przez nauczyciela,

będziesz poznawał rodzaje, budowę i zastosowanie obwodów prądu przemiennego. Zakres
treści jednostki modułowej jest bardzo szeroki.
Po wykonaniu zaplanowanych ćwiczeń, sprawdź poziom swoich postępów wykonując
„Sprawdzian postępów”.

Odpowiedzi Nie wskazują luki w Twojej wiedzy, informują Cię również, jakich

zagadnień jeszcze dobrze nie poznałeś. Oznacza to także powrót do treści, które nie są
dostatecznie opanowane.

Poznanie przez Ciebie wszystkich lub określonej części wiadomości będzie stanowiło dla

nauczyciela podstawę przeprowadzenia sprawdzianu poziomu przyswojonych wiadomości
i ukształtowanych umiejętności. W tym celu nauczyciel może posłużyć się zadaniami
testowymi.

W poradniku jest zamieszczony sprawdzian osiągnięć, który zawiera przykład takiego

testu oraz instrukcję, w której omówiono tok postępowania podczas przeprowadzania
sprawdzianu i przykładową kartę odpowiedzi, w której, w przeznaczonych miejscach zakreśl
właściwe odpowiedzi spośród zaproponowanych.

Bezpieczeństwo i higiena pracy

W czasie pobytu w pracowni musisz przestrzegać regulaminów, przepisów

bezpieczeństwa i higieny pracy oraz instrukcji przeciwpożarowych, wynikających z rodzaju
wykonywanych prac. Przepisy te poznasz podczas trwania nauki.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

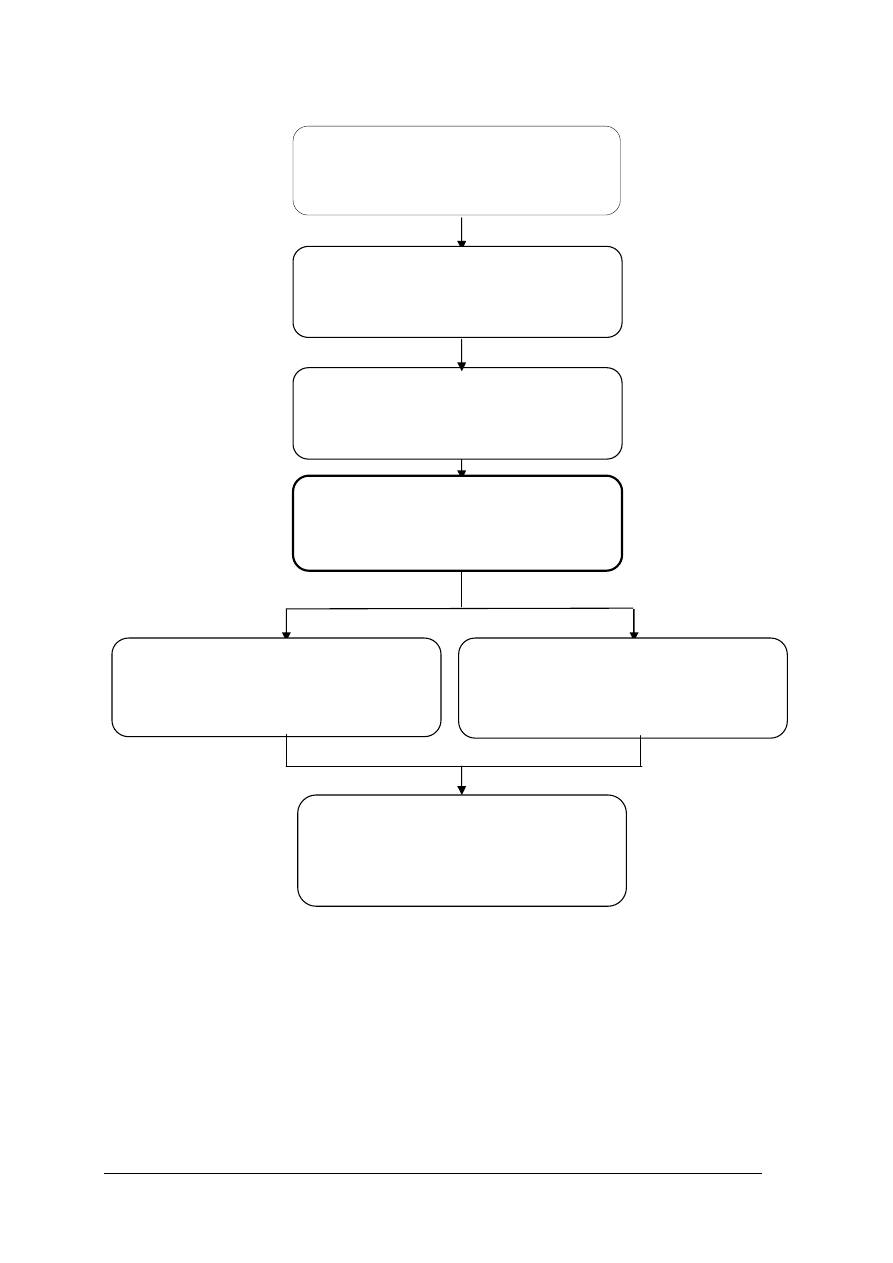
725[01].O1

Pomiary parametrów elementów

i układów elektronicznych

725[01].O1.06

Analizowanie działania maszyn i urządzeń

elektrycznych

725[01].O1.04

Badanie i pomiary elektronicznych

układów analogowych

725[01].O1.01

Przygotowanie do bezpiecznej pracy

725[01].O1.03

Badanie i pomiary obwodów prądu

przemiennego

725[01].O1.05

Badanie i pomiary elektronicznych

układów cyfrowych

725[01].O1.02

Badanie i pomiary obwodów prądu stałego

Schemat układu jednostek modułowych

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

2. WYMAGANIA WSTĘPNE

Przystępując do realizacji programu jednostki modułowej powinieneś umieć:

−

klasyfikować materiały ze wzglądu na właściwości elektryczne,

−

rozróżniać podstawowe wielkości elektryczne,

−

rozróżniać podstawowe materiały stosowane w elektrotechnice,

−

porównywać właściwości materiałów stosowanych w konstrukcjach maszyn i urządzeń
elektrycznych,

−

stosować i przeliczać podstawowe jednostki wielkości elektrycznych w układzie SI,

−

stosować podstawowe prawa elektrotechniki,

−

posługiwać się symbolami graficznymi elementów elektrycznych,

−

rozróżniać połączenia szeregowe, równoległe i mieszane elementów obwodu
elektrycznego,

−

rozróżniać elementy struktury obwodu elektrycznego,

−

obliczać parametry zastępcze źródeł napięcia połączonych szeregowo i równolegle,

−

określać stany pracy źródła energii elektrycznej,

−

określać warunki dopasowania odbiornika do źródła,

−

obsługiwać woltomierz, amperomierz, omomierz i miernik uniwersalny,

−

stosować metody pomiaru podstawowych wielkości elektrycznych,

−

planować pomiary w obwodzie elektrycznym,

−

organizować stanowisko pomiarowe,

−

stosować różne sposoby połączeń elektrycznych,

−

łączyć obwód elektryczny zgodnie ze schematem,

−

przedstawiać wyniki pomiarów w formie tabel i wykresów,

−

odczytywać informację z tabeli i wykresu,

−

oceniać dokładność pomiarów,

−

współpracować w grupie,

−

korzystać z różnych źródeł informacji,

−

stosować przepisy bezpieczeństwa i higieny pracy, ochrony przeciwpożarowej i ochrony
stanowiska pracy.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

3. CELE KSZTAŁCENIA

W wyniku realizacji programu jednostki modułowej powinieneś umieć:

–

rozróżnić parametry charakteryzujące przebieg prądu przemiennego,

–

rozróżnić różne typy kondensatorów i cewek,

–

narysować wykresy wektorowe dla zadanego elementu R, L, C,

–

przeanalizować proste układy prądu przemiennego,

–

obliczyć i oszacować podstawowe wielkości elektryczne w układach prądu przemiennego,

–

zinterpretować podstawowe zjawiska z zakresu elektrotechniki,

–

określić warunki rezonansu napięć i prądów,

–

sklasyfikować i scharakteryzować filtry,

–

sklasyfikować i scharakteryzować transformatory,

–

rozróżnić stany pracy transformatora,

–

obsłużyć oscyloskop,

–

dobrać przyrządy pomiarowe do pomiaru wielkości elektrycznych w obwodach prądu
przemiennego, połączyć układ do pomiaru podstawowych wielkości w układach prądu
przemiennego,

–

dokonać pomiarów podstawowych wielkości elektrycznych w układach prądu przemiennego,

–

zlokalizować zwarcia i przerwy w prostych układach,

–

przedstawić wyniki w formie tabeli i wykresu,

–

przeanalizować i zinterpretować wyniki pomiarów oraz sformułować wnioski praktyczne,

–

zademonstrować poprawność wykonywania pomiarów,

–

przewidzieć zagrożenia dla życia i zdrowia w czasie realizacji ćwiczeń z prądem
przemiennym,

–

dokonać pomiarów w układach prądu przemiennego w sposób bezpieczny,

–

zastosować procedurę postępowania w sytuacji zagrożenia.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

4. MATERIAŁ NAUCZANIA

4.1. Pole elektryczne i kondensator

4.1.1. Materiał nauczania

Ładunek elektryczny

Występujące przyrodzie ładunki elektryczne są związane z materią w postaci ładunku

cząsteczek elementarnych, tj. elektronów i protonów. Stwierdzono z dużą dokładnością, że
atomy są elektrycznie obojętne, tzw. że ładunki ujemne elektronów i dodatnie protonów
równoważą się w obrębie każdego atomu.

Ładunku elektrycznego nie można stworzyć, ani zniszczyć, można jedynie spowodować

przejście pewnej liczby elektronów z jednego ciała na drugie, na przykład przez zetknięcie
dwóch ciał elektroizolacyjnych, a jeszcze łatwiej przez pocieranie. Ładunek elektronu jest
ujemny, a ładunek protonu dodatni.

Prawo Coulomba. Przenikalność elektryczna
Dwa naelektryzowane ciała, dostatecznie małe, aby ich ładunki równe Q

i Q

można

było uważać za punktowe, oddziałują na siebie siłą, która jest proporcjonalna do iloczynu ich
ładunków, odwrotnie proporcjonalnie do kwadratu odległości r między nimi.

F =

4π

⋅

Siła ta zależy od właściwości otaczającego środowiska, zwane przenikalnością

elektryczną ε.

⋅

gdzie:

−









⋅

−

8,85

4π

stała elektryczna zwana też przenikalnością

elektryczną próżni,

−

przenikalność elektryczna względna środowiska.

Przenikalność elektryczna próżni

ε jest jedną ze stałych fizycznych, a jej wartość została

określona w układzie SI i ma wymiar farada na metr. Przenikalność elektryczna względna
podaje nam, ile razy przenikalność określonego środowiska jest większa od przenikalności
próżni. Przenikalność względna jest wielkością bezwymiarową.
Siła F działa wzdłuż prostej łączącej oba ładunki w kierunku:
–

odpychania, gdy ładunki są jednoimienne tj. oba dodatnie lub oba ujemne; wtedy ich
iloczyn jest dodatni.

–

przyciągania, gdy ładunki są różnoimienne, tj. jeden dodatni o drugi ujemny; wtedy ich
iloczyn jest ujemny.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

Rys. 1. Oddziaływanie wzajemne dwóch ładunków elektrycznych:

a), b) jednoimienne; c) różnoimienne [3, s. 29]

Prąd elektryczny. Jednostki prądu i ładunku
Stosunek ilości ładunku ΔQ przepływającego przez przekrój przewodnika w małym

przedziale czasu Δt do tego czasu nazywamy prądem elektrycznym.

i =

Δt

ΔQ

Jeżeli w równych dowolnie małych przedziałach czasu przepływają jednakowe ładunki
elektryczne, można określić prąd za pomocą wzoru

I =

I – prąd taki nazywamy prądem stałym w odróżnieniu od prądu zmieniającego się w czasie,
który oznaczamy małą literą i. Prąd elektryczny określa się jednostką zwaną amperem (1 A).
Wszystkie pozostałe jednostki elektryczne i magnetyczne można wyrazić za pomocą ampera
oraz metra, kilograma i sekundy.
Jeden kulomb jest to ładunek elektryczny przenoszony w ciągu jednej sekundy przy nie
zmieniającym się w czasie prądzie równym jednemu amperowi.

1[Q] = 1A · 1s = 1C = 1 kulomb (amperosekunda)

Pole elektryczne. Natężenie pola elektrycznego

Dookoła ciała naelektryzowanego powstaje pole elektryczne, które działa na inne

umieszczone w nim ładunki elektryczne, jak też powoduje przemieszczanie się elektronów
swobodnych na umieszczonych w nim przewodnikach.

Rys. 2. Pole elektryczne [3, s. 35]

Przyjmijmy, że dany jest odosobniony ładunek punktowy Q w próżni i chcemy zbadać

jego pole elektryczne. Użyjemy do tego tak małego ładunku q, aby można było pominąć jego
wpływ na badane pole. Umieścimy ładunek próbny q w dowolnym punkcie P pola
w odległości r od ładunku Q. Na ładunek działa q, zgodnie z prawem Coulomba siła

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

F =

πr

gdzie: Q – ładunek punktowy,

q – mały ładunek,

r – odległość,

ε – przenikalność elektryczna.

Siła F jest proporcjonalna do ładunku q.

Pole elektryczne wytworzone przez ładunki elektryczne nieruchome i niezmienne

w czasie nazywamy polem elektrostatycznym.
Natężenie pola elektrycznego w dowolnym punkcie pola jest równe stosunkowi siły
działającej na mały próbny dodatni ładunek elektryczny, umieszczony w dowolnym punkcie,
do tego ładunku.

E =

[ ]

[

]

[

]

[ ]

[

]

[

]

[

]









⋅

Napięcie i potencjał

Siła działająca w polu elektrycznym na ładunek próbny q może spowodować jego

przesunięcie w kierunku działania siły. Iloczyn siły i przesunięcia jest równy wykonywanej
przy tym pracy.

Rys. 3. Napięcie i potencjał [3, s. 36]

Napięcie elektryczne między dwoma dowolnymi punktami A, B w polu elektrycznym jest
równe stosunkowi pracy przy przenoszeniu małego dodatniego ładunku próbnego q, z punktu
A do punktu B, do tego ładunku.

Jednostkę napięcia określamy na podstawie pracy lub mocy mierzonej podczas przepływu
prądu elektrycznego przez przewód.
Prąd stały o wartości jednego ampera przenosi w ciągu jednej sekundy ładunek równy
jednemu kulombowi. Jeżeli wydatkowana przy tym praca jest równa jednemu dżulowi, albo
moc tracona jest równa jednemu watowi, to napięcie jest równe jednemu woltowi(1 V).

1V = 1

= 1

⋅

= 1

Obok napięcia jest jeszcze używana wielkość zwana potencjałem. Aby wyznaczyć potencjał
w dowolnym punkcie A pola elektrycznego umieszczamy w tym punkcie ładunek próbny q
i przesuwamy go bardzo daleko do „nieskończoności”, oznaczamy symbolem

∞

Potencjał (oznaczamy literą V) w dowolnym punkcie pola elektrycznego jest równy

stosunkowi pracy wykonanej przy przesunięciu dodatniego ładunku próbnego z danego
punktu pola do nieskończoności do tego ładunku

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

Napięcie pomiędzy dwoma punktami pola elektrycznego jest równe różnicy potencjałów tych
punktów.

= V

– V

Jednostką napięcia i potencjału jest wolt (V)

Jeden wolt jest różnicą potencjałów między dwoma punktami przewodu, między którymi

nie zmieniający się w czasie prąd jednego ampera wywołuje stratę mocy równą jednemu
watowi.
Jednostką natężenia pola elektrycznego jest wolt na metr:

1[E] = 1

Kondensatory

Kondensatorem nazywamy układ dwóch elektrod przedzielonych dielektrykiem,

wykonanych celowo dla uzyskana potrzebnej pojemności.

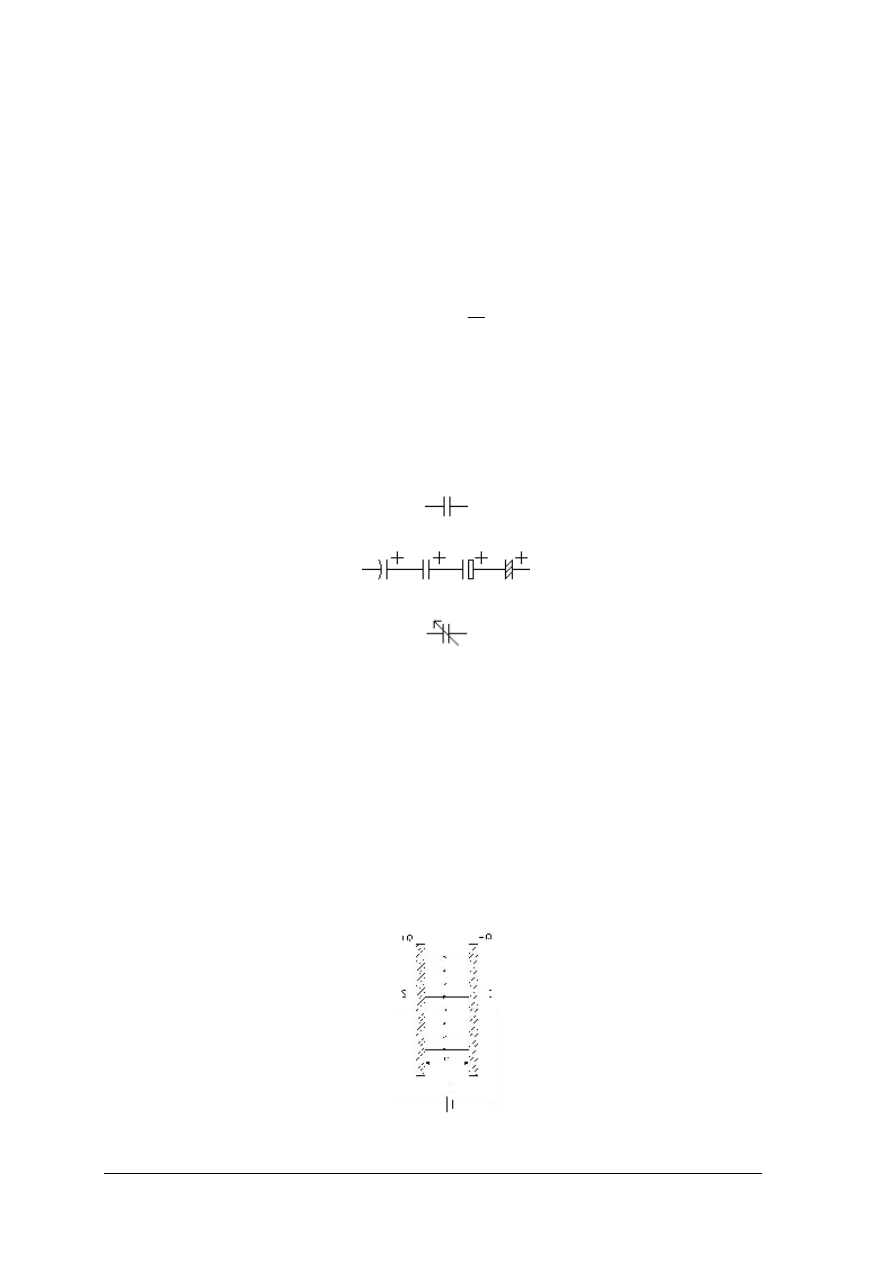
Symbole kondensatorów

−

Zwykły

−

Spolaryzowany (Elektrolityczny)

−

Zmienny (Trymer)

Rodzaje kondensatorów:

−

kondensator płaski, to dwie płytki przewodnika (tzw. okładki), rozdzielone izolatorem
(dielektrykiem). Pojemność kondensatora płaskiego jest tym większa, im większa jest
powierzchnia okładzin i przenikalność elektryczna względna dielektryka oraz im
mniejszy jest odstęp między okładzinami,

−

rurowy ceramiczny, którym rurka materiału ceramicznego o dużej przenikalności
elektrycznej, jest powleczony wewnątrz i zewnątrz warstewką metalu,

−

wielopłytkowy obrotowy o pojemności nastawianej przez zmianę zagłębienia zespołu
płytek ruchomych między płytkami nieruchomymi,

−

elektrolityczny, w którym dielektrykiem jest cieniutka warstewka wodorotlenku glinu
uformowana na folii aluminiowej stanowiącej biegun dodatni.

Rys. 4. Kondensator płaski (przekrój poprzeczny) [1, s. 94]

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

Pojemność kondensatora płaskiego można obliczyć ze wzoru:

C =

⋅

gdzie: C

–

pojemność kondensatora w [F],

–

powierzchnia okładziny w [m

–

przenikalność bezwzględna dielektryka









–

odstęp między okładzinami w m.

Jednostką pojemności jest Farad [1F]

1[C] = 1

[V]

[Q]

= 1

⋅

= 1 F

mniejsze jednostki to: milifarad

1 mF = 10

–3

mikrofarad 1 μ F = 10

–6

nanofarad

1 nF = 10

–9

pikofarad

1 pF = 10

–12

Ładunek zgromadzony na jednej z okładzin nazywamy ładunkiem kondensatora.
Ładunek jest wprost proporcjonalny do napięcia, czyli:

Q = C · U

C – jest pojemnością kondensatora.
Stosunek ładunku kondensatora do napięcia występującego pomiędzy jego okładzinami
nazywamy pojemnością kondensatora.

C =

[ ]

[ ] [ ]

Parametry kondensatorów

−

pojemność znamionowa – jest to pojemność (wyrażona w faradach) określona przez
producenta i podana na oznaczeniu kondensatora; określa zdolność kondensatora do
gromadzenia ładunku,

−

pojemność rzeczywista – dokładna pojemność, jaką posiada kondensator,

−

tolerancja – (klasa dokładności) – ponieważ ze względu na rozrzuty produkcyjne
kondensatory nie mają pojemności dokładnie zgodnej z pojemnością znamionową,
podaje się maksymalne dopuszczalne odchyłki, tolerancję wyraża się w procentach
wartości znamionowej,

−

napięcie znamionowe – jest to maksymalne napięcie, które można doprowadzić do
zacisków kondensatora, napięcie przewyższające tę wartość powoduje przebicie
dielektryka i zwarcie kondensatora,

−

prąd upływowy – prąd przewodzenia pojawiający się po doprowadzeniu do końcówek
kondensatora napięcia stałego,

−

temperaturowy współczynnik pojemności – określa względną zmianę pojemności,
zależną od zmian temperatury,

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

−

wytrzymałością elektryczną – nazywamy maksymalną wartość natężenia pola, która
jeszcze nie niszczy własności izolacyjnych dielektryka,

−

reaktancja pojemnościowa – jest to opór zależny od częstotliwości, jaki posiada
kondensator podczas przepływu prądu zmiennego.

Pojemnością przewodnika odosobnionego nazywamy stosunek ładunku nagromadzonego na
przewodniku do jego potencjału względem obranego punktu w polu elektrycznym, któremu
przypisujemy potencjał równy zeru, czyli:

C =

gdzie: Q – ładunek zgromadzony na przewodniku,

ϕ – potencjał tego ładunku.

Łączenie kondensatorów.

Rozróżniamy dwa rodzaje połączeń kondensatorów: połączenie szeregowe i połączenie

równoległe.
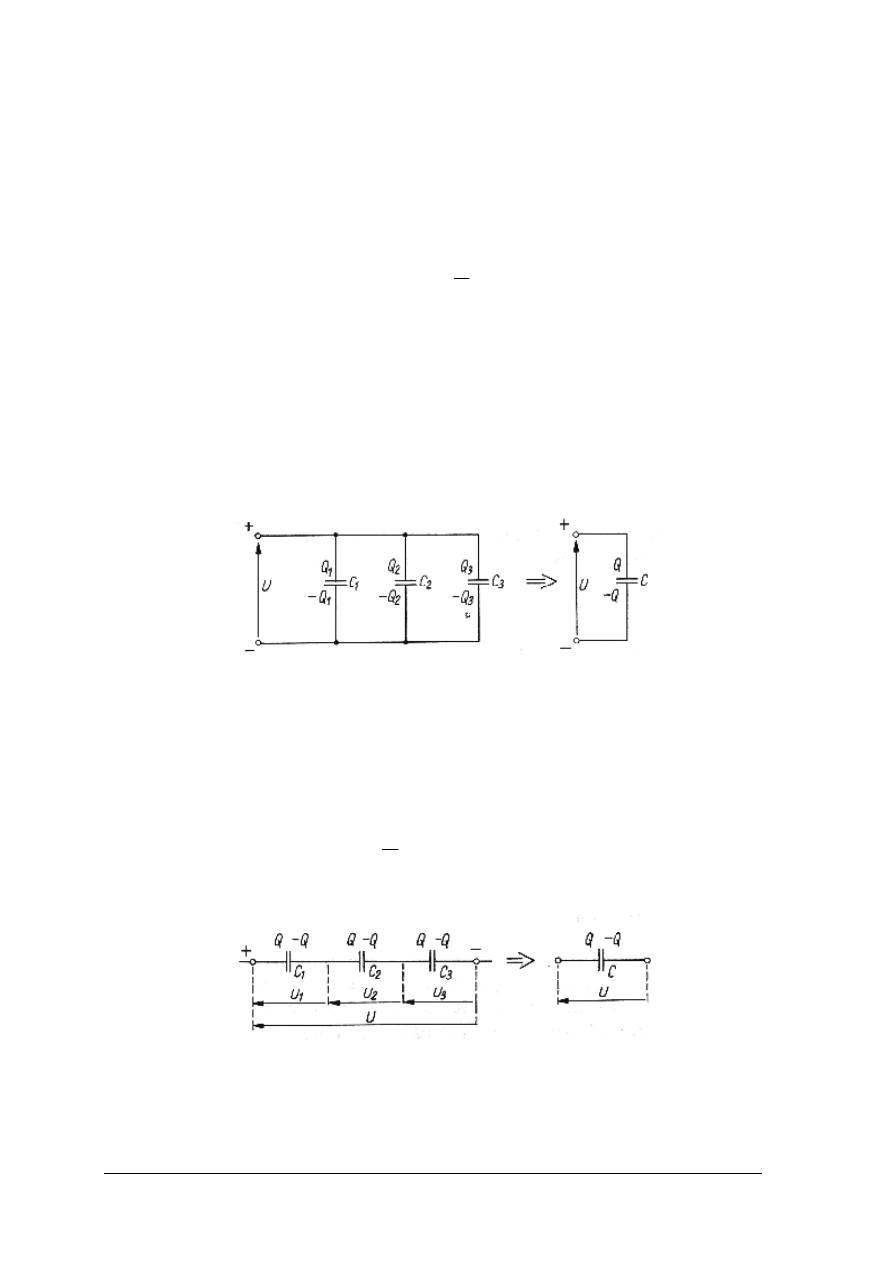
Połączenie równoległe

Przy połączeniu równoległym kondensatorów napięcie na zaciskach każdego

kondensatora jest takie samo.

Rys. 5. Połączenie równoległe kondensatorów (przekrój poprzeczny) [3, s. 138]

Przy połączeniu równoległym kondensatorów pojemność zastępcza jest równa sumie
pojemności poszczególnych kondensatorów.

C = C

Połączenie szeregowe

Rys. 6. Połączenie szeregowe kondensatorów (przekrój poprzeczny) [3, s. 136]

Przy połączeniu szeregowym kondensatorów wszystkie kondensatory mają taki sam

ładunek.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

Przy połączeniu szeregowym kondensatorów odwrotność pojemności zastępczej jest równa
sumie odwrotności pojemności poszczególnych kondensatorów.
Przy połączeniu szeregowym kondensatorów o jednakowej pojemności, pojemność zastępcza
jest równa pojemności jednego z kondensatorów podzielonej przez liczbę połączonych
kondensatorów.

jeżeli: C

= C

= C to C

4.1.2. Pytania sprawdzające

Odpowiadając na pytania, sprawdzisz, czy jesteś przygotowany do wykonania ćwiczeń.

1. Co to jest pole elektryczne?
2. Co to jest przenikalność względna środowiska?
3. Jakie znasz podstawowe własności pola elektrycznego?
4. Jak brzmi prawo Coulomba?
5. W jaki sposób oblicza się pojemność kondensatora płaskiego?
6. Czy potrafisz narysować i omówić sposoby łączenia kondensatorów?
7. Jakie znasz podstawowe parametry kondensatora?

4.1.3. Ćwiczenia

Ćwiczenie 1

Trzy kondensatory o pojemności C

= 6 μF, C

= 18 μF, C

= 9 μF włączono w szereg na

napięcie U = 6000 V. Oblicz ładunek Q i napięcie na poszczególnych kondensatorach.

Sposób wykonania ćwiczenia

Aby wykonać ćwiczenie, powinieneś:

1) obliczyć pojemność zastępczą,
2) obliczyć ładunek Q,
3) następnie obliczyć napięcie na poszczególnych kondensatorach.

Wyposażenie stanowiska pracy:

–

poradnik dla ucznia,

–

kalkulator,

–

zeszyt, przybory do pisania,

–

literatura wskazana przez nauczyciela.

Ćwiczenie 2

Reaktancja pojemnościowa kondensatora o pojemności 4,7 μF, przy określonej

częstotliwości doprowadzonego napięcia, wynosi 10 Ω. Oblicz wartość tej częstotliwości.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

Sposób wykonania ćwiczenia

Aby wykonać ćwiczenie, powinieneś:

1) skorzystać ze wzoru X

2π

⋅

2) obliczyć częstotliwość.

Wyposażenie stanowiska pracy:

–

poradnik dla ucznia,

–

kalkulator,

–

zeszyt, przybory do pisania,

–

literatura wskazana przez nauczyciela.

Ćwiczenie 3

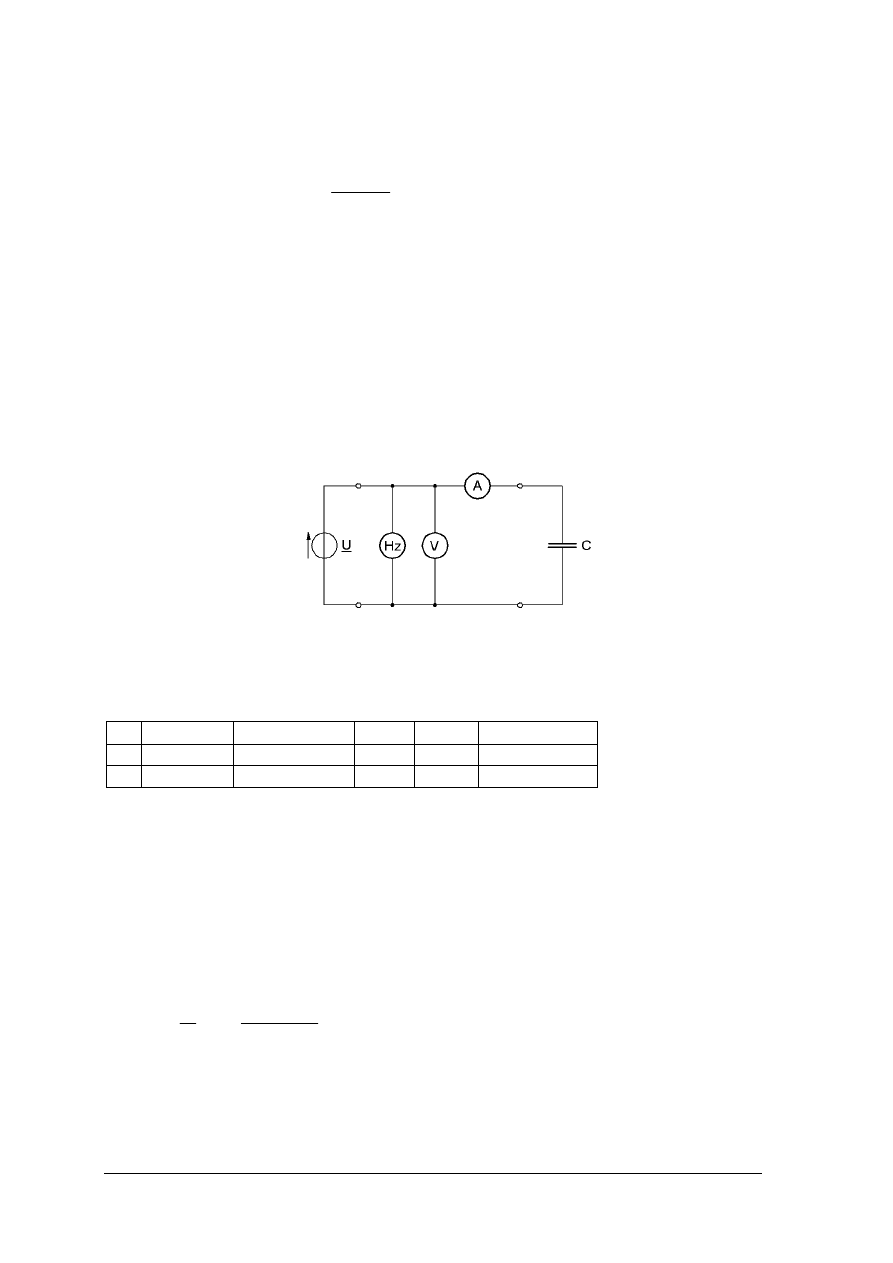
Wykonaj pomiar pojemności metodą techniczną elementów zaproponowanych przez

nauczyciela.

Rysunek do ćwiczenia 3. Układ do pomiaru pojemności metodą techniczną

Tabela wyników pomiarów i obliczeń.

Lp. U [V]

I [mA]

[

Ω

] f

[Hz] C [nF lub

100

Sposób wykonania ćwiczenia.

Aby wykonać ćwiczenie, powinieneś:

1) zanalizować schemat pomiarowy,
2) skompletować potrzebną aparaturę i elementy,
3) połączyć obwód elektryczny i zasilić go sygnałem sinusoidalnie zmiennym o U = 5 V

i f = 100 Hz,

4) wykonać pomiary wartości skutecznych prądu oraz napięcia,
5) obliczyć wartości pojemności na podstawie wzorów:

⋅

6) porównać obliczone wartości pojemności z oznaczeniami na wybranych elementach,
7) oszacować dokładność pomiarów i sformułować wnioski.

Wyposażenie stanowiska pracy

–

częstościomierz,

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

–

generator funkcyjny,

–

multimetr cyfrowy i analogowy,

–

kondensatory: C = 10 nF, C = 0,22

F, C = 0,47

F, C = 22 nF, C = 0,1

–

literatura wskazana przez nauczyciela,

–

materiały i przybory do pisania.

4.1.4. Sprawdzian postępów

Czy potrafisz:

Tak

Nie

1) obliczyć pojemność zastępczą kondensatora płaskiego?

2) narysować układ szeregowy kondensatorów?

3) narysować układ równoległy kondensatorów?

4) wyjaśnić co to jest przenikalność elektryczna w próżni?

5) zdefiniować pojemność elektryczną?

6) zdefiniować prawo Coulomba?

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

4.2. Pole magnetyczne i elektromagnetyczne

4.2.1. Materiał nauczania

Zapoznanie się z podstawowymi właściwościami pola magnetycznego pozwala

zrozumieć zjawiska, w których biorą udział magnesy trwałe i elektromagnesy. Oddziaływania
elektromagnetyczne stanowią bowiem podstawę dla nieomal wszystkich dziedzin
elektrotechniki.

Magnesy naturalne i sztuczne. Igły magnetyczne

W kompasie najważniejszym elementem jest niewielki magnes trwał – igła magnetyczna.

Jeden z końców igły zawsze zwraca się w kierunku północy, dlatego ten koniec magnesu
trwałego nazywa się biegunem północnym i oznaczamy literą N. Przeciwległy biegun
magnesu trwałego jest biegunem południowym oznaczamy literą S. Obserwując zachowanie
dwóch magnesów trwałych zauważono, że dwa bieguny jednoimienne (tj. dwa N lub dwa S)
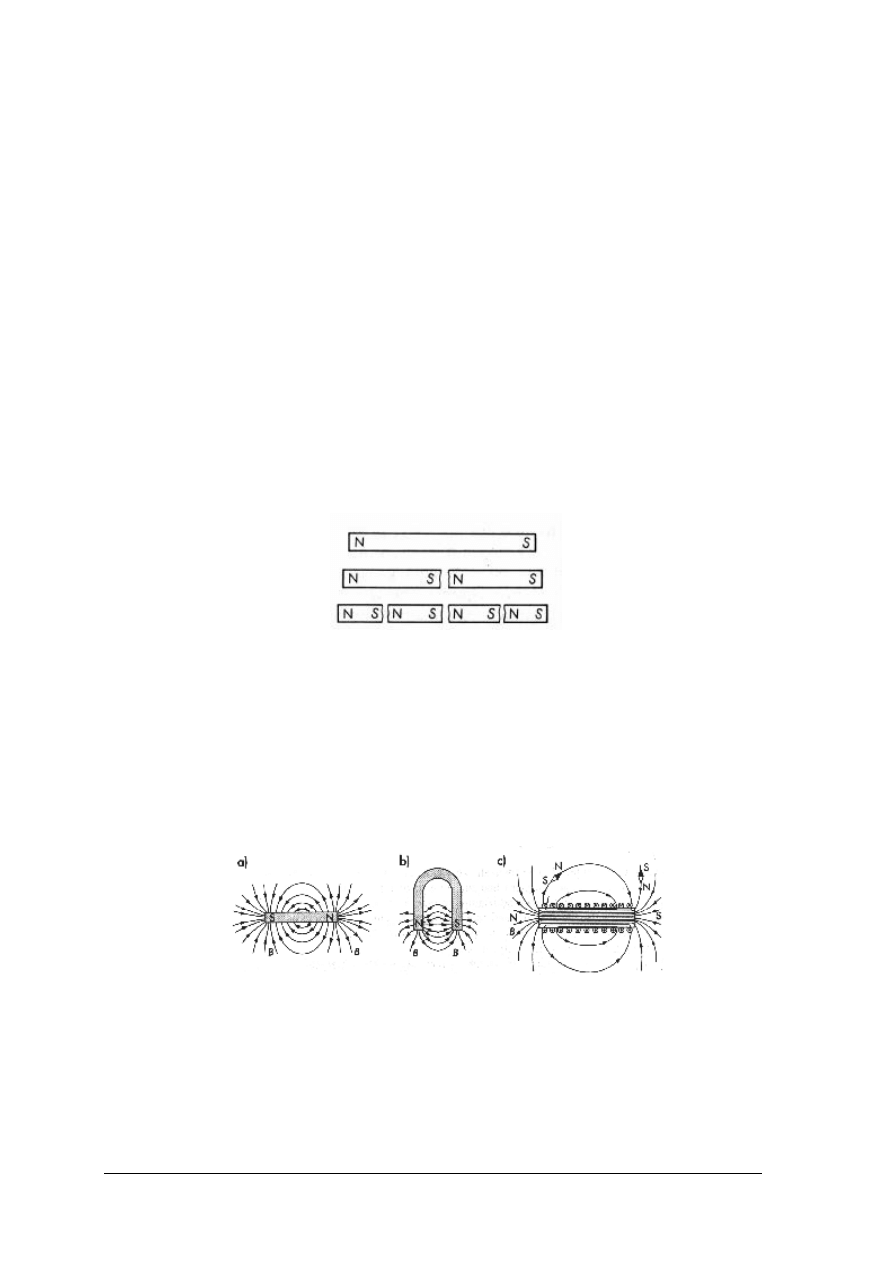
odpychają się wzajemnie zaś dwa magnesy różnoimienne (N i S) przyciągają się wzajemnie.
Bieguny magnetyczne występują zawsze parami nie jest możliwe oddzielenie bieguna
magnetycznego N lub tylko S.

Rys. 7. Magnesy (przekrój poprzeczny) [3, s. 140]

Istotą oddziaływania magnetycznego są tzw. siły elektrokinetyczne występujące

pomiędzy ładunkami elektrycznymi będącymi w ruchu.

Prąd w dowolnym obwodzie elektrycznym wywołuje w otaczającej przestrzeni pola

elektrokinetyczne, nazwane tradycyjnie polem magnetycznym.

Obraz graficzny pola magnetycznego

Obrazem pola magnetycznego są linie sił tego pola.

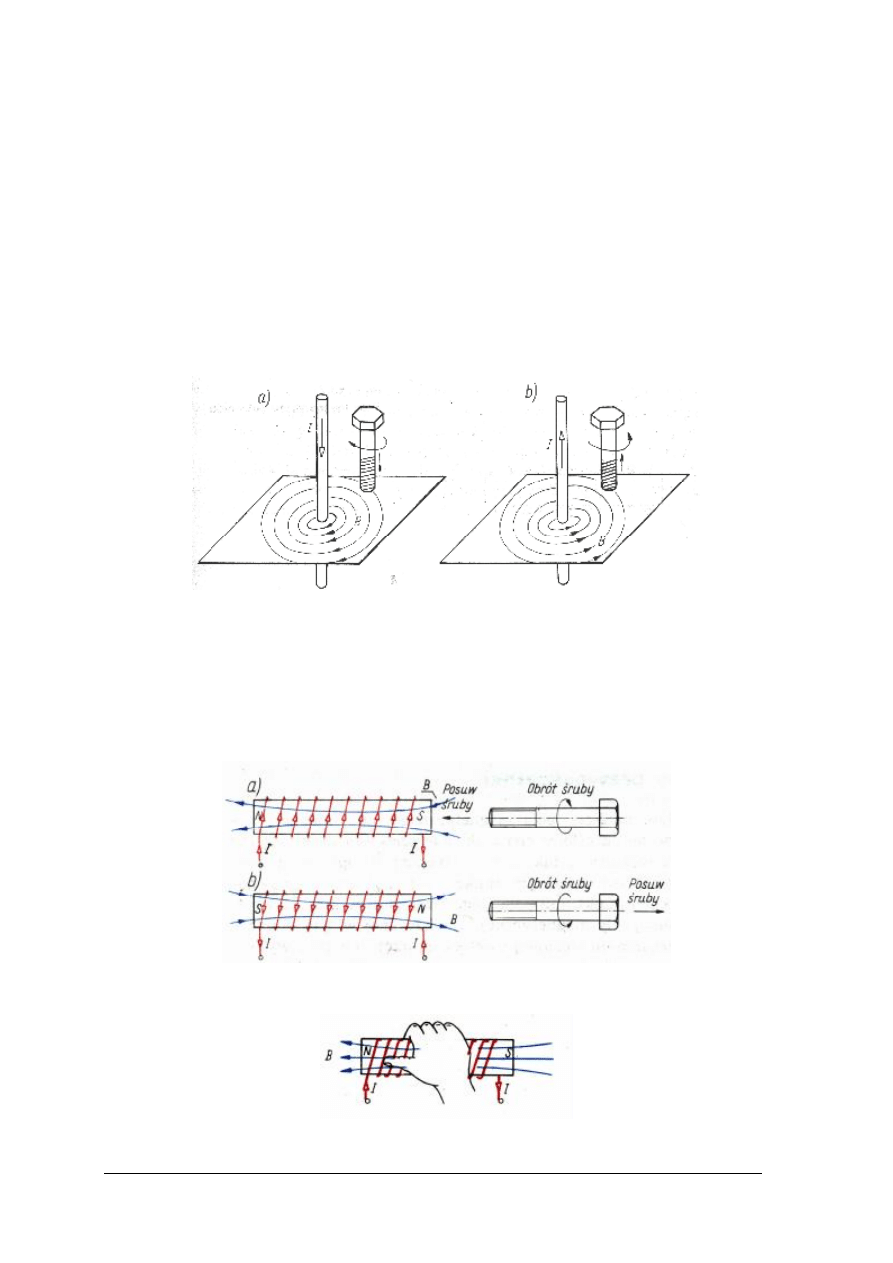
Rys. 8. Linie pola magnetycznego wokół: a) magnesu trwałego sztabkowego;

b) magnesu trwałego o kształcie podkowy; c) solenoid z prądem elektrycznym [6, s. 28]

Linie sił pola wokół magnesu trwałego rys. 8a i b wychodzą z jednego bieguna północnego
(oznaczonego N) i wchodzą do bieguna południowego (oznaczonego S).W przewodniku,
przez który przepływa prąd elektryczny linii sił pola magnetycznego przybierają kształt
okręgów prostopadłych do przewodu.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

Obraz pola magnetycznego wokół magnesu trwałego, przewodnika z prądem lub solenoidu
rys. 8c można uzyskać za pomocą opiłków stalowych rozsypanych na kartce papieru lub szkle.

Reguła śruby prawoskrętnej

W każdym punkcie pola magnetycznego igła magnetyczna przyjmuje ściśle określony

kierunek. Kierunek ten przyjmujemy za kierunek wektora indukcji magnetycznej B.
Wektor B jest w każdym punkcie pola styczny do przechodzącej przez ten punkt linii pola.
Przy wyznaczaniu kierunku wektora indukcji B w polu wytworzonym przez prąd elektryczny
posługujemy się regułą śruby prawoskrętnej.
Chcąc wyznaczyć kierunek i zwrot wektora B w otoczeniu przewodu prostoliniowego
układamy śrubę prawoskrętną w osi przewodu i obracamy ją tak, aby posuw śruby był zgodny
ze zwrotem prądu I.

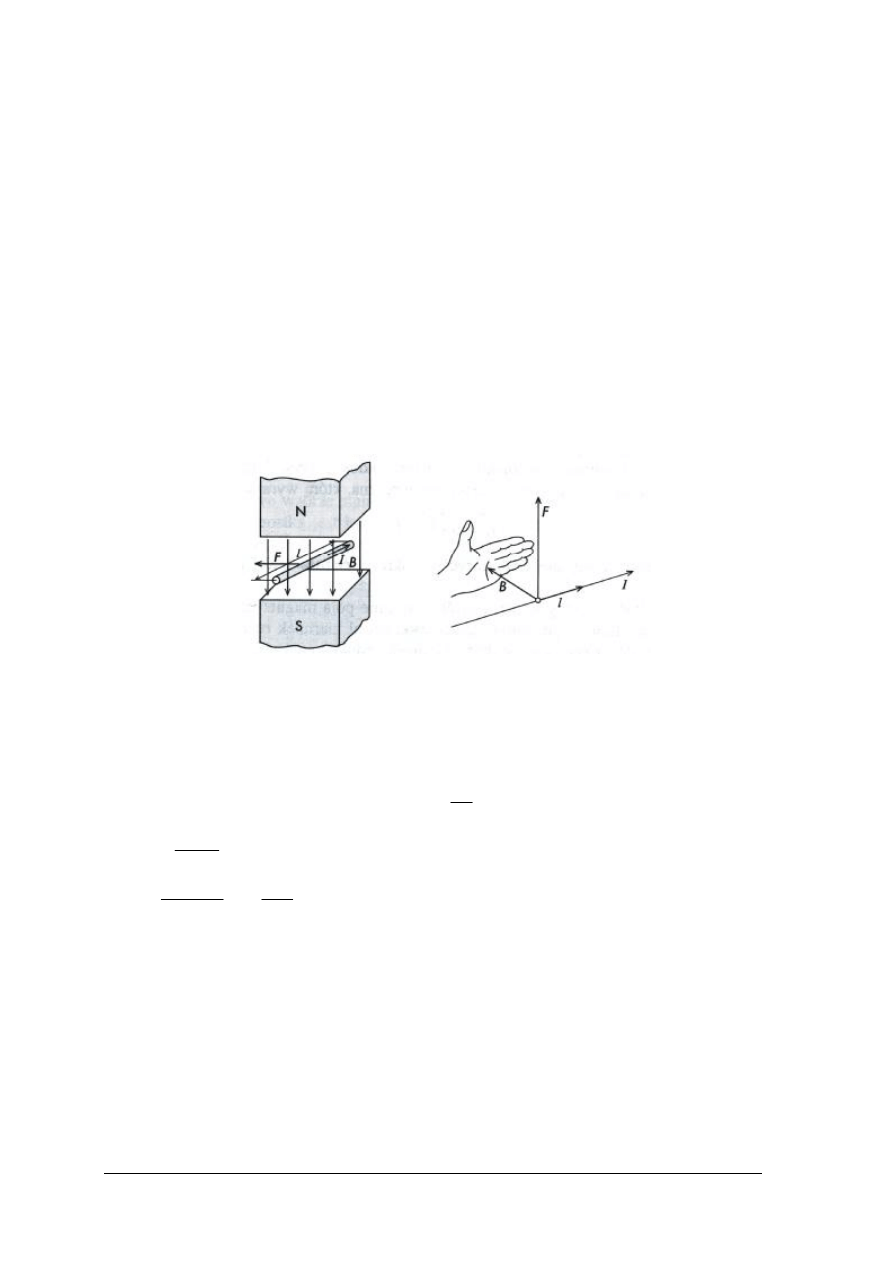
Rys. 9. Pole magnetyczne w otoczeniu przewodu prostoliniowego o prądzie I

a), b) widok perspektywiczny [3, s. 143]

Linie pola są okręgami leżącymi w płaszczyznach prostopadłych do osi przewodu. Obrót

śruby prawoskrętnej wyznacza obieg linii pola, a wektor B jest styczny do przechodzącego
przez dany punkt okręgu, którego środek leży w osi przewodu.

W zastosowaniu do solenoidu jest stosowana reguła prawej ręki.

Rys. 10. Stosowanie reguły śruby prawoskrętnej do solenoidu przy różnych zwrotach prądu [3, s. 146]

Rys. 11. Wyznaczanie kierunku pola magnetycznego w solenoidzie za pomocą reguły prawej ręki [3, s. 146]

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

Prawa rękę należy położyć na solenoidzie tak, aby cztery palce obejmujące solenoid były

skierowane zgodnie z prądem. Odchylony duży palec wskazuje zwrot linii pola wewnątrz
solenoidu.

Działanie pola magnetycznego na prąd elektryczny. Indukcja magnetyczna

Podstawową wielkością magnetyczną charakteryzującą stan pola magnetycznego

w danym miejscu jest indukcja magnetyczna B.

Na przewodnik o długości l, przez który przepływa prąd I umieszczony w polu

magnetycznym o indukcji B oddziałuje siła, którą wyznacza się:

F = B

⋅

gdzie: F – siła, B – indukcja magnetyczna, l – długość.

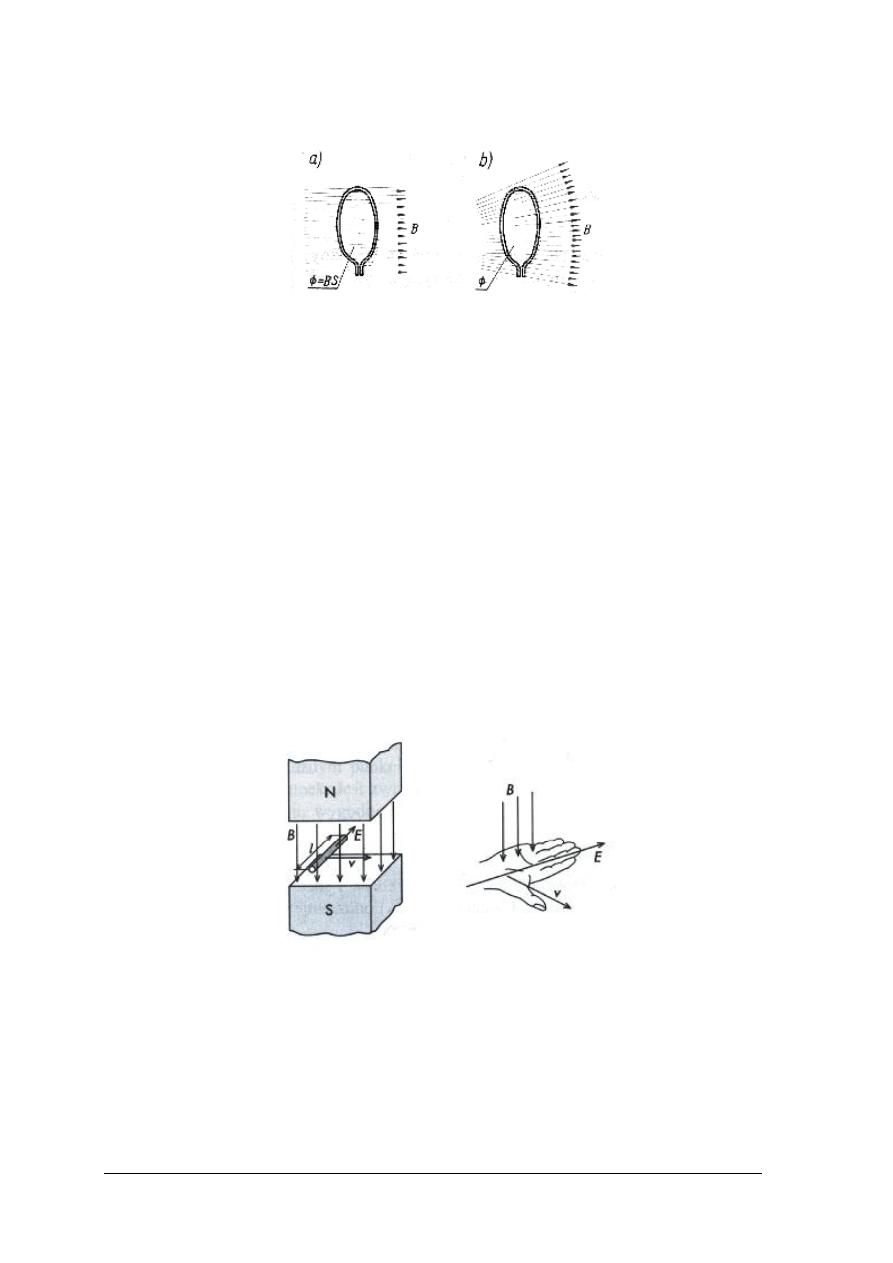
Jeżeli lewą dłoń ułożymy tak, aby linie pola magnetycznego były skierowane do dłoni,

a cztery palce zgodnie z prądem, to odchylony wielki palec wskaże kierunek siły F.

Rys. 12. Reguła lewej reki – linie indukcji pola magnetycznego są skierowane kierunku dłoni,

a cztery palce wskazują kierunek przepływu prądu.

Odchylony w górę kciuk wskazuje kierunek działania siły F [6, s. 29]

Znając siłę F, możemy obliczyć wartość indukcji magnetycznej:

B =

⋅

1[B] = 1

⋅

uwzględniając, że 1 N = 1 J/m = 1 V

s/m

⋅

1[B] =

⋅

= 1

⋅

= 1 T = 1 tesla

Jednostką indukcji magnetycznej jest tesla [T]

Jedna tesla jest indukcja magnetyczną wywierająca siłę jednego niutona (N) na metr

(m) długości przewodu prostoliniowego o prądzie równym jednemu amperowi (A),
umieszczonego prostopadle do linii indukcji.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

Strumień magnetyczny

Rys. 13. Strumień magnetyczny w polu: a) równomiernym; b) nierównomiernym [3, s. 149]

W elektrotechnice często posługujemy się pojęciem strumienia magnetycznego. Jest to

wielkość proporcjonalna do sumy wszystkich linii pola magnetycznego w danym punkcie.
W równomiernym polu magnetycznym strumień magnetyczny Φ stanowi iloczyn indukcji B
i pola powierzchni S, prostopadłej do wektora indukcji:

Φ = B S

⋅

Jednostką strumienia magnetycznego jest weber [Wb] = [

⋅

Zjawisko indukcji elektromagnetycznej

⋅

, B = [T]

Zwrot indukowanej siły elektromotorycznej określa reguła lewej ręki.

Jeżeli prawą dłoń ułożymy w taki sposób, aby linie pola magnetycznego były skierowane

do dłoni, a odchylony kciuk wskazywał kierunek ruchu przewodu, to pozostałe cztery palce
wskażą kierunek indukowanej siły elektromotorycznej.

Rys. 14. Ilustracja zjawiska indukcji elektromagnetycznej

– ruchomy przewodnik w polu magnetycznym [6, s. 30]

Indukcyjność własna i wzajemna cewki

Indukcyjność własna

Stosunek strumienia skojarzonego z cewki Ψ do prądu I płynącego przez cewkę

nazywamy indukcyjnością własną cewki.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

L =

gdzie: L – indukcyjność własna, Ψ – strumień magnetyczny.

Jednostka indukcyjności jest 1 henr [1 H].

L =

[A]

[Wb]

[A]

⋅

= [Ω s

⋅

] = [H]

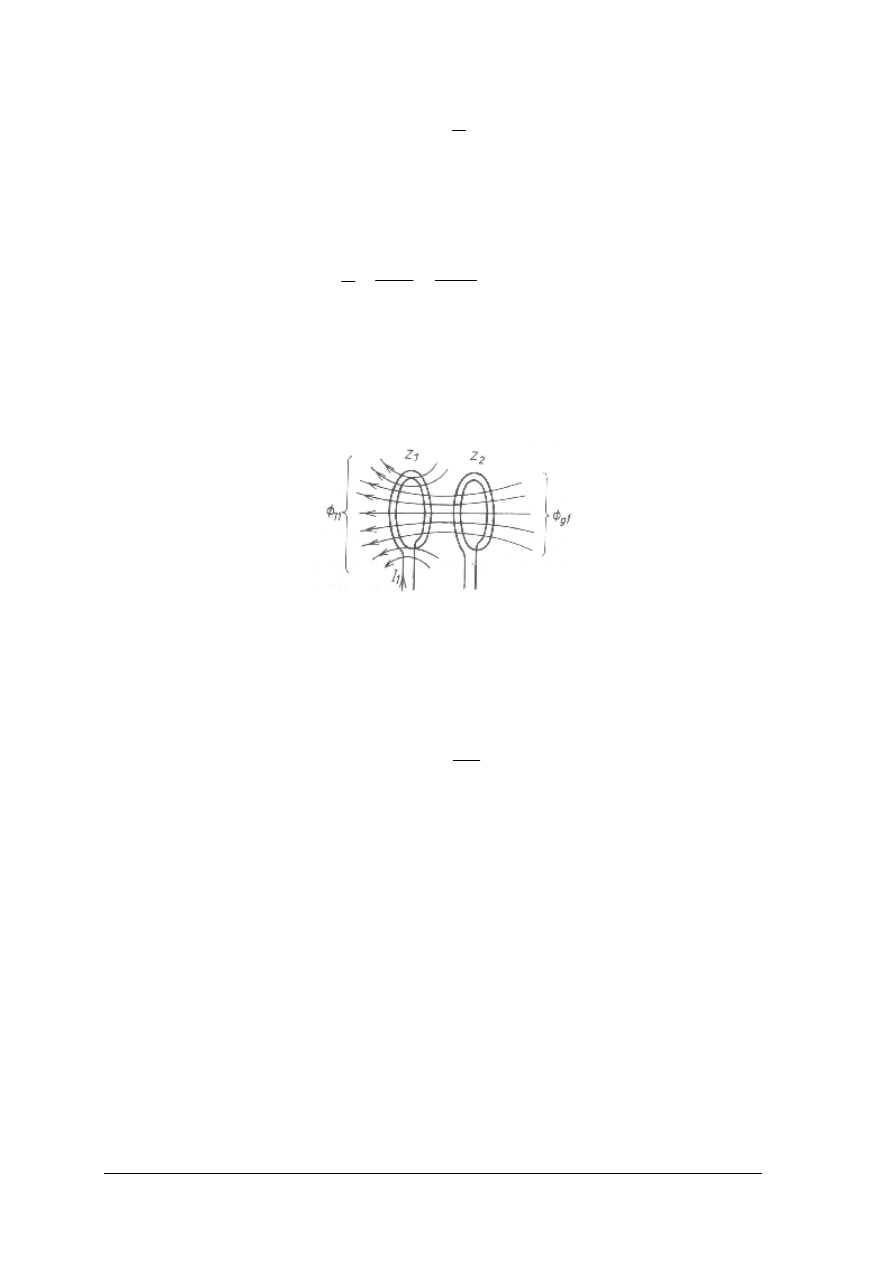
Indukcyjność wzajemna

Dwa elementy ułożone względem siebie w taki sposób, że pole magnetyczne jednego

z nich przenika, choćby częściowo, element drugi nazywamy elementami sprzężonymi
magnetycznie.

Rys. 15. Dwie cewki sprzężone magnetycznie [1, s. 127]

Indukcyjnością wzajemną cewki pierwszej z drugą nazywamy stosunek strumienia

magnetycznego wytworzonego w cewce pierwszej 1 i skojarzonego z cewką drugą 2, do
prądu płynącego w cewce 1. Oznaczamy M

gdzie: M

– indukcyjność wzajemna,

– strumień magnetyczny,

– natężenie prądu.

Współczynnikiem sprzężenia cewki pierwszej z cewką drugą (drugiej z pierwszą) nazywamy
stosunek strumienia magnetycznego głównego cewki pierwszej (drugiej) do strumienia
całkowitego tej cewki.

Zapamiętaj! – Cewka jest elementem zdolnym do gromadzenia energii w polu

magnetycznym.

Obwody magnetyczne, przenikalność magnetyczna

Obwodem magnetycznym nazywamy zespół elementów, tworzących zamkniętą drogę dla

strumienia magnetycznego Φ. Elementami obwodu magnetycznego są źródła strumienia
(magnesy trwałe, elektromagnesy) oraz elementy, wzdłuż których strumień się zamyka
(rdzenie szczeliny powietrzne).W każdym punkcie obwodu magnetycznego pole magnetyczne

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

można scharakteryzować dwiema wielkościami: indukcja magnetyczna B i natężenia pola
magnetycznego H.

B = μ H

⋅

gdzie: μ – przenikalność magnetyczna bezwzględna.

Jednostką jest henr

μ =

⋅

gdzie:

μ – przenikalność magnetyczna próżni,

μ = 4

−

⋅

[H/m],

μ – przenikalność magnetyczna względna środowiska.

Własności magnetyczne materiałów.

Ze względu na przenikalność magnetyczną względną

μ rozróżniamy następujące grupy

materiałów:

−

ferromagnetyczne – w których pod wpływem zewnętrznego pola magnetycznego
następuje znaczny wzrost indukcji (stal elektrotechniczna, stopy Alnico, ferryty),
w których

μ jest dużo większa od 1,

−

paramagnetyczne – w których własne pole magnetyczne jest zgodne ze zwrotem pola
zewnętrznego (platyna, powietrze, aluminium), w których

μ jest nieco większa od 1,

−

diamagnetyczne – w których własne pole magnetyczne osłabia zewnętrzne pole
magnetyczne,

μ jest nieco mniejsza od 1. Przykładami diamagnetyków są: woda, rtęć,

miedź, wszystkie gazy szlachetne (np. neon, argon, ksenon, krypton).
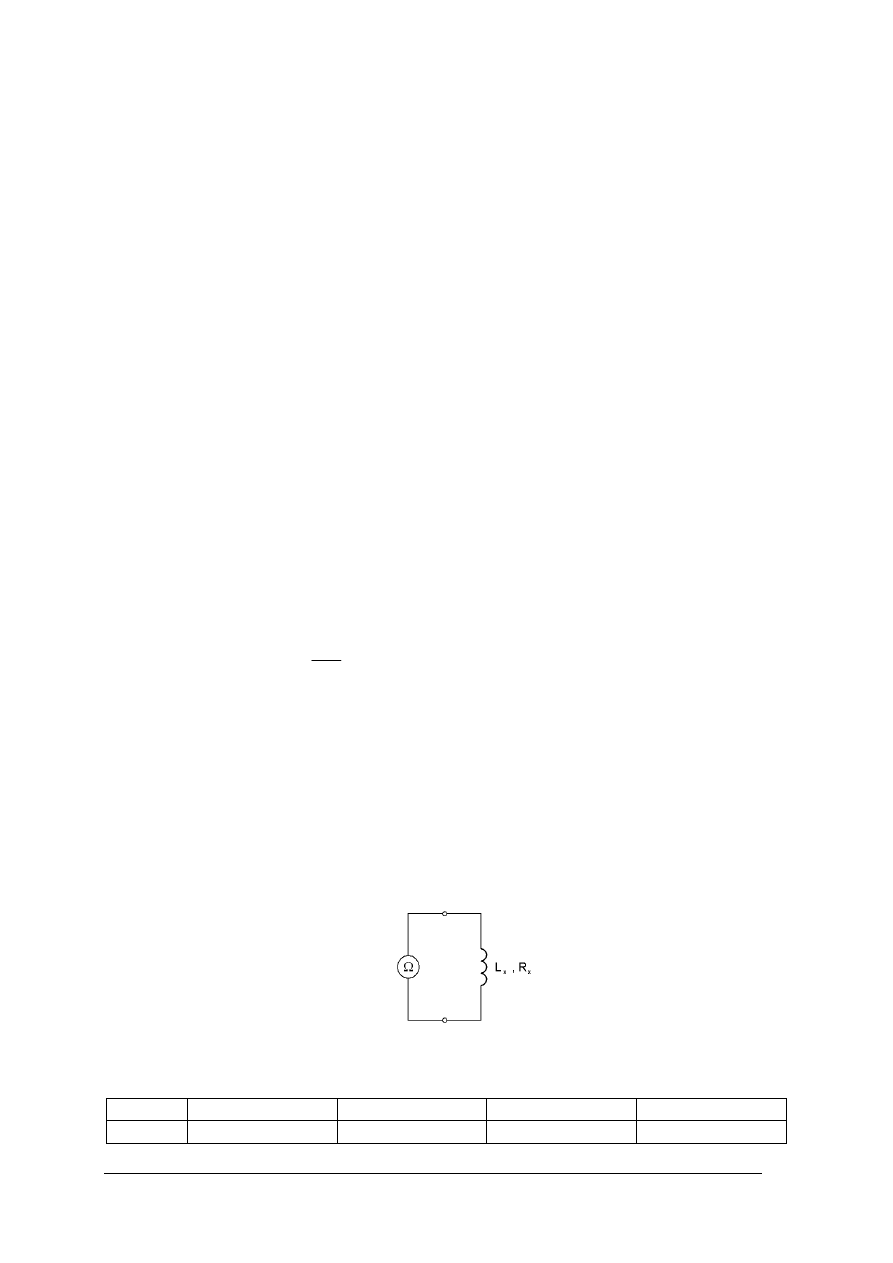
W zależności od kształtu krzywej histerezy rozróżniamy materiały:

−

magnetyczne miękkie a)

−

magnetyczne twarde 2b)

Rys. 16. Pętla histerezy materiału magnetycznego: a) pętla histerezy z punktami charakterystycznymi

b) porównanie pętli histerezy materiału magnetycznie twardego i miękkiego [6, s. 32]

Pole pętli histerezy jest proporcjonalne do straty energii na jeden zamknięty cykl
przemagnesowania w jednostce objętości.
Zastosowanie materiałów magnetycznych:
Materiały magnetycznie miękkie stosujemy się do budowy:

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

−

silników elektrycznych (blachy twornika),

−

przekaźników,

−

transformatorów sieciowych,

−

cewek z rdzeniem (ferryty).

Materiały magnetycznie twarde stosujemy się do budowy magnesów trwałych.

4.2.2. Pytania sprawdzające

Odpowiadając na pytania, sprawdzisz, czy jesteś przygotowany do wykonania ćwiczeń.

1. Czy potrafisz zdefiniować strumień magnetyczny?
2. Na czym polega zjawisko indukcji elektromagnetycznej?
3. Jaki związek zachodzi między indukcja B a natężeniem pola magnetycznego H?
4. Czy potrafisz zdefiniować natężenie prądu elektrycznego?

5. Co to jest indukcja własna?
6. Co określa reguła lewej dłoni?

4.2.3. Ćwiczenia

Ćwiczenie 1

Oblicz natężenie pola magnetycznego w odległości a = 15 cm od przewodu

prostoliniowego o prądzie I = 30 A.

Sposób wykonania ćwiczenia

Aby wykonać ćwiczenie, powinieneś:

1) skorzystać z wzoru: H=

2) obliczyć natężenie pola magnetycznego.

Wyposażenie stanowiska pracy

–

poradnik dla ucznia,

–

kalkulator,

–

zeszyt, przybory do pisania,

–

literatura wskazana przez nauczyciela.

Ćwiczenie 2

Wykonaj pomiar rezystancji cewek cyfrowym multimetrem.

Rysunek do ćwiczenia 2. Układ do pomiaru rezystancji cewek multimetrem cyfrowym

Tabela wyników pomiarów

= 10 mH

= 33mH

= 100mH

= 220mH

R [

Ω

]

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

Sposób wykonania ćwiczenia

Aby wykonać ćwiczenie, powinieneś:

1) zanalizować schemat pomiarowy,
2) skompletować potrzebną aparaturę i elementy,
3) połączyć obwód elektryczny,
4) wykonać pomiar rezystancji cewek omomierzem,
5) oszacować dokładność pomiarów i sformułować wnioski.

Wyposażenie stanowiska pracy:

−

cyfrowy multimetr,

−

cewki: L = 10 mH, L= 33 mH, L = 100 mH, L = 200 mH,

−

literatura wskazana przez nauczyciela,

−

materiały i przybory do pisania.

Ćwiczenie 3

Wykonaj pomiar indukcyjności metodą rezonansową, elementów zaproponowanych

przez nauczyciela.

Rysunek do ćwiczenia 3. Układ do pomiaru indukcyjności metodą rezonansową

Tabela wyników pomiarów i obliczeń.

Lp.

[Hz]

L [mH]

Sposób wykonania ćwiczenia

Aby wykonać ćwiczenie, powinieneś:

1) zanalizować schemat pomiarowy,
2) skompletować potrzebną aparaturę i elementy,
3) połączyć obwód elektryczny i zasilić go sygnałem sinusoidalnie zmienny o U = 1 V,

zmieniając częstotliwość od 100 Hz do 100 kHz,

4) określić częstotliwość rezonansową f

przy której wskazanie woltomierza jest największe,

5) obliczyć wartość indukcyjności każdej z badanych cewek na podstawie wzoru:

⋅

6) oszacować dokładność pomiarów i sformułować wnioski.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

Wyposażenie stanowiska pracy:

−

generator funkcyjny,

−

częstościomierz,

−

multimetr analogowy,

−

kondensator C = 22 nF,

−

cewki L = 10 mH, L = 33 mH, L = 100 mH, L = 220 mH,

−

rezystor R = 100

Ω

/2 W,

−

literatura wskazana przez nauczyciela,

−

przybory do pisania.

4.2.4. Sprawdzian postępów

Czy potrafisz:

Tak

Nie

1) określić własności magnetyczne materiałów?

2) podać, regułę śruby prawoskrętnej?

3) wyjaśnić, co to jest przenikalność elektryczna w próżni?

4) wyznaczyć kierunek pola magnetycznego w solenoidzie?

5) dokonać podziału, materiałów magnetycznie miękkich?

6) wyjaśnić co nazywamy indukcją wzajemną?

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

4.3. Właściwości i parametry charakterystyczne dla prądu

przemiennego jednofazowego i trójfazowego

4.3.1. Materiał nauczania

W praktyce częściej niż prądem stałym mamy do czynienia z prądem przemiennym. Jest

on powszechnie stosowany w elektroenergetyce. To właśnie w postaci prądu przemiennego
energia elektryczna jest dostarczana do domowych i przemysłowych instalacji elektrycznych.
Prąd przemienny odznacza się tym, że wartość jego natężenia i kierunek przepływu zmieniają
się okresowo w czasie.

Wielkości charakterystyczne prądu sinusoidalnego

Wartość chwilowa i =

ωt

sin

⋅

gdzie: I

– wartość maksymalna (amplituda),

ω – pulsacja (prędkość kątowa),

t – czas.

Okresem oznaczonym literą T, nazywa się czas, po którym przebieg się powtarza.

Okres prądu sinusoidalnego T =

2π

[s].

Pulsacja ω = 2 π f [rad/s].
Odwrotnością kresu jest częstotliwość f, wyrażająca liczbę okresów przypadających na jedną
sekundę

f =

Jednostką częstotliwości jest herc [Hz], 1 Hz =

Wartością skuteczną prądu przemiennego nazywa się taką wartość prądu stałego, który
płynąc przez rezystor spowoduje wydzielanie się takiej samej ilości ciepła (energii) co
płynący w tym samym czasie prąd przemienny (sinusoidalnie zmienny).

I =

oraz U =

gdzie: I – natężenie prądu,

– wartość maks. natężenia prądu,

U – napięcie,

– wartość maks. napięcia.

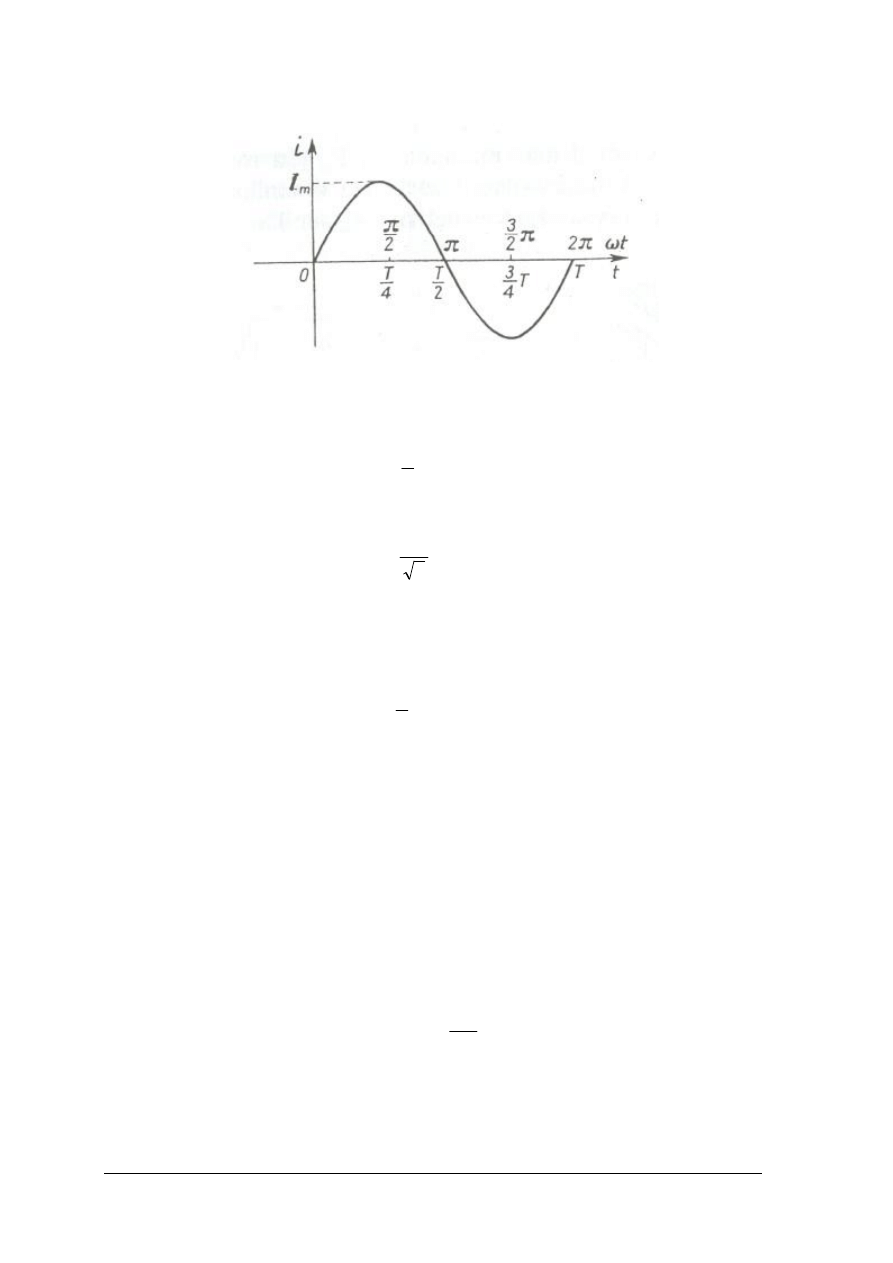
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

Rys. 17. Wykres prądu sinusoidalnie zmiennego [7, s. 32]

Wartość średnia półokresowa prądu sinusoidalnego I

śr

= 0,637 I

Analogicznie określa się wartość skuteczną i średnią napięcia sinusoidalnego

U =

= 0,707 U

gdzie: U – napięcie,

– wartość maks. napięcia

śr

– wartość średnia napięcia.

śr

= 0,637 U

Wartość skuteczna określa się dużymi literami bez wskaźników. Wartości skuteczne

prądów i napięć można mierzyć za pomocą mierników elektrodynamicznych
i elektromagnetycznych.
Wartości średnie prądów i napięć można mierzyć miernikami magnetoelektrycznymi.
W praktyce posługujemy się wartościami skutecznymi napięć i prądów.

Elementy R, L, C w obwodzie prądu sinusoidalnego

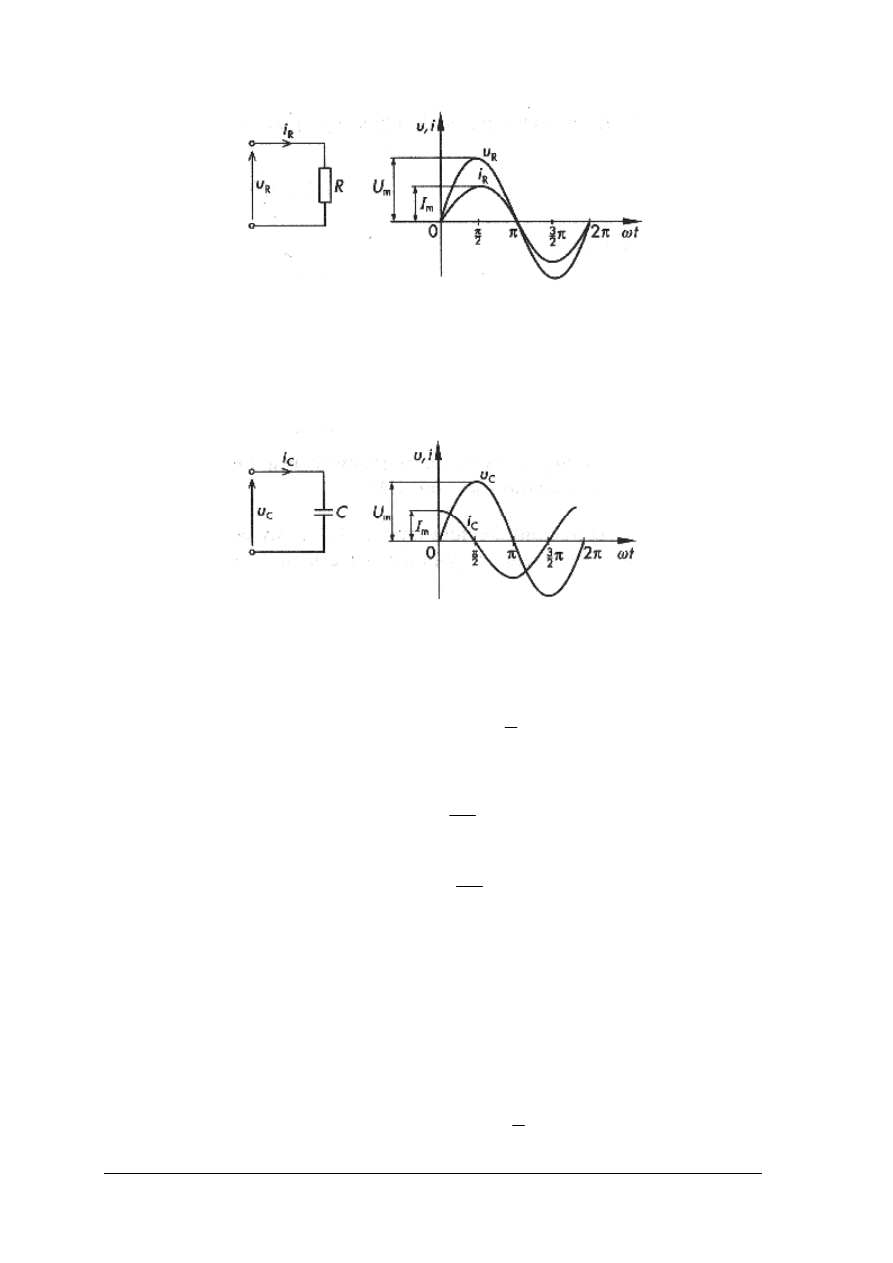
Gdy do rezystora R doprowadzi się napięcie sinusoidalnie zmienne:

= U

sin ω t

Amplituda prądu:

Prąd elektryczny w rezystorze zamienia się zgodnie ze zmianami napięcia w czasie. Tak

więc prąd płynący w rezystorze nie jest przesunięty w fazie względem napięcia.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

Rys. 18. Przebieg czasowy napięcia i prądu sinusoidalny – rezystora [6, s. 51]

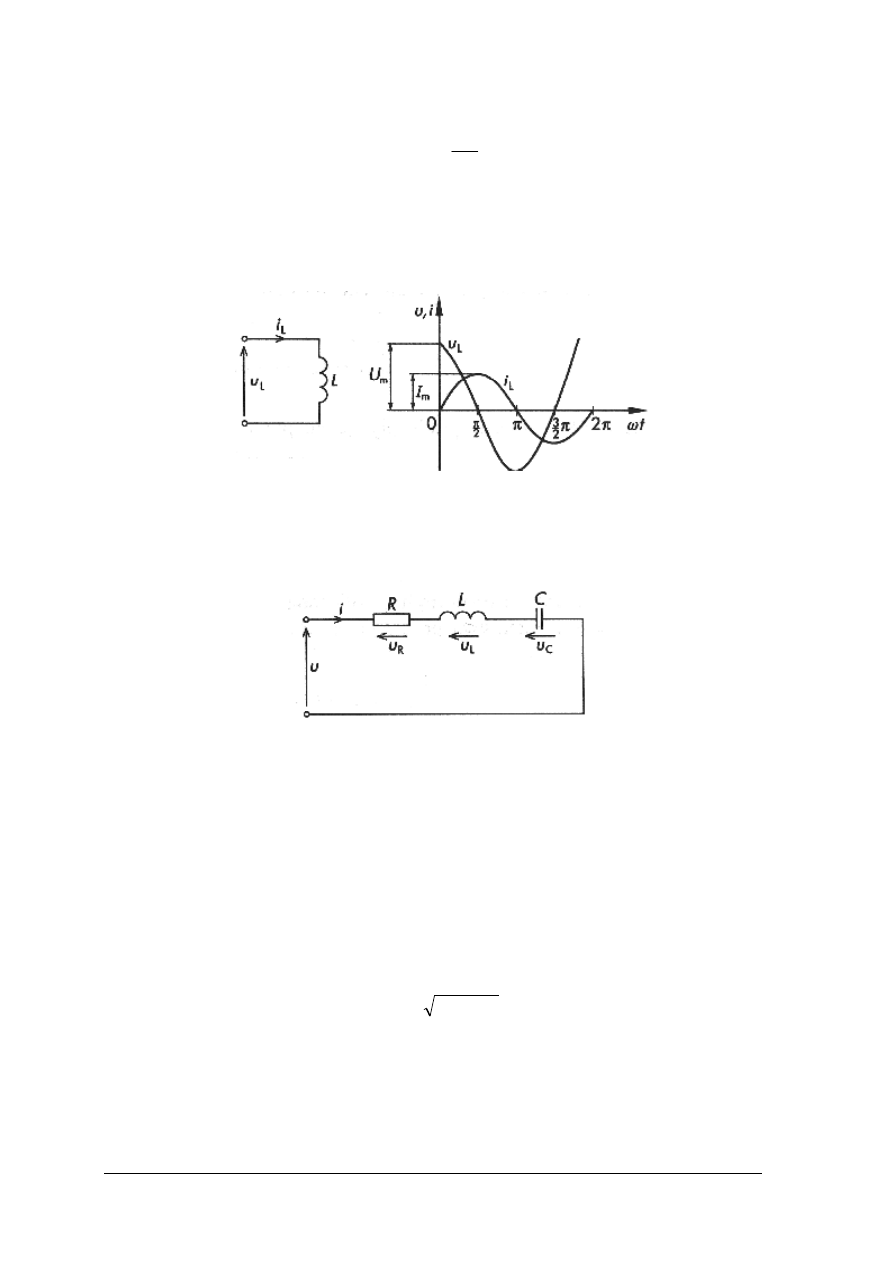
W kondensatorze umieszczonym w obwodzie prądu sinusoidalnego, energia elektryczna

jest zamieniana na energię pola elektrycznego i magazynowania w dielektryku znajdującym
się pomiędzy jego okładzinami.

Rys. 19. Przebieg czasowy napięcia i prądu sinusoidalny – kondensatora [6, s. 51]

Przebieg prądu płynącego przez kondensator wyprzedza w fazie o kąt π/2 (90º) napięcie
panujące na kondensatorze.

= I

sin ( ω t +

)

Wartość skuteczna prądu płynącego przez kondensator:

ωC

– reaktancja pojemnościowa kondensatora.

Jednostką reaktancji pojemnościowej jest om [Ω].

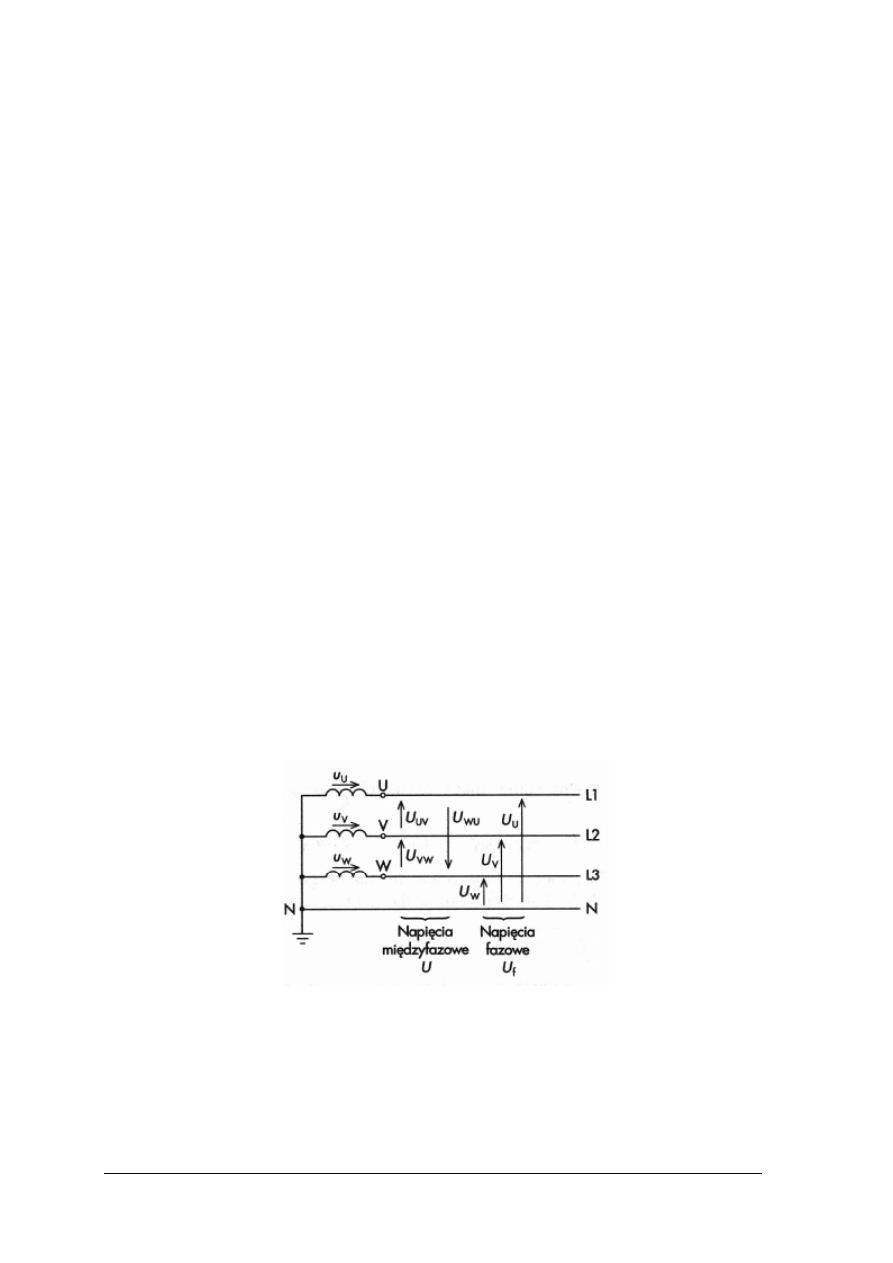
W cewce indukcyjnej mamy do czynienia z magazynowaniem energii w polu

magnetycznym.
Przebieg prądu płynącego przez cewkę opóźnia się w fazie o kąt π/2 (90º) względem napięcia
panującego na cewce.

= I

·sin(ωt –

)

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

Wartość skuteczna prądu płynącego przez cewkę:

= ω∙L

– reaktancja indukcjyjna cewki.

Jednostka reaktancji cewki jest om [Ω].

Rys. 20. Przebieg czasowy napięcia i prądu sinusoidalny – cewki [6, s. 51]

Obwód prądu sinusoidalnego z szeregowo połączonymi elementami R, L, C.

Rys. 21. Przebieg czasowy napięcia i prądu sinusoidalnego [6, s. 53]

Wartość skuteczna napięcia

U = Z∙I

gdzie: U – napięcie,

I – natężenie prądu,

R – rezystancja,

X – reaktancja,

Z – impedancja.

Z =

Z – impedancja.
Jednostką impedancji jest om [Ω].

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

Moc prądu sinusoidalnego

W obwodzie prądu sinusoidalnego podobnie jak i w obwodzie prądu stałego, rezystor

pobiera energię elektryczną i przetwarza na ciepło.

Moc czynna (P) stanowi iloczyn wartości skutecznych napięcia i prądu oraz cosφ kąta

przesunięcia fazowego między przebiegami prądu i napięcia.

P = U ∙I ∙cosφ

cosφ – współczynnik mocy

Jednostką mocy czynnej jest wat [W].

Moc bierna (Q) stanowi iloczyn wartości skutecznych napięcia i prądu oraz sinφ kąta

przesunięcia fazowego między przebiegami prądu i napięcia.

Q = U ∙I ∙ sinφ

Jednostką mocy biernej jest war [var].

Moc pozorna (S) stanowi iloczyn wartości skutecznych napięcia i prądu.

S = U ∙I

Jednostką mocy pozornej jest woltoamper [V∙A].

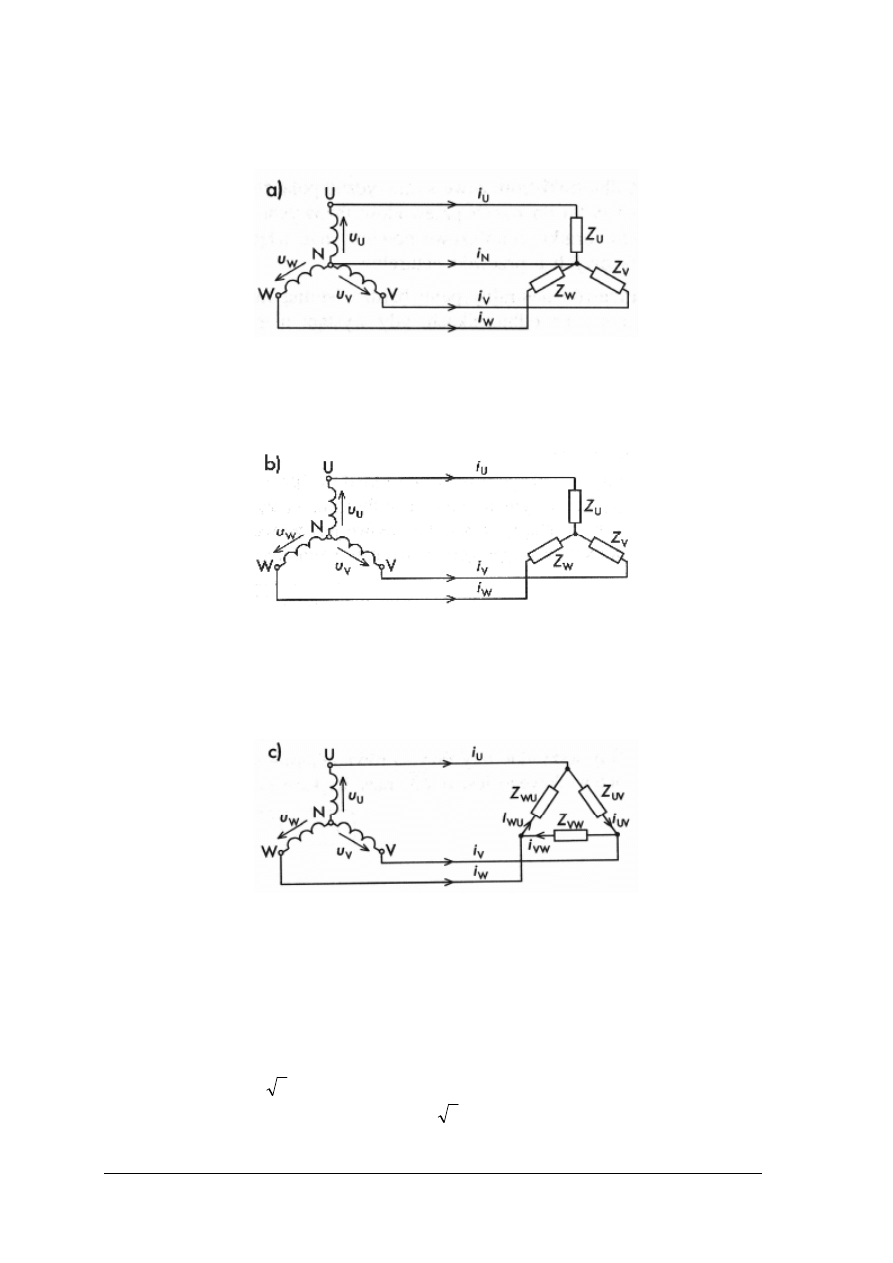
Obwody trójfazowe

Układem trójfazowym nazywamy zbiór trzech obwodów elektrycznych, w którym

działają trzy napięcia źródłowe sinusoidalnie zmienne o jednakowej częstotliwości,
przesunięte względem siebie o kąt 120° i wytwarzane w jednym źródle energii, którym
najczęściej jest generator lub prądnica trójfazowa.

Prądem przewodowym nazywamy prąd płynący w przewodzie fazowym i oznaczamy: I

, I

Prądem fazowym nazywamy prąd płynący w fazie źródła lub odbiornika i oznaczamy: I

, I

Rys. 22. Napięcia międzyfazowe i fazowe w układzie czteroprzewodowym [6, s. 57]

Trójfazowe źródło lub odbiornik energii elektrycznej może być połączony w:

−

trójkąt,

−

gwiazdę.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

Układ połączeń w gwiazdę występuje w dwóch odmianach:

−

czteroprzewodowa z przewodem neutralnym

Rys. 23. Układ trójfazowy prądu przemiennego:

a) czteroprzewodowy z połączeniem odbiornika w gwiazdę [6, s. 57]

−

trójprzewodowy

Rys. 24. Układ trójfazowy prądu przemiennego:

b) trójprzewodowy z połączeniem odbiornika w gwiazdę [6, s. 57]

Układ połączeń w trójkąt

Rys. 25. Układ trójfazowy prądu przemiennego:

c) trójprzewodowy z połączeniem odbiornika w trójkąt [6, s. 57]

W tym przypadku odbiornik łączy się z siecią zasilającą trzema przewodami. Napięcie
międzyfazowe jest wówczas równe napięciu fazowemu (czyli napięciu występującemu na
uzwojeniu jednej fazy):

U = U

Gdy wszystkie trzy fazy są równomiernie obciążone, wówczas natężenie prądu

przewodowego jest o 3 razy większe od prądu fazowego.

I = 3 ∙I

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

Moc prądu trójfazowego oblicza się ze wzorów:

Moc czynna:

cos

⋅

Moc bierna:

sin

⋅

Moc pozorna:

⋅

ϕ =

gdzie: S – moc pozorna,

P – moc czynna,

Q – moc bierna,

– napięcie międzyfazowe,

U – napięcie,

– natężenie pradu trójfazowego,

I – natężenie prądu.

Rezonans napięć i prądów

Zjawisko rezonansu przedstawia taki stan pracy obwodu elektrycznego, przy którym

reaktancja wypadkowa obwodu lub susceptancja wypadkowa jest równa zeru. Napięcie i prąd
na zaciskach rozpatrywanego obwodu są zgodne w fazie.
Częstotliwością rezonansową (f

) nazywamy częstotliwość, przy której reaktancja wypadkowa

lub susceptancja wypadkowa obwodu jest równa zeru.

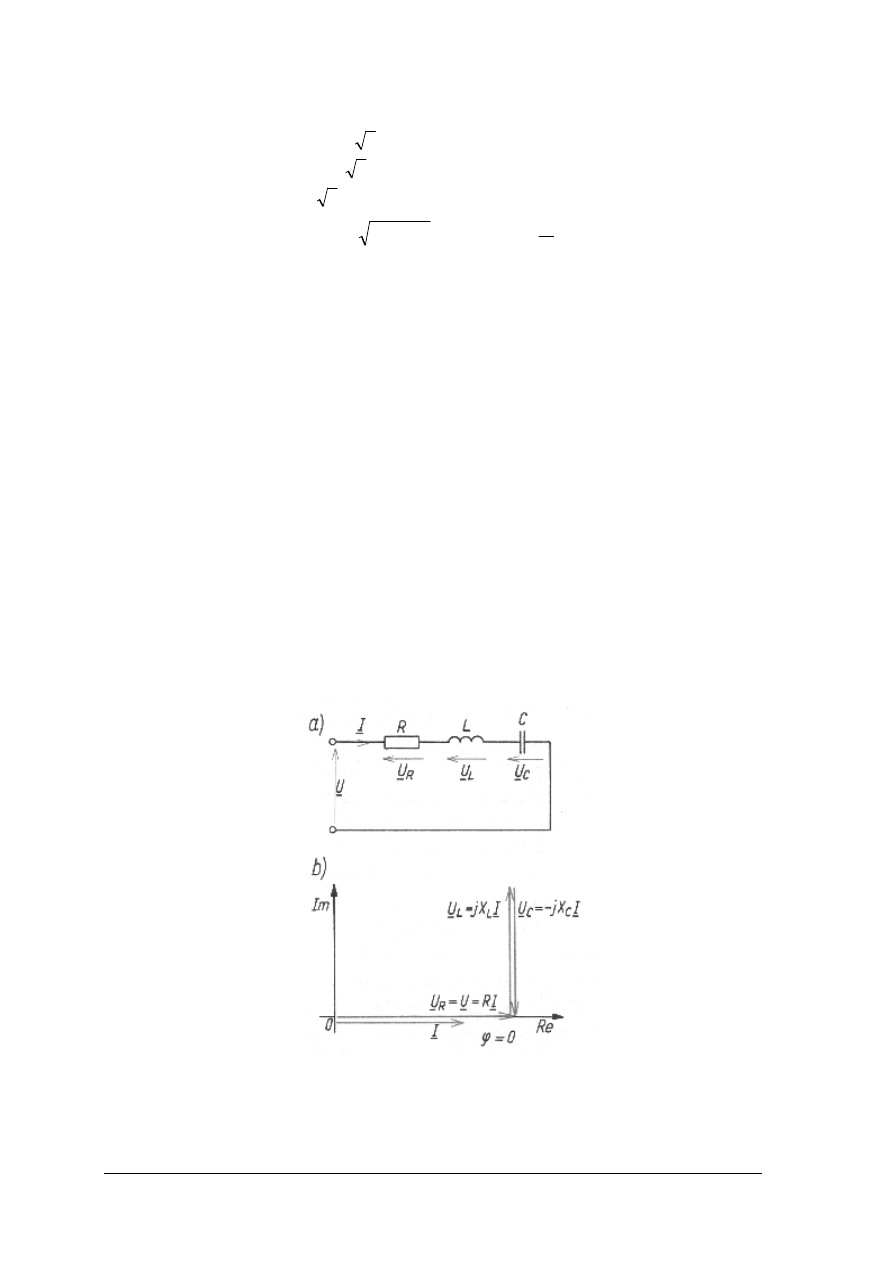
Rezonans napięć

Rezonansem napięć lub rezonansem szeregowym nazywamy rezonans występujący

w obwodzie o połączeniu szeregowym elementów R, L, C charakteryzujący się równością
reaktancji indukcyjnej i reaktancji pojemnościowej.

Rys. 26. Rezonans napięć w dwójniku szeregowym R, L, C:

a) schemat obwodu; b) wykres wektorowy w stanie rezonansu [1, s. 209]

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

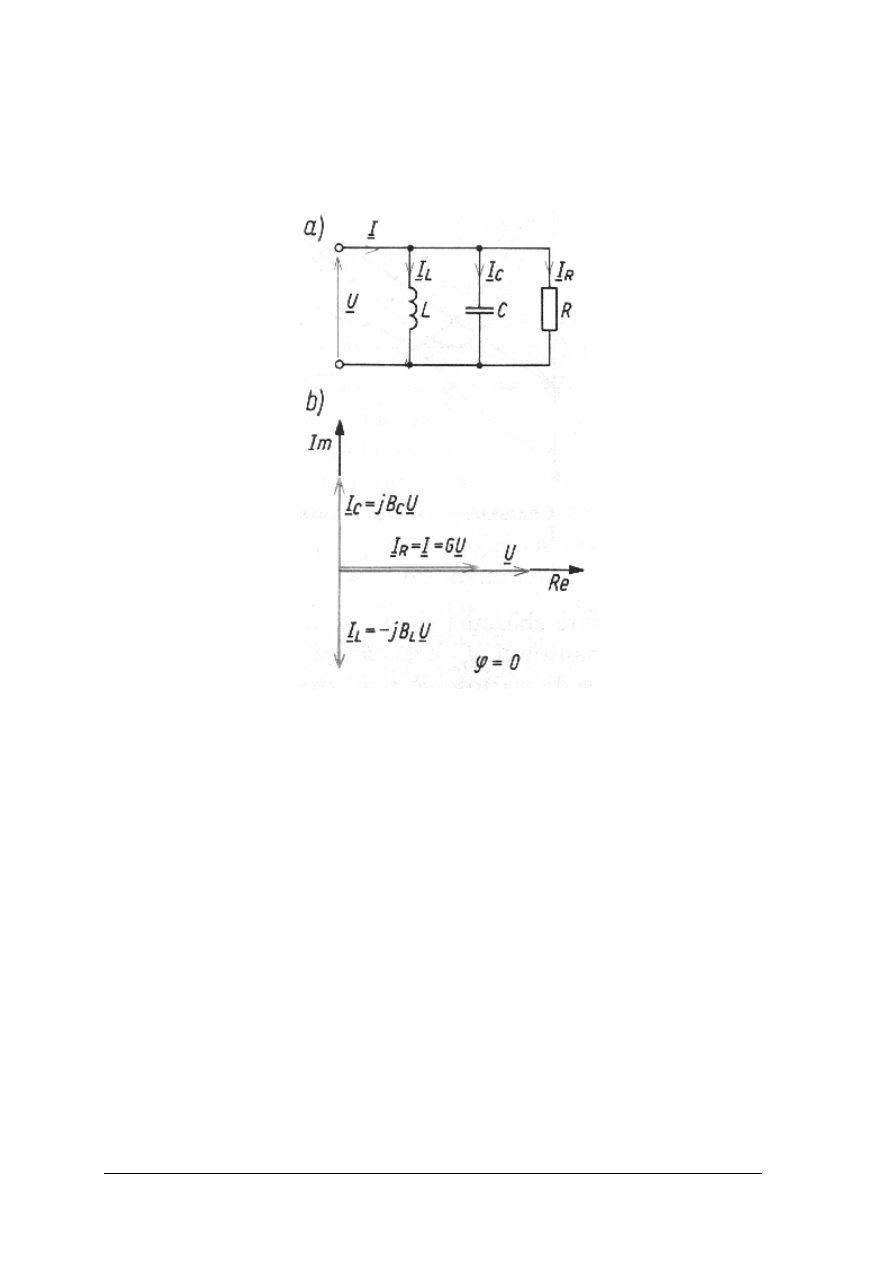
Rezonans prądów

Rezonansem prądów lub rezonansem równoległym nazywamy rezonans występujący

w obwodzie o połączeniu równoległym elementów R, L, C, charakteryzujący się równością
susceptancji indukcyjnej i susceptancji pojemnościowej.

Rys. 27. Rezonans prądów w dwójniku równoległym R, L, C:

a) schemat obwodu; b) wykres wektorowy w stanie rezonansu [1, s. 212]

4.3.2. Pytania sprawdzające

Odpowiadając na pytania, sprawdzisz, czy jesteś przygotowany do wykonania ćwiczeń.

1. Co nazywamy wartością skuteczną?
2. Jakie znasz wielkości charakterystyczne prądu sinusoidalnego?
3. Na czym polega zjawisko rezonansu?
4. Jaka jest zależność między mocą czynną, bierną i pozorną?
5. Co nazywamy układem trójfazowym?
6. W jaki sposób można łączyć źródła i odbiorniki trójfazowe?
7. Co to jest reaktancja cewki i kondensatora?
8. Co nazywamy rezonansem prądów?

4.3.3. Ćwiczenia

Ćwiczenie 1

Oblicz częstotliwość rezonansową obwodu, w którym wystąpił rezonans równoległy, jeśli

dane są następujące wielkości: C = 1 μF, L = 10 H.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

Sposób wykonania ćwiczenia

Aby wykonać ćwiczenie, powinieneś:

1) skorzystać z wzoru f

2π

⋅

2) obliczyć częstotliwość rezonansową f

Wyposażenie stanowiska pracy:

–

poradnik dla ucznia,

–

kalkulator,

–

zeszyt, przybory do pisania,

–

literatura wskazana przez nauczyciela.

Ćwiczenie 2

Cewkę o indukcyjności L = 0,127 H i rezystancji R

= 5 Ω włączono w szereg

z rezystorem o rezystancji R

= 25 Ω na napięcie sinusoidalne o wartości skutecznej

U = 230 V i częstotliwości f = 50 Hz. Obliczyć prąd pobierany z sieci moce: czynną i pozorną
oraz współczynnik mocy danego układu szeregowego.

Sposób wykonania ćwiczenia

Aby wykonać ćwiczenie, powinieneś:

1) obliczyć rezystancję całkowitą,
2) obliczyć reaktancję indukcyjną,
3) obliczyć impedancję układu szeregowego,
4) obliczyć wartość skuteczną prądu,

5) obliczyć współczynnik mocy cosφ =

6) obliczyć moc: czynną, bierną i pozorną.

Wyposażenie stanowiska pracy:

–

poradnik dla ucznia,

–

kalkulator,

–

zeszyt, przybory do pisania,

–

literatura wskazana przez nauczyciela.

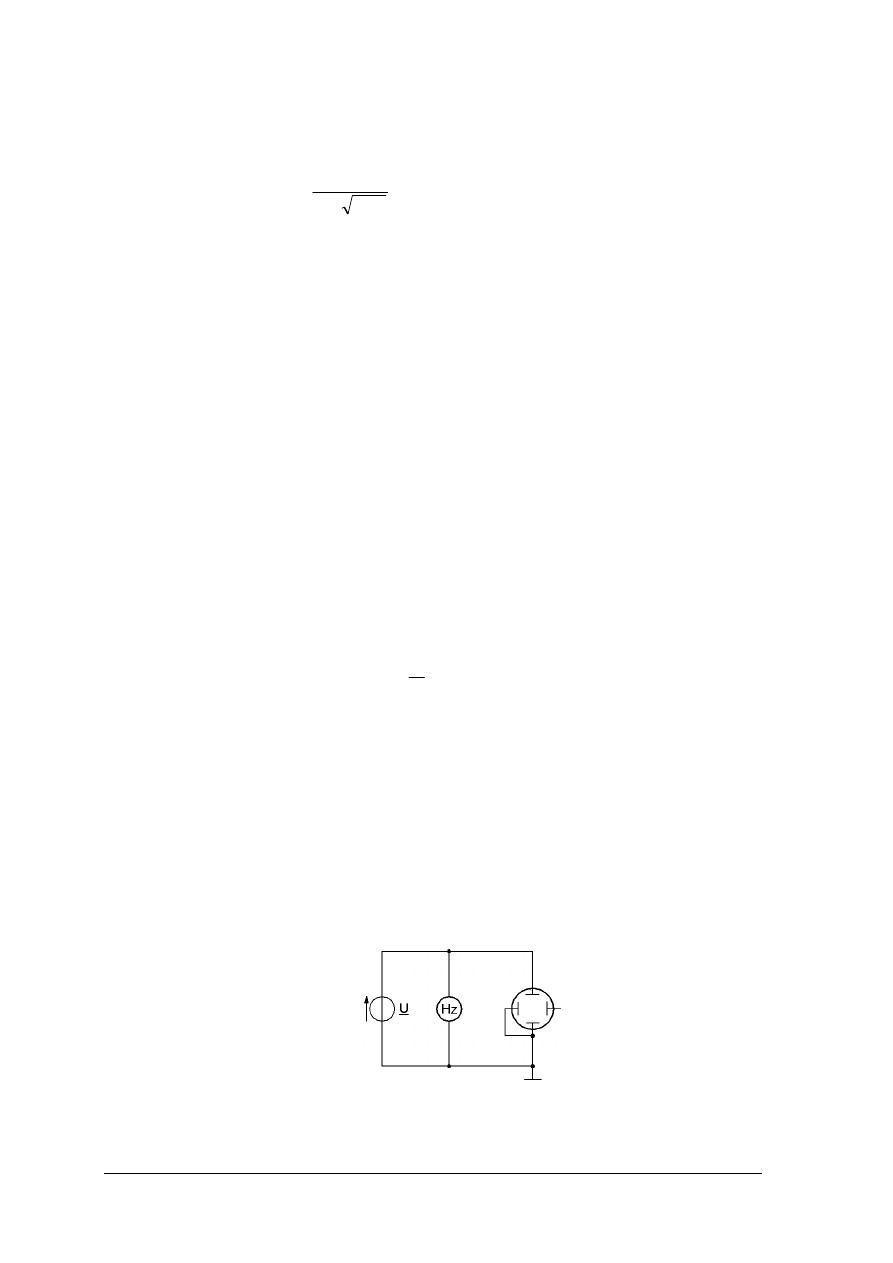
Ćwiczenie 3

Wykonaj pomiar częstotliwości oraz okresu napięcia sinusoidalnie zmiennego za pomocą

oscyloskopu i częstościomierza.

Rysunek do ćwiczenia 3. Układ do pomiaru częstotliwości i okresu napięcia sinusoidalnie zmiennego

oscyloskopem i częstościomierzem.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

Tabela wyników pomiarów i obliczeń.

Lp. L

[działki] C

[ms/działki] T

[ms] f

[Hz] Wskazanie częstościomierza [Hz]

wartość okresu z oscylogramu; C

współczynnik odchylania poziomego oscyloskopu.

Sposób wykonania ćwiczenia

Aby wykonać ćwiczenie, powinieneś:

1) zanalizować schemat pomiarowy,
2) skompletować potrzebną aparaturę,
3) połączyć obwód elektryczny i zasilić go napięciem sinusoidalnie zmiennym,
4) wykonać pomiary częstotliwości napięcia sinusoidalnie zmiennego, częstościomierzem,
5) przerysować zaobserwowane oscylogramy, a wyniki pomiarów zapisać w tabeli,
6) obliczyć wartości T

, f

na podstawie wzorów:

⋅

7) porównać obliczone wartości częstotliwości ze wskazaniami częstościomierza,
8) oszacować dokładność pomiarów i sformułować wnioski.

Wyposażenie stanowiska pracy:

−

generator funkcyjny,

−

częstościomierz,

−

oscyloskop,

−

literatura wskazana przez nauczyciela,

−

materiały i przybory do pisania.

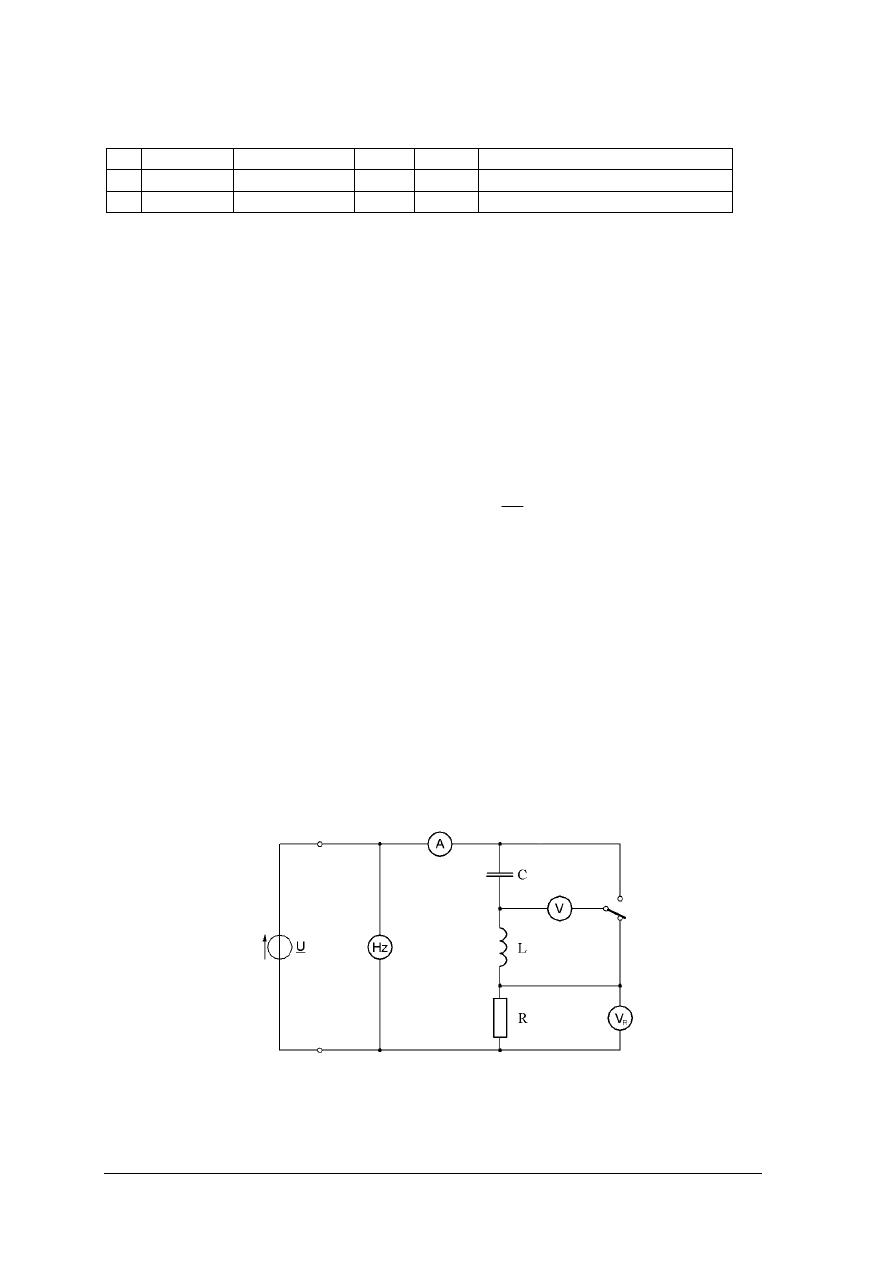
Ćwiczenie 4

Zbadaj obwód szeregowy RLC.

Rysunek do ćwiczenia 4. Układ do badania obwodu szeregowego RLC

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

Tabela wyników pomiarów i obliczeń

f[kHz]

0,1

0,5

I [mA]

[V]

[

Ω

]

[

Ω

]

Ω

]

Sposób wykonania ćwiczenia

Aby wykonać ćwiczenie, powinieneś:

1) zanalizować schemat pomiarowy,
2) skompletować potrzebną aparaturę,
3) połączyć obwód elektryczny i zasilić go,
4) wykonać pomiary prądu I, napięcia: U

– na rezystorze, U

– na kondensatorze i U

– na

cewce,

5) obliczyć wartości reaktancji pojemnościowej X

, reaktancji indukcyjnej X

i impedancji

z obwodu z zależności:

⋅

)

−

6) wyznaczyć charakterystyki impedancji Z, reaktancji pojemnościowej X

, indukcyjnej X

oraz napięć: U

– na rezystorze, U

– na kondensatorze i U

– na cewce w funkcji

częstotliwości,

7) odczytać z otrzymanych wykresów wartość częstotliwości rezonansowej fr,
8) obliczyć wartość częstotliwości rezonansowej fr na podstawie zależności:

⋅

9) porównać wartości fr otrzymane z wykresów i obliczeń,
10) oszacować dokładność pomiarów i sformułować wnioski.

Wyposażenie stanowiska pracy

−

generator funkcyjny,

−

częstościomierz,

−

2 multimetry cyfrowe i multimetr analogowy,

−

rezystor R = 470

Ω

/2 W,

−

cewka L = 33 mH,

−

kondensator C = 47 nF/250 V,

−

literatura wskazana przez nauczyciela,

−

materiały i przybory do pisania.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

4.3.4. Sprawdzian postępów

Czy potrafisz:

Tak

Nie

1) obliczyć wartość reaktancji indukcyjnej obwodu na podstawie jego

parametrów?

2) wyjaśnić pojęcia: moc bierna, czynna i pozorna?

3) narysować układ trójfazowy symetryczny połączony w gwiazdę?

4) narysować układ trójfazowy symetryczny połączony w trójkąt?

5) wyjaśnić,

różnice

pomiędzy

układem

trójprzewodowym

a czteroprzewodowym?

6) wyjaśnić co to jest napięcie fazowe?

7) narysować wykres przebiegu czasowego na podstawie parametrów

przebiegu sinusoidalnego?

8) określić zmiany reaktancji indukcyjnej przy zmianach częstotliwości?

9) zanalizować schemat pomiarowy obwodu szeregowego RLC?

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

4.4. Filtry częstotliwościowe

4.4.1. Materiał nauczania

Filtr jest to fragment obwodu elektrycznego lub obwodu elektronicznego

odpowiedzialny za przepuszczanie lub blokowanie sygnałów o określonym zakresie
częstotliwości lub zawierającego określone harmoniczne.

Ze względu na przeznaczenie filtry można podzielić na cztery podstawowe rodzaje:

−

dolnoprzepustowe,

−

górnoprzepustowe,

−

środkowoprzepustowe,

−

środkowozaporowe.
Ze względu na konstrukcję i rodzaj działania filtry można podzielić na:

−

pasywne – nie zawierają elementów dostarczających energii do obwodu drgającego,
zawierają tylko elementy RLC,

−

jednostopniowe,

−

wielostopniowe,

−

aktywne – zawierają zarówno elementy RLC, jak również i elementy dostarczające
energię do filtrowanego układu np. wzmacniacze, układy nieliniowe.
Filtry można również podzielić na typy obwodów w jakich są używane:

−

analogowe,

−

cyfrowe.
Parametry filtrów częstotliwościowych to:

−

pasmo przepustowe – zakres częstotliwości, które filtry przepuszczają,

−

pasmo tłumieniowe – zakres częstotliwości, które filtry tłumią,

−

częstotliwość graniczna f

– oddziela pasmo przepustowe i tłumieniowe,

−

współczynnik tłumienia a – miara zmian napięcia przy przejściu od zacisków
wejściowych do zacisków wyjściowych filtra, w paśmie przepustowym a = 0 (lub jest
bliskie zeru ), w paśmie tłumieniowym a jest bardzo duże,

−

charakterystyka częstotliwościowa – określa napięcie wyjściowe w funkcji częstotliwości

(zwyczajowo jest to funkcja pulsacji

Filtry mogą mieć strukturę czwórników typu:

lub

Filtry dolnoprzepustowe

Filtr dolnoprzepustowy to układ elektroniczny, optyczny, akustyczny lub inny element

przetwarzający sygnał (np. odpowiedni algorytm) przepuszczający częstotliwości sygnału
poniżej ustalonej częstotliwości granicznej, tłumi składowe widma leżące w górnej jego
części. Układ elektroniczny zbudowany jest zazwyczaj z cewki lub rezystora i kondensatora.
Ma jedno pasmo przepustowe i jedno tłumiące. Filtr dolnoprzepustowy jest układem
całkującym stratnym. Wielkością charakteryzującą taki układ jest transmitancja, określana
jako stosunek napięcie wyjściowego do wejściowego.

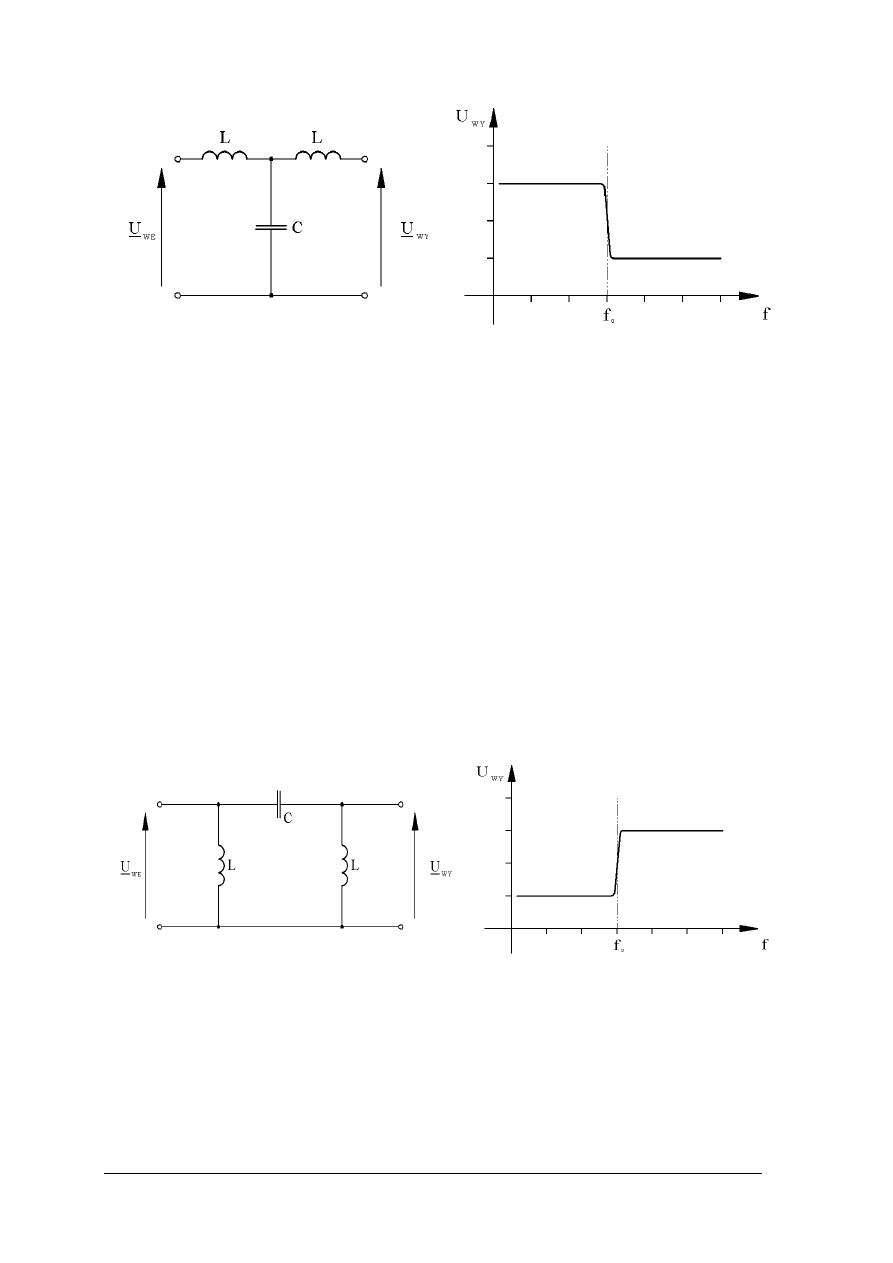
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

Rys. 28. a) Filtr dolnoprzepustowy, b) charakterystyka częstotliwościowa filtru dolnoprzepustowego [1, s. 308]

Przykładem optycznego filtra dolnoprzepustowego jest płytka z kryształu dwójłomnego
znajdująca się przed przetwornikiem optoelektronicznym (np. CCD, CMOS) w cyfrowym
aparacie fotograficznym.

Filtry górnoprzepustowe

Filtr górnoprzepustowy to układ elektroniczny, przepuszczający częstotliwości sygnału

powyżej ustalonej częstotliwości granicznej, a tłumi składowe widma leżące w dolnej jego
części.

W zależności od konstrukcji filtr taki zbudowany jest jako:

−

reaktancyjne L, C, zbudowane z cewek i kondensatorów,

−

pojedyncza cewka bądź kondensator,

−

bezindukcyjne, pasywne R, C,

−

piezoceramiczne,

−

aktywne – zawierające wzmacniacze,

−

cyfrowe.

Rys. 29. a) Filtr górnoprzepustowy; b)charakterystyka częstotliwościowa filtru górnoprzepustowego [1, s. 308]

Filtry pasmowe

Filtry pasywne są wykonane tylko z pasywnych elementów RLC. Przy odpowiednim

połączeniu elementów można uzyskać wszystkie typy filtrów. Filtry pasywne wykonuje się
też jako elementy z materiałów piezoelektrycznych z odpowiednio napylonymi elektrodami.

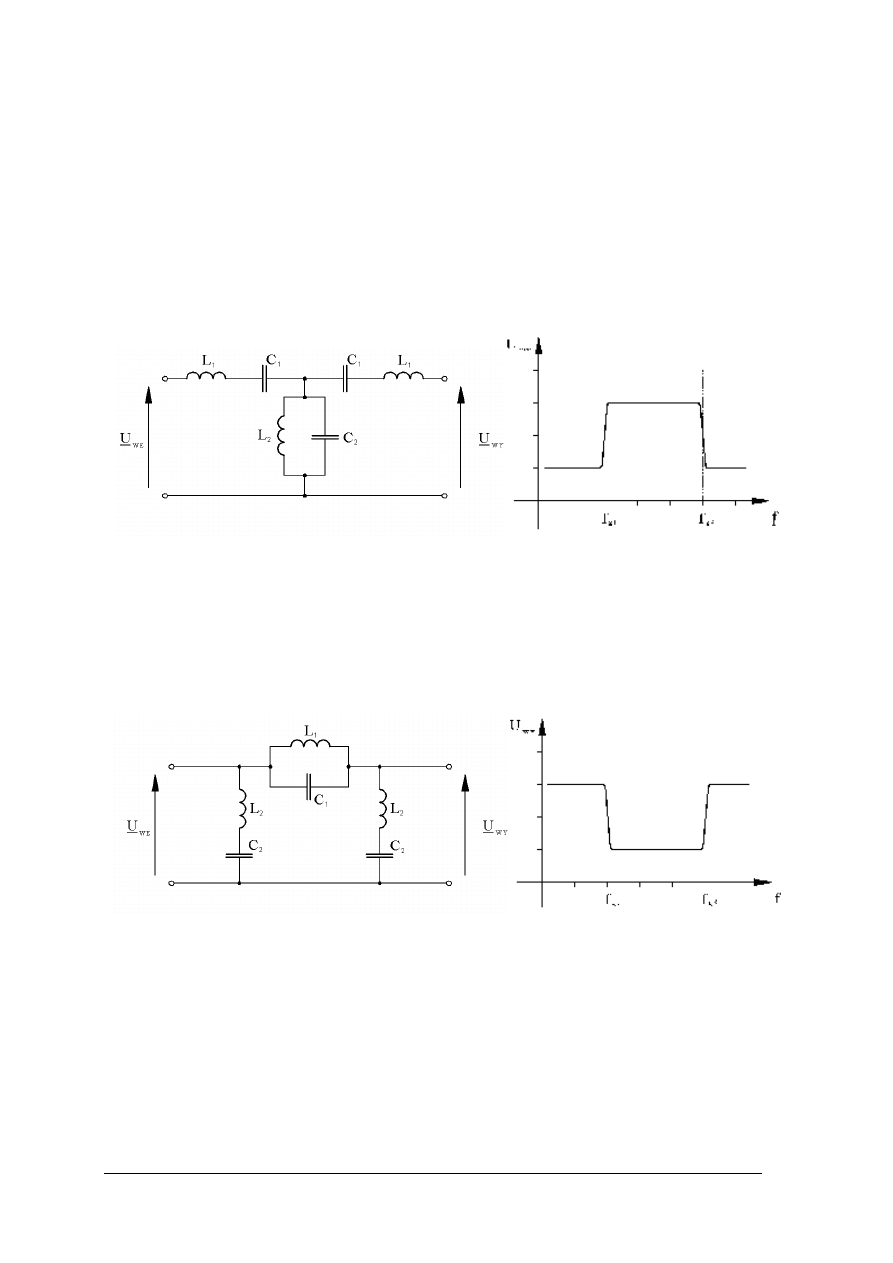
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

Najprostszym rodzajem filtra pasywnego szeroko stosowanego w elektronice jest filtr

dolnoprzepustowy w postaci kondensatora o dużej pojemności połączonego równolegle do
filtrowanego napięcia (z ewentualnym szeregowym rezystorem). Urządzenia elektroniczne są
często zasilane z sieci energetycznej za pomocą zasilaczy. Napięcie sieci (o skutecznej
wartości 230 V) jest transformowane na niskie napięcie użyteczne (np. 12 V), które jest
następnie prostowane za pomocą prostownika dwupołówkowego. Napięcie wyjściowe takiego
prostownika ma przebieg tętniący. Dopiero równoległe dołączenie kondensatora
o dpowiedniej pojemności powoduje znaczne zmniejszenie amplitudy tętnień, czyli właśnie
proces filtrowania. Im większa jest pojemność użytego kondensatora tym bardziej napięcie
wyjściowe ma przebieg zbliżony do przebiegu stałego.

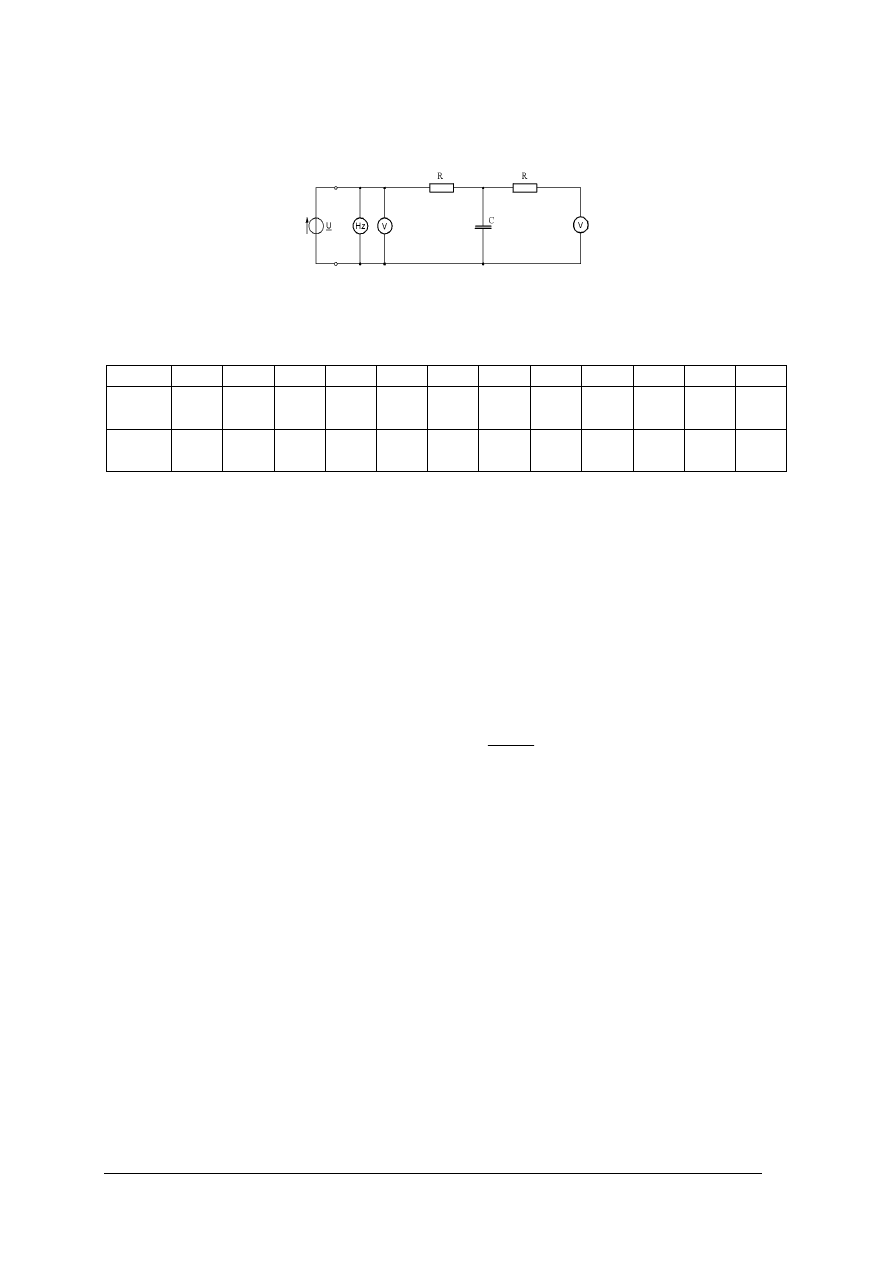
Rys. 30. a) Filtr pasmowy; b) charakterystyka częstotliwościowa filtru pasmowego [1, s. 311]

Filtry zaporowe

Filtry zaporowe przepuszczają sygnały o wszystkich częstotliwościach za wyjątkiem

sygnałów określonego pasma ograniczonego częstotliwościami granicznymi f

i f

g2.

gałęziach

podłużnych

tych

filtrów

występują

obwody

rezonansu

prądów,

a w poprzecznych obwody rezonansu napięć.

Rys. 31. a) Filtr zaporowy; b) charakterystyka częstotliwościowa filtru zaporowego [1, s. 311]

Filtry pasywne RC

Realizowane są za pomocą rezystorów i kondensatorów. W konstrukcji tych filtrów

zrezygnowano z cewek, ponieważ elementy te sprawiają największe kłopoty, przede
wszystkim nie mogą być realizowane w technice scalonej.
Mają one parametry porównywalne z parametrami filtrów reaktancyjnych. Najczęściej
wykonywane są jako układy zminiaturyzowane.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

Rys. 32. Filtr RC [1, s. 312]

= R, φ = 45º

2π

⋅

– częstotliwość graniczna.

Filtry aktywne

Budowane

są

wykorzystaniem

wzmacniaczy

operacyjnych,

rezystorów

i kondensatorów. Prócz właściwości typowych filtrów wzmacniają również przepuszczane
sygnały.

4.4.2. Pytania sprawdzające

Odpowiadając na pytania, sprawdzisz, czy jesteś przygotowany do wykonania ćwiczeń.

1. Jak dzielimy filtry ze względu na budowę?
2. Jakie są podstawowe parametry filtrów częstotliwościowych?
3. Czym charakteryzują się filtry pasywne?
4. Jak zbudowane są i czym charakteryzują się filtry dolnoprzepustowe?
5. Jakie są różnice w budowie między filtrami reaktancyjnymi a pasywnymi RC?

4.4.3. Ćwiczenia

Ćwiczenie 1

Filtr dolnoprzepustowy RL o rezystancji równej 2,2 kΩ ma częstotliwość graniczną

= 500 Hz. Oblicz wartość indukcyjności cewki filtra.

Sposób wykonania ćwiczenia

Aby wykonać ćwiczenie, powinieneś:

1) skorzystać z wzoru L =

2π

⋅

2) obliczyć indukcyjność cewki.

Wyposażenie stanowiska pracy

−

poradnik dla ucznia,

−

kalkulator,

−

zeszyt, przybory do pisania,

−

literatura wskazana przez nauczyciela.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

Ćwiczenie 2

Zbadaj filtr dolnoprzepustowy RC.

Rysunek do ćwiczenia 2. Układ do badania filtra dolnoprzepustowego RC

Tabela wyników pomiarów i obliczeń

f[Hz]

100

200

400

800

10k

20k

[V]

Sposób wykonania ćwiczenia

Aby wykonać ćwiczenie, powinieneś:

1) zanalizować schemat pomiarowy,
2) skompletować potrzebną aparaturę i elementy,
3) połączyć obwód elektryczny i zasilić go sygnałem napięcie sinusoidalnie zmiennym

o U=1V i częstotliwościach zmienianych w zakresie od 40 Hz do 20k Hz,

4) wykonać pomiarów napięcia U

na wejściu układu i U

na jego wyjściu,

5) wyznaczyć charakterystykę częstotliwościową badanego filtra,
6) określić wartość częstotliwości granicznej f

oraz pasmo przepustowe filtra,

7) obliczyć stałą czasową

τ badanego obwodu z zależności:

⋅

i na jej podstawie

ponownie określają częstotliwość graniczną f

⋅

8) porównać obie wartości częstotliwości granicznej f

9) oszacować dokładność pomiarów i sformułować wnioski.

Wyposażenie stanowiska pracy:

−

generator funkcyjny,

−

dwa multimetry cyfrowe,

−

częstościomierz,

−

dwa rezystory R = 470 Ω/2 W,

−

kondensator C = 0,22 μF/400 V,

−

materiały i przybory do pisania.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

4.4.4. Sprawdzian postępów

Czy potrafisz:

Tak

Nie

1) dokonać pomiaru filtra dolnoprzepustowego?

2) zanalizować schemat pomiarowy filtra dolnoprzepustowego RC?

3) narysować charakterystykę częstotliwościową filtru zaporowego?

4) narysować charakterystykę częstotliwościową filtru górnoprzepustowego?

5) określić parametry filtrów częstotliwościowych?

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

4.5. Transformator

4.5.1. Materiał nauczania

Transformator jest to urządzenie elektroenergetyczne przetwarzające energię

elektryczną

energię

elektryczną

innych

parametrach,

pomocą

pola

elektromagnetycznego bez udziału ruchu. Przy przetwarzaniu uzyskuje się zmianę napięcia
i prądu przy stałej wartości częstotliwości.

Rys. 33. a) Transformator zasilający małej mocy; b) transformator energetyczny średniego napięcia [10]

Do podstawowych zadań transformatorów należy:

−

zmiana wartości napięcia sinusoidalnie zmiennego,

−

oddziaływanie (separacja odbiornika) obwód dla prądu stałego,

−

dopasowanie obwodów elektrycznych prądu zmiennego.

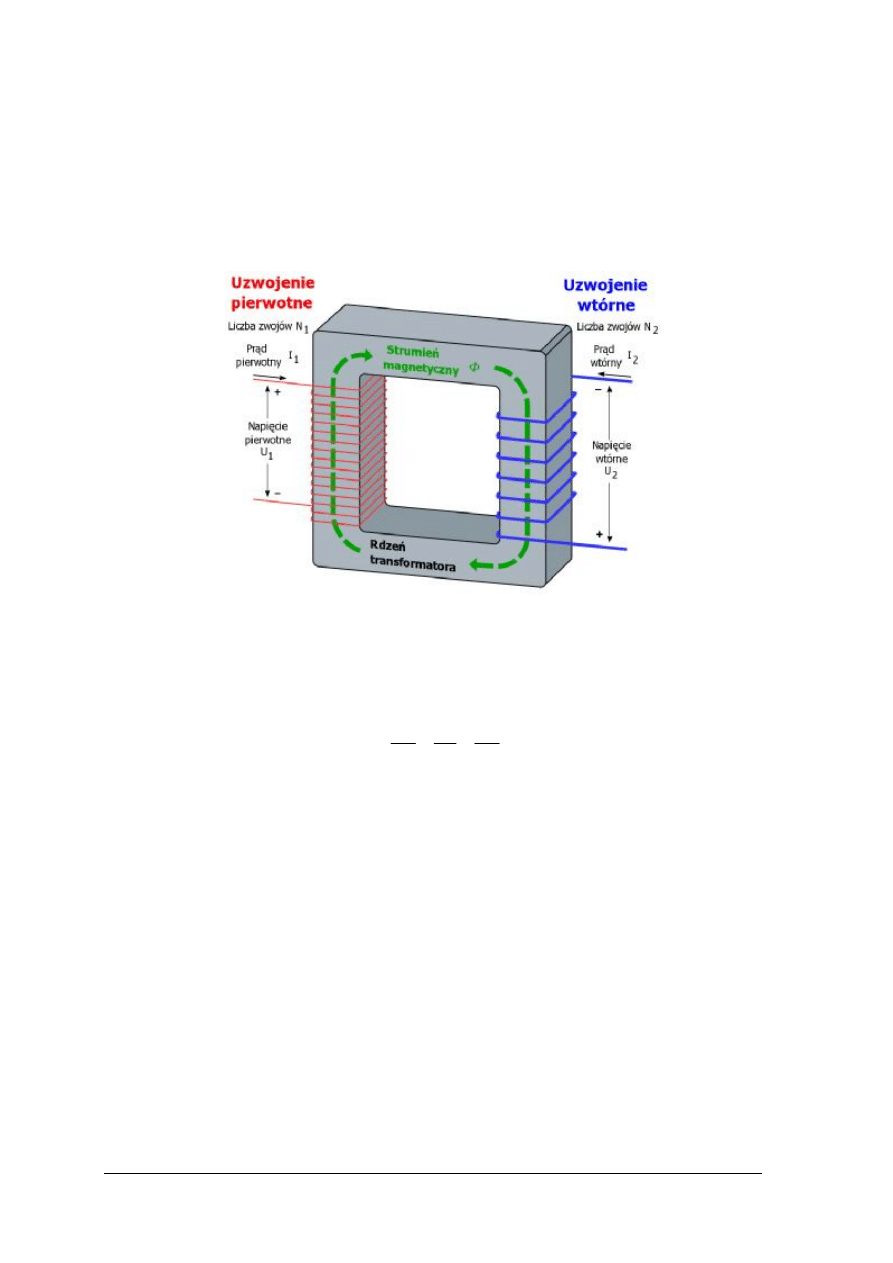
Podstawowe elementy transformatora

Transformator zbudowany jest z dwóch lub więcej cewek (zwanych uzwojeniami)

nawiniętych na wspólny rdzeń magnetyczny wykonany zazwyczaj z materiału
ferromagnetycznego.
Jedno z uzwojeń (nazywamy pierwotnym) podłączone jest do źródła prądu przemiennego,
powoduje to przepływ w nim prądu przemiennego. Prąd przemienny wywołuje powstanie
zmiennego pola magnetycznego, pole to przenika przez druga cewkę (uzwojenie wtórne)
i w wyniku indukcji elektromagnetycznej powstanie w nich zmiennej siły elektromotorycznej
(napięcia).

U

≈

= 4,44

⋅

≈

= 4,44

⋅

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

gdzie: E

– siła elektromotoryczna pierwotna,

– napięcie pierwotne,

– liczba zwojów pierwotnych,

– siła elektromotoryczna wtórna,

– napięcie wtórne,

– liczba zwojów wtórnych,

– strumień magnetyczny.

Rys. 34.

Schematyczne przedstawienie idealnego transformatora [10]

Przekładnia transformatora jest równa stosunkowi liczby zwojów uzwojenia

pierwotnego do liczby zwojów uzwojenia wtórnego.
Stosunek sił elektromotorycznych nazywa się przekładnią transformatora

K =

≈

gdzie: U – napięcie elektryczne,

E – siła elektromotoryczna,

N – liczba zwojów.

Wyższe napięcie transformatora nazywa się napięciem górnym, a napięcie niższe – dolnym.

Podstawowe parametry transformatora:

−

moc pozorna,

−

przekładnia napięciowa,

−

liczba zwojów na wolt,

−

sprawność transformatora.

Transformator może pracować w trzech stanach pracy:

−

w stanie jałowym,

−

w stanie obciążenia,

−

w stanie zwarcia.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

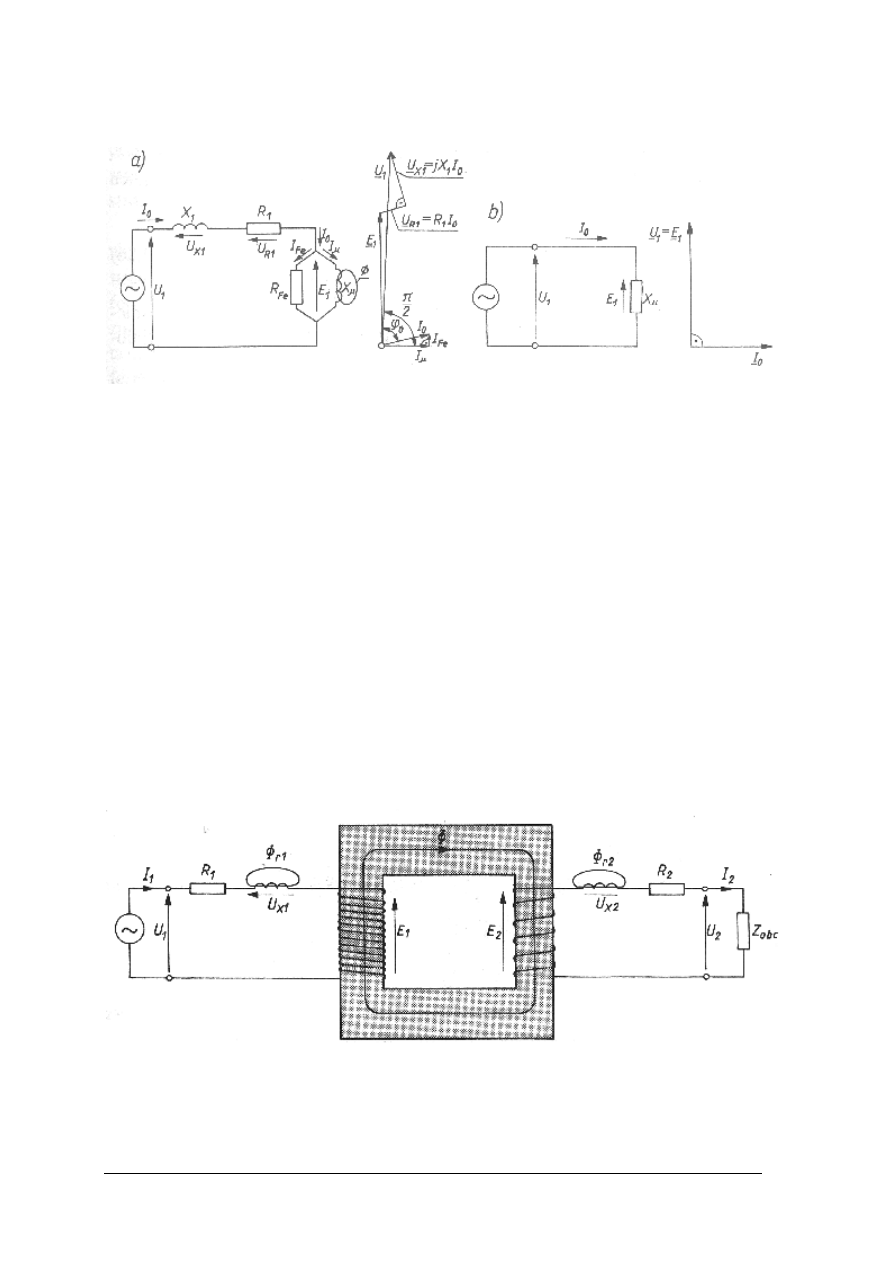
Stan jałowy transformatora

Rys. 35. Transformator w stanie jałowym [2, s. 95]

Stan, w którym uzwojenie pierwotne transformatora jest połączone z siecią zasilającą,

a uzwojenie wtórne jest rozwarte, nazywa się stanem jałowym transformatora.

Prąd płynący w uzwojeniu pierwotnym nazywamy prądem jałowym; w mocy stanowi

około 1…10% prądu znamionowego.
Straty w rdzeniu stanowią zwykle 0,15….1,5% mocy znamionowej.

Przekładnia transformatora jest równa stosunkowi napięcia pierwotnego do napięcia

wtórnego w stanie jałowym transformatora.

Stan obciążenia transformatora

Stanem obciążenia transformatora nazywamy taki stan pracy, w którym uzwojenie

pierwotne jest zasilane napięciem znamionowym, a w obwód wtórny jest włączony odbiornik.
W stanie obciążenia transformatora w obu uzwojeniach płyną prądy. Prąd strony wtórnej I

zależy od napięcia na zaciskach tej strony oraz od parametrów odbiornika. Natomiast prąd
strony pierwotnej I

zawsze dopasowuje się do prądu obciążenia.

Przy obciążeniu transformatora prądy pierwotny wtórny, są w przybliżeniu odwrotnie

proporcjonalne do liczby zwojów uzwojenia pierwotnego i wtórnego, natomiast napięcia są
wprost proporcjonalne do liczby zwojów.

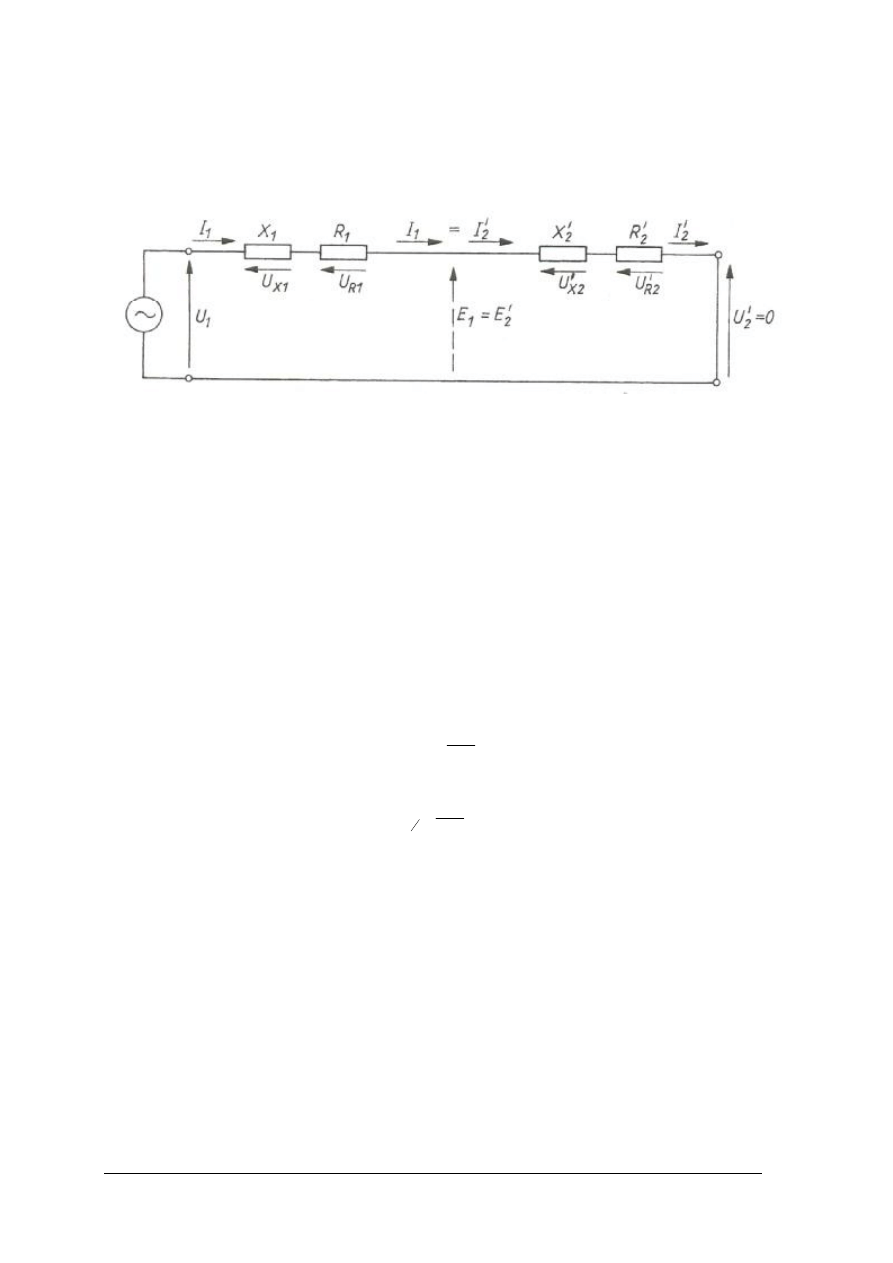
Rys. 36. Transformator w stanie obciążenia [2, s. 105]

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

Stan zwarcia transformatora

Stanem zwarcia transformatora nazywamy taki stan, w którym do uzwojenia pierwotnego

jest doprowadzone napięcie zasilające, a uzwojenie wtórne jest zwarte.
Napięcie na zaciskach zwartego uzwojenia jest równe zero.

Rys. 37. Transformator w stanie zwarcia [2, s. 113]

Zwarciem awaryjnym nazywamy zwarcie występujące przy pełnym napięciu zasilającym.
Prąd płynący w uzwojeniach transformatora jest wówczas od kilku do kilkudziesięciu razy
większy od prądu znamionowego.
Stan ten jest niebezpieczny dla transformatorów z dwóch powodów:

−

powstają duże siły dynamiczne działające na uzwojenia,

−

całkowita moc pobrana w tym stanie wydziela się w postaci ciepła, co powoduje wzrost
temperatury uzwojeń a w konsekwencji uszkodzenie transformatora.

Zwarcie pomiarowe realizowane jest w warunkach laboratoryjnych.

Napięcie zwarcia transformatora jest to napięcie mierzone na jego zaciskach

pierwotnych, gdy przy zwartych zaciskach wtórnych prąd pierwotny jest równy prądowi
znamionowemu.

100

⋅

gdzie: u

– względne napięcie zwarcia,

– napięcie zwarcia,

– napięcie znamionowe.

Ustalony prąd zwarciowy transformatora (przy pełnym napięciu) jest tyle razy większy od
prądu znamionowego, ile razy napięcie zwarcia jest mniejsze od napięcia znamionowego.

Transformatory specjalne
Duże zastosowanie w technice znalazły transformatory specjalne.

Zaliczamy do nich np.:

−

autotransformator jest odmianą transformatora, który ma tylko jedno uzwojenie (część
uzwojenia jest wspólna zarówno dla pierwotnego jak i wtórnego napięcia);

−

transformatory trójuzwojeniowe mają po trzy uzwojenia na każdej kolumnie. Są to:
uzwojenie górne (GN), średnie napięcie (SN) i dolne napięcie (DN);

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

−

przekładniki stosowane w celu obniżenia wartości napięcia lub prądu dla dokonania
pomiarów lub dla galwanicznego oddzielenia obwodu pomiarowego od sieci wysokiego
napięcia;

−

transformator separujący jest transformatorem dwuuzwojeniowym, którego używa się
do zasilania urządzeń napięciem odizolowanym od podstawowej sieci zasilającej.
W laboratoriach pomiarowych stosuje się go np. tam, gdzie nie można używać
uziemionych wyjść sieciowych, ponieważ wtedy otrzyma się pętlę uziemień, które mogą
mieć wpływ na wynik pomiarów Bieguny sieci mają jak wiadomo 230 V i 0 V
w stosunku do ziemi. Uzwojenie wtórne transformatora separującego można pozostawić
nieuziemione i w takim wypadku nie daje ono napięcia w stosunku do ziemi (napięcie
wtórne pozostanie "pływające") To pływające napięcie zmniejsza zasadniczo ryzyko dla
osób pracujących w laboratorium. Transformator może być wyposażony w ekran
pomiędzy stroną pierwotną i wtórną, aby zapobiec zakłóceniom przenoszonym
pojemnościowo;

−

transformator bezpieczny i pośredni do celów ochronnych winny być używane, aby
ograniczyć ryzyko porażenia prądem w urządzeniach elektrycznych i przedmiotach
powszechnego użytku. Transformatory te muszą mieć zapewnioną izolację pomiędzy
stroną pierwotną i wtórną, a także ograniczone napięcie wyjściowe, które może wynosić
12, 24, 42 i 115 V w zależności od wymaganego zastosowania;

−

transformatorem bezpiecznym nazywamy taki transformator, który posiada tzw.
bezpieczne niskie napięcie pracy, najwyżej 50 V, transformator pośredni dla celów
ochrony to taki, który dostarcza napięcia w zakresie pomiędzy 50 i 125 V;

−

transformator dzwonkowy to transformator przeznaczony do dzwonków drzwiowych
i podobnych zastosowań. Może mieć on wartość prądu zwarciowego najwyżej 10 A, aby
uniknąć ewentualnego uszkodzenia przewodów dzwonkowych, które mogą przenosić
tylko krótkotrwałe obciążenia;

−

transformatory małej częstotliwości do zastosowań Hi – Fi muszą przenosić cały
zakres częstotliwości akustycznych 20 Hz do 20 kHz bez zmian w tłumieniu i bez
większych przesunięć fazowych. Oznacza to w praktyce, że muszą one przenosić jeszcze
szerszy zakres częstotliwości. Dlatego jest znacznie trudniej skonstruować i zbudować
transformator małej częstotliwości, niż transformator sieciowy, który musi funkcjonować
dobrze tylko przy jednej częstotliwości.

Straty i sprawność transformatorów

Sprawnością (η) nazywamy stosunek mocy czynnej oddanej P

od mocy czynnej

pobranej P

Różnica między mocą dostarczaną P

a oddaną P

określa straty mocy czynnej transformatora

ΔP = P

– P

Straty mocy w rdzeniu, nazywamy stratami w żelazie ΔP

, zalicza się do strat jałowych

ΔP

transformatora nie zależą od one od mocy transformatora.

Straty mocy, których wartość zależy od prądu obciążenia, nazywa się stratami
obciążeniowymi ΔP

obc,

praktycznie są nimi straty mocy w uzwojeniach.

Straty mocy w transformatorze przy pominięciu strat dodatkowych:

ΔP = ΔP

+ ΔP

obc

≈

ΔP

+ ΔP

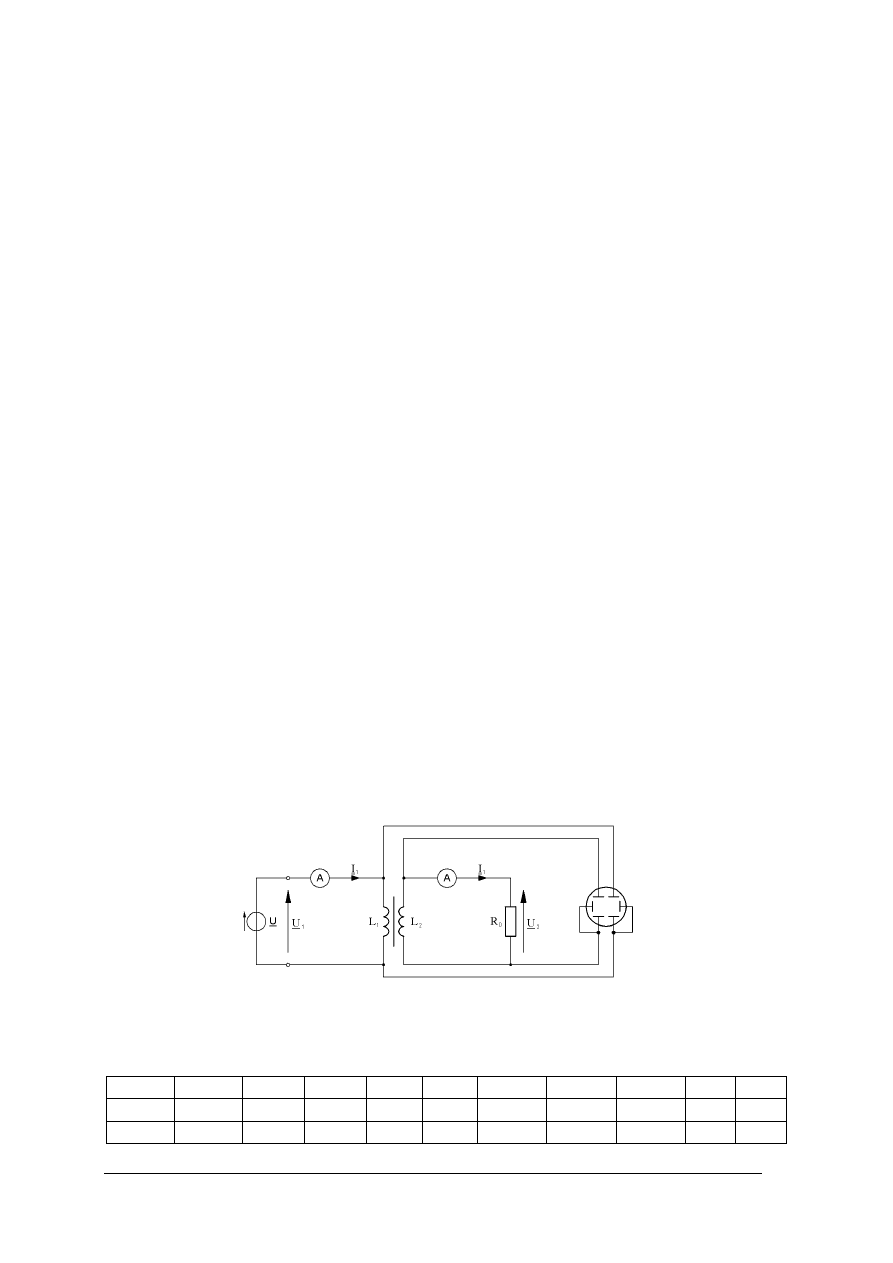
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

4.5.2. Pytania sprawdzające

Odpowiadając na pytania, sprawdzisz, czy jesteś przygotowany do wykonania ćwiczeń.

1. Z czego zbudowany jest transformator jednofazowy?
2. Co nazywamy stanem jałowym, a co stanem zwarcia transformatora?
3. Co nazywamy przekładnią transformatora?
4. Od czego zależy sprawność transformatora?
5. Co nazywamy napięciem zwarcia transformatora?
6. Jakie podstawowe zadania spełnia transformator?
7. Z jakich podstawowych elementów zbudowany jest transformator?
8. Jakie znasz transformatory specjalne?

4.5.3. Ćwiczenia

Ćwiczenie 1

Moc znamionowa transformatora na napięcie 5000/400 V wynosi 4 kVA. Współczynniki

mocy mają wartość: cosφ

= 0,85 i cosφ

= 0,81. Sprawność transformatora wynosi 93%.

Oblicz moc czynną po stronie wtórnej transformatora oraz straty mocy.

Sposób wykonania ćwiczenia

Aby wykonać ćwiczenie, powinieneś:

1) obliczyć moc czynną po stronie wtórnej P

2) obliczyć straty mocy ΔP.

Wyposażenie stanowiska pracy:

−

poradnik dla ucznia,

−

kalkulator,

−

zeszyt, przybory do pisania,

−

literatura wskazana przez nauczyciela.

Ćwiczenie 2

Wykonaj badania transformatora jednofazowego.

Rysunek do ćwiczenia 2. Układ do badania transformatora jednofazowego

Tabele wyników pomiarów i obliczeń

1SS

[V] U

2SS

[V] I

[mA] I

[mA]

Ω

] P

[mW] P

[mW]

1700 1700

∞

1700 1700

0,1

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

1700 1700

4,7

1700

850

1700

Sposób wykonania ćwiczenia

Aby wykonać ćwiczenie, powinieneś:

1) zanalizować schemat pomiarowy,
2) dobrać (skompletować) potrzebną aparaturę i elementy,
3) połączyć obwód elektryczny i zasilić go sygnałem sinusoidalnie zmiennym wartości

międzyszczytowej U

=6 V i f=1 kHz,

4) wykonać pomiary napięcia i prądu po stronie pierwotnej układu i po stronie wtórnej

zmieniając liczbę uzwojeń N

i N

oraz wartość rezystancji obciążenia R

powtórzyć

pomiary po włożeniu między rdzeń transformatora izolatora (kawałka papieru),

5) obliczyć moc pobraną przez uzwojenie pierwotne transformatora P

, moc oddana

przezuzwojenie wtórne P

, sprawność transformatora

i przekładnię zwojową

według zależności:

⋅

;

⋅

;

100

⋅

;

6) oszacować dokładność pomiarów i sformułować wnioski.

Wyposażenie stanowiska pracy:

−

multimetr analogowy i cyfrowy,

−

generator funkcyjny,

−

oscyloskop dwukanałowy,

−

cewki z rdzeniem ferromagnetycznym L = 70 mH o liczbie zwojów N

= 850,

L = 140 mH o liczbie zwojów N

= 1700,

−

rezystor R = 100 Ω/2W, R = 4,7 kΩ/1 W, R = 1 kΩ/1 W.

4.5.4. Sprawdzian postępów

Czy potrafisz:

Tak

Nie

1) wyjaśnić zasadę działania transformatora?

2) określić podstawowe parametry transformatora?

3) narysować schemat zastępczy transformatora w stanie obciążenia?

4) wyjaśnić co należy do podstawowych zadań transformatora?

5) dokonać badania transformatora jednofazowego?

6) wyjaśnić co nazywamy zwarciem awaryjnym?

7) zanalizować schemat pomiarowy transformatora?

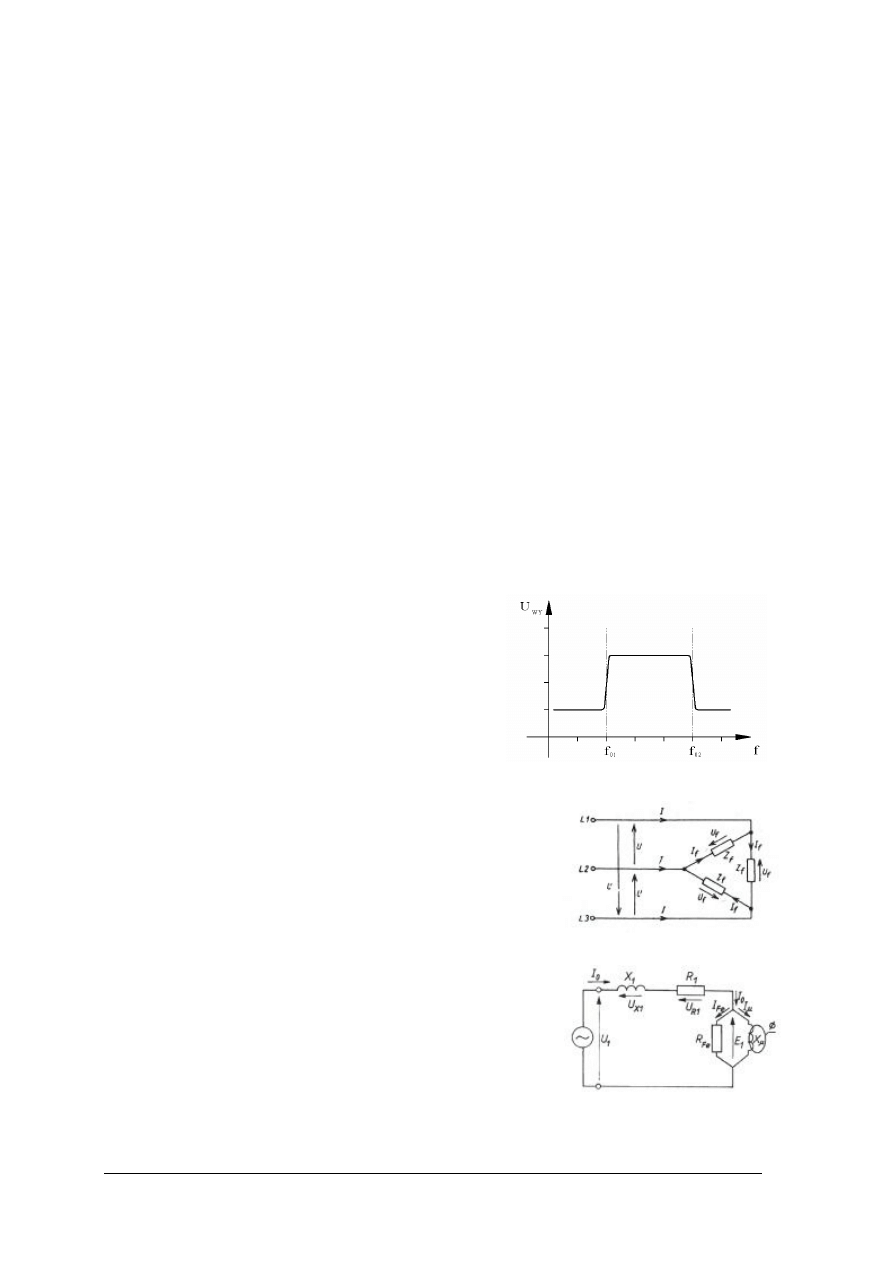
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

5. SPRAWDZIAN OSIĄGNIĘĆ

INSTRUKCJA DLA UCZNIA

1. Przeczytaj uważnie instrukcję.
2. Podpisz imieniem i nazwiskiem kartę odpowiedzi.
3. Zapoznaj się z zestawem zadań testowych.
4. Test zawiera 20 zadań o różnym stopniu trudności. Wszystkie zadania są zadaniami

wielokrotnego wyboru i tylko jedna odpowiedź jest prawidłowa.

5. Udzielaj odpowiedzi tylko na załączonej karcie odpowiedzi – zaznacz prawidłową

odpowiedź znakiem X (w przypadku pomyłki należy błędną odpowiedź zaznaczyć
kółkiem, a następnie ponownie zakreślić odpowiedź prawidłową).

6. Pracuj samodzielnie, bo tylko wtedy będziesz miał satysfakcję z wykonanego zadania.
7. Kiedy udzielenie odpowiedzi będzie Ci sprawiało trudność, wtedy odłóż jego

rozwiązanie na później i wróć do niego, gdy zostanie Ci czas wolny. Trudności mogą
przysporzyć Ci zadania: 17–20, gdyż są one na poziomie trudniejszym niż pozostałe.
Przeznacz na ich rozwiązanie więcej czasu.

8. Na rozwiązanie testu masz 90 minut.

Powodzenia

ZESTAW ZADAŃ TESTOWYCH

1. Rysunek przedstawia charakterystykę częstotliwościową filtra

a) górnoprzepustowego.
b) zaporowego.
c) pasmowego.
d) dolnoprzepustowego.

2. Rysunek przedstawia układ połączeń

a) w gwiazdę.
b) w trójkąt.
c) w zygzak.
d) w trójkąt–gwiazdę.

3. Schemat przedstawia

a) transformator w stanie jałowym.
b) transformator w stanie zwarcia.
c) transformator w stanie obciążenia.
d) schemat zastępczy transformatora.

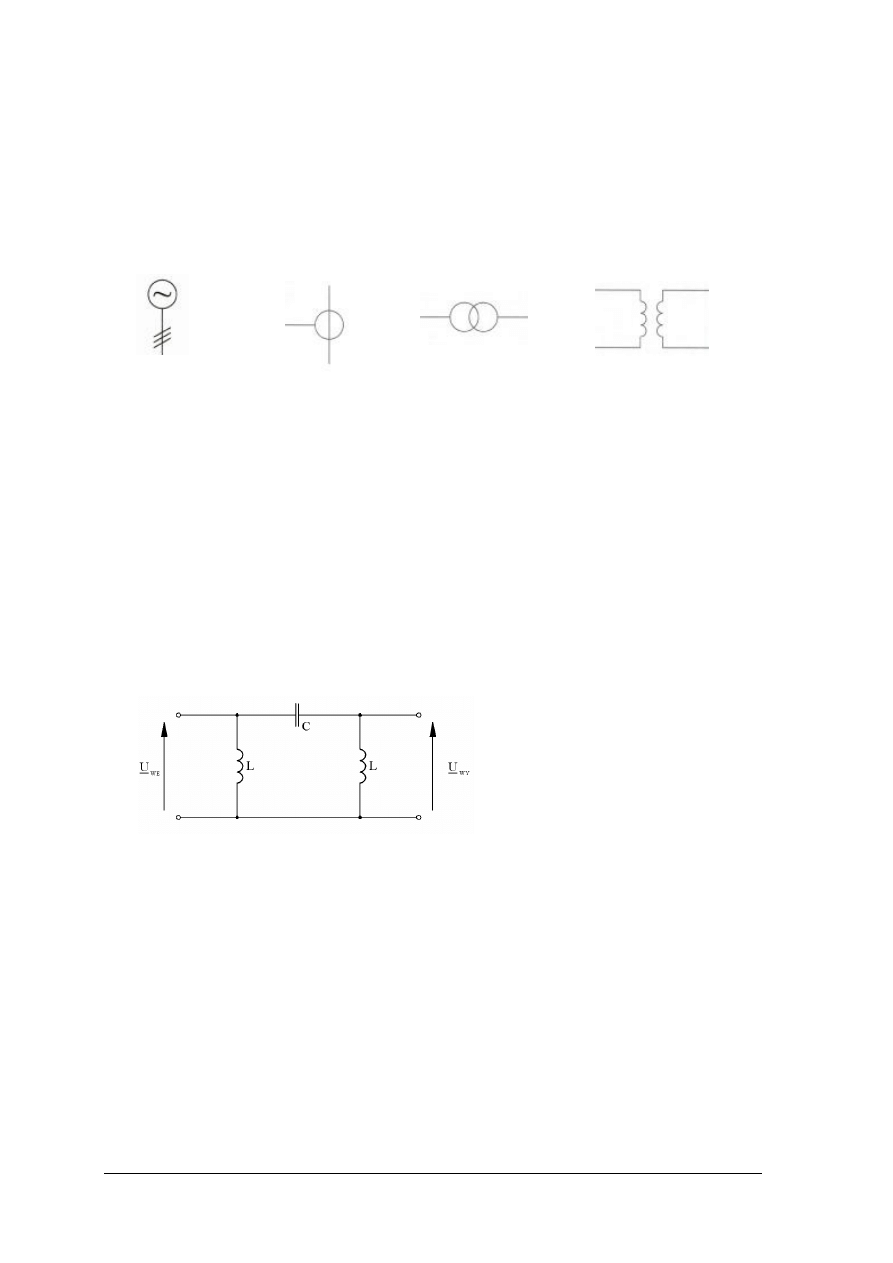
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

4. Uzwojenie strony wtórnej oznaczamy

a) U

b) I

c) N

d) P

5. Symbol przedstawiający transformator na schemacie jednoliniowym to

6. Z ekranu oscyloskopu odczytano wartość odpowiadającą okresowi przebiegu

sinusoidalnie zmiennego, która wynosi 4 działek. Współczynnik odchylania poziomego
C

wynosi 200 ms/działkę, częstotliwość f badanego przebiegu wynosi

a) 125 Hz.
b) 250 Hz.
c) 1250 Hz.
d) 2500 Hz.

7. Rysunek przedstawia schemat filtra

a) górnoprzepustowego.
b) pasmowego LC.
c) aktywnego.
d) dolnoprzepustowego

8. ε

oznacza

a) przenikalność elektryczna względna środowiska.
b) przenikalność elektryczna próżni.
c) przenikalność elektryczna.
d) ładunek elektryczny.

9. Obecność rdzenia ferromagnetycznego wewnątrz cewki powoduje:

a) spadek wartości indukcyjności cewki.
b) wzrost wartości indukcyjności cewki.
c) wzrost wartości natężenia prądu w obwodzie.
d) spadek wartości natężenia prądu w obwodzie.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

10. Wykres który przedstawia zależność wartości natężenia prądu od częstotliwości

w obwodzie szeregowym RLC to

11. Układ szeregowy kondensatorów o pojemnościach C

=1,5 μF i C

= 4,7 μF jest ładowany

w czasie t = 1,2s prądem o natężeniu 3 mA. Ładunek zgromadzony na kondensatorach
wynosi
a) 2,6 mAs.
b) 3,6 mAs.
c) 3,9 mAs.
d) 4,6 mAs.

12. Reaktancja indukcyjna wraz ze wzrostem częstotliwości

a) maleje.
b) oscyluje.
c) rośnie.
d) nie zmienia się.

13. Urządzenie, które zamienia energię elektryczną na elektryczną to

a) prądnica.
b) silnik.
c) transformator.
d) generator.

14. W tanie rezonansu obwodu zawierającego elementy R, L i C zachodzi następująca

zależność
a) obwód ma charakter indukcyjny i pojemnościowy.
b) napięcia na wszystkich elementach są jednakowe.
c) prądy płynące przez wszystkie elementy są jednakowe.
d) odwód ma charakter czysto rezystancyjny.

15. Moc czynną prądu jednofazowego określa wzór

a) Q = U

sin

⋅

b) P = 3 U

cos

⋅

c) P =

cos

⋅

d) Q = 3 U

sin

⋅

16. Woltomierz o zakresie pomiarowym 100 V i kasie dokładności 1 wskazuje 50 V.

Maksymalny błąd względny pomiaru wynikający z klasy miernika wynosi
a) 5%.
b) 2%.
c) 1,0%.
d) 0,5%.

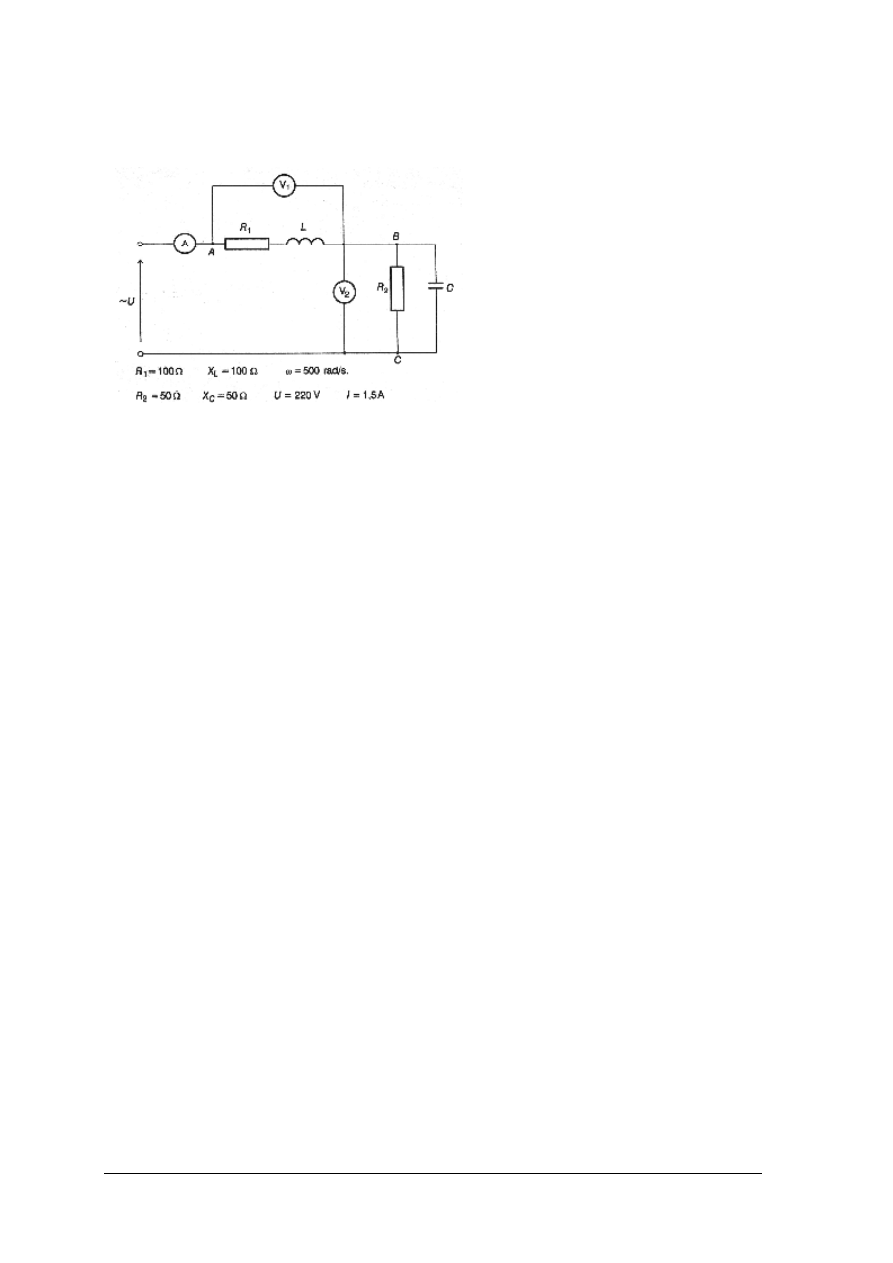
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

Rysunek do zadania od 17 do 20.
Oblicz obwód i na jego podstawie rozwiąż zadania:

17. Indukcyjność cewki zastosowanej w podanym obwodzie wynosi

a) 5 H.
b) 15 H.
c) 200 mH.
d) 500 mH.

18. Układ pobiera moc czynną

a) 150 W.
b) 199 W.
c) 250 W.
d) 281 W.

19. Amplituda napięcia zasilającego obwód wynosi

a) 150,1 V.
b) 311,1 V.
c) 156,5 V.
d) 355,4 V.

20. Wskazanie woltomierza V

wynosi

a) 17,7 V.
b) 53 V.
c) 38,5 V.
d) 60 V.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

KARTA ODPOWIEDZI

Imię i nazwisko ……………………………………………………..

Badanie i pomiary obwodów prądu przemiennego

Zakreśl poprawną odpowiedź.

zadania

Odpowiedź

Punkty

Razem:

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

6. LITERATURA

1. Bolkowski S.: Podstawy elektrotechniki. WSiP, Warszawa 1995
2. Goźlińska E.: Maszyny elektryczne. WSiP, Warszawa 1995
3. Kurdziel R.: Elektrotechnika dla ZSZ, cz. I i II. WSiP, Warszawa 1995
4. Kuźniarki A.: Pracownia elektryczna dla ZSZ. PWSZ, Włocławek 1972
5. Morusek A.: Urządzenia elektroniczne dla ZSZ, cz. II. WSiP, Warszawa
6. Nowicki J.: Podstawy elektrotechniki i elektroniki dla ZSZ. WSiP, Warszawa 1999
7. Orlik W.: Egzamin kwalifikacyjny elektryka. Wydawnictwo „KABe”, Krosno 1999
8. Praca zbiorowa: Poradnik elektryka. WSiP, Warszawa 1995
9. Stein Z.: Maszyny elektryczne. WSiP, Warszawa 1995
10. www.pl.wikipedia.org

Wyszukiwarka

Podobne podstrony:

więcej podobnych podstron