Digital Object Identifier (DOI) 10.1007/s00193-002-0139-0

ShockWaves (2002) 12: 121–128

Spectral intensity measurement for soot formation of benzene

behind reflected shock waves

T. Tsuboi, K. Ishii, H. Omura

Department of Mechanical Engineering, Faculty of Engineering, Yokohama National University, 79-5 Tokiwadai, Hodogaya,

Yokohama 240-8501, Japan

Received 5 February 2002 / Accepted 13 February 2002

Published online 11 June 2002 – c

Springer-Verlag 2002

Abstract. Soot formation of benzene was observed using He-Ne laser extinction at 632.8 nm as well as the

visible and infrared thermal radiation at 0.63, 0.80, 1.12, 1.52, 2.3, 3.4, 3.9, 4.3

µ

m. From the light extinction

we determined the temperature-dependent soot formation rate. Also from the visible and infrared radiation

we calculated the temperature of soot particles and kcl-values which were dependent on the soot volume

concentration. The temperature dependence of soot formation rates below 2500 K was obtained in the

early part of soot formation and that above 1900 K was obtained in the later part of soot formation for

the cases of the laser extinction and the visible-infrared radiation intensities, respectively.

Key words: Soot formation, Benzene, IR-emission, Spectral intensity, Hottel-Broughton equation

1 Introduction

Soot formation has been studied from various standpoints.

Several groups observed soot formation and the optical in-

dex in burner flames (Bonne and Wagner 1965; D’Alessio

et al. 1972; Wersborg et al. 1975). Others (Frey and Corn

1967, Kham et al. 1971, Sj¨ogren 1973 and Kadota et al.

1977) observed the formation of soot or particulates in

diesel exhaust gas. On the other hand Radcliffe and Ap-

pleton 1971 and Park and Appleton 1973 observed the

oxidation or the O-atom reaction with soot. Shock tube

techniques were also applied for the basic study of soot

formation (Yoshizawa et al. 1979; Frenklach et al. 1983a;

Frenklach et al. 1983b; Johnson et al. 1983; Bauer and

Zhang 1983; B¨ohm et al. 1998). One of us (TT) observed

soot formation behind shock waves using visible and in-

frared He-Ne laser light extinction (Tsuboi et al. 1992).

The G¨ottingen group also used a near-infrared semicon-

ductor laser along with a visible He-Ne laser as the light

source (Tanke et al. 1998). Darzell and Sarofim were the

first group who obtained the complex index of soot par-

ticles (Darzell and Sarofim 1969), and other groups fol-

lowed after them to study the complex index experimen-

tally and theoretically Graham 1974, Chippett and Gray

1978. Wagner 1979 and Calcote 1981 gave overviews of

soot studies. Many of the measurements in flame and in

diesel exhaust gas were focused on technical applications.

Correspondence to: T. Tsuboi (e-mail: [e-mail])

An abridged version of this paper was presented at the 23rd

Int. Symposium on ShockWaves at Fort Worth, Texas, from

July 22 to 27, 2001

The shock tube measurements were performed for the el-

ementary study of soot formation and were used for the

visible and infrared laser absorption studies. In spite of

many attempts there are still unclear aspects of the soot

formation mechanism as well as the thermodynamic prop-

erties. One of the authors (T.T.) (Tsuboi et al. 1986) tried

to measure the average density of soot under the condition

of high temperature in a shock wave using infrared He-Ne

laser extinction and they (Tsuboi et al. 1992) calculated

also the latent heat and surface tension of phase change by

using a model of soot formation. Since the results of these

attempts were still uncertain, we have performed further

study. The previous workers observed the later part of the

light extinction signal as the soot signal, because the early

stage of the light extinction signals could include also the

molecules, which were produced as intermediates during

the soot formation process. We ventured to analyze the

early stage of light extinction of the soot formation pro-

cess by measuring the visible and infrared radiation inten-

sities, and the light extinction simultaneously. From these

measurements we could obtain the time histories of the

spectral intensities and calculated the concentration and

the temperature of the radiating particles, by using the

Hottel-Broughton equation.

2 Experimental apparatus,

and light extinction and emission

Experiments for soot formation were performed in a stain-

less shock tube with 100 mm diameter. The low pressure

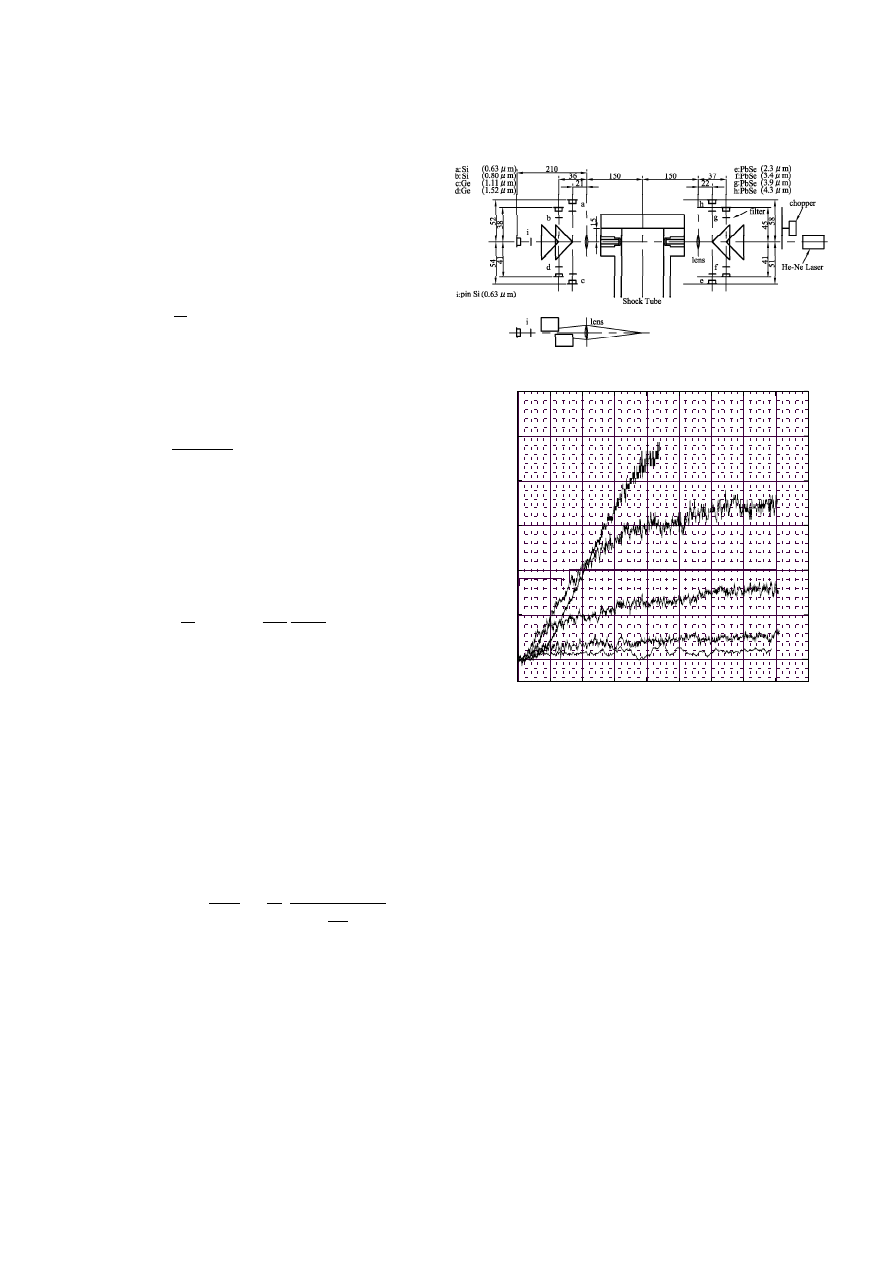
122

T. Tsuboi et al.: Soot formation of benzene

section was 4200 mm long, while the high pressure sec-

tion was 2200 mm long. The leakage of the tube was 0.1

Pa/min. Further details of the shock tube can be seen in

Tsuboi et al. 1992.

He-Ne laser at 632.8 nm was used as the light source for

the light extinction measurements. The monochromatic

light extinction is described as follows:

I

I

0

= exp(−CextNL) .

(1)

Here, I

0

is the incident light intensity and I is the trans-

mitted light intensity through the column length L with

the concentration N of absorbing species, whose cross sec-

tion is Cext. This cross section Cext can be expressed as:

C

ext

=

36πV n

2

κ

Z

1

here, Z

1

= (n

2

+ n

2

κ

2

)

2

+ 4(n

2

− n

2

κ

2

) + 4 .

The variables n, κ are those of the complex index m =

n(1 − κi). In this paper we used n = 1.57, nκ = 0.44 at

632.8 nm (Darzell and Sarofim 1969). In the case that the

particle diameter is much smaller than the wavelength of

the light source, Eq. (1) can be recalculated

ln

I

I

0

= −36π

n

2

κ

Z

1

N

S

V

S

L

λ .

(2)

Here, N

S

is the number density of soot particles, V

S

is

the volume of one soot particle and the light path length

L = 10 cm. Therefore one could calculate the time history

of total soot volume per cm

3

, N

S

V

S

.

The visible and infrared emission intensities were mea-

sured at wavelengths of 0.63, 0.80, 1.12, 1.52, 2.3, 3.4,

3.9, and 4.3

µ

m using narrow band pass filters. Figure

1 shows the optical setup for measurement of the IR-

emission. Simultaneously, the He-Ne laser run from right

to left through the small gap between prism reflectors and

the light extinction was measured at place ”i” on the left

side. Using the Hottel-Broughton equation the spectral

intensity is described as follows:

I

λ

=

1 − exp

−

kcl

λ

0.95

1

λ

5

C

1

exp

C

2

λT

− 1

.

(3)

The best-fit I

λ

–λ of this equation gave the temperature

T and the kcl-value, which was proportional to the total

volume of soot N

S

V

S

.

3 Results

Soot formation behind reflected shock waves was followed

at temperatures 1400–4000 K in the density range between

1 and 8×10

−5

mol/cm

3

for mixtures between 0.5 and 1.0%

C

6

H

6

in argon. The measurements of laser light extinction

and visible-infrared radiation intensities were performed

simultaneously.

Fig. 1. Optical system for measurement of infrared emission

0

500

0

2

4

6

N

S

V

S

[x10

6

cm

3

/cm

3

]

Time t [

µ

s]

2100K

2230K

2290K

2340K

1940K

0.5 % C

6

H

6

ρ

= 2x10

–5

[mol/cm

3

]

Model 1

Model 2

Region1

Region2

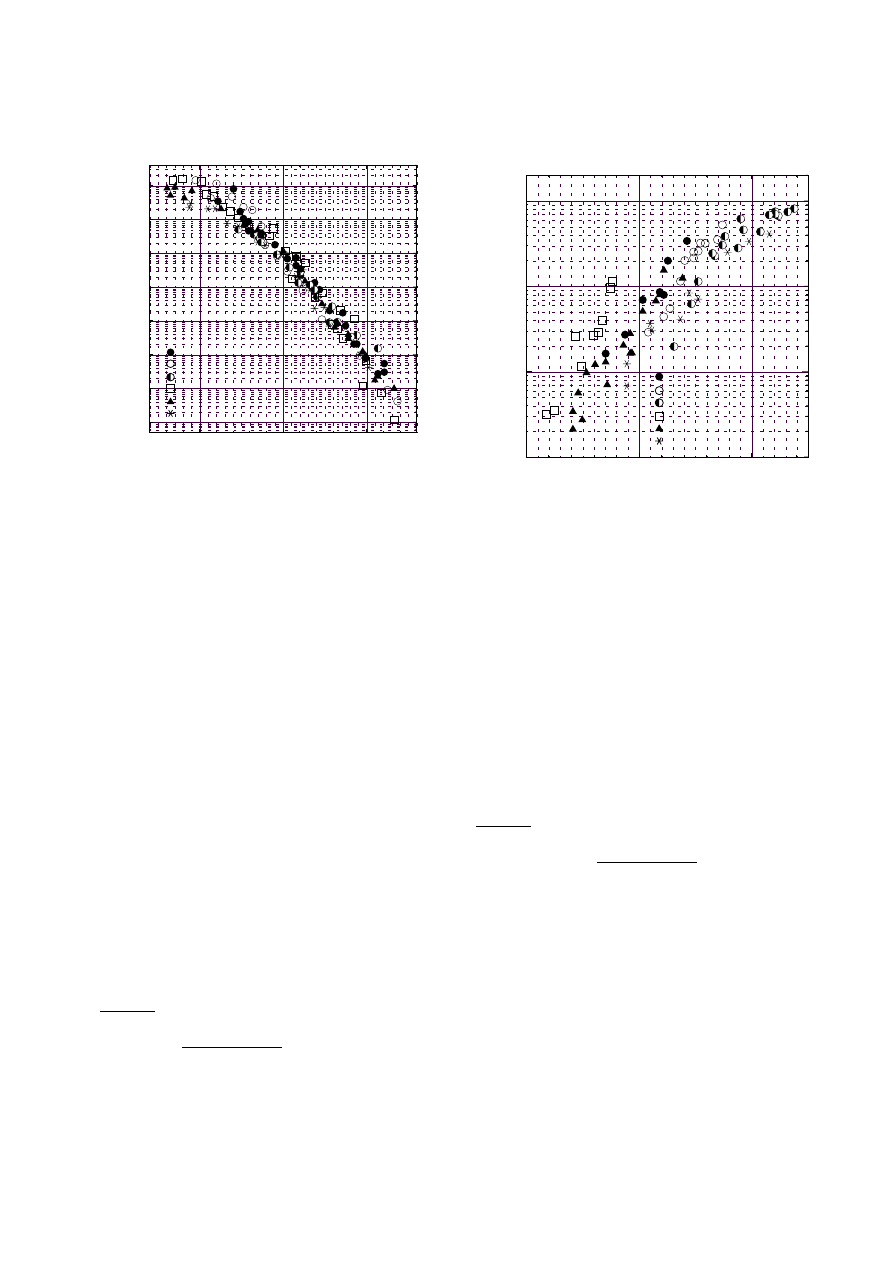
Fig. 2. Soot volume profiles N

S

V

S

at various temperatures

3.1 Laser extinction

Figure 2 shows the profiles of total soot volume N

S

V

S

at

temperatures of 1940, 2100, 2230, 2290 and 2340 K. At

low temperatures the total soot volume increased rapidly

in the early part (region 1) of the reaction time and

the growth rate increased with increasing temperature

till about 2250 K, and in the later part (region 2) the

growth rate decreased. At high temperatures above about

2250 K the region 1 was shortened and could not be recog-

nized above 2300 K. The soot production rate decreased

with increasing temperature. These phenomena were

clearly observed especially in the later part (region 2) of

reaction time where the total soot volume increases lin-

early.

Previous workers (Frenklach et al. 1983a; Frenklach

et al. 1983b; Tanke et al. 1998) observed soot formation

mainly in the later part of the time history of light ex-

tinction. We tried to measure the early part of the time

history of soot formation, though there was some influ-

ence of species other than soot particles. For calculation

of soot production we made some assumptions (Tsuboi et

al. 1992):

N

S

V

S

= at

n

,

T. Tsuboi et al.: Soot formation of benzene

123

4

5

6

10

2

10

4

10

6

10

8

k

S

V

S

=[3xdN

S

V

S

/d(t

3

)][C

6

H

6

]

–

2.6

[Ar]

–

0.2

10

4

/T

5

[1/K]

: P

4

=1.4MPa(0.5%C

6

H

6

)

: P

4

=0.6MPa(0.5%C

6

H

6

)

: P

4

=0.3MPa(0.5%C

6

H

6

)

: P

4

=1.4MPa(1%C

6

H

6

)

: P

4

=0.6MPa(1%C

6

H

6

)

: P

4

=0.3MPa(1%C

6

H

6

)

cm

3

/

µ

s

–

3

(mol/cm

3

)

–

2.8

]

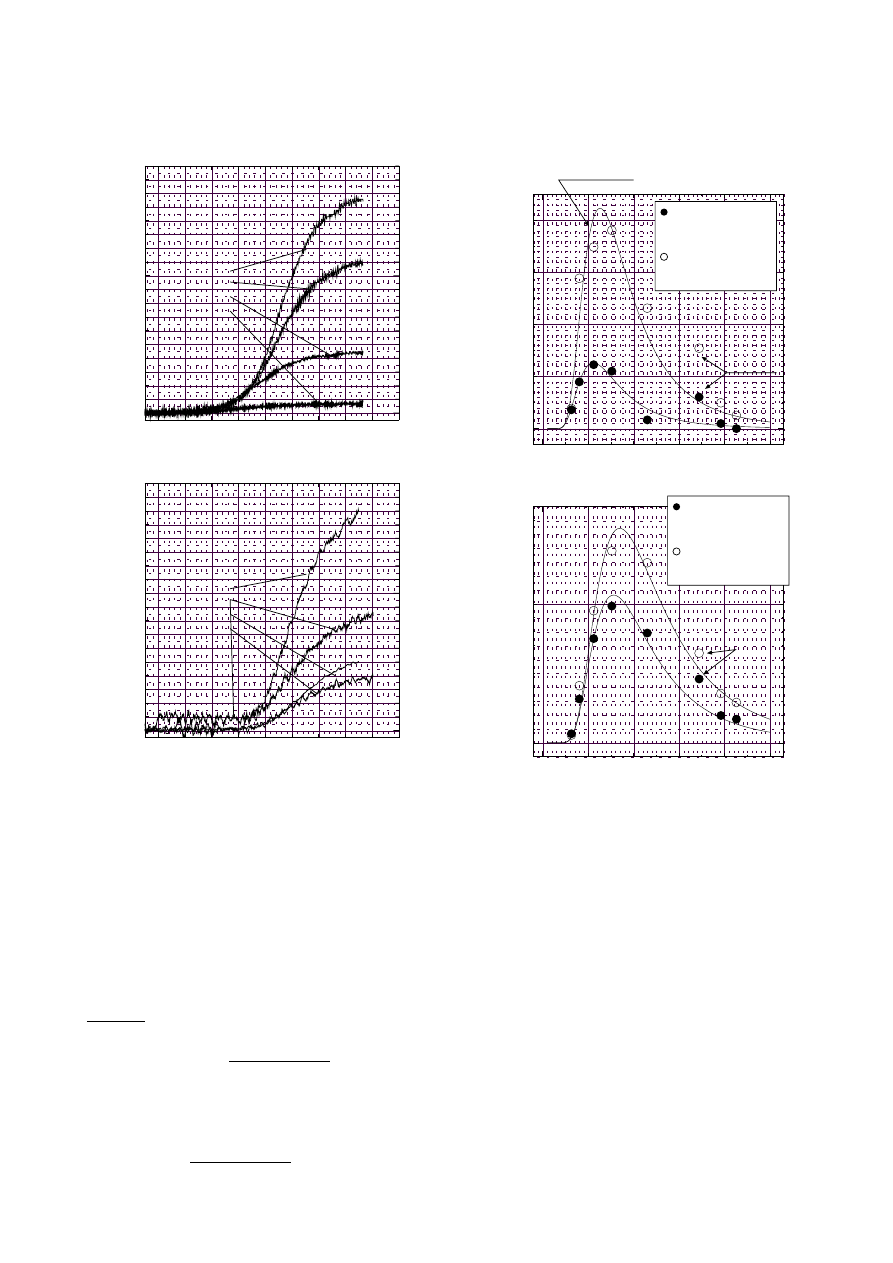
Fig. 3. Temperature-dependent reduced rates of soot forma-

tion at low temperature (region 1). Data were obtained from

the laser extinction signals

here N

S

and V

S

are the number density of the soot parti-

cles and the average volume of a soot particle, respectively.

That is: when the number density of soot whose volume

is V

S

i

is N

S

i

, the total soot volume per unit gas mixture

is

i

N

S

i

V

S

i

. The suffix S

i

is described as the i-th soot-

particle in the modeling. The variable N

S

V

S

is the total

volume of soot per unit gas volume. The variable t is time.

The variable n could be estimated from the experiment

and it was about 3 under our conditions.

The experimental results for the soot production is

shown by an equation:

k

S

V

S

1

= 3a = [3d(N

S

V

S

)/dt

3

][C

6

H

6

]

−2.6

[Ar]

−0.2

= [3d(I

0

/I)/dt

3

][C

6

H

6

]

−2.6

[Ar]

−0.2

/[36πn

2

κL/(Z

1

λ)] .

(4)

The definition of k

S

V

S

1

is given in Eq. (19). The pre-factor

3 came from the differential of dt

3

. The production rate in-

creased with increasing temperature and depended mainly

on the production rate of the intermediates B. Figure 3

shows such temperature dependent rates in reduced form.

The influence of benzene concentration on the soot pro-

duction rate was 2.6 and that of argon was 0.2. The val-

ues n, κ and Z

1

were the factors of wavelength-dependent

complex index of soot particles and the related variables.

Under 2000 K one could express the relation as follows:

3

d(N

S

V

S

)

dt

3

= (6 ± 5) × 10

23

[C

6

H

6

]

2.6±0.1

[Ar]

0.2±0.1

×exp

−

640000 ± 40000

RT

[cm

3

/cm

3

µ

s

3

] .

(5)

The overall activation energy contained the activation

energy (E

a

) due to chemical reactions and the activation

energy (E

b

= ∆G

∗

) due to phase change. The influence of

an activation energy (E

b

) due to this phase change on the

overall activation energy increased with increasing tem-

perature and the activation energy (E

b

) increased with

3

4

5

10

–1

10

0

10

1

10

2

[dN

S

V

S

/dt][C

6

H

6

]

–

2.6

[Ar]

1.7

[1/

µ

s(mol/cm

3

)

–

0.9

]

: P

4

=1.4MPa(0.5%C

6

H

6

)

: P

4

=0.6MPa(0.5%C

6

H

6

)

: P

4

=0.3MPa(0.5%C

6

H

6

)

: P

4

=1.4MPa(1%C

6

H

6

)

: P

4

=0.6MPa(1%C

6

H

6

)

: P

4

=0.3MPa(1%C

6

H

6

)

10

4

/T

5

[1/K]

Fig. 4. Temperature-dependent reduced rates of soot forma-

tion at high temperature (region 2). Data were obtained from

the laser extinction signals

increasing temperature, as described in Eq. (11). When

this activation energy (E

b

) increased, the rate of phase

change decreased. Therefore, the apparent activation en-

ergy of soot-particles production rate decreased with in-

creasing temperature especially above 2000 K. A large rate

of soot production was still observed shortly behind the

reflected shock wave between 2000 and 2200 K but the rate

became small after the early part of light extinction. How-

ever the rate did not go to zero. The soot was produced

slowly and the extinction signal increased linearly with

time. Figure 4 shows the temperature dependence in re-

duced form. The increasing rate decreased with increasing

temperature. The following expression was experimentally

determined:

d(N

S

V

S

)

dt

= (7 ± 6) × 10

−6

[C

6

H

6

]

2.6±0.2

[Ar]

−1.7±0.1

×exp

266000 ± 50000

RT

[cm

3

/cm

3

µ

s] . (6)

3.2 IR-emission

The above Eqs. (5) and (6) were obtained only from a sin-

gle absorption line (632.8 nm). Though it was previously

confirmed that these particles have the characteristic of

black body radiation Tsuboi et al. 1986, the time histo-

ries of spectral intensities of the particles were followed

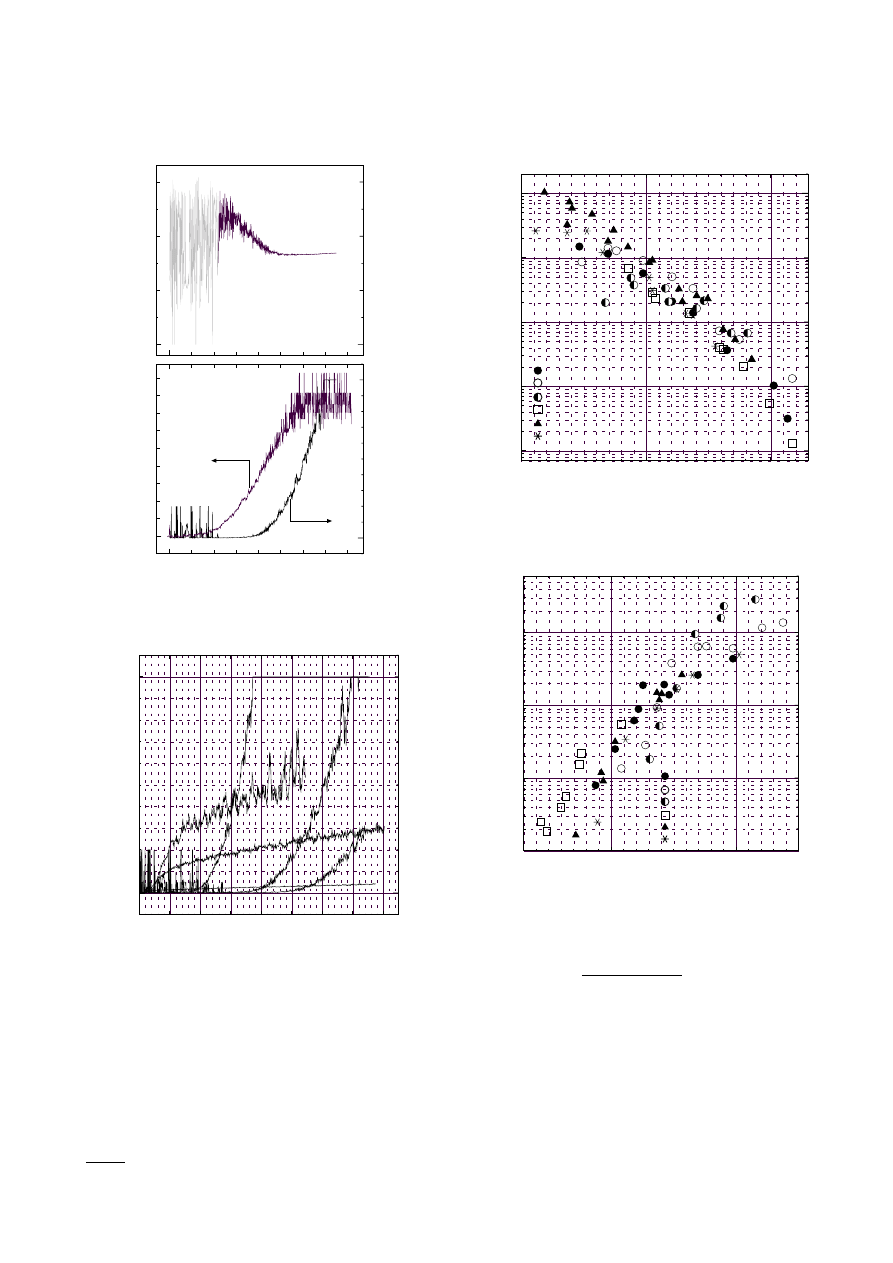
in order to obtain more information. Figure 5 shows the

time histories of monochromatic emissive powers. From

these spectra we could calculate the time histories of soot

temperature and of a term which was proportional to the

total soot volume, by using the Hottel-Broughton equa-

tion. Figure 6 shows the best-fit of the Hottel-Broughton

equation.

Figure 7 shows the kcl-value, which is proportional to

the volume density of soot at various temperatures. As

124

T. Tsuboi et al.: Soot formation of benzene

0

0.5

0

50

100

150

Time t [ms]

E

λ

kW/m

2

µ

m]

1 % C

6

H

6

in Ar

T

5

= 1780 K

ρ

5

= 3.46 x 10

–5

mol/cm

3

1.52

µ

m

1.12

µ

m

0.80

µ

m

0.63

µ

m

0

0.5

0

50

100

150

Time t [ms]

E

λ

kW/m

2

µ

m]

1 % C

6

H

6

in Ar

T

5

= 1780 K

ρ

5

= 3.46 x 10

–5

mol/cm

3

2.3

µ

m

3.4

µ

m

3.9

µ

m

4.3

µ

m

Fig. 5. Monochromatic emissive powers at 0.63, 0.80, 1.12,

1.52

µ

m and at 2.3, 3.4, 3.9, 4.3

µ

m

seen in the lower figure the sensitivities obtained from in-

frared signals were not as high as that of the light extinc-

tion of laser. The kcl profile was observed after the appear-

ance of N

S

V

S

-signal obtained by light extinction. There-

fore, for the empirical expression it was better to use the

variable τ (so-called induction period). Thus we defined,

as the increasing velocity of kcl, the rate 3d(kcl)/d(t−τ)

3

,

which was similar to the expression used in the analysis

of light extinction signals. The expression found was:

3

d(kcl)

d(t − τ)

3

= (2 ± 1) × 10

16

[C

6

H

6

]

1.8±0.1

[Ar]

0.7±0.2

×exp

−

280000 ± 40000

RT

[

µ

m

0.95

/

µ

s

3

](7)

τ = (4 ± 2) × 10

10

[C

6

H

6

]

−0.22±0.07

[Ar]

−0.74±0.12

× exp

−

240000 ± 40000

RT

[s] .

(8)

0

2

4

0

20

40

Wave length [

µ

m]

E

λ

[kW/m

2

µ

m]

E

λ

=

ε

λ.

E

b

λ

: t=0.30 [ms]
T

P

=2180 [K]

kcl=0.024 [

µ

m

0.95

]

: t=0.40 [ms]
T

P

=1950 [K]

kcl=0.169 [

µ

m

0.95

]

3.44

µ

m

0

2

4

0

100

Wave length [

µ

m]

E

λ

[kW/m

2

µ

m]

: t=0.50 [ms]
T

P

=1670 [K]

kcl=1.603 [

µ

m

0.95

]

: t=0.60 [ms]
T

P

=1660 [K]

kcl=4.983 [

µ

m

0.95

]

3.44

µ

m

Fig. 6. Best fit of Hottel-Broughton equation for calculation

of T

P

and kcl, obtained from Fig. 5

Figure 8 shows the kcl-value profiles at temperatures

1710, 1780, 1890, 2270, 2390 and 2540 K. These kcl-value

profiles were similar to the N

S

V

S

profiles in Fig. 2. At

low temperature the soot volume grew rapidly in the

early part of reaction time and the growth rate increased

with increasing temperature till about 2270 K, and in the

later part the growth rate decreased. At high temperature

above about 2270 K the region 1 in Fig. 2 was shortened

and could not be recognized above 2270 K. The soot pro-

duction rate decreased with increasing temperature. This

phenomenon was clear especially in the later part of reac-

tion time (the region 2 in Fig. 2) where the soot volume

increased linearly.

Figure 9 shows the reduced relation [d(kcl)/d(t−τ)

3

]×

[C

6

H

6

]

−1.8

[Ar]

−0.7

versus reciprocal temperature.

The profile of soot formation above 2200 K could not

be measured with our measuring system shortly behind

reflected shock waves, because the time constant of our

measuring system was large, while the reaction velocity

T. Tsuboi et al.: Soot formation of benzene

125

0

1000

2000

3000

0

0.2

0.4

0.6

0.8

0

5

0

10

T

P

[K]

kcl [

µ

m

0.95

]

Time [ms]

N

S

V

S

[x10

6

cm

3

/cm

3

]

1 % C

6

H

6

in Ar

T

5

= 1780 K

ρ

5

= 3.46x10

–5

mol/cm

3

Fig. 7. T

P

, kcl of soot particles calculated from Fig. 5 and

N

S

V

S

from light extinction

0

200

400

600

800

0

10

kcl [

µ

m

0.95

]

Time t [

µ

s]

1 % C

6

H

6

in Ar at P

4

=0.6MPa.

1710K

1780K

1890K

2270K

2390K

2540K

Fig. 8. Soot formation rates at temperatures 1710, 1780, 1890,

2270, 2390 and 2540 K

(soot production velocity) was much larger. However, the

slow increase of soot concentration was observed after this

fast soot production, which was similar to the light ex-

tinction experiment (Fig. 2). Figure 10 shows the reduced

temperature dependence, and the reduced relation is as

follows:

d(kcl)

dt

= (1.0 ± 0.6) × 10

8

[C

6

H

6

]

4.7±0.3

[Ar]

−2.8±0.1

4

5

6

10

6

10

8

10

10

: P

4

=1.4MPa(0.5%C

6

H

6

)

: P

4

=0.6MPa(0.5%C

6

H

6

)

: P

4

=0.3MPa(0.5%C

6

H

6

)

: P

4

=1.4MPa(1%C

6

H

6

)

: P

4

=0.6MPa(1%C

6

H

6

)

: P

4

=0.3MPa(1%C

6

H

6

)

10

4

/T

5

[1/K]

[dkcl/d(t

–

τ

)

3

][C

6

H

6

]

–

1.8

[Ar]

–

0.7

[

µ

m

0.95

/

µ

s

3

(mol/cm

3

)

–

2.5

]

Fig. 9. Temperature-dependent reduced rates of soot forma-

tion. Data were obtained from the thermal radiation at 0.63,

0.80, 1.12, 1.52

µ

m and at 2.3, 3.4, 3.9, 4.3

µ

m. Region 1

4

5

10

14

10

15

10

16

10

17

: P

4

=1.4MPa(0.5%C

6

H

6

)

: P

4

=0.6MPa(0.5%C

6

H

6

)

: P

4

=0.3MPa(0.5%C

6

H

6

)

: P

4

=1.4MPa(1%C

6

H

6

)

: P

4

=0.6MPa(1%C

6

H

6

)

: P

4

=0.3MPa(1%C

6

H

6

)

[dkcl/dt][C

6

H

6

]

–

4.7

[Ar]

2.8

[

µ

m

0.95

/

µ

s(mol/cm

3

)

–

1.9

]

10

4

/T

5

[1/K]

Fig. 10. Temperature-dependent reduced rates of soot forma-

tion. Data were obtained from the thermal radiation at 0.63,

0.80, 1.12, 1.52

µ

m and at 2.3, 3.4, 3.9, 4.3

µ

m. Region 2

×exp

343000 ± 50000

RT

[

µ

m

0.95

/

µ

s] .

(9)

4 Discussion

The soot formation process was followed by observing

both the light extinction and the visible and infrared ra-

diation. The technique to obtain the soot volume by mea-

suring the laser extinction was used by previous workers

(Frenklach et al. 1983a; Frenklach et al. 1983b; Tanke et

al. 1998; Tsuboi et al. 1986), though it was not certain

whether the measured signal was only due to soot. One of

126

T. Tsuboi et al.: Soot formation of benzene

us (TT) confirmed the visible and the infrared radiation

were the black body radiation in the later part of soot

formation (Tsuboi et al. 1986). As one technique to de-

cide whether the signal is due to soot, one can measure

the light signals at various wavelengths, simultaneously.

We tried to measure the visible and infrared radiation.

The radiation must have black body radiation, if it is due

to soot. Figure 6 shows that the spectral intensities are

similar to the black body radiation (Figs. 5,6).

In the wavelength region used for the soot measure-

ment there must be some absorption and emission due to

complex molecules beside soot particles. At 3.4

µ

m there

was emission due to benzene and related intermediates.

Therefore we omitted the emission signal at 3.4

µ

m for

calculation of the temperature and the kcl-value.

The temperature, which was calculated from emission

signals, was higher than that of equilibrium temperature

in the early stage of the formation. The nucleation of soot

is an exothermic reaction and the heat goes to argon as

the heat bath, i.e. heat conduction from soot particles to

argon. Therefore our measured temperature was probably

higher than the equilibrium temperature in the early stage

of the time history of soot.

The radiation signal appeared behind the laser extinc-

tion, since the sensitivity of the optical system for IR-

radiation was not as high as that of laser extinction, as

mentioned above. However, the inferred kcl-value showed

similar profile with the He-Ne-laser extinction. Therefore,

we decided one could measure the soot signal with our

optical systems.

The previous workers expressed their experimental re-

sults with the induction period, soot formation rate and

soot yield (Frenklach et al. 1983a; Frenklach et al. 1983b;

Tanke et al. 1998). In our experiments the rate of soot pro-

duction was still not zero in the region of the soot yield,

where the soot formation was defined to be practically

zero by previous workers. Furthermore, we observed the

early part of soot signals and took information from these

data.

For the soot formation mechanism in this region we at-

tempted to do the following modeling (Tsuboi et al. 1992)

and the expression obtained was compared qualitatively

with the experimental results:

(1) Benzene reaction and the production of one or some

complex species (clusters) B. The cluster B was not only

one species but they must be several species. These re-

actions must occur in the gas phase and there must also

some chain reactions.

n

1

A → B

l

( k

a

) .

(2) Phase change Bto soot S

1

(coagulation)

n

2

B → S

1

( k

b

) .

(3) Growth of soot particles

S

1

+ B → S

2

( k

1

)

S

2

+ B → S

3

( k

2

)

............

S

n

+ B → S

n+1

( k

n

) .

(4) Cohesion of soot particles

S

i

+ S

j

→ S

i+j

( k

c

) .

The rate of volume N

S

i

V

S

i

of soot particle S

i

are

d

d

t

(N

S

1

V

S

1

) = k

b

N

n

2

B

V

S

1

− k

1

N

B

N

S

1

V

S

1

d

d

t

(N

S

2

V

S

2

) = k

1

N

B

N

S

1

V

S

2

− k

2

N

B

N

S

2

V

S

2

d

d

t

(N

S

3

V

S

3

) = k

2

N

B

N

S

2

V

S

3

− k

3

N

B

N

S

3

V

S

3

.........

d

d

t

(N

S

n

V

S

n

) = k

n−1

N

B

N

S

n−1

V

S

n

− k

n

N

B

N

S

n

V

S

n

.

The total volume rate of soot particles is

d

dt

(N

S

V

S

) =

n

i=1

d

dt

(N

S

i

V

S

i

)

= k

b

N

n

2

B

V

S

1

+ N

B

V

B

n

i=1

k

i

N

S

i

.

(10)

Here, V

S

i

− V

S

i−1

= V

B

. The rate k

i

is equivalent to the

collision frequency between S

i

and B, which is given as

follows.

k

i

=

πd

2

S

i

B

σ

S

i

B

·

8kT

πµ

1/2

.

The rate k

b

is the rate constant of phase change to soot

from the gas phase of C-species and given in Tsuboi et al.

1992:

k

b

= k

b0

exp (−∆G

∗

/RT )

and

∆g =

16πγ

3

3∆H

v

(T

0

)

2

·

1

(1 − T/T

0

)

2

∆G

∗

= N

0

∆g .

(11)

Here, γ is the surface tension, ∆H

v

(T

0

) is the latent heat

of soot from gas phase at T

0

, ∆g and ∆G

∗

are the ac-

tivation energy to form the soot. Strictly speaking, ∆G

∗

is the activation energy to make the minimum soot par-

ticle (embryo) from the unstable species of the radius

r = 0. However the species Bhas already some size.

Therefore, one should consider that k

b

is proportional to

k

b0

exp (−∆G

∗

/RT ).

The rate of N

B

is

d

dt

N

B

= k

a

N

n

1

A

− k

b

N

n

2

B

−N

B

(k

1

N

S

1

+ k

2

N

S

2

+ · · ·k

n

N

S

n

) . (12)

When one uses the early part of soot formation, the first

term of Eq. (12) must be rate determining, then one ob-

tains,

d

dt

N

B

∼ k

a,0

e

k

r

t

N

n

1

A

.

(13)

T. Tsuboi et al.: Soot formation of benzene

127

If one takes only the first step of reactions for the forma-

tion of B-species, the over-all rate constant k

a

in Eq. (13)

can be constant. However, if one considers the period un-

til the beginning of soot formation, one probably must as-

sume that some chain reactions occur. Therefore k

a,0

e

k

r

t

had to be applied for the rate k

a

of over-all reactions which

produce the B-species. The second and the third terms in

Eq. (12) must be still small. If one integrates the equation

N

B

=

k

a,0

k

r

e

k

r

t

− 1

N

n

1

A

(14)

by considering V

S

1

= n

2

V

B

, Eq. (10) can be substituted

for Eq. (14).

d

dt

(N

S

V

S

) = n

2

k

b

N

n

2

B

V

B

1 +

N

B

V

B

n

i=1

k

i

N

S

i

n

2

k

b

N

n

2

B

V

B

. (15)

At the beginning of the reaction one can take the first

part of the Eq. (15), because probably, k

B

≈ k

i

, k

b

N

n

2

B

>

N

B

×

k

i

N

S

i

in the early stage of the soot formation, then

N

A

= constant and we obtain the following equation:

d

dt

(N

S

V

S

) = n

2

k

b

k

a

k

r

e

k

r

t

− 1

N

n

1

A

n

2

V

B

.

(16)

If one calculates the above equation further, then one can

obtain

d

dt

(N

S

V

S

) = n

2

k

b

k

n

2

a

t

n

2

N

n

1

n

2

A

V

B

N

S

V

S

=

n

2

n

2

+ 1

k

b

k

n

2

a

t

n

2

+1

N

n

1

n

2

A

V

B

(17)

for the time t ≈ 0 and at the time k

r

t > 1 one can obtain

d

dt

(N

S

V

S

) = n

2

k

b

k

a

k

r

n

2

e

2k

r

t

N

n

1

n

2

A

V

B

N

S

V

S

= n

2

k

b

1

2k

r

k

a

k

r

n

2

e

n

2

k

r

t

N

n

1

n

2

A

V

B

. (18)

The time history of N

S

V

S

, which is obtained from Eq. (2),

indicates that n

2

∼ 2. Using Eq. (17), one can obtain the

relation N

S

V

S

= a × t

3

, given in Eq. (4) and then one can

obtain 2 k

S

V

B

(= k

S

V

S

1

).

3d(N

S

V

S

)

dt

3

= 2k

b

k

2

a

V

B

N

2n

1

A

= 2k

S

V

B

N

2n

1

A

= k

S

V

S

1

N

2n

1

A

(19)

This expression is equivalent to the experimental expres-

sion with Eqs. (4), (5) and (7). The signals of infrared

emission to measure the kcl-value are less sensitive than

those of He-Ne laser light extinction. The time history of

NV

S

of He-Ne laser was in the region k

r

< 1 and one can

use Eq. (17). On the contrary the time history of kcl ob-

tained from infrared emission was in the region k

r

> 1 and

one can use Eq. (4).

This analysis could be used in the temperature region

under 2100 K. The time interval when the B-species was

produced decreased with increasing temperature. Then

one cannot explain the soot formation with Eqs. (17) and

(4). Above 2300 K the concentration N

B

might not be

time-dependent and can be constant. Namely,

N

B

= n

N

A

(= constant) .

(20)

Then one can obtain from Eq. (15)

d

dt

(N

S

V

S

) = k

b

N

n

2

B

V

Si

= k

b

n

N

A

n

2

V

Si

(21)

then

N

S

V

S

= k

b

n

N

A

n

2

V

S

i

t + C .

(22)

Here C is a constant at t = 0. This expression is equivalent

to Eqs. (6) and (9). The activation energy −∆G

∗

/RT of

the rate constant k

b

is strongly temperature-dependent.

With increasing temperature the energy increases until

T = T

0

. Therefore, the rate constant k

b

decreases with

increasing temperature. The negative temperature depen-

dence in Fig. 10 shows this effect. This effect can be seen

in Figs. 3, 9. Namely, the apparent activation energy of

soot formation rate decreased at above 2200 K.

Since this modeling is a rough estimation of soot for-

mation, it cannot be explained precisely, however one can

understand the temperature dependence of the soot for-

mation rate.

5 Conclusion

The time histories of soot volume, kcl-value and temper-

ature were followed by observing the light extinction of

He-Ne laser and the thermal radiation at 0.63, 0.80, 1.12,

1.52, 2.3, 3.4, 3.9, 4.3

µ

m. The following expressions were

obtained.

(1) From laser extinction:

under 2000 K in the early stage of soot formation,

3

d(N

S

V

S

)

dt

3

= (6 ± 5) × 10

23

[C

6

H

6

]

2.6±0.1

[Ar]

0.2±0.1

× exp

−

640000 ± 40000

RT

[cm

3

/cm

3

µ

s

3

]

above 2100 K in the later stage of soot formation,

d(N

S

V

S

)

dt

= (7 ± 6) × 10

−6

[C

6

H

6

]

2.6±0.2

[Ar]

−1.7±0.1

×exp

266000 ± 50000

RT

[cm

3

/cm

3

µ

s] .

(2) From thermal radiation:

under 2000 K in the early stage of soot formation,

3

d(kcl)

d(t − τ)

3

= (2 ± 1) × 10

16

[C

6

H

6

]

1.8±0.1

[Ar]

0.7±0.2

×exp

−

280000 ± 40000

RT

[

µ

m

0.95

/

µ

s

3

]

τ = (4 ± 2) × 10

10

[C

6

H

6

]

−0.22±0.07

[Ar]

−0.74±0.12

×exp

−

240000 ± 40000

RT

[s]

128

T. Tsuboi et al.: Soot formation of benzene

above 2100 K in the later stage of soot formation,

d(kcl)

dt

= (1.0 ± 0.6) × 10

8

[C

6

H

6

]

4.7±0.3

[Ar]

−2.8±0.1

×exp

343000 ± 50000

RT

[

µ

m

0.95

/

µ

s] .

Acknowledgements. This project is partially supported by

Joint Program of JSPS-NEDO Matching Fund (No.25) in 1999.

References

Bauer SH, Zhang LM (1983) ShockTube Pyrolysis of Poly-

cyclic Aromatics – Detection of Precursors. Proceedings

of the 14th International Symposium on ShockTubes and

Waves, pp. 654–661

B¨ohm H, Jander H, Tanke D (1998) PAH Growth and Soot For-

mation in the Pyrolysis of Acetylene and Benzene at high

Temperatures and Pressures: Modeling and Experiment.

27th Symposium (International) on Combustion, pp. 1605–

1612

Bonne U, Wagner HGg (1965) Untersuchung des Reaktions-

ablaufs in fetten Kohlenwasserstoff-Sauerstoff-Flammen.

III. Optische Untersuchungen an rußenden Flammen.

Berichte der Bunsengesellschaft f¨ur Physikalische Chemie

69:35–48

Calcote HF (1981) Mechanisms of Soot Nucleation in Flames-

A Critical Review. Combustion and Flame 42:215–242

Chippett S, Gray WA (1978) The Size and Optical Properties

of Soot Particles Combustion and Flame 31:149–159

D’Alessio A, Beretta F, Venitozzi C (1972) Optical Investiga-

tions on Soot Forming Methane-Oxygen Flames. Combus-

tion Science and Technology 3:263–272

Darzell WH, Sarofim AF (1969) Optical Constants of Soot and

Their Application to Heat-Flux Calculations.. Transactions

of the ASME, Journal of Heat Transfer (1969-2), pp. 100–

104

Frenklach M, Taki S, Likwok Cheong CK (1983a) Soot Particle

Size and Soot Yield in ShockTube Studies. Combus. Flame

51:37–43

Frenklach M, Taki S, Durgaprasad, Matula, RA (1983b) Soot

formation in shock-tube pyrolysis of acetylene, allene, and

1,3-butagiene. Combus. Flame 54:81–101

Frey JW, Corn M (1967) Physical and Chemical Characteris-

tics of Particulates in a Diesel Exhaust. American Indus-

trial Hygiene Association Journal, pp. 468–478

Graham SC (1974) The Refractive Indices of Isolated and of

Aggregated Soot Particles. Combustion Science and Tech-

nology 9:159–163

Johnson BE, Lester TW, Merklin JF, Sorenson CM (1983)

Soot from Benzene/Cyclohexane Pyrolysis. Proceedings of

the 14th International Symposium on ShockTubes and

Waves, pp. 648–653

Kadota T, Hiroyasu H, Farazandehmehr (1977) Soot Forma-

tion by Combustion of a Fuel Droplet in High Pressure

Gaseous Environments. Combustion and Flame 29:67–75

Kham IM, Wang CHT, Langridge BE (1971) Coagulation and

Combustion of Soot Particles in Diesel Engines. Combus-

tion and Flame 17:409–419

ParkC, Appleton JP (1973) Shock-Tube Measurements of Soot

Oxidation Rates. Combustion and Flame 20:369–379

Radcliffe SW, Appleton JP (1971) Shock-Tube Measurements

of Carbon to Oxygen Atom Ratios for Incipient Soot For-

mation with C

2

H

2

, C

2

H

4

and C

2

H

6

Fuels. Combustion Sci-

ence and Technology 3:255–262

Sj¨ogren A (1973) Soot Formation by Combustion of an At-

omized Liquid Fuel. 14th Symposium (International) on

Combustion, pp. 919–927

Tanke D, Wagner HGg, Zaslonko IS (1998) Mechanism of

the Action of Iron-Bearing Additives on Soot Formation

behind ShockWaves. 27th Symposium (International) on

Combustion, pp. 1597–1604

Tsuboi T, Kamei M, Kobayashi K, Ikuta Y, Katoh R (1986)

Optische Messungen der Dichte der von Azetylen gebilde-

ten Rußteilchen. Japan. J. Appl. Phys. 25:1165–1168

Tsuboi T, Kamei M, Kobayashi K, Ikuta Y (1992) ¨Uber Ruß-

bildung des Azetylenes hinter reflektierten Stoßwellen. J.

Phys. Soc. Japan 61:4643–4649

Wagner HGg (1979) Soot Formation in Combustion. 17th Sym-

posium (International) on Combustion, pp. 3–19

Wersborg BL, Fox LK, Howard JB (1975) Soot Concentration

and Absorption Coefficient in a Low-Pressure Flame. Com-

bustion and Flame 24:1–10

Yoshizawa Y, Kawada H, Kurokawa M (1979) A Shock-Tube

Study on the Process of Soot Formation from Acetylene

Pyrolysis. 17th Symposium (International) on Combustion,

pp. 1375–1381