Całki funkcji wymiernych

mgr Zofia Makara

27 czerwca 2004

1

Całki funkcji wymiernych - metody całowania

Calki funkcji wymiernych nie posiadają żadnych specjalnych metod całowa-
nia, ale znajomość niekórych faktów może uprościć ich obliczanie.
Kilka uwag:

1. jeśli stopień wielomianu w liczniku jest większy lub równy stopnio-

wi wykładnika w mianowniku, to licznik dzielimy przez mianownik
i otrzymujemy całkę wielomianu i całkę funkcji wykładniczej, której
stopień wielomianu w liczniku jest mniejszy niż w mianowniku;

2. jeśli istniej możliwość i widoczna jest konieczność funkcję wymierną al-

bo dzielimy na wilele funkcji wymiernych, albo rozkładamy na ułamki
proste;

3. znanymi metodami calkowania obliczamy daną calkę.

Przykład 1

Z

2x + 1

x

2

+ 2x + 2

dx =

Z

2x + 2 − 1

x

2

+ 2x + 2

dx =

Z

2x + 2

x

2

+ 2x + 2

dx −

Z

1

x

2

+ 2x + 2

dx =

Z

(x

2

+ 2x + 2)

0

x

2

+ 2x + 2

dx −

Z

1

(x + 1)

2

+ 1

dx

= ln(x

2

+ 2x + 2) + arc (x + 1) +C

C ∈ R.

Przykład 2

Z

x

6

+ 9x

4

+ 10x

2

+ 10

x

4

+ 8x

2

− 9

dx =

Z

(x

2

+ 1)(x

4

+ 8x

2

− 9) + 1 + x

2

x

4

+ 8x

2

− 9

dx =

Z

(x

2

+ 1)(x

4

+ 8x

2

− 9) + 1 + x

2

x

4

+ 8x

2

− 9

dx =

Z

x

2

+ 1 dx+

Z

1 + x

2

x

4

+ 8x

2

− 9

dx =

1

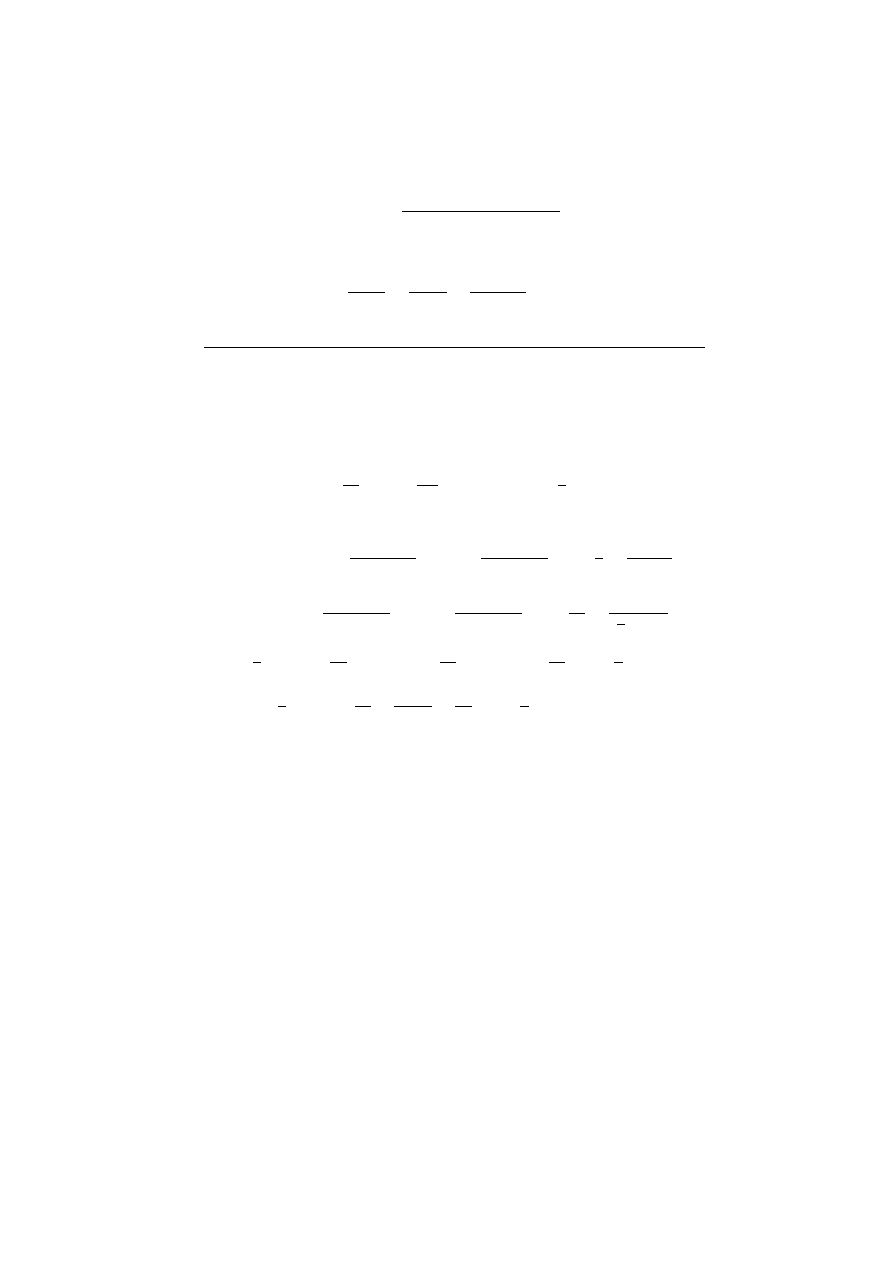
Z

x

2

+ 1 dx +

Z

1 + x

2

(x − 1)(x + 1)(x

2

+ 9)

dx = ∗

Można zauważyć, że można rozłożyć dany ułamek na ułamki proste:

A

x − 1

+

B

x + 1

+

Cx + D

x

2

+ 9

=

=

(A + B + C)x

3

+ (A − B + D)x

2

+ (9A + 9B − C)x + (9A − 9B − D)

(x − 1)(x + 1)(x

2

+ 9)

Stąd:

A + B + C = 0; A − B + D = 1; 9A + 9B − C = 0; 9A − 9B − D = 1;

Więc

A =

1

10

; B =

−1

10

; C = 0; D =

4

5

;

Zatem

∗ =

Z

x

2

+ 1 dx +

Z

1

10(x − 1)

dx −

Z

1

10(x + 1)

dx +

4

5

Z

1

x

2

+ 9

dx

=

Z

x

2

+ 1 dx +

Z

1

10(x − 1)

dx −

Z

1

10(x + 1)

dx +

4

45

Z

1

(

x
3

)

2

+ 1

dx =

=

1

3

x

3

+ x +

1

10

ln (x − 1) −

1

10

ln (x + 1) +

4

45

arc tg

x

3

+ C

=

1

3

x

3

+ x +

1

10

ln

x − 1

x + 1

+

4

45

arc tg

x

3

+ C

C ∈ R.

Zatem wynikiem całkowania funkcji wymiernych są: funkcje wymierne, lo-
garytm naturalny, funkcje potęgowe i arcus tangens.

2

Zadania

1.

Z

x

2

− 3x dx;

2.

Z

8x

7

− 3x

2

+ 4x − 5 dx;

3.

Z

(x − 2)

8

− (x + 5)

3

dx;

2

4.

Z

8(x − 3)

7

− 5(x − 3)

4

dx;

5.

Z

1

1 − x

dx;

6.

Z

1

3x − 5

dx;

7.

Z

2x

1 − x

dx;

8.

Z

2x − 3

1 − x

dx;

9.

Z

1 − x

2

1 − x

dx;

10.

Z

3 + 2x

9 − 4x

2

dx;

11.

Z

x

2

− 3x + 2

x

2

+ 2x − 3

dx;

12.

Z

x + 1

x

3

+ x

2

− 4x − 4

dx;

13.

Z

x

x

2

+ 1

dx;

14.

Z

2x

2

+ 3

x

2

+ 9

dx;

3

15.

Z

x + 3

x

2

+ 4

dx;

16.

Z

1

x

2

+ 6x + 14

dx;

17.

Z

2x + 7

x

2

+ 6x + 14

dx;

18.

Z

1

x

2

+ 6x − 7

dx;

19.

Z

2x − 5

x

2

+ 6x − 7

dx;

20.

Z

x

3

− 2x

x

2

+ 6x − 2

dx;

21.

Z

2x − 5

(x − 2)

9

dx;

22.

Z

9

(x − 5)

8

dx;

23.

Z

5x

2

(x

3

+ 1)

5

dx

24.

Z

2x

x

4

+ 4

dx;

25.

Z

2x

4

+ 2x + 18

x

4

+ 9

dx

4