
1
Wykład 12.
Elektryczność i magnetyzm. Prawo Gaussa
1. Pole elektryczne
1.1
Wektor natężenia pola elektrycznego E.
Pole elektryczne definiuje się jako stosunek siły elektrycznej działającej na
ładunek jednostkowy:
q
F
E
r
r
=
,
(1.1.1)
gdzie E – natężenie pola elektrycznego, F – siła elektryczna (prawo Coulomba),
q ładunek próbny (dodatni).
Z prawa Coulomba otrzymamy pole elektryczne ładunku punktowego (w
próżni):
r
r
q
q
r
r
q
q
F
r
r
2
2
1
0
2
1
0
4
1
ˆ
4
1
ε
π
ε
π
=
=
,
(1.1.2)
gdzie:
0
ε
- przenikalność elektryczna próżni, r odległość między ładunkami, a
pozostałe wielkości opisano na rysunku 1.1.
Rys 1.1 Siły działające między dwoma ładunkami. Prawo Coulomba.
Pola elektryczne wypełnia zasadę superpozycji – natężenia pól elektrycznych
dodaję się wektorowo. Jeżeli mamy wiele ładunków, to całkowite pole
elektryczne jest równe:

2
∑
=
+
+
+
=
i
i
E
E
E
E
E
r
K
r
r
r
r
3
2
1
(1.1.3).
gdzie E
i
- natężenie ładunku punktowego dane jest przez równania 1.1.1 i 1.1.2.
Równie 1.3 możemy zastosować również do obliczenie natężenia pola
elektrycznego wytwarzanego przez nieskończoną ilość, nieskończenie małych
ładunków, modyfikując je odpowiednio. Pole elektryczne zdefiniowane jest
wówczas przez całkę (sumę nieskończonej liczby nieskończenie małych
elementów):
∫
=
r
d
r
r
E
ˆ
ˆ
4
1
3
2
0
ρ
ε
π
r
(1.1.4).
Na koniec, natężenie pola elektrycznego związane jest z potencjałem
zależnością:
)
(
)
(
r
r
grad
E
φ
φ
−∇
=
−
=
r
,
(1.1.5).
Natężenie pola elektryczne jest przeciwnie skierowane do gradientu potencjału
skalarnego pola elektrycznego.
1.2
Indukcja pola elektrycznego oraz przenikalność elektryczna ośrodka
Jak będzie wyglądało pole elektryczne w ośrodku różnym od próżni: w cieczach,
gazach, czy ciałach stałych, czyli ośrodkach charakteryzujących się różną od
jedności względną przenikalnością elektryczną? Musimy prowadzić nową
wielkość. Pole elektryczne definiujemy w takich ośrodkach poprzez wektor
indukcji pola elektrycznego D w sposób następujący:
E
D
r
r
ε
=
,
(1.2.1).
gdzie: D – wektor indukcji pola elektrycznego, E – wektor natężenia pola
elektrycznego,
ε
- przenikalność elektryczna ośrodka.
Przenikalność elektryczna ośrodka
ε
jest skalarem w ośrodku izotropowym,
czyli takim, którego własności elektryczne są takie same niezależnie od kąta w
jakim dokonujemy pomiary. Oznacza to, że w ośrodku izotropowym wektory D
i E są do siebie równoległe. W ośrodku anizotropowym, którego własności
elektryczne zależą od kąta, w którym dokonuje się pomiarów, przenikalność
elektryczna ośrodka
ε
jest tensorem 2-go rzędu (macierzą dwuwymiarową), a
wektory D i E przestają być równoległe.
Przykład bryły izotropowej: kula.

3
Przykład bryły anizotropowej: sześcian, ogólnie każda bryła nie będąca kulą
(sferą).
Przenikalność elektryczna ośrodka definiujemy jako iloczyn
r
ε
ε
ε
0
=
(1.2.2)
gdzie:
0
ε
- przenikalność elektryczna próżni, fundamentalna stała przyrody
Względna przenikalność elektryczna ośrodka
r
ε
(stała bezwymiarowa) określa
ile razy przenikalność danego ośrodka
ε
jest większa od przenikalności
elektrycznej próżni
0
ε
.
0
ε
ε
ε
=
r
(1.2.2a)
Dla próżni
1
=
r
ε
. Względna przenikalność elektryczna zależy od budowy
cząstek (molekuł) tworzących materiał. Może być skalarem lub tensorem rzędu
2-go. W zmiennym polu elektrycznym względna przenikalność elektryczna jest
funkcją częstotliwości zmian pola elektrycznego. Dla stałego pola elektrycznego
mamy do czynienia ze stała przenikalnością statyczną. Ze względu na własności
elektryczne materiały dzielimy ją na trzy rodzaje: dielektryki, paraelektryki i
ferroelektryki. Wartości względnej przenikalności elektrycznej dla niektórych
materiałów podano w tabeli 1.
Tabela 1 Wartości względnej przenikalności elektrycznej dla kilku wybranych
materiałów.
ośrodek
r
ε
przenikalność
elektryczna
próżnia
1
powietrze
1.00056
diament
5,5–10
krzem (Si)
11,68
alkohol metylowy (CH
3
OH)
30
alkohol etylowy (C
2
H
5
OH)
27
woda (H
2
O) (temp. 0
0
- 20
0
C)
80 – 88
ferroelektryki
> 1000
Warto tu przypomnieć związek między elektrycznymi i magnetycznym
własnościami próżni a prędkością światła:

4
0
0
1
µ
ε
=
c
,
(1.2.3)
gdzie: ε
0
– podatność elektryczna, µ
0
– podatność magnetyczna próżni.
Przenikalność elektryczna poprzez indukcję elektryczną D określa odpowiedź
ośrodka (materiału) na przyłożone zewnętrzne pole elektryczne E.
Przyłożone pole elektryczne oddziałuje na ośrodek dwojako. Ośrodek wpływa
na oddziaływanie, modyfikując je w istotny sposób, ale też pole elektryczne
oddziałuje na ośrodek (zjawisko polaryzacji polaryzacja elektrycznej ośrodka).
Widać to w prędkości światła. W ośrodku o określonej podatności elektryczne i
magnetyczne, wynosi:
µ
ε
1
=
c
,
(1.2.4)
gdzie: ε to podatność elektryczna ośrodka, µ podatność magnetyczna ośrodka.
Prędkość światła w ośrodku jest różna (niższa) od prędkości światłą w próżni.
Materiał wpływa na propagację fali elektromagnetycznej (światła). Zmienia
(obniża) prędkość światła.

5
2. Prawo Gaussa
Carl Friedrich Gauss (1777 - 1855)
Prawo Gaussa stosujemy dla pola grawitacyjnego oraz pola elektrycznego. Ma
ono analogiczną postać w przypadku obu tych pól, jakże przecież różnych, W
fizyce (i matematyce) prawo Gaussa definiuje związek strumieniem pola
grawitacyjnego,
pola
elektrycznego,
przechodzącego
przez
dowolną
powierzchnię zamkniętą, a masą, odpowiednio ładunkiem, zamkniętym
wewnątrz tej powierzchni.
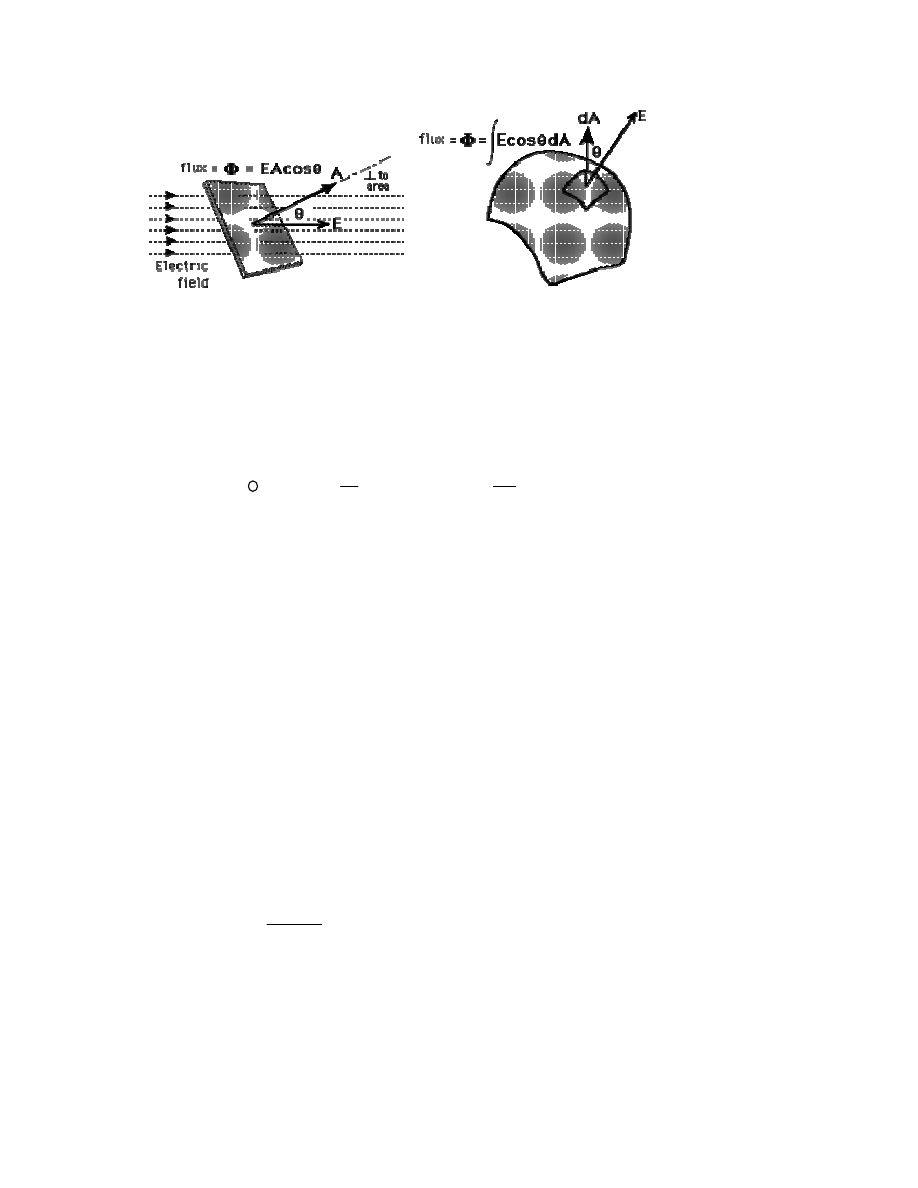
Strumień pola elektrycznego, w ośrodku o przenikalności elektrycznej ośrodka
ε
, definiujemy następująco:
)
,
(
cos
A
E
A
E
A
E
E
r
r
<
r
r
⋅
=
⋅
=
Φ
(2.1a).
gdy powierzchnia jest płaska i tworzy stały kąt ze z natężeniem (patrz rys. 2.1).
W przypadku dowolnej powierzchni (zakrzywionej) strumień definiujemy jako
nieskończoną sumę nieskończenie małych przyczynków (różniczek) strumienia
(patrz rys. 2.1):
∫
∫
=
=
Φ
A
A
E
A
d
D
A
d
E
r
r
r
r
ε
1
(2.1b).
gdzie:
E
Φ
- strumień pola elektrycznego, D, E – wektory pola elektrycznego, A
powierzchnia zamknięta.
6
Rys 2.1 Strumień pola elektrycznego
Prawo Gaussa:
(postać całkowa prawa Gaussa)
ε
ρ
ε
Q
dV
r
A
d
E
V
A
E
=
=
=
Φ
∫
∫
)
(
1
r
r
(2.2).
gdzie: A – powierzchnia obejmująca objętość V.
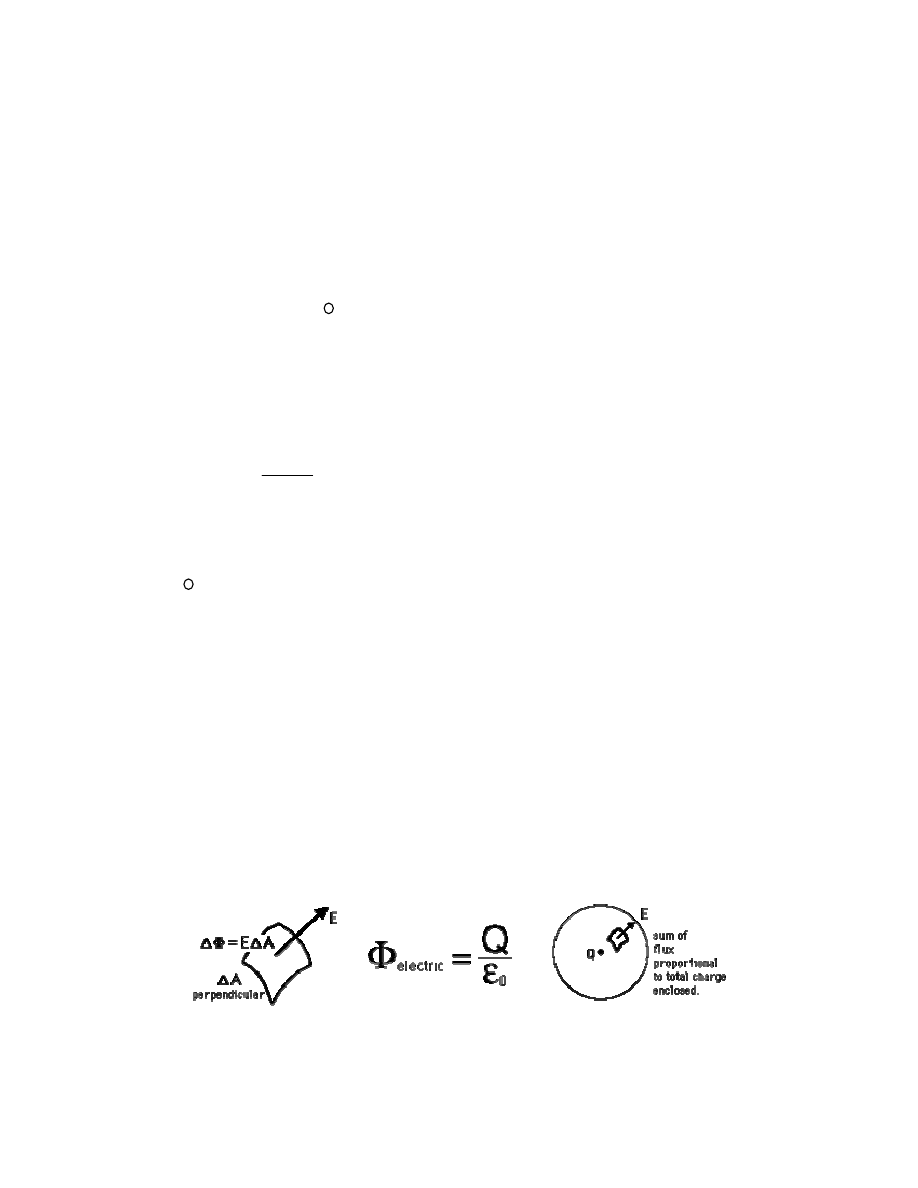
Strumień pola elektrycznego przechodzącego przez dowolną powierzchnię
zamkniętą jest proporcjonalny do całkowitego ładunku elektrycznego
zamkniętego przez tą powierzchnię. Inaczej mówiąc, prawo Gaussa głosi, że
pole elektryczne jest polem źródłowym. Istnieją ładunki elektryczne, które
wytwarzają pole elektryczne.
Prawo Gaussa:
(postać różniczkowa prawa Gaussa)
ε
ε
ρ
ρ
0
)
(
lub
)
(
r
E
div
r
D
div
=
=
r
r
(2.3).
gdzie
ρ
jest to gęstość ładunku [C/m
3
]
7
Pole elektryczne jest polem źródłowym. Postać prawa Gaussa, czy to całkowa,
czy różniczkowa, są sobie równoważne. Przejście między nimi umożliwia
twierdzenie Gaussa – Ostrogradzkiego.
*********************************
Dodatek matematyczny
Twierdzenie Gaussa – Ostrogradskiego
∫
∫
∂
=
V
V
A
d
F
dV
F
div
r
r
r
(2.4).
*********************************
W próżni prawo Gaussa będzie wyglądało następująco:
0
)
(
ε
ρ
r
E
div
=
(2.5).
Jeszcze raz prawo Gaussa, czyli I prawo Maxwella.
ρ
=
=
∫
D
div
Q
A
d
D
A
r
r
r
(2.6).
postać całkowa i różniczkowa.
Prawo Gaussa stosuje się nie tylko do pola elektrycznego. Jest prawdziwe dla
każdego pola, którego natężenie zmienia się jak odwrotność kwadratu odległości
~1/r
2
. Obowiązuje również np. dla pola grawitacyjnego, dla intensywności
promieniowania.
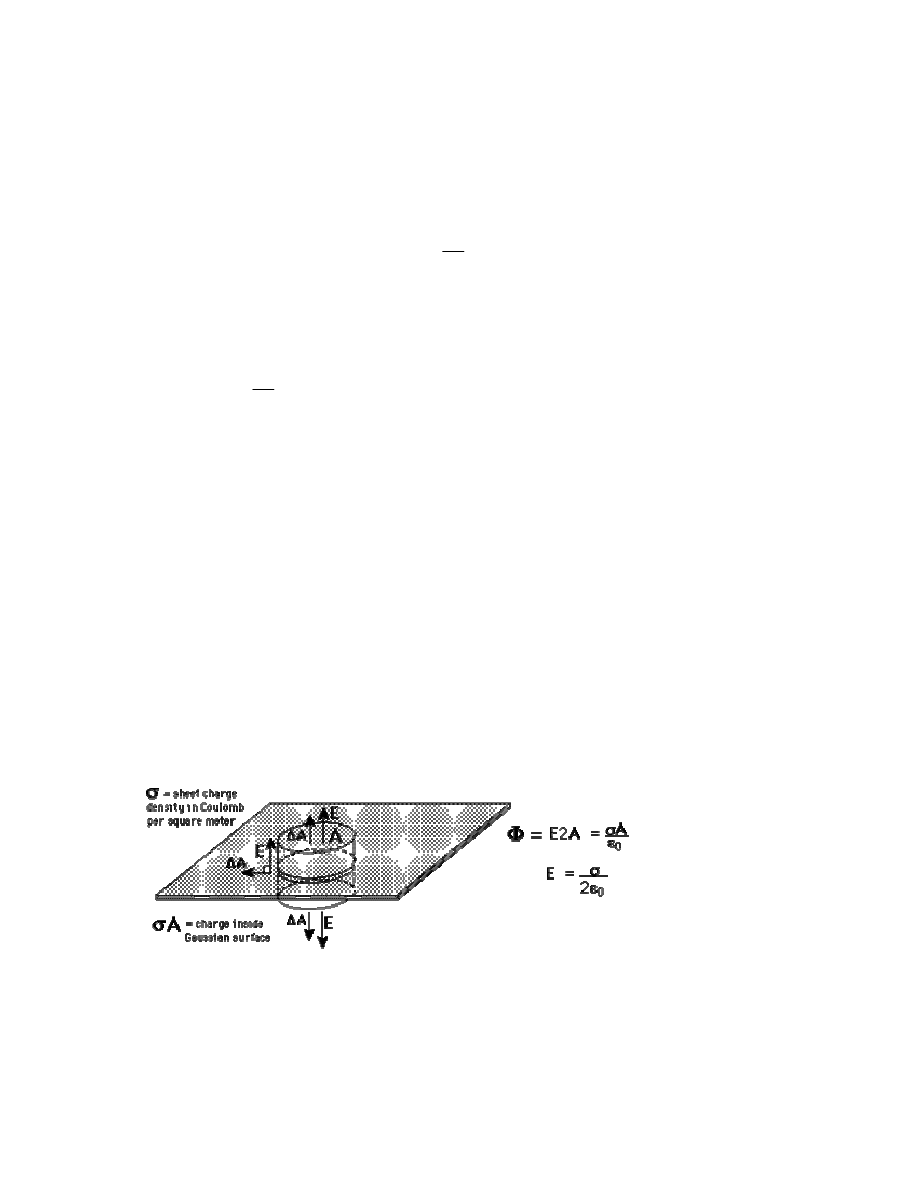
Zadanie: wykazać, że prawo Coulomba wynika z prawa Gaussa (patrz rys. 2.2)
Rys. 2.2 Strumień pola elektrycznego dla ładunku punktowego
8
Prawo Gaussa definiuje pole elektryczne jako pole źródłowe. Ale wiemy, że
natężenie pola elektrycznego związane jest potencjałem skalarnym równaniem
1.1.5. Podstawiając to do prawa Gaussa otrzymamy:
ε
ρ
φ
φ
=
∇
⋅
∇
=
)
(
)
(grad
div
(2.7).
Równanie to możemy zapisać:
ε
ρ
φ
=
∇
2
(2.8),
nosi ono nazwę równania Poissona. Jest to równanie różniczkowe rzędu
drugiego. W ogólnym przypadku jest ono trudne do rozwiązania.
Jednakże, gdy w ośrodku nie ma ładunków elektrycznych, np. w próżni,
równanie 2.7 upraszcza się:
0
2
=
∇
φ
(2.9),
równanie to nosi nazwę równania Laplace’a.
Opisuje ono pole elektryczne w próżni, bez ładunków punktowych.
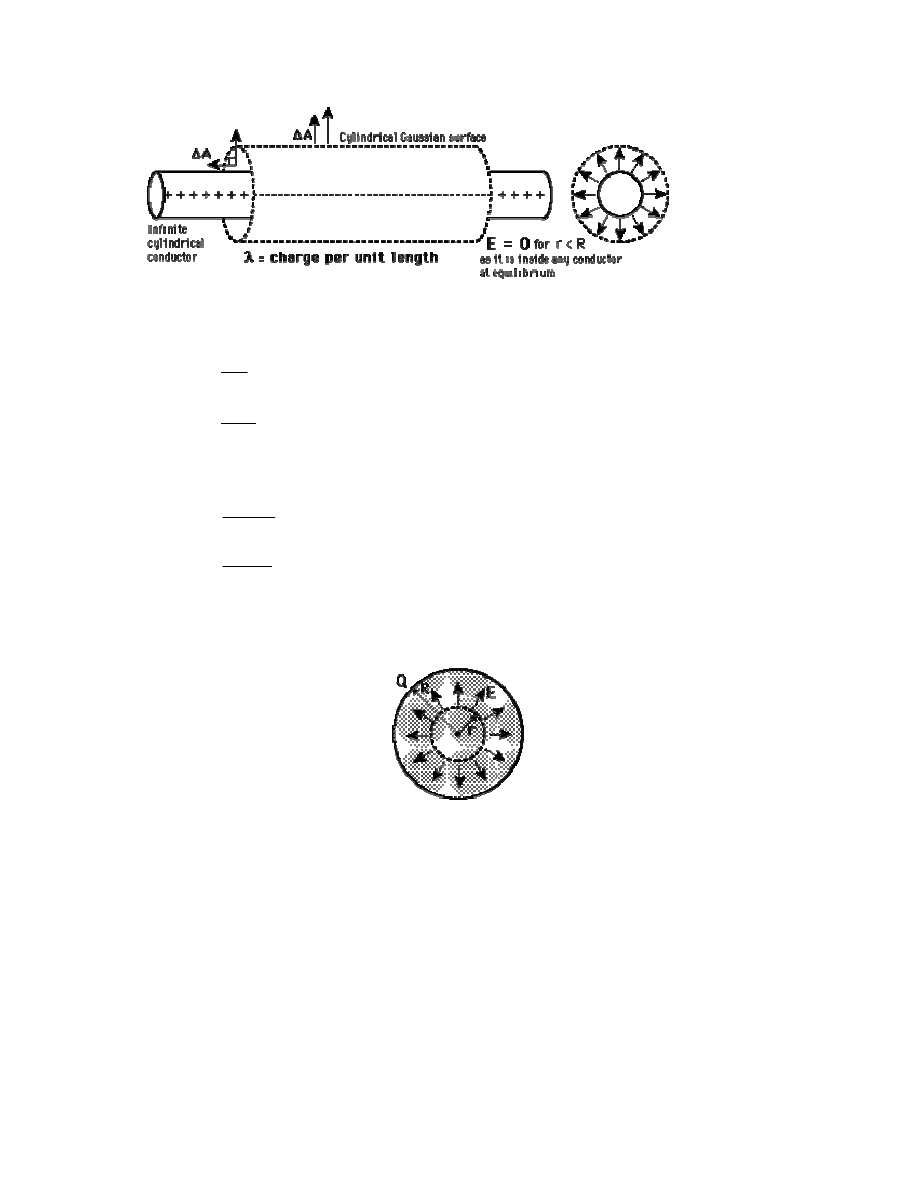
Zadanie:
Korzystając z prawa Gaussa obliczyć pole elektryczne ładunków
rozmieszczonych na:
a) jednorodna naładowana płaszczyzna
b) naładowanego cylindra o promieniu R
9
Odpowiedź:
R
r
dla
r
R
E
R
r
dla
r
E
≥
=
<
=
0
2
0
2
2
ε
ρ
ε
ρ
b) naładowanej kuli o promieniu R
Odpowiedź:
R
r
dla
r
Q
E
R
r
dla
R
r
Q
E
≥
=
<
=
2
0
3
0
4
4
πε
πε
przypadek na zewnątrz kuli jest równoważny polu ładunku punktowego,
przypadek wewnątrz kuli pomoże rozwiązać rysunek:
d) dwóch naładowanych, równoległych płaszczyzn
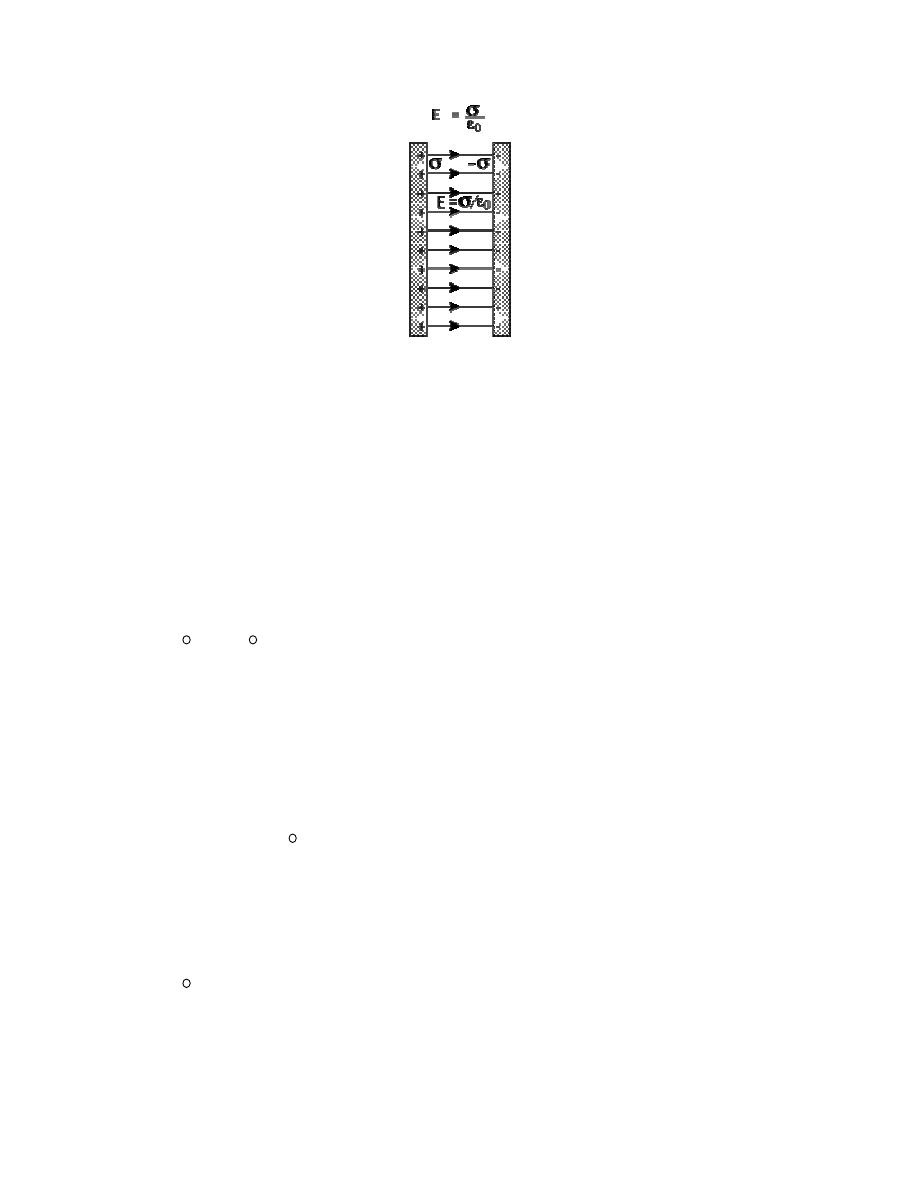
10
3. II równanie Maxwella
Praca wykonana przy przesunięciu ładunku między dwoma punktami wynosi:
∫
∫
=
=
→
2
1
2
1
1
2
1
)
(
r
r
r
r
l
d
E
q
l
d
F
r
r
W
r
r
r
r
,
(3.1),
Pole elektryczne jest polem zachowawczym. Praca wykonana po dowolnej
drodze zamkniętej równa się zero.
∫
∫
=
=
0
l
d
E
dW
r
r
,
(3.2),
Skorzystamy tutaj z twierdzenia Stokes’a.
*********************************
Dodatek matematyczny
Twierdzenie Stokes’a
∫
∫
∂
=
A
A
l
d
F
dA
F
rot
r
r
r
(3.3).
*********************************
Korzystając z prawa Stokesa mamy:
∫
∫
=
=
S
L
S
d
E
rot
l
d
E
0
r
r
r
r
(3.4),
Otrzymujemy stąd zależność (postać całkowa i różniczkowa):

11
0
0
=
=
∫
E
rot
l
d
E
L
r
r
r
(3.5).
znaną jako II równanie Maxwella.
4. Dipol elektryczny
Dipol elektryczny: układ dwóch ładunków: +q i –q odległych o stałą odległość d.
Rys. 3.1 Dipol elektryczny
Moment dipolowy cząsteczki jest zdefiniowany jako:
d
q
p
r
r
=
,
(4.1),
Na rys 4.2 przedstawiono powierzchnie ekwipotencjalne, czyli potencjał
skalarny dipola elektrycznego.
Pole elektryczne dipola elektrycznego konstruuje się jak suma (wektorowa) pól
elektrycznych pochodzących od ładunku dodatniego q i ujemnego -q.
Łatwiej jednak jest wyznaczyć skalarny potencjał dipola, który jest sumą
(algebraiczną) potencjałów skaranych pochodzących od dodatniego i ujemnego
ładunku (patrz rys. 4.2).
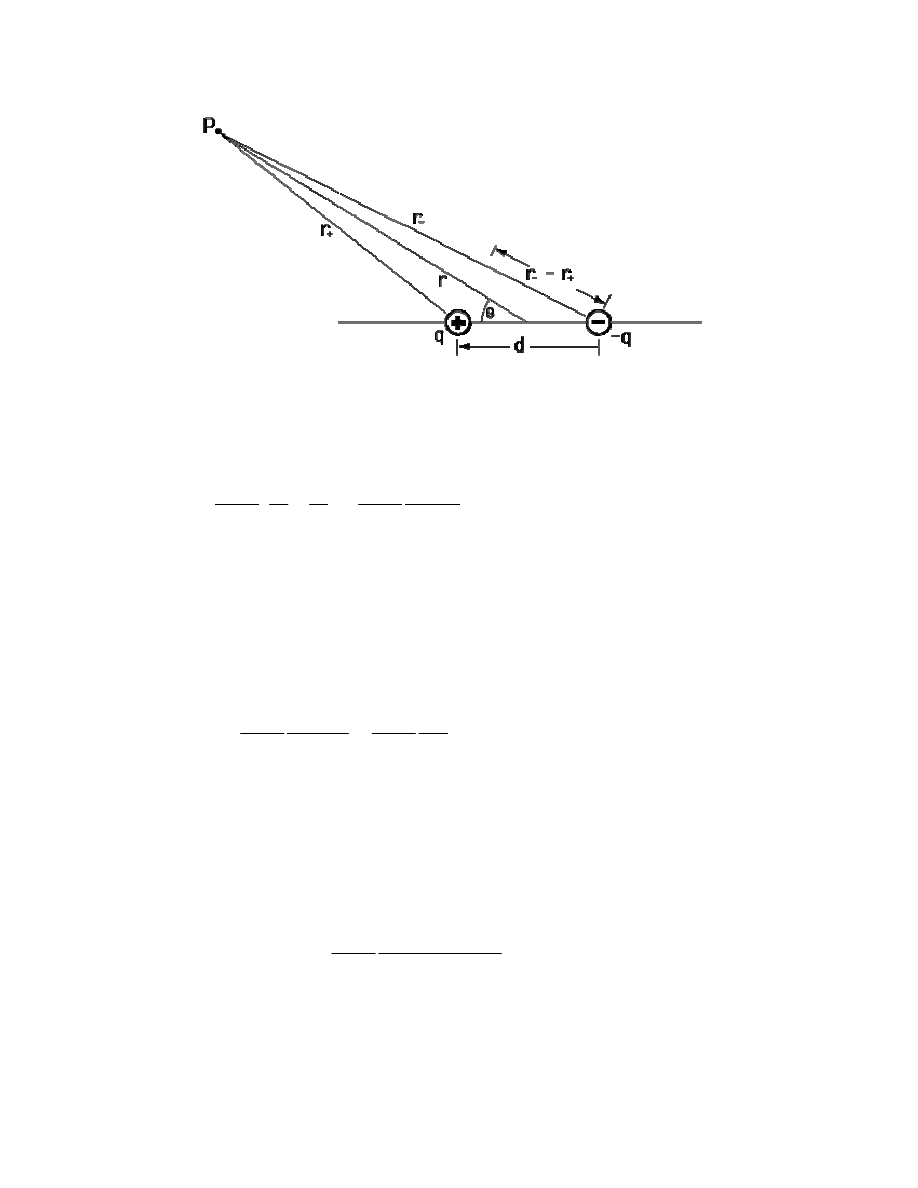
12
Rys. 4.2 Obliczanie potencjału skalarnego dipola elektrycznego
Potencjał w punkcie P wynosi:
−
+
+
−
−
+
−
=
−
=
r
r
r
r
q
r
r
q
0
0
4
)
1
1
(
4
πε
πε
φ
,
(4.2),
Interesujące wynik otrzymujemy, gdy r >> wówczas. Stosujemy przybliżenie:
2
,
cos
r
r
r
d
r
r
≈
≈
−
+
−
+
−
θ
,
(4.3).
Potencjał dipola elektrycznego zapisujemy następująco:
2
0
2
0
ˆ
4
1
cos
4
)
(
r
r
p
r
d
q
r
r
πε
θ
πε
φ
=
=
,
(4.4).
Obliczeń dokonano w próżni. W przypadku dipola elektrycznego w ośrodku
należy zmodyfikować wzór 4.4, uwzględniając względną przenikalność
elektryczną ośrodka.
Mając dany potencjał skalarny dipola elektrycznego możemy obliczyć pole
elektryczne na podstawie wzoru 1.1.5:
3
0
)
ˆ
)
ˆ
(
3
(
4
1
)
(
)
(
r
p
r
r
p
r
r
E
r
r
r
−
⋅
=
−∇
=
πε
φ
,
(4.4).
Jest to znany wzór na pole elektryczne dipola elektrycznego.

13
W przypadku, gdy oś Z skierowana jest wzdłuż osi dipola elektrycznego,
składowa z – owa pola elektrycznego jest równa:
3
2
0
)
1
)
(cos
3
(
4
r
p
E
z
−
=
θ
πε
,
(4.4).
4.1 Oddziaływanie dipola z polem elektrycznym
Umieszczenie dipola elektrycznego o momencie dipolowym p w polu
elektrycznym o natężeniu E, powoduje, że na dipol zaczyna działać moment siły:
E
p
M
r
r
r
×
=
,
(4.1.1).
Moment siły działający na dipol będzie obracał dipol ustawiając go równolegle
do linii natężenia pola elektrycznego, gdyż w takim położeniu dipol elektryczny
minimalizuje swoją energię potencjalną równą:
E
p
U
r
r
⋅
−
=
,
(4.1.2).
Dipol elektryczny m maksymalną energię, gdy dipol jest antyrównoległy do E.
Pole elektryczne działa porządkująco na zbiór chaotycznie skierowanych dipoli
elektrycznych.
4.2 Wektor indukcji pola elektrycznego
Wektor indukcji pola elektrycznego, również określany jako wektor
przesunięcia, jest zdefiniowany jako:
P
E
D
r
r
r
+
=
0
ε
(4.2.1).
gdzie: P – wektor polaryzacji. Jest on wprost proporcjonalny do natężenia pola
elektrycznego, co zapisujemy następująco:
E
P
r
r
χ
ε
0
=
(4.2.2).
Po podstawieniu o wzoru 4.2.1 otrzymamy zależność opisującą wartość indukcji
pola elektrycznego:

14
E
E
P
E
D
r
r
r
r
r
ε
ε
χ
ε
ε
0
0
0
)
1
(
=
+
=
+
=
(4.2.3).
Współczynnik
χ
ε
+
=
1
nazywamy względną przenikalnością elektryczną
dielektryka, zaś współczynnik
χ
nazywany jest podatnością elektryczną
dielektryka.
4.3 Własności materii a pole elektryczne
Materię dzielimy, ze względu na to jak reaguje na przyłożone zewnętrzne pole
elektryczne, na dwie główne grupy:
•
dielektryki (
1
≥
ε
),
•
paraelektryki (
1
>
ε
),
•
ferroelektryki(
1
>>
ε
).
To, do jakiej grupy przynależy konkretny materiał, zależy od jego budowy
molekularnej. W ogólnym przypadku przenikalność elektryczna
ε
jest macierzą
(tensorem drugiego rzędu). Pomiar przenikalności elektrycznej materiału
dostarcza informacji o strukturze cząstek tworzących tą materię.
Tablica Przykładowe wartości przenikalności elektrycznej
Dielektryki
ε
Paraelektryki
ε
He
1.00007
woda (H
2
O)
~81
H
2
1.00027
etanol (C
2
H
5
OH)
27
N
2
1.00058
Dielektryki tworzą materiały, zbudowane z cząsteczek niepolarnych, czyli
cząsteczek, które nie posiadają trwałych elektrycznych momentów dipolowych.
Obecności pola elektrycznego powoduje indukowanie momentu dipolowego,
poprzez przesunięcie środków ciężkości ładunków dodatnich i ujemnych.
Zjawisko to nosi nazwę polaryzacji elektronowej. Pole elektryczne porządkuje
jednocześnie dipole elektryczne zgodnie z zwrotem pola (wzory 4.1.1 oraz
4.1.2). Jest to polaryzacja kierunkowa.
Cząstki niepolarne to cząstki o budowie symetrycznej, jak: H
2
, N
2
, O
2
, czy gazy
szlachetne. Paraelektryki to materiały, których cząsteczki posiadają trwały
elektryczny moment dipolowy również w nieobecności pola elektrycznego. Są
to tzw. cząstki polarne. Doskonałym przykładem jest cząsteczka wody (H
2
O)
(patrz rys. 4.3). W nieobecności zewnętrznego pola elektrycznego paraelektryki
nie wykazują pola elektrycznego, ponieważ dipole elektryczne są zorientowane
w sposób przypadkowy, chaotyczny, i pola dipoli wzajemnie się znoszą.
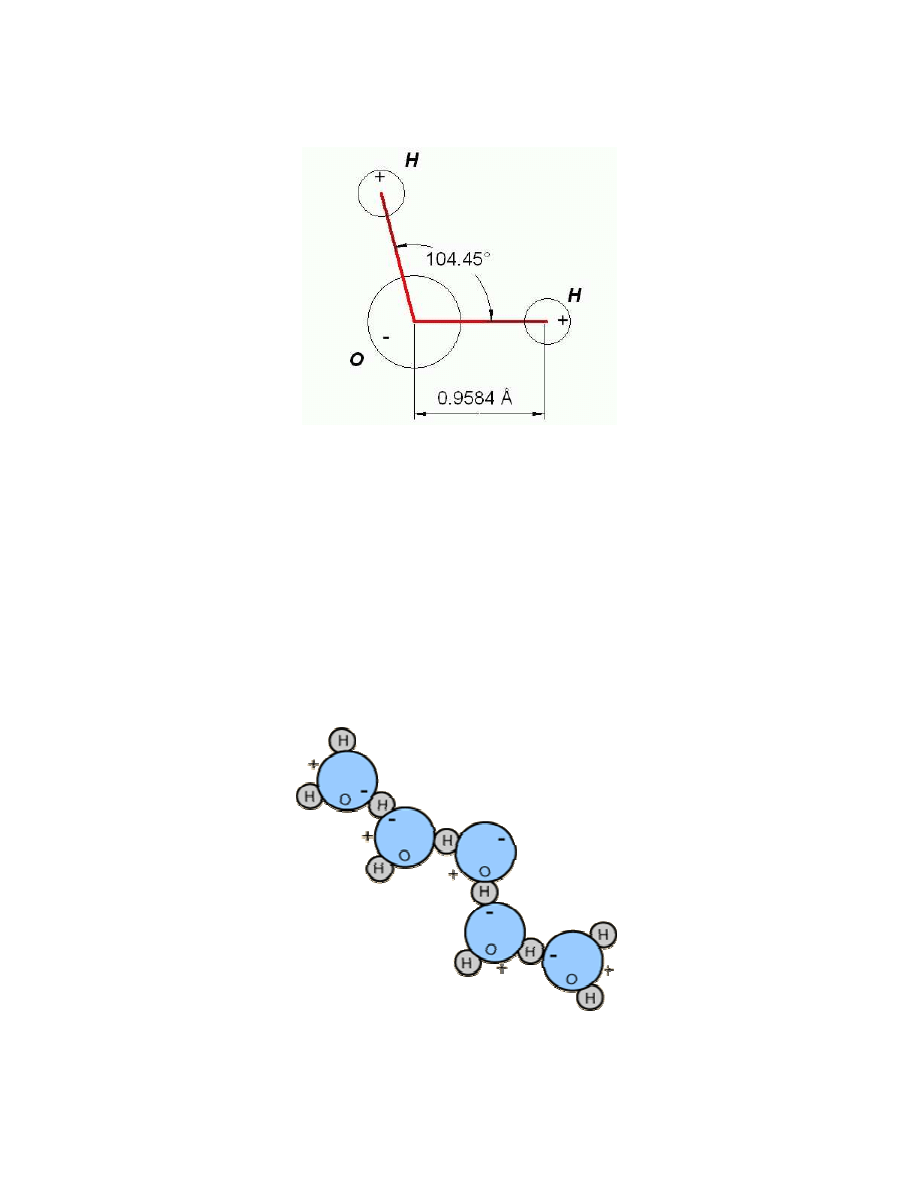
15
Znamy także inne rodzaje polaryzacji: jonowa, atomowa ale nie będzie się o
nich rozwodzić, zostawiając to specjalistom.
Rys. 4.3 Cząsteczka wody
Rysunek 4.3 ukazuje budowę cząsteczki wody. Między tlenem (O) a wodorami
(H) występują wiązania wodorowe. Bardzo ważne dla własności wody są
odległości i kąt jaki tworzą jony odoru. Cząstka wody posiada moment
dipolowy. Jest to cząstka polarna. Pole elektryczne działając na cząsteczki
polarne porządkuje ułożenie dipoli elektrycznych (polaryzacja kierunkowa albo
orientacyjna). Własności elektryczne istotnie wpływają na inne własności
materii. Widać to wyraźnie na przykładzie wody (patrz rys 4.4). Taka budowa
determinuje niezwykłe własności wody np.: punkt potrójny (w 0.01
0
C przy
ciśnieniu normalnym) czy anomalna rozszerzalność wody.
Rys. 4.4 Wiązania cząsteczek wody

16
Anomalna rozszerzalność wody - zmniejszanie się objętości wody (i wzrost
gęstości wody) w miarę wzrostu temperatury w przedziale od 0
0
do 4
0
Celsjusza.
Oznacza to, że lód jest lżejszy od wody. Przyczyna dla której kostka lodu nie
tonie w szklance a zbiorniki wodne nie zamarzną do samego dna nawet podczas
największych mrozów.
Trzeci rodzaj materii: ferroelektryki, są materiały wykazujące pole elektryczne
w nieobecności zewnętrznego pola elektrycznego. Charakterystyczną cechą
ferroelektryków jest struktura domenowa, co powoduje np. występowanie
histerezy elektrycznej podobnie jak histerezę magnetyczną obserwujemy dla
ferromagnetyków. Analogicznie, w przypadku pola magnetycznego materię
dzielimy na diamagnetyki, paramagnetyki, ferromagnetyki.
Wyszukiwarka
Podobne podstrony:
więcej podobnych podstron