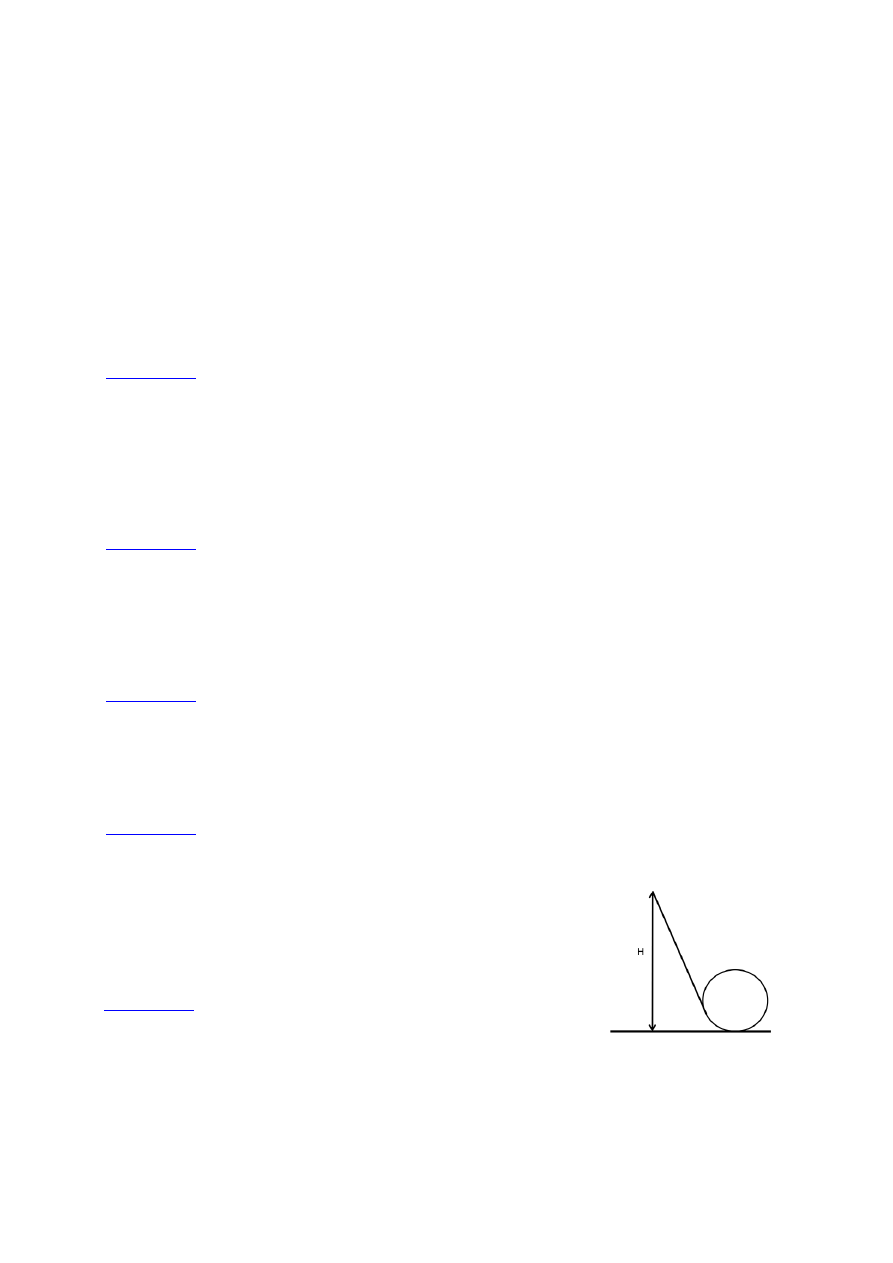
Praca i energia. Zasada zachowania energii mechanicznej. Środek masy.

Praca

Uwaga: Zadania w tej części rozwiązujemy przy pomocy twierdzenia o pracy i energii kinetycznej lub

zasady zachowania energii mechanicznej.

104. Jaką prędkość początkową v

0

trzeba nadać ciału o masie m, aby wjechało na szczyt równi o

długości d i kącie nachylenia

α

jeżeli współczynnik tarcia wynosi f ? Oblicz czas t trwania ruchu.

Przyspieszenie ziemskie g



dane. Wykonać rysunek.

Rozwiązanie:

105

.

Blok o masie m = 15 kg jest przesuwany po poziomej powierzchni pod działaniem siły F = 70 N

skierowanej pod kątem 30

o

do poziomu. Blok przesunięto o s = 5 m, a współczynnik tarcia f = 0,25.

Obliczyć pracę: a) siły F; b) składowej pionowej wypadkowej siły działającej na blok; c) siły
grawitacji; d) siły tarcia.

Rozwiązanie:

106. Klocek o masie m = 0,7 ześlizguje się z równi pochyłej o długości 6 m i kącie nachylenia 30

o

, a

następnie zaczyna poruszać się po poziomej płaszczyźnie. Współczynnik tarcia na równi i poziomej
powierzchni wynosi f = 0,2. Jaka jest prędkość klocka na końcu równi oraz po przebyciu drogi 1 m po
poziomej powierzchni? Jaką odległość przebędzie klocek do momentu zatrzymania się?

Rozwiązanie:

107. Auto o masie 1500 kg rusza i przyspiesza jednostajnie do prędkości 10 m/s w czasie 3 sekund.

Obliczyć: a) pracę wykonaną nad autem; b) średnią moc silnika w pierwszych 3 sekundach ruchu; c)
moc chwilową dla t = 2 sekundy.

Rozwiązanie:

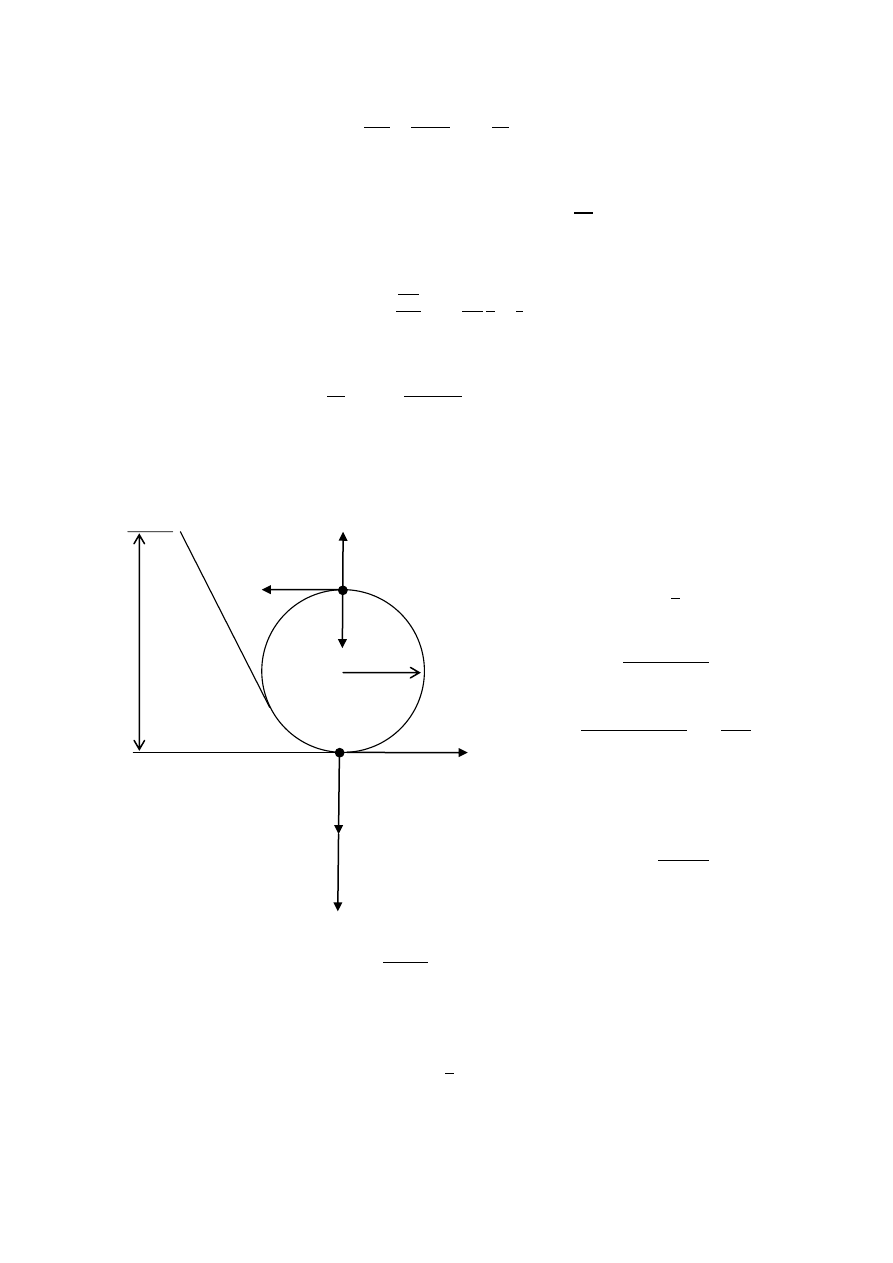
108. Paciorek nadziany na drut ślizga się bez tarcia po
nachylonym drucie zakończonym pętlą (patrz rysunek obok) o
promieniu R. Jeśli H = 3,5 R, to jaką prędkość ma paciorek w
najwyższym punkcie pętli? Ile wynosi nacisk paciorka na drut
w najniższym i najwyższym punkcie pętli?

Rozwiązanie:

109. Ciało znajdujące się na wysokości h rzucono pionowo do góry z prędkością 5 m/s. Prędkość

końcowa ciała wyniosła 25 m/s. Wyznaczyć h. Na jaką maksymalną wysokość H wzniosło się to
ciało? Jakie będą prędkości tego ciała na wysokościach H/4 i h/4?

Rozwiązanie:

110. Kamień rzucono pionowo do góry. Mija on punkt A z prędkością v, a punkt B, leżący 3 m wyżej

niż A, z prędkością v/2. Oblicz: a) prędkość v, b) maksymalną wysokośc wzniesienia się ciała ponad
punkt B.

Rozwiązanie:

113. Ciało rzucono pionowo w dół z wysokości H, nadając mu prędkość v

0

= 5 m/s. Ciało uderzyło w

ziemie z prędkością 35 m/s. Ile wynosi H? Jaką prędkość miało to ciało po przebyciu drogi H/6?

Rozwiązanie:

114. Kamień rzucono ukośnie z powierzchni ziemi. Na wysokości 9,1 m jego prędkość jest równa v =

(7,6i + 6,1j). Jaka jest maksymalna wysokość rzutu? Jaka była prędkość wyrzutu? Z jaką prędkością
kamień spadł na ziemię?

Rozwiązanie:

115. Wartość prędkości początkowej kamienia rzuconego ukośnie jest 5 razy większa od jego

prędkości w najwyższym punkcie toru. Pod jakim katem wyrzucono kamień?

Rozwiązanie:

116. Balon porusza się ruchem jednostajnym prostoliniowym na wysokości H = 2 km z prędkością u =

20 m/s. Z balonu wyrzucono metalową kulkę nadając jej prędkość poziomą 5 m/s względem balonu w
chwili, gdy przelatywał nad punktem A płaskiego terenu. Wyznaczyć prędkości kulki na wysokości
2H/3. Rozpatrzyć dwa przypadki rzutu: w kierunku ruchu balonu i w kierunku przeciwnym do jego
prędkości chwilowej.

Rozwiązanie:

112. Dwie masy m i M (M>m) są połączone nieważką nicią przewieszoną
przez nieważki krążek. Stosując zasadę zachowania energii mechanicznej
wyznaczyć prędkość V masy m w momencie, gdy jej środek masy podniesie
się na wysokość H. Założyć, że krążek nie obraca się, a nić ślizga się po jego
powierzchni bez tarcia. Jaka będzie prędkość ciała m, jeśli odstąpimy od
założenia o idealnie gładkiej powierzchni krążka i przyjmiemy, że na drodze
H praca sił tarcia będzie równa W?

Rozwiązanie:

M

117. Ciało o masie 0,5 kg ślizga się po poziomym chropowatym torze kołowym o promieniu 2 m. Jego

prędkość początkowa wynosiła 8 m/s, a po jednym pełnym obiegu toru spadła ona do wartości 6 m/s.
Wyznaczyć pracę sił: a) tarcia, b) dośrodkowej. Obliczyć współczynnik tarcia. Po jakim czasie ciało to
się zatrzyma? Ile razy obiegnie ono tor do momentu zatrzymania się?

Rozwiązanie:

118. Rozciągnięcie sprężyny o 10 cm wymaga pracy 4 J. Ile potrzeba pracy, aby rozciągnąć tę

sprężynę do 20 cm? Ws-ka: wartość pracy wykonanej nad sprężyną o współczynniku sprężystości k
rozciągniętej o x wynosi kx

2

/2.

Rozwiązanie:

119. Kula o masie 0,005 kg i prędkości 600 m/s zagłębiła się w drewnie na głębokość 2 cm.

Wyznaczyć średnią wartość siły oporu działającej w drewnie na kulkę. Zakładając, że siła oporu jest
stała, obliczyć czas hamowania kulki. Z jaką przemianę energii mamy w tym zjawisku do czynienia?

Rozwiązanie:

121. Jaką pracę wykonał silnik pociągu elektrycznego o masie

ton

100



m

, który poruszając się

ruchem jednostajnie przyspieszonym w czasie

s

15



t

uzyskał prędkość

h

km

108

v



. Efektywny

współczynnik tarcia wynosi

05

,

0



f

a przyspieszenie ziemskie przyjąć równe

2

s

m

10



g

.

Rozwiązanie:

122. Ciało o masie

kg

2



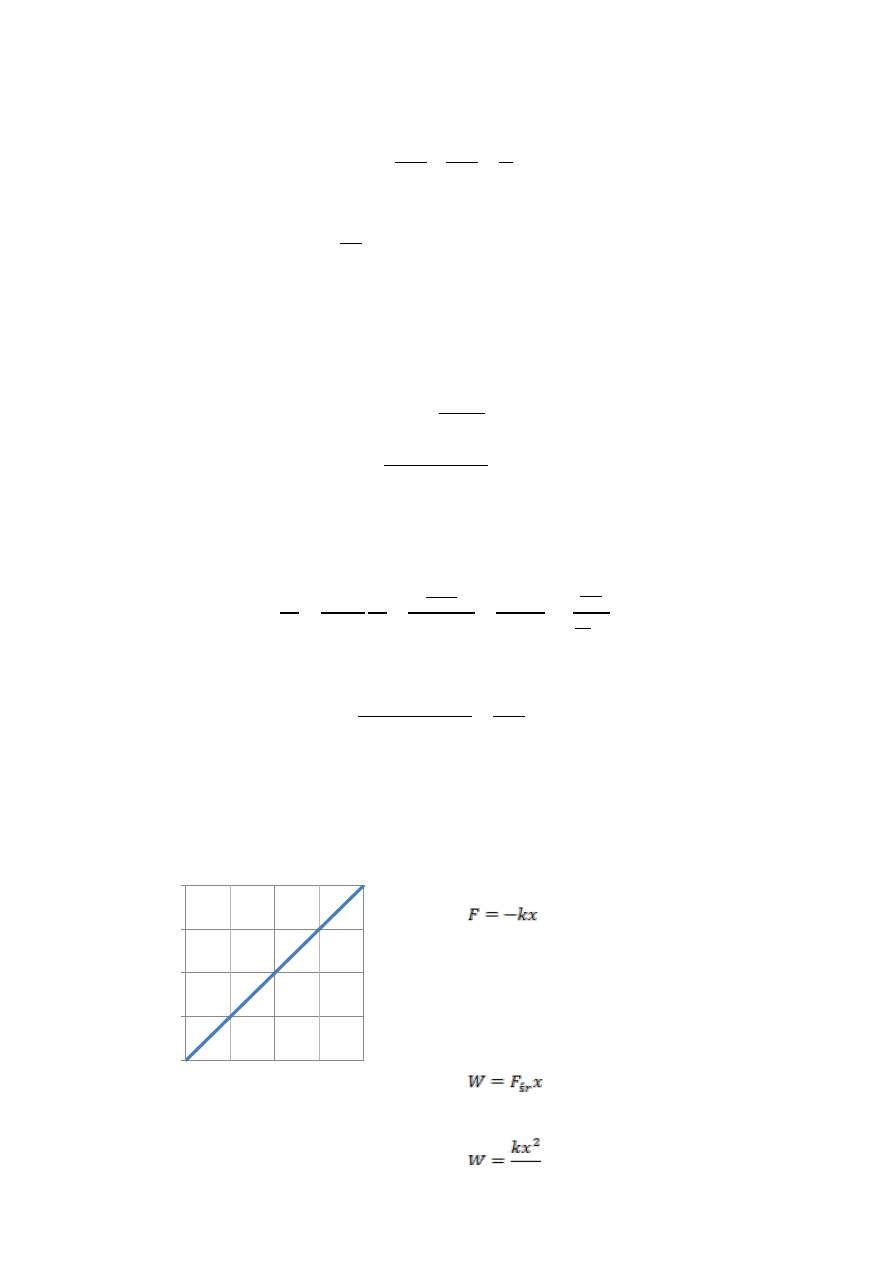
m

zsuwa się po równi pochyłej ze stałą prędkością

s

m

25

,

0

v



.

Współczynnik tarcia wynosi

5

,

0



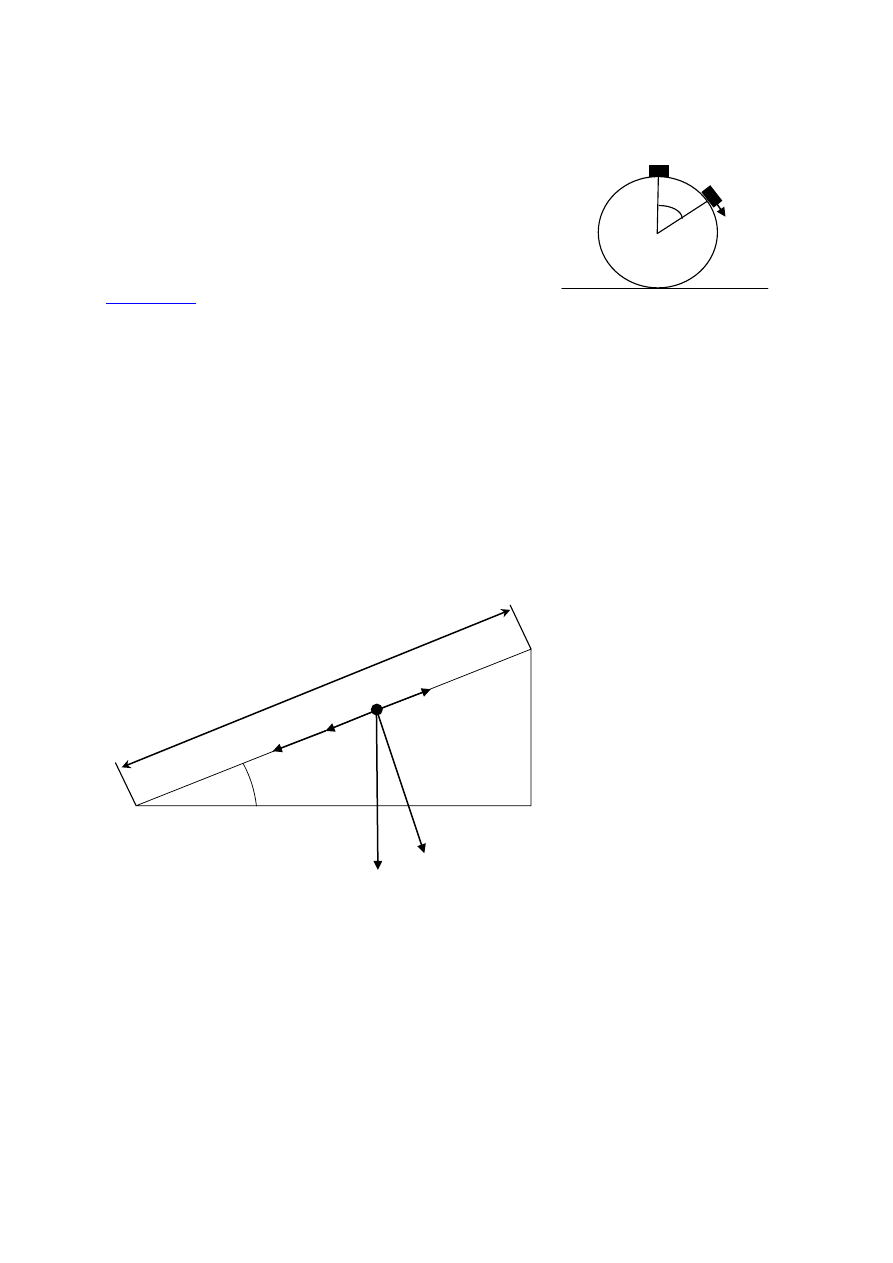
f

. Oblicz moc siły zsuwającej ciało.

Rozwiązanie:

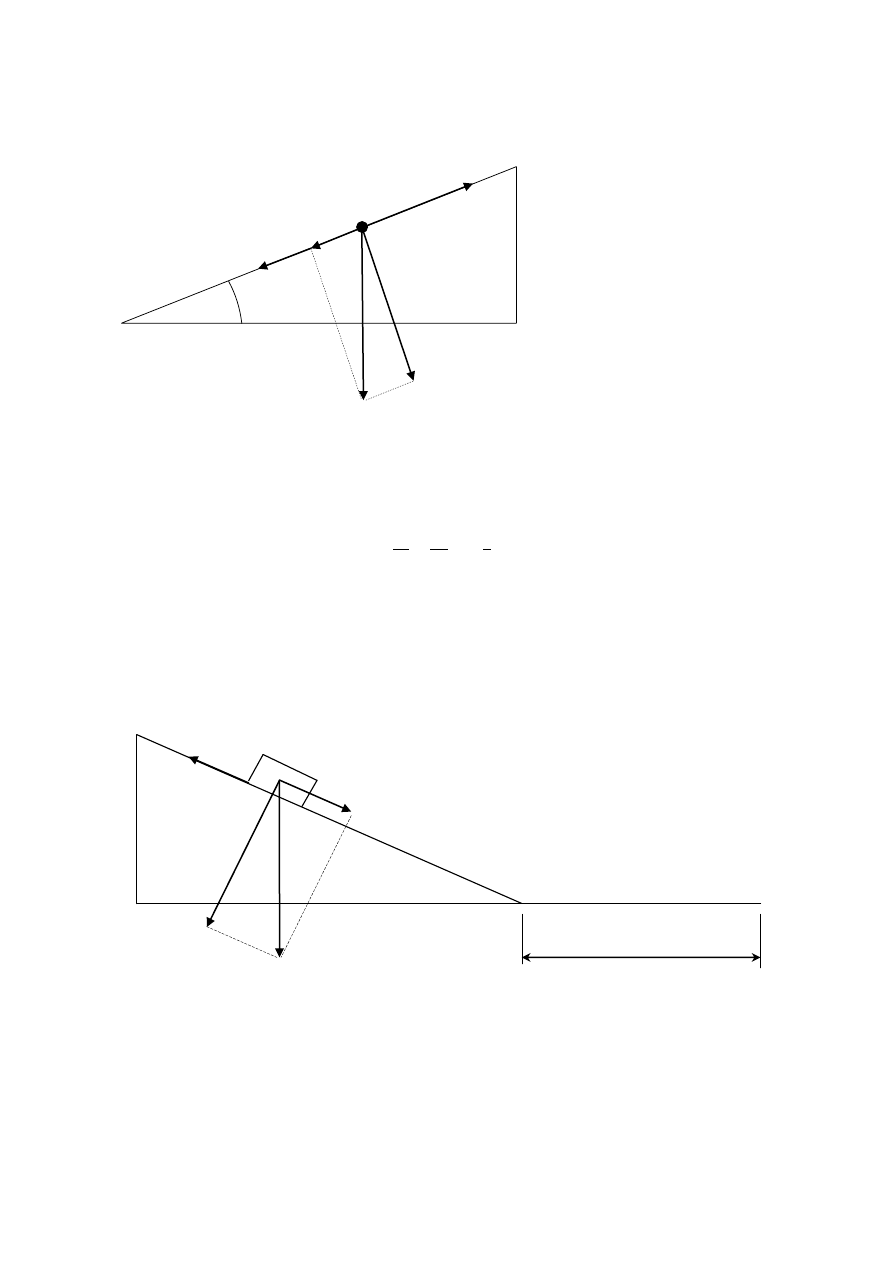
123. Sanki ześlizgują się z pagórka, którego zbocze ma długość

m

10



d

i jest nachylone pod kątem





30



do poziomu. Jaką odległość x przebędą sanki na odcinku poziomym po zjechaniu ze zbocza,

jeżeli na całej drodze współczynnik tarcia wynosi

2

,

0



f

?

Rozwiązanie:

120. Współczynnik tarcia miedzy masą m (patrz rysunek
obok) a podłożem wynosi 0,2. Jeśli początkowo oba ciała
spoczywają ruszą, to ile wynosi prędkość obu mas po
przebyciu przez M drogi 0,6 m? Masę nici i krążka
zaniedbujemy. Nitka ślizga się po krążku bez tarcia

Rozwiązanie:

v

F

n

mg

F

s

F

T

d





m

124. W najwyższym punkcie kuli o promieniu R znajduje
się małe ciało w położeniu równowagi chwiejnej. Przy
najmniejszym wychyleniu z tego położenia ciało zacznie
się zsuwać po powierzchni kuli. Wyznacz kąt α jaki
zatoczy promień kuli do miejsca oderwania się

Rozwiązanie:

---------------------------------------------------------------------------------------------------------------------------,

Autor rozwiązań

Mgr. W. Magierski

RZad104

W trakcie wjeżdżania na
szczyt równi początkowa
energia

kinetyczna

ciała

u podnóża równi jest tracona
na

wykonanie

pracy

przeciwko

sile

tarcia

i zamienia się w energię
potencjalną.

Ponieważ siła tarcia ma stałą
wartość, to praca przeciwko
tej sile daje się przedstawić
jako

iloczyn

siły

i

przesunięcia:

𝑊

𝑇

= 𝐹

𝑇

𝑑

Korzystając z zasady zachowania energii oraz równoważności pracy i energii możemy napisad:

𝐸

𝑘0

= 𝑚𝑔𝑕 + 𝑊

𝑇

Przy czym wysokośd równi h wyraża się wzorem:

𝑕 = 𝑑 sin 𝛼

Zgodnie z definicją siła tarcia to:

𝐹

𝑇

= 𝑓𝐹

𝑛

= 𝑓𝑚𝑔 cos 𝛼 .

Początkowa energia kinetyczna ciała wynosi:

R

R



v

𝐸

𝑘0

=

𝑚𝑣

0

2

2

.

Podstawiając do bilansu energii mamy:

𝑚𝑣

0

2

2

= 𝑚𝑔𝑑 sin 𝛼 + 𝑓𝑚𝑔 𝑑cos 𝛼

skąd

𝑣

0

= 2𝑔𝑑 sin 𝛼 + 𝑓 cos 𝛼 .

Sprawdzamy jednostki:

𝑣

0

=

m

s

2

m =

m

s

.

RZad105

Zgodnie z definicją, praca stałej
siły wyraża się przez iloczyn
skalarny siły i przesunięcia:

𝑊 = 𝐅 ∙ 𝐬 = 𝐹𝑠 cos α

Składowa pionowa wypadkowej
siły działającej na blok będzie
różnicą pomiędzy siłą ciężkości a
składową

pionową

siły

zewnętrznej:

𝐹

𝑛

= 𝑚𝑔 − 𝐹"

Siła ta, będąc prostopadła do
kierunku

przesunięcia,

nie

wykona żadnej pracy – podobnie jak siła grawitacji.

Siła tarcia natomiast wykona pracę:

𝑊

𝑇

= 𝐅

𝐓

∙ 𝐬 = 𝐹

𝑇

𝑠 cos 180° = −𝑓𝐹

𝑛

𝑠

Podstawiając za siłę nacisku i zauważając, że 𝐹" = 𝐹 sin 𝛼 otrzymujemy:

𝑊

𝑇

= −𝑓 𝑚𝑔 − 𝐹 sin 𝛼 𝑠

Sprawdzamy jednostki:

𝑊 = kg

m

s

2

m = Nm = J

i obliczamy:

𝑊 = 70 ∙ 5 ∙ cos 30° = 350

3

2

≅ 303J

𝑊

𝑇

= −0,25 ∙ (15 ∙ 10 − 70 sin 30°) ∙ 5 = −1,25 150 − 35 = −143,75 ≅ −144 J

F

F’

F”

F

T

mg

m





Odp. Praca siły F wynosi 303J a praca siły tarcia –144J. Siła nacisku i siła ciężkości nie wykonały
pracy.

RZad106

Zgodnie z zasadą zachowania energii i równoważności pracy i energii początkowa energia potencjalna
klocka zostanie zużyta na wykonanie pracy przeciwko sile tarcia a reszta zamieniona na energię
kinetyczną klocka u podstawy równi. Ta reszta z kolei zostaje rozproszona przez siłę tarcia na
poziomym torze.

Rozważmy najpierw ruch po równi, gdzie mamy:

𝑚𝑔𝑕 =

𝑚𝑣

𝑘

2

2

+ 𝑊

𝑇

przy czym wysokośd równi h wiąże się z długością równi d zależnością:

𝑕 = 𝑑 sin 𝛼 ;

v

k

oznacza prędkośd klocka u podstawy równi, a praca siły tarcia wynosi:

𝑊

𝑇

= 𝑓𝐹

𝑛

𝑑 = 𝑓𝑚𝑔 𝑑cos 𝛼

Podstawiając otrzymujemy:

𝑚𝑔𝑑 sin 𝛼 =

𝑚𝑣

𝑘

2

2

+ 𝑓𝑚𝑔𝑑 cos 𝛼

skąd

𝑣

𝑘

= 2𝑔𝑑(sin 𝛼 − 𝑓 cos 𝛼)

Prędkośd ta staje się prędkością początkową w ruchu poziomym i znowu bilansujemy pracę i energię,
zakładając, że s oznacza drogę w tym ruchu:

𝑚𝑣

𝑘

2

2

=

𝑚𝑣

2

2

+ 𝑊

𝑇

′

F

s

mg

F

T

m

F

n





s

Praca na drodze s przeciwko sile tarcia wyniesie:

𝑊

𝑇

′

= 𝑓𝑚𝑔𝑠 .

Podstawiamy i otrzymujemy:

𝑣

𝑘

2

= 𝑣

2

+ 2𝑓𝑔𝑠

skąd

𝑣 = 𝑣

𝑘

2

− 2𝑓𝑔𝑠 = 2𝑔𝑑 sin 𝛼 − 𝑓 cos 𝛼 − 2𝑓𝑔𝑠

Kładąc v = 0 obliczymy drogę do momentu zatrzymania:

𝑠 =

𝑣

𝑘

2

2𝑓𝑔

=

𝑑 sin 𝛼 − 𝑓 cos 𝛼

𝑓

Obliczenia:

prędkośd klocka u podstawy równi:

𝑣

𝑘

= 2 ∙ 10 ∙ 6(sin 30° − 0,2 cos 30°) = 120(0,5 − 0,1 3) = 39,2 = 6,3

m

s

prędkośd klocka po przebyciu drogi s = 1m

𝑣 = 2 ∙ 10 ∙ 6(sin 30° − 0,2 cos 30°) − 2 ∙ 0,2 ∙ 10 ∙ 1 = 39,2 − 4,0 = 5,9

m

s

droga przebyta przez klocek do momentu zatrzymania:

𝑠 =

6(sin 30° − 0,2 cos 30°)

0,2

= 30 0,5 − 0,1 3 = 9,8 m

RZad107

Zgodnie z zasadą równoważności pracy i energii, praca wykonana nad autem równa jest przyrostowi
jego energii kinetycznej:

𝑊 = ∆𝐸

𝑘

=

1
2

𝑚𝑣

2

kg

m

2

s

2

= Nm = J

Wartośd tej pracy:

𝑊 = 0,5 ∙ 1500 ∙ 10

2

= 75 000 J = 75 kJ

Dzieląc tę pracę przez czas rozpędzania do prędkości v otrzymamy średnią moc silnika:

𝑃

ś𝑟

=

𝑊

𝑡

J

s

= W

Moc ta wyniesie:

𝑃

ś𝑟

=

75 000

3

= 25 000 W = 25 kW

Moc chwilowa jest pochodną pracy po czasie i może byd przedstawiona jako:

𝑃 =

d𝑊

d𝑡

=

𝐅 ∙ d𝐬

d𝑡

= 𝐅 ∙

d𝐬
d𝑡

= 𝐅 ∙ 𝐯

W przypadku stałej siły działającej w kierunku ruchu równanie jest skalarne:

𝑃 = 𝐹 ∙ 𝑣 = 𝑚𝑎𝑣 = 𝑚𝑎 𝑎𝑡 = 𝑚𝑎

2

𝑡 = 𝑚

∆𝑣

∆𝑡

2

𝑡

Jednostka:

𝑃 = kg

m

2

s

2

s

= kg

m

2

s

2

1

s

=

J

s

= W

Wartośd mocy chwilowej:

𝑃 = 1 500 ∙

10

3

2

∙ 2 =

300 000

9

= 33 333 W = 33,3 kW

RZad108

W najwyższym punkcie pętli paciorek ma
prędkość spełniająca bilans energii:

𝑚𝑔𝐻 = 𝑚𝑔2𝑅 +

1
2

𝑚 𝑣"

2

skąd

𝑣" = 2𝑔(𝐻 − 2𝑅)

Po uwzględnieniu warunków zadania

𝑣" = 2𝑔(3,5𝑅 − 2𝑅) = 3𝑔𝑅

Nacisk N” paciorka na drut w tym miejscu
będzie różnicą pomiędzy siłą ciężkości
a siła odśrodkową:

𝑁" = 𝑚𝑔 −

𝑚 𝑣"

2

𝑅

Wstawiając

znalezioną

prędkość

w najwyższym punkcie otrzymamy:

𝑁" = 𝑚𝑔 −

𝑚3𝑔𝑅

𝑅

= 𝑚𝑔 − 3𝑚𝑔 = −2𝑚𝑔

Znak minus oznacza, że siła nacisku jest skierowana w górę.

Postępując podobnie znajdziemy prędkość w najniższym punkcie toru:

𝑚𝑔𝐻 =

1
2

𝑚 𝑣′

2

skąd

F”

od

v”

mg

R

H

mg

F’

od

v’

𝑣′ = 2𝑔𝐻

Po uwzględnieniu warunków zadania

𝑣′ = 2𝑔3,5𝑅 = 7𝑔𝑅

Nacisk N’ paciorka na drut w najniższym miejscu będzie sumą siłą ciężkości i siły odśrodkowej:

𝑁

′

= 𝑚𝑔 +

𝑚 𝑣′

2

𝑅

Wstawiając znalezioną prędkość w najniższym punkcie otrzymamy:

𝑁

′

= 𝑚𝑔 +

𝑚7𝑔𝑅

𝑅

= 8𝑚𝑔

RZad109

Zad. 109. Ciało znajdujące się na wysokości h rzucono pionowo do góry z prędkością 5 m/s. Prędkość

końcowa ciała wyniosła 25 m/s. Wyznaczyć h. Na jaką maksymalną wysokość H wzniosło się to
ciało? Jakie będą prędkości tego ciała na wysokościach H/4 i h/4?

Oznaczmy przez v

0

prędkość początkową ciała (tę na wysokości h) a przez v

k

prędkość końcową ciała

na wysokości równej zero. Zgodnie z zasadą zachowania energii mamy:

𝑚𝑔𝑕 +

𝑚𝑣

0

2

2

=

𝑚𝑣

𝑘

2

2

zatem

𝑕 =

𝑣

𝑘

2

2𝑔

−

𝑣

0

2

2𝑔

=

𝑣

𝑘

2

− 𝑣

0

2

2𝑔

𝑚

2

𝑠

2

𝑚

𝑠

2

=

𝑚

2

𝑠

2

𝑠

2

𝑚

= 𝑚

Po podstawieniu danych:

𝑕 =

25

2

− 5

2

2 ∙ 10

=

600

20

= 30 𝑚

Maksymalne wzniesienie spełni równośd energii:

𝑚𝑔𝑕 +

𝑚𝑣

0

2

2

= 𝑚𝑔𝐻

skąd

𝐻 = 𝑕 +

5

2

2𝑔

Po podstawieniu danych:

𝐻 = 30 +

5

2

2 ∙ 10

= 30 + 1,25 = 31,25 [m]

Prędkośd v

1

na wysokości H/4 spełni równanie

𝑚𝑔𝑕 +

𝑚𝑣

0

2

2

= 𝑚𝑔

𝐻

4

+

𝑚𝑣

1

2

2

skąd

𝑣

1

= 2𝑔 𝑕 −

𝐻

4

+𝑣

0

2

𝑚

𝑠

Po podstawieniu:

𝑣

1

= 2 ∙ 10 30 −

31,25

4

+ 5

2

= 20 ∙ 22,2 + 25 = 469 = 21,7

𝑚

𝑠

Analogicznie prędkośd v

2

na wysokości h/4 wyniesie

𝑚𝑔𝑕 +

𝑚𝑣

0

2

2

= 𝑚𝑔

𝑕
4

+

𝑚𝑣

2

2

2

skąd

𝑣

2

= 2𝑔 𝑕 −

𝑕
4

+𝑣

0

2

=

3𝑔𝑕

2

+𝑣

0

2

𝑚

𝑠

Po podstawieniu:

𝑣

2

= 1,5 ∙ 10 ∙ 30 + 5

2

= 450 + 25 = 475 = 21,8

𝑚

𝑠

RZad110

Oznaczmy wysokość punktu A przez h a różnicę wysokości punktów A i B przez



h = 3m. Zgodnie z

zasadą zachowania energii mamy:

𝑚𝑣

2

2

+ 𝑚𝑔𝑕 =

𝑚

𝑣

2

2

2

+ 𝑚𝑔(𝑕 + ∆𝑕)

zatem

𝑣

2

+ 2𝑔𝑕 =

𝑣

2

4

+ 2𝑔𝑕 + 2𝑔∆𝑕

stąd

𝑣 =

8𝑔∆𝑕

3

= 2

2𝑔∆𝑕

3

m

s

2

m =

m

s

Po podstawieniu

𝑣 = 2

2 ∙ 10 ∙ 3

3

= 20 = 4,5

m

s

Oznaczmy szukaną maksymalną wysokośd wzniesienia ponad punkt B jako H, mamy:

𝑚𝑣

2

2

+ 𝑚𝑔𝑕 = 𝑚𝑔(𝑕 + ∆𝑕 + 𝐻)

skąd po podstawieniu otrzymanej wcześniej prędkości v dostajemy:

𝑚

2

8𝑔∆𝑕

3

+ 𝑚𝑔𝑕 = 𝑚𝑔𝑕 + 𝑚𝑔∆𝑕 + 𝑚𝑔𝐻

i wyznaczamy

𝐻 =

1
3

∆𝑕

W pamięci obliczamy

𝐻 = 1[m]

RZad112

Zgodnie z zasadą zachowania energii obniżenie się środka masy układy oznacza zmniejszenie energii
potencjalnej układu, co musi skutkować wzrostem energii kinetycznej układu mas – tak aby całkowita
energia mechaniczna została zachowana. Oczywiście, prędkość v ciała o masie m będzie taka sama jak
prędkość ciała o masie M, choć przeciwnie skierowana.

Oznaczmy przez h

1

wysokość położenia środka masy układu w chwili początkowej, a przez h

2

wysokość położenia środka masy układu w chwili końcowej i wyznaczmy te położenia. Zgodnie z
definicją środka masy mamy:

𝑀 𝑕 − 𝑕

1

= 𝑚𝑕

1

𝑕

1

𝑀 + 𝑚 = 𝑀𝐻

𝑕

1

=

𝑀

𝑀 + 𝑚

𝐻

Analogicznie w chwili koocowej:

𝑚 𝑕 − 𝑕

2

= 𝑀𝑕

2

𝑕

2

𝑀 + 𝑚 = 𝑚𝐻

𝑕

2

=

𝑚

𝑀 + 𝑚

𝐻

Obniżenie ∆𝑕 środka masy będzie równe:

∆𝑕 = 𝑕

1

− 𝑕

2

=

𝑀 − 𝑚
𝑀 + 𝑚

𝐻

Zmiana energii potencjalnej układu przełoży się na energię kinetyczną ciał:

𝑀 + 𝑚 𝑔∆𝑕 =

𝑀𝑣

2

2

+

𝑚𝑣

2

2

=

1
2

𝑀 + 𝑚 𝑣

2

skąd

𝑣

2

= 2𝑔∆𝑕 = 2𝑔𝐻

𝑀 − 𝑚
𝑀 + 𝑚

Ostatecznie:

𝑣 = 2𝑔𝐻

𝑀 − 𝑚
𝑀 + 𝑚

𝑚

𝑠

2

𝑚 =

𝑚

𝑠

W sytuacji gdy tarcie na krążku spowoduje rozpraszanie energii należy to uwzględnid dodając straty
energii (równe pracy sił tarcia) do bilansu energii:

𝑀 − 𝑚 𝑔𝐻 =

1
2

𝑀 + 𝑚 𝑣

2

+ 𝑊

i wówczas

𝑣 = 2𝑔𝐻

𝑀 − 𝑚
𝑀 + 𝑚

−

2𝑊

𝑀 + 𝑚

RZad113

Zgodnie z zasadą zachowania energii energia potencjalna i kinetyczna w chwili startu równa będzie
energii kinetycznej w momencie uderzenia w ziemię:

Oznaczmy przez v

k

prędkość z jaką ciało uderzyło w ziemię, mamy wówczas:

𝑚𝑔𝐻 +

𝑚𝑣

0

2

2

=

𝑚𝑣

𝑘

2

2

stąd

𝐻 =

𝑣

𝑘

2

2𝑔

−

𝑣

0

2

2𝑔

=

𝑣

𝑘

2

− 𝑣

0

2

2𝑔

m

2

s

2

m

s

2

= m

Obliczamy:

𝐻 =

35

2

− 5

2

2 ∙ 10

=

1200

20

= 60 [m]

W drugiej części zadania zastosujemy ten sam sposób, trzeba tylko zauważyd, że po przebyciu H/6
drogi ciało będzie na wysokości 5H/6. Oznaczmy prędkośd w tym momencie przez v i układamy bilans
energii:

𝑚𝑔𝐻 +

𝑚𝑣

0

2

2

= 𝑚𝑔

5𝐻

6

+

𝑚𝑣

2

2

skąd

6𝑔𝐻 − 5𝑔𝑕 = 3𝑣

2

− 3𝑣

0

2

3𝑣

2

= 𝑔𝐻 + 3𝑣

0

2

i ostatecznie:

𝑣 =

𝑔𝐻

3

+ 𝑣

0

2

m

s

Obliczamy:

𝑣 =

10 ∙ 60

3

+ 25 = 225 = 15

m

s

RZad114

Oznaczmy wysokość daną w zadaniu przez h, a maksymalną wysokość przez H. Wektorowy zapis
prędkości oznacza, że składowe wektora prędkości wynoszą:

𝑣

𝑥

= 𝑣

0𝑥

= 7,6

m

s

𝑣

𝑦

= 6,1

m

s

Wartośd prędkości na wysokości h wyniesie:

𝑣 = 𝑣

𝑥

2

+ 𝑣

𝑦

2

Policzmy tę prędkośd, bo będzie potrzebna do wyznaczenia energii kinetycznej

𝑣 = 7,6

2

+ 6,1

2

= 95 = 9,75

m

s

Bilansując energię całkowitą w momencie wyrzutu i na wysokości h, mamy:

𝑚𝑣

0

2

2

=

𝑚𝑣

2

2

+ 𝑚𝑔𝑕

Wyznaczymy stąd prędkośd początkową wyrzutu v

0

:

𝑣

0

= 𝑣

2

+ 2𝑔𝑕

Wartośd tej prędkości:

𝑣

0

= 9,75

2

+ 2 ∙ 10 ∙ 9,1 95 + 182 = 277 = 16,6

m

s

Bilans energii w najwyższym punkcie pozwoli wyznaczyd tę wysokośd:

𝑚𝑣

0

2

2

= 𝑚𝑔𝐻

𝐻 =

𝑣

0

2

2𝑔

m

2

s

2

m

s

2

= m

Obliczamy:

𝐻 =

16,6

2

2 ∙ 10

= 13,8 [m]

Prędkośd z jaką kamieo upadnie na ziemię jest oczywiście równa prędkości wyrzutu i wynosi

𝑣

𝑘

= 16,6

m

s

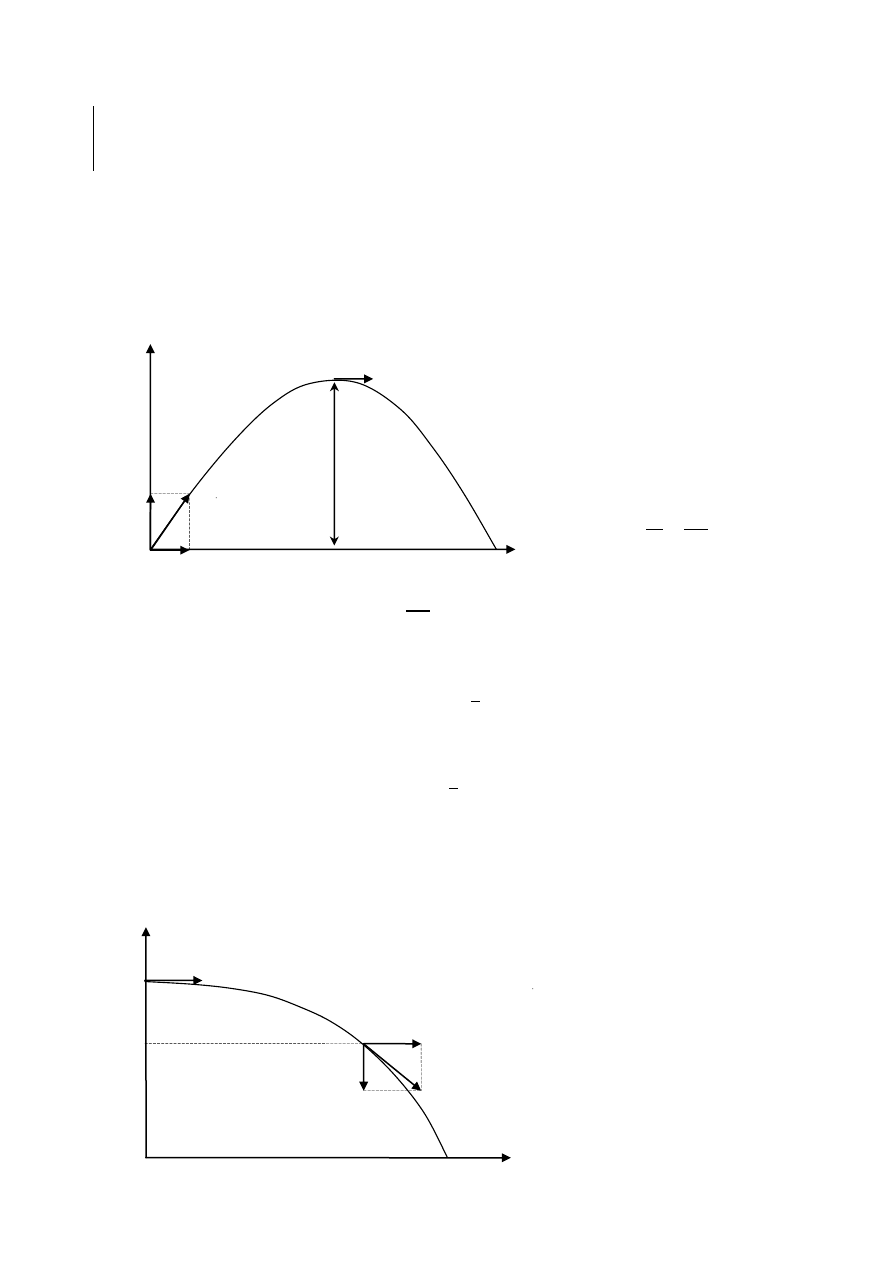
RZad115

W

najwyższym

punkcie

toru

prędkość ciała ma tylko składową
poziomą równą składowej poziomej
prędkości początkowej.

𝑣 = 𝑣

0𝑥

Oznaczmy

przez

k

stosunek

prędkości dany w zadaniu:

𝑘 =

𝑣

0

𝑣

=

𝑣

0

𝑣

0𝑥

Z drugiej strony:

𝑣

0𝑥

𝑣

0

= cos 𝛼

Zatem

cos 𝛼 =

1
𝑘

Podstawiamy i mamy

cos 𝛼 =

1
5

= 0,2

𝛼 = 78°28′

RZad116

Oznaczmy prędkość własną kulki
przez w. Prędkość początkowa v

0

kulki może być zatem sumą lub
różnicą prędkości u i w. Te dwa
przypadki najwygodniej będzie
rozważyć

w

ostatnim

etapie

rozwiązania przyjmując:

𝑣

0

= 𝑢 + 𝑤

𝑣

0

= 𝑢 − 𝑤

y

x

v

0x



v

0

v = v

0x

v

0y

H

x

v

0x

h

v

v

0

= v

0x

v

y

H

A

y

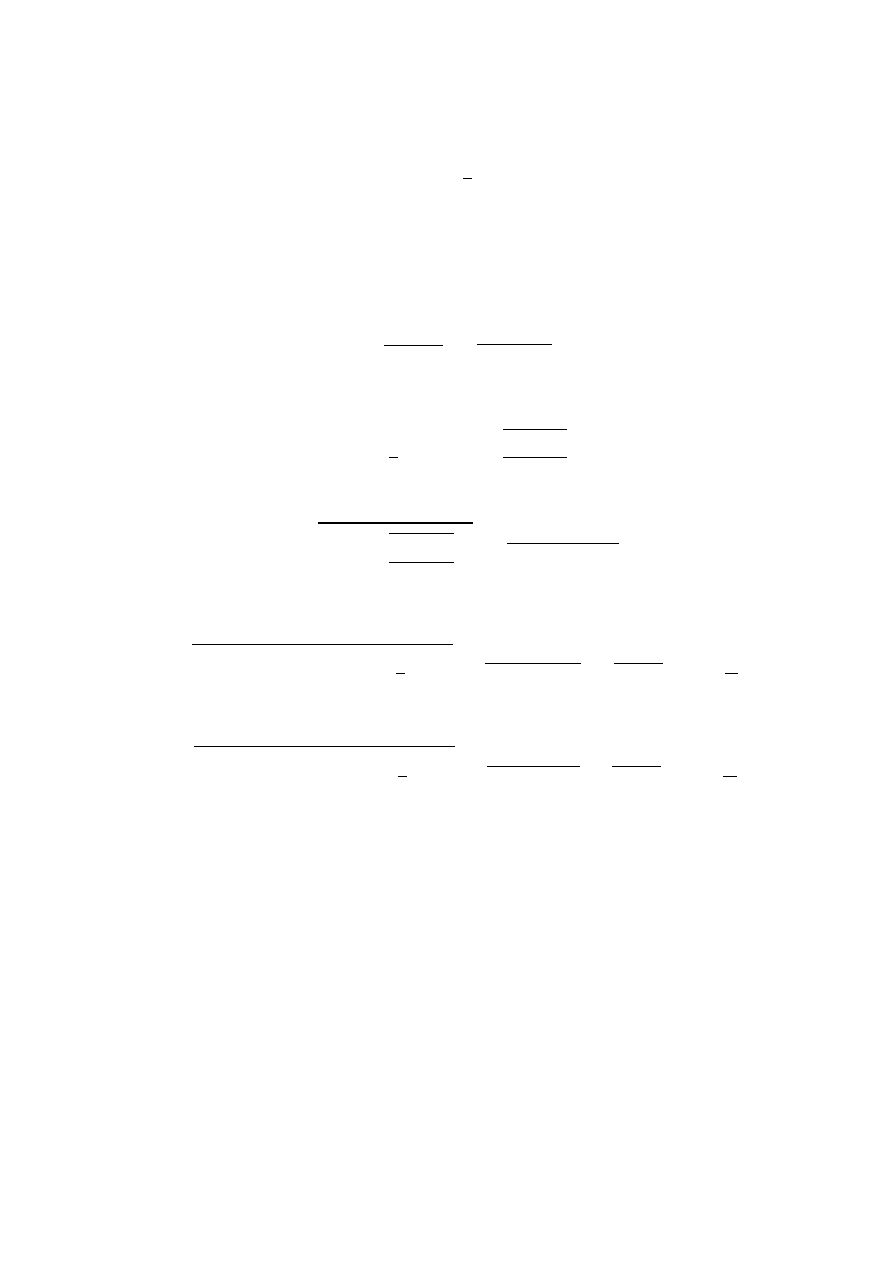
Napiszmy kinematyczne równania ruchu w przypadku rzutu poziomego:

𝑥 = 𝑣

0

𝑡

𝑦 = 𝐻 −

1
2

𝑔𝑡

2

Różniczkując po czasie te równania otrzymamy współrzędne prędkości:

𝑣

𝑥

= 𝑣

0

𝑦

𝑦

= −𝑔𝑡

Znak minus oznacza prędkośd zorientowaną przeciwnie do kierunku (w górę) przyjętego za dodatni.
Szukana prędkośd jest przekątną prostokąta prędkości:

𝑣 = 𝑣

𝑥

2

+ 𝑣

𝑦

2

= 𝑣

0

2

+ 𝑔𝑡

2

Czas t znajdziemy kładąc y = h w równaniu ruchu:

𝑕 = 𝐻 −

1
2

𝑔𝑡

2

𝑡 =

2(𝐻 − 𝑕)

𝑔

Prędkośd zatem wyrazi się wzorem:

𝑣 = 𝑣

0

2

+ 𝑔

2 𝐻 − 𝑕

𝑔

2

= 𝑣

0

2

+ 2𝑔(𝐻 − 𝑕)

Obliczamy prędkośd w przypadku rzutu w kierunku ruchu balonu:

𝑣 = (20 + 5)

2

+ 2 ∙ 10 ∙ 2000 −

2
3

2000 = 625 + 13 332 = 13 957 = 118

m

s

i w kierunku przeciwnym:

𝑣 = (20 − 5)

2

+ 2 ∙ 10 ∙ 2000 −

2
3

2000 = 225 + 13332 = 13 557 = 116

m

s

RZad117

Praca w ruchu obrotowym wyraża się wzorem:

𝑊 = 𝑀

ś𝑟

𝜑

gdzie



oznacza drogę kątową a M

śr

to średni moment siły – w naszym przypadku siły tarcia

hamującej ruch po okręgu. Ponieważ siła hamująca ma stała wartośd, to jej wartośd średnia równa
jest chwilowej, a jej moment wyniesie:

𝑀 = 𝑀

ś𝑟

= 𝐹

𝑇

𝑅 = 𝑓𝑚𝑔𝑅

gdzie R oznacza promieo okręgu, m masę ciała a f współczynnik tarcia. Podstawiając do wzoru na
pracę otrzymujemy:

𝑊 = 𝑓𝑚𝑔𝑅𝜑

Praca ta spowodowała zmniejszenie energii kinetycznej poruszającego się ciała:

𝑊 = ∆𝐸

𝑘

=

𝑚𝑣

2

2

2

−

𝑚𝑣

1

2

2

=

𝑚

2

𝑣

2

2

− 𝑣

1

2

i możemy wyznaczyd pracę siły tarcia:

𝑊 =

0,5

2

6

2

− 8

2

= 0,25 −28 = −7 [J]

Praca siły tarcia jest ujemna, bo powoduje zmniejszanie się prędkości.

Praca siły dośrodkowej jest równa zero, bo jej moment jest równy zero z racji równoległości
wektorów siły i promienia.

Współczynnik tarcia policzymy ze wzoru na pracę zauważając, że 1 obrót to 2



radianów:

𝑓 =

𝑊

𝑚𝑔𝑅𝜑

𝑓 =

7

0,5 ∙ 10 ∙ 2 ∙ 2𝜋

= 0,11

Liczbę N obrotów do momentu zatrzymania otrzymamy dzieląc przez 2



drogę kątową

odpowiadająca pracy W’ siły tarcia do momentu zatrzymania równą początkowej energii kinetycznej
ciała.

𝑁 =

𝜑

2𝜋

=

𝑊′

𝑓𝑚𝑔𝑅

1

2𝜋

=

𝑚𝑣

1

2

2

2𝜋𝑓𝑚𝑔𝑅

=

𝑣

1

2

4𝜋𝑓𝑔𝑅

𝑚

2

𝑠

2

𝑚

𝑠

2

𝑚

= 1

Obliczamy:

𝑁 =

8

2

4𝜋 ∙ 0,11 ∙ 10 ∙ 2

=

64

8,8𝜋

= 2,3

RZad118

0

40

80

120

160

0

0.1

0.2

siła

*N

+

wydłużenie [m]

Siła sprężystości jest proporcjonalna do
wydłużenia sprężyny:

gdzie minus oznacza przeciwny do wydłużenia
kierunek

działania

siły

–

model

jednowymiarowy.

Praca z kolei może byd przedstawiona jako
iloczyn średniej siły i wydłużenia:

Korzystając ze wskazówki mamy:

Porównując oba wzory na pracę i wykorzystując definicję siły sprężystości otrzymujemy:

𝐹

ś𝑟

𝑥 =

𝑘𝑥

2

2

𝐹

ś𝑟

=

𝑘𝑥

2

=

𝐹

2

a zatem średnia siła jest równa połowie wartości siły maksymalnej. Wykres przedstawia zależność siły
sprężystości od wydłużenia a praca na tym wykresie jest polem pod krzywą (prostą). Jak widać
dwukrotne zwiększenie wydłużenia powoduje czterokrotne zwiększenie pracy.

Przyjmijmy, że W

1

to praca włożona w rozciągnięcie sprężyny o x

1

, a W

2

to praca wymagana aby

rozciągnąć sprężynę o x

2

. Mamy zatem:

𝑊

1

=

𝑘𝑥

1

2

2

𝑘 =

2𝑊

1

𝑥

1

2

oraz:

𝑊

2

=

𝑘𝑥

2

2

2

=

2𝑊

1

𝑥

1

2

𝑥

2

2

2

= 𝑊

1

𝑥

2

𝑥

1

2

Podstawiając dane otrzymujemy:

𝑊

2

= 4

0,2
0,1

2

= 4 ∙ 4 = 16 [J]

RZad119

Energia kinetyczna kuli zostaje zużyta na



wykonanie pracy przeciwko siłom spójności drewna,



wykonanie pracy odkształcania materiału kuli,



podniesienie temperatury kuli



lokalne podniesienie temperatury drewna,

jednym słowem zostanie rozproszona.

Stosując definicję pracy w postaci:

Stosując definicję pracy w postaci:

𝑊 = 𝐹

ś𝑟

𝑑

możemy zbilansowad energię i pracę:

𝑚𝑣

2

2

= 𝐹

ś𝑟

𝑑

gdzie d oznacza głębokośd kuli po zderzeniu i otrzymujemy:

𝐹

ś𝑟

=

𝑚𝑣

2

2𝑑

,

kg

m

s

2

m

=

kg ∙ m

s

= N

Znajomośd siły pozwoli znaleźd przyspieszenie:

𝐹

ś𝑟

= 𝑚𝑎

bo z drugiej strony:

𝑎 =

∆𝑣

∆𝑡

=

𝑣

𝑡

zatem:

𝐹

ś𝑟

= 𝑚

𝑣

𝑡

skąd

𝑡 =

𝑚𝑣

𝐹

ś𝑟

,

kg

m

s

N

=

kg ∙ m

s

s

2

kg ∙ m

= s

Po podstawieniu otrzymujemy:

𝑡 =

2𝑚𝑣𝑑

𝑚𝑣

2

=

2𝑑

𝑣

,

Obliczenia

𝐹

ś𝑟

=

𝑚𝑣

2

2𝑑

=

0,005 ∙ 600

2

2 ∙ 0,02

=

360 000

8

= 45 000 J = 45 kJ

𝑡 =

2𝑑

𝑣

=

2 ∙ 0,02

600

=

0,02

300

=

2

30 000

= 6,7 ∙ 10

−5

𝑠 = 67[μs]

RZad120

Oznaczmy drogę masy M przez h – będzie to obniżenie wysokości tej masy i jednocześnie droga jaką
pokona masa m. Stosując zasadę zachowania energii dochodzimy do wniosku, że zmniejszenie energii
potencjalnej masy M powoduje zwiększenie energii kinetycznej obu mas, a część zostanie zużyta na
wykonanie pracy przeciwko sile tarcia pomiędzy masą m a podłożem.

𝑀𝑔𝑕 =

1
2

𝑀𝑣

2

+

1
2

𝑚𝑣

2

+ 𝑊

𝑇

Praca przeciwko sile tarcia będzie iloczynem siły tarcia (współczynnik tarcia f razy nacisk mg) i drogi h:

𝑊

𝑇

= 𝑓𝑚𝑔𝑕

Podstawiamy i mamy:

2𝑀𝑔𝐻 − 2𝑓𝑚𝑔𝑕 = 𝑚 + 𝑀 𝑣

2

skąd

𝑣 = 2𝑔𝑕

𝑀 − 𝑓𝑚

𝑚 + 𝑀

,

m

s

2

m

kg
kg

=

m

s

Aby wykonad obliczenia musimy znad obie masy albo przynajmniej ich iloraz.

RZad121

Ruch jednostajnie przyspieszony odbywa się pod wpływem stałej siły (siła wypadkowa). Siła
wypadkowa to, z jednej strony, różnica pomiędzy siłą napędową F

n

pochodzącą od silnika a siłą tarcia

F

T:

𝐹 = 𝐹

𝑛

− 𝐹

𝑇

a z drugiej iloczyn masy i przyspieszenia:

𝐹 = 𝑚𝑎

Zatem siła napędowa:

𝐹

𝑛

= 𝐹 − 𝐹

𝑇

= 𝑚𝑎 − 𝑓𝑚𝑔

Praca tej siły może byd przedstawiona jako iloczyn siły i przesunięcia:

𝑊 = 𝐹

𝑛

𝑠

gdzie s jest drogą w ruchu jednostajnie przyspieszonym:

𝑠 =

𝑎𝑡

2

2

i przyspieszenie:

𝑎 =

∆𝑣

∆𝑡

=

𝑣

𝑡

Ostatecznie siła napędowa wyraża się wzorem:

𝐹

𝑛

= 𝑚

𝑣

𝑡

− 𝑓𝑚𝑔

i praca tej siły wyniesie:

𝑊 = 𝑚

𝑣

𝑡

− 𝑓𝑚𝑔 𝑠 = 𝑚

𝑣

𝑡

− 𝑓𝑚𝑔

𝑎𝑡

2

2

= 𝑚

𝑣

𝑡

− 𝑓𝑚𝑔

𝑣

𝑡

𝑡

2

2

Ostatecznie:

𝑊 =

𝑚𝑣

2

2

1 − 𝑓

𝑔𝑡

𝑣

kg

m

2

s

2

= Nm = J

Po podstawieniu danych (zamieniamy km/h na m/s) otrzymujemy:

𝑊 =

100000 ∙ 108

1000

3600

2

2

1 − 0,05

10 ∙ 15

108

1000

3600

= 45 ∙ 10

6

∙ 0,75 [J] = 33,75 [MJ}

F

F

n

mg

F

s





m

F

T

RZad122

Załóżmy, że siła zsuwająca
ciało działa w dół równi.
Ponieważ prędkość zsuwania
jest stała to mamy do czynienia
z równowagą sił działających w
kierunku wektora prędkości:

𝐹 + 𝐹

𝑠

= 𝐹

𝑇

Podstawiając znane zależności
otrzymujemy:

𝐹 + 𝑚𝑔 sin 𝛼 = 𝑓𝑚𝑔 cos 𝛼

Skąd

𝐹 = 𝑚𝑔𝑓 cos 𝛼 − sin 𝛼

Aby wyznaczyd moc stałej siły dokonajmy prostych przekształceo:

𝑃 =

𝑊

𝑡

=

𝐹𝑠

𝑡

= 𝐹

𝑠

𝑡

= 𝐹𝑣

Zatem:

𝑃 = 𝑚𝑔 𝑓 cos 𝛼 + sin 𝛼 𝑣Aby dokonać obliczeń trzeba znać kąt nachylenia równi.

RZad123

Zgodnie z zasadą zachowania energii i równoważności pracy i energii początkowa energia potencjalna
sanek zostanie zużyta na wykonanie pracy przeciwko sile tarcia a reszta zamieniona na energię
kinetyczną sanek u podstawy równi. Ta reszta z kolei zostaje rozproszona przez siłę tarcia na
poziomym torze.

Rozważmy najpierw ruch po równi, gdzie mamy:

F

s

mg

F

T

m

F

n





x

𝑚𝑔𝑕 =

𝑚𝑣

𝑘

2

2

+ 𝑊

𝑇

przy czym wysokośd równi h wiąże się z długością równi d zależnością:

𝑕 = 𝑑 sin 𝛼 ;

v

k

oznacza prędkośd klocka u podstawy równi, a praca siły tarcia wynosi:

𝑊

𝑇

= 𝑓𝐹

𝑛

𝑑 = 𝑓𝑚𝑔 𝑑cos 𝛼

Podstawiając otrzymujemy:

𝑚𝑔𝑑 sin 𝛼 =

𝑚𝑣

𝑘

2

2

+ 𝑓𝑚𝑔𝑑 cos 𝛼

skąd

𝑣

𝑘

= 2𝑔𝑑(sin 𝛼 − 𝑓 cos 𝛼)

Prędkośd ta staje się prędkością początkową sanek w ruchu poziomym a energia kinetyczna z nią
związana zostaje zużyta na pracę przeciwko sile tarcia na drodze x, tzn. do momentu zatrzymania.
Bilansujemy pracę i energię:

𝑚𝑣

𝑘

2

2

= 𝑊

𝑇

′

Praca na drodze x przeciwko sile tarcia wyniesie:

𝑊

𝑇

′

= 𝑓𝑚𝑔𝑥 .

Podstawiamy i otrzymujemy:

𝑣

𝑘

2

= 2𝑓𝑔𝑥

skąd:

𝑥 =

𝑣

𝑘

2

2𝑓𝑔

Po podstawieniu znalezionej wcześniej prędkości v

k

otrzymujemy koocowy rezultat:

𝑥 = 𝑑

sin 𝛼 − 𝑓 cos 𝛼

𝑓

[m]

Obliczenia:

𝑥 =

10(sin 30° − 0,2 cos 30°)

0,2

= 50 0,5 − 0,1 3 = 16,3 m

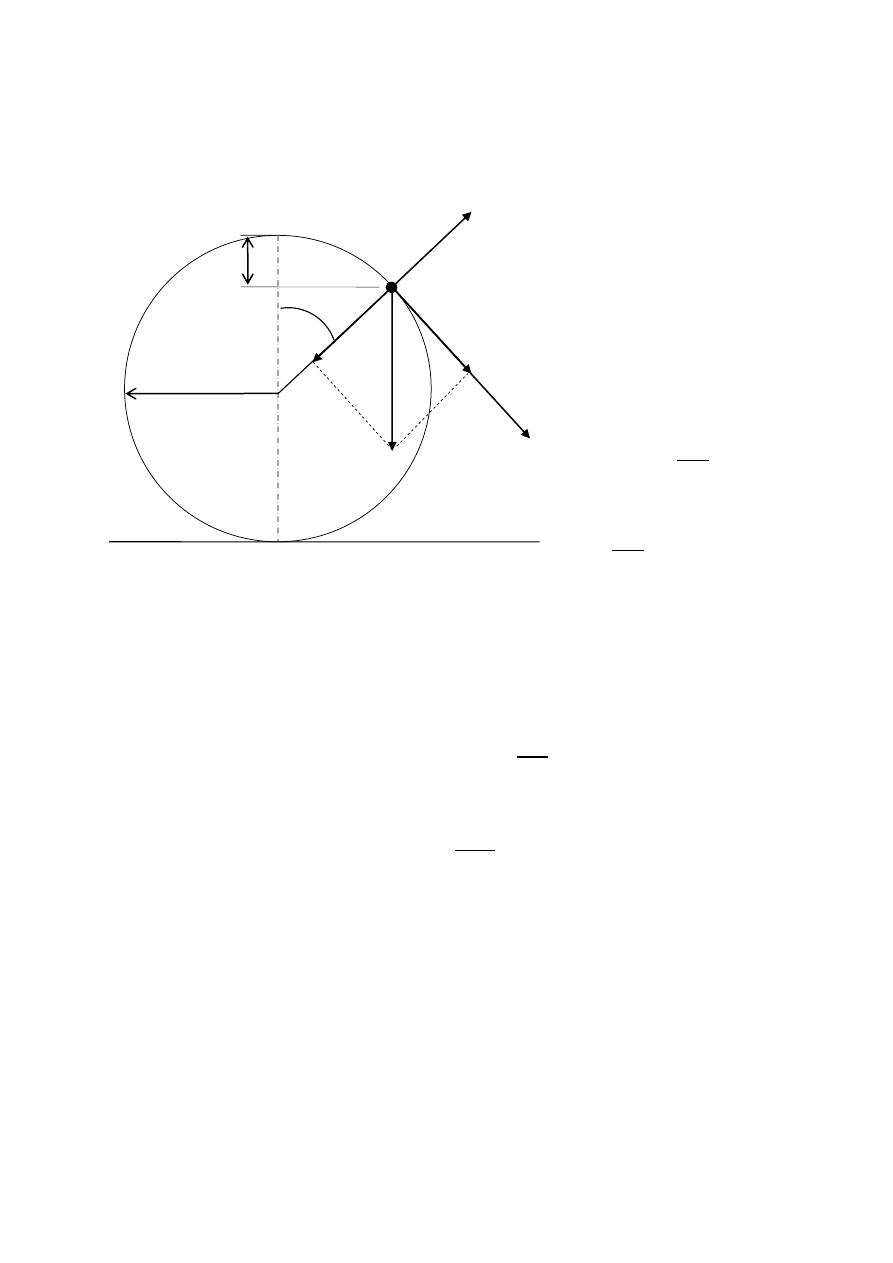
RZad124

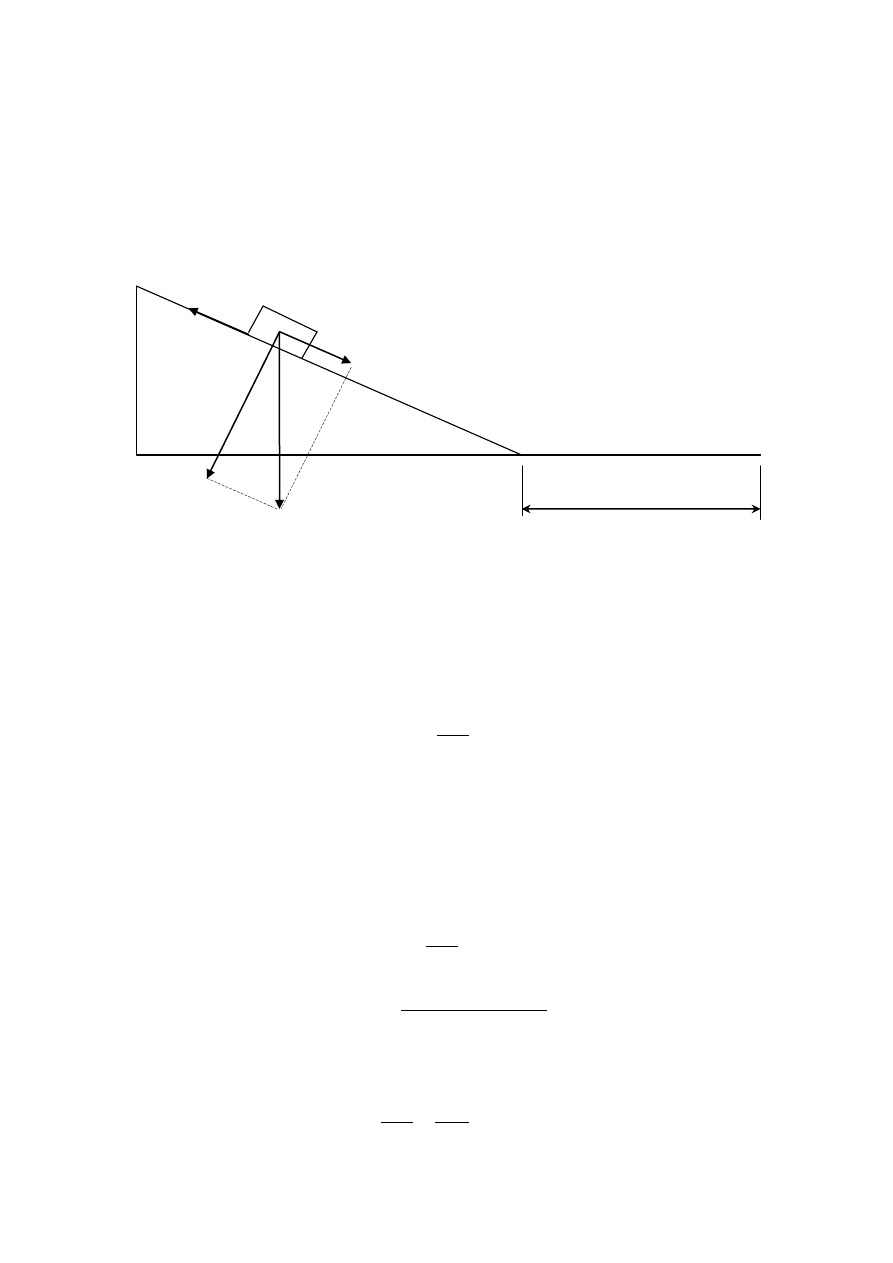
Miejsce oderwania zsuwającego
się ciała wyznacza warunek
równowagi sił: odśrodkowej F

od

i

składowej normalnej F

n

siły

ciężkości mg:

𝐹

𝑜𝑑

= 𝐹

𝑛

Łatwo zauważyd, że:

𝐹

𝑛

= 𝑚𝑔 cos 𝛼

i pamiętamy, że:

𝐹

𝑜𝑑

=

𝑚𝑣

2

𝑅

Podstawiamy i mamy:

𝑚𝑣

2

𝑅

= 𝑚𝑔 cos 𝛼

skąd

𝑣

2

= 𝑔𝑅 cos 𝛼

Zdając sobie sprawę z tego, że ze wzrostem kąta



rośnie prędkośd zsuwania v szukamy zależności

między tymi wielkościami. Skorzystamy z zasady zachowania energii porównując początkową energię
potencjalną ciała w najwyższym punkcie kuli z energią mechaniczną w momencie oderwania:

𝑚𝑔2𝑅 = 𝑚𝑔 2𝑅 − 𝑕 +

𝑚𝑣

2

2

Zauważmy też, że:

cos 𝛼 =

𝑅 − 𝑕

𝑅

Po prostych przekształceniach otrzymujemy:

𝑕 = 𝑅 1 − cos 𝛼

a po wstawieniu do bilansu energii:

𝑣

2

= 2𝑔𝑅 − 2𝑔𝑅 cos 𝛼

Porównując ten rezultat z wcześniejszym równaniem dla v

2

dostajemy:

2𝑔𝑅 − 2𝑔𝑅 cos 𝛼 = 𝑔𝑅 cos 𝛼

skąd

R

h

F

od

F

s

v

mg

F

n





cos 𝛼 =

2
3

𝛼 ≅ 48°

Odp. Zsuwające się po powierzchni kuli ciało oderwie się gdy jego promień wodzący zakreśli kąt 48°.

---------------------------------------------------------------------------------------------------------------------------

***