
Raport Laboratorium z Fizyki 3
ĆWICZENIE NR 30
POMIAR TEMPERATURY PIROMETREM OPTYCZNYM
Imi i Nazwisko,
ę
Nr indeksu, Wydzia
ł
Termin zaj
ęć
Data oddania
sprawozdania
ocena ko cowa
ń
Zatwierdzam wyniki pomiarów.
Data i podpis prowadzącego kurs ............................................................
Adnotacje dotyczące wymaganych poprawek oraz daty otrzymania poprawionego
sprawozdania
1. Zestaw przyrządów :
- pirometr optyczny;
- zasilacz stabilizowany;
- amperomierz prądu stałego;
- woltomierz napięcia stałego;
- żarówka 50W/12V .
2. Cel ćwiczenia:
Określenie temperatury włókna żarówki w zależności od dostarczonej mocy.
3. Wiadomości wstępne:
Każde ciało znajdujące się w temperaturze wyższej niż 0 K jest źródłem promieniowania
termicznego, wywołanego ruchem cieplnym cząsteczek i atomów. W chwili, gdy ciało osiąga
temperaturę 950 K zaczyna emitować promieniowanie widzialne - początkowo tylko czerwoną
część widma, które następnie stopniowo się rozszerza, tak aby przy 1800 K objąć cały zakres
widzialny. Pirometrią nazywa się metody pomiaru temperatury ciał polegające na porównywaniu
ich całkowitej lub spektralnej zdolności emisyjnej. Urządzenia służące do pomiaru wysokich
temperatur i wykorzystujące powyższą własność noszą nazwę pirometrów optycznych .
W niniejszym ćwiczeniu do pomiaru temperatur został wykorzystany pirometr optyczny
monochromatyczny z zanikającym włóknem. Obserwator patrzący przez okular (w którym znajduje
się filtr przepuszczający tylko promieniowanie o barwie czerwonej (
λ
=650 nm)) widzi włókno
żarówki (znajdującej się wewnątrz pirometru) na tle obrazu badanego ciała:
U
U
a b c
Zachodzą trzy możliwe przypadki:
a) włókno jaśniejsze od badanego ciała,
b) włókno znika w tle,
c) włókno ciemniejsze od badanego ciała;
W chwili, gdy włókno żarówki znika na tle badanego ciała ze skali galwanometru
G (wyskalowanego w jednostkach temperatury [
°
C]) odczytuje się wartość temperatury czarnej
TCZ badanego ciała, czyli temperatury ciała doskonale czarnego (ciała o 100-procentowej
zdolności emisji i absorpcji w każdej temperaturze), które w pewnym małym umownym przedziale
długości fal
∆λ
promieniuje z takim samym natężeniem jak badany obiekt:
E(
λ
,T
CZ
)
∆λ
=A(T
RZ
)E(
λ
,T
RZ
)
∆λ
Żarówka jest włączona w jedno z ramion mostka Wheatstone'a, a galwanometr G w jego przekątną.
Metoda pomiarowa wykorzystuje własność włókna żarówki polegającą na wzroście jego rezystancji
wraz ze wzrostem temperatury. Zmniejszając wartość rezystancji R powoduje się wzrost
temperatury włókna, a tym samym wychylenie wskazówki galwanometru (który do temperatury
około 800
°
C pozostaje niewzbudzony, gdyz mostek jest zrównoważony) proporcjonalne do
temperatury badanego ciała.
Związek pomiędzy temperaturą czarną i temperaturą rzeczywistą można wyznaczyć z
następującej równości:
C
C
T
A
T C
C
T
CZ
CZ
RZ
1
5
2
1
1
5
2
1
1
1
λ
λ
λ
λ
λ
−
−
−
−
−
=
−
[(exp
)
]
( ,
)
[(exp
)
]
z której po uproszczeniu otrzymuje się:
1
1
2
T
T
C
A
T
RZ
CZ
CZ
=
+ λ
λ
ln ( ,
)
C
2
=0.0144 mK
λ
=650 nm
Α(λ, Τ
ΧΖ
)=0.476
4.
Wyniki:
Tabela z wynikami pomiarów przy U=5 [V], I=2,4 [A]
Tabela z wynikami pomiarów przy U=7 [V], I=2,9 [A]
Zakres pomiarowy nr 2
Nomogram
Lp. U [V]
I [A]
P [W]
1
1530
11
1803,15 1931,99
1540
1813,15
2
1550
-9
1823,15 1955,41
1562
1835,15
3
1540
1
1813,15 1944,00
1550
1823,15
4
1530
11
1803,15 1931,99
1540
1813,15
5
7
0,15
2,9 0,04 20,3
0,71
3,5
1530
1541
11
1803,15 1931,99 1944,91 12,79
1540
1813,15
6
1540
1
1813,15 1944,00
1550
1823,15
7
1530
11
1803,15 1931,99
1540
1813,15
8
1560
-19
1833,15 1966,95
1570
1843,15
9
1550
-9
1823,15 1955,41
1562
1835,15
10
1550
-9
1823,15 1955,41
1562
1835,15
∆U [V]
∆I [A]
∆P [W] E
p
[%] T
cz
[ºC] Tcz
śr
[ºC] ∆T
cz
[ºC] T
cz
[K]
T
rz
[K]
Trz
śr
[K] ∆T
rz
T
rz
[ºC]
T
rz
[K]
Zakres pomiarowy nr 1
Nomogram
Lp. U [V]
I [A]
P [W]
1
1380
-24
1653,15 1759,00
1430
1703,15
2
1350
6
1623,15 1717,32
1390
1663,15
3
1340
16
1613,15 1714,67
1385
1658,15
4
1360
-4
1633,15 1737,31
1400
1673,15
5
5
0,15 2,4 0,04 12,0
0,6
5,0
1340
1356
16
1613,15 1714,67 1729,98 9,04
1385
1658,15
6
1370
-14
1643,15 1748,55
1420
1693,15
7
1350
6
1623,15 1717,32
1390
1663,15
8
1380
-24
1653,15 1759,00
1430
1703,15
9
1350
6
1623,15 1717,32
1390
1663,15
10
1340
16
1613,15 1714,67
1385
1658,15
∆U [V]
∆I [A]
∆P [W] E
p
[%] Tcz [ºC] Tcz
śr
[ºC] ∆T
cz
[ºC]
T
cz
[K]
T
rz
[K]
Trz
śr
[K] ∆T
rz
T
cz
[ºC]
T
rz
[K]
Tabela z wynikami pomiarów przy U=10 [V], I=3,65 [A]
5. Obliczenia:
Dane:
T 273,15=T
cz
[
K ]
1
T
rz
=
1
T
cz
C
2
lnA
- monochromatyczny współczynnik widmowy, dla wolframu:
A=0,476−2∗10
−
5
T
cz
- długość fali:
=
650∗10
−
9
[
m]
C
2
=
1,44∗10
−
2
[
mK ]
kl
V
= 1,5 [%]
−
klasa woltomierza,
U
Z
= 10 V
−
zakres woltomierza,
kl
A
= 0,5 [%]
−
klasa amperomierza,
I
Z
= 7,5 A
−
zakres amperomierza
Zakres I:
1.
T
cz
=
1653,15[ K ]
- obliczanie wartości temperatury rzeczywistej :
Zakres pomiarowy nr 3
Nomogram
Lp. U [V]
I [A]
P [W]
1
1850
19
2123,15 2308,40
1772
2045,15
2
1840
29
2113,15 2296,21
1760
2033,15
3
1870
-1
2143,15 2331,76
1790
2063,15
4
1850
19
2123,15 2308,40
1772
2045,15
5
10
0,15 3,65 0,04 36,5
0,9
2,5
1880
1869
-11
2153,15 2344,11 2330,97 21,81
1800
2073,15
6
1870
-1
2143,15 2331,76
1790
2063,15
7
1860
-9
2133,15 2319,64
1782
2055,15
8
1890
-21
2163,15 2357,37
1820
2093,15
9
1880
-11
2153,15 2344,11
1800
2073,15
10
1900
-31
2173,15 2367,98
1830
2103,15
∆U [V]
∆I [A]
∆P [W] E
p
[%] T [ºC] Tcz
śr
[ºC] ∆T
cz
[ºC]
T
cz
[K]
T
rz
[K]
Trz
śr
[K] ∆T
rz
T
rz
[ºC]
T
rz
[K]
Tabela z wynikami pomiarów dla U=3 [V] do U=10 [V]
Nomogram
Lp. U [V]
I [A]
P [W]
1
3
1,9
5,7
0,4
7,01
1270
1543,15 1636,7
1338
1611,15
2
4
2,2
8,8
0,5
5,7
1380
1653,15
1759
1430
1703,15
3
5
2,4
12
0,6
5
1370
1643,15 1748,55
1420
1693,15
4
6
2,7
16,2
0,64
3,9
1440
1713,15 1834,86
1478
1751,15
5
7
0,15
2,9 0,04 20,3
0,71
3,5
1540
1813,15
1944
1976,07
1550
1823,15
6
8
3,2
25,6
0,8
3,1
1630
1903,15 2053,39
1622
1895,15
7
8,5
3,3
28,05
0,83
2,9
1660
1933,15 2118,64
1643
1916,15
8
9
3,4
30,6
0,87
2,8
1700
1973,15 2132,20
1680
1953,15
9
9,5
3,5
33,25
0,9
2,7
1790
2063,15 2237,14
1740
2013,15
10
10
3,6
36
0,94
2,6
1840
2113,15 2296,21
1760
2033,15
∆U [V]
∆I [A]
∆P [W] E
p
[%] T [ºC]
T
cz
[K]
T
rz
[K]
Trz
śr
[K]
T
cz
[ºC]
T
rz
[K]
1
T
rz
=
1
1653,15
650∗10
−
9
1,44∗10
−
2
∗
ln 0,4676− 2∗10
−
5
∗
1653,15
1
T
rz
=
6,05∗10
−
4
4,51∗10
−
5
∗
ln 0,476−0,033
1
T
rz
=
6,05∗10
−
4
−
3,65∗10
−
5
T
rz
=
1759[ K ]=1485,86[◦C ]
2. T
cz
=
1623,15[ K ]
1
T
rz
=
1
1623,15
650∗10
−
9
1,44∗10
−
2
∗
ln 0,4676− 2∗10
−
5
∗
1623,15
1
T
rz
=
6,16∗10
−
4
−
3,37∗10
−
5
T
rz
=
1717,32[ K ]=1444,17[◦C ]
3.
T
cz
=
1613,15[ K ]
1
T
rz
=
1
1613,15
650∗10
−
9
1,44∗10
−
2
∗
ln 0,4676− 2∗10
−
5
∗
1613,15
1
T
rz
=
6,199∗10
−
4
−
3,664∗10
−
5
T
rz
=
1714,67[ K ]=1441,52[◦C ]
4. T
cz
=
1633,15[ K ]
1
T
rz
=
1
1633,15
650∗10
−
9
1,44
∗
10
−
2
ln 0,4676−2∗10
−
5
∗
1633,15
1
T
rz
=
6,123∗10
−
4
−
3,67∗10
−
5
T
rz
=
1737,31[ K ]=1464,16[◦C ]
5.
T
cz
=
1613,15[ K ]
T
rz
=
1714,67[ K ]=1441,52[◦C ]
6.
T
cz
=
1643,15[ K ]
1
T
rz
=
1
1643,15
650∗10
−
9
1,44∗10
−
2
∗
ln 0,4676− 2∗10
−
5
∗
1643,15
1
T
rz
=
6,086∗10
−
4
−
3,67∗10
−
5
T
rz
=
1748,55[ K ]=1475,40[◦C ]
7. T
cz
=
1623,15[ K ]
T
rz
=
1717,32[ K ]=1444,17[◦C ]
8. T
cz
=
1653,15[ K ]
T
rz
=
1759[ K ]=1485,86[◦C ]
9. T
cz
=
1623,15[ K ]
T
rz
=
1717,32[ K ]=1444,17[◦C ]
10. T
cz
=
1613,15[ K ]
T
rz
=
1714,67[ K ]=1441,52[◦C ]
- obliczanie średniej wartości temperatury rzeczywistej:

Trz
śr
=
∑
i=1
n
Trz
i
n
=
17591717,321714,671737,311714,671748,551717,3217591717,321714,67
10
=
1729,98[ K ]
- obliczanie wartości bezwzględnego błędu pomiaru prądu:
[ ]
A
A
A
I
kl
I
z
A
04
,
0
0375
,
0
%
100
5
,
7
%
5
,
0
%
100
≈
=
⋅
=
⋅
=
∆
- obliczanie wartości bezwzględnego błędu pomiaru napięcia:
V
V
U
kl
U
Z
U
15
,
0
%
100
10
%
5
,
1
%
100
%
=
⋅
=
⋅
=
∆
- obliczanie wartości pobieranej mocy:
P=U∗I=5∗2,4=12[W ]
- obliczanie wartości błędu bezwzględnego pobieranej mocy:
P=I∗U U ∗ I=2,4∗0,15−5∗0,04=0,6[W ]
- wyznaczenie błędu względnego pomiaru mocy:
E
p
=
P
i
P
i
∗
100 %=0,2−12∗100 %=5 %
- wyznaczenie błędu bezwzględnego poszczególnych pomiarów temperatuty:
T =T
śr
−
T
i
=
1356−1380=−24
- wyznaczenie średniego błędu kwadratowego:
T
cz
=
∑
i=1
n
T
i
2
n−1
=
2240
9
=
15,18
- wyznaczanie błędu bezwzględnego temperatury rzeczywistej:
K =
1
T
cz
C
2
ln A
A=2∗10
−
5
∗
T
cz
K =
T
cz
T
cz
2
C
2
∗
A
A
T
rz
=
K
K
2
=
T
cz
T
cz
2
C
2
∗
A
A
∗
T
rz
2
T
rz
=
15,18
1626,15
2
650∗10
−
5
1,44∗10
−
2
∗
2∗10
−
5
∗
1626,15
0,476−2∗10
−
5
∗
1729,98
2
5,74∗10
−
6
4,51∗10
−
5
∗
0,032
0,48
∗
2330,97
2
=
5,74∗10
−
6
4,51∗10
−
5
∗
0,067∗2992830,8
5,74∗10
−
6
9,04=9,04
Zakres II:
1.
T
cz
=
1803,15[ K ]
1
T
rz
=
1
1803,15
650∗10
−
9
1,44∗10
−
2
∗
ln 0,4676− 2∗10
−
5
∗
1803,15
1
T
rz
=
5,546∗10
−
4
−
3,7∗10
−
5
T
rz
=
1931,99[ K ]=1658,84[◦C ]

2. T
cz
=
1823,15[ K ]
1
T
rz
=
1
1823,15
650∗10
−
9
1,44∗10
−
2
∗
ln 0,4676− 2∗10
−
5
∗
1823,15
1
T
rz
=
5,485∗10
−
4
−
3,71∗10
−
5
T
rz
=
1955,41[ K ]=16582,26[◦C ]
3.
T
cz
=
1813,15[ K ]
1
T
rz
=
1
1813,15
650∗10
−
9
1,44∗10
−
2
∗
ln 0,4676− 2∗10
−
5
∗
1813,15
1
T
rz
=
5,515∗10
−
4
−
3,705∗10
−
5
T
rz
=
1944[ K ]=1670,86[◦C ]
4. T
cz
=
1803,15[ K ]
T
rz
=
1931,99[ K ]=1658,84[◦C ]
5. T
cz
=
1803,15[ K ]
T
rz
=
1931,99[ K ]=1658,84[◦C ]
6. T
cz
=
1813,15[ K ]
T
rz
=
1944[ K ]=1670,86[◦C ]
7. T
cz
=
1803,15[ K ]
T
rz
=
1931,99[ K ]=1658,84[◦C ]
8. T
cz
=
1833,15[ K ]
1
T
rz
=
1
1833,15
650∗10
−
9
1,44∗10
−
2
∗
ln 0,4676− 2∗10
−
5
∗
1833,15
1
T
rz
=
5,455∗10
−
4
−
3,709∗10
−
5
T
rz
=
1966,95[ K ]=1693,80[◦C ]
9.
T
cz
=
1823,15[ K ]
T
rz
=
1955,41[ K ]=1682,26[◦C ]
10.
T
cz
=
1823,15[ K ]
T
rz
=
1955,41[ K ]=1682,26[◦C ]
- obliczanie średniej wartości temperatury czarnej:
Trz
śr
=
∑
i=1
n
Trz
i
n
=
1931,991955,4119441931,991931,9919441931,991966,951955,411955,41
10
=
1944,91[ K ]
- obliczanie wartości bezwzględnego błędu pomiaru prądu:
[ ]
A
A
A
I
kl
I
z
A
04
,
0
0375
,
0
%
100
5
,
7
%
5
,
0
%
100
≈
=
⋅
=
⋅
=
∆
- obliczanie wartości bezwzględnego błędu pomiaru napięcia:
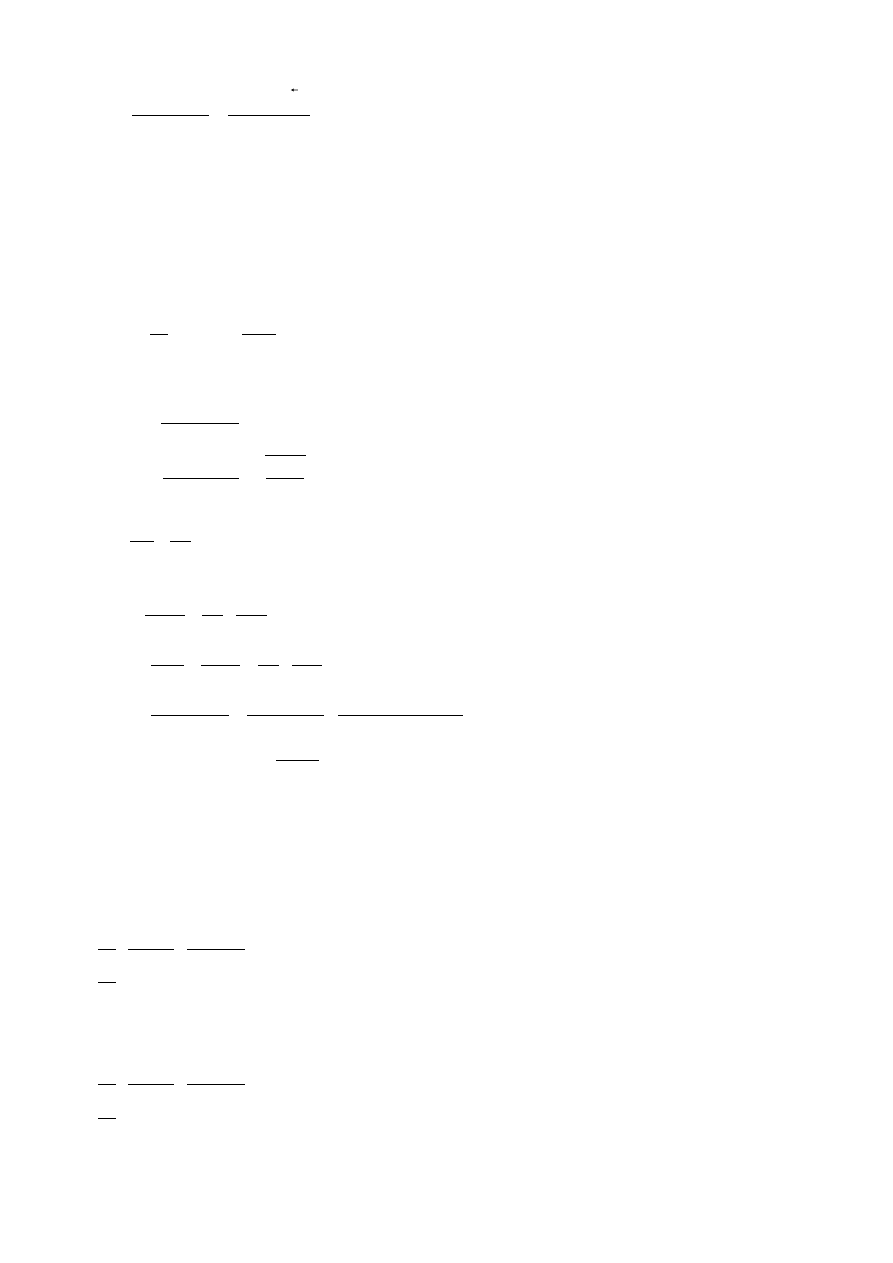
V
V
U
kl
U
Z
U
15
,
0
%
100
10
%
5
,
1
%
100
%
=
⋅
=
⋅
=
∆
- obliczanie wartości pobieranej mocy:
P=U∗I=7∗2,9=20,3[W ]
- obliczanie wartości błędu bezwzględnego pobieranej mocy:
P=I∗ U U ∗ I=2,9∗0,157∗0,04=0,71[W ]
- wyznaczenie błędu względnego pomiaru mocy:
E
p
=
P
i
P
i
∗
100 %=
0,16
20,3
∗
100 %=3,5 %
- wyznaczenie błędu bezwzględnego poszczególnych pomiarów temperatuty:
T =T
śr
−
T
i
=
1541−1530=11
- wyznaczenie średniego błędu kwadratowego:
T
cz
=
∑
i=1
n
T
i
2
n−1
=
1090
9
=
11
- wyznaczanie błędu bezwzględnego temperatury rzeczywistej:
K =
1
T
cz
C
2
ln A
A=2∗10
−
5
∗
T
cz
K =
T
cz
T
cz
2
C
2
∗
A
A
T
rz
=
K
K
2
=
T
cz
T
cz
2
C
2
∗
A
A
∗
T
rz
2
T
rz
=
11
1817,15
2
650∗10
−
5
1,44∗10
−
2
∗
2∗10
−
5
∗
1814,15
0,476−2∗10
−
5
∗
1944,91
2
3,33∗10
−
6
4,51∗10
−
5
∗
0,036
0,48
∗
2330,97
2
=
3,33∗10
−
6
4,51∗10
−
5
∗
0,075∗3782674,91
4,17∗10
−
6
12,79=12,79
Zakres III:
1. T
cz
=
2123,15[ K ]
1
T
rz
=
1
2123,15
650∗10
−
9
1,44∗10
−
2
∗
ln 0,4676−2∗10
−
5
∗
2123,15
1
T
rz
=
4,332∗10
−
4
−
3,77∗10
−
5
T
rz
=
2308,40 [K ]=2035,25[◦C ]
2.
T
cz
=
2113,15[ K ]
1
T
rz
=
1
2113,15
650∗10
−
9
1,44∗10
−
2
∗
ln 0,4676−2∗10
−
5
∗
2113,15
1
T
rz
=
4,732∗10
−
4
−
3,77∗10
−
5
T
rz
=
2296,21[ K ]=2023,06 [◦C ]
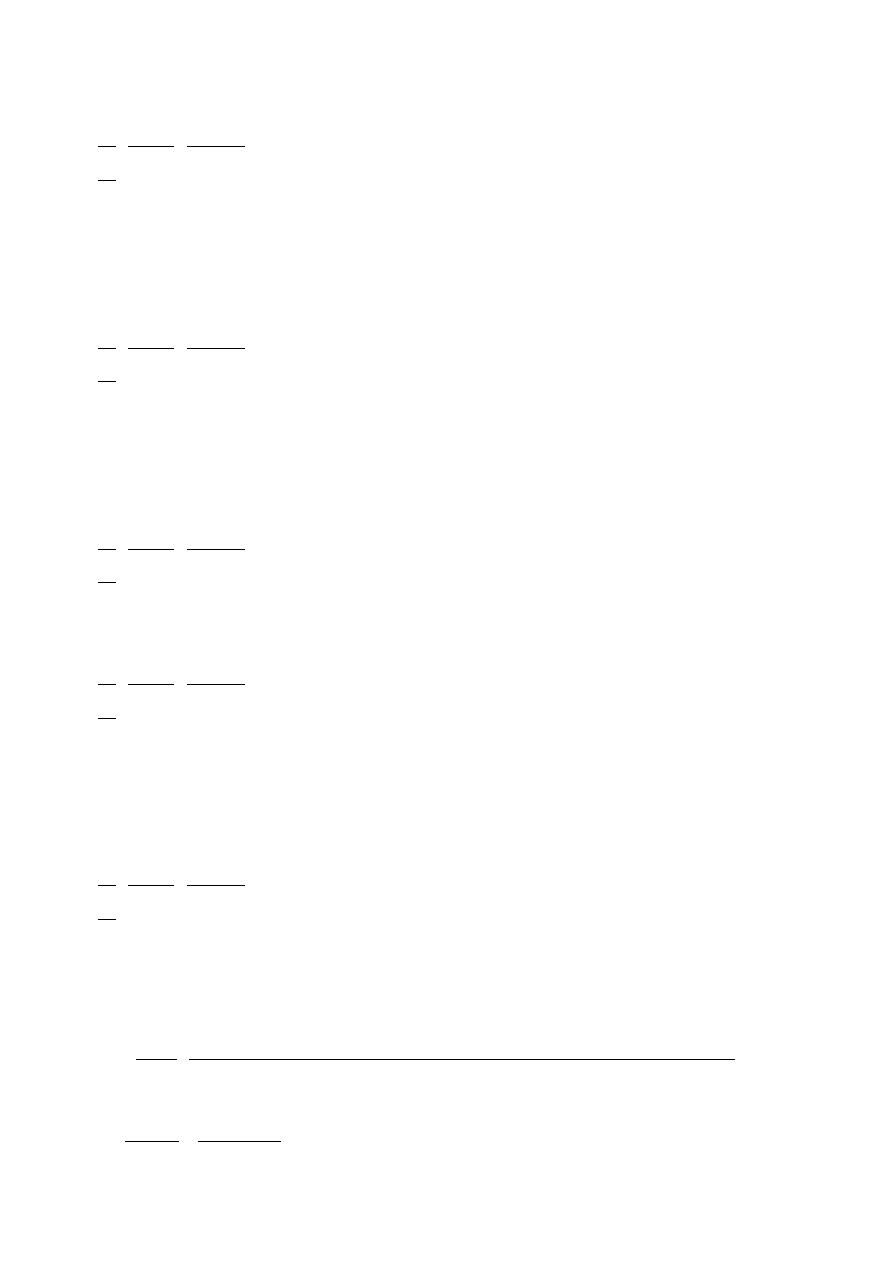
3. T
cz
=
2143,15[ K ]
1
T
rz
=
1
2143,15
650∗10
−
9
1,44∗10
−
2
∗
ln 0,4676−2∗10
−
5
∗
2143,15
1
T
rz
=
4,666∗10
−
4
−
3,773∗10
−
5
T
rz
=
2331,76[ K ]=2058,61[◦C ]
4.
T
cz
=
2123,15[ K ]
T
rz
=
2308,40 [K ]=2035,25[◦C ]
5.
T
cz
=
2153,15[ K ]
1
T
rz
=
1
2153,15
650∗10
−
9
1,44∗10
−
2
∗
ln 0,4676−2∗10
−
5
∗
2153,15
1
T
rz
=
4,644∗10
−
4
−
3,776∗10
−
5
T
rz
=
2344,11[ K ]=20370,96 [◦C ]
6. T
cz
=
2143,15[ K ]
T
rz
=
2331,76[ K ]=2058,61[◦C ]
7. T
cz
=
2133,15[ K ]
1
T
rz
=
1
2133,15
650∗10
−
9
1,44∗10
−
2
∗
ln 0,4676−2∗10
−
5
∗
2133,15
1
T
rz
=
4,688∗10
−
4
−
3,77∗10
−
5
T
rz
=
2319,64 [K ]=2046,49[◦C ]
8.
T
cz
=
2163,15[ K ]
1
T
rz
=
1
2163,15
650∗10
−
9
1,44∗10
−
2
∗
ln 0,4676−2∗10
−
5
∗
2163,15
1
T
rz
=
4,623∗10
−
4
−
3,81∗10
−
5
T
rz
=
2357,37[ K ]=2084,22[◦C ]
9. T
cz
=
2153,15[ K ]
T
rz
=
2344,11[ K ]=2070,96 [◦C ]
10. T
cz
=
2173,15[ K ]
1
T
rz
=
1
2173,15
650∗10
−
9
1,44∗10
−
2
∗
ln 0,4676−2∗10
−
5
∗
2173,15
1
T
rz
=
4,601∗10
−
4
−
3,779∗10
−
5
T
rz
=
2367,98[ K ]=2094,83 [◦C ]
- obliczanie średniej wartości temperatury czarnej:
Trz
śr
=
∑
i=1
n
Trz
i
n
=
2308,402296,212331,762308,402344,112331,76 2319,642357,372344,112367,98
10
=
2330,97[ K ]
- obliczanie wartości bezwzględnego błędu pomiaru prądu:
[ ]
A
A
A
I
kl
I
z
A
04
,
0
0375
,
0
%
100
5
,
7
%
5
,
0
%
100
≈
=
⋅
=
⋅
=
∆
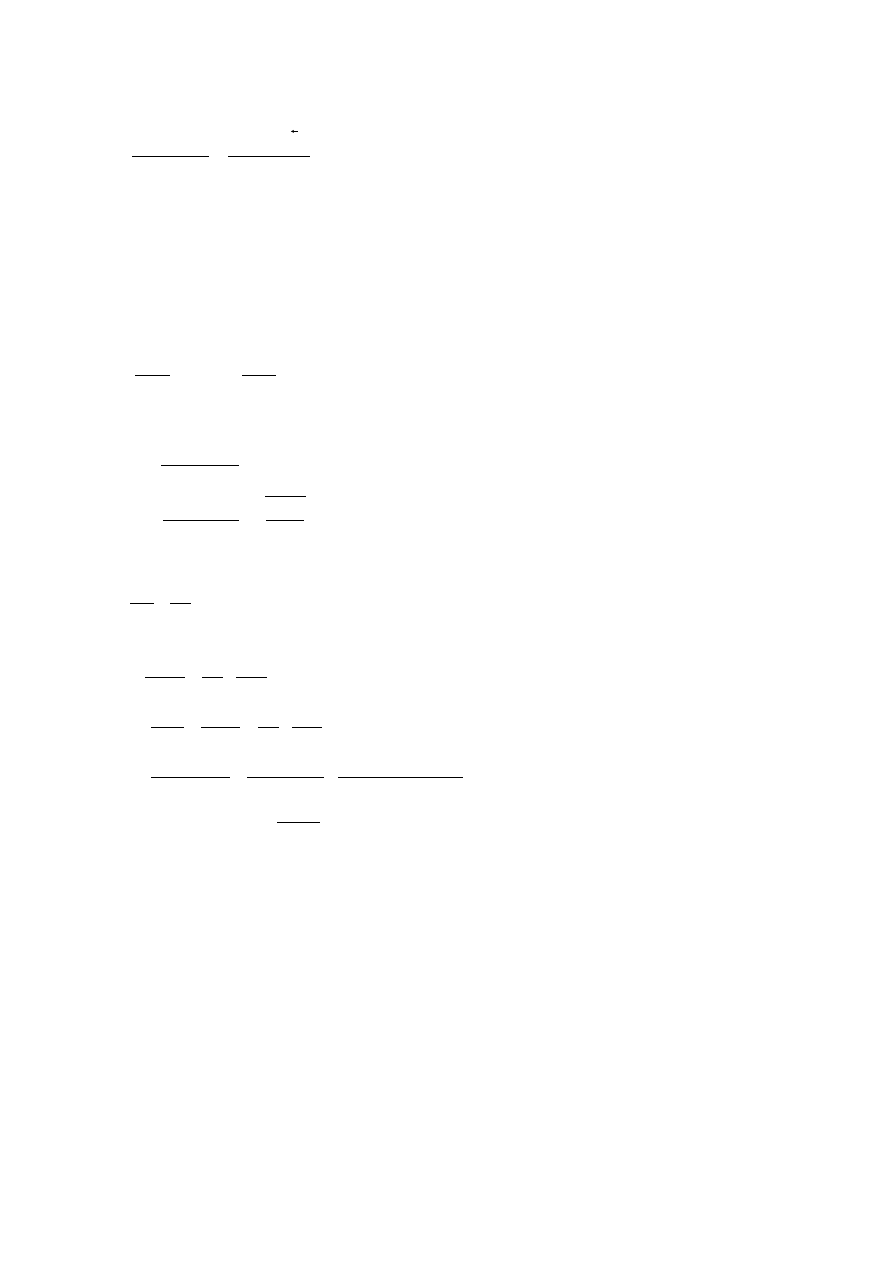
- obliczanie wartości bezwzględnego błędu pomiaru napięcia:
V
V
U
kl
U
Z
U
15
,
0
%
100
10
%
5
,
1
%
100
%
=
⋅
=
⋅
=
∆
- obliczanie wartości pobieranej mocy:
P=U∗I=10∗3,65=36,5[W ]
- obliczanie wartości błędu bezwzględnego pobieranej mocy:
P=I∗ U U ∗ I=3,65∗0,15−10∗0,04=0,9 [W ]
- wyznaczenie błędu względnego pomiaru mocy:
E
p
=
P
i
P
i
∗
100 %=
0,2
36,5
∗
100 %=2,5 %
- wyznaczenie błędu bezwzględnego poszczególnych pomiarów temperatuty:
T
i
=
T
śr
−
T
i
=
1869−1850=19
- wyznaczenie średniego błędu kwadratowego temperatury czarnej:
T
cz
=
∑
i=1
n
T
i
2
n−1
=
3290
9
=
19,12
- wyznaczanie błędu bezwzględnego temperatury rzeczywistej:
K =
1
T
cz
C
2
ln A
A=2∗10
−
5
∗
T
cz
K =
T
cz
T
cz
2
C
2
∗
A
A
T
rz
=
K
K
2
=
T
cz
T
cz
2
C
2
∗
A
A
∗
T
rz
2
T
rz
=
19,12
2142,15
2
650∗10
−
5
1,44∗10
−
2
∗
2∗10
−
5
∗
2142,15
0,476−2∗10
−
5
∗
2330,97
2
4,17∗10
−
6
4,51∗10
−
5
∗
0,043
0,48
∗
2330,97
2
=
4,17∗10
−
6
4,51∗10
−
5
∗
0,089∗5433421,14
4,17∗10
−
6
21,81=21,81
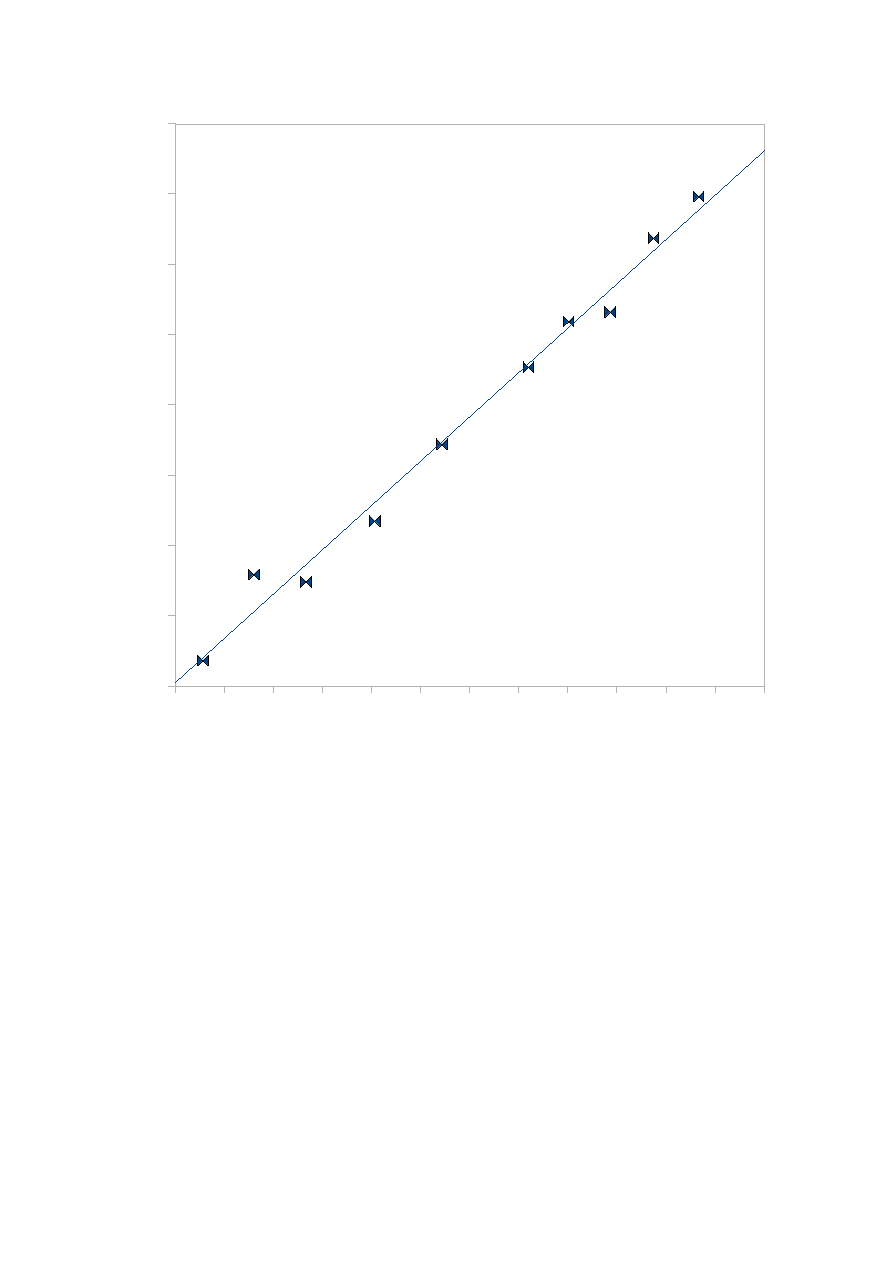
4
7
10
13
16
19
22
25
28
31
34
37
40
1600
1700
1800
1900
2000
2100
2200
2300
2400
Zależność Trz od mocy P
Moc P[W]
Te
m
pe
ra
tu
ra
T
rz
[
K
]

6. Wnioski:
Błędy wyliczone w trakcie wykonywania ćwiczenia powstały w wyniku następujących przyczyn:
- niedoskonałości ludzkiego oka, które nie pozwala na dokładne wyznaczenie momentu
kiedy barwa badanego ciała jest identyczna z barwy włókna żarówki pirometru. Dlatego
wystąpiły duże rozbieżności w odczycie T
CZ
.
- niezbyt dobra stabilizacja napięcia zasilającego żarówkę, a tym samym mocy wydzielanej na
żarówce.
- mierniki używane w ćwiczeniu miały określoną klasę dokładności (amperomierz-0.5,
woltomierz-1,5) co wpłyneło bezpośrednio na błędy wyznaczenia napięcia i prądu i pośrednio na
błąd dotyczący mocy wydzielonej na badanej żarówce.
Pirometr optyczny monochromatyczny z zanikającym włóknem służy do pomiaru
temperatur w zakresie około 800 - 2300
°
C. W przypadku temperatur z górnej części zakresu stosuje
się osłabiacz zmniejszający w określony sposób natężenie promieniowania . Po zastosowaniu
większej ilości osłabiaczy możliwy jest pomiar wyższych temperatur jednak jego dokładność
będzie zdecydowanie niższa. Pirometry wykorzystywane się m. in.
w metalurgii do pomiarów temperatur wewnątrz pieców.
Wielkość błędów średnich kwadratowych wyznaczonych przy seriach 10-pomiarów okazała
sie niewielka , najwykszy z nich nie przekroczył 3.8% wielkości mierzonej . Wydaje się więc, że
dokładność pomiarów jest dość dobra.
Wyszukiwarka
Podobne podstrony:
więcej podobnych podstron