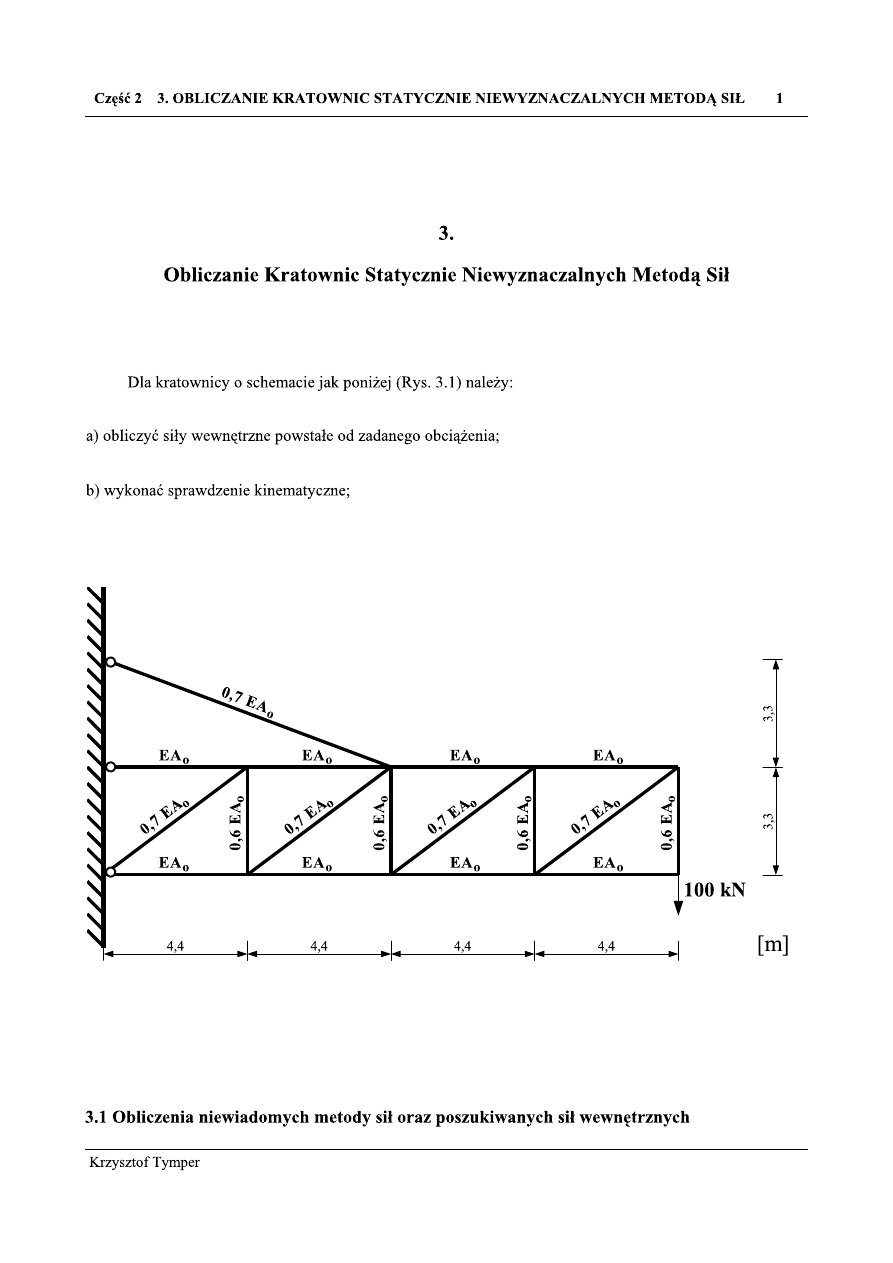
Rys. 3.1 Rozpatrywana kratownica

Mechanika Budowli

AlmaMater

Zgodnie ze sposobem rozwiązywania układów statycznie niewyznaczalnych (hiperstatycznych)

metodą sił, zamieniamy rozpatrywany, jednokrotnie statycznie niewyznaczalny układ (Rys. 3.1.1 a)), na tzw.
układ podstawowy (układ zastępczy), tak samo obciążony i geometrycznie identyczny z rozpatrywanym ale
statycznie wyznaczalny (Rys. 3.1.1 b)).

[m]

4,4

3

,3

4,4

4,4

4,4

3

,3

1

1

[m]

4,4

3

,3

4,4

4,4

4,4

3

,3

[m]

3

,3

3

,3

K

5

K

1

K

2

K

3

K

4

G

1

G

2

G

3

G

4

D

1

D

2

D

3

D

4

S

1

S

2

S

3

S

4

K

1

G

1

D

1

K

2

G

2

D

2

K

3

G

3

D

3

K

4

G

4

D

4

K

5

K

5

S

1

S

2

S

3

S

4

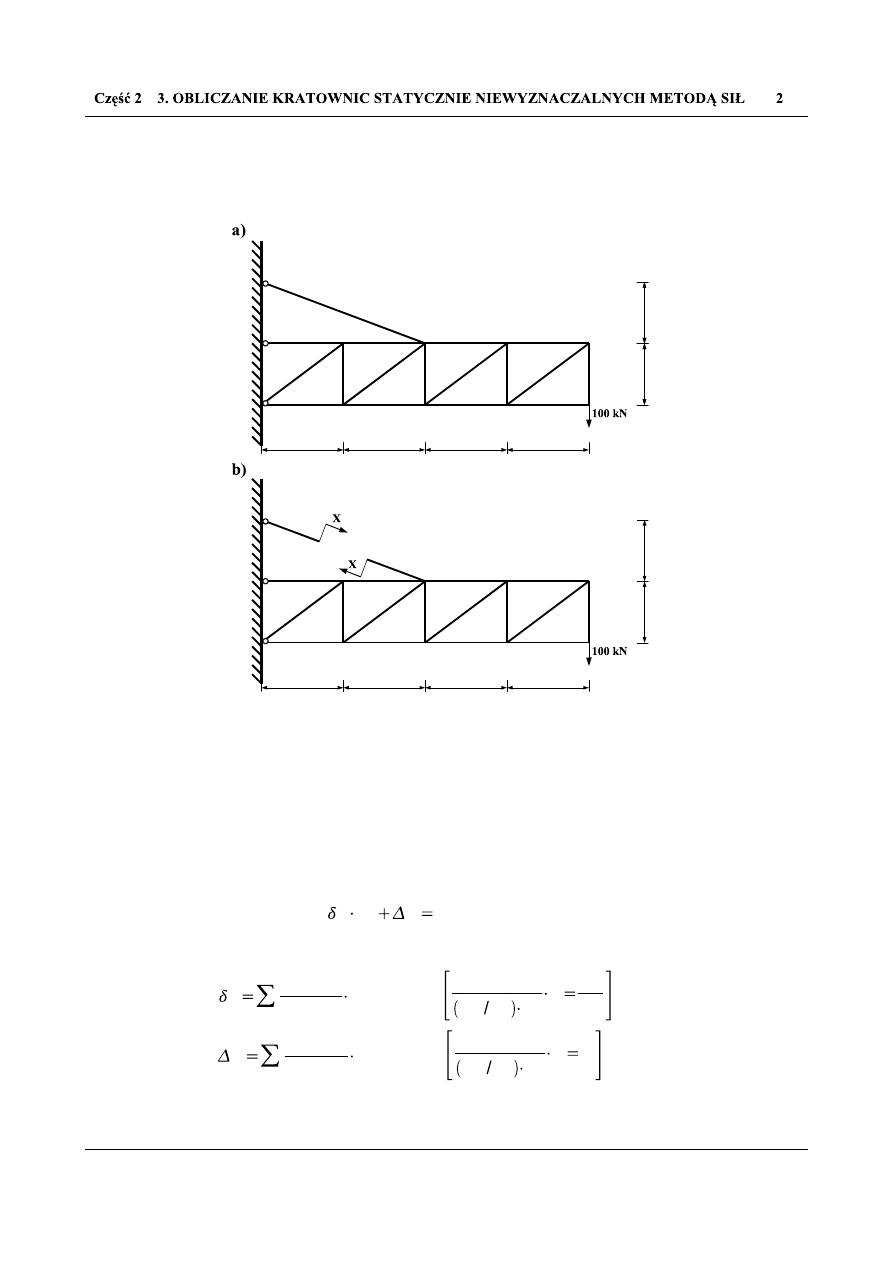
Rys. 3.1.1 Dany układ: a) rzeczywisty jednokrotnie statycznie niewyznaczalny; b) układ podstawowy (zastępczy),

statycznie wyznaczalny, z niewiadomą siłą X

1

Powyższy układ podstawowy (Rys. 3.1.1 b)) dla dowolnych X

1

nie spełnia warunku identyczności

kinematycznej z rzeczywistym układem, ponieważ dozna on przemieszczenia na końcach rozciętego pręta.
Aby spełnić ten warunek, do układu podstawowego wprowadzamy dodatkowy warunek na X

1

, w postaci

równania liniowego (tzw. równania kanonicznego), wyrażających zgodność przemieszczeń układu
rzeczywistego i podstawowego, przez liczenie przemieszczeń w układzie statycznie wyznaczalnym, takich
punktów, których znamy konkretne wartości w układzie statycznie niewyznaczalnym. Dla naszego
przypadku równanie kanoniczne przyjmie postać (3.1.1):

1 1

X

1

1 p

0

(3.1.1)

gdzie δ

11

i ∆

1p

to odpowiednie przemieszczenia wyrażone następującymi wzorami:

1 1

j

S



j



1

S



j



1

EA

j

l

j

1

kN m

2

m

2

m

m

kN

(3.1.2)

1 p

j

S



j



1

S



j



p

EA

j

l

j

kN

kN m

2

m

2

m m

(3.1.3)

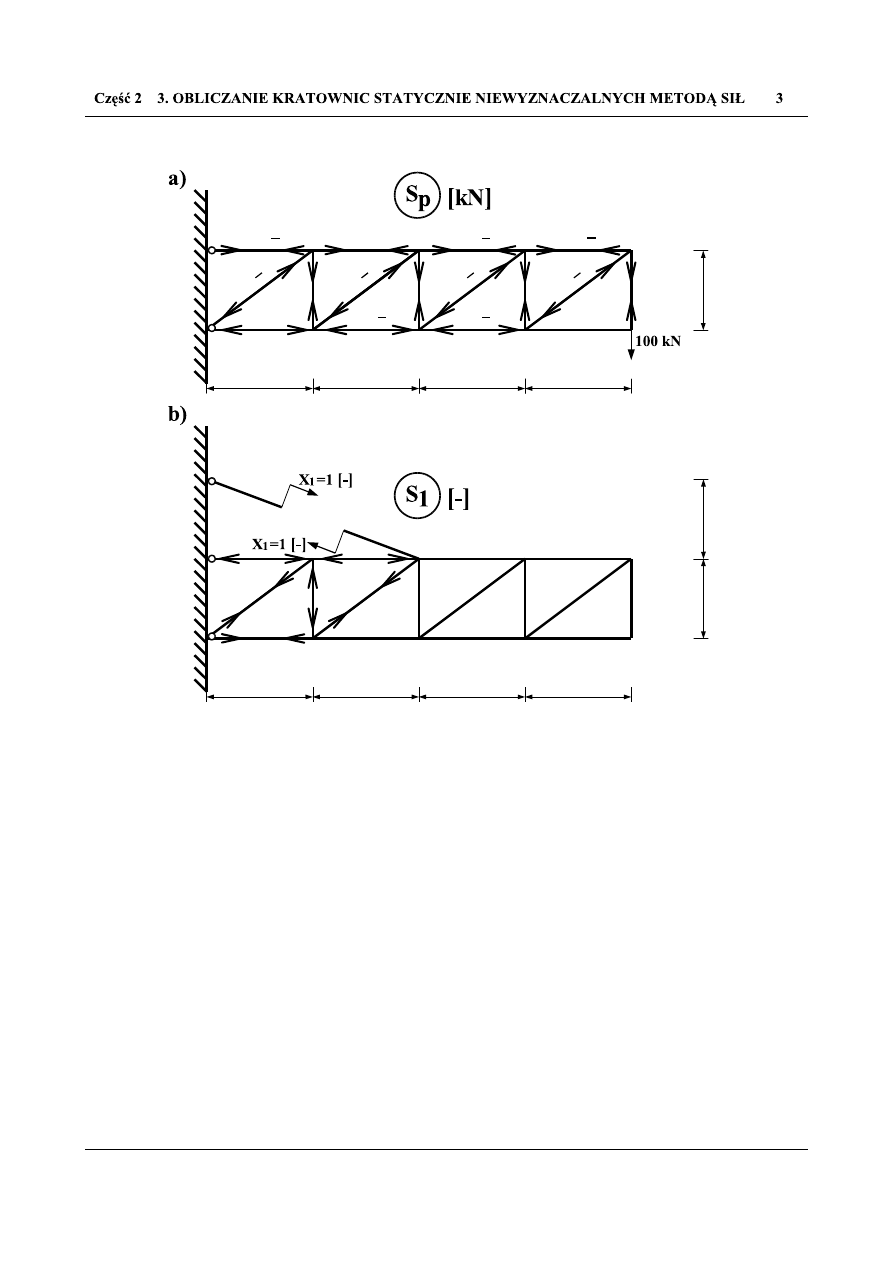
W celu obliczenia powyższych współczynników (3.1.2 i 3.1.3), znajdujemy odpowiednie wielkości sił

normalnych w danych prętach kratownicy (Rys. 3.1.2).

Krzysztof Tymper Mechanika Budowli

AlmaMater

[m]

4,4

3

,3

4,4

4,4

4,4

3

,3

[m]

4,4

3

,3

4,4

4,4

4,4

533

1
3

400

266

2
3

133

1
3

266

2
3

133

1
3

0

400

100

100

100

100

16

6

2

3

16

6

2

3

16

6

2

3

16

6

2

3

0,468

1,872

0,351

0

0

0

0

0

0

0

0

0

0

0,5

85

0,5

85

1,404

Rys. 3.1.2 Wartości siły normalnej w danych prętach kratownicy, w układzie podstawowym powstałe wskutek

działania: a) obciążenia zewnętrznego; b) siły jedynkowej przyłożonej w miejsce niewiadomej X

1

Poszukiwane współczynniki otrzymano po odpowiednich sumowaniach (Tab. 3.1.1), a następnie na ich

podstawie uzyskano wartość poszukiwanej niewiadomej X

1

(Tab. 3.1.1), co z kolei pozwoliło na znalezienie

poszukiwanych rzeczywistych sił wewnętrznych w rozpatrywanym układzie statycznie niewyznaczalnym
(Tab. 3.1.1 oraz Rys.3.1.3).

Tab. 3.1.1 Obliczenia poszukiwanych sił wewnętrznych

Krzysztof Tymper Mechanika Budowli

AlmaMater

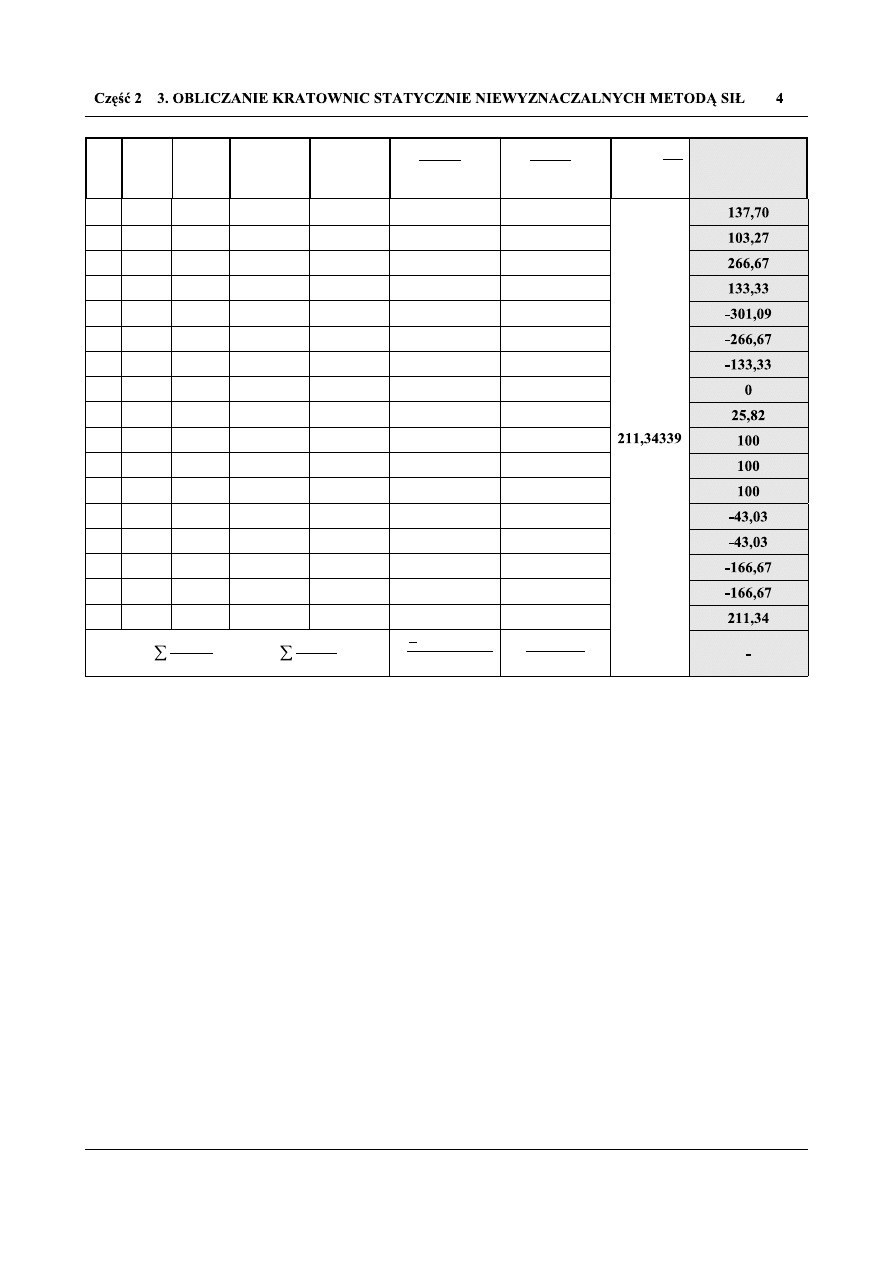
Pręt

l

j

[m]

EA

j

[kN]

S

(j)

P

[kN]

S

(j)

1

[-]

S



j



1

S



j



P

EA

j

⋅

l

j

[m]

S



j



1

S



j



1

EA

j

⋅

l

j

[m/kN]

X

1

=

−



1 p



1 1

[kN]

S

(j)n

= S

(j)

1

.

X

1

+S

(j)

P

[kN]

G

1

4,4

EA

0

533,3333

-1,872

-4392,95973

15,41929

G

2

4,4

EA

0

400

-1,404

-2471,04

8,67335

G

3

4,4

EA

0

266,6667

0

0

0

G

4

4,4

EA

0

133,3333

0

0

0

D

1

4,4

EA

0

-400

0,468

-823,68

0,96371

D

2

4,4

EA

0

-266,6667

0

0

0

D

3

4,4

EA

0

-133,3333

0

0

0

D

4

4,4

EA

0

0

0

0

0

S

1

3,3

0,6 EA

0

100

-0,351

-193,05386

0,67762

S

2

3,3

0,6 EA

0

100

0

0

0

S

3

3,3

0,6 EA

0

100

0

0

0

S

4

3,3

0,6 EA

0

100

0

0

0

K

1

5,5

0,7 EA

0

-166,6667

0,585

-766,08644

2,68896

K

2

5,5

0,7 EA

0

-166,6667

0,585

-766,08644

2,68896

K

3

5,5

0,7 EA

0

-166,6667

0

0

0

K

4

5,5

0,7 EA

0

-166,6667

0

0

0

K

5

9,3984 0,7 EA

0

0

1

0

13,42655



1 p

=

j

S



j



1

S



j



p

EA

j

⋅

l

j

,



1 1

=

j

S



j



1

S



j



1

EA

j

⋅

l

j

9412,90647

EA

0

44,53845

EA

0

Krzysztof Tymper Mechanika Budowli

AlmaMater

[m]

4,4

3,

3

4,4

4,4

4,4

3,

3

o

o

o

o

o

o

o

o

[m]

4,4

3,

3

4,4

4,4

4,4

103,27

0

301,09

25,82

100

100

100

211,3

4

137,70

43

,03

43

,03

266,67

133,33

266,67

133,33

16

6,6

7

16

6,6

7

Rys. 3.1.3 Zestawienie wyników (rzeczywistych wartości siły normalnej w danych prętach) dla rozpatrywanej

kratownicy statycznie niewyznaczalnej

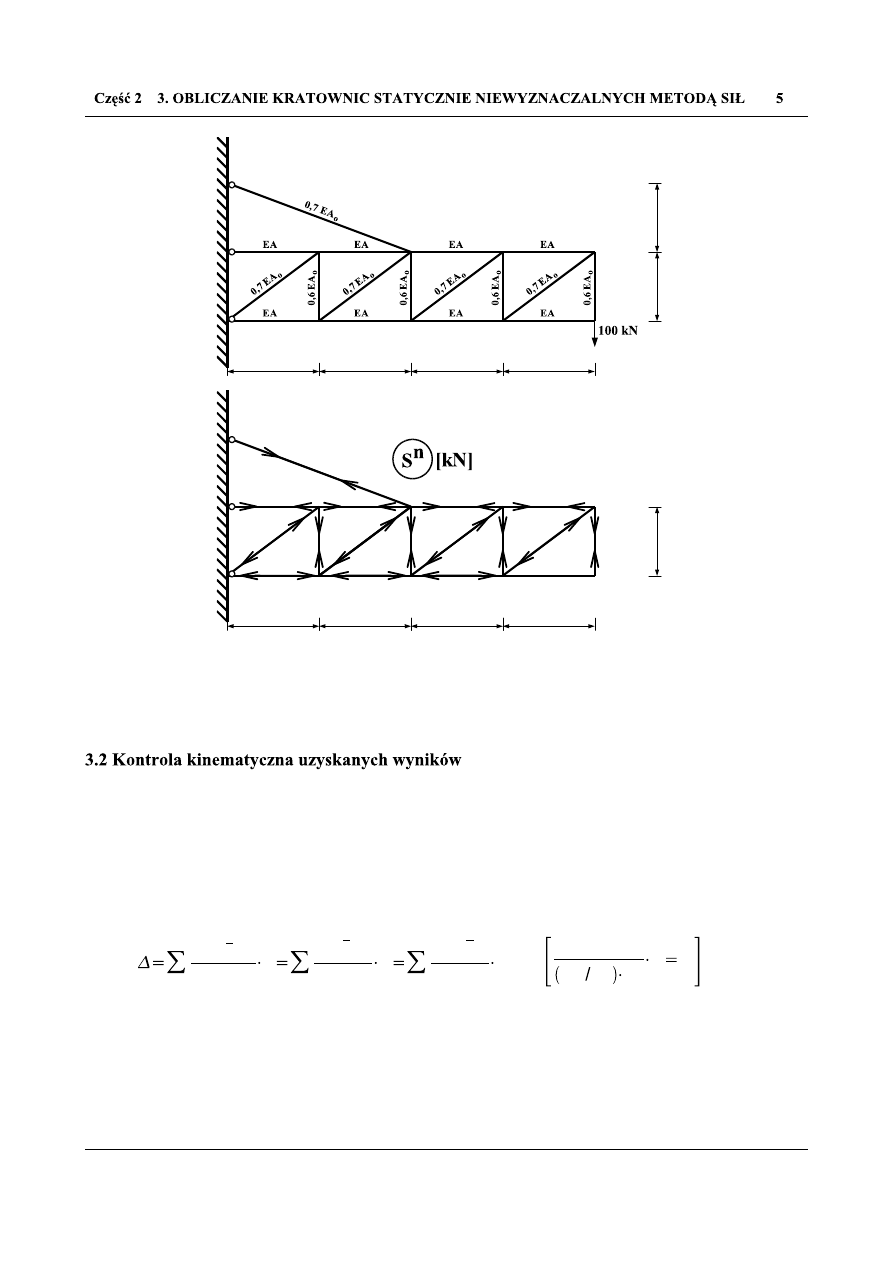
Jest to najważniejsze sprawdzenie w metodzie sił, gdyż dopiero one daje nam pewność poprawności

uzyskanych wyników. Polega na wykazaniu, że dla wybranych punktów (na ogól punktów, które nie doznają
przemieszczeń

w

układzie

statycznie

niewyznaczalnym)

przemieszczenia

są

równe

wartościom

rzeczywistym tam występującym. Przemieszczenia wyliczymy korzystając z równania pracy wirtualnej oraz
z twierdzeń redukcyjnych, z których wynika, że licząc przemieszczenia w układzie statycznie
niewyznaczalnym, jeden ze stanów (rzeczywisty lub wirtualny), możemy wyliczyć dla dowolnego układu
podstawowego (3.2.1).

j

S



j



n

S



j



n

EA

j

l

j

j

S

o



j



S



j



n

EA

j

l

j

j

S



j



n

S

o



j



EA

j

l

j

kN

kN m

2

m

2

m m

(3.2.1)

Z uwagi na specyfikę oraz prostotę rozpatrywanej przez nas kratownicy (układ jednokrotnie wewnętrznie
statycznie niewyznaczalny), kontrola kinematyczna nie jest w tym przypadku do końca miarodajna. Wynika
to z faktu, że w

szystkie możliwe do zastosowania układy podstawowy są ze sobą tożsame. Dlatego sprawdzenia

dokonamy (Tab. 3.2.1) wykorzystując ten sam co poprzednio (użyty podczas liczenia współczynników równania
kanonicznego) układ podstawowy (Rys. 3.1.1 b)).

Krzysztof Tymper Mechanika Budowli

AlmaMater

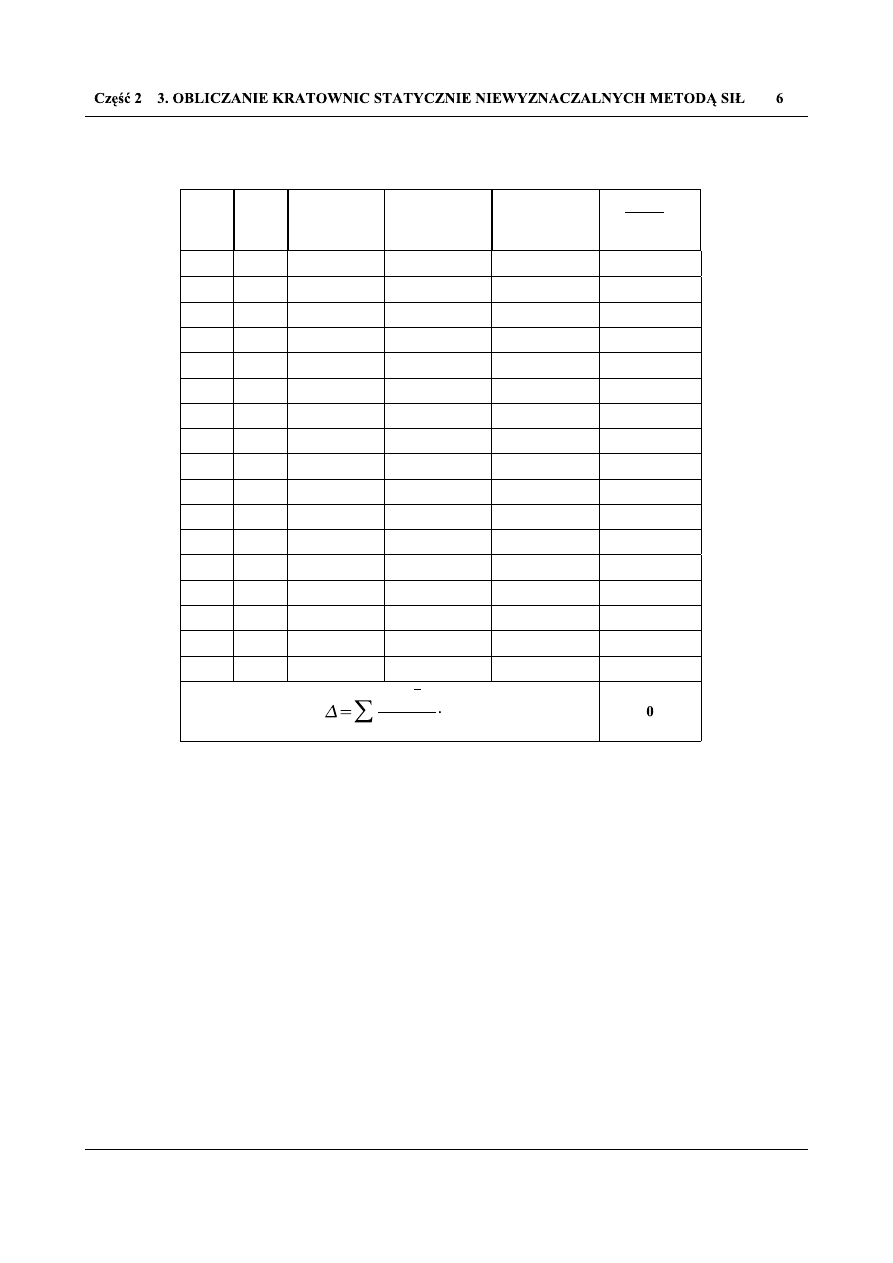
Tab. 3.2.1 Kontrola kinematyczna rozpatrywanego układu kratowego

Pręt

l

j

[m]

EA

j

[kN]

S



j



n

[kN]



S

o



j



[-]

S



j



n



S

o



j



EA

j

⋅

l

j

[m]

G

1

4,4

EA

0

137,70

-1,872

-1134,19482

G

2

4,4

EA

0

103,27

-1,404

-637,98474

G

3

4,4

EA

0

266,67

0

0

G

4

4,4

EA

0

133,33

0

0

D

1

4,4

EA

0

-301,09

0,468

-620,00719

D

2

4,4

EA

0

-266,67

0

0

D

3

4,4

EA

0

-133,33

0

0

D

4

4,4

EA

0

0

0

0

S

1

3,3

0,6 EA

0

25,82

-0,351

-49,84355

S

2

3,3

0,6 EA

0

100

0

0

S

3

3,3

0,6 EA

0

100

0

0

S

4

3,3

0,6 EA

0

100

0

0

K

1

5,5

0,7 EA

0

-43,03

0,585

-197,79158

K

2

5,5

0,7 EA

0

-43,03

0,585

-197,79158

K

3

5,5

0,7 EA

0

-166,67

0

0

K

4

5,5

0,7 EA

0

-166,67

0

0

K

5

9,3984

0,7 EA

0

211,34

1

2837,61346

j

S



j



n

S

o



j



EA

j

l

j

Na zakończenie warto dodać że w przypadku bardziej skomplikowanych układów kratowych wewnętrznie
statycznie niewyznaczalnych sprawdzenia uzyskanych wyników można również dokonać w następujący
sposób:

- obliczyć rzeczywiste przemieszczenie danego punktu, w dwóch różnych układach dla wirtualnego stanu
obciążenia (wykorzystując twierdzenie redukcyjne w dwóch różnych układach podstawowych), które musi
być takie samo;

- ponownie przeprowadzić obliczenia metodą sił, ale dla innego układu podstawowego i porównać
otrzymane w ten sposób wyniki, z wyliczonymi wcześniej;

Krzysztof Tymper Mechanika Budowli

AlmaMater