Discrimination testing: a few ideas, old and new

Michael O’Mahony

a,

*, Benoıˆt Rousseau

b

a

Department Food Science and Technology, University of California, Davis, CA 95616, USA

b

The Institute for Perception, 2306 Anza Avenue Davis, CA 95616, USA

Accepted 21 July 2002

Abstract

The present article provides an overview of our current knowledge on the topic of discrimination testing. First, the various goals

of discrimination testing are outlined in terms of the objective of the investigation: psychophysics (understanding how the human
senses work), Sensory Evaluation I (using the human senses as instruments to evaluate food characteristics) and Sensory Evaluation
II (investigating the consumer’s ability to discriminate between foods). Then, theories are described allowing the selection of the
most appropriate protocol based on the aim of the study. These theories include the Thurstonian approach to product measure-
ments, taking into account the central processing of information in the brain. The effect of experimental factors such as memory,
sensory ‘fatigue’, sample retasting and practice are also considered. The consideration of all these variables will allow the selection
of the most suitable protocol for investigations involving discrimination testing.
#

2002 Elsevier Science Ltd. All rights reserved.

Keywords:

Discrimination; Thurstonian; Perceptual variance; Memory; Sensory fatigue

Discrimination tests are the basis for sensitivity mea-

surements in psychophysics, and are also used by the
industry for discrimination among very similar products
for quality assurance, product development, ingredient
specification, storage studies, etc. Discrimination tests
are suitable for distinguishing between confusable sti-
muli, as opposed to easily discriminable stimuli, which
are best discriminated using rating techniques. In psycho-
physics, the ‘confusable’ stimuli can be two similar, yet
different intensities of a stimulus, or they can be the pre-
sence or absence of a low intensity, ‘threshold’ stimulus.

1. Response bias

The central problem in discrimination testing is

response bias, sometimes called criterion variation. This
has been reviewed (Green & Swets, 1966; O’Mahony,
1992; O’Mahony, 1995b; Rousseau, 2001), so it will be
only mentioned briefly here. The problem is one of getting

a judge who can discriminate between two stimuli to
report that he can. The exact nature of the problem
depends on the nature of the test being used.

First consider a threshold test in which a judge is

required to detect sweetness in a series of low con-
centration sucrose solutions and distilled water stimuli.
Some of the stimuli will taste obviously sweet and some
obviously not sweet. Yet, others will be more difficult to
assess. The judge will tend to ‘draw a line’, a criterion
sensation of sweetness. Anything stronger will be called
‘‘sweet’’; anything weaker will be called ‘‘unsweet’’. This
line can be called the b-criterion. It basically answers the
question: ‘‘How sweet does a stimulus need to be before
being called sweet?’’. Where the line is drawn is a cog-
nitive decision. It will vary with the circumstances of the
experiment. Therefore, if the judge says he detects
sweetness, it is because his taste receptors can detect the
sweetness and his b-criterion is in such a position that
this sensation can be called ‘‘sweet’’. However, on a
different occasion, the criterion might be in such a
position that the same sensation will be called
‘‘unsweet’’. The usual way of solving this problem is to
use a forced choice procedure where two stimuli are
presented to the judge. One will be distilled water, the
other will be a low concentration of sucrose, and the

0950-3293/02/$ - see front matter # 2002 Elsevier Science Ltd. All rights reserved.
P I I : S 0 9 5 0 - 3 2 9 3 ( 0 2 ) 0 0 1 0 9 - X

Food Quality and Preference 14 (2002) 157–164

www.elsevier.com/locate/foodqual

* Corresponding author. Tel.: [phone]; fax: [phone].

E-mail address:

[e-mail] (M. O’Mahony),

[e-mail] (B. Rousseau).

judge is required to indicate which one is the sucrose.
This has the effect of stabilizing the b-criterion in a sui-
table position so that the distilled water will be called
‘‘unsweet’’ and the sucrose solution will be called
‘‘sweet’’. Tests like the 2-Alternative Forced Choice (2-
AFC or paired comparison) or 3-AFC (two distilled
water, one sucrose solution) use this strategy. This
method can be extended to the sensory evaluation of
foods (sweet vs. unsweet cakes, beverages etc), personal
care products, etc.

The other type of criterion is the t-criterion which

answers the question ‘‘how different must stimuli be to
be called different?’’ This is more a distance-based cri-
terion used for tests which ask whether stimuli are dif-
ferent or not. This strategy assumes that the judge has a
cognitive ‘yardstick’, which needs to be exceeded by two
perceptions in order for the two corresponding stimuli
to be reported as ‘different’. Again, in the same manner
as for the b-criterion, forced choice procedures like the
triangle or duo-trio test circumvent this problem.

2. Choosing a discrimination test

In sensory science, there are several goals for

measurement, and for a more detailed review see
O’Mahony (1995a). Psychophysics has a range of goals:
the study of the sensory response to the physical prop-
erties of a stimulus, the mechanisms of this response,
and any associated information processing in the brain
which can affect how the judge reports these sensations.
For what has been called Sensory Evaluation I, the goal
is to use the human senses as instruments for measuring
foods or other products. For what was called Sensory
Evaluation II, the goal is to measure product perception
in conditions as close as possible to realistic consump-
tion situations.

For Sensory Evaluation I, the human senses are used

as an analytical tool: for example, the nose is an alter-
native to a gas chromatograph for detecting volatile
chemicals. The focus here is to study the properties of
the foods or other products, it is not to study how well
consumers can discriminate between them. In descrip-
tive analysis the various attributes of a product which
elicit sensations in the judge, are rated, resulting in a
profile of that particular product. These profiles are
then compared among products. Yet, if the products
were not easily discriminable, difference tests could be
used to make these comparisons. In this case, it would
seem sensible to use the most sensitive and statistically
powerful test available in the same way that we would
choose the most sensitive analytical instrument. Thus,
for Sensory Evaluation I, we look for the most powerful
and sensitive test.

For Sensory Evaluation II, we are looking for a test

which will predict how well consumers can discriminate

in natural conditions of consumption or use. The focus
here is to study the sensitivity of consumers to differ-
ences between products. The test procedure chosen will
depend on the particular product, so that one cannot
make firm generalizations. However, some principles
can be proposed. A test that is more statistically pow-
erful will not require such a large sample of consumers
to detect a difference of a given size. It is thus more
efficient and less expensive. The test should be matched
in sensitivity to normal conditions of consumption,
which may mean that we do not necessarily want the
most sensitive test.

For psychophysics, discrimination tests are generally

used for measurement of sensitivity to various stimuli or
sensitivity to differences between different intensities of
a stimulus. To enable efficient comparisons, the main
requirement is standardization of testing procedures. As
in Sensory Evaluation I, a statistically more powerful
test would be more suitable.

In the choice of these tests, there are several theore-

tical strands that can be drawn upon. Firstly, there is
probabilistic modeling. This is sometimes referred to,
and will be here, as Thurstonian modeling, to honor the
pioneering development of these ideas by Thurstone
(1927). This approach considers the efficiency of the
central processing that takes place in the brain. This
provides a theoretical framework for assessing the suit-
ability of various difference tests. It also provides a
generalized measure of degree of difference, d

0

, which

can be used for comparing the results obtained from
different testing procedures. For instance, the results
from a triangle test can be compared to those from a
duo-trio test, despite their different chance probabilities.
More important still, Thurstonian modeling allows the
comparison of the relative power of testing procedures.
This framework can be expanded by further considera-
tion of carry-over effects, memory effects, retasting, etc.

3. Thurstonian modeling

As mentioned earlier, Thurstonian modeling is based

on ideas first developed by Thurstone (1927). It was a
precursor to the development of signal detection theory
(Green & Swets, 1966; Macmillan & Creelman, 1991),
and has recently been applied to sensory evaluation (for
reviews, see Ennis, 1990; Ennis, 1993b; O’Mahony,
1995b; O’Mahony, Masuoka, & Ishii, 1994; Rousseau,
2001). It is based on two ideas: variation of product
perception and what can be called the decision rule or
cognitive strategy.

When a food is tasted repeatedly, the perception of its

flavor will vary over repeated tastings. This variation
has several sources. In the judge, there is random noise
in the nervous system, sensory adaptation especially due
to residuals from prior tasted stimuli, variability in the

158

M. O’Mahony, B. Rousseau / Food Quality and Preference 14 (2002) 157–164

number of receptors triggering a response at the per-
ipheral level, etc. In the product, there can be variation
due to non-homogeneity both within and between sam-
ples. Because of these variations, the intensity of pro-
duct perception will not be constant, but will vary
slightly according to a frequency distribution usually
assumed to be normal. The height of the distribution at
a given intensity indicates the likelihood of that inten-
sity occurring at any given moment (intensities around
the mean are more likely to occur than those towards
the tails of the distribution.) Using this approach, two
confusable stimuli, the sort that are so similar that they
need to be distinguished by formal testing, can be
represented as two overlapping distributions This is
illustrated in Fig. 1. The distributions are usually
assumed to have the same variance, and this has been
confirmed experimentally as being a suitable assump-
tion (e.g. Hautus & Irwin, 1995; O’Mahony, 1972). The
degree of difference between the products is called or
d

0

( the population parameter, d

0

its experimental esti-

mate) which is the distance between the means of the
distributions measured in terms of their standard
deviations. The larger the d

0

, the more different the per-

ception of the products. A d

0

of 1 can be considered

as a threshold value in psychophysics (76% correct in
a 2-AFC test).

The second idea in Thurstonian modeling is the con-

cept of a decision rule. Each discrimination test has at
least one specific decision rule that the judge will use to
generate an answer. The two main decision rules have
been described by O’Mahony et al. (1994) as the ‘com-
parison of distances’ (triangle, duo-trio) and ‘skimming’
(2-AFC, 3-AFC) strategies. Tables have been developed
for these and other tests relating the proportion of tests
correct to d

0

(Ennis, 1993b; Ennis & Mullen, 1986;

Ennis, Ennis, Yip, & O’Mahony, 1998; Hacker & Rat-
cliff, 1979; Frijters, 1982; Frijters, Kooistra, & Ver-
eijken, 1980; Rousseau & Ennis, 2001).

Because some decision rules are more efficient than

others, a judge will exhibit better performance with
some tests than others, even if the underlying sensory
difference between the products (d

0

) is the same. This

illustrates their difference in statistical power: some tests
are more suitable for detecting small sensory differences
than others (Ennis, 1993b). An alternative way of con-
sidering the statistical power of tests is that some will
require smaller sample sizes than others for detecting a
given degree of difference. For example, to have 80%

chance of detecting a d

0

of 1, at a significance level of

5%, the 2-AFC will require 21 judgments, the 3-AFC
15, the triangle 198 and the duo-trio 225. This disparity
in sample size becomes even more extreme when looking
at smaller differences (d

0

<

1) or larger power require-

ments (power > 80%).

The Thurstonian assumptions and predictions have

been confirmed in many experimental applications. One
of the most notorious is the paradox of discriminatory
non-discriminators (attributed to Gridgeman, 1970)
based on Byer and Abrams’ data (1953). In this para-
dox, when comparing exactly the same stimuli, judges
perform a higher proportion of 3-AFC tests correctly
than triangle tests. This paradox was solved by Frijters
(1979) using Thurstonian ideas, and has been confirmed
many times since (see for example Delwiche & O’Mah-
ony, 1996; Frijters, 1981; Masuoka, Hatjopoulos, &
O’Mahony, 1995; Rousseau & O’Mahony, 1997; Still-
man, 1993; Tedja, Nonaka, Ennis, & O’Mahony, 1994).
Thurstone’s ideas were also confirmed (different tests
yielding the same d

0

values for the same stimuli and

judges) using a variety of discrimination procedures
(Delwiche & O’Mahony, 1996; Geelhoed, MacRae, &
Ennis, 1994; Hautus & Irwin, 1995; Huang & Lawless,
1998; Kuesten, 2001; Masuoka et al., 1995; Rousseau,
Meyer, & O’Mahony, 1998; Rousseau & O’Mahony,
2000; 2001; Stillman & Irwin, 1995).

Based on the Thurstonian approach, the 3-AFC and

2-AFC tests using the ‘skimming’ decision rule, turn out
to be statistically the most powerful. The 3-AFC is
slightly more powerful than the 2-AFC. The triangle
and duo-trio which use the ‘comparison of distances’
strategy are less powerful, and thus require larger samples
of data in order to detect the same degree of difference.

At this stage of the proceedings, it would appear that

the 3-AFC is the most desirable test for Sensory Eva-
luation I, closely followed by the 2-AFC. These tests
require specification in the test instructions of the nature
of the attributes on which the stimuli should be dis-
criminated. As the judges in Sensory Evaluation I will
very likely be trained sufficiently to identify the relevant
attribute of the food (as with descriptive analysis), there
should be no problem with this. However, should it not
be possible to specify the relevant attribute, the ‘warm-
up’ procedure (O’Mahony, Thieme, & Goldstein, 1988)
can be used to induce the judges to specify the difference
(Thieme & O’Mahony, 1990; Rousseau & O’Mahony,
1997). If the nature of the products eliminates the possi-
bility of a ‘warm-up’ because of excessive ‘‘taste fatigue’’
or trigeminal effects, then a test where the attribute is not
specified must be chosen. The commonly used methods
in this category are the duo-trio and triangle tests.

The same-different test is also a possibility. In this

test, a judge is presented with a pair of stimuli and sim-
ply required to state whether he perceives them as
‘‘same’’ or ‘‘different’’. However, it is important to spe-

Fig. 1. Thurstonian representation of the difference/similarity between
two products.

M. O’Mahony, B. Rousseau / Food Quality and Preference 14 (2002) 157–164

159

cify exactly what is meant by a same–different test. In
the shorter version of the test, a trial is defined as the
presentation of a single pair of stimuli which are either
the same or different. In the longer version, a trial is
defined as the presentation of two pairs of stimuli, one
the same, one different; these pairs are presented suc-
cessively to the judge, who is not aware that one pair is
the same and the other is different. Unpublished mod-
eling (Ennis, 2001) has demonstrated that in this ver-
sion, while still less powerful than the 2-AFC and 3-
AFC, the same–different test is more powerful than the
triangle and duo-trio. Thus, when the attribute cannot
be specified, the longer version of the same–different test
seems like the best alternative.

Unlike the triangle, duo-trio, 2-AFC and 3-AFC tests,

d

0

values cannot be computed simply from the propor-

tion of tests correct: the size of the t criterion matters.
For a given d

0

value, each value of t will yield a different

proportion of tests correct. Therefore, the computation
of d

0

will involve the prior estimation of t. This compu-

tation is described in the Appendix and tables have been
published based on this computation (Kaplan, Macmil-
lan, & Creelman, 1978; Macmillan, & Creelman, 1991).

These same arguments would appear to hold if the

goal was psychophysical testing or Sensory Evaluation
II. However, in the latter case under ordinary condi-
tions of consumption, attribute differences are not spe-
cified. This would eliminate the 2-AFC and 3-AFC. The
triangle, duo-trio and same-different are more realistic.
Of these remaining tests where attributes are not speci-
fied, the same-different test is more powerful. Further-
more, this test has simplicity because it corresponds
more to realistic everyday judgments that are made by
consumers. Therefore, at this stage, the same-different
test would appear the strongest contender for Sensory
Evaluation II.

4. Expanding the Thurstonian models: factors that add
perceptual variance

Upto now, for the same judge and same stimuli, dif-

ferent methods would yield different proportions of tests
correct, but will yield the same d

0

value. This allows

simple cross-comparison among protocols. However,
sometimes other factors can interfere with this. They
can be seen as increasing the variance of the perceptual
distribution, thus decreasing d

0

, or the opposite effect,

decreasing the variance of the perceptual distribution,
thus increasing d

0

. Fig. 2 illustrates why an increase of

perceptual variance will result in a measured lower d

0

value. A d

0

value is measured in terms of the standard

deviation of the distributions. Since the variance of the
distributions is larger in the bottom part of the figure,
the corresponding d

0

value will be smaller (bigger mea-

suring ‘unit’). Therefore, the more a factor increases the

perceptual variance, the smaller the d

0

value will be.

Thus, if a factor interferes with two protocols to a dif-
ferent extent, those protocols will yield different d

0

values.

The first of those factors involves the sequence of

presentation of the stimuli in a test. For example, the
taste of a stimulus can be affected to a greater or a lesser
degree by the stimulus that preceded it. Sensory adap-
tation would render a strong tasting stimulus as not
appearing so strong if it were tasted immediately after
another strong tasting stimulus. Also, an increase in
stimulus concentration can be more easily detected than
a decrease (O’Mahony & Goldstein, 1987). The effects
of these factors have been modeled by treating the two
stimuli (A and B) as four stimuli (A tasted after A, A
after B, B after A, B after B). One model, the condi-
tional stimulus model (Ennis & O’Mahony, 1995), uses
four perceptual distributions rather than two. The other
model, Sequential Sensitivity Analysis model (O’Mah-
ony, 1995b; O’Mahony & Odbert, 1985), is an ordinal
model. The latter predicts that the 2-AFC would yield a
higher d

0

than other tests, i.e. its sequences of tasting

will increase the perceptual variances to a lesser extent.
This was confirmed experimentally versus the 3-AFC
test (Dessirier & O’Mahony, 1999; Rousseau &
O’Mahony, 1997).

The second factor is memory. In a discrimination

task, a stimulus being tasted is compared to the memory
of a stimulus tasted beforehand. Inconstancy in the
memory of that stimulus would be adding perceptual
variance, thus decreasing d

0

. As the number of samples in

a test or the time between tasting stimuli increases, var-
iance based on inconstancy of memory also increases.
Therefore, performance on a two stimulus test would be
expected to yield a higher d

0

than on a test involving three

or more stimuli. This provides an additional explana-
tion to the sequence effects for the differences observed
between the 2-AFC and 3-AFC tests. Furthermore, in
the face of contrary predictions from sequence effects,
the two stimulus same–different test gave equal or
higher d

0

values than the three stimulus triangle and

duo-trio tests (Kuesten, 2001; Rousseau et al., 1998;
Rousseau, Rogeaux & O’Mahony, 1999; Stillman, &
Irwin, 1995), showing the importance of memory.

Fig. 2. Decrease in d

0

value due to an increase in the perceptual var-

iances.

160

M. O’Mahony, B. Rousseau / Food Quality and Preference 14 (2002) 157–164

Returning to the selection of an appropriate test for

Sensory Evaluation I, it would appear that because of
possible memory and sequence effects, the 2-AFC would
yield a larger d

0

value and thus provide more statistical

power. For psychophysics, the same would be true, and
the 2-AFC is generally used in such discrimination-
based methods. For Sensory Evaluation II, the same–
different test would still seem to be the method of
choice.

5. Factors that decrease perceptual variance

Decreasing the variance of the perceptual distribu-

tions will result in the measure of larger d

0

values (cf.

Fig. 2, opposite effect). Two factors having such an
effect can be mentioned: sample retasting and training.

Rather than the two intensity distributions represent-

ing the two stimuli to be discriminated (Fig. 2), consider
instead a distribution of the perceptual differences
between the two stimuli generated by repeated tastings
(Fig. 4). Sometimes this perceptual difference will be
greater than d

0

sometimes it will be less. Yet, the mean

of the distribution will be d

0

. In a 2-AFC, retasting the

stimuli has been described as decreasing the variance of
this distribution of differences (Juslin & Olsson, 1997).
Because this difference distribution arises from the two
intensity distributions, it can be modeled as a decrease
in the variance of the perceptual distributions, thus an
increase in d

0

. This prediction has been confirmed

experimentally, showing how allowing judges to re-
sample stimuli up to three times significantly improved
their performance in the triangle, same-different and
dual-pair methods (Rousseau & O’Mahony, 2000).

Regarding

training

or

practice,

it

is

generally

observed that sensitivity to various attribute changes
increases upon repeated exposure to products during
various descriptive analysis procedures. Such an effect
was formally observed in discrimination testing with
model systems (Tedja et al., 1994). This increase in per-
formance can again be viewed as a decrease in percep-
tual variance. As part of an ongoing research project in
the authors’ laboratory, the sensitivity of a trained ice
cream tasting panel was compared to that of consumers.
Same–different tests were used to discriminate between
ice creams varying in composition. The panel had been
in operation for a period of several months. As pre-
dicted, the trained panel exhibited a higher sensitivity
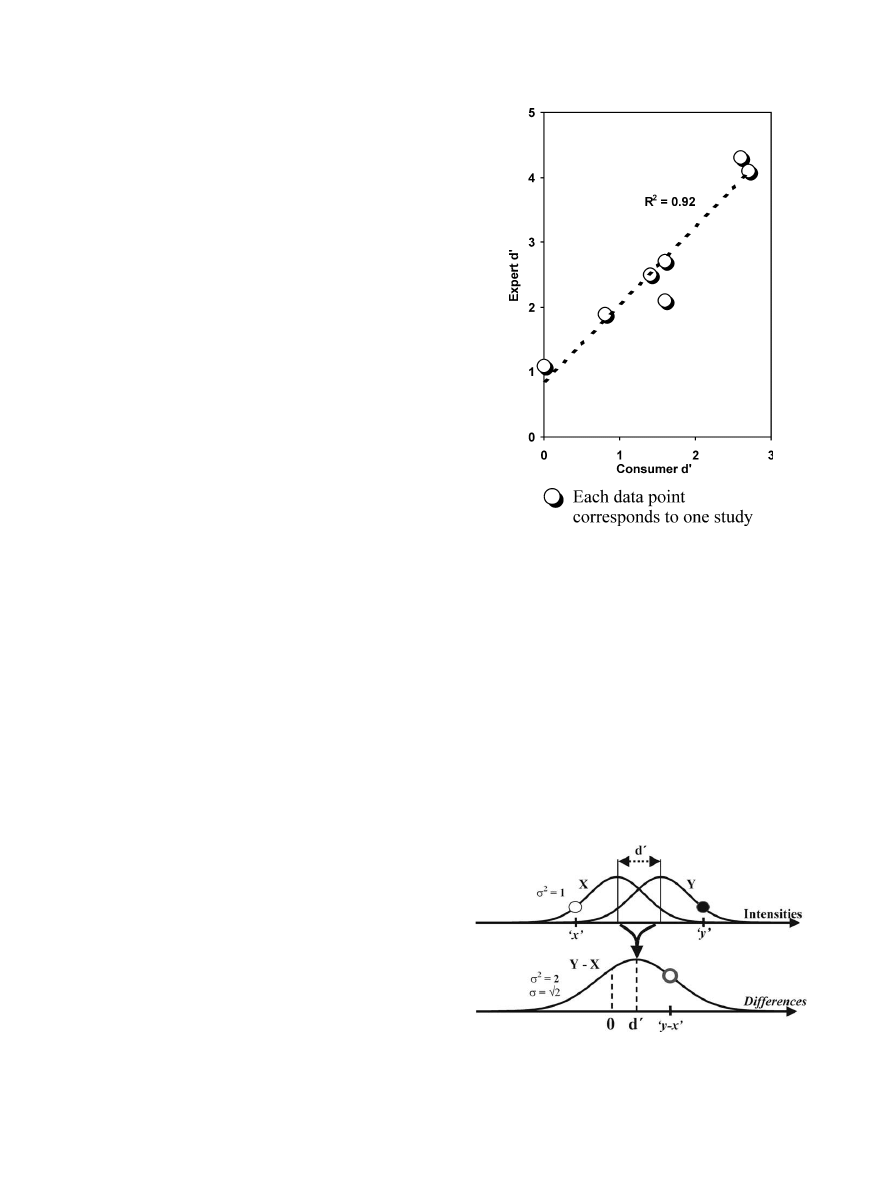
than consumers as is illustrated in Fig. 3. For this par-
ticular type of product, the consumers seem to start
discriminating (d6¼0) when the trained panel’s d

0

has a

value of 1. Such comparisons can be used for predicting
consumer discrimination from ‘in-house’ trained panels,
resulting in a reduction of time and cost requirements. This
approach has been used previously with R-index values
for whisky discrimination (Takagi & Asakura, 1985).

6. Difference tests involving more than two stimuli

Most difference tests were designed for discriminating

between two stimuli. However, in some situations, it is
desirable to measure the degree of discrimination
among more than two stimuli. It would be time-con-
suming to perform a succession of triangle or 2-AFC
tests on the assorted pairs of stimuli. An alternative
approach would be to use a test that incorporates more
than two stimuli. Ranking is one possibility, should a
suitable dimension be identified along which to rank.

Yet, when such a dimension cannot be identified, a

Torgerson test (Torgerson, 1958) can be used. This test

Fig. 3. Relationshipbetween the sensitivities of a trained panel and a
consumer panel for vanilla flavored ice cream.

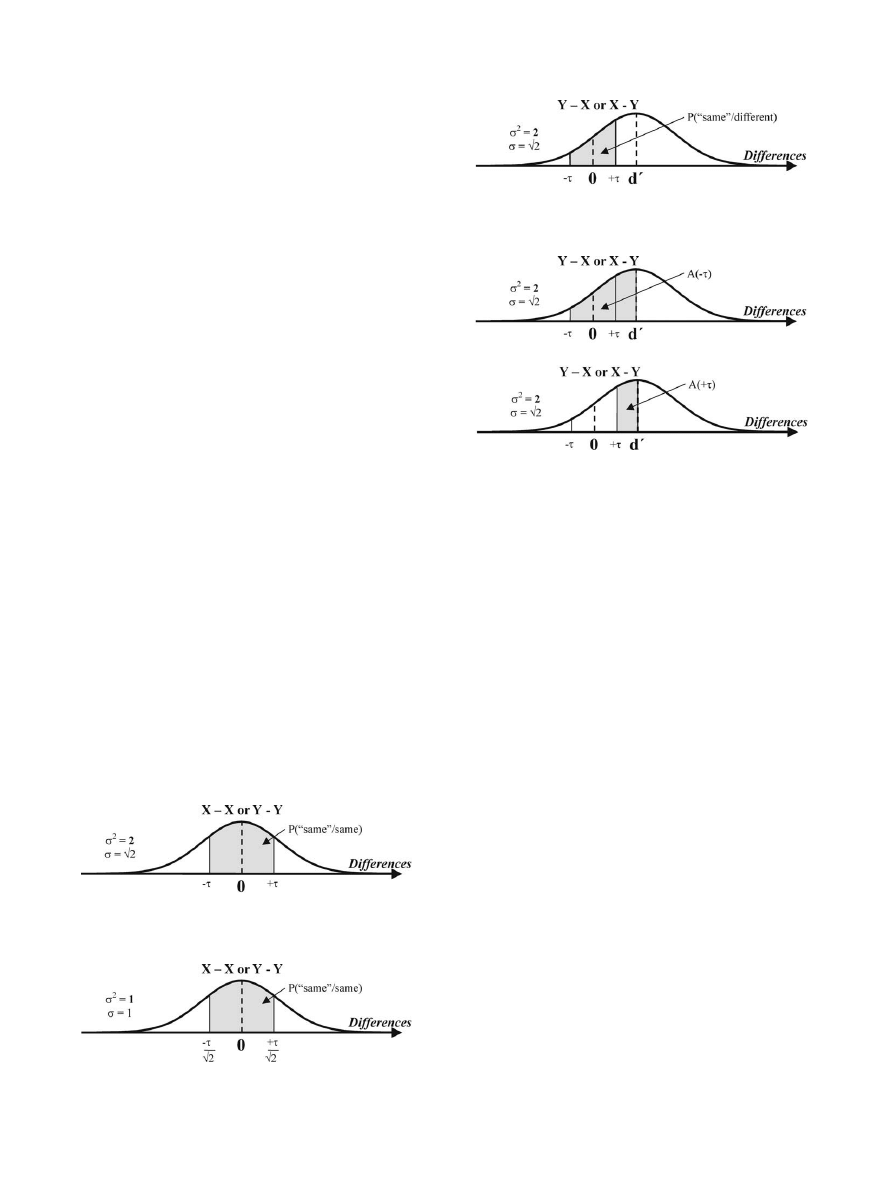
Fig. 4. Development of a distribution of differences in perceptual
intensity, illustrated through the presentation of a pair of different yet
confusable samples X and Y, engendering ‘x’ and ‘y’ momentary
perceptions.

M. O’Mahony, B. Rousseau / Food Quality and Preference 14 (2002) 157–164

161

resembles the duo-trio test except that neither of the
comparison stimuli is the same as the reference. The
judge’s task is to select which of these two stimuli is
closer to the reference. In fact, the duo-trio is a special
case of Torgerson’s method. A Thurstonian model of
the task is available for this test (Ennis, Mullen, & Frij-
ters, 1988). Unfortunately, no tables are available for
the computation of d

0

because of its complexity; soft-

ware is required. Recent experimental evidence con-
firmed the validity of this model, by demonstrating how
the Torgerson test gave the same d

0

values as a series of

successive duo-trios (Rousseau, O’Mahony, & Ennis,
2001). However, for the same precision of measurement,
the Torgerson method requires a smaller sample size. It
also permits the estimation of the dimensionality of the
solution: it can be determined whether the several pro-
ducts being compared vary along the same dimension or
not. Alternative approaches include the multiple dual-
pair method (Rousseau & Ennis, 2002) and Richard-
son’s method of triads (Ennis et al., 1988; Richardson,
1938), which both require similar computations.

These methods have applications in both Sensory

Evaluation I and II. It needs to be kept in mind that
their power is similar to that of the duo-trio test.
Nevertheless, they can provide solutions to situations
when the similarities of more than two products must be
obtained simultaneously. A particular application is the
consideration of batch-to-batch variability when com-
paring two or more products. The Torgerson’s method,
for instance, permits a measure of the similarity between
two products, taking into account such variability.

7. Summary

In situations where memory and sequence effects do

not play a significant role, the 3-AFC provides a mar-
ginally greater statistical power than the 2-AFC, yet
uses more samples. In situations where memory and
sequence effects play a significant role, the 2-AFC
because of its greater sensitivity (larger d

0

) overcomes

the marginal advantage of the 3-AFC, resulting in
slightly greater statistical power. This makes it a sui-
table candidate where the attribute change can be spe-
cified.

Generally,

this

would

apply

to

Sensory

Evaluation I (use of human senses to measure the sen-
sory properties of food) and psychophysics (study of
human sensory mechanisms per se). When the attribute
cannot be specified, which often occurs in Sensory Eva-
luation II (study of consumer perception), the same-
different test would seem a more suitable candidate than
other tests due to its greater statistical power.

It would be unwise to generalize over all situations

regarding the appropriateness of various discrimination
tests. However, understanding the underlying theory and
the behavior of various sensory and cognitive variables

can provide some useful pointers. With more experi-
mental research and development of further theory, the
conclusions presented here might need to be altered.

Although this article has concentrated on discrimina-

tion between confusable stimuli, the same ideas can be
applied to discrimination among more easily discrimin-
able stimuli, using category rating scales (Kim, Ennis, &
O’Mahony, 1998). As evidence of their universality,
they have been applied to hedonic measurements such
as hedonic and just-about-right scales, and preference
tests (see for instance Geelhoed et al., 1994; Ennis,
1993a). These applications were again included in
Thurstone’s pioneering work. Because of its general
utility, further theoretical developments will probably
be made within the context of what we have called
Thurstonian modeling.

Appendix

Calculation of d

0

values from the same–different

method.

In this Appendix, we describe the various steps

necessary to calculate a d

0

value from same-different test

results. This approach is analogous to that described in
Signal Detection Theory for the yes/no (A/Not A)
paradigm. The same-different test can involve a b- or t–
criterion (independent-observations and differencing
models, see for example Hautus and Irwin, 1995). The
calculation described thereafter applies only to the t–
criterion situation. Two steps are necessary: the estima-
tion of the size of the criterion t, then, knowing t, the
calculation of d

0

.

Unlike the yes/no paradigm d

0

calculation, which

deals with absolute intensities to estimate d

0

, the same-

different d

0

calculation requires the use of a distribution

of intensity differences as shown in Fig. 4.

From Fig. 4, we see that two independent normal

distributions of intensities of variance 1 can be repre-
sented by a normal distribution of differences of var-
iance 2 (standard deviation

ffiffiffi

2

p

) when pairs of samples

are presented and compared. If d

0

=0, X and Y lie on

topof one another and the distribution of differences is
centered at 0.

Step1: Estimation of the size of t
Like d

0

, t is measured in terms of the standard devia-

tion of the intensity distributions, or z-values. To esti-
mate t, the results from the presentation of identical
samples (XX and YY) are considered. As described
previously, the two overlapping intensity distributions
will produce a difference distribution. When the stimuli
are the same the mean of this distribution (d

0

) will be

zero and the standard deviation will be

ffiffiffi

2

p

. As descri-

bed earlier, a judge will answer that the samples pre-
sented are different if the perceived difference is larger
than t. Therefore, any perceived difference smaller than

162

M. O’Mahony, B. Rousseau / Food Quality and Preference 14 (2002) 157–164

t will induce a response ‘‘same’’. The proportion of
‘‘same’’ responses is equivalent to the area under the
curve between t and +t. This is illustrated in Fig. 5.

Tables exist giving the relationshipbetween the area

under the standard normal and z-values [see for instance
O’Mahony (1986), Table G1]. However, these tables
have been generated for normal distributions centered
at 0 with a standard deviation of 1. Thus, in order for
them to be used, it is necessary standardize the dis-
tribution of differences so that it also has a standard
deviation of 1, rather than

ffiffiffi

2

p

. This can be done simply

by dividing all current z-values by

ffiffiffi

2

p

. The resulting

distribution is shown in Fig. 6.

If, when the samples were the same, the proportion of

‘‘same’’ responses [P(‘‘same’’/same)] was say, 60%, the
proportion between 0 and +t would be 30%. From the
Table G1 of O’Mahony (1986), we find that for a pro-
portion of area under the curve of 30%, z=0.84.

Thus, t=0.84 X

ffiffiffi

2

p

=1.19

Step2: Calculation of d

0

Now that we know t, we will calculate d

0

using the

distribution of differences obtained from the presenta-
tion of pairs of samples that were different (XY and
YX). This time the mean of the distribution will be d

0

rather than zero; it is the situation illustrated in Fig. 4.
Imagine that the proportion ‘‘same’’ responses with the
products now being different [P(’’same’’/different)] is
40%. The grey area in Fig. 7 represents the proportion
of times that pairs of different samples were called
‘‘same’’ (40%).

The computation of d

0

is not straightforward because

there is insufficient information available. It is not sim-
ply a matter of using normal distribution tables to find
z

-values corresponding to an area under the curve, as in

the calculation of . However, the grey area (40%) can
be seen as the difference between two areas: the area
between d

0

and t minus the area between d

0

and +t

(see Fig. 8).

If A is the normal distribution function of parameters

d

0

and

ffiffiffi

2

p

. We can write:

A

(t)A(+t)=40%

This equation cannot be solved readily. Its root, d

0

,

needs to be found iteratively. Nevertheless, this can be
done using any currently available statistical package.

The tables published by (Kaplan et al. (1978) and

Macmillan and Creelman (1991) are based on such
computations.

References

Byer, A. J., & Abrams, D. (1953). A comparison of the triangular and

two-sample taste-test methods. Food Technology, 7, 185–187.

Delwiche, J., & O’Mahony, M. (1996). Flavour discrimination—an

extension of Thurstonian paradoxes to the tetrad method. Food
Quality and Preference

, 7, 1–5.

Dessirier, J. M., & O’Mahony, M. (1999). Comparison of d

0

values for

the 2-AFC (paired comparison) and 3-AFC discrimination meth-
ods: Thurstonian models, Sequential Sensitivity Analysis and
power. Food Quality and Preference, 10, 1–8.

Ennis, D. M. (1990). Relative power of difference testing methods in

sensory evaluation. Food Technology, 44, 114–118.

Ennis, D. M. (1993a). A single multidimensional model for dis-

crimination, identification and preferential choice. Acta Psycholo-
gica

, 84, 17–27.

Ennis, D. M. (1993b). The power of sensory discrimination methods.

Journal of Sensory Studies

, 8, 353–370.

Ennis, D.M. (2001). Personal communication.
Ennis, D. M., & Mullen, K. (1986). A multivariate model for discrimina-

tion methods. Journal of Mathematical Psychology, 30, 206–219.

Ennis, D. M., & O’Mahony, M. (1995). Probabilistic models for

sequential taste effects in triadic choice. Journal of Experimental
Psychology-Human Perception & Performance

, 21, 1088–1097.

Fig. 5. Estimation of the size of t. Use of the distribution differences
elicited by the presentation of identical samples.

Fig. 6. Standardized normal distribution of differences originating
from pairs of identical samples.

Fig. 7. Distribution of differences elicited by the presentation of dif-
ferent samples.

Fig. 8. Areas used to estimate d

0

.

M. O’Mahony, B. Rousseau / Food Quality and Preference 14 (2002) 157–164

163

Ennis, D. M., Mullen, K., & Frijters, J. E. (1988). Variants of the

method of triads: unidimensional Thurstonian models. British
Journal of Mathematical and Statistical Psychology

, 41, 25–36.

Ennis, J. M., Ennis, D. M., Yip, D., & O’Mahony, M. (1998). Thur-

stonian models for variants of the method of tetrads. British Journal
of Mathematical & Statistical Psychology

, 51, 205–215.

Frijters, J. E. R. (1979). The paradox of discriminatory non-

discriminators resolved. Chemical Senses & Flavor, 4, 355–358.

Frijters, J. E. R. (1981). An olfactory investigation of the compatibility

of oddity instructions with the design of a 3-AFC signal detection
task. Acta Psychologica, 49, 1–16.

Frijters, J. E. R. (1982). Expanded tables for conversion of a propor-

tion of correct responses (Pc) to the measure of sensory difference
(d

0

) for the triangular method and the 3-alternative forced choice

procedure. Journal of Food Science, 47, 139–143.

Frijters, J. E. R., Kooistra, A., & Vereijken, P. F. G. (1980). Tables of

d

0

for the triangular method and the 3-AFC signal detection proce-

dure. Perception and Psychophysics, 27, 176–178.

Geelhoed, E. N., MacRae, A. W., & Ennis, D. M. (1994). Preference

gives more consistent judgments than oddity only if the task can be
modeled as forced choice. Perception and Psychophysics, 55, 473–477.

Green, D. M., & Swets, J. A. (1966). Signal Detection Theory and

Psychophysics

. New York: Wiley.

Gridgeman, N. T. (1970). A re-examination of the two-stage triangle

test for the perception of sensory differences. Journal of Food
Science

, 35, 87–91.

Hacker, M. J., & Ratcliff, R. (1979). A revised table of d

0

for M-

alternative forced choice. Perception and Psychophysics, 26, 168–
170.

Hautus, M. J., & Irwin, R. J. (1995). Two models for estimating the

discriminability of foods and beverages. Journal of Sensory Studies,
10

, 203–215.

Huang, Y. T., & Lawless, H. T. (1998). Sensitivity of the ABX dis-

crimination test. Journal of Sensory Studies, 13, 229–239.

Juslin, P., & Olsson, H. (1997). Thurstonian and Brunswikian origins

of uncertainty in judgment: a sampling model of confidence in sen-
sory discrimination. Psychological review, 104, 344–366.

Kaplan, H. L., Macmillan, N. A., & Creelman, C. D. (1978). Tables of

d

0

for

variable-standard

discrimination

paradigms.

Behavior

Research Methods & Instrumentation

, 10, 796–813.

Kim, K. O., Ennis, D. M., & O’Mahony, M. (1998). A new approach

to category scales of intensity II. Use of d

0

values. Journal of Sensory

Studies

, 13, 251–267.

Kuesten, C. L. (2001). Sequential use of the triangle, 2-AC, 2-AFC,

and same–different methods applied to a cost-reduction effort: con-
sumer learning acquired throughout testing and influence on pref-
erence judgements. Food Quality and Preference, 12, 447–455.

Macmillan, N. A., & Creelman, C. D. (1991). Detection theory: a

user’s guide

. New York, NY, USA: Cambridge University Press.

Masuoka, S., Hatjopoulos, D., & O’Mahony, M. (1995). Beer bitter-

ness detection: testing Thurstonian and Sequential Sensitivity Ana-
lysis models for triad and tetrad methods. Journal of Sensory
Studies

, 10, 295–306.

O’Mahony, M. (1972). Salt taste sensitivity: a signal detection

approach. Perception, 1, 459–464.

O’Mahony, M. (1986). Sensory Evaluation of Food: Statistical methods

and Procedures

. New York: Dekker.

O’Mahony, M. (1992). Understanding discrimination tests: a user-

friendly treatment of response bias, rating and ranking R-index tests
and their relationshipto signal detection. Journal of Sensory Studies,
7

, 1–47.

O’Mahony, M. (1995a). Sensory measurement in food science—fitting

methods to goals. Food Technology, 49, 72–82.

O’Mahony, M. (1995b). Who told you the triangle test was simple?.

Food Quality and Preference

, 6, 227–238.

O’Mahony, M., & Goldstein, L. (1987). Tasting successive salt and

water stimuli: the roles of adaptation, variability in physical signal
strength, learning, supra- and subadapting signal detectability.
Chemical Senses

, 12, 425–436.

O’Mahony, M., & Odbert, N. (1985). A comparison of sensory differ-

ence testing procedures: sequential sensitivity analysis and aspects of
taste adaptation. Journal of Food Science, 50, 1055–1058.

O’Mahony, M., Masuoka, S., & Ishii, R. (1994). A theoretical note on

difference tests: models, paradoxes and cognitive strategies. Journal
of Sensory Studies

, 9, 247–272.

O’Mahony, M., Thieme, U., & Goldstein, L. (1988). The warm-up

effect as a means of increasing the discriminability of sensory dif-
ference tests. Journal of Food Science, 53, 1848–1850.

Richardson, M. W. (1939). Multidimensional psychophysics. Psycho-

logical Bulletin

, 35, 659–660.

Rousseau, B. (2001). The b-strategy: an alternative and powerful cog-

nitive strategy when performing sensory discrimination tests. Jour-
nal of Sensory Studies

, 16, 301–318.

Rousseau, B., & Ennis, D. M. (2001). A Thurstonian model for the

dual-pair (4IAX) discrimination method. Perception and Psycho-
physics

, 63, 1083–1090.

Rousseau, B., & Ennis, D. M. (2002). The multiple dual-pair method.

Perception and Psychophysics (in press).

Rousseau, B., & O’Mahony, M. (1997). Sensory difference tests:

Thurstonian and SSA predictions for vanilla flavored yogurts.
Journal of Sensory Studies

, 12, 127–146.

Rousseau, B., & O’Mahony, M. (2000). Investigation of the effect of

within-trial retasting and comparison of the dual-pair, same–different
and triangle paradigms. Food Quality and Preference, 11, 457–464.

Rousseau, B., & O’Mahony, M. (2001). Investigation of the dual-pair

method as a possible alternative to the triangle and same–different
tests. Journal of Sensory Studies, 16, 161–178.

Rousseau, B., Meyer, A., & O’Mahony, M. (1998). Power and sensi-

tivity of the same–different test: comparison with triangle and duo-
trio methods. Journal of Sensory Studies, 13, 149–173.

Rousseau, B., O’Mahony, M., & Ennis, D. M. (2001). Simultaneous

estimations of multiple sample similarities using a multivariate var-
iant of the duo-trio test. Paper presented at the 4th Rosemary
Pangborn Symposium, Dijon, France.

Rousseau, B., Rogeaux, M., & O’Mahony, M. (1999). Mustard

discrimination by same–different and triangle tests: Aspects of
irritation, memory and t criteria. Food Quality and Preference,
173–184.

Stillman, J. A. (1993). Response selection, sensitivity, and taste-test

performance. Perception and Psychophysics, 54, 190–194.

Stillman, J. A., & Irwin, R. J. (1995). Advantages of the same–differ-

ent method over the triangular method for the measurement of taste
discrimination. Journal of Sensory Studies, 10, 261–272.

Takagi, M., & Asakura, Y. (1985). Atarashii shikibetsugata kanno

Kensa-R-index ho- no jicchi rei. Engineers, 3, 24–28.

Tedja, S., Nonaka, R., Ennis, D. M., & O’Mahony, M. (1994). Triadic

discrimination testing—refinement of Thurstonian and Sequential
Sensitivity Analysis approaches. Chemical Senses, 19, 279–301.

Thieme, U., & O’Mahony, M. (1990). Modifications to sensory test

protocols: the warmed up paired comparison, the single standard
duo-trio and the A-not A test modified for response bias. Journal of
Sensory Studies

, 5, 159–176.

Thurstone, L. L. (1927). A law of comparative judgment. Psychologi-

cal Review

, 34, 273–286.

Torgerson, W. S. (1958). Theory and methods of scaling. New York:

Wiley.

164

M. O’Mahony, B. Rousseau / Food Quality and Preference 14 (2002) 157–164