An Introduction to Strategy Proof Mechanism Design*

Nick Baigent

Institute of Public Economics, Graz University

nicholas.baigent@kfunigraz.ac.at

August, 2003

The purpose of these notes is to introduce the subject of mechanism design. Ideally,
these notes would be read after reading “Mechanism Design: A quick tour” in Baigent
(2003). There are some modest mathematics perquisites that would easily be satisfied
by any student early in a masters course in economics. They can easily be obtained
from Stewart and Tall (1977).

Part 1 reviews some basic game theory, part 2 presents Direct Revelation
Mechanisms, and part 3 presents General Mechanisms and implementation in
Dominant Strategies.

Genuine attempts to do the exercises are essential for two reasons. First, some
exercises attempt to lead students to discover important points by themselves.
Second, the answers to many exercises are used later, especially those marked by *.

* Both Daniel Eckert and Christian Klamler read the entire manuscript and
commented in detail. I am very grateful to both. The usual disclaimer is accepted.

1: Review of Game theory

1.1 Introduction

Conflict and co-operation are essential features in many situations in economics,

politics, business management and other areas. There are many examples.

The performance of a group or organisation may be improved if the people in it work

hard. However, individuals may also like to shirk (not work hard). Indeed, if the

benefits of success are shared, individuals may have an incentive to shirk, hoping to

receive benefit without supplying much effort to get that benefit.

Two regions may have to reduce greenhouse gas emissions in order to achieve

environmental benefits. If the total reduction of both regions is all that matters, each

region may prefer the other to make higher reductions while they make lower

reductions. However, neither region may agree to reductions unless the other also

makes reductions. A similar situation can arise with the use of renewable resources

such as fish and forests. Conservation may require reducing harvests. While each

fisherman or forester would like to require the others to reduce their harvest more than

they do themselves, they may have to reduce harvests themselves in order to get the

others to make the required reductions.

The price that one firm gets for its output will depend not only on its own output, but

also on the output, and therefore the price, of its competitors. Countries negotiate

over trade agreements, and other sorts of agreements (taxation, migration, use of

rivers, lakes and sea) where the actions of each affect the others. People who live

together are affected by whether, or how often, the other does the washing up,

cleaning, gardening and looks after the

children. The retired are affected by

whether the young are prepared to go on paying their pensions by taxation. In

democracies, governments are obtained not by the actions of 1 person, but from the

votes of all citizens.

Everywhere in private, social, economic and political life, one finds interdependence.

To analyse what rational individuals would do in such situations of strategic

interdependence is the main purpose of game theory.

1.2

Strategies, outcomes and mechanisms.

Consider two individuals, 1 and 2, working to produce some output. They can either

work (w) or shirk (s). These are called their strategies. Thus, the set of all possible

strategies of 1 is

and the set of all possible strategies of 2 is

{ , }

w s

{ , }

w s

The possible strategy lists may therefore be expressed as follows, writing the strategy

of 1 first followed by the strategy of 2:

(w,w) they both work.

(w,s) 1 works and 2 shirks.

(s,s) they both shirk.

(s,w) 1 shirks and 2 works.

Thus, the set of all strategy lists is

{( , ),( , ),( , ),( , )}

S S

w w w s s w s s

= ×

, the

Cartesian Product of the set of all possible strategies of 1 with the set of all possible

strategies of 2.

You will need to understand the following concepts from mathematics: Sets: (set membership

(

x S

∈

), union, intersection, empty set, power set and Cartesian products of sets. Functions: (Domain,

codomain and range.) Composition of functions. The use of quantifiers: (“For all” (

) and “for

some” (

∃

)). All of these will be used many times in these notes. If you do not understand any of them

you must look them up yourself in a mathematics book. Both Hülsmann et al (1998) and Stewart and
Hall (1977) cover the required mathematics.

∀

The possible outcomes of the choice given by strategy lists may be described as

follows:

(s,w) leads to outcome a. In this outcome, success is medium (e.g. medium output), 1

has low work effort and 2 has high work effort.

(w,w) leads to outcome b. In this outcome both supply high effort and a high level of

success is therefore obtained.

(s,s) leads to outcome c in which there is low success obtained with low effort from

both 1 and 2.

(w,s) leads to outcome d in which there is medium success, but high effort from 1 and

low effort from 2.

The important thing is that outcomes are determined by all of the agents’ choices; that

is by the whole strategy list. In our example, this may be expressed in the form of a

table as follows.

Outcome determination table

ww ss ws sw

b c

So far, we have two sets, a set of all possible strategy lists S, and a set of all outcomes

X, and we also have a function that shows what outcomes are determined by each

possible strategy list. Such an outcome function is called a mechanism. It is a

function

m S

that assigns an outcome to all strategy lists in its domain.

In our

example

and

→

( , )

, ( , )

m w s

d m w w

( , )

m s s

( , )

m s w

= , as in the table.

Exercise 1.1:

The outcome determination table completely describes the
mechanism. Therefore, give a definition of a mechanism in terms of
a table. What advantages and disadvantages does your definition
have compare with the one given.

A mechanism can also be expressed using a different table as follows.

w b

s a

In this table, each row corresponds to a strategy choice of agent 1 and each column

corresponds to a strategy choice of agent 2. Therefore, each strategy list is a

combination of row and column. The outcome for any strategy list is given by the

cell in the intersection of the row and column corresponding to the strategies in the

strategy list.

Unfortunately, the terminology is not standardised and mechanisms are also called outcome functions,

game forms, institutions, organisations or rules.

1.3

Preferences, utilities and games in normal form.

Will the individuals choose to work or shirk? To answer this, we need to know their

preferences. Preferences rank outcomes. The following table gives a plausible list of

preferences in which

R is 1’s preference and

R is 2’s preference:

These rankings are obtained as follows. They both top rank the outcome in which

they shirk and the other works. So, the reduced success compared with both working

is more than offset by not having to work. They both bottom rank the outcome in

which they work and the other shirks. In between are the outcomes in which they

either both work or both shirk. Between these, the high success from both working

offsets their high work effort and they both prefer this to both shirking and the low

success this achieves.

It is useful to describe a preference ranking by a utility function. A utility function

uses numbers to describe a ranking, assigning higher numbers to higher ranked

outcomes. Thus, given 1’s ranking

R , let 1’s utility of a be

, 1’s utility of

b be u b

, 1’s utility of c be u c

( ) 4

( )

= and 1’s utility of d be u d

. In the

same way, let 2’s utility levels of the outcomes be

( )

( ) 1

u d

and u a

( )

u b

= 4

( ) 1

u c

( ) 0

( ) 10

u a

Thus, for both individuals, there are four levels to their rankings and therefore four

utility levels. 10 for the top ranked outcome, 4 for the second ranked outcome, 1 for

the third ranked outcome and 0 for the fourth ranked outcome.

Of course, these numbers are not the only ones that can describe these preference

rankings. Any assignment of numbers to outcomes that give higher numbers to more

preferred outcomes would also describe these preferences.

Exercise 1.2*: Give the domain, codomain and range of the utility function.

In exercises 1.3 – 1.7, preferences refer to those used in the “work – shirk” example.

Exercise 1.3:

Describe the preferences of 1 and 2 by utility functions that are
different from the ones using values 0, 1, 4 and 10.

Exercise 1.4:

Describe 1’s preference by a utility function such that the utility of b
is equal to 0. Describe 2’s preference by a utility function such that
the utility of c is equal to –5.

Exercise 1.5:

A utility function is not the only way to describe a preference as a
function. It can also be done with a function that has the set of all
subsets of outcomes as its range. Give a precise definition of such a
function (i.e. give its domain, codomain and range, and the rule for
assigning range elements to domain elements). (You may have to
think quite hard to do this.)

Exercise 1.6:

Express the preferences of 1 and 2 using tables obtained from the
function given in the previous exercise.

Exercise 1.7*: In the work-shirk example, give the composition of the utility

function of person 1 with the outcome function. See figure 1.1.
Express this composition in the form of a table. Do the same for
person 2.

The composite functions in exercise 1.7 are called payoff functions and are

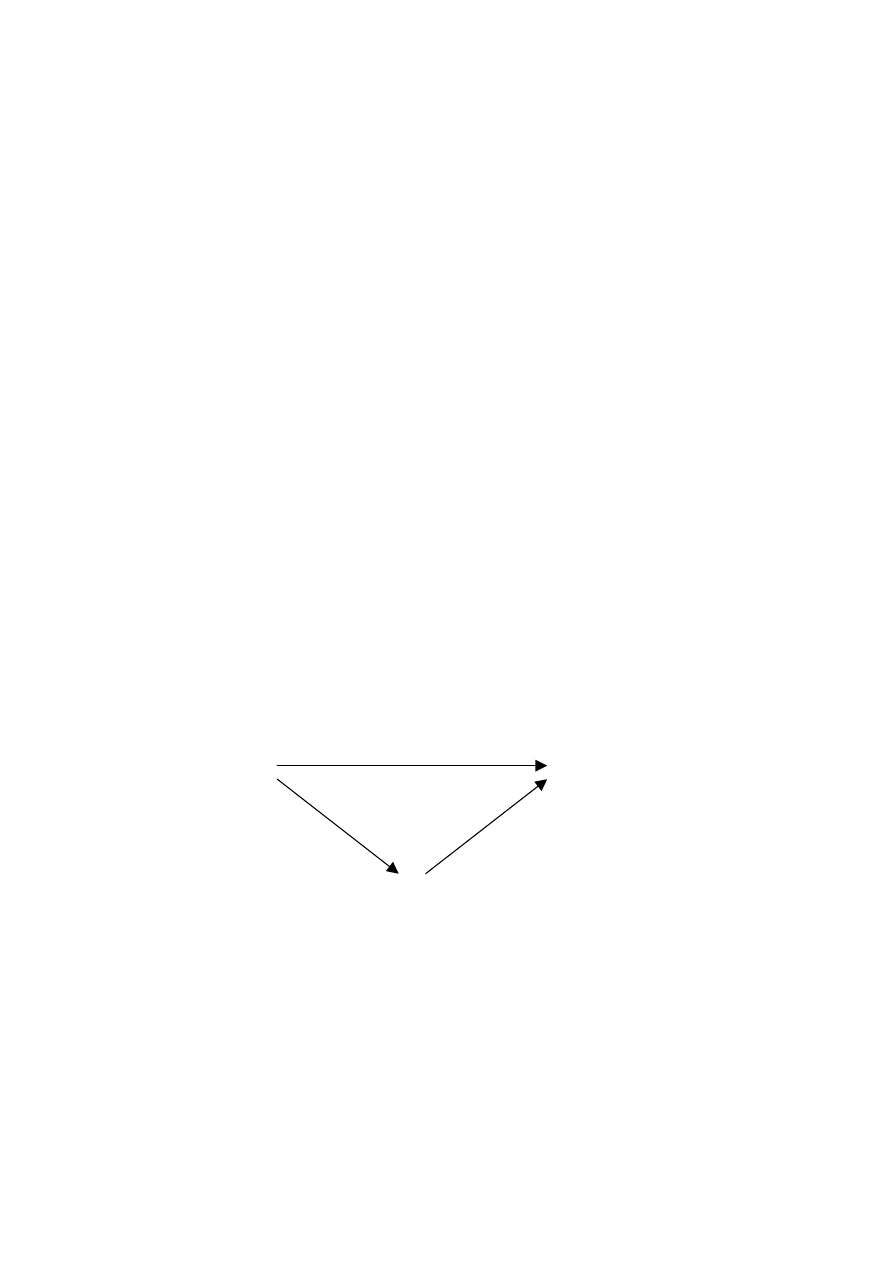
illustrated in figure 1.1.

figure 1.1

These payoff functions determine a game known as the Prisoners’ Dilemma game.

The name comes from another interpretation of the strategies. Although our

interpretation is different, we follow the usual practice of calling this game the

Prisoners’ Dilemma (PD) game. It is an example of what is called a game in normal

form or a game in strategic form. In general, a game in normal form is a set of

players, a strategy set for each player and a payoff function for each player.

Both payoff functions can also be expressed in a single game table, or bimatrix, as

follows where, as usual, the rows w and s denote the strategies of 1 and the columns w

and s denote the strategies of 2:

Prisoners’ Dilemma table

w s

4,4 0,10

10,0 1,1

The 4 cells in the table each have a pair of numbers. In each case, these numbers are

the payoffs resulting from the strategy given by the row and column of that cell. The

first number is 1’s payoff and the second number is 2’s payoff. Thus, for the strategy

list (s,w) given by the second row and the first column, 1 gets a payoff of 10 and 2

gets a payoff of 0. For 2 person games in which there are a finite number of

strategies, such tables are often used to present the information contained in the

payoff functions. However, for games with either more people or an infinite number

of strategies, such tables cannot be used, even though the definition given above is

still satisfactory.

Exercise 1.8:

Formulate a model of a duopoly. What are the strategy sets of the
two firms? What are their payoff functions? What are their utility
functions?

Exercise 1.9:

Formulate a model of a committee that uses majority voting to
determine outcomes. What are the strategy sets in your model and
what are the payoff functions?

Exercise 1.10: Construct an example giving strategy sets, mechanism, utility

functions and payoff functions for a situation in which there are 3
players with different size strategy sets. Can this game be expressed
by a table?

1.4

Dominant Strategy Equilibrium and Pareto Optimality.

In the prisoners’ dilemma game, which strategies would 1 and 2 choose? What would

the outcome be? What criteria could be used for deciding whether the outcomes

determined by the strategies they choose are good outcomes? According to these

criteria, would rational choices lead to good outcomes? It is to these issues that we

now turn.

Games in which binding agreements can be made are called cooperative games.

Games in which binding agreements are not possible are called non cooperative

games

. We will assume that binding agreements are not possible.

Exercise 1.11: If they could make binding agreements in the Prisoners’ Dilemma

game, what would they agree to do? Give your reasons. Give some
examples of situations that are cooperative games.

Given that they cannot make binding agreements in the Prisoners’ Dilemma game,

agent 1 might reason as follows.

“If 2 works, I will get 10 rather than 4 if I shirk. If 2 shirks, I will get 1 rather than
0 from shirking. Therefore, whatever 2 does, I am better off shirking.”

In a similar way, agent 2 would conclude that shirking is the best choice, whatever 1

chooses. That is, shirking is a best reply for both to whatever the other could do.

Thus, if they are rational they will both shirk. However, they would both be better off

by working. If they both worked, they would each get a payoff of 4 which is higher

than the payoff of 1 that they would each get by rationally shirking.

A change from strategy list (s,s) to (w,w) is an example of a Pareto improvement. A

strategy list from which there are no Pareto improvements is called Pareto optimal.

Exercise 1.12: In the PD game, which of the outcomes are Pareto optimal?

Exercise 1.13: Consider the list of three preferences in the following table.

x z y

y x z

z y x

Which outcomes are Pareto Optimal?

Exercise 1.14: Construct an example in which there are two agents and 5 outcomes

such that there is only one Pareto Optimal outcome.

Exercise 1.15*: Give a definition of “Pareto optimal”. (Hint: Pareto Optimality is a

property. So, what is Pareto Optimality a property of? Think about
a general format for defining properties that will always make clear
what a property is a property of!)

Exercise 1.16: A parent has one bar of chocolate to divide between two children.

Give all the Pareto Optimal ways to do this. Would the answer be
significantly different if there were more than two children?

In solving the PD game, use was made of the concept of best reply. This concept is

very important and used to define other equilibrium solutions for games in normal

form, such as Nash Equilibrium.

Exercise 1.17*: Give a definition of “best reply”. (Hint: Structure you definition as

follows. A --- is a best reply to --- if and only if ...)

In any game in normal form, a strategy that is a best reply to all the strategies of

others is called a dominant strategy. A list of strategies in which all strategies in the

list are dominant strategies is called a dominant strategy equilibrium. In the

prisoners’ dilemma game,

is a dominant strategy equilibrium.

( , )

s s

Exercise 1.18*: In the payoff table for the Prisoners’ Dilemma game, is it possible

to change the payoffs of 2 in such a way that shirking is not a
Dominant Strategy for 1?

Exercise 1.19: Consider the game given by the following table:

left right

top

a, e

c, f

bottom

b, g

d, h

Give values for e, f, g and h such that left is a dominant strategy for
all values of a, b, c and d.

Exercise 1.20: In the Prisoners’ Dilemma game, assume that neither player knows

the payoff function of the other but that they could buy this
information. How much would they be prepared to pay for this
information?

Exercise 1.21: In the Prisoners’ Dilemma game, it was assumed that binding

agreements were not possible but nothing was said about the
possibilities for communication between 1 and 2. If they could
communicate, would this make any difference?

Exercise 1.22: Draw a diagram using a horizontal axis for 1’s payoffs and the

vertical axis for 2’s payoffs. For each strategy list, show the pairs
of payoffs given by the payoff function.

Exercise 1.23: Is it possible to have a 2 person game in which all strategies are

dominant strategies? If so, give an example.

Exercise 1.24*: Consider two agents each of which have “human rights”. Each

agent can choose r, (to respect the other’s rights) or v, (to violate
the others rights). The preferences of the agents are simple.

Each

only cares whether the other respects or violates their rights.
Formulate this as a game. Find the dominant strategies. Which
strategy lists are Pareto Optimal?

Exercise 1.25: Suppose that you know the payoff function of a game, but not the

mechanism. For each strategy and for each person, can you still

This game requires that agents are indifferent between some pairs of outcomes.

determine whether or not it is a dominant strategy? If you do not
need to know the mechanism in order to solve a game, does game
theory need the concept of mechanism? If it does, what does it need
it for?

Exercise 1.26*: The following table shows a mechanism in which 1 chooses a

preference given by a row and 2 chooses a preference given by a
column. Their choices thus reveal a preference. Therefore, for
each revealed preference list, given by a row and a column, the cells
show the outcome. Of course, the preferences revealed by strategy
choices may not be true preferences.

x
y

y
x

x
y

y
x

x
y

x x x y x x

x x x x x z

y
x

x x y y x y

y x y y z y

x
y

x x x z z z

y
x

x z y y z z

Suppose that 1 has a true preference of y strictly preferred to z and z
strictly preferred to x, and suppose that 2 has a true preference of z
strictly preferred to x and x strictly preferred to y. Let the utility of
a top ranked outcome be 2, the utility of a second ranked outcome
be 1 and the utility of a bottom ranked outcome be 0.

Give the payoff table for the game using the mechanism given by the
table and for the preferences given in the previous paragraph. Is it
a dominant strategy for 1 to choose the row in which their choice is
also their true preferences? Is it a dominant strategy for 2 to
choose the column in which their choice is also their true
preference? In general, do you think it is always rational for
committee members to reveal their true preferences? Is this a cause
for concern? Why?

In our study of mechanism design, Dominant Strategy equilibria are the only methods

we will need to solve games. However, for the sake of completeness and given its

general importance, section 1 concludes with a brief introduction to solving games

using Nash Equilibrium.

1.5 Nash

Equilibrium.

Dominant Strategy equilibria, at least when they are unique, give a very convincing

way to solve a game. A player who has a dominant strategy has good reason to

choose it, and arguably no good reasons to choose any other strategy. This is fine as

far as it goes. The problem is that in many games, not all players have dominant

strategies in which case the game has no dominant strategy equilibria.

For example, consider the game given in the following table in which 1 chooses rows

and two chooses columns.

Left

Right

Top 7,5

5,4

Bottom 6,4

6,3

1 has no dominant strategy since Top is only a best reply to Left but not a best reply

to Right. However, if 1 and 2 are rational, it is fairly clear what they would do. To

begin with, 1 would see that Left is a dominant strategy for 2. Therefore, not only

would 2 choose Left but 1 would confidently expect 2 to choose Left. This makes 1’s

choice easy since Top is the best reply to Left. Therefore (Top, Left) is a convincing

solution to this game.

There is a name for the procedure we have just used. It is called elimination of

weakly dominated strategies

. First, Right was eliminated because it was weakly

dominated.

This left a game in which 1 had two choices, Top and Bottom, but 2 only

had one choice, Top. In this smaller game, 1 does have a dominant strategy since Top

dominates Bottom. Eliminating Bottom, we are left with (Top, Left) as the solution to

the game.

This is also all right as far as it goes. The problem is that not all games can be solved

in this way.

Consider the game given by the following table in which 1 must choose from Top,

Middle or Bottom and 2 must choose from Left, Centre or Right.

Left

Centre

Right

Top 10,0

0,10

3,3

Middle 2,10

10,2

6,4

Bottom

3,3 4,6 6,6

No strategies are dominated, and there are certainly no dominant strategies. The best

reply of each depends on what the other will do. A Nash Equilibrium is a strategy

list in which each strategy in the list is a best reply to all the other strategies in the

list. Note carefully exactly how this differs from the definition of a Dominant

Strategy equilibrium and that a Dominant Strategy equilibrium must be a Nash

In this example we have strict domination, since for each row, 2’s payoffs are greater in the first

column than in the second column. If one were greater than and the other were equal to, then we
would have weak dominance.

Equilibrium but the converse is not generally true. In the game given by the table,

(Bottom, Right) is the unique Nash Equilibrium.

It will be useful later to go deeper into why a Nash Equilibrium is a reasonable

solution. In the game given in the table on the previous page, best reply rows vary

from column to column. For example, Top is the best reply to Left but Middle is the

best reply to Centre.

Thus, for rational players to choose the strategies in a particular strategy list, they

must believe that other players would choose the other strategies in that list. For

(Top, Left) to be chosen, 1 must believe that 2 will choose Left and 2 must believe

that 1 would choose Top. But could they rationally have these beliefs?

Assume they both know the table.

Then, for 1 to expect 2 to choose Left, 2 must

expect 1 to choose Top. But if 2 does expect 1 to choose Top then 2’s best reply

would be Centre and with this expectation 2 would not in fact want to choose Left.

Furthermore, 1 could not therefore rationally expect 2 to expect that 1 would choose

Top! On the other hand, for Nash Equilibria, each player can expectations that

support their Nash Equilibrium strategy as a best reply.

More specifically, assume that they both know each others payoffs, they both know that each other

knows that they know this, and that they know that each other knows that they know this and so on.
This important assumption is called “Common Knowledge”.

This view of Nash Equilibrium builds on the concepts of “Rationalizability” introduced by D. G.

Pearce in “Rationalizable Strategic Behaviour and the Problem of Perfection”, Econometrica 52
(1984): 1029-1050, and D. Bernheim, “Rationalizable Strategic Behaviour”, Econometrica 52 (1984):
1007-1028. A simple treatment may be found in “Strategy: An Introduction to Game Theory” (2002),
Norton, New York, by Joel Watson.

Exercise 1.27: What do you think rational players would choose in the following

game?

shirk

work

shirk

1, 1

1, 0

work

0, 1

2, 2

Give your reasons. Why do you think games like this are called
“coordination games”?

Exercise 1.28: The following table shows a different game for each possible value

of x.

left

right

top x,

x x, 0

bottom

0, x

4, 4

For what values of x is there a unique Dominant Strategy
equilibrium? Give the Dominant Strategy equilibrium for each of
these values of x. Are there any values of x such that there are Nash
Equilibria that are not Dominant Strategy equilibria? Give all of
the Nash Equilibria in these cases and say which one has the
strategies that you think will be chosen. Give your reasons.

This is all right as far as it goes. The problem is that not all games have a Nash

Equilibrium. Consider the game given by following table in which 1 again chooses

rows and 2 again chooses columns.

Left

Right

Top

1, -1

-1, 1

Bottom

-1, 1

1, -1

Starting in the top left pair of payoffs and going around them in a clockwise way: Left

is not a best reply to Top, Top is not a best reply to Right, Right is not a best reply to

Bottom and Bottom is not a best reply to Left. In this case, neither player can develop

consistent reasons to expect the other to choose any particular strategy.

It may seem as though this is the end of the road. However, in the game in the table

on the previous page, let 1 think that 2 will choose Left with probability p and choose

Right with probability 1 – p. In the same way, let 2 think that 1 will choose Top with

probability q and Bottom with probability 1 – q. Probabilities p and 1 – p are called a

mixed strategy for 2 (even though they are 1’s expectations) and probabilities q and 1

– q are called a mixed strategy for 2 (even though they are 1’s expectations). The

rows and columns are now called pure strategies. Note that, as defined, pure

strategies are a special case of mixed strategies.

Given these mixed strategies, the expected payoff of 1 is:

[ , ]

) (1

)

)(1

)

2) 2

E p q

pq p

p q

−

− −

+ +

− −

The next step is to determine what value of p* of p would maximise the expected

payoff of 1 for all possible values of q. It is easily seen that if

then

; if

then

and if

then p* may be any value between 0 and 1

inclusive. A similar argument shows that the value q* of q that maximises 2’s

expected payoff for any particular value of p is as follows: If

1 2

then

; if

* 0

1 2

then

and q* may be any value between 0 and 1 inclusive if

* 1

1 2

* 1

1 2

* 0

1 2

Now let us see what values of p and q we might consider as solutions for this game.

Let us consider

and

. This could only be regarded as a solution if 1

expected 2 to choose Left with probability

, and 2 expected 1 to choose Top

with probability

2 3

. But if they did have these expectations they would not in

fact choose with the probabilities

expected by each other, and they could

1 3

both figure this out! Indeed, it is only by each choosing their two strategies by tossing

a fair coin, so that

p q

, that these expectations can be consistently held and

the actions justified. Thus, a Nash Equilibrium in mixed strategies is a list of

mixed strategies, one for each player, such that each maximises that player’s expected

payoff given the other mixed strategies in the list. In other words, a Nash Equilibrium

in mixed strategies is a list of mixed strategies in which each one is a best reply to the

others in the list.

1 2

= =

Guess what. All games with a finite number of players and a finite number of

strategies have at least one Nash Equilibrium. Of course, there may be more than one.

This concludes the review of the game theory background that is required for

mechanism design. It should be emphasised that the coverage is minimal. This is

particularly true with respect to Nash Equilibria, especially in mixed strategies. There

are many good textbooks in game theory, and most microeconomics textbooks now

include some game theory though the amount varies a lot from one book to another.

Exercise 1.29: Give all the Nash Equilibria in pure and mixed strategies for the

game in the following table:

left

right

top

2, 1

0, 0

work

0, 0

1, 2

Which Nash Equilibria are Pareto Optimal?

2: Direct Revelation Mechanisms

You should begin this section by reviewing exercise 1.26. In that exercise, the

possible strategy sets were revealed preferences. Such mechanisms are called Direct

Revelation Mechanisms

. Of course, they are a special case of general mechanisms

in which the strategy sets need not be preferences. This section presents an important

result, the Gibbard-Satterthwaite theorem, about Direct Revelation mechanisms.

Later, we will see that the Gibbard-Satterthwaite theorem is very useful for the

analysis of general mechanisms too. First, we must develop formal notation and

define concepts more carefully.

2.1

Notation and Definitions

{1, , },

n n

= …

> : Finite set of agents.

{ , , }

x y

… : Finite set of at least 2 outcomes.

R i N

∈ : Preference ranking of i N

∈ . This is a transitive ranking of outcomes in

which every pair of outcomes is ranked and there is no indifference

between distinct pairs. This is only for simplicity and it does not affect

any of the results. In some exercises, such as the one about the human

rights game, indifference between distinct pairs is allowed.

ℜ

: The set of all preference rankings.

( , ,

)

…

: A list of preference rankings, one for each agent.

Π = ℜ : The set of all preference lists (Cartesian product of the sets of all possible

preference rankings with each other.)

(

, *

)

R R

−

: The preference list obtained from

( , ,

)

…

by replacing

R by *

R .

That is, (

, ,

)

, *) ( , ,

R R

…

−

. (

−

is called an i-

variant of

R R

, *)

R R

Exercise 2.1:

Prove that every preference list is an i-variant of itself. If there are
two agents and three outcomes, how many i-variants are there for
any preference list, assuming only strict preferences. Construct
several examples of i-variants.

s : A strategy (action) choice for i N

∈ .

S : The set of all possible strategy choices for i N

∈ .

( , , )

…

: A strategy list, one strategy for each

i N

∈ .

= × ×

…

: The set of all possible strategy lists (Cartesian product of the sets of

all possible individual strategies with each other).

( , *

s s

−

) : The strategy list obtained from

( , , )

…

, , )

…

by replacing

s by

. That

is, ( ,

−

*) ( , ,

, *,

s s

s S

∈

m S

→

= Π

A mechanism is a function

that assigns an outcome

to all strategy

lists

. It is assumed that agents know the mechanism and their preferences. A

Direct Revelation Mechanism

is a mechanism

for which

Thus,

m S

→

( )

m s

If there is indifference between distinct pairs of alternatives, this definition is easily extended.

a Direct Revelation mechanism will be written

, and strategy choices

reveal a preference

}

{ , }

)

∈Π

m u

Π →

A preference game is any pair

consisting of a mechanism and a preference

list.

( , )

m R

Exercise 2.2*: Let

{1,2}

{ , , ,

x y w

b , and

{ , }

l r

. The

mechanism

m S

,is given in the following table:

→

left

right

top x w

work y

Give preference lists

( ,

and

( ,

)

R R

′ ′

∈Π with

utility representations for

, for

u′ for

R′ and for

u′

from which payoff functions

m u

and

such that the Prisoners’ Dilemma game is obtained

with

and

, and the human rights game of exercise 1.24 is

obtained with

′ and

′ . In what sense is the mechanism used in

the Prisoners’ Dilemma game the same, and what sense is it
different, from the mechanism used in the human rights game?

R′

′

m u

′

Strategy,

∈

is a Dominant Strategy for i N

∈ in preference game

if and

only if, for all

( , )

m R

−

or ( , )

−

( )

m s

is a Dominant

Strategy equilibrium

of the preference game (

if and only if

m R)

∈ is a

Dominant Strategy for all i N .

∈

s S

∈

( , )

( )

m s s R m s

∈

Now, consider the following example.

{ , }

a b

and there are two agents, 1 and 2,

with

and

. The mechanism m is given by the following table:

{ , }

u d

{ , }

l r

u x

d x

Let R denote the preference list in which both 1 and 2 prefer x to y. Then, the

Dominant Strategy equilibrium is

and the Dominant Strategy equilibrium

outcome is x. We may write this as e m

( , )

u l

( , ) ( , )

u l

and

( , )

m R

m e

(

)

More generally, we may write e m

( , )

∈ for a Dominant Strategy equilibrium

outcome given mechanism m and preference list R. If there are multiple Dominant

Strategy Equilibria, then

selects one of them. Clearly,

( ,

e m )

( , )

m R

m e

denotes a

Dominant Strategy equilibrium outcome for mechanism m and preferences list R.

(

)

It follows that

is a function that assigns an equilibrium strategy list to all

preference lists in

( , )

e m i

Π . It will be called a Dominant Strategy equilibrium behaviour

function

Exercise 2.3:

Let m be the mechanism of the Prisoners’ Dilemma game. Give
examples of

such that

and e m

( ,

)

e m R′′

( , )

w s

)

( ,

) ( ,

s w

′′′ =

, ,

R R R

′ ′′ ′′′∈ Π

( , ) ( , )

e m R

w w

′ =

is only required because we do not allow indifference between distinct outcomes.

( , )

( )

m s s

m s

−

It is possible to define

more generally, so that it depends on customs, social norms and a

variety of other things. Also, Dominant Strategy equilibrium could be replaced by Nash Equilibrium.

( , )

e m R

Since the Dominant Strategies of a player only depend on that player’s preferences,

we can write

for the Dominant Strategy for i in preference game (

Therefore, e m

can be written as follows:

( , )

e m R

, )

m R

( , )

(

)

( ,

)

m R

( , )

( , ), ,

e m R

…

Exercise 2.4:

Let m be the mechanism used in the Prisoners’ Dilemma game.
Give examples of preference lists

and

such that:

, e m

)

s and e m

( ,

( , )

s w

)

R′′′

. Now

give e m

, e m

( , )

R′

( , )

R′ , e m

( ,

)

R′′ , e m

( , R )

′′

( ,

)

R′′′

, e m

and

( ,

)

e m R′′′

R′ R′′

R′′′

( , ) ( , )

e m R

w w

′ =

( ,

) ( ,

′′ =

For any mechanism m, let e m

denote the subset of strategy lists that are

equilibrium behaviour choices for some preference game

( , )

. Let

denote the subset of outcomes

( , )

m e m

x X

∈ such that

(

)

( ,

m e m R)

for some

∈Π .

( , ),

m R R

∈ Π

(

)

Exercise 2.5:

For the mechanism given by the table on page 21, give e m

and

( , )

(

)

( , )

m e m

2.2 Strategy

Proofness

Let

, and

{1,2,3}

{ , , , }

w x y z

. Consider the preference list R

∈ Π given in the

following table:

x y y

y x x

w w w

z z z

Recall exercises 1.18, 1.19 and 1.20.

Let

denote the following method suggested by Borda in 1781. For all

preference lists

Π →

, let an outcome be given points equal to the number of

outcomes below it in each preference in the preference list. Then let the chosen

outcome

be the one that has the highest score. Ties are broken alphabetically.

( )

m R

∈ Π

( )

m R

)

Thus, for the preference list given in the table above, the scores are as follows: y gets

8 points, x gets 7 points, w gets 3 points and z gets 0 points. Therefore,

Now consider the preference list

(

R R

−

defined in the following table:

x y y

w x x

z w w

y z z

Thus, the preference list (

)

R R

−

is obtained from R by changing the ranking of

person 1, lowering y from second to bottom. In all other respects, the preference list

)

(

R R

−

is the same as the preference list R. The scores obtained by the outcomes

from preference list

(

)

R R

(

, R

−

are: x gets 7 points, y gets 6 points, w gets 4 points and z

gets 1 point. Therefore, m R

) x

= .

Thus, if person 1 thinks that 2 and 3 will express the preferences

R and

R as in the

tables above, then 1 can bring about the outcome x by expressing

R or the outcome y

by expressing

R . If

R is 1’s true preference, then according to this preference, it

would be rational, in the sense of maximising true preference, to express

R rather

than

R . Such strategic misrepresentation of preferences is called manipulation. In

this example, this is expressed more precisely by saying that person 1 can manipulate

at R via

Π → X

R since

xR y

Π →

or, equivalently,

)

(

)

(

m R R R m R

−

∈ N

∈ℜ

(

−

m R R

Π →

∈

∈ N

∈ℜ

More generally:

can Manipulate m

X at

∈ Π via *

if and only if

)

( )

R m R

Note that this definition specifies four things: who can manipulate (person i); what

can or cannot be manipulated (the mechanism,

); where it can be

manipulated (at the preference list

in its domain); and finally, how it can be

manipulated (by expressing preference

R ). Roughly speaking, for i

to be able

to Manipulate, he or she must be able to do two things. First, at some preference list,

must be able to change the outcome. Second, the change must be in i’s favour.

∈ Π

A Direct Revelation mechanism m

Π →

is Strategy Proof if and only if there is

that can Manipulate m

→

at any

via any

∈

Thus, for a strategy proof mechanism :

Π →

, no one has a reason to

misrepresent their preferences. Nothing can be gained by revealing a false preference.

Exercise 2.6:

Construct an example showing that the Borda Score is not Strategy
Proof when there are three outcomes and three individuals. Show
that if there are only two outcomes then, for any finite number of
individuals, the Borda Score is Strategy Proof.

Truthful revelation of preferences is very important in economics, particularly in

connection with public good problems. Later, it will become clear that its

significance is both deeper and wider

than this. Before that, the question arises

as to whether there are any mechanisms m

that are Strategy Proof. After all,

our example shows that for three outcomes and three individuals, the Borda score is

not Strategy Proof.

Π →

2.3

The Gibbard-Satterthwaite theorem

There are some Strategy Proof mechanisms m :

Π →

as the following exercises

show.

Exercise 2.7*: Let

{ , }

x y

, and let there be any finite number of individuals

who can have any strict preference ranking of outcomes. Consider
the Direct Revelation mechanism that gives outcome for which there
is a majority, with ties broken alphabetically. Show that this
mechanism is Strategy Proof?

Exercise 2.8*: Let

{ , , }

x y z

, let there be any finite number of at least 2

individuals, and for all

, m

is the highest ranked outcome

according to

R d N

∈ (ties broken alphabetically). Show that this

Direct Revelation mechanism is Strategy Proof?

∈Π

( )

Exercise 2.9*: Let

{ , , }

x y z

, let there be any finite number of at least 2

individuals. Let

be a constant function so that there is

an outcome x

∈ such that

for all

. Show that

this Direct Revelation mechanism is Strategy Proof?

Π →

( )

m R

∈Π

From exercise 2.7, it follows that strategic misrepresentation of preferences is not

really a problem for situations in which there are only two outcomes. For situations in

which there are a larger number of outcomes, exercises 2.8 and 2.9 offer somewhat

unattractive possibilities for attaining Strategy Proofness. In our search for Strategy

Proof Direct Revelation mechanisms we will therefore limit our attention to others.

This is done as follows.

Given a mechanism,

, an individual

Π →

∈

is called a Dictator for that

Direct Revelation mechanism if and only if, for all preference lists

and all

∈Π

pairs of outcomes x and y, if d strictly prefers x to y then y is not chosen. If there is no

Dictator for m

then it is said to be Non Dictatorial. This property rules out

the Direct Revelation mechanisms in exercise 2.8.

( ) 3

Π ≥

Π →

Confining attention to Direct Revelation mechanism for which at least 3 outcomes are

achievable (

)

, rules out those in exercise 2.9, since such functions cannot

be constant.

Exercise 2.10: Assume there that

∈

is a Dictator for the Direct Revelation

mechanism m :

Π →

where there are 27 outcomes in X. What is

the value of

(

)

? Let

Π →

be a constant function.

What is the value of

(

)

Note that if a Direct Revelation mechanism :

Π →

has the Weak Pareto property

then it is not constant. The Weak Pareto property requires that for all preference lists

and all pairs of outcomes x and y, if everyone Strictly Prefers x to y then y is not

chosen.

Exercise 2.11*: Show that, for any Direct Revelation mechanism m

X that

has the Weak Pareto property,

Π →

( )

Π =

Exercise 2.12: Do all, some or no Dictatorial mechanisms have the Weak Pareto

property?

Thus, we are led to ask whether there are non dictatorial Strategy Proof Direct

Revelation mechanisms that can achieve more than two outcomes? The answer is

“no”, as shown by the famous Gibbard-Satterthwaite theorem:

Theorem:

(Gibbard-Satterthwaite): Let the Direct Revelation mechanism

Π →

be such that

( )

Π >

. Then it is either Dictatorial or

not Strategy Proof.

For any set Y, |Y| denotes the number of elements in it.

For proofs, see Gibbard (1973) or Kelly (1987).

Exercise 2.14: Use a table to prove the Gibbard-Satterthwaite theorem for the case

of 2 agents and 3 outcomes.

Exercise 2.14: Consider the set of all Direct Revelation mechanisms

such that

Π →

( )

Π >

. Draw a Venn diagram to illustrate the

Gibbard-Satterthwaite theorem.

Exercise 2.15*: Show that if X has more than two outcomes, then the only Weakly

Paretian Strategy Proof mechanisms are Dictatorial.

Exercise 2.16: For the Direct Revelation mechanism given in the table below, each

row corresponds to a strict preference ranking for person 1 and
each column corresponds to a strict preference ranking for person
2. Thus, any row and column determines a strategy list of chosen,
or revealed, preferences. Is the mechanism constant? Is it
Dictatorial? Is it Strategy Proof? If it is not Strategy Proof, give
full details of all cases of manipulability. (That is, give all cases of
who, where and how.)

x
y

y
x

x
y

y
x

x
y

x x x x z z

y
x

y y y y z z

x
y

z z z z z z

y
x

z z z z z z

Exercise 2.17: Given three outcomes and two individuals, make your own tables

like the one in exercise 2.16 that give a Non Dictatorial Direct
Revelation mechanism without the Weak Pareto property. Then do
a table for one that has the Weak Pareto property but not the
Strategy Proofness property. Now make a table for one that does not
have the Non Dictatorship property. Does it have the Weak Pareto
property?

Exercise 2.18: Let there be 2 individuals and three alternatives and consider a

Direct Revelation mechanism in which all strict preference rankings
are possible strategies. Using a table, give a mechanism for which
both of the following are true: (i) Any outcome ranked top by both
preferences is the outcome chosen for that list, and (ii) the Weak
Pareto property is violated.

Exercise 2.19*: Using the Direct Revelation mechanism given in the table in

exercise 2.16, for each true preference that 1 could have, is
truthfully revealing that preference a best reply to all preferences
that 2 could reveal? For each true preference that 2 could have, is
truthfully revealing that preference a best reply to all preferences
that 1 could reveal?

Exercise 2.20: Assume that there are only 2 individuals and 2 outcomes, use a

table to give a Direct Revelation mechanism such that, for all true
preferences that either person could have, expressing true
preference is a best reply to all preferences that the other might
choose.

2.4

A Game Theoretic version of the Gibbard-Satterthwaite theorem

The Gibbard-Satterthwaite theorem as presented above, is a theorem about the

properties of Direct Revelation mechanisms. Preference games played no explicit

role. However, the exercises 1.26 and 2.16 strongly suggest that the Gibbard-

Satterthwaite theorem may be closely related to game theory. In fact, the theorem can

be equivalently presented using (preference) games.

Consider a preference game in which individuals have (true) preferences

and in which the mechanism is a Direct Revelation

mechanism,

. Recall that is a Dominant Strategy for i

if and

only if it is a best reply to all the preferences that others could choose from their

∈

( , , , ,

)

∈Π

…

Π →

strategy sets. This implies that, for all

, either

(

, )

( )

m R R

m R

−

. For such a preference game, a strategy list of chosen preferences

is a Dominant Strategy Equilibrium if and only if every chosen preference in the

list is a dominant strategy.

( , )

m R

∈Π

(

, )

( )

m R R R m R

−

For a Direct Revelation mechanism m, and a preference game

, if R is a

Dominant Strategy equilibrium then rational choice may be said to reveal preferences

truthfully. While desirable, the possibilities for this are very limited, as the following

important result shows.

Theorem:

(Gibbard-Satterthwaite game theoretic theorem): Let

be a

non Dictatorial Direct Revelation mechanism and let e m be a
Dominant Strategy equilibrium behaviour function. If

, then

≠ for some

Π →

( , )

(

)

( , )

m e m

Π >

( , )

e m R

∈Π

Exercise 2.21: Deduce this theorem from the earlier statement of the Gibbard-

Satterthwaite theorem.

Thus, given Dominant Strategy equilibria, either there is a Dictator or only 2

outcomes are achievable. Of course, this only tells us about Direct Revelation

mechanisms, and these are very special cases of the general mechanisms that are

much more common in practice.

Exercise 2.22: In the Gibbard-Satterthwaite theorem, individuals may have any

possible preference ranking of the outcomes since the domain of the
mechanism is

Π . Can you find an “escape” from the Gibbard-

Satterthwaite impossibility result by restricting the domain of the
mechanism to some proper subset of

Π .

Exercise 2.23: Consider a situation in which there are two agents, 1 and 2, and

three outcomes, x, y and z. For all preference lists, if 1 and 2 have
the same top ranked outcome, then assign this to that list. If they
have different top ranked outcomes then assign the top ranked
outcome that is alphabetically prior. Is this Direct Revelation
mechanism Strategy Proof? If it is not Strategy Proof, show how it
can be manipulated.

3 General

Mechanisms

Direct Revelation mechanisms are very special cases of general mechanisms.

However, from any general mechanism, a Direct Revelation mechanism can be

derived in a specific way. The derived Direct Revelation mechanism is, in a precise

sense, equivalent to the general mechanism from which it was derived. Because of

this, properties of general mechanisms can be obtained by analysing the much simpler

derived Direct Revelation mechanism. Furthermore, given dominant strategy

behaviour, it can be shown that in all preference games using the derived Direct

Revelation mechanism, a strategy choice revealing true preference is a dominant

strategy. This has the major advantage that we do not need to worry about strategic

misrepresentation of preferences in these cases.

All this is shown in a useful and elegant result called the Revelation Principle. The

ideas will be developed gradually with the help of an example.

3.1 MIFA

Example

MIFA, the Ministry for Interfering in Family Affairs, is responsible for divorce law.

That is, it must design a mechanism in which the actions of partners determine

whether they get a divorce or stay married. The MIFA example may also be easily

adapted for terminating other relationships such as business partnerships and

agreements between cities, regions or governments.

Consider individuals, 1 and 2, who can either stay married for which we write

σ ,

(think of this as the status quo), or they can divorce,

δ , which terminates the

relationship. Thus, the set of outcomes is

. There are only two preferences

{ , }

σ δ

that 1 and 2 can have. For the preference ranking

σ is strictly preferred to δ

and for the preference ranking

δ is strictly preferred to σ . Thus, there are four

lists in : (

and (

R R

~ c

)

R R

(

)

R R

(

)

R R

)

Remembering that in the status quo they are married, if they want to divorce they can

go to court and c will denote this strategy. Of course, if they want to stay married,

they would not go to court and

will denote this strategy. Thus, the sets of

possible strategies for 1 and 2 are

and

. It is assumed that

only dominant strategies are chosen.

( , )

m R

{ ,~ }

Recall the following. For any general mechanism

and preference list

, there is a preference game

. For each such preference game, e m

a Dominant Strategy Equilibrium and

is a Dominant Strategy equilibrium

outcome of that preference game. Now, consider ˆ

( ,

m m e m

( , )

e m i

( , )

m m e m

, the composition of

and

. See figure 3.1.

Π →

e m

m S

→

∈Π

( , )

(

)

( , )

m e m R

)

Exercise 3.1:

What is the domain, codomain and range of

( , )

figure 3.1

For any general mechanism m, the Direct Revelation mechanism will be

called the derived Direct Revelation mechanism. It is derived from the

General Mechanism m and the Dominant Strategy equilibrium behaviour

function e m

. Many preference games ( ,

can be obtained using ,

one for every

∈ Π

( , )

•

)

m R

∈ Π

Exercise 3.2:

Give a mechanism m for the MIFA problem such that, for some

, e

is not Pareto Optimal.

∈ Π

( , )

m R

Exercise 3.3:

Give a mechanism m for the MIFA problem such that, for all

m e

is the top ranked outcome for agent 1.

(

)

R R

( ,

(

)

( , )

m R

(

)

Exercise 3.4:

Give a mechanism m for the MIFA problem such that

= 1. For this mechanism, give a preference list

such that

is not Pareto Optimal.

( , )

m e m

∈ Π

( , )

e m R

Exercise 3.5:

Give a mechanism m for the MIFA problem such that for

, e m

)

Exercise 3.6*: (i) Consider the “Vatican mechanism”

, defined by the

following table.

Π →

~ c

(ii) For which preference lists is

m e

Pareto Optimal?

(

)

( , )

m R

( , )

e m

(iii)

Give

m m

, and show that

m e

for all

~ c

(

)

( , )

( )

m R

∈Π

( , )

e m R

(iv) Show that

= for all

∈Π

Π →

Exercise 3.7*: For the MIFA example, consider the mechanism

given

by the following table.

~ c

In the next table, the first column gives all the preference lists. In the
second column, fill in the Dominant Strategy equilibria. In the third
column, fill in the Dominant Strategy equilibrium outcomes. Are all
the entries in the third column Pareto Optimal for the preference lists
in the same row?

( , )

e m i

(

)

( , )

m e m i

(

)

R R

(

)

R R

(

)

R R

(

)

R R

Fill in columns 2 and 3 of the following table.

( , )

e m i

(

)

( , )

m e m i

(

)

R R

(

)

R R

(

)

R R

(

)

R R

Compare the third columns in the previous two tables and discuss
the relationship between the two.. Compare the first two columns of
the previous table and discuss the relationship between the two.

Exercise 3.8:

For the MIFA problem, consider the Direct Revelation mechanism

given by the following table.

m m′

= =

Give two general mechanisms m and

m′

such that

and

m m′

≠

m S

→

( , )

e m i

3.2

The Revelation Principle

Some of the exercises in the previous section show how a General Mechanism and the

Derived Direct Revelation mechanism are related in the MIFA example. We saw that

telling the truth is a Dominant Strategy equilibrium for all preference games using the

Derived Direct Revelation mechanism. The following result shows that this is not just

a peculiar feature of the MIFA example.

Theorem:

(Revelation

Principle): For all mechanisms

, Dominant

Strategy equilibrium behaviour functions

and all preference

lists

∈ Π

( ,

e m

)

The relationship between general mechanisms and Derived Direct Revelation

mechanisms is illustrated in figure 3.2.

The arrow going northeast from

illustrates that truth-telling is a

Dominant Strategy equilibrium as given by the Revelation Principle. It is shown as

the identity function since any true preference at the beginning of the arrow is also

revealed by the Dominant Strategy equilibrium choice at the end of the arrow. Also,

ˆS = Π

( , )

e m i

That is,

is the identity function on

going from left to right, the composition of the two top arrows is the same function as

the composition of the two bottom arrows. In this precise sense, which may be called

Outcome Determination Equivalence

, a general mechanism and its Derived Direct

Revelation mechanism are equivalent.

( , )

e m i

( , )

e m

ˆS = Π

figure 3.2

Exercise 3.9*: Prove the Revelation Principle. (Don’t be afraid. It is very easy.

You will need to use the definition of Dominant Strategy
equilibrium. See Gibbard (1973) and Kreps (1990, pages 712-713).

Exercise 3.10: Let m and R be the mechanism and preference list that is used in the

Prisoners’ Dilemma. Give

and

ˆ ( )

m R

e m

( , R)

(

)

( , )

m R

( , )

e m R

≠

m e

Exercise 3.11: Consider a situation in which there are two agents, 1 and 2, and

three outcomes, x, y and z. Each agent must suggest an outcome,
and the outcome determined by the mechanism m is the most
popular suggestion with ties broken alphabetically. Is it always a
Dominant Strategy for agents to suggest their most preferred
outcome? Give the derived Direct Revelation mechanism for this
general mechanism. Give a preference list R such that

Exercise 3.12

Consider the mechanism and preferences for the human rights game
of exercise 1.24. There are four Dominant Strategy Equilibria.
Does it matter which one is used in the Revelation Principle?

The Revelation Principle still holds even if preference lists include preferences in which there is

indifference between distinct outcomes.

3.3 General

Outcome

Determination

At this point, we know something about Direct Revelation mechanisms (Gibbard-

Satterthwaite theorem), we know how to get a Direct Revelation mechanism from a

general mechanism (composition), we know something about the Derived Direct

Revelation mechanism and how it is related to the general mechanism from which it

was derived (Revelation Principle). But we know little about general mechanisms.

For this, we need GOD.

Group Outcome Determination

(GOD) is a pair

(

)

, ( , )

m e m i

( ,

e m

consisting of a

mechanism and a Dominant Strategy equilibrium behaviour function. The

terminology GOD is appropriate since, given any mechanism and any equilibrium

behaviour function, an outcome is determined. However, both items in GOD,

and

, are required for outcome determination. Either one by itself is not sufficient.

)

d N

∈

x y X

∈

xR y

(

)

( , )

m e m R

≠

(

)

, ( , )

m e m i

( , )

e m

GOD is Dictatorial if and only if there is an individual

such that, for all

and all

implies

∈Π

Exercise 3.13: Prove the following. If GOD

is Dictatorial then the

Direct Revelation mechanism m m

is Dictatorial.

We now have all we need. It is time to put it all together to establish something

important about general mechanisms.

Theorem

(Dictatorial GOD). Let

be a mechanism and

be a

Dominant Strategy equilibrium behaviour function such that

. Then the GOD

is Dictatorial.

( , )

e m i

m S

→

(

)

( , )

m e m

Π >

(

)

, ( , )

m e m i

Exercise 3.14: Prove the previous theorem. (Hint: Use the Revelation Principle

and then use the Gibbard-Satterthwaite theorem on the Derived
Direct Revelation mechanism. Finally, show that if the Derived
Direct Revelation mechanism is Dictatorial then so is GOD using

the general mechanism.)

Exercise 3.15: Let

, let

and let m be the mechanism used

in the Prisoners’ Dilemma. Is GOD

(

)

, ( , )

m e m i

(

)

Dictatorial? Is

? Explain why this is not a counter example to the

equation above.

{1,2}

{ , , , }

a b c d

( , )

m e m

Π >

Exercise 3.16: Discuss the significance of the previous theorem.

Appendix:

Summary

Notation

{1, , },

= …

{ , , }

x y

…

> : Finite set of agents.

: Finite set of at least 2 outcomes.

R i N

∈

: Preference ranking of i

∈ ; (a ranking of outcomes such that every pair

of outcomes is transitively ranked with no indifference).

ℜ

( , ,

)

: The set of all preference rankings.

…

Π = ℜ

(

, *)

: A list of preference rankings, one for each agent.

: The set of all preference lists (Cartesian product of the sets of all possible

preference rankings with each other.)

R R

−

( , ,

)

: The preference list obtained from

by replacing R by

That is, (

…

, *) ( , ,

, *,

, ,

)

R R

−

…

s : A strategy (action) choice for i N

∈ .

S : The set of all possible strategy choices for i N

∈ .

( , , )

…

i N

: A strategy list, one strategy for each

∈ .

= × ×

…

: The set of all possible strategy lists (Cartesian product of the sets of

all possible individual strategies with each other).

( , *)

s s

−

( , , )

: The strategy list obtained from

by replacing s by

. That

is, ( ,

…

*) ( , ,

, *,

, , )

s s

−

…

Definitions

1. A mechanism is a function

that assigns an outcome

to all

preference lists

m S

→

( )

m s

s S

∈

→

2. A mechanism

m S

is a Direct Revelation mechanism if and only if

= Π

3. A preference game is a pair (

consisting of a mechanism

and

a preference list

, )

m R

m S

→

∈ Π

4. Strategy, s

∈ is a Dominant Strategy for i

in preference game (

if and only if, for all

or m s

∈

, )

m R

s S

∈

( , )

( )

m s s R m s

−

( , )

( )

m s

−

is a Dominant Strategy equilibrium of the preference game

and only if

is a Dominant Strategy for all i N .

m R

∈

(

)

6. For all mechanisms

, a Dominant Strategy equilibrium Behaviour

function is a function e m

that assigns a Dominant Strategy

equilibrium,

, to all preference lists

m S

→

( , ) :

Π →

( , )

e m R

∈

∈ Π

( , )

m R

( , )

)

7. For all preference games

with Dominant Strategy equilibrium e m

is a Dominant Strategy equilibrium outcome.

(

( ,

m e m

8. For any mechanism m, e m

is the subset of strategy lists that are

( , )

equilibrium behaviour choices for some preference game

( ,

m R R

m e

∈ Π

(

)

( , )

x X

∈

( ,

is the subset of outcomes

such that

for

some

is the number of outcomes in

(

)

m e

∈Π

(

)

( , )

m e m

(

)

( , )

m e m

∈

10. i

can Manipulate

via

if and only if

Π →

( )

m R

∈ Π

∈ℜ

(

, *)

m R R R

−

11. A Direct Revelation mechanism m

is Strategy Proof if and only if

there is no i

that can Manipulate m

at any

via any

Π →

∈

Π →

∈ Π

∈ℜ

12. A Direct Revelation mechanism m

is not Dictatorial if and only if,

there is no i

such that, for all

and all

implies

Π →

∈ Π

x y X

∈

xP y

( )

m R

≠

13. A Direct Revelation mechanism m

has the Weak Pareto property if

and only if, for all

and all

for all i

∈ implies

Π →

∈ Π

x y X

∈

xP y

( )

m R

≠

( , )

14. For a mechanism

and a Dominant Strategy equilibrium behaviour

function e m , the Derived Direct Revelation mechanism

the composition of

m S

and e m . Therefore,

for all

m S

→

( , )

m m e m

→

( , )

(

)

ˆ ( )

( , )

m R

m e m R

∈ Π

15. Group Outcome Determination (GOD) is a pair

(

)

, ( , )

m e m i

consisting of a

mechanism and a Dominant Strategy equilibrium behaviour function.

( , )

e m i

16. GOD

is Dictatorial if and only if there is a

such that, for all

and all

implies

(

, (

m e

∈ Π

(

)

( , )

m R

m e

)

, )

m i

∈

( ,

m R

)

m R

( )

Π >

m S

→

)

x y X

∈

xP y

≠

Results

Preliminary remark: The Dominant Strategy of i

in preference game

may

be written e m

and

∈

)

( , ),

(

, ), ( ,

m R e m

Π →

( )

Π >

( , )

(

), , ( ,

e m R

…

Theorem

(Gibbard-Satterthwaite): For all Direct Revelation mechanisms

such that

is Strategy Proof if

and only if it is Dictatorial.

→

Proof

Gibbard (1973) or Kelly (1987).

Corollary If

X has at least three outcomes, then a Weakly Paretian Direct

Revelation mechanism

is Strategy Proof if and only if it

is Dictatorial.

Π →

Proof:

This follows from the Gibbard-Satterthwaite theorem and the fact

that the Weak Pareto property implies that

if there are at

least 3 outcomes.

Theorem (Revelation

Principle): For all mechanisms

, Dominant

Strategy equilibrium behaviour functions

and all preference

lists

= . (That is,

is the identity function

Π .)

(

e m,i

∈ Π

( , )

e m R

Proof: (See Kreps (1990) and Gibbard (1973).

Theorem

(Dictatorial GOD). If

is a mechanism and

is a

Dominant Strategy equilibrium behaviour function such that

, then GOD

is Dictatorial.

m S

→

( , )

e m i

(

)

( ,

m e m

)

(

)

, ( , )

m e m i

References

Baigent, N., (2003a): “Mechanism Design: A quick tour”, Institute of Public
Economics, Graz University.

Gibbard, A., (1973): “Manipulation of Voting Schemes: A General Result”,
Econometrica, 41, 587-602.

Hülsmann, J.: W. Gamerith, U. Leopold-Wildburger and W. Steindl, (1998):
“Einführung in die Wirtschaftsmathematik, Springer, chapter 1.

Kelly, Jerry S., (1987): Social Choice Theory: An Introduction; Berlin; Springer
Verlag.

Kreps, D.M., (1990): “A Course in Microeconomic Theory”, Harvester Wheatsheaf,
New York; pages 712-713.

Stewart, I. and D. Tall (1977): “The Foundations of Mathematics”, Oxford University
Press, chapters 3, 5 and 6 (pages 113-116).

Document Outline

b
a
- - 3General Mechanisms
Notation
Definitions
Results

Wyszukiwarka

Podobne podstrony:
Zizek, Slavoj Looking Awry An Introduction to Jacques Lacan through Popular Culture
An Introduction to the Kabalah
An Introduction to USA 6 ?ucation
An Introduction to Database Systems, 8th Edition, C J Date
An Introduction to Extreme Programming
Adler M An Introduction to Complex Analysis for Engineers
An Introduction to American Lit Nieznany (2)
(ebook pdf) Mathematics An Introduction To Cryptography ZHS4DOP7XBQZEANJ6WTOWXZIZT5FZDV5FY6XN5Q
An Introduction to USA 1 The Land and People
An Introduction to USA 4 The?onomy and Welfare
An Introduction to USA 7 American Culture and Arts
An Introduction To Olap In Sql Server 2005
An Introduction to Yang Mills Theory
An Introduction to Linux Systems?ministration
An introduction to the Analytical Writing Section of the GRE
An Introduction to USA 5 Science and Technology
Geiss An Introduction to Probability Theory
Poisonous and Edible Mushrooms An Introduction to Mushrooms in Norway (2012)
An Introduction to USA 3 Public Life and Institutions

więcej podobnych podstron

Baigent Nick An Introduction to Strategy Proof Mechanism Design

Document Outline