International Conference
20th EURO Mini Conference
“Continuous Optimization and Knowledge-Based Technologies”
(EurOPT-2008)
May 20–23, 2008, Neringa, LITHUANIA
ISBN 978-9955-28-283-9
L. Sakalauskas, G.W. Weber and
E. K. Zavadskas (Eds.): EUROPT-2008
Selected papers. Vilnius, 2008, pp. 137–142
© Institute of Mathematics and Informatics, 2008
© Vilnius Gediminas Technical University, 2008
137
PORTFOLIO DESIGN AND OPTIMIZATION USING NEURAL NETWORK BASED
MULTIAGENT SYSTEM OF INVESTING AGENTS
Darius Plikynas
Vilnius Management School,
J. Basanavičiaus g. 29a, 03109 Vilnius, Lithuania
E-mail: darius.plikynas@vva.lt
Abstract: Efficiency of the simulation methods in the social domain remains jeopardized by the multi
scale complexity and vague representation of it in the mostly symbolic models applied. There is a clear
need for connectionist approach in designing robust real-life applications. This paper reports about a new
approach meant for designing intelligent investing agents capable to simulate well known investing
strategies by making timely market decisions and optimizing their multi asset portfolios in terms of profit-
risk estimates in the real life investment markets. For this reason proposed multi-layered framework con-
structs (i) an intelligent agent composed by a few trained neural networks each specialized to make in-
vestment decisions according to the assigned investment strategy in the different markets, (ii) multi-agent
system of such agents, which are trained to follow different investing strategies in order to optimize their
portfolios. Simulation gives an opportunity to simulate multi-agent competitive system for the search of
the best profit-risk performing agents, i.e. investing strategies. This gives an edge over costly and time
consuming actual experimenting in the diversified investment markets having real-life index funds (or
stocks) and non-risky financial assets. In our model, agents follow different investing strategies according
to the defined portfolio, saving and risk aversion preferences using forecasts based on the technical analy-
sis. Simulations show that proposed NN-based multi-agent system produces similar results in terms of
e.g. wealth distribution comparing with empirical evidences from the real investment markets behaviour
as described by Pareto wealth and Levy returns distributions. The proposed approach is flexible and com-
plex enough to be extended using field-based framework and evolutionary computation, which will lead
to the dynamic system of adaptive and collaborating agents capable to change their behaviour “on the fly”
depending on the profit-risk performance and market situation. The author argues that in the near future
such evolving multi-agent platforms designed to learn from experience added with fundamental analysis
facilities will produce superior agents capable to substitute humans in terms of profit-risk optimization in
the investing markets
Keywords: Investment Strategies, Neural Networks, Agent-Based Computational Finance, Artificial
Stock Markets, Behavioural Finance.
1. Introduction
Following a rationality assumption, our agent is a subjective (expected) utility maximizer. We hold
this assumption true when designing our model. The level of savings, the portfolio and risk aversion that
agents choose may be affected by these individual factors. One way to think of this is to think of agents
who have the same objective but different expectations, and, therefore, hold different portfolios. This will
cause wealth to flow between the agents over time (Jones, 2002).
In the economy where agents have heterogeneous beliefs or heterogeneous learning rules, structure
on long-run prices arises from the forces of market selection. It has long been assumed that those with
better beliefs will make better decisions, driving out those with worse beliefs, and thus determining long
run assets prices and their own welfare (Sapienza, 2003; Hoffmann, 2007).
So, why instead of constructing agents, who are strictly bounded to some explicit investing algo-
rithms, not to simulate more or less successful investing strategies, which are currently employed in the
market. In fact, well known investors’ behaviour (e.g. Peter Lynch, Warren Buffett, George Soros etc) is
obviously too complicated for algorithmic description, but could be learned by AI techniques, e. g. neural
networks (NN) can simulate those complex winning strategies etc. Having enough historical data, the
proposed research is capable to learn complex nonlinear behaviour and simulate it in the real investment
markets.
D. Plikynas
138
In essence, we don’t make here risky inferences about how real market behaves and who our agents
are in logical terms (symbolic approach). Instead, proposed agents learn from experience and behave ac-
cording to the simulated strategies in order to find the best behaviour scenario. Such knowledge compila-
tion helps an agent cope with complexity by matching efficient solutions to common problems (meta-
reasoning, see (Wilson, 2001; Miller, 2007)).
The employed connectionist approach is working rather like reactive system, implementing direct
mappings from perception to action that avoid expensive intermediate steps of representation and reason-
ing. In the proposed hybrid behavior-based model, direct mappings of this kind can be learned from ex-
perience. This somewhat is following (Minsky, 1986) idea that intelligent systems should be constructed
from large numbers of separate agents, each with percepts, actions, and goals of its own.
However, for the effective implementation of the model we have to discuss about empirical evi-
dences which could be used as quantitative validity test of the proposed approach. Sure there are em-
ployed some intermediate checks, e.g. neural networks forecasting and recognition performance using
standard estimates like mean square error, determination coefficient etc or some validity checks for the
separate agent performance, but, obviously, the ultimate final criteria have to deal with the end result, i.e.
how well simulated multi-agent system performs comparing with the real market behaviour.
In fact, there are multitudes of possible criteria, but there is chosen the distribution of investing
agents’ portfolios as the final check. The plausibility of this approach is its empirical simplicity as, know-
ing how portfolio distributions of the real investors are looking like; we can compare them with our
agents’ portfolios and make some inferences about model’s overall validity. In fact, following statistical
physics, it is becoming clear that almost any system comprised of the large number of interacting units
has the potential of displaying power-law behaviour. Since economic systems are comprised of a large
number of interacting units, it is perhaps not unreasonable to examine economic phenomena within the
conceptual framework of scaling and universality (Mantegna, 2000; Hoffmann, 2007).
Recent extensive analysis of short-term returns has shown that price differences, log-returns, and
rates of return are described extremely well by a truncated Levy distribution (Blume, 2006). In this re-
spect, proposed research is also significant, since it provides a simulation framework within which em-
pirical laws like power-law and Levy distribution can be observed and studied within the parameters
space of the simulated model (McCauley, 2004; Sapienza, 2003; Moss, 2005).
2. General Research Framework
During the phase of model construction, two main conflicting goals were arising: short term task to
make a system just fine to tackle the problem in the chosen investment domain and the second - long term
goal to build a new simulation platform altogether for much wider class of applications. Current research
report is in the middle of both. The author admits the delicate problem to represent well both issues at
once in such a short paper.
Briefly, the strategic goal (which is well beyond the scope of the presented paper) is construction of
the novel field-based framework for simulation of adaptive complex social systems acting as information
networks composed from nodes of intelligent (information transforming) agents. In fact, uncoupled and
indirect interactions among agents require the capability of affecting the context and of perceiving it. The
context will be modelled as virtual data fields, where each spatial (or logical) node stores the pervasive
field values, which are defined by the field dispersion equations in the grid space (Marco, 2006).
The prospective approach promotes mediated interactions by exploiting some sort of distributed in-
formation that can be used as a means to enforce indirect and uncoupled interactions among agents and
that can also be expressive enough to represent contextual information in a form locally accessible and
immediately usable by agents.
One of the closest examples in this area is amorphous computing (Nagpal, 2004). Another interesting
proposal in that direction is the Multilayered Multi Agent Situated System (MMASS), defining a formal
and computational framework relying on a layered environmental abstraction (De Paoli, 2003). MMASS
were related to the simulation of artificial societies and social phenomena, for which the physical layers
of the environment were also virtual spatial abstractions. In the last decade, a number of other field-based
approaches were introduced like Gradient Routing (GRAd), Directed Diffusion, “Co-Fields” at TOTA
Programming Model, CONRO etc (Mamei, 2006).
The current paper describes only the first phase, i.e. construction of the intelligent agents and design
of the simulation framework. So, as a number of theoretical and empirical studies have suggested, the
ORTFOLIO DESIGN AND OPTIMIZATION USING NEURAL NETWORK BASED MULTIAGENT SYSTEM OF INVESTING AGENTS
139
proposed investment simulation approach has micro (for each investing agent) and macro (for the whole
system of agents) goals. The micro goals are to maximize agents’ disposable capital and survive in the
long run (the current research phase). Meanwhile, the macro goals (the prospective research phases) are
to create self-organized social system.
The prospective approach is going to employ these five main components: 1) resources (information
and natural resources), 2) wavelike transformation (WT), 3) neural networks (NN), 4) evolutionary com-
puting (EC), 5) production rules (PR). For the current research stage, though, we have only designed and
optimized the neural network component and simulation environment.
Neural network component is about a set of initially trained NNs, which are arranged to deal with
different markets and make their appropriate decisions. In fact, an agent is a modular entity composed
from this set of NNs (each NN is dealing with the different market data). NN are initially trained to fore-
cast and recognize in order to simulate some investing strategies (investing timing, behavioral rules,
risk/pofit preferences etc), see
http://vlab.vva.lt/
.
3. Application Domain
According to the above discussion, this section discusses research issues related with the investment
market, which is represented using the real time series from S&P500, Dow Jones Composite and US
Treasury Bonds indices (value, open/close values, trade volumes, volatility etc). Each agent, according to
his investment strategy (see next section) is optimized for the best possible forecasting of index fund
movements in order to place profitable and risk adjusted decisions. System of agents is targeted to find
optimal risk-profit on the efficient frontier according to Markowitz theory (Markowitz, 1991).
Since this research aims to make an application in the investment domain, we have to mention
briefly about underlying assumptions concerning capital market. In short, we construct the portfolio based
on the CAPM (capital asset pricing model) policy statements. Because of the complexity of the real
world, following CAPM, additional assumptions are made to make agents more alike:
In the proposed model, each agent is forming his portfolio composed from the three investment op-
tions (in the next version the number of portfolio assets will not be bound to only three assets): two index
funds and a Treasury bond, see above. This is a minimum set of assets needed for the design of profit-risk
adjusted portfolio, where Treasury bond is assumed as almost risk free asset.
It is important to notice that during simulation an agent can change one owned asset to another hav-
ing associated transaction costs, but no liquidity issues are associated with. Besides, he can’t borrow
money and buy more assets than he already has in his owned assets portfolio. He can only make transfers
of currently available funds (aggregated portfolio market price) through transferring own capital from one
asset to another. The transfer of owned asset is via current selling market price and buying of another as-
set is via current market buying price. Therefore, there is no need to design any auctioning mechanism
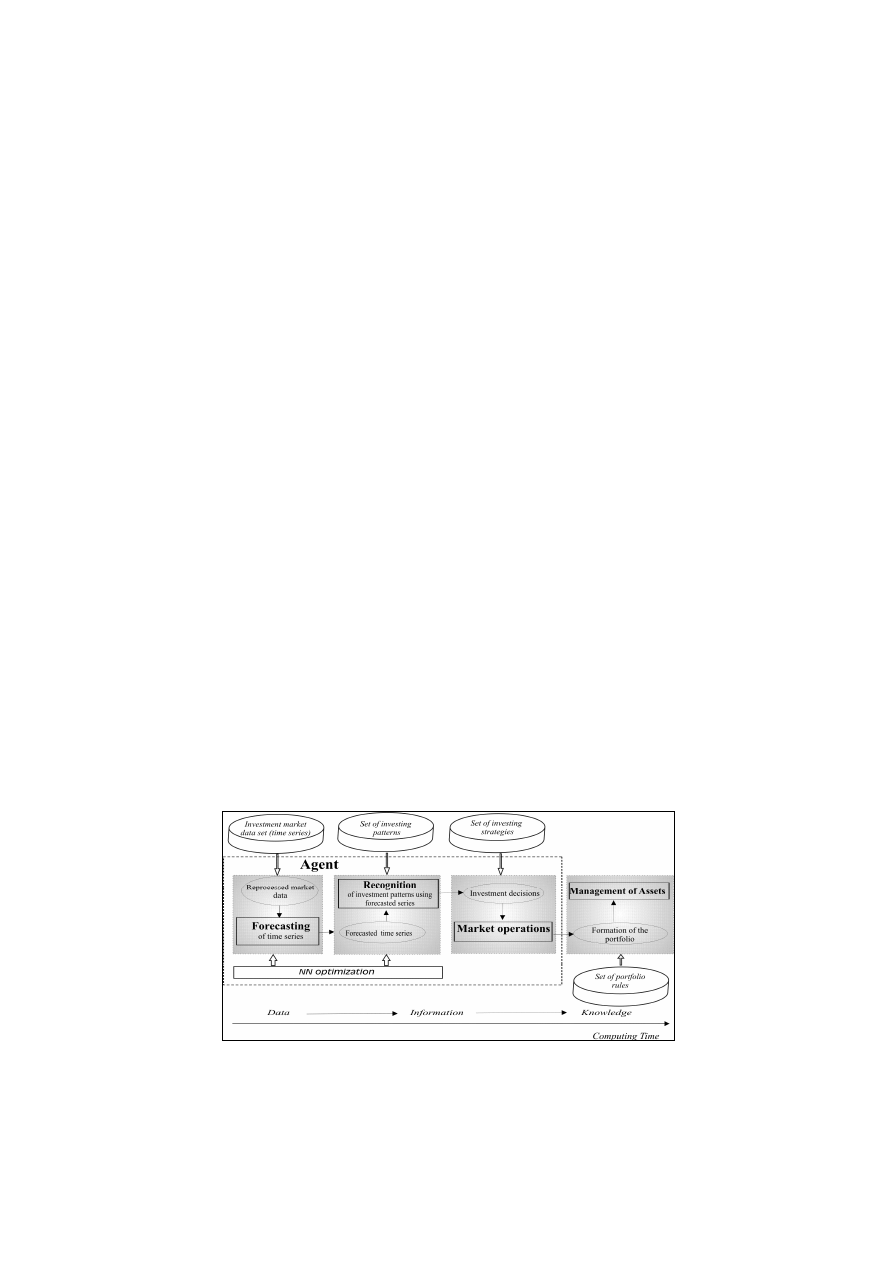
and take care about liquidity issues, see Fig. 1.
Fig. 1. General model scheme
Based on this, each agent enters the investment market with the same initial capital K
0
, which is fur-
ther allocated according to individual investment preferences. In short, each agent has to perform 1) to
learn his investment strategy from the sample data, 2) to make forecasting in order to adjust his expecta-
tions and prepare for the market intervention according to his investment strategy, 3) to apply timely mar-
D. Plikynas
140
ket interventions (buying/selling) according to agent’s investment strategy, 4) to redistribute available
capital according to portfolio rules and estimate the final portfolio.
In terms of wealth, initially homogenous agents are gradually collecting different wealth depending
on luck and performance of the investment strategies they employ. The discussion above gives some un-
derstanding how portfolio theory is applied in the current research, but not less important is to discuss
how close wealth accumulated in the simulated portfolios is to the real investors’ wealth distributions. If
our simulations are showing that proposed NN-based multi-agent system produces similar results in terms
of wealth distribution comparing with empirical evidences from the real investment markets behaviour as
described by Pareto wealth and Levy returns distributions (Levy, 1997), then we can conclude at this
stage that proposed model is close to reality (obviously, more sophisticated tests additionally are needed
as above assumption is necessary, but not sufficient for such conclusion).
4. Experimental setup
Hence, after description of the general research framework and particular application domain (for the
current research stage), we finally can give some details about the actual experimental setup, methodical
issues, constraints and model implementation issues.
In the proposed model, each investor is represented as an agent. Initially, the set of agents can be di-
vided to the clusters, which equal sizes are defined by the experimenter. Cluster types are outlined by the
investment strategies picked up for the simulation or by a type of agents (different sets of internal parame-
ters). Depending on the simulation parameter set, the total number of agents can be chosen varying from a
few to even thousands. The author has been experimenting with a different number of them reaching as
much as 5000.
In methodical sense, agents are modelled using multilayer perceptron (MLP) backpropagation neu-
ral networks [NN] with fast Levenberg-Marquardt learning algorithm (Haikin, 1999). The application is
compiled using MatLab environment and NN Toolbox in particular. To summarize, the virtual lab soft-
ware platform is based on Condor, Tomcat server and Oracle XE DB. The Win2003 server is running on
Intel Core2 Quad Q6600 2.4 GHz/1066FSB/8MB/RAID2*500GB HDD hardware server platform (inte-
grated 4 processors).
The first version of the model is already available via web using our virtual lab environment, which
is intended to enable others to access the model and make experimentations using it (
http://vlab.vva.lt/
).
In the next version, we are planning to add some GUI and user friendly interface. Besides, the author
plans to “dehardwire” the application currently bounded only to the described data set, see below. So, it
will make our model even more applicable for the broader class of assets, portfolio configurations, strate-
gies and data structures.
Concerning the “internals” of an agent, each investment asset is analyzed by a dedicated NN (neural
network), see Fig. 2. It means, that an agent is a modular entity composed from a number of different
NNs, where separate NNs are dealing with different market data, e.g. time series analyses, forecasting,
recognition (which and when investment strategy to employ) etc, see Fig. 1. This is the case for those
agents, which are static in the sense of the strategy they have been assigned to use in the simulation setup
as they can’t change it during the running time.
Actually, the stage of forecasting and recognition usually goes one after another, though, in this par-
ticular model NN learns forecasting and recognizing at the same time (the initial data set has been pre-
processed to add needed technical indicators for the recognition of strategies). MSE-mean square error
and R-square were used mainly as performance criteria comparing with the standard multivariate regres-
sion. As a matter of fact a novel type of NN has been designed, which has a unique input weight matrix
(Plikynas, 2006).
In reality, the initial data set has to be expanded before feeding it to the NNs, i.e. auto regression sets
were generated, adding technical indicators and other factors needed for the NN to recognize the market
situation (see Fig. 2) for making appropriate investment decisions (according to the ascribed investment
strategy). In that regard, 6 major investment strategies (the sets of technical trading rules following Wall
Street definition) were simulated, i.e. “buy and hold”(naiv trading), “bull”, Support&Resistance, Con-
trary, Risk averse, Filter rule.
After all, 15 trading rules were designed for an agent’s index fund (single) asset management. We
have based our technical analysis approach on a number of theoretical and empirical studies (Jones, 2002;
Hoffmann, 2007), which have suggested that technical analysis remains popular with many investors. The
ORTFOLIO DESIGN AND OPTIMIZATION USING NEURAL NETWORK BASED MULTIAGENT SYSTEM OF INVESTING AGENTS
141
leading experts in the field (see Jones, 2002; Darley, 2007; Sharpe, 1964) have published a number of
papers providing support for some basic technical indicators, e.g. MACD – moving average conver-
gence/divergence, W%R – Williams’ oscillator, MFI – money flow index, WMA – weighted moving av-
erage etc (see Table 2). Following their advice, these technical indicators were adopted as benchmarks in
the presented model.
Fig. 2. Investment market data (autoregression time series) and technical
preprocessed data projected as inputs to the forecasting MLP NN.
5. Some results and conclusions
In fact, NN training and testing results indicate when NN are ready for simulations and inclusion in
the agent’s model, see Table 1. Though, NN optimization task is not automated yet. The experimenter has
to spend great deal of time only for tuning NN parameters in order to outperform the MLR in strategy
recognition.
Table 1.
NN optimisation: learning and testing performance having various NN configurations
MLP configurations (S&P500 data set)
Inv. strat. recognition:
learning and testing stage
Pure_linear Logsig_32 layers Tansig_32 layers separated_1 separated_2
mse_regr_learning_strat
0.005
0.005
0.005
0.017
0.005
mse_nn_learning_strat
0.005
0.005
0.005
0.021
0.004
r2_regr_learning_strat
0.181
0.181
0.181
0.247
0.181
r2_nn_learning_strat
0.179
0.206
0.246
0.361
0.214
mse_regr_testing_strat
0.008
0.008
0.008
0.040
0.008
mse_nn_testing_strat
0.008
0.006
0.005
0.028
0.005
r2_regr_testing_strat
0.165
0.165
0.165
0.205
0.165
Opt
im
iza
tion
cr
ite
ria
r2_nn_testing_strat
0.170
0.195
0.187
0.292
0.220
After NNs are optimized, we can generate a chosen number of agents for each investing strategy.
Sure, we allocate first initial capital (initial capital by default is 1, but it is shared among the three assets
proportionally 0.33:0.33:0.33) and then start simulation.
Below are given only some visual examples out of multitude of other simulation results, see Fig. 3.
Unfortunately, the limited space available doesn’t allow to deliver more empirical results here. In short,
simulations of over 500 agents are generating distributions of returns, which are in close proximity to the
Levy returns distribution and agents’ portfolio distributions are reasonably close to the Pareto wealth dis-
tribution. An interested reader can obtain more evidences and numerical results for the chosen setup by
running the model via our virtual lab (http://vlab.vva.lt).
In summary, simulation of each investing strategy, facilitated by a set of appropriate technical indi-
cators and procedures, once satisfied gives incentives for the appropriate market interventions, which in
turn are coordinated by the multi asset portfolio management algorithm (composed by 9 rules). Adopted
D. Plikynas
142
approach makes agent’s decisions effective in real time, where agent is able to execute intelligent market
timing decisions (interventions). Diversity of investing strategies makes agents’ to execute different in-
vestment patterns following chosen profit/risk targets.
Fig. 3. Simulation results (strat. S
4
) for one agent: top left – NN testing performance
(S&P500 forecasting), top right – NN testing performance (inv. strategy recognition),
bottom left – dynamics of agent’s capital distribution, bottom right – distribution of portfolio returns
To the author‘s knowledge, there is no experiment in the field that focuses on the market mecha-
nisms in such a virtual setting. Management of agents’ operational procedures thus gives us a unique tool
for the simulation of investment strategies. Future research will focus on experimenting with more repre-
sentative investment portfolios as well as search for better fitted algorithmic parameters. The proposed
NN modularity approach enables us envisage a system of networking social agents, which will interact
among each other creating behavioral patterns and social phenomena in general.
References
Blume, L. E.; Durlauf, S. N. (eds.). 2006. The Economy as an Evolving Complex System III. A Volume in the Santa
Fe Institute in the sciences of complexity. Oxford University Press, New York.
De Paoli, F.; Vizzari, G. 2003. Context dependent management of field diffusion: an experimental framework, in
Proceedings of the Workshop from Object to Agents. WOA, Piagora Editrice, Cagliari, Italy.
Jones, C. P. 2002. Investments: Analysis and Management. John Wiley&Sons, eight ed.
Hoffmann, A. O. I.; Jager, W.; Von Eije, J. H. 2007. Social Simulation of Stock Markets: Taking It to the Next
Level, Journal of Artificial Societies and Social Simulation 10(2): 7.
Levy, M.; Solomon, S. 1997. New Evidence for the Power-Law Distribution of Wealth. Physica A 242.
Mamei, M. and Zambonelli, F. 2006. Field-Based Coordination for Pervasive Multiagent Systems. Springer-Verlag.
241 p.
Mantegna, R. N.; Staney, H. E. 2000. An Introduction to Econophysics: Correlations and Complexity in Finance.
Cambridge University Press.
Markowitz, H. M. 1991. Portfolio Selection: Efficient diversification of investments. Blackwell Publishers.
McCauley, J. L. 2004. Dynamics of Markets: Econophysics and Finance. Cambridge University Press.
Miller, J. H. and Page, S. E. 2007. Complex Adaptive Systems: an Introduction to Computational Models of Social
Life. Princeton University Press. 260 p.
Moss, S.; Edmonds, B. 2005. Towards Good Social Science, Journal of Artificial Societies and Social Simulation
8(4). Available from Internet: < http://jasss.soc.surrey.ac.uk/8/4/13.html>
.
Plikynas, D. and Akbar, Y. 2006. Application of Modified MLP Input Weights' Matrices: An Analysis of Sectoral
Investment Distribution in the Emerging Markets, Neural Computing and Applications Journal. Publisher
Springer London.