Development of Enhanced Electric Arc Furnace Models for Transient Analysis

Gilsoo Jang

Korea University

Seoul, Korea

Weiguo Wang

ESCA-Alstom

Tacoma, WA

USA

G. T. Heydt Ari-

zona State Univer-

sity

Tempe, AZ

USA

S. S. Venkata

Iowa State Uni-

versity

Ames, IA

USA

Byongjun Lee

Korea University
Korea University

Seoul, Korea

ABSTRACT

Electric arc furnaces (EAFs) are a main cause of voltage flicker due to the interaction of the high demand

currents of the loads with the supply system impedance. In order to adequately understand and analyze

the effects on the power system from these loads, obtaining an accurate representation of the characteris-

tics of the loads is crucial. In this paper, a mixed chaotic EAF model to represent the low frequency and

high frequency variations of the arc current respectively and a chain-shaped chaotic EAF model to char-

acterize the current variation have been proposed. The concept of chaotic parameters, such as chaotic

resistance, inductance or admittance has been also proposed for the characterization of arc furnace opera-

tion and the highly nonlinear physical processes. In addition, a DLL--Dynamic Link Library module,

which is a FORTRAN interface with TACS--Transient Analysis of Control Systems, is developed to im-

plement the chaotic load models in the EMTP--Electromagnetic Transients Program. The simulation

results are presented in comparison with the actual data to illustrate the validity of the models.

Keywords: Chaos, Load modeling, Arc furnace, EMTP, TACS, FORTRAN interface, Flicker, Power

quality indices

I. INTRODUCTION

A large amount of steel accounting for 40% of total tonnage in the United States was made in electric arc

furnaces (EAFs) [1]. Besides, the power fluctuation of EAFs appears to be of concern in the degradation

of the electric power quality of the interconnected system. Because of its severe impact on the power

quality problems due to its nonlinear and highly varying characteristics, the dynamic characteristics of

EAFs have been a subject of study to provide high quality power to all customers. Even though the EAF

has been studied for many years, it is still difficult to obtain a complete representation of such load and its

impact on the power system. Some researchers used the stochastic models to represent the operation of

the EAF because of the aperiodic, seemingly random behavior of these loads [2-4]. An alternative ap-

proach to include the deterministic chaos in the modeling of the EAF [5] was proposed, for chaos has

been detected in the arc current. This chaotic model proves to be a better representation of the EAF opera-

tion when assessing the impact of the EAF on power systems.

The main purpose of this paper is to develop enhanced chaotic EAF models which have a better represen-

tation of the EAF operation when assessing the impact of the EAF on power systems. New chaotic mod-

els, such as mixed chaotic model and chain-shaped chaotic model, have been proposed in this paper to

serve as the improvements of the model based on the chaos theory. The mixed chaotic model combines

both the Lorenz system and the logistic system to represent the low frequency and high frequency com-

ponents in EAF current, and the chain-shaped chaotic model uses the patterns detected in the EAF current

to characterize its variation. In addition, EMTP EAF modules of the proposed models have been devel-

oped to simulate the power systems which contains EAFs and it allows to verify the accuracy of the

chaos-based models and to illustrate their capabilities.

II. EAF EQUIVALENT SYSTEM

The main discussion in this paper relates to AC electric arc furnaces, although a similar modeling ap-

proach is possible for dc furnaces. Electric arc furnace operation may be classified into several stages,

depending on the melting status and the time lapse from the initial energization of the unit. During the

melting period, sets of steel nearly create a short circuit on the secondary side of the furnace transformer,

and it creates large fluctuations of current at low power factors. These current fluctuations cause varia-

tions in reactive power, which cause a momentary voltage drop or flicker, both at the supply bus and at

nearby buses in the interconnected system. The arc currents are more uniform during the refining period,

and result in less impact on the power quality of the system.

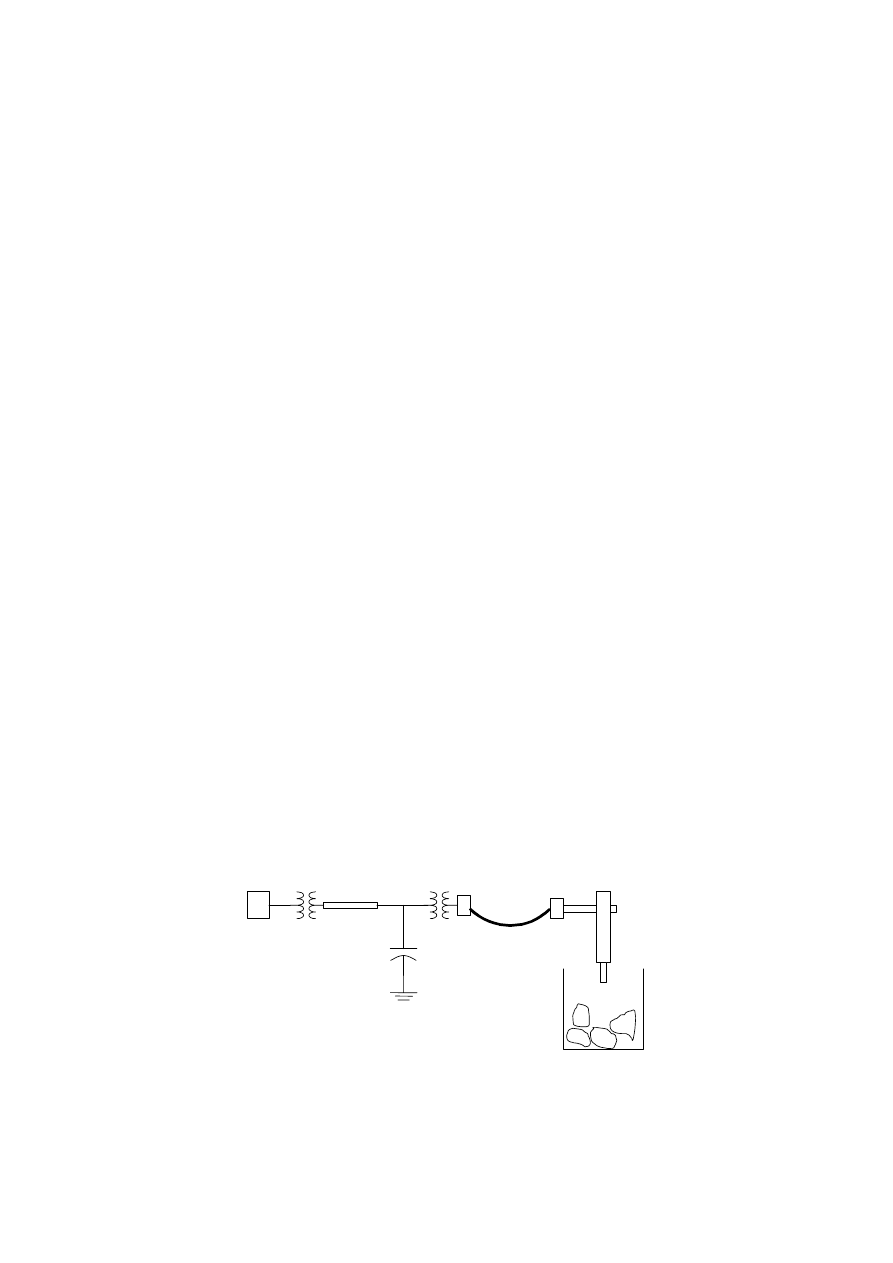
A typical and detailed arc furnace structure is shown in Figure 1. It includes a system equivalent at sub-

station bus S, substation transformer T

s

, cable run to furnace D

1

, power factor correction equipment C, arc

furnace transformer T

a

, flexible cables D

2

, bus conductors B, graphite electrodes G and the melting vessel

M.

M

B

C

G

S

T

S

D

1

T

a

D

2

Figure 1 Structure of a Typical Arc Furnace

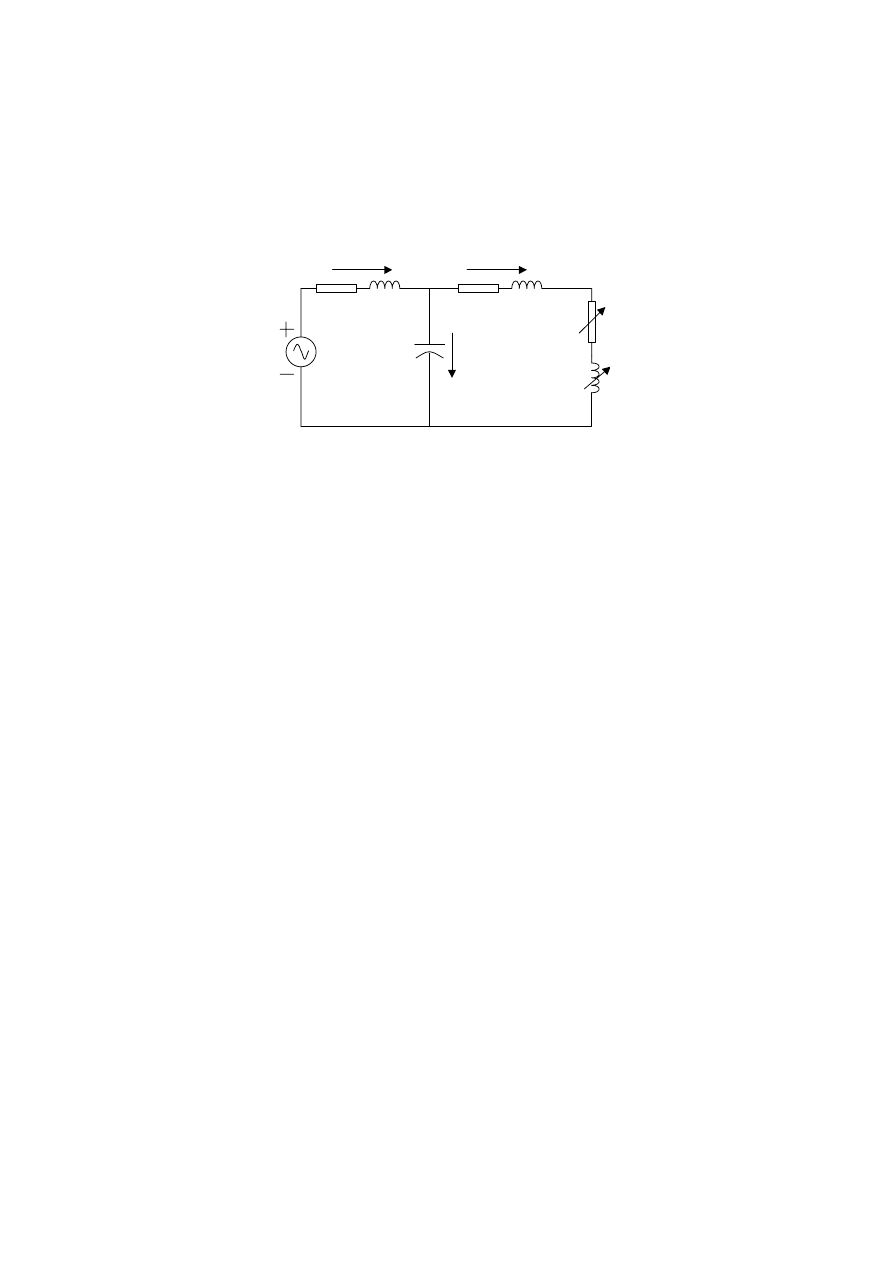
In order to analyze the arc process and the interaction between the arc furnace and power system, a

mathematical simplification of the given system is performed. The simplification in Figure 2 is reason-

able because the mechanical process is much slower than the electrical dynamics.

C

e

R

1

L

1

R

2

L

2

R

f

L

f

i

1

i

2

i

c

, v

c

Figure 2 Circuit Representation of the Arc Furnace

In Figure 2, R

1

and L

1

represent the resistance and the reactance of power system at substation level, the

substation transformer winding and the cable run to the furnace transformer, and R

2

and L

2

represents the

resistance and the reactance of the flexible cables, the bus conductors and the graphite electrodes. The

dynamic variation of arc resistance and inductance is represented by R

f

and L

f

, and both nonlinear vari-

ables are time varying and bounded. All the circuit parameters except the R

f

and L

f

can be obtained from

the given conditions.

III. MODELING OF ARC FURNACES USING CHAOS THEORY

The modeling of AC electric arc furnaces has traditionally been done with either fixed circuit elements or

fixed elements plus a stochastic component. However, recent tests using actual furnace load data suggest

that there may be a chaotic component to the model. The term chaos in this context implies a mathemati-

cal property in which the dynamic model is highly sensitive to starting point of the system state vector. If

the evolution of an initial state is denoted as X(t), and the evolution from a very nearby initial state is

X'(t), then X-X' is found to diverge even if the initial states become close together. Chaotic properties are

observed in some physical systems that are nonlinear and high order. There are some tests for chaos, and

AC arc furnace data appear to qualify as having a chaotic component. Note that chaos is a deterministic

phenomenon -- there is no stochastic element. It is possible that actual EAF load currents have a usual

linear and nonlinear component, a chaotic component, and a stochastic component. In this study, focus

on the chaotic component is made and found to give reasonable results.

A. Lorenz Model

In references [5,6], evidence of chaotic behavior is shown in the current from an AC EAF. The calcula-

tion of the largest Lyapunov exponent of the EAF provides a mathematical support for the modeling of

arc furnaces using chaos theory. In the chaotic model in [5], load current data from an EAF is used as

inputs to a feed-forward model which is composed of tuning and simulation stages. A time scaled version

of the Lorenz system[7] is used to represent the highly varying behavior of the currents in an EAF. The

scaled version of the Lorenz system is shown in equation (1). A time scale factor of 30 is needed to model

the highly varying load at 60 Hz. The state variables are x, y and z, whereas

σ

, r and b are constants

whose values were initialized as 10, 8/3, and 28 respectively,

bz

xy

z

y

z

r

x

y

x

y

x

30

30

30

)

(

30

)

(

30

−

=

−

−

=

−

=

&

&

&

σ

(1)

In the Lorenz model, the arc resistance is expressed as below

x

C

R

f

1

=

(2)

In (2), C

1

is a constant and x is one of the state variables. According to [8], the value of arc reactance is

proportional to the arc resistance with coefficient

α

. i.e.

1

2 f

R

L

f

f

π

α

=

(3)

where, f

1

is the network frequency.

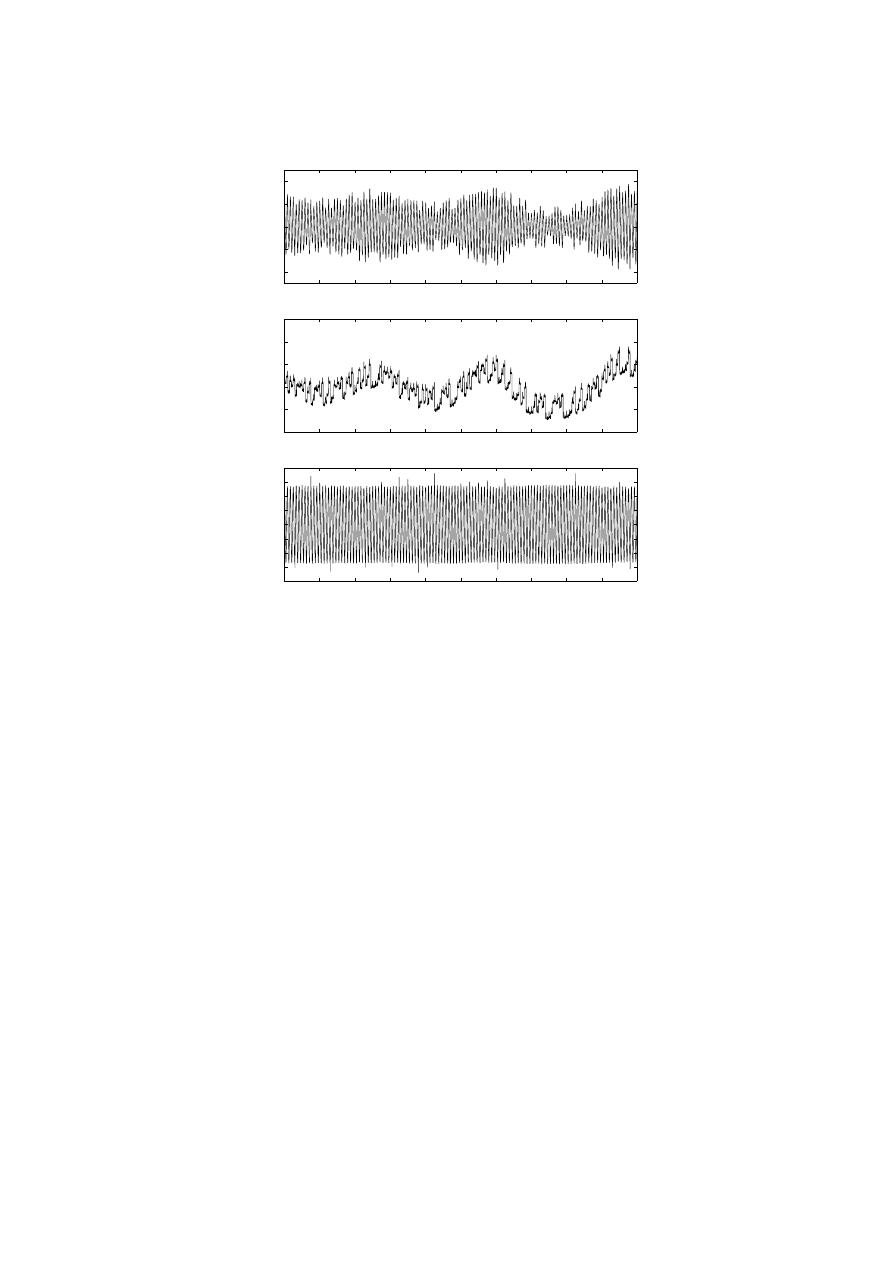
Using this Lorenz model together with a typical 50 MVA EAF system [9], the simulation has been per-

formed. The simulated arc current and arc admittance are shown in Figure 3.

0.2

0.4

0.6

0.8

1

1.2

1.4

1.6

1.8

2

−2000

−1000

0

1000

2000

Arc Current(A)

Arc Current and Admittance in Lorenz Model

0.2

0.4

0.6

0.8

1

1.2

1.4

1.6

1.8

2

0

0.02

0.04

0.06

0.08

0.1

Arc Admittance

Time(S)

Figure 3 AC Electric Arc Current and Admittance in Lorenz Model

B. Logistic Model

The logistic equation is a classical iterative equation with the appropriate value of parameter k. The for-

mula is rewritten in equation (4).

]

1

,

0

[

,

)

1

(

0

1

∈

−

⋅

=

+

x

x

x

k

x

n

n

n

(4)

Because x

n

is a discrete time series with an unknown time step, we could designate different time steps or

different chaotic frequencies to characterize the variation of arc admittance Y. Hence, Y consists of the

summation of the time series from the logistic equation with different chaotic frequencies.

...

3

3

2

2

1

1

+

+

+

=

f

f

f

f

X

a

X

a

X

a

Y

(5)

where, X

1f

, X

2f

, X

3f

, … represent the time series with different chaotic frequencies like 30Hz, 60Hz,

120Hz and so on.

Therefore, the arc admittance corresponding to different harmonic components can be represented by this

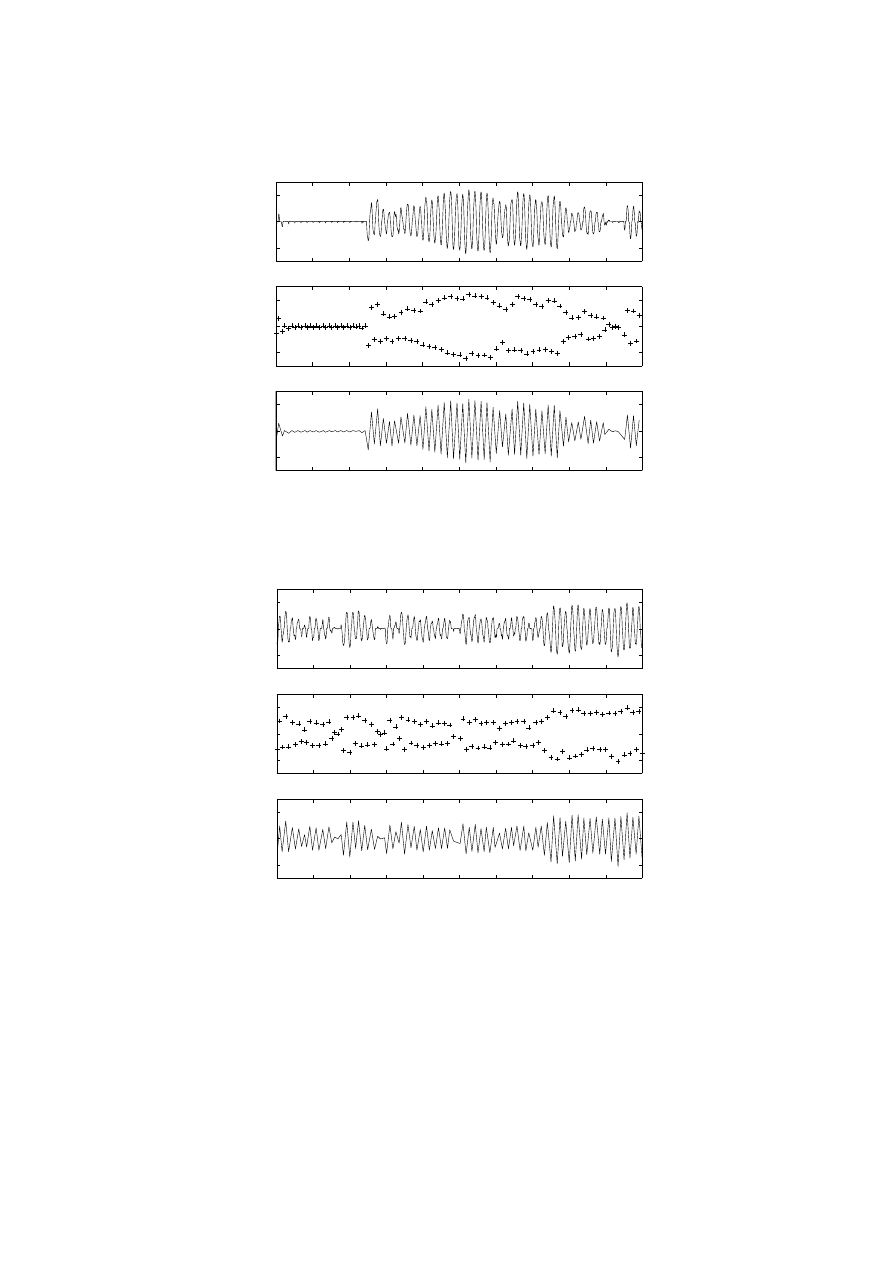
model. Figure 4 shows the simulated arc current, arc admittance and arc voltage using this model.

0

0.2

0.4

0.6

0.8

1

1.2

1.4

1.6

1.8

2

−2000

−1000

0

1000

2000

Arc Current(A)

Arc Current, Admittance and Voltage in Logistic Model

0

0.2

0.4

0.6

0.8

1

1.2

1.4

1.6

1.8

2

0

0.05

0.1

Arc Admittance

0

0.2

0.4

0.6

0.8

1

1.2

1.4

1.6

1.8

2

−4

−2

0

2

4

x 10

4

Arc Voltage(V)

Time(s)

Figure 4 Simulated Arc Furnace Current, Arc Admittance and Arc Voltage using Logistic Model

This model covers the characteristics of the high frequency behavior of an EAF like the harmonics. The

voltage drop on the transformer winding impedance is caused by the nonlinear variation of the arc resis-

tance and inductance. Largely the voltage drop due to the winding inductance is caused by the erratic arc

current variation.

C. Mixed Chaotic Models

A mixed chaotic model is proposed to represent the dynamic characteristics of EAFs in wide frequency

ranges. As in equation (6), the Lorenz contributes to the low frequency components of arc current and the

logistic system to the high frequency components.

02

.

0

,

003

.

0

,

005

.

0

2

1

0

log

2

1

0

=

=

=

+

+

=

C

C

Y

Y

C

Y

C

Y

Y

istic

lorenz

f

(6)

In (6), Y

0

is fixed admittance, and Y

f

represents the total admittance of the arc furnace. C

1

and

C

2

are constants, depending on the historical data and scaling of both systems. Y

lorenz

represents the con-

tribution of admittance from the Lorenz system. Y

logistic

represents the contribution of admittance from the

logistic equation. These parameters can be optimized and tuned to further characterize the operation of

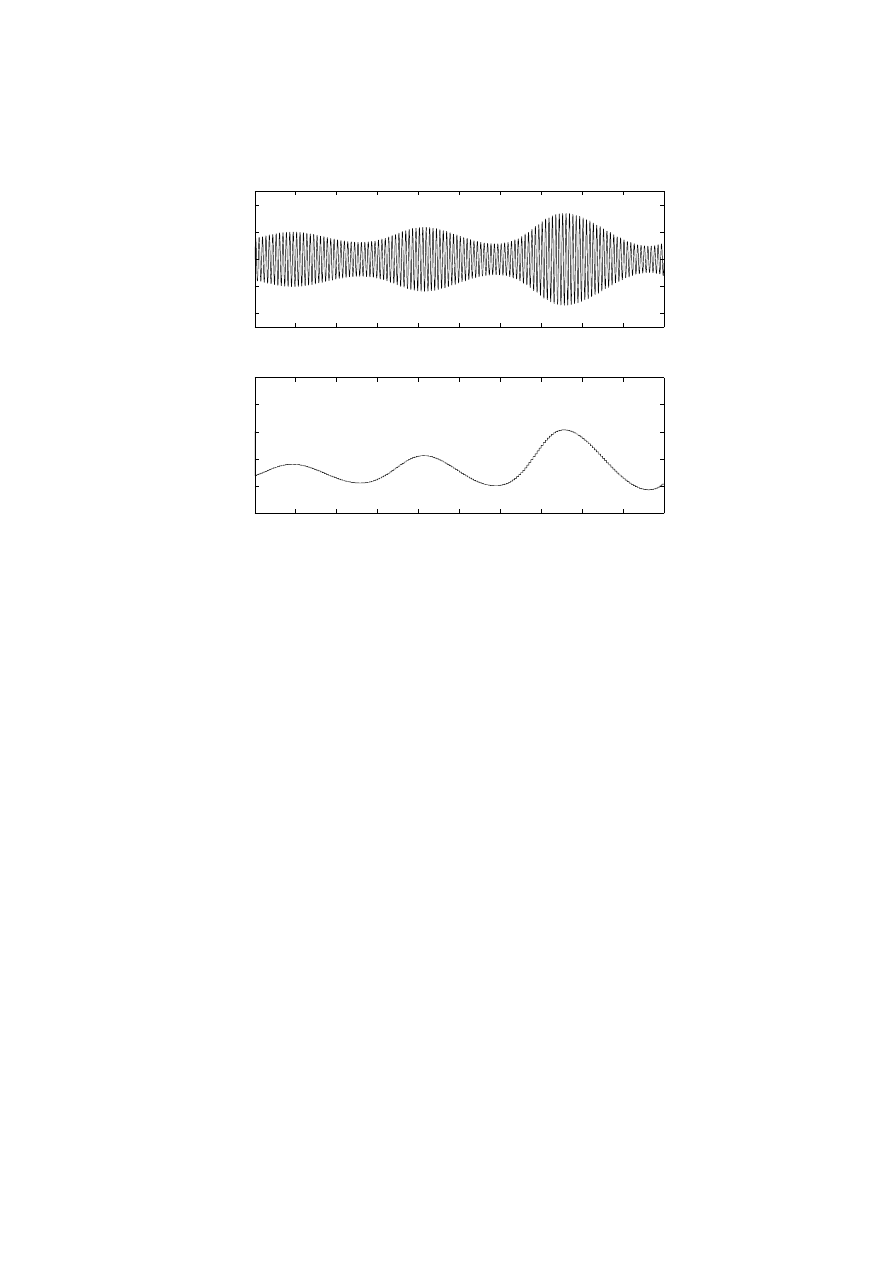
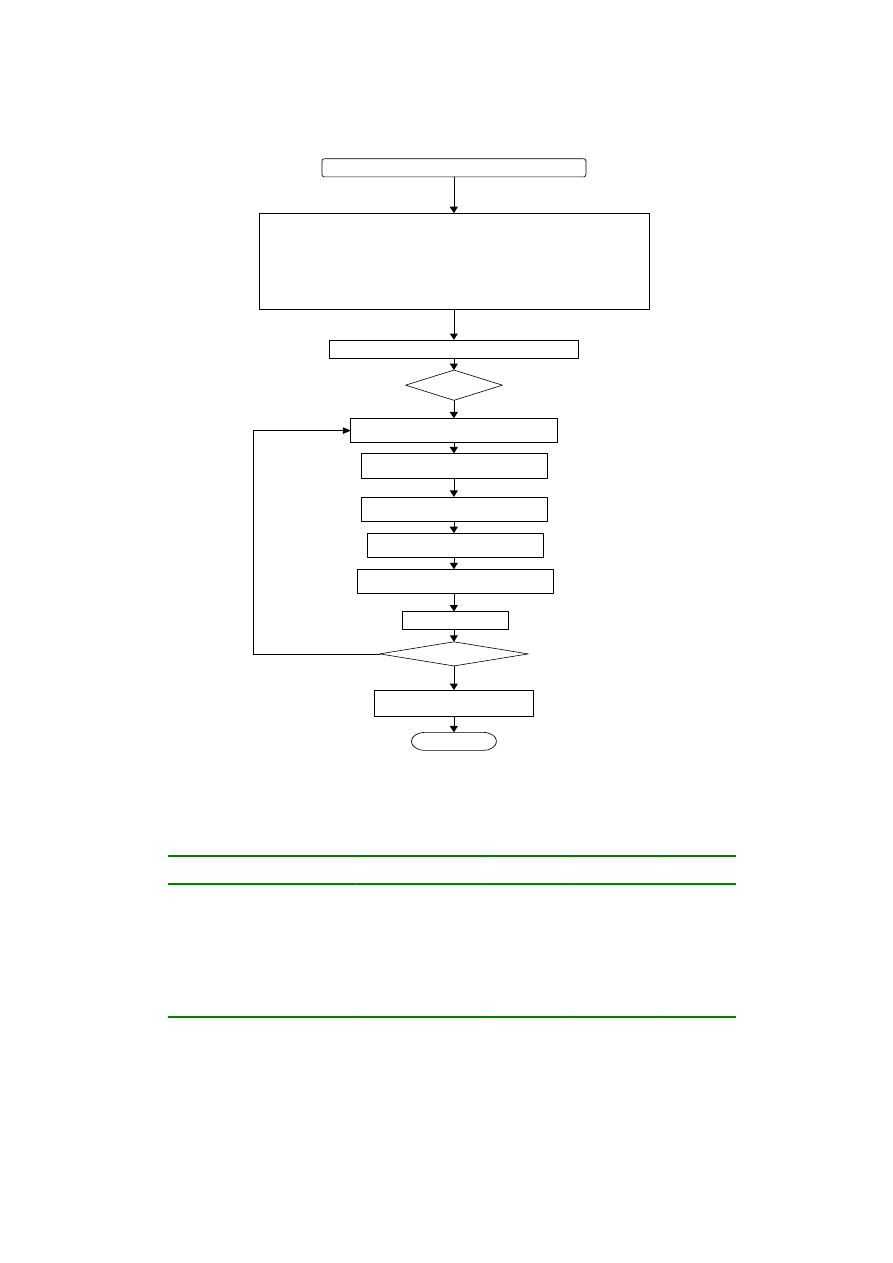
the arc furnace. Figure 4 shows the procedure to develop the proposed model. The simulated arc current

and voltage in the test system [9] are shown in

Figure 5

Figure 5

. The power quality indices are calculated from the simulated waveforms and compared with

those from the actual waveforms in Table 1. Clearly we can see they are matched very well through the

comparison with the actual power quality indices.

Table 1 Power Quality Indices in the Mixed Chaotic Model

Power Quality Indices

Simulated Data

Min

Max

Average

THD

0.037378

0.029583

0.061930

0.044522

K-Factor

1.021513

1.008624

1.073438

1.034753

Crest Factor

2.888085

2.496126

3.146561

2.824822

Zero-Peak Flicker Factor

1.176755

0.907654

1.534109

1.291042

RMS Flicker Factor

0.047134

0.039731

0.112681

0.077426

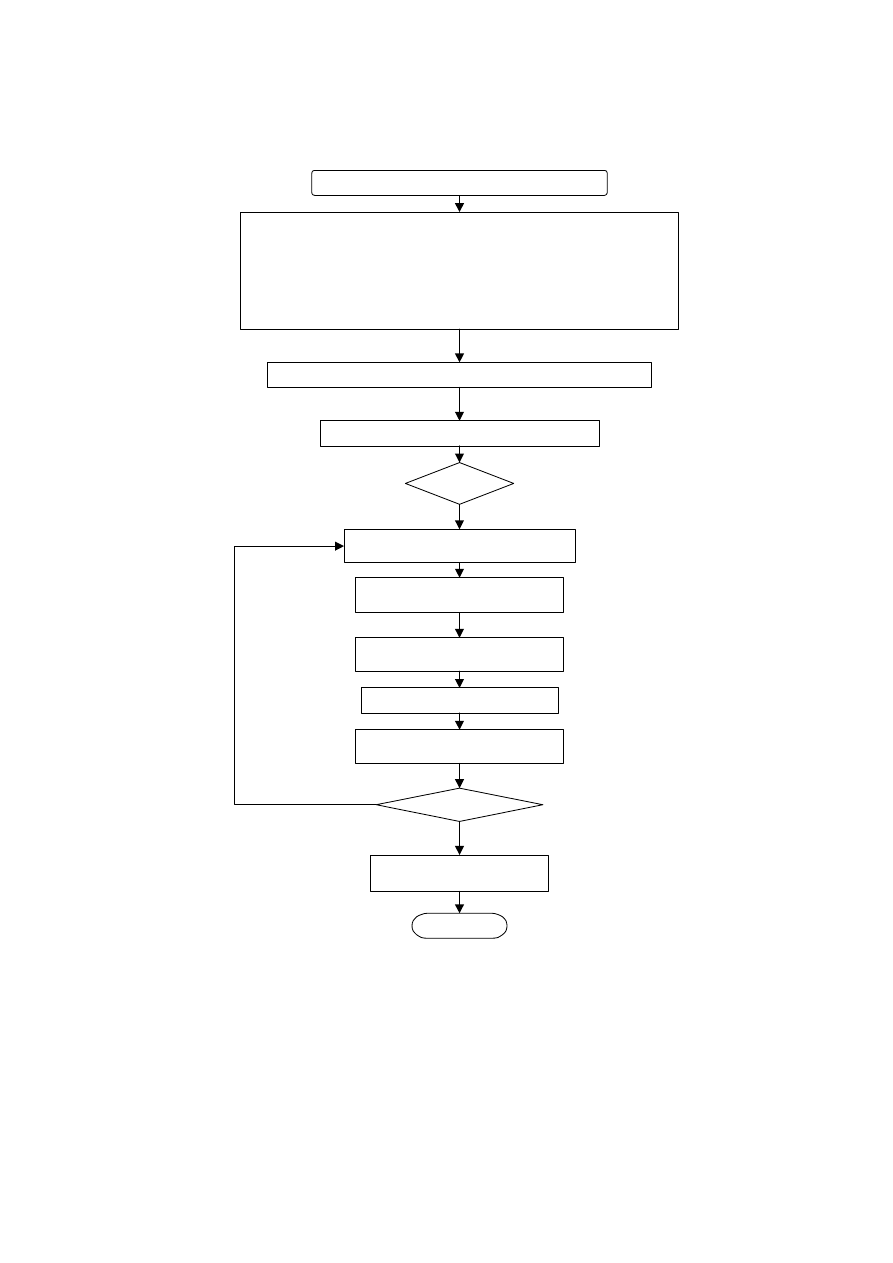
Start to run the program for simulation of the electric arc furnace

Set Circuit Parameters like R

1

, R

2

, L

1

, L

2

, and Prop(X

f

=Prop*R

f

), Network Frequency

Set step length for integration and total integration time :h=0.0001, ShowTime=20 (Simlation time)

Set the fixed part of chaotic admittance:Adf0=0.016(fixed part of chaotic admittance)

Set the parameter for Lorenz system:Sigma=10, r=28, b=8/3

Set the chotic frequency for logistic system: Fchaotic=100

Set the initial value and coefficients for Lorenz system

Go through the transients for Lorenz system

Reset the initial value for Lorenz system after transients

Set the initial value and coefficients for harmonic compensation

Set the initial value and coefficients for Logistic system

Calculate the initial value of chaotic admittance for R

f

and L

f

using coefficient of Prop

Set the initial value of state variable of arc current ifur=0

k=1

Calculate the admittance contribution from Lorenz

system(low frequency)

Calculate the admittance contribution from

Logistic system(high frequency)

Calculate the admittance contribution for

harmonic compensation(harmonics)

Get the total admittance of the arc furnace

Integrate the system with one step and get the

arc current-- ifur and other variables

k >= Num-1?

Data analysis to get the power quality

indices for the simulated data

Terminate

Figure 4 Flow Chart of the Mixed Chaotic Model

0.2

0.4

0.6

0.8

1

1.2

1.4

1.6

1.8

2

−2000

−1000

0

1000

2000

Arc Current(A)

Arc Current from the Mixed Chaotic Model

0.2

0.4

0.6

0.8

1

1.2

1.4

1.6

1.8

2

0

0.02

0.04

0.06

0.08

0.1

Admittance

Nonlinear Admittance from the Mixed Chaotic Model

0.2

0.4

0.6

0.8

1

1.2

1.4

1.6

1.8

2

−4

−3

−2

−1

0

1

2

3

4

x 10

4

Arc Voltage(V)

Arc Voltage from the Mixed Chaotic Model

Time(S)

Figure 5 Simulated Arc Current, Admittance and Bus Voltage According to the Mixed Chaotic Model

D. Chain-Shaped Chaotic Model

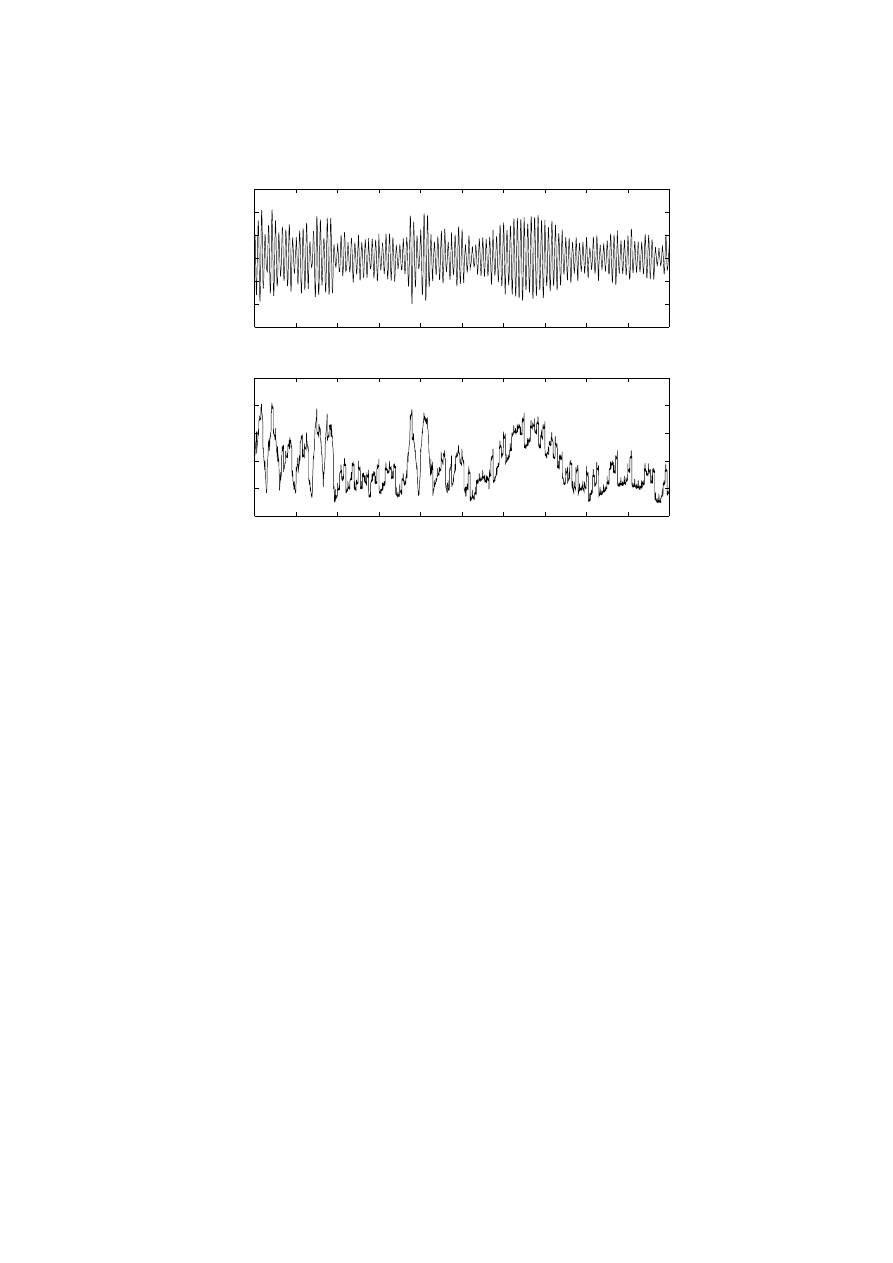
A pattern, chain-shaped envelope pattern, is detected from a typical EAF, and it can be identified in Fig-

ure 6 and 7 in which some sample waveforms together with their tuned waveforms are shown. It is just

like someone’s drawing which is composed of a lot of sinusoidal arcs (not the physical arc) with different

length, magnitude, angle and frequencies. With the following assumptions, the chain-shaped chaotic

model to represent this pattern can be developed.

•

The length of the arc varies chaotically

•

The magnitude of the arc varies randomly

•

The angle of the arc keeps constant

•

The frequency of the sinusoidal arc varies chaotically with logistic equation

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

1

−2000

0

2000

Current(A)

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

1

−2000

0

2000

Current(A)

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

1

−2000

0

2000

Current(A)

Time(S)

Figure 6 Tuned Arc Current Waveforms-Sample A (first 1 second)

9.1

9.2

9.3

9.4

9.5

9.6

9.7

9.8

9.9

10

−2000

0

2000

Current(A)

9.1

9.2

9.3

9.4

9.5

9.6

9.7

9.8

9.9

10

−2000

0

2000

Current(A)

9.1

9.2

9.3

9.4

9.5

9.6

9.7

9.8

9.9

10

−2000

0

2000

Current(A)

Time(S)

Figure 7 Tuned Arc Current Waveforms—Sample B ( between 9 and 10 seconds)

The arc admittance from this model can be expressed as follows.

001

.

0

,

0003

.

0

,

001

.

0

,

0003

.

0

,

001

.

0

,

001

.

0

,

004

.

0

...

5

5

4

3

2

1

0

3

3

2

2

1

1

sin

0

=

=

=

=

=

=

=

+

+

+

+

+

=

a

a

a

a

a

a

Y

Y

a

Y

a

Y

a

Y

Y

Y

f

f

f

arc

f

(7)

In (7), Y

1f

, Y

2f

, etc. are chaotic time series generated from the logistic equation with different time steps

and initial values, and a

1,

a

2

, etc. are scaling constants. Y

0

is a constant which can characterize the mini-

mum variation of arc admittance. Y

sinarc

is given by

0

,

5

.

0

)

sin(

0

0

0

sin

=

=

+

=

θ

θ

ω

M

M

arc

Y

t

Y

Y

(8)

Here Y

M

is the magnitude of the sinusoidal arc,

θ

0

is the initial angle of the sinusoidal arc served as the

low frequency envelope, and

ω

is the frequency governed by the logistic equation. The outcome of this

simulation model is promising in characterizing the general behavior of the arc furnace. The procedure

for developing this model is illustrated in Figure 8. The simulation results using this model are shown in

Figure 9 and Table 3. The power quality indices derived from the simulated arc current matched well with

those from the actual data. As seen from Table 1 and Table 2, the chain-shaped chaotic model has better

results than the mixed chaotic model in terms of power quality indices. Hence, the chain-shaped chaotic

model is suitable to characterize the general behavior of the electric arc furnace operation.

S t ar t t o ru n t h e p r o g r a m f or s im u la tio n of th e e le c tric a rc fu rn a c e

S e t C irc u it P a r a m e t e rs lik e R

1

, R

2

, L

1

, L

2

, a n d P r o p (X

f

= P r o p * R

f

), N e tw o rk F r e q u e n c y

S et s t e p le n g th f or in t e g r a tio n a n d t o t a l in t e g r a tio n tim e : h = 0 .0 0 0 1 , S h o w T i m e = 2 0 (S im la tio n tim e)

C alc u la t e t h e t o t a l n u m b e r of in t e g r a ti o n s t e p s : N u m = S h o w T im e /h

C alc u la te th e n u m b e r o f d a t a p o in ts in e ac h d at a p ie c e : D at a N u m = 1 /h

S et th e in it ia l c h a o t ic f r eq u e n c y f o r th e v a ria tio n of th e e n v e lo p : F li c k F r e q = 0 .8 * 1 0

S et th e in it ia l c o u n te r v a lu e f o r e ac h c h a in a rc : d u r c o u n t e r

S et th e in it ia l a n g le of t h e e n v e lo p e : S it a = r a n d

S e t th e in it ia l m a g n it u d e of t h e e n v e lo p e : M a g = 0 . 5

S et th e in itia l v a l u e o f t h e L o g is tic s ys t e m : x 1 = r a n d

S et th e in it ia l v a lu e a n d c o e ff ic ie n ts f o r h ar m o n ic c o m p e n s a tio n

S et th e in itia l v a l u e o f s t a t e v a ria b le of arc c u r r e n t i fu r = 0

k = 1

C a lc u la te th e a n g le o f th e c h a in a rc S it a

C a lc u la te th e v a ria t io n o f th e a d m itt a n c e

A d m it = ( 0 .1 + v a r i)/ 1 0

C a lc u lat e t h e a d m itt a n c e c o n tr ib u tio n f r om th e

L o g is tic s ys t e m

C a lc u lat e t h e a d m it ta n c e c o n tr ib u tio n f r om

th e h a r m o n ic c o m p e n s a tio n

M o d if y th e c o u n t er v a lu e a c c or d in g t o F lic k F r e q

a n d g e t th e t o t a l a d m itta n c e o f a rc fu r n ac e

k > = N u m - 1 ?

D at a a n a lys is to g e t t h e p o w e r q u a lity

in d ic e s f or t h e s im u lat e d d a t a

T er m in a te

In t e g r a te th e s ys te m

Figure 8 Flowchart for the Chain-shaped Chaotic Model

Table 2 Power Quality Indices from the Chain-shaped Chaotic Model

Power Quality Indices

Simulated Data

Min

Max

Average

THD

0.035140

0.029583

0.061930

0.044522

K-Factor

1.016711

1.008624

1.073438

1.034753

Crest Factor

2.786330

2.496126

3.146561

2.824822

Zero-Peak Flicker Factor

1.118353

0.907654

1.534109

1.291042

RMS Flicker Factor

0.067070

0.039731

0.112681

0.077426

0.2

0.4

0.6

0.8

1

1.2

1.4

1.6

1.8

2

−3000

−2000

−1000

0

1000

2000

3000

Arc Current from the Chain−Shaped Chaotic Model

Time(S)

Arc Current(A)

0.2

0.4

0.6

0.8

1

1.2

1.4

1.6

1.8

2

0

0.02

0.04

0.06

0.08

0.1

Time(S)

Arc Admittance

Nonlinear Admittance from the Chain−Shaped Chaotic Model

Figure 9 Simulated Arc Current from the Chain-Shaped Chaotic Model

E. Development of an EAF EMTP Model

The Electromagnetic Transients Program (EMTP) is a computer program for simulating electromagnetic,

electromechanical, and control system transients on multiphase electric power systems. The basis of the

software is the companion circuit method. EMTP is used to solve the ordinary differential and/or alge-

braic equations associated with an "arbitrary" interconnection of different electric power system and con-

trol system components [10]. The chaos-based load models for EAFs are developed in FORTRAN. Since

the developed model involves two different processes for the tuning and simulation, it can not be re-

garded as the typical nonlinear element in the EMTP. In order to implement the model for the study on

system performance and design into the EMTP, a FORTRAN interface is used with TACS in the EMTP.

In the interface, the EAF model is treated as a user-defined EMTP source in order to pass its current to

TACS and the electrical network treats this user-defined source as an independent current source. For

detailed information about using the EMTP source, please refer to EMTP rulebook [11]. The mechanism

of interaction among the EAF model, TACS and EMTP network is shown in Figure 10. Once the user-

supplied input variables have been transferred to the EAF model, the model performs the tuning and

simulation in its own subroutines and the output of the model is sent to TACS through the interface at

each time step. Then, TACS passes the data to electrical network defined in EMTP. Finally, the EMTP

simulates the electrical network using the data from TACS. Nonlinear analysis and chaos theory are used

to model the arc currents in an EAF. At the same time, a DLL module, which is a FORTRAN interface

with TACS is developed to implement the chaotic load model in the EMTP. The simulation results to il-

lustrate the validity of this model were produced using the EAF EMTP module. The EAF EMTP module

will be used for the proper assessment of the power quality impact, and the performance of control de-

vices on power distribution systems.

TACS

EAF Model

P

P

r

r

o

o

v

v

i

i

d

d

e

e

D

D

a

a

t

t

a

a

f

f

o

o

r

r

E

E

M

M

T

T

P

P

S

S

o

o

u

u

r

r

c

c

e

e

R

R

e

e

t

t

u

u

r

r

n

n

s

s

t

t

h

h

e

e

V

V

a

a

l

l

u

u

e

e

t

t

o

o

T

T

A

A

C

C

S

S

/

/

E

E

M

M

T

T

P

P

S

S

o

o

u

u

r

r

c

c

e

e

C

C

a

a

l

l

l

l

F

F

O

O

R

R

T

T

R

R

A

A

N

N

I

I

n

n

t

t

e

e

r

r

f

f

a

a

c

c

e

e

E

E

M

M

T

T

P

P

C

C

u

u

r

r

r

r

e

e

n

n

t

t

S

S

o

o

u

u

r

r

c

c

e

e

Figure 10 Use of TACS-EMTP Source

IV. CONCLUSIONS AND FUTURE WORK

In this paper, different chaotic models are proposed to predict the general behavior of the arc furnace op-

eration. In the mixed EAF chaotic model proposed in this paper, the logistic system is added to make bet-

ter representation of high frequency components in the electric arc current to the EAF chaotic model

based on the Lorenz system. This model is useful when assessing the harmonic property of EAFs. An

argument, and evidence is presented for the detection of chaos in electric arc furnace loads. Chain-shaped

chaotic model mathematically interpret the low frequency variation of the arc current, and the simulation

results showed the model is suitable to represent the general behavior of the EAFs. A FORTRAN inter-

face with EMTP/TACS has been developed to implement the chaotic load models, by which EMTP simu-

lation results have been presented to compare with the actual data to illustrate the validity of the models.

Simulation results show that the mixed chaotic model and chain-shaped chaotic model appropriately

characterize the behavior of the arc furnace operation in the sense of power quality indices and other cri-

teria presented, and the EMTP module together with the chaotic EAF models can be used for the proper

assessment of the power quality impact on power distribution systems with and without compensation

devices.

Although electric arc furnace loads are typically isolated from the distribution system

and subtransmission supply through transformer reactance and filtered with simple

tuned filters, the nonsinusoidal current can not be effectively attenuated by the fixed and

passive devices. Having obtained the model for the furnace, it may be utilized to assess

the impact of an existing load in the system, and to find ways of reducing such impact.

The model can also be used for planning purposes, e.g. to study the impact of a pro-

posed installation in a power system. Although the focus of this paper is on AC electric

arc furnaces, the results apply to certain nonlinear loads that behave similarly, such as

plasma torches and arc welders

In light of the patterns detected in the EAF current, neural networks

could be used to train the system which governs the variation of arc admittance and thereof to predict the

arc current based on the history input data. Such a system should have the function of identifying the dif-

ferent melting phases (different variation style of arc current) and come up with reasonable neural net-

work parameters.

V. REFERENCES

[1] Nadira, Ramon Usoro, Patrick B., "Self-Adjusting Model Algorithmic Control Of A Three-Phase

Electric Arc Furnace," Journal ofDynamic Systemas and Measurement Control, Transactions ASME, vol.

110, no. 4, Dec. 1988, pp. 361-366.

[2] G. C. Montanari, M. Loggini, A. Cavallini, L. Pitti, D. Zaninelli, "Arc Furnace Model for the Study

of Flicker Compensation in Electric Networks," IEEE Transactions on Power Delivery, vol. 8, no. 4,

1994, pp.2026-2036.

[3] S. Varadan, E. B. Makrwn, A. A. Girgis, "A New Time Domain Voltage Source Model for an Arc

Furnace using EMTP, "IEEE Transactions on Power Delivery, vol. I 1, no. 3, July 1996, pp. 1685-1691.

[4] R. Collantes, T. Gomez, "Identification and Modeling of a Three Phase Arc Furnace for Voltage

Disturbance Simulation," IEEE Transactions on Power Delivery, vol. 12, no. 4, Oct. 1997, pp. 1812-

1817.

[5] E. O’Neill-Carrillo, G. Heydt, E. J. Kostelich, S. S. Venkata, A. Sundaram, “Nonlinear Determinis-

tic Modeling of Highly Varying Loads,” submitted for publication to the IEEE Power Engineering Soci-

ety, 1998

[6] G. T. Heydt, E. O'Neill-Carrillo, R. Y. Zhao, “The Modeling of Nonlinear Loads as Chaotic Systems

in Electric Power Engineering,” Proceedings of the 1996 IEEE/PES International Conference on Har-

monics and Quality of Power, Las Vegas, Oct. 1996, pp. 704-711.

[7] K. Alligood, T. Sauer, J. Yorke, Chaos: An Introduction to Dynamical Systems, Springer-Verlag,

New York, 1997.

[8] Aly A. Mahmoud, "Modeling of a Resistance Regulated Arc furnace," IEEE Transaction on Power

Apparatus and Systems, vol. PAS-104, no. 1, Jan. 1985, pp. 58-66

[9] G. Jang, W. Wang, "Electric Arc Furnaces: Chaotic Load Models and Transient Analysis," Lescope

Conference, July 1998

[10] IEEE Standard 519-1992, “IEEE Recommended Practices and Requirements for Harmonic Control

in Electrical Power Systems,” New York, 1992.

[11] EMTP Rule Book, Electric Power Research Institute, Palo Alto, CA, November, 1996.

[12] Garnett P. Williams, Chaos Theory Tamed. Washington, D.C.: Joseph Henry Press, 1997.