Solar Energy Vol. 65, No. 3, pp. 143–157, 1999

1999 Elsevier Science Ltd



Pergamon

P I I : S 0 0 3 8 – 0 9 2 X ( 9 8 ) 0 0 1 3 9 – X

All rights reserved. Printed in Great Britain

0038-092X / 99 / $ - see front matter

DESIGN OF HYBRID-PHOTOVOLTAIC POWER GENERATOR, WITH

OPTIMIZATION OF ENERGY MANAGEMENT

†

M. MUSELLI , G. NOTTON and A. LOUCHE

´

`

Universite de Corse-URA CNRS 2053, Centre de Recherches Energie et Systemes, Route des Sanguinaires,

F-20 000 Ajaccio, France

Received 26 February 1998; revised version accepted 14 October 1998

Communicated by ROBERT HILL

Abstract—A methodology is developed for calculating the correct size of a photovoltaic (PV)-hybrid system
and for optimizing its management. The power for the hybrid system comes from PV panels and an
engine-generator – that is, a gasoline or diesel engine driving an electrical generator. The combined system is a
stand-alone or autonomous system, in the sense that no third energy source is brought in to meet the load. Two
parameters were used to characterize the role of the engine-generator: denoted SDM and SAR, they are,
respectively, the battery charge threshold at which it is started up, and the storage capacity threshold at which
it is stopped, both expressed as a percentage of the nominal battery storage capacity. The methodology
developed is applied to designing a PV-hybrid system operating in Corsica, as a case study. Various sizing
configurations were simulated, and the optimal configuration that meets the autonomy constraint (no loss of
load) was determined, by minimizing of the energy cost. The influence of the battery storage capacity on the
solar contribution is also studied. The smallest energy cost per kWh was obtained for a system characterized by
an SDM 5 30% and an SAR 5 70%. A study on the effects of component lifetimes on the economics of
PV-hybrid and PV stand-alone systems has shown that battery size can be reduced by a factor of two in
PV-hybrid systems, as compared to PV stand-alone systems.



1999 Elsevier Science Ltd. All rights

reserved.

1. INTRODUCTION

the physical, technical and economical hypothesis,
in Section 2, in which the detailed sizing meth-

As opposed to the PV-only system, the PV-hybrid

odology is also explained. Section 3 examines the

system – consisting of a photovoltaic system

effect of the battery storage capacity on the solar

backed-up by an engine-generator set – has

contribution

and

the

effect

of

the

engine-

greater reliability for electricity production, and it

generator’s operating strategy on the energy costs.

often represents the best solution for electrifying

Finally, an economic study is reported that com-

remote areas (van Dijk, 1996). The engine-

pares the roles of the various subsystems in

generator set (or simply engine-generator) reduces

determining the lifetime of the total system.

the PV component size, while the PV system
decreases the operating time of the generator,
reducing its fuel consumption, O&M, and replace-

2. SIZING METHODOLOGY

ment costs. This study’s primary objectives have

2.1. System configuration

been (i) to develop a sizing methodology for
PV-hybrid systems that supply small and medium

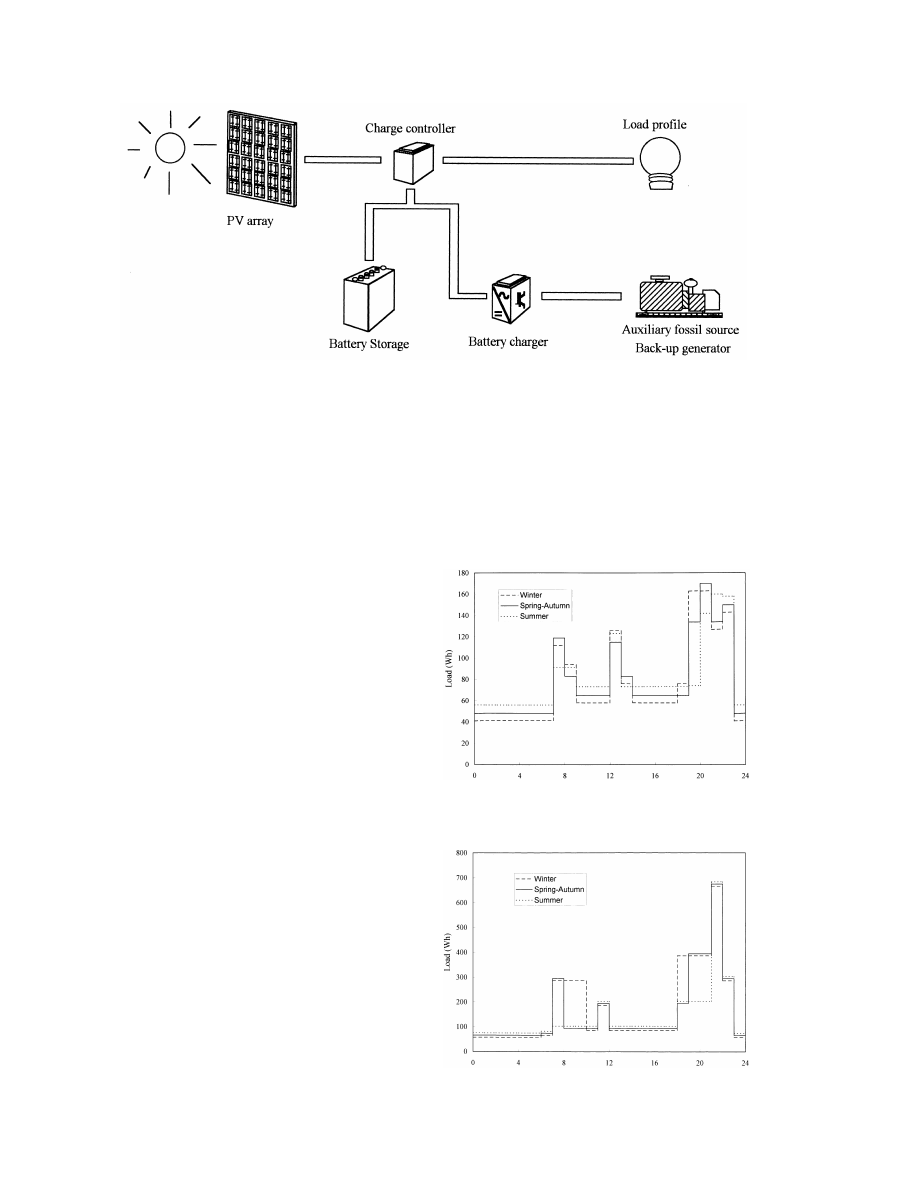
The system (Fig. 1) consists of a PV array, a

power levels to remote areas, and (ii) to study the

battery bank, a back-up generator (3000 rpm or

influence of load profiles and of certain engine-

1500 rpm) driven by a gasoline- or diesel-engine,

generator parameters, such as their type, starting

a charge controller, and an AC / DC converter.

threshold, and stopping threshold. A case study of

The engine-generator will be used only as a

the approach developed is performed for Ajaccio,

battery charger (this reduces its required rated

Corsica (418559N, 88399E).

power), and so its rated power is directly linked to

A brief description of the overall sizing meth-

the nominal battery capacity, C

.

max

odology is presented in Section 1. The paper gives

2.2. Description of the sizing method

The system must be autonomous, i.e. the load

must be totally met by the system at all times.

†Author to whom correspondence should be addressed. Tel.:

Such a constraint still permits an infinite number

133-4-9552-4141;

fax:

133-4-9552-41

2;

e-mail:

[e-mail]

of possible system configurations. From solar

143

144

M. Muselli et al.

Fig. 1. Sketch of the PV-hybrid system studied.

radiation data and from assumed daily load pro-

and have a higher price than conventional

files, the system behavior can be simulated, and a

appliances.

system meeting the constraints can be sized.

In our study, two possible hourly DC-load profiles

However, finding the best system must be done on

have been chosen to represent the load. The first,

the basis of an overall systems approach. First,

the ‘Low Consumption’ profile (Fig. 2), is based

certain physical and technical constraints are used

on ‘adapted’ loads. It has a mean daily energy

to reduce the system parameters to a realistic

consumption of 1.8 kWh per day and a peak

domain. Then minimizing the energy cost leads to
the optimal solution.

3. OPERATING AND DESIGN SIMULATIONS

3.1. Solar irradiation and load profiles

The sizing of PV-hybrid systems for Ajaccio

will be based on 19 years of hourly total irradia-
tion on a horizontal plane, collected at the site.
The PV modules will be tilted, and so hourly total
irradiation on tilted planes had to be computed,
and this was done using the models of Hay and
Davies (1980); Orgill and Hollands (1977). The
resulting errors (RMBE 5 1.4% and RRMSE 5

Fig. 2. ‘Low Consumption’ load profile used in the study.

7% for Hay and Davies model; RMBE 5 2
2.41% and RRMSE 5 8.81% for the Orgill and
Hollands model) have been shown to be quite
small (Poggi, 1995) for the site. In this way,
hourly values of solar irradiation, I (t), on the PV

b

array were calculated for a tilt angle of 308, and
this data provided the input data of the simula-
tions.

Two different types of load can be identified:

1. That provided by ‘conventional’ appliances

available on the market that typically have a
low energy efficiency and have been optimized
not from an energy point of view, but rather
from a quality–price point of view;

2. That provided by ‘adapted’ or ‘high efficiency’

appliances that are rather scarce on the market

Fig. 3. ‘Standard’ load profile used in the study.

Design of hybrid-photovoltaic power generator, with optimization of energy management

145

power demand of 170 W, which occurs in spring

and for these supports, the average price falls to

and autumn. The second, the ‘Standard’ profile

$US 0.83 / Wp (0.69 ECU / Wp).

(Fig. 3), is based on the French utility data

Battery bank: The battery bank can be char-

(EDF), as reported by Eliot (1982). It has a daily

acterized by its nominal capacity C

, its (maxi-

max

average load of 3.7 kWh per day and a peak

mum) depth of discharge DOD, taken in this study

power of 680 W, the latter occurring in the

to be 70% (Tsuda et al., 1994), and two conver-

summer. For each profile, the consumption is

sion efficiencies r

and r

, respectively, for

ch

dch

represented by a sequence of powers P (t), each

charge and discharge, which were taken to equal

c

taken as constant over the simulation time-step,

to 85% (Oldham France, 1992; Manninen and

Dt, which is normally taken as 1 h.

Lund, 1989). The cost of the battery is quite
significant, because the initial investment is high
and the battery has to be replaced several times

3.2. System characteristics

during the PV system lifetime. The battery bank

3.2.1. Photovoltaic subsystem. PV modules:

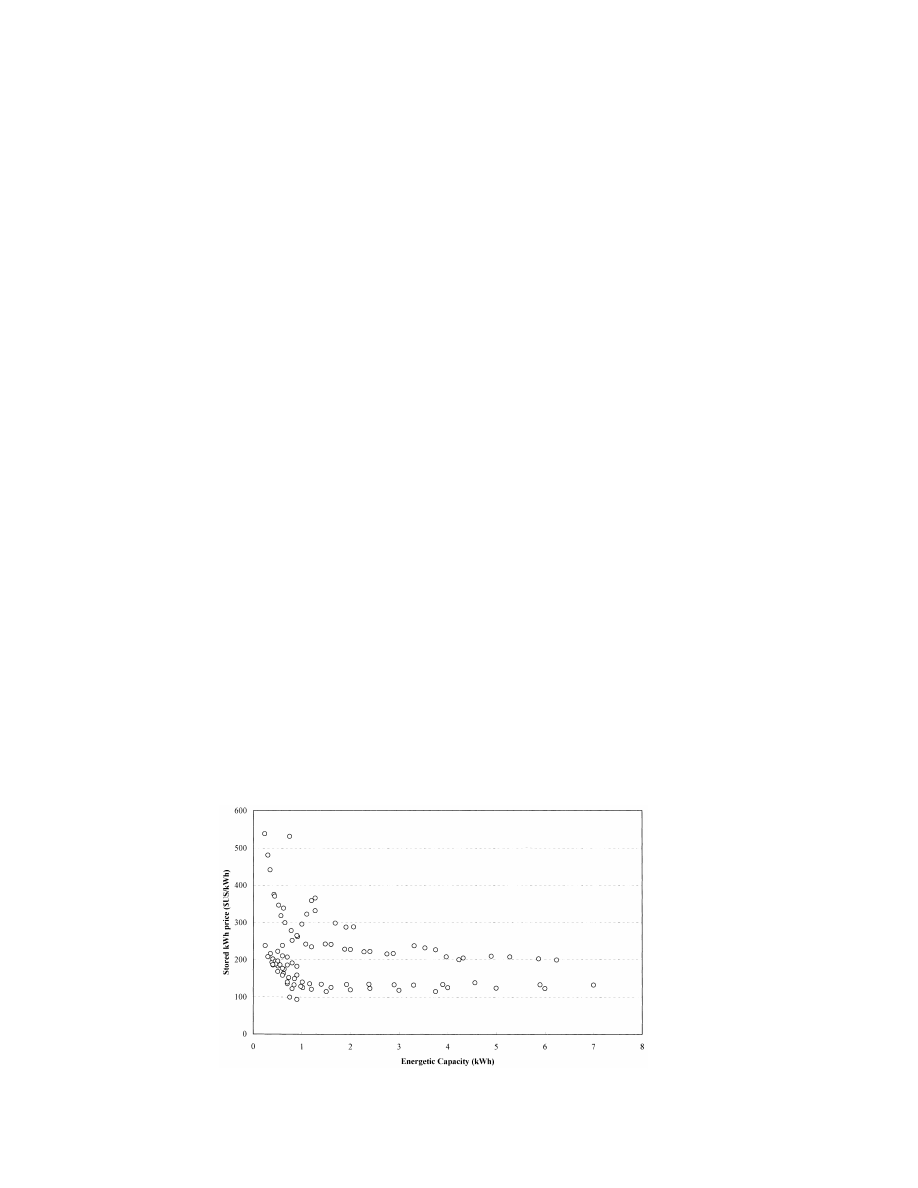
typically accounts for about 40% of the total

For the PV subsystem, we assume a constant PV

system cost (Notton et al., 1996a). Costs of

efficiency h

of 10%. The PV power production

batteries per kilowatt-hour stored capacity are

PV

P (t) is then computed as the product of the PV

plotted in Fig. 4, for the various battery types

p

efficiency, the hourly irradiation I (t) and the PV

marketed by several French suppliers. The battery

b

module area, as has been proposed by several

cost is strongly affected by its type; in particular,

works (Iskander and Scerri, 1996). The ‘peak-

whether it is the stationary type used in many PV

Watt’ (or ‘Wp’) price was used as a fixed econ-

applications or the starter type more readily

omic parameter, as has been done by several

available in developing countries. Frequently-en-

authors (Keller and Afolter, 1995; Biermann et

countered are costs of $US 130 / kWh and $US

al., 1995). It was set equal to $US 5.8 / Wp (5

217 / kWh (110 and 183 ECU / kWh). Thus, an

ECU / Wp), in accordance with the prices of the

average price of $US 180 / kWh (150 ECU / kWh)

French producer PHOTOWATT and others sup-

may be used for estimating the battery cost. The

pliers.

battery lifetime is linked to physical parameters,

Module supports: A literature survey shows

such as the charge–discharge rate, temperature

that the costs of module supports are in the range

and maximum discharge; it is very difficult to

$US 0.35 / Wp (0.28 ECU / Wp) to $US 1.9 / Wp

correlate the lifetime with these parameters. Based

(1.5 ECU / Wp) (Imamura et al., 1992; Palz and

on our own experiences, a battery lifetime equal

Schmid, 1990). Using data collected from four

to five years has been considered in this work.

PV suppliers (Wind and Sun, Eurosolare, Photo-

Charge controller: Regulator costs vary widely.

watt, Siemens), support costs per Wp versus the

Not all regulators work on the same electronic

number of modules per frame are equal to $US

principle, and they can include special options,

1.63 / Wp (1.28 ECU / Wp). However, generally

such as lightning protection, digital displays, etc.

PV frames are used with four modules or more,

We estimated the average price to be $US 0.65 /

Fig. 4. Price of battery storage as a function of the nominal battery storage capacity.

146

M. Muselli et al.

Wp (0.55 ECU / Wp) (Iskander and Scerri, 1996),

where P

and Q are the generator power (kW)

G

v

0

0

which is close to the GTZ value (Biermann et al.,

and the hourly consumption (l / h), P

and Q are

G

v

1995), and we based our model on this price.

respectively the rated power and the consumption

Photovoltaic subsystem installation cost: There

at this rated power, and PCI is the heating value

v

21

is considerable experience in the installation of

of the fuel (PCI

510.08 kWh?l

and

v / diesel

21

small PV systems. In some PV-system projects in

PCI

59.43 kWh?l

).

v / gasoline

0

0

Corsica, the installation cost was 25% of the PV

The ratio Q /P

is the specific consumption,

v

G

panel cost, and this is in agreement with some

defined as the fuel consumption required to

references (Illiceto et al., 1994; Paish et al., 1994;

produce, at nominal power, one kilowatt-hour of

Abenavoli, 1991). Thus this percentage was used

energy. Using a power law model for the con-

for the present study.

sumption at rated power of gasoline engines we

Photovoltaic subsystem O&M cost: Concerning

have:

the maintenance of the PV subsystem, we have

20.2954

0

0

Q 5 0.7368.P

(3)

considered an annual O&M equal to 2% of the

v

G

PV system investment, and a PV system lifetime

and assuming a constant value of 0.3 l / kWh

of 20 years (Notton et al., 1998).

(Thabor, 1988; Calloway, 1986) for diesel en-

3.2.2. Engine-generator

subsystem.

Engine-

gines, allows the determination of the reduced

generators may be compared using many different

consumption versus reduced power:

characteristics, including fuel consumption, motor
speed, continuous or periodic output, load factor,

Q

P

v

G

]

]

2 for diesel generators:

5 0.22 1 0.78

0

0

and noise level, etc. The higher the engine speed,

Q

P

v

G

the faster the wear of the parts and the shorter the

(4)

lifetime; thus, a 3000 or 3600-rpm engine can
only be used for a short time whereas a 1500 or

Q

v

]

2 for gasoline generators:

5

1800-rpm engine can be used continuously. One

0

Q

v

must also compare gasoline engines with 1500

P

10.2954

10.2954

and 3000-rpm diesel engines. In this study, just

G

0

0

]

f

1 2 0.576P

g

1 0.576P

(5)

G

G

0

two parameters, ‘SDM’ and ‘SAR’ are used as

P

G

indices of the engine-generator‘s role, at least so

As an example, g 50.22 and j 50.78 for all diesel

far as the simulations are concerned. SDM and

generators, and g 50.29 and j 50.71 for a 2-kW

SAR are the thresholds in battery charge at which

gasoline engine. We note the presence of a

the engine-generator is switched on or off, respec-

consumption at zero load: 20% and 30% of the

tively, each expressed as a fraction of the battery

full

load

for

diesel

and

gasoline

back-up

capacity.

generators. These results are in agreement with

Fuel consumption: A back-up generator is

recent works (Beyer et al., 1995a).

characterized by its efficiency h and its consump-

c

By using data collected from back-up generator

tion in relation to the produced electrical power as

manufacturers, we have computed the efficiencies

follows:

for each type of generator, and summarize these

P

G

results in Table 1.

]]]

h 5

(1)

c

PCI Q

Engine-generator price: The engine price de-

v

v

pends on nominal power, the price per unit kW,

Q

P

v

G

tending to decrease with increasing nominal

]

]

5

g 1 j

0

0

Q

P

power. To represent this scale effect, a power law

v

G

has been used:

0

0

P

P

P

G

G

G

]]]]

]]]]

]

0

2

a

5 1 2

1

F

G F

G

0

0

0

C 5 C (P )

(6)

G

0

G

h .PCI .Q

h .PCI .Q

P

c

v

v

c

v

v

G

(2)

where C

is the cost per kW of engine-generator

G

0

Table 1. Nominal engine generator efficiencies (h )

c

Minimum

Maximum

Standard

Average

value (%)

value (%)

deviation (%)

value (%)

Gasoline

16.5

30.9

3.4

21.1

Diesel 3000 rpm

29.8

44.6

4.8

35.3

Diesel 1500 rpm

22.3

40.2

3.2

29.9

Design of hybrid-photovoltaic power generator, with optimization of energy management

147

Table 2. Statistical coefficients for the prices of back-up generators (Eq. (6))

MBE

RMSE

RMBE

RRMSE

Type

C

a

($US / kW)

($US / kW)

(%)

(%)

0

Gasoline

718.1

20.585

226.3

180.3

5.4

23.2

Diesel 3000 rpm

704.1

20.2626

210.8

100.6

2.3

22.0

Diesel 1500 rpm

3362.2

20.7184

212.3

145.8

1.5

17.2

capacity, C the cost coefficient, and a the scale

way, 1986; Cramer et al., 1990; Energie Relais,

0

factor. The coefficients in this equation, obtained

1995;

Sandia

National

Laboratories,

1990;

by fits to data provided by French suppliers, are

Energelec, 1995) are very different; we used a

presented in Table 2.

lifetime of 6000 h and 10 000 h for diesel 3000-

Components of the engine-generator: We have

rpm and 1500-rpm engine generators respectively.

allowed for a fuel storage tank, at a price of $US

Engine-generator installation cost: According to

1.7 / l (1.43 ECU / l), in accordance with literature

Paish et al. (1994); Calloway (1986), the engine-

from the French manufacturer GENELEC. The

generator installation cost is equal to 10% of the

storage capacity is taken to be the equivalent of

initial investment for the engine-generator. This

20 h of continuous engine-generator operation (in

includes bedding, exhaust, and automatic control

fact the engine runs for only a few hours a day, on

costs.

average).

Engine generator subsystem O&M cost: While

The fuel price is strongly dependent on the

the installation cost of an engine-generator system

energy policy of the country. A study (Hille and

is relatively low, the annual O&M cost is rela-

Dienhart, 1992) illustrated the diversity of fuel

tively high. It is often estimated as being propor-

prices. Prices range from $US 0.02 / l (0.016

tional to the total hardware cost (Biermann et al.,

ECU / l) to $US 0.75 / l (0.63 ECU / l), the last

1995; Paish et al., 1994; EGAT, 1990). The

figure representing that in developing countries.

proportionality constant ranges from 5% to 20%.

Transport costs can increase the fuel price by $US

However, such an hypothesis must be considered

0.12–$US 0.23 / l (0.1 ECU–0.19 ECU / l) for

prudently, because the more an engine-generator

each 1000 kilometers of distance the fuel must be

runs, the more costly is its annual maintenance;

moved by ground transport, and this is increased

thus, it is good to take into account the annual

by a factor of nearly 40, if air transport is used.

operating

time

of

the

engine-generator

We have considered a price of $US 0.55 / l (0.46

(Abenavoli, 1991; Calloway, 1986). Recently,

ECU / l) and $US 1.15 / l (0.97 ECU / l) for diesel

some authors have calculated the maintenance

and gasoline fuels, respectively.

cost as a fixed cost per kWh, thus linking it to the

Engine generator lifetime: The engine-genera-

operating time (Benyahia, 1989).

tor lifetime is expressed as a function of the

Faced with all these various assumptions in the

operating hours. Table 3 summarizes the predic-

literature, we estimated the O&M cost based on

tions available in the literature. For gasoline

the cost and occurrence of various maintenance

engines, in accordance with the great majority of

operations; thereby, the O&M cost (including oil

authors (Sandia National Laboratories, 1990;

changes) is linked to the operating time. Our

Energelec, 1995), we have used the mean value of

assumptions are (i) that oil (costing 4.49 $US (3.8

the range, which is an engine lifetime equals to

ECU) per l) is replaced every 100 h for all

3500 h. For diesel engines, the 1500-rpm diesel

gasoline and all 3000-rpm diesel engines, and

lifetime is greater than the 3000-rpm diesel life-

every 150 h for all 1500-rpm diesel engines; (ii)

time, because of the reduced rotational speed of

that skilled laborer costs are $US 21.8 / h (18.5

the generator. The literature predictions (Callo-

ECU / h); (iii) that each oil change, complete with

Table 3. Back-up generator lifetime in hours (literature)

References

Type

Operating hours

Abenavoli (1991)

Gasoline

15 000

Calloway (1986)

Diesel

5000

Beyer et al. (1995a)

Diesel

30 000

Energie Relais (1995)

Diesel

1200

Sandia National Laboratories (1990)

Gasoline

2000 to 5000

Sandia National Laboratories (1990)

Diesel

6000

Energelec (1995)

Gasoline

1800

Energelec (1995)

Diesel 3000

8000

Energelec (1995)

Diesel 1500

12 000

148

M. Muselli et al.

an air-filter cleaning, requires 40 min of skilled

consumed energy L

(T) over the same period.

labour, (14.80 $US or 12.5 ECU); (iv) that the oil

Thus

filter (costing 9.10 $US or 7.7 ECU) is replaced

T

after every two oil changes; (v) that the air-filter

L(T ) 5

O

P (t).dt 5h

.S

.H (T )

(11)

c

PV

Ref

b

(10.9 $US or 9.2 ECU), and the fuel filter (5.4
$US or 4.6 ECU for gasoline and 10.9 $US or 9.2

where H (T ) is the global daily irradiation inci-

b

ECU for diesel engine) and the spark plugs (4.6

dent on PV modules inclined with an angle b and

$US or 3.9 ECU for gasoline engine) are changed

the summation is taken over all the days in the

after four oil changes. Each of these operations

period T. We then define the dimensionless PV

take 2 h (43.7 $US or 37 ECU). Accordingly, the

area S

as the ratio of the actual module area to

Dim

O&M costs (in ECU / h) are to be computed from

the reference area S

.

Ref

the following equations:

We also define a dimensionless storage capacity

(i) for gasoline engines, C

5



(0.4005

C, which is expressed in terms of days of

O

& M

autonomy. C is obtained by dividing the actual

1 0.1532.P

) 3 15.2 1 120.1



/ 400

(7)

gene

storage capacity by the annual mean of the daily
load consumption:

(ii) for 3000 rpm diesel engines, C

O

& M

C

5



(0.747 1 0.1184.P

) 3 15.2 1 120.8



/ 400

max

gene

]]

C 5

(12)

¯

L

daily

(8)

3.4. PV-hybrid system behavior. Simulation

(iii) for 1500 rpm diesel engines, C

O

& M

calculations

5



(0.242 1 0.3505.P

) 3 15.2 1 120.8



/ 600

gene

The system simulation is performed by consid-

(9)

ering a Loss of Load Probability equal to 0%; in
other words, the system reliability is 100%,

Notton et al. (1997) have shown that the above

leading to autonomy for the system.

costing hypothesis is consistent with the findings

Given the values of irradiation on tilted planes

of several earlier studies.

and the consumption patterns previously de-

Battery charger: The nominal power of the

scribed, the system behavior can be simulated

battery charger is related to its nominal storage

using an hourly time step-several workers (Man-

capacity. One must take into account that the

ninen and Lund, 1989; Beyer et al., 1995b)

electrical current produced by the generator must

having shown that the simulation of PV systems

not be greater than one fifth of the ampere-hour

requires only an hourly series of solar data. Based

capacity of the battery (Sandia National Lab-

on a system energy balance and on the storage

oratories, 1990):

continuity equation, the simulation method used

C

max

0

here is similar to that used by others (Sidrach de

]]

P

5

(10)

charger

5

Cardona and Mora Lopez, 1992; Kaye, 1994).
Considering the battery charger output power

A battery charger’s efficiency h

is equal to

charger

P

(t), the PV output power P (t) and the load

90% according to the manufacturers MASTER-

charger

p

power P (t) on the simulation step Dt, the battery

VOLT and PRIMAX. For its cost, a power law

c

energy benefit during a charge time Dt is given

relationship was used. The different parameters

1

by (Dt ,Dt):

and the statistical errors associated are as follows:

1

C 51099, a 5 20.691, MBE5 2113 $US / kW,

0

RMSE5418

$US / kW,

RMBE5 20.5%

and

C (t) 5 r

E

[P (t) 1 P

(t) 2 P (t)] dt

(13)

RRMSE519%.

1

ch

p

charger

c

Dt

1

3.3. Relevant dimensionless variables

The battery energy loss during a discharge time

Two dimensionless variables characterize the

Dt is given by (Dt ,Dt):

2

2

PV-hybrid system: the PV module surface and the
battery storage capacity; both are independent of

1

the daily load. For the PV area, we first define a

]]

C (t) 5

E

[P (t) 1 P

(t) 2 P (t)] dt

2

S D

2

p

charger

c

reference area, S

as the PV module area (m )

r

ref

dch

Dt

2

that will produce, over the simulation period T
(say 19 years), an electrical energy equal to the

(14)

Design of hybrid-photovoltaic power generator, with optimization of energy management

149

The state of charge of the battery is defined

SOC is compared with the intrinsic parameters

during a simulation time-step Dt by:

(maximum and minimum capacities). If SOC(t),
C

the system is failing and if SOC(t).C

,

min

max

C(t) 5 C(t 2 Dt) 1 C (t) 1 C (t)

(15)

1

2

the system produces wasted energy.

By simulating many PV-hybrid systems having

If C

(t) reaches SAR by an energy benefit C (t)

1

the same load, one can, in principle, find an

during the charge period with the engine-genera-

infinite set of physical solutions, each solution

tor working, the generator has to be stopped and

being characterized by a PV module area S

, a

Dim

the charge time Dt

during Dt is calculated

1

storage capacity C

, and a nominal engine-

max

assuming a linear relation:

generator power. Each solution defines a ‘pair’

Dt

SAR 2 C(t 2 Dt)

1

(S

, C

). Several technical constraints, for

Dim

max

]

]]]]]

5

(16)

U

U

Dt

C (t)

example, the available products, reduces the

1

infinite number of solutions to a finite number of

Moreover, if during the discharge period when the

configurations. For each configuration, some

engine generator is stopped, C(t) reaches SDM,

physical variables are calculated by simulations:

the motor is started and the discharge time Dt

2

the wasted energy, the working time and the fuel

during Dt is calculated by a linear relation as:

consumption of the engine- generator, and the
times when certain subsystems need replacement.

Dt

C(t 2 Dt) 2 SDM

2

]

]]]]]

5

(17)

U

U

The energy cost is then computed for each pair,

Dt

C (t)

2

and the minimization of this parameter yields the
optimal operating configuration.

As an input of a simulation time-step Dt (taken as
1 h), several variables must be determined: PV
output power, load power, battery state of charge,

4. SIMULATION RESULTS

and back-up generator state (ON or OFF) in the
previous time-step. A battery energy balance

4.1. Operating mode

indicates the operating strategy of the PV-hybrid

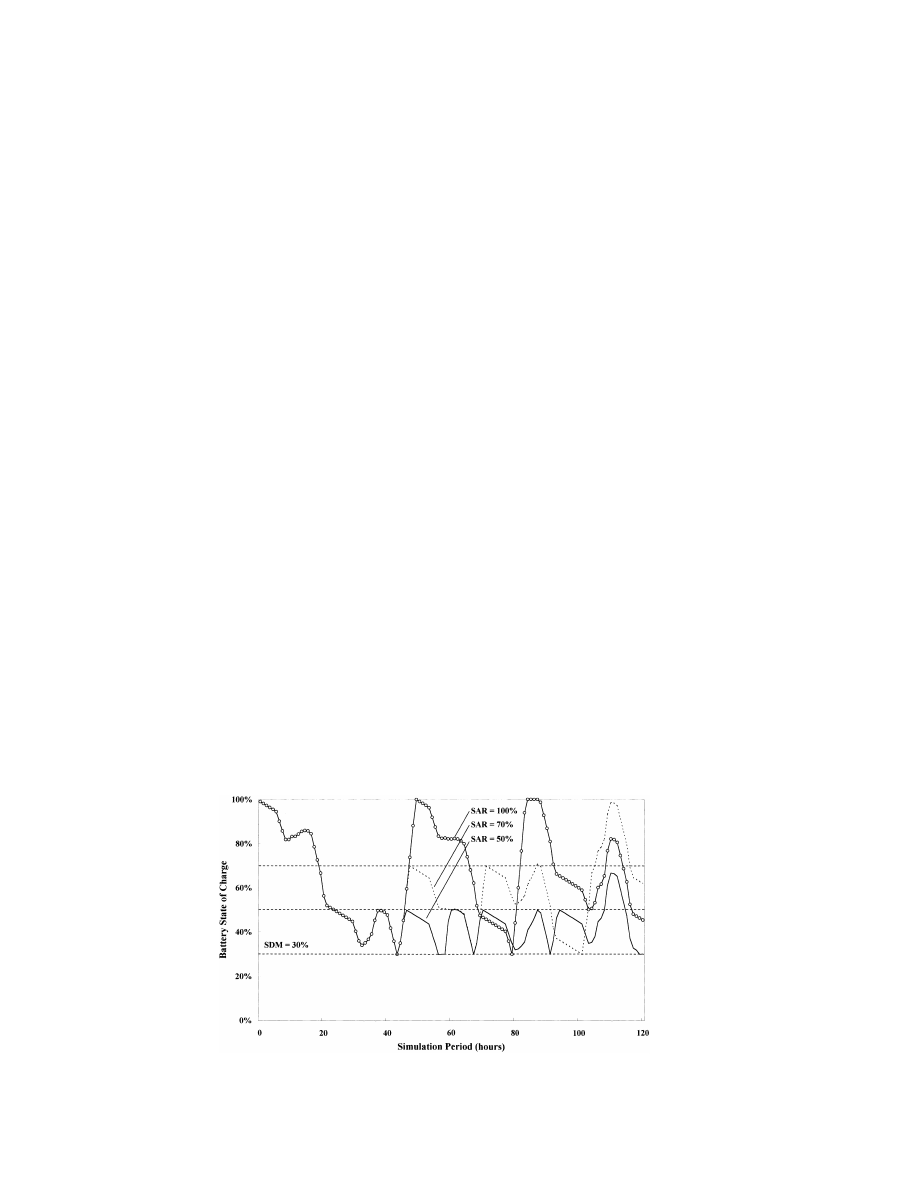
To illustrate the battery energy state evolution

system: charge (energy balance positive) or dis-

as a function of the engine-generator thresholds,

charge (energy balance negative). Some tests are

we have plotted in Figs. 5 and 6, which show,

necessary to study the SOC variations as com-

respectively, the energy stored and the engine-

pared to the starting and stopping thresholds. If

generator operating hours as a function of time,

SOC(t) falls below SDM, the motor is started; and

over five days. Assumed parameter settings for

if SOC(t) exceeds SAR, it is stopped. So, the

the figures are as follows: C 5two days, the initial

charge and discharge times (Eqs. (16) and (17))

charge on the battery5100% of capacity, dimen-

must be calculated on the simulation time-step in

sionless PV module surface50.94, SDM530%

order to compute the different energy flows in the

and SAR550%, 70% and 100%. Also, the ‘Low

system (Eqs. (13) and (14)). Then, the battery

Fig. 5. Evolution of the battery state of charge for several assumed values of the thresholds (SDM, SAR) governing the operation

of the engine-generator.

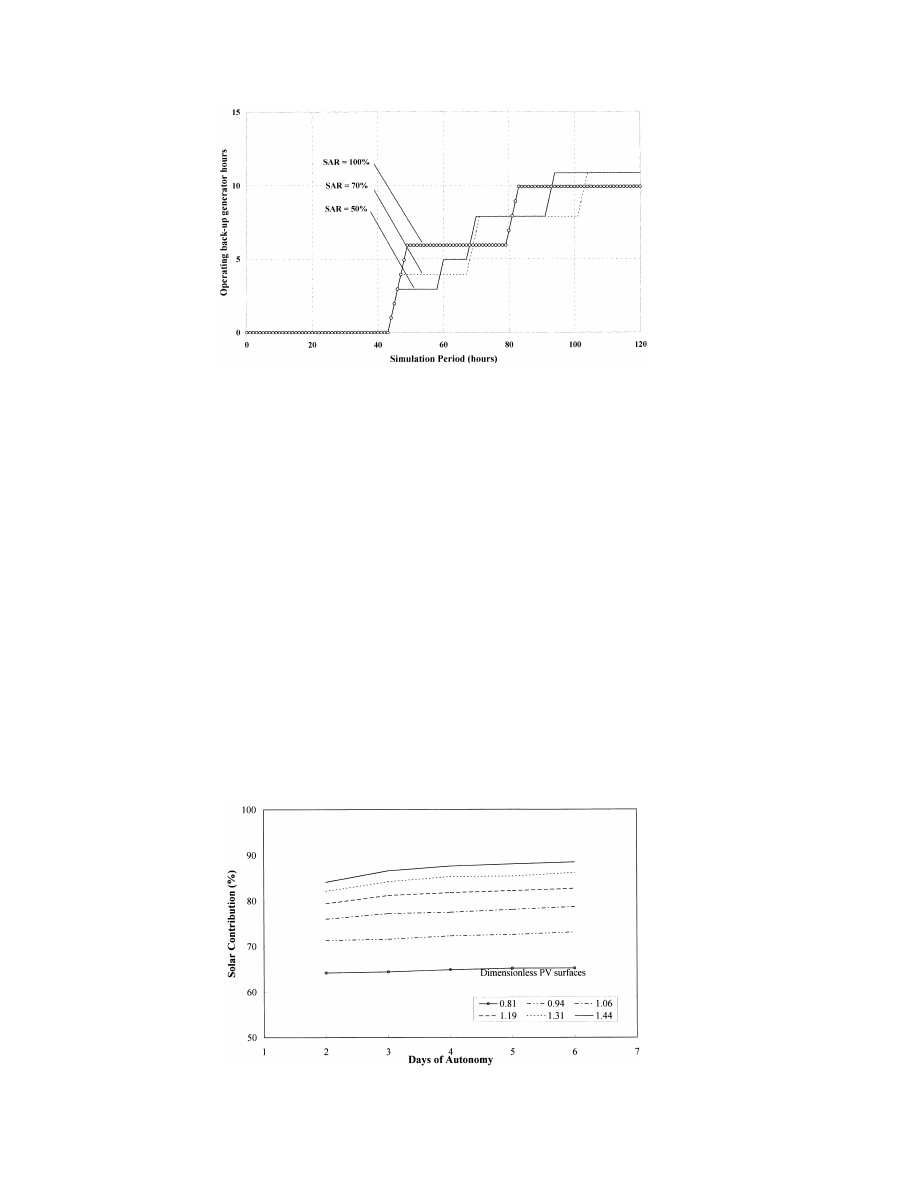
150

M. Muselli et al.

Fig. 6. Plot of the back-up generator operating time for several assumed values of the thresholds (SDM, SAR) governing the

operation of the engine-generator.

Consumption’ load profile was used, and a

nominal engine-generator power is undersized and

gasoline engine was assumed.

the autonomy constraint is not respected. Thus, in
the remainder of this paper, only batteries with

4.2. PV-hybrid system sizing curves

capacities greater than to two days will be consid-

Fig. 7 presents the solar contribution (defined

ered.

as the percentage that the PV production is of the

Fig. 8 presents the sizing curve, as obtained

total energy production) versus dimensionless

assuming the Standard load profile, the SDM and

storage capacities (one to six days). These plots

SAR are equal to 30% and 80%, respectively, and

have been parameterized using dimensionless PV

a gasoline-driven engine. The existence of some

areas ranging from 0.81 to 1.44. We concluded

‘discontinuities’ in Fig. 8 are due to the number of

that it was not necessary to consider a PV-hybrid

changes of the engine-generator with the decrease

system with a storage capacity greater than two or

in dimensionless PV areas. The optimal configura-

three days of autonomy. Sidrach de Cardona and

tion, i.e., the one corresponding to the lowest

Mora Lopez (1992) have obtained the same

energy cost, is determined for each sizing curve.

conclusion considering a PV-hybrid system in

In Figs. 9 and 10 (which apply to ‘Low Consump-

which the back-up generator was applied directly

tion’ and ‘Standard’ profiles respectively), we

to the load and to a battery charger, at the same

have plotted the sizing curves parameterized by

time. The simulations demonstrate that for a

the storage capacities (two to six days) for

system with only one day of autonomy, the

SDM530% and SAR580%.

Fig. 7. Solar contribution (%) as a function of dimensionless storage capacities 2 to 6 days.

Design of hybrid-photovoltaic power generator, with optimization of energy management

151

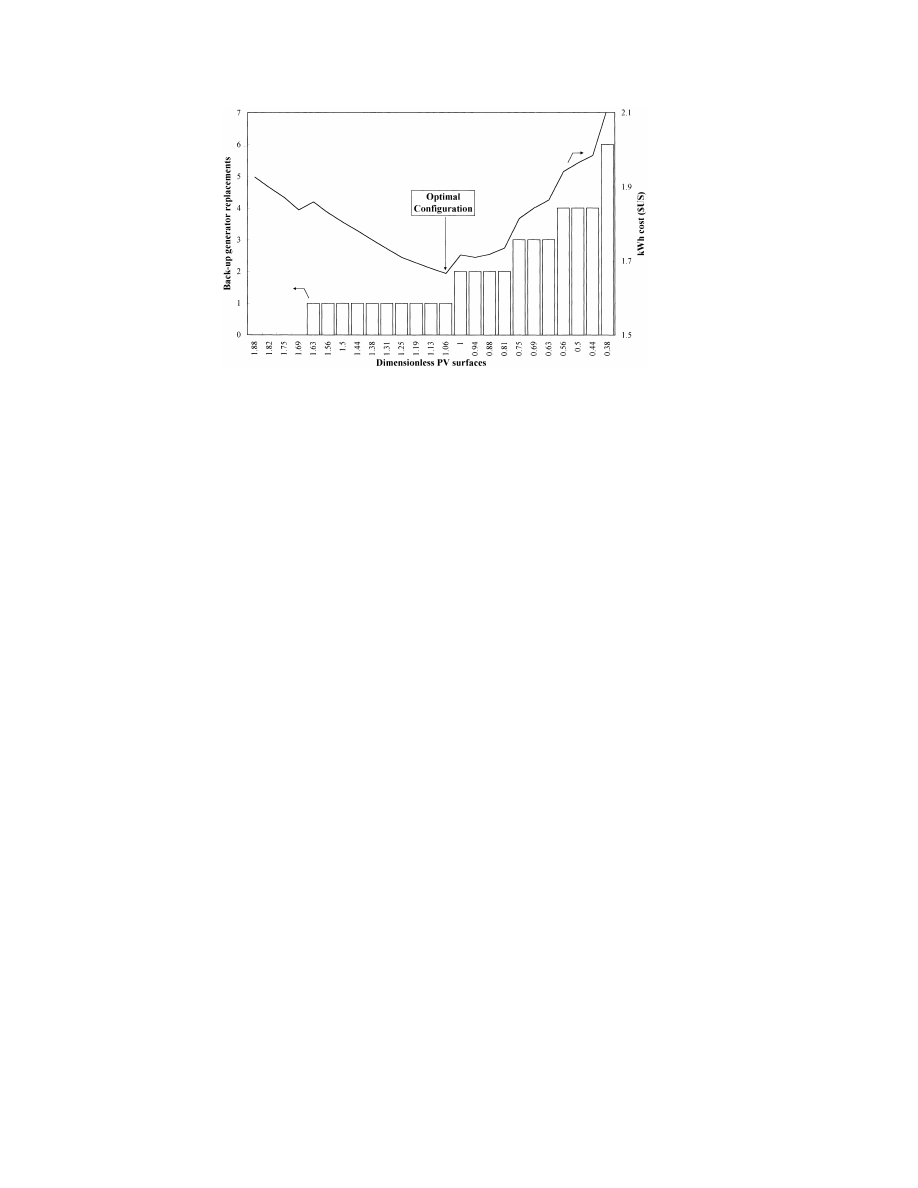
Fig. 8. Sizing curve of PV-hybrid systems for a gasoline engine, ‘Standard’ load profile, and SDM and SAR equal to 30% and

80%, respectively.

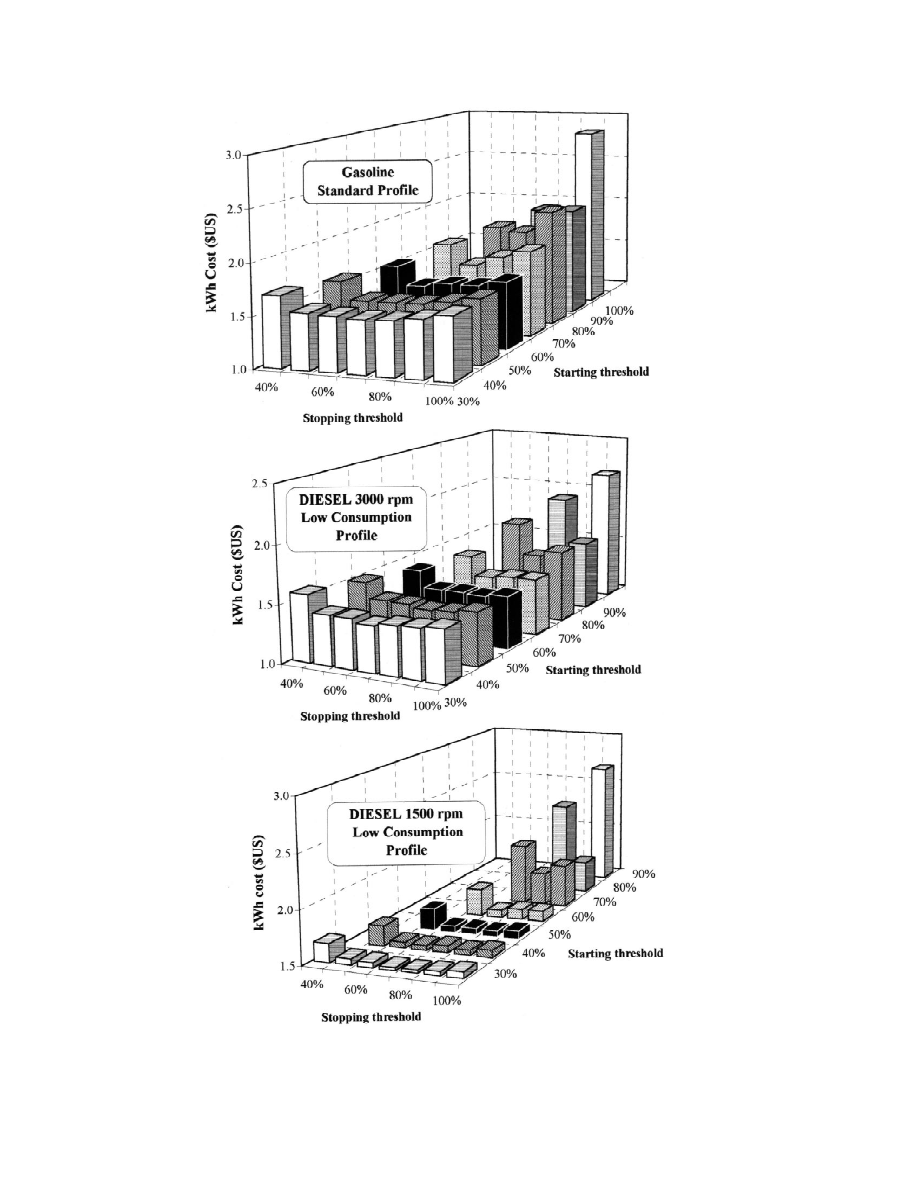
The lowest points on the curve define the

(S

50.97, 0.95 and 0.73 for the three cases in

Dim

optimal configuration. Although the locations of

Fig. 11). The optimal size of the engine generator

the lowest points are indistinct around the optimal

is easily deduced from the optimal capacity (two

point, the optimal configuration is always ob-

days) and from Eq. (10), by dividing the battery

tained when the storage capacity equals two days

charger rated power by the charger efficiency

of autonomy. These findings have been confirmed

h

.

charger

for other values of the starting and stopping

For the combinations of SDM and SAR and for

thresholds.

the optimal pairs (S

, C

) of Fig. 11, we have

Dim

max

To make these results more general, a sensitivi-

combined the solar contribution curves obtained

ty analysis of the energy costs to various parame-

for a battery capacity of two days to deduce

ters must be performed. A short sensitivity study

optimal solar and fossil fuel contributions for each

presented in a previous paper (Notton et al.,

engine-generator type, and these are given in

1998) confirmed the main conclusions shown

Table 4.

here.

In previous works in our laboratory Notton et

al. (1996b) applied such an optimization to a

4.3. Influence of the back-up generator

hybrid-system, but without including the engine-

operating strategy

generator behavior in the system simulation. In

In accordance with the above results, a storage

that work, the stand-alone PV system without the

capacity of two days will be used for the analysis

engine-generator had been sized for several loss-

of the back-up generator operating strategy. Also,

of-load probabilities, and then the energy deficit

the energy cost has been calculated for various

was supplied by the engine-generator. This con-

combinations of SDM and SAR, by varying them

figuration has led to identical optimal contribu-

by steps of 10%, (i.e., SDM[[30%; 90%] and

tions (75% solar and 25% fossil), whichever the

SAR[[40%; 100%]). For each combination, we

engine type. In this study, the results have been

computed the optimal pair leading to the lowest

found to depend on the engine type. The varia-

energy cost. Fig. 11 presents the results for each

tions in the contributions for the diesel 1500-rpm

engine type and for both load profiles. The

type can be linked to its longer lifetime, which

optimal configuration is obtained when SDM5

leads to reduced replacement costs. The results

30% and SAR570%, regardless of the load

are very dependent on the lifetime and mainte-

profile and the engine-generator type.

nance of the engine, and have been calculated by

Thus we have now demonstrated that the

optimizing these two parameters (Notton et al.,

optimal size of the battery capacity is two days

1997).

and the best energy management is obtained when

4.4. Wasted energy

SDM and SAR are respectively equal to 30% and
70% of the nominal storage capacity. The optimal

We have also studied, over a given time period,

PV area for each configuration is close to unity

say T, the influence of the engine-generator

152

M. Muselli et al.

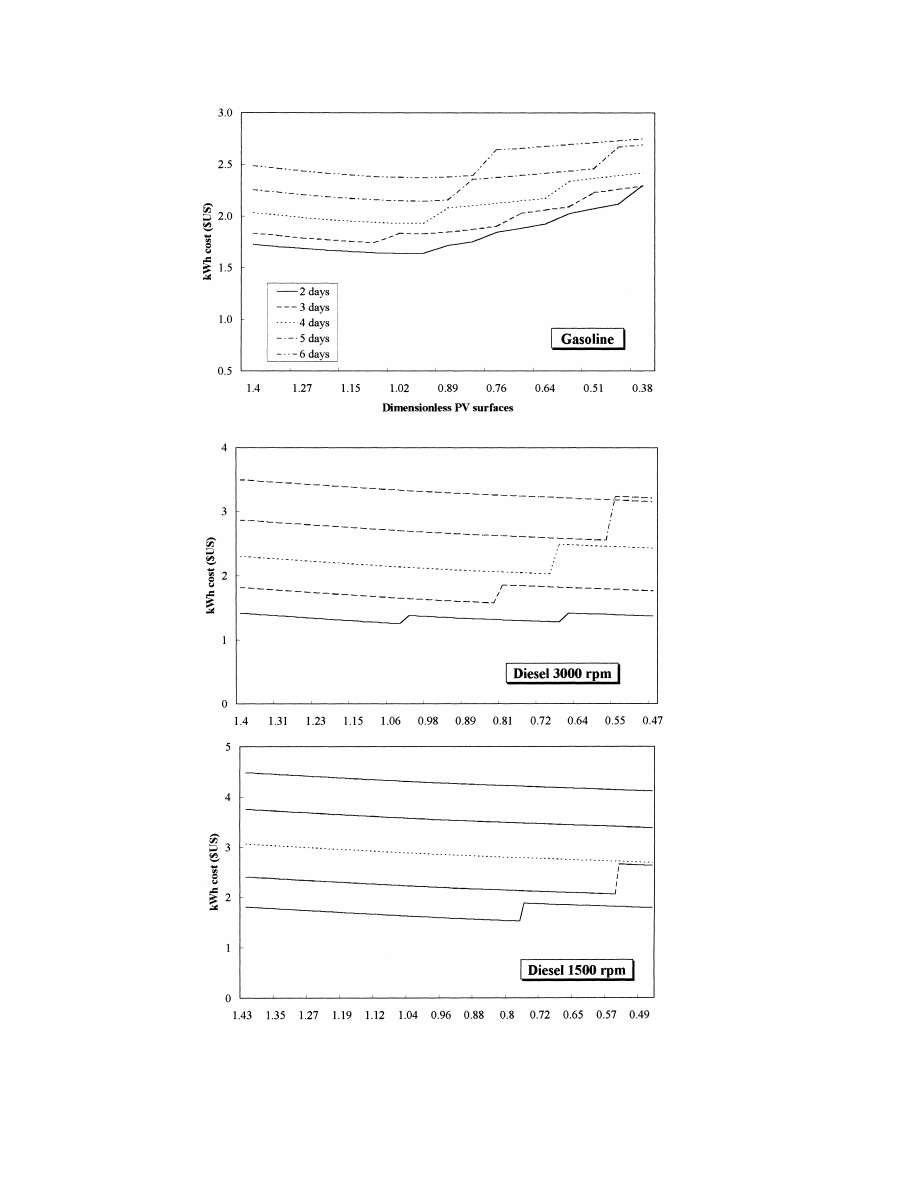
Fig. 9. Sizing curves obtained for a storage capacity ranging from 2 to 6 days of autonomy, for each engine type (The Low

Consumption load profile is assumed).

Design of hybrid-photovoltaic power generator, with optimization of energy management

153

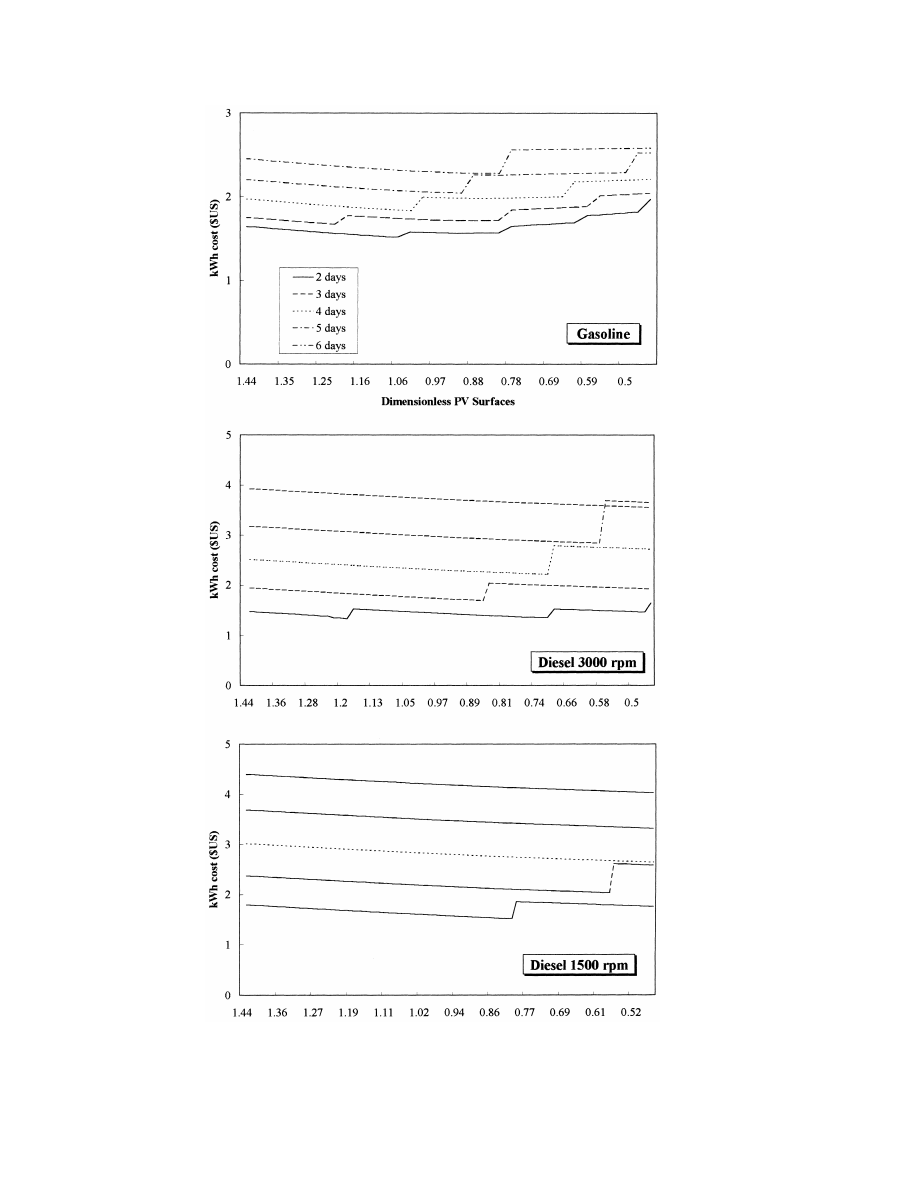
Fig. 10. Sizing curves obtained for storage capacities ranging from 2 to 6 days of autonomy, for each engine type (Standard load

profile is assumed.)

154

M. Muselli et al.

Fig. 11. Influence of back-up generator operating strategy according to engine type.

Design of hybrid-photovoltaic power generator, with optimization of energy management

155

Table 4. Optimal contributions for each back-up generator type

Optimal contributions

Motor type

Load profiles

Solar source (%)

Fossil source (%)

Gasoline

Low consumption / standard

75

25

Diesel 3000 rpm

Low consumption / standard

80

20

Diesel 1500 rpm

Low consumption / standard

65

35

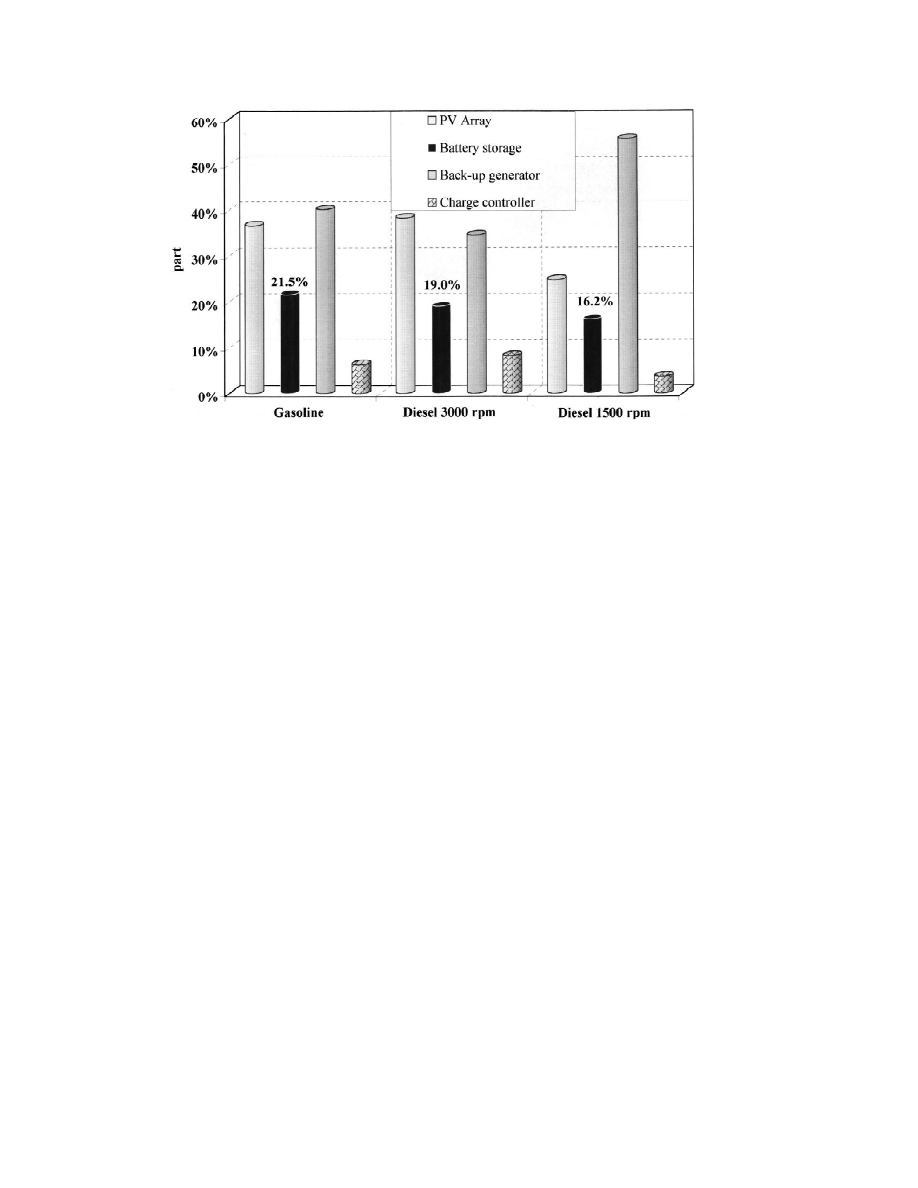
operating strategy on the wasted energy WE(T )

subsystem during its lifetime. The results are

produced by the system,

presented in Fig. 13. For hybrid systems using
gasoline and 3000-rpm diesel engine-generators,

T

the PV contribute 35% and the engine contributes

WE(T ) 5

O

[P (t) 2 P (t)] dt

(18)

p

c

40% of the total cost. The total investment cost is

P (t ).P (t )

p

c

made up of the following: PV modules about

C(t ).C

max

30%, engine-generator about 20%, PV support

For example, for a gasoline engine the influence

about 4%, O&M for the engine-generator about

of the stopping threshold (SAR[[40%; 70%]) on

5%, and the charge controller about 3.5%. With

the wasted energy for a given starting threshold

the lifetime of a gasoline engine being lower than

(SDM530%) is shown in Fig. 12. We found a

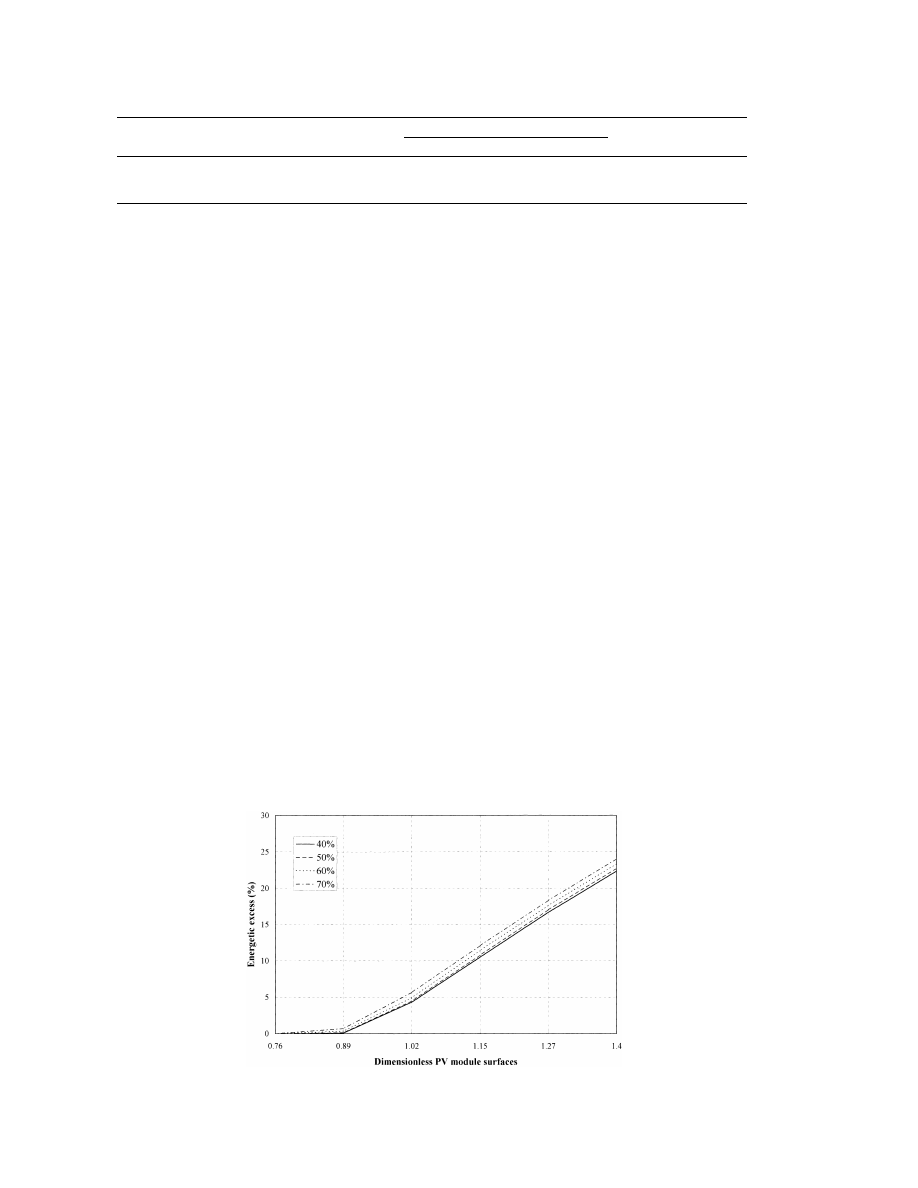
the lifetime of a 3000-rpm diesel engine, the

trivial result: increasing the PV module increases

gasoline engine must be replaced during the

the energy excess. On the other hand, the charge

hybrid-system lifetime, whereas the diesel engine

strategy represented by the SAR variation is not

does not. Moreover, the fuel consumption cost is

significant. The increase of SAR causes an in-

greater for the gasoline engine, because its fuel

crease from 2 to 4% of the energy surplus over all

consumption and its fuel prices are higher than

PV area ranges. We note that, considering the

those for a 3000-rpm diesel engine. For the

optimal configurations previously given (S

5

Dim

system using the 1500-rpm diesel engine, the

0.97 for gasoline engine), the energy surplus is

initial costs are more important: the PV and

inferior to 5%; this demonstrates the competitive-

engine-generator investment (about 20% and

ness of hybrid-PV systems, as compared to stand-

50%), PV support parts (about 3%), the O&M

alone PV/ battery systems with an energy excess

back-up generator (about 3%), and the charge

about 50%.

controller investment (about 3%). We note that the
battery contribution to the cost is about 20%

4.5. Economical study on the PV-hybrid system

(made up of about 9% for investment and 11% for

lifetime

replacement) regardless of the engine type. This
result agrees with previous findings (Notton et al.,

From optimal configurations previously de-

1996a) relating to stand-alone PV/ battery sys-

scribed (SDM530% and SAR570%), for each

tems, for which the storage represents 40% on the

engine type and for the Low Consumption load

total lifetime cost. Thus the addition of a back-up

profile, we have determined the investment,

generator to a traditional PV system cuts the

maintenance and replacement costs for each

Fig. 12. Influence of the stopping threshold on the energy excess (SDM set equal to 30%).

156

M. Muselli et al.

Fig. 13. Breakdown of the contributions (investment, maintenance, replacement) of each subsystem in determining the PV-hybrid

system lifetime.

battery’s contribution to the total cost by a factor

FOSSIL, the contribution of fossil in the latter
combination being higher, because of the longer

of two. Previously, Notton et al., 1996b showed

lifetime of a diesel engine. The work has demon-

that the energy cost produced by a PV hybrid

strated the competitiveness of PV-hybrid systems,

system is half of a traditional PV/ battery stand-

which can work with an energy excess as low as

alone system.

5% and a battery storage half of that of the
traditional stand-alone PV system, based on the

5. CONCLUSIONS

system lifetime. In conclusion, the approach
presented here appears to be a valuable tool for

In this paper, we have studied the behavior of a

the design and evaluation of PV-hybrid systems

stand-alone PV-hybrid (PV and engine-generator)

supplying power in remote areas.

system. We have considered the sizing of PV
systems by using hourly total irradiation values on

NOMENCLATURE

tilted surfaces and hourly load profiles taken as
constant over the seasons. The study has shown

Dimensionless battery storage

C

that the optimal configuration, i.e., the configura-

capacity

tion that minimizes the energy cost, is obtained

C(t)

Battery state of charge

Wh

with a battery storage capacity of two days. The

C (t)

Battery energy benefit during the

Wh

1

influence of the engine-generator’s operating

period Dt

C2(t)

Battery energy loss during the

Wh

strategy has also been studied. It was found that

period Dt

an optimal configuration is one where the engine-

C

Cost coefficient

$US

0

generator is switched on when the battery charge

C

kW price

$US

G

is at 30% of maximum battery capacity and where

C

Nominal storage capacity

Wh

max

it is turned off when the battery charge is 70% of

C

Minimal storage capacity

Wh

min

DOD

Depth of discharge

%

maximum battery capacity. The study has de-

22

H (T )

Solar irradiation received by PV

Wh?m

b

termined optimal contributions for both solar and

modules on a tilted plane

fossil fuel energy sources. For gasoline powered

22

I (t)

Hourly solar irradiation on tilted

Wh?m

b

engine-generators,

the

combination

of

75%

plane

SOLAR with 25% FOSSIL are the most econ-

L(T )

Energy consumed by load in the

Wh

period T

omical solutions, and 3000-rpm diesel powered

P (t)

Instantaneous power to the load

W

c

engine-generators, 80% SOLAR and 20% FOS-

PCI

Heating value of fuel

kWh per l

v

SIL are the most economical solutions. For 1500-

P

Generator power

W

G

rpm diesel powered engine-generators, the opti-

P (t)

Instantaneous power represent-

W

c

mal combination is 65% SOLAR with 35%

ing the load

Design of hybrid-photovoltaic power generator, with optimization of energy management

157

Hille G. and Dienhart H. (1992) Economic analysis of hybrid

P

Generator power

W

G

0

systems for decentral electricity generation in developing

P

Nominal power of the battery

W

charger

countries. In Proceedings of the

11th European Photo-

charger

voltaic Solar Energy Conference, pp. 1559–1563, Mon-

P

Power of the battery charger

W

charger(t )

treux.

available at the instant t

Illiceto A., Previ A. and Zuccaro C. (1994) Experiences of

0

P

Rated

power

of

the

engine

W

G

rural electrification in southern Italy by means of PV plants.

generator

In Proceedings of the

12th European Photovoltaic Solar

P (t)

Instantaneous

PV

produced

W

Energy Conference, pp. 210–211, Amsterdam.

p

Imamura M.S., Helm P., and Palz W. (1992) In Photovoltaic

power

System Technology

: An European Handbook, Stephen H. S.

Q

Back-up generator consumption

l / h

v

and Associates (Eds), Commission of the European Com-

per h

0

munities, Bedford.

Q

Consumption of the motor at

l / h

v

Iskander C. and Scerri E. (1996) Performance and cost

this rated power per h

evaluation of a stand-alone photovoltaic system in Malta.

SAR

Stopping threshold

Wh

World Renewable Energy Congress 8, 1–4, pp. 437–440,

S

Dimensionless PV surface

Dim

Denver, Colorado.

SDM

Starting threshold

Wh

Kaye J. (1994) Optimizing the value of photovoltaic energy in

2

S

PV Reference surface

m

electricity supply systems with storage. In Proceedings of

ref

the

12th European Photovoltaic Solar Energy Conference,

WE(T )

Wasted energy on the period T

Wh

pp. 431–434, Amsterdam.

a

Scale factor

Keller L. and Afolter P. (1995) Optimizing the panel area of a

h

Back-up generator efficiency

%

c

PV system in relation to the static inverter–practical results.

h

Battery charger efficiency

%

charger

Solar Energy 55, 1–7.

h

PV array efficiency

%

PV

Manninen L.M. and Lund P.D. (1989) Dynamic simulation

r , r

Charge and discharge battery

%

ch

dch

and sizing of photovoltaic and wind power systems. In

efficiencies

Proceedings of the

9th European Photovoltaic Solar Energy

Dt

Simulation time-step

h

Conference, pp. 546–549, Freiburg.

Dt

Battery charge time during the

h

Notton G., Muselli M., Poggi P. and Louche A. (1996)

1

period Dt

Autonomous photovoltaic systems: influencies of some
parameters on the sizing: simulation time-step, input and

Dt

Battery discharge time during

h

2

output power profile. Renewable Energy 7, 353–369.

the period Dt

Notton G., Muselli M. and Louche A. (1996) Autonomous

hybrid photovoltaic power plant using a back-up generator:
a case study in a Mediterranean island. Renewable Energy

REFERENCES

7, 371–391.

Notton G., Muselli M., Poggi P. and Louche, A. (1997) What

Abenavoli R. I. (1991) Technical and economic comparison of

hypothesis used for an economic study of electric generators

electric generators for rural area. Solar Energy 47, 127–135.

for rural area? literature survey and new suggestions. In

Benyahia Z. (1989) Economic viability of photovoltaic sys-

Proceedings of the

14th European Photovoltaic Solar

tems as an alternative to diesel power plants. In Proceedings

Energy Conference, pp. 2534–2537, Barcelona.

of the

9th European Photovoltaic Solar Energy Conference,

Notton G., Muselli M. and Poggi P. (1998) Costing of a

pp. 173–175, Freiburg.

stand-alone photovoltaic system. Energy 23(4), 289–308.

Beyer H. G., Degner T. and Gabler H. (1995) Operational

Oldham France S.A. (1992) Technical documentation.

behavior of wind diesel systems incorporating short-term

Orgill J. F. and Hollands K. T. G. (1977) Correlation equation

storage: an analysis via simulation calculations. Solar

for hourly diffuse radiation on horizontal surface. Solar

Energy 54, 429–439.

Energy 19, 357–359.

Beyer H. G., Bolhen M. and Schumacher, J. (1995b) GENG.

Paish O., MacNellis B. and Derrick A. (1994) Solar Electrici-

A solar modelisation data generation for the simulation

ty. Ch. V: Applications, John Wiley and Sons.

system INSES. In Proceedings of the

13th European

Palz W. and Schmid J. (1990) Electricity production costs

Photovoltaic Solar Energy Conference, pp. 982–985, Nice.

from photovoltaic systems at several selected sites within

¨

Biermann E., Corvinus F., Herberg T. and Hofling H. (1995)

the European Community. Int

. J. Solar Energy 8, 227–231.

Basic Electrification for Rural Household. GTZ (Deutsche

`

´

Poggi P. (1995) Contribution a l’etude de l’insertion de

Gesselschaft fur Technische Zuzammenarbeit).

`

¨

´

systemes photovoltaıques dans un reseau insulaire. Ph.D.

Calloway T.M. (1986) Design of an intermediate-sized au-

Thesis, University of Corsica.

tonomous photovoltaic–diesel power plant. Sandia National

Sandia National Laboratories (1990) Stand-alone Photovoltaic

Laboratory Report, SAND85-2136.

Systems. SAND87-7023.

Cramer G., Kleinkauf W. and Schott T. (1990) Wind / diesel /

Sidrach de Cardona M. and Mora Lopez L.I. (1992) Optimiz-

battery systems – Applications, experience, economy of

ing of hybrid photovoltaic generator systems for installa-

different system configurations and sizes. European Com-

tions of rural electrification. In Proceedings of the

11th

munity Wind Energy Conference, pp. 575–579, Madrid.

European Photovoltaic Solar Energy Conference, pp. 1287–

EGAT (1990) Economic analysis of photovoltaic system.

1290, Montreux.

EGAT Report.

Thabor M.Z. (1988) Small diesel power. International Confer-

´

Eliot P. (1982) Analyses d’un habitat PV en site isole. Ph.D.

ence on Small Power Supplies, Tasmanie.

Thesis, University of Nice.

Tsuda I., Kurokawa K. and Nozaki K. (1994) Annual simula-

ENERGELEC Back-Up Generators (1995) Technical Docu-

tion results of PV system with redox flow battery. Solar

mentation (French suppliers).

Energy Mater

. Solar Cells 35, 503–508.

ENERGIE RELAIS Back-Up Generators (1995) Technical

van Dijk V.A.P. (1996) Hybrid photovoltaic solar energy

Documentation (French suppliers).

systems: design, operation and optimization of the Utrecht

Hay, J.E. and Davies J.A. (1980) Calculation of the solar

PBB system. Ph.D. Thesis, University of Utrecht.

radiation incident on an inclined surface. In Proceedings
First Canadian Solar Radiation Data Workshop, pp. 59–72.